Summary
How does robust and tunable behavior emerge in a complex biological network? We sought to understand this for the signaling network controlling pattern-triggered immunity (PTI) in Arabidopsis. A dynamic network model containing four major signaling sectors, the jasmonate, ethylene, PAD4, and salicylate sectors, which together explain up to 80% of the PTI level, was built using data for dynamic sector activities and PTI levels under exhaustive combinatorial sector perturbations. Our regularized multiple regression model had a high level of predictive power and captured known and unexpected signal flows in the network. The sole inhibitory sector in the model, the ethylene sector, was central to the network robustness via its inhibition of the jasmonate sector. The model's multiple input sites linked specific signal input patterns varying in strength and timing to different network response patterns, indicating a mechanism enabling tunability.
Introduction
Inducible immunity is a major component of plants' immunity against pathogens (Jones and Dangl, 2006) in which plants recognize pathogen attack and transduce this information through signaling networks within the cell, to different cells, and to distant tissues. This culminates in activation of defense responses, which could affect fitness of the pathogen. Although this sequence of recognition, signal transduction, and response is the common theme in biological responses to stimuli, plant inducible immunity is unique in that pathogens not only initiate the signaling event but also attack the signaling network.
In pattern-triggered immunity (PTI), a well-defined mode of plant inducible immunity (Dodds and Rathjen, 2010; Jones and Dangl, 2006; Tsuda and Katagiri, 2010), pattern recognition receptors (PRRs) of a plant recognize molecular patterns relatively conserved among similar types of microbes (microbe-associated molecular patterns, MAMPs). For example, a part of bacterial flagellin (flg22), a part of bacterial elongation factor-Tu (elf18), and an oligosaccharide part of fungal cell walls (chitin) are recognized in Arabidopsis thaliana by the receptor-like kinase PRRs, FLS2, EFR, and CERK1, respectively (Chinchilla et al., 2006; Miya et al., 2007; Wan et al., 2008; Zipfel et al., 2006). Such recognition of MAMPs by the cognate PRRs initiates PTI signaling. A successful pathogen overcomes PTI by delivering effectors that interfere with PTI signaling (Dodds and Rathjen, 2010; Jones and Dangl, 2006). For example, the Gram-negative bacterial pathogen Pseudomonas syringae delivers various proteinaceous effectors via its type III secretion system into host plant cells (Lindeberg et al., 2012). As microbial pathogens can evolve much faster than plants, it seems unlikely that plants can keep up with evolution of pathogens by depending mainly on simple adaptation (Katagiri and Tsuda, 2010).
Previously we investigated quantitative relationships among four major signaling sectors, the jasmonate (JA), ethylene (ET), PAD4, and salicylate (SA) sectors, which provide much of the network backbone during PTI in Arabidopsis (Tsuda et al., 2009). JA, ET, and SA are phytohormones important for immune signaling, and their signaling can be abolished by mutations in the genes DDE2, EIN2, and SID2, respectively (Alonso et al., 1999; Park et al., 2002; Wildermuth et al., 2001). The PAD4 gene affects the SA level as well as many SA-independent responses (Glazebrook et al., 2003; Jirage et al., 1999); the latter were defined as the PAD4 effect in our study. In a quadruple mutant, dde2/ein2/pad4/sid2, the level of immunity triggered by flg22 (flg22-PTI) against P. syringae pv. tomato DC3000 (Pto) was diminished to 20% of the wild-type level (Tsuda et al., 2009). Signaling allocation analysis was used to determine the contributions to flg22-PTI of the four signaling sectors and the sector interactions (Tsuda et al., 2009). Signaling allocation analysis conceptually reconstitutes the signaling network step-by-step from the near-ground state of the quadruple mutant based on immunity level measurements in all 16 Arabidopsis combinatorial genotypes regarding the four sectors (dde2/ein2/pad4/sid2, dde2/ein2/pad4, dde2/ein2 /sid2, dde2/pad4/sid2, ein2/pad4/sid2, dde2/ein2, dde2/pad4, dde2/sid2, ein2/pad4, ein2/sid2, pad4/sid2, dde2, ein2, pad4, sid2, and wild type). In flg22-PTI, the interactions that involve both the PAD4 and SA sectors had synergistic contributions to immunity, but the other interactions were compensatory. The compensatory interactions indicate robustness against perturbations, which could provide a mechanism for the network to withstand attack from fast-evolving pathogens.
The plant immune signaling network response should be tunable, as well as robust, to accommodate the following aspects. First, unnecessary induction of immunity negatively impacts plant fitness. Second, signals indicating pathogen attack may not be reliable. For example, both pathogenic and non-pathogenic microbes may present the same MAMPs (Boller and Felix, 2009). Strong induction of immunity by MAMPs from non-pathogens would incur a fitness cost, thus the level of immunity should be tuned probabilistically according to the reliability of pathogen attack signals (Katagiri and Tsuda, 2010). Third, different types of defense responses have different efficacies against different types of pathogens (Glazebrook, 2005). Thus, the spectrum of defense responses should be tuned to respond efficiently to different types of pathogens.
Robustness of the network output to perturbations may suggest inflexibility in the network response and appears inconsistent with tunability of the response. Investigating how the apparently contradictory network properties of robustness and tunability emerge in the plant immune signaling network is a main motive of the current study. Our experimental system, consisting of 16 Arabidopsis combinatorial genotypes, allows investigation of complex interactions among four signaling sectors. We built a quantitative model describing signaling dynamics in the four-sector network during PTI, based on the sector activities at two time points and the immunity levels against two P. syringae strains after flg22, elf18, a modified chitin, or mock treatment in 16 genotypes. The model demonstrated predictive power. Contrary to current understanding, the model predicted a positive regulatory role of the JA sector on the SA sector, which was confirmed by SA level measurement. The inhibitory effect of the ET sector on the JA sector, which was predicted by the model and confirmed by JA measurement, was central to the robustness of the network output. The network response to different MAMPs was tuned by different intensity and timing patterns of inputs to three sectors. Particularly, the network may have evolved to switch among four qualitative states of the JA and PAD4 sectors: only JA on, only PAD4 on, both on, and neither on.
Results
The modeling approach
Two types of data were collected: (1) the mRNA levels of marker genes for each of four signaling sectors as proxies of sector activities (Supplemental Information and Figure S1A); (2) apoplastic growth of Pto and P. syringae pv. maculicola ES4326 (Pma). The mRNA level and bacterial count measurements were performed after treatment with mock, flg22, elf18, or chitosan (a modified chitin (Silipo et al., 2010)) in 16 combinatorial genotypes of Arabidopsis. The mRNA levels of the marker genes were measured three and nine hours post treatment (hpt). The bacterial strains were infiltrated into leaves 24 hpt, and the bacterial growth was measured two days after infiltration. The log2-transformed mRNA level values were non-linearly scaled for a homogenous noise level (Figures S1B-D). These preprocessed mRNA level values were used in modeling and are called the sector activity values hereafter. The log10-transformed bacterial counts were used in modeling, and the decrease due to MAMP vs. mock treatment of the same genotype is called the (MAMP-induced) immunity level hereafter.
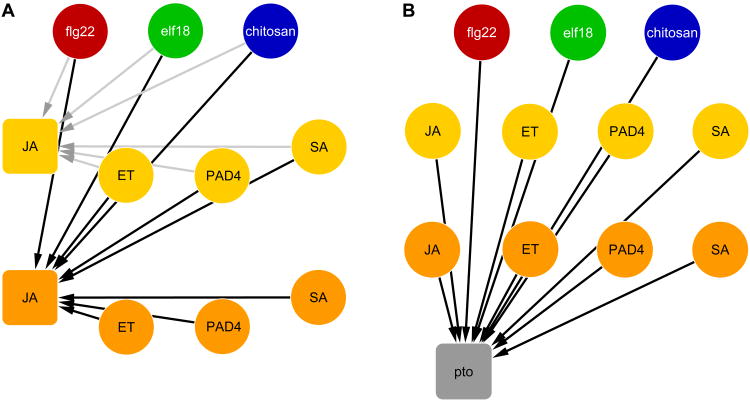
There are four layers of nodes in our model. The top layer consists of three MAMP nodes, flg22 (red), elf18 (green), chitosan (blue), and mock (not shown). After fitting the model, all MAMP inputs were calculated relative to mock inputs, so the mock node is not included in the visualization. The yellow and orange nodes of the second and third layers represent the 3-and 9-hpt states, respectively, of the four signaling sectors. The gray output node in the bottom layer represents the immunity level measured with either Pto or Pma. A multiple regression model with each of the sector and output nodes as the response (targets of directed links) and the nodes in the preceding or same layers as the explanatory variables (sources of directed links) was set up as the starting model (Figures 1). The link from the 3-hpt to the 9-hpt sector nodes within each signaling sector (i.e., JA 3-hpt to JA 9-hpt in Figure 1A) was omitted from the starting model because it is not linearly independent of a link from any MAMP node to the 9-hpt node. Thus, the link from a MAMP node to a 9-hpt node represents the sum of those from the MAMP node and from the early node of the same sector. The starting model was fit using Lasso regression with varying penalty (λ) values (Friedman et al., 2010) in combination with a bagging approach (Hastie et al., 2009), and the predictive power of the model structure (i.e., non-zero link parameters) obtained for each λ value was evaluated. A compact model structure maintaining high predictive power was selected in this way and refit to the complete dataset using least squares to estimate the parameter values (Figure 2A, Table S1). We also built a Bayesian network model (Supplemental Information and Figure S2A) and a multiple regression model with the same starting structure as the Bayesian model, which were found to have lower predictive power than the full regression model described above (Figures S2A and S2B). Thus, we focused our efforts on the full regression model.
Figure 1.
Starting network structures of regression models for (A) the JA sector and (B) the immunity against Pto as examples. Our model consists of four layers, listed from the top: (1) three MAMP treatment inputs (flg22 (red), elf18 (green), and chitosan (blue)); (2) activities of four signaling sectors at 3 hpt (yellow nodes); (3) activities of the signaling sectors at 9 hpt (orange nodes); and (4) two immunity outputs (against Pto and Pma strains, pto gray node shown). Each link represents a directional dependency between an explanatory variable “source” node and a response “target” node. Gray and black links in (A) represent the models for 3 and 9 hpt, respectively. See also Figure S1.
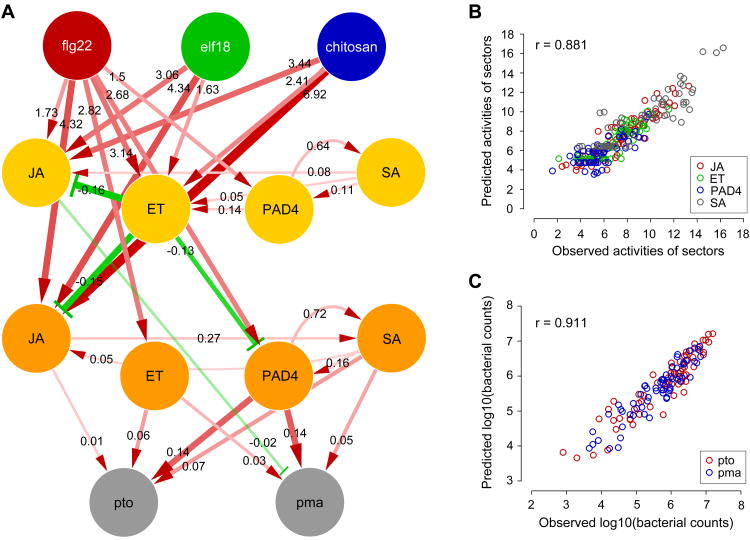
Figure 2.
The PTI signaling network model has a high level of predictive power. (A) The obtained model. Directional links in red and green represent the significant parameters, indicating activation and inhibition, respectively. The width and color intensity of the links represent parameter values. The links to the immunity nodes are scaled differently from those to the sector nodes for better visualization. The links from the MAMP nodes to the immunity nodes are not shown as they represent the immunity level that is not explained by the four sectors. The estimated mean parameter value for each link is indicated. (B and C) The model predictions vs. the observed data of the sector activities across the treatment:genotoype:time:sector combinations (B) and the immunity level across the treatment:genotype:strain combinations (C). The associated Pearson correlation coefficients are shown as r. Red circle, JA; green, ET; blue, PAD4; gray, SA in (B) and red, Pto; blue, Pma in (C). See also Figures S1F, S2, and S3 and Table S1.
The obtained model has a high level of predictive power
Model predictions for each treatment:genotype:time:sector activity and each treatment:genotype:strain immunity level were made by a bagging approach, fitting the fixed model structure shown in Figure 2A with least squares. Figures 2B and C show high Pearson correlation coefficients (PCCs) between the predicted values and the mean observed values for the sector activities (0.881) and the log10 of bacterial counts (0.911), demonstrating high levels of predictive power.
If the starting model structure was too complex, the structure of the final regularized model could vary with relatively small changes in the data. To test the stability of the model, random noise at varying levels was generated and added to the original dataset, the same modeling procedure was performed on the noise-added data, and the obtained models were compared to the original model (Figures S3A and S3B). Even when the standard deviation (SD) of the added noise was twice as large as the SD of the residuals associated with the original model (log2k = 1), the parameter values were quite consistent, suggesting that the model inference process is largely stable.
We further tested the contributions of the inter-sector links to the model performance. When all links between signaling sectors were removed from the starting model structure, the PCCs between the predicted and observed data were reduced to 0.681 for the sector activity and 0.887 for log10 of bacterial counts (Table S2), indicating sector cross-talk links help capture the network's behavior.
The roles of the PAD4 and SA sectors in immunity against the P. syringae strains
A positive feedback loop structure consisting of the PAD4 and SA sectors, which is well established (Jirage et al., 1999; Shah, 2003), was correctly captured by the model (bidirectional red links between the PAD4 and the SA nodes at both 3 and 9 hpt in Figure 2A). SA signaling is a positive regulator of immunity against biotrophic and hemibiotrophic pathogens, such as P. syringae (Glazebrook, 2005); our model concurred (red links from the SA 9-hpt to the pto and pma nodes). Although SA-independent functions of PAD4 have been described (Glazebrook et al., 2003), the primary role of PAD4 has often been characterized as positive regulation of SA signaling (Vlot et al., 2009). The high orders of network perturbation used in our study revealed a direct (i.e., not via SA) and strong contribution of PAD4 to immunity (thick red links from the PAD4 9-hpt to the pto and pma nodes). EDS1, which forms a heterodimer with PAD4, is likely involved in this direct immune contribution of PAD4 (Wiermer et al., 2005). The SA sector activation by MAMPs is indirect (Figure 2A), which may be the basis of delayed activation of SA signaling during flg22-PTI (Tsuda et al., 2008), possibly limiting the negative impacts of misfired immunity (Katagiri and Tsuda, 2010).
The JA sector activates the SA sector
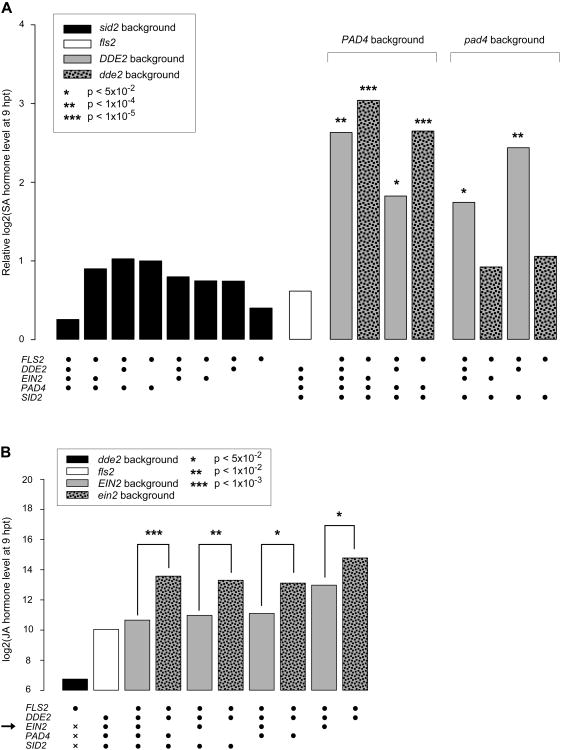
Although it is often thought that JA signaling inhibits SA signaling (Vlot et al., 2009), the JA sector activated the SA sector in our model (the red link from the JA to SA nodes at 9 hpt in Figure 2A). We tested this model prediction by directly measuring the SA level at zero and 9 hpt with flg22 in 16 combinatorial genotypes and a flg22-receptor mutant, fls2. Figure 3A shows that the SA increase was dependent on flg22 treatment since the increase in fls2 (white bar) was not different from the sid2-containing mutants (black bars). In the pad4-containing genotypes, the SA increase completely depended on the wild-type allele of DDE2, indicating that the JA sector is required for the SA increase (gray and mottled bars under “pad4 background”). The PAD4 sector was required for SA increase in dde2-containing genotypes (compare left 2 bars to right 2 bars among 4 mottled bars). Since the SA increases were lower in the DDE2/PAD4-containing genotypes than in the corresponding dde2/PAD4–containing genotypes (gray and mottled bars under “PAD4 background”), the JA and PAD4 sectors are compensatory in activation of the SA sector. Thus, this positive JA sector effect on the SA sector became evident only under high order perturbation of the system. These observations of higher SA increases in dde2/PAD4– containing genotypes than in the corresponding DDE2/PAD4-containing genotypes are reminiscent of the notion that JA signaling inhibits SA signaling. However, the higher SA increases occurred not because the JA sector per se inhibits the SA sector activation but because the dde2 mutation eliminates the above-noted compensation (i.e., a negative interaction) between the JA and PAD4 sectors on SA activation. This is an example of the fact that in a web-like network, the effect of removal of a single network component is not necessarily the opposite of the component's function (Katagiri and Tsuda, 2010).
Figure 3.
Confirmation of predicted regulatory relationships. (A) SA upregulation after flg22 treatment required the JA sector or the PAD4 sector in a compensatory manner. The means of three biological replicates for the log2-transformed SA level increase from 0 to 9 hpt with flg22 in the indicated genotypes (black dot and blank for the wild-type and mutant alleles, respectively) are shown as bars. Significant differences from the aggregated mean of the sid2-containing genotypes (black bars) are indicated by asterisks. (B) The JA level was lowered by the ET sector activity at 9 hpt with flg22. The bars show the means of the log2-transformed JA levels in three biological replicates for the indicated genotypes as in (A). The dde2-containing genotypes were aggregated to one as many measurements were below detection (black bar; x for the genotype represents either wild-type or mutant alleles). Asterisks indicate significant differences in the comparisons between EIN2 (gray bars) and ein2 (mottled bars) of the same genetic backgrounds.
Inhibition of the JA sector by the ET sector is important for robustness of the PTI network output
Our model predicts that the ET sector is the sole source of inhibitory effects in the immune signaling network (Figure 2A). In particular, the model highlights inhibition of the JA sector by the ET sector. We tested this prediction by directly measuring the JA level at 9 hpt with flg22 in 16 combinatorial genotypes and fls2 (Figure 3B). The JA levels in ein2-containing genotypes were always higher than the corresponding EIN2-containing genotypes (paired mottled and gray bars), indicating that the ET sector inhibits the JA sector regardless of the states of the other sectors.
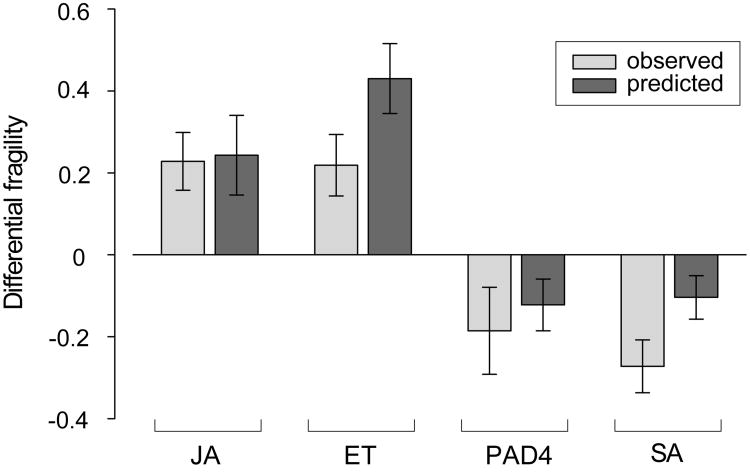
One signaling sector inhibiting another, if both regulate network output, can produce robust network output. When the first sector is compromised by, for example, a pathogen effector, the second sector is released from inhibition and backs up the function of the first sector, which we referred to as “sector-switching” (Sato et al., 2010). We tested whether the ET sector inhibition of the JA sector contributes to network robustness. We measured how much loss of a sector in question affects network fragility, which we defined as the impact on network output further removing another (secondary) sector. For example, the impacts of removing the PAD4 sector (a secondary sector) when the JA sector is in question was calculated for each treatment:strain combination as |mdde2/pad4 − mdde2| for the dde2 background and |mpad4 − mwt| for the DDE2 background, where mk is the mean immunity level of genotype k. The differential fragility of the JA sector for the treatment:strain:PAD4 combinations was calculated by |mdde2/pad4 − mdde2| − |mpad4 − mwt|. If a differential fragility is positive or negative, removal of the sector in question decreases or increases robustness, respectively. The fragility values for each treatment:strain:secondary_sector combination in the absence vs. the presence of each sector in question are plotted in Figure S4. Figure 4 shows the mean and standard error of the differential fragility values. The differential fragilities were calculated from either the observed data or model predictions (light and dark gray bars, respectively), demonstrating consistent results between them. Loss of the JA or ET sectors increased network fragility, indicating both the JA and ET sectors are important for network robustness. Removal of either the source (ET) or target (JA) sector would eliminate the ET to JA inhibitory link. We conclude that this inhibitory link is important for network robustness.
Figure 4.
The JA and ET sectors are salient factors in network robustness. The differential fragility was calculated for predicted (light gray bars) and observed (dark gray bars) immunity levels. A positive differential fragility means that removal of the indicated sector decreases network robustness. Each bar shows the mean and standard error across the appropriate treatment:strain:secondary_sector combinations. See also Figure S4.
MAMP treatments tune the response of an invariant network using different input patterns
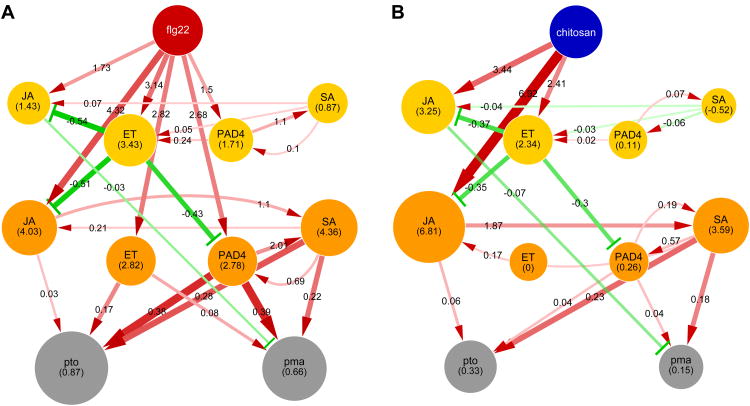
The model with the link parameter values (Figure 2A) does not allow easy visualization of signal flow, which is the product of the source node activity and the link parameter for each link. To facilitate model interpretation, we made “network activity maps,” in which the sector node size represents the sector activity and the link width and color intensity represent the amount of signal flow (Figure S5). In the network activity maps, it is evident that flg22 treatment strongly activates the JA, ET, and PAD4 sectors whereas chitosan treatment predominantly activates the JA sector (Figure 5). This difference in network input pattern results in much stronger activation of the 9-hpt PAD4 sector node by flg22 treatment than by chitosan treatment; the 9-hpt PAD4 sector activity largely explains the higher levels of immunity to both Pto and Pma induced by flg22 than by chitosan. In addition, flg22 treatment, but not chitosan treatment, also activates the 9-hpt ET sector node, which raises immunity levels. The differential signal flows activated by the two treatments strongly suggest that one way to tune the network response is to change the intensity and timing pattern of the inputs to the signaling sectors.
Figure 5.
Treatments of wild type with flg22 (A) and chitosan (B) have different signal input patterns, which results in distinct network responses. These “network activity maps” make visual the model-predicted relative sector activity and immunity level by the respective node sizes, and the relative amount of signal flow by the width and color intensity of the link. Link values were calculated relative to mock treatment for each MAMP treatment. The range of immunity levels was scaled from 0 to 1, and the links targeting the immunity nodes were scaled according to the scaled immunity level. The predicted relative sector activity and the relative signal flow values are indicated in the node and along the link, respectively. Otherwise, the representation is the same as the model with parameter values in Figure 2A. See also Figure S5.
Another possible explanation for different efficacies in immunity conferred by different MAMP treatments is that the signaling network structure changes according to MAMP treatments. To explore this possibility, we fit separate models for different treatments (treatment-specific models; Figure S3C) and compared the predictive power of the obtained models to the original treatment-invariant model (Figure 2A) across all treatments. The predictions of the sector activities and the immunity levels by the invariant model were as good as or better than those by the treatment-specific models (Table S3), and the invariant model was less complex (the total numbers of parameters were 45 and 82, respectively). Thus, the invariant model is the better representation of the signaling network, and differential network responses to different MAMP treatments are likely achieved by different signal input patterns.
If the hypothesis that an invariant network is tuned by different input patterns is correct, we should be able to predict the network response to an arbitrary MAMP as long as we know the input signal pattern. To test this, the model parameters were fit to subsets of the observations in which the data from one of the three MAMPs were withheld. Using only the sector activities of the wild-type genotype after treatment with the withheld MAMP, the input signal pattern was inferred, and the sector activities and the immunity levels of the other genotypes after treatment with the withheld MAMP were predicted (See Supplementary Information). Predicted immunity and sector activities were compared with the actual observations for each withheld MAMP treatment (Figure S3D). The PCCs between the model predictions and observed data ranged from 0.623 to 0.725 for the sector activities and 0.684 to 0.807 for the immunity level. This level of predictive power supports the hypothesis and suggests that the invariant model captures the core network parameters well. Furthermore, it indicates that the same invariant model will likely be able to predict the sector activities and the immunity levels across the genotypes for any other MAMPs given only sector activity measurements after MAMP treatment of the wild-type genotype.
Discussion
In the current study, we built a multiple regression model of the signal flow dynamics in the network consisting of four major signaling sectors during PTI. The revealed signal flows provide mechanistic explanations for the static sector interactions described in our prior study (Tsuda et al., 2009). For example, we showed that inhibition of the JA sector by the ET sector is a main cause of observed partial robustness against network perturbations during PTI. Our model was based on expression levels of sector marker genes as proxies for the sector activities. We strictly selected the marker genes to minimize systematic error of known sources, which included the phytohormones gibberellic acid, auxin, abscisic acid and brassinosteroid, as well as the response specificity to JA, ET, and SA. However, such strict selection in the response specificity does not completely exclude the possibility that marker gene expression is affected by some signals we did not consider and that the resulting model might be affected by such unknown signals. This is the reason we used direct hormone measurement to validate some of the key model predictions, inhibition of the JA sector by the ET sector and activation of the SA sector by the JA sector (Figure 3): since we defined the corresponding hormone levels as the sector activities, these predictions were firmly validated. Despite the fact that our model exhibited a high level of predictive power, our model is unlikely to be the perfect model. The complexity of our data was vastly increased by high orders of genetic perturbation of the network compared to conventional types of data, and this data complexity supported our current modeling study (see below). However, it is conceivable that future data with even higher complexity would support more complex models. Nevertheless, our current model explained known network responses well and generated several testable hypotheses, which demonstrates its utility.
The multi-factorial features of the dataset were important for obtaining a high performance model
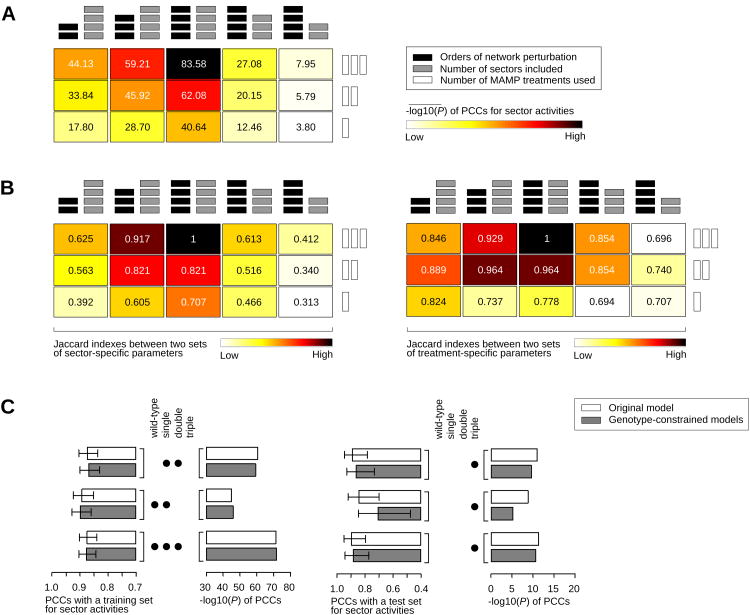
Our sector activity model was built on a multi-factorial dataset: four signaling sectors, 16 exhaustive combinatorial genotypes regarding the signaling sectors, three MAMP (and one mock) treatments, and two time points. We examined the importance of (1) the number of explanatory sectors used to decipher network activity and output (four sectors), (2) high orders of sector perturbation represented by the combinatorial genotypes (16 genotypes), and (3) several network stimuli (three MAMP treatments). First, the predictive power was compared between the original model with four sectors and models with fewer sectors (Figure 6A, three columns on the right). For example, in modeling with three sectors, one sector and the links connected to the sector were removed from the starting model, and the data from genotypes containing the mutation for that sector were removed. The significance of the PCC (-log10P) between the observed and the predicted sector activity values decreased in the models with fewer sectors. The structures of the models with fewer sectors were substantially different from that of the corresponding part of the original model as shown by the Jaccard index (Figure 6B). These results indicate that inclusion of all four highly interacting sectors was important for high predictive power of the model, suggesting that this inclusion also captured mechanistic relationships among the sectors more accurately.
Figure 6.
The multi-factorial nature of the dataset was important in obtaining a sector activity model with high predictive power. (A) Models having limited sectors or obtained with limited data have lower predictive power than the original model. The significance of the PCCs (-log10P) between the predictions of different models and the observed data are shown with darker colors for higher significances. The limited models were made with fewer signaling sectors (4, 3, and 2 sectors for the three right columns) or with datasets with lower orders of perturbations (up to triple, double, and single mutants for the three left columns) and with fewer MAMP treatments (3, 2, and 1 MAMP treatment(s), plus mock treatment, for the three rows). The average significance values for the limited models of the same class are shown. The middle cell in the top row represents the original model. (B) The structures of the limited models are substantially different from that of the original model. The Jaccard indices between the original model and the limited models used in (A) are shown. (C) Models obtained with lower orders of sector perturbation have poor predictive power of data collected from higher orders of perturbation. The PCCs between the model predictions and observed data for the triple mutants are shown. See also Figures S6 and S7.
Second, the models built on lower orders of sector perturbations were compared, i.e., modeling was performed with the datasets in which the data from higher orders of multiple mutants were removed. When four-sector models were made using only lower orders of sector perturbations, the predictive power and the structural similarity to the original model decreased (Figures 6A and B, three columns on the left). In this case, we further tested whether the structure of the original model was not only different but also more accurate than those of the models with lower orders of sector perturbations. Figure 6C shows that the models built on the datasets with up to single mutants poorly predicted the sector activity values for the higher orders of mutants, indicating that the mechanistic relationships captured based only on lower orders of sector perturbation were not accurate.
We similarly demonstrated the importance of having multiple MAMP inputs for the predictive power and structure of the model (Figures 6A and B, rows of the cells). Thus, our multifactorial dataset was important in obtaining a model with high predictive power and with accurate mechanistic relationships. Although we only tried a limited number of modeling approaches, we anticipate that our multifactorial dataset will provide a rich basis for further modeling work. All raw and preprocessed data are included in Data S1 and S2.
Limited statistical power associated with the immunity data
The above-noted importance of including four highly interacting signaling sectors implies the importance of inter-sector links in the model. In fact, a sector activity model devoid of inter-sector links performed poorly in predicting sector activity across the treatments and genotypes (Table S2). On the other hand, the starting model for the immunity level did not contain terms for further interactions downstream of the sectors; such interactions might be significant. For example, SA signaling inhibits some downstream transcriptional responses requiring activation of both the JA and ET sectors (Van der Does et al., 2013), which could be included as an interaction term in the immunity model. However, as the immunity level is already well explained by the original model, our current dataset is unlikely to have the power to investigate such interaction terms. To gain sufficient power to test interaction terms in the immunity level model, it will be necessary to measure the activities directly corresponding to the interactions in question, such as the expression level of a marker gene that reports inhibition by SA signaling of signaling requiring both JA and ET sector activation. This discussion also reveals that immunity is a highly summarized phenotype and that immunity level data alone do not have much power to elucidate the underlying mechanisms.
Inhibitory regulation in the immune network may increase plant fitness
Inhibition of the JA sector by the ET sector was important in the robustness of the network output against perturbations (Figure 4), suggesting that the intact network internally represses signaling sector(s), keeping the network output suppressed relative to its maximum possible activity. This suppression could be interpreted as a tradeoff of gaining network robustness, but plants may not benefit from higher levels of PTI. Non-pathogenic microbes also present MAMPs, and responding to non-pathogens with a strong immune response would reduce plant fitness. It is conceivable that the level of inhibition by the ET sector on the JA sector has been selected to probabilistically optimize plant fitness in two ways: limiting response to imperfect information and conferring network robustness against potential network perturbations by pathogen effectors.
Tuning of the network response according to the input pattern may provide immunity to specific pathogens
Our network activity maps revealed how different MAMP treatments lead to very different responses of the same network (Figure 5). The network response is modulated by a combination of multiple input points and the patterns of intensity and timing on these inputs. For example, flg22 is a MAMP derived from Gram-negative bacteria, such as P. syrinage (Zipfel et al., 2004). Treatment with flg22 activated the JA, ET, and PAD4 sectors at similar levels, which resulted in strong immunity against P. syringae, as PAD4 sector activation at 9 hpt strongly contributes to immunity. In contrast, chitin is a MAMP derived from fungi (Silipo et al., 2010), which include necrotrophs. Chitosan treatment predominantly activated the JA sector, which controls responses effective against necrotrophs. Thus, the network input patterns associated with flg22 and chitin may be selected to optimize the network response for immunity against bacterial and fungal pathogens, respectively.
Treatment with elf18, a bacterial MAMP (Zipfel et al., 2006), had an input pattern more similar to chitosan than flg22 (Figure S5). This might indicate that the JA sector contributes to immunity against bacterial necrotrophs, such as Pectobacterium species (Davidsson et al., 2013). Another possibility is that the input pattern from EFR, the elf18 receptor, has not yet been adapted well as EFR seems to have evolved relatively recently (Lacombe et al., 2010; Saijo et al., 2009). Yet another possibility is that EFR may also be involved in recognition of other microbes. The chitin receptor CERK1 is also a co-receptor of the bacterial MAMP peptidoglycan (Willmann et al., 2011), which raises the possibility that a single PRR may be involved in recognition of different types of microbes. If this is the case, the spectrum of microbes recognized by a PRR would probabilistically shape the signal input pattern from the PRR to the invariant network, and the signal input pattern could be locally adapted to variable microbe spectra. Such intraspecific local adaptation could be observed as variation in the signal input pattern mediated by the PRR. Although this is an interspecific comparison, chitin-induced immunity in tomato is quite effective against a biotrophic fungus, Cladosporium fulvum (de Jonge et al., 2010), suggesting variation in chitin-triggered immune signaling between the tomato variety used and Arabidopsis accession Col-0.
An invariant signaling network whose response is tuned by differential input patterns, determined by MAMPs, allows us to predict the network response and output under other input scenarios. Once input patterns are determined (e.g. through measurement of sector activities upon MAMP treatment of a wild-type plant), the network response and the induced immunity level against Pto and Pma in different genotypes can be predicted using the network model (Figure S3D). In nature, a single microbe is likely to present multiple MAMPs. With their collective signal input pattern information, our model should be able to predict the network response and the triggered immunity level after treatment with such collective MAMPs.
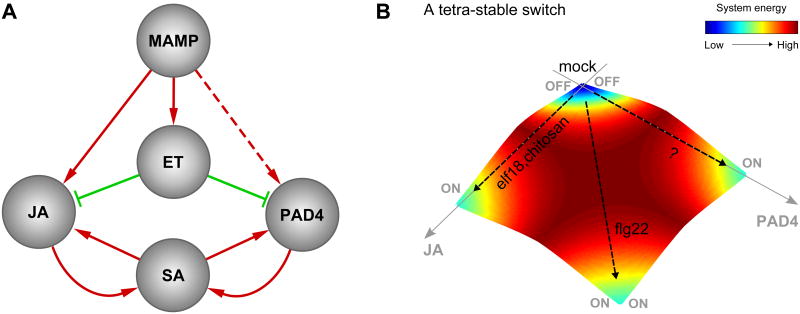
Symmetric roles of the JA and PAD4 sectors: inhibition by the ET sector and positive feedback loops with the SA sector
Figure 7A depicts a static summary of major regulatory relationships in the model shown in Figure 2A. This summary network suggests that the JA and PAD4 sectors play symmetric roles in the sense that they are both inhibited by the ET sector and are involved in positive feedback loops with the SA sector. The observation that the JA and PAD4 sectors are compensatory in activation of the SA sector (Figure 3A) is consistent with this symmetry. A characteristic property of a positive feedback loop is a bistable switch (Ferrell and Xiong, 2001). It is conceivable that both the JA-SA and PAD4-SA feedback loops function as compensatory bistable switches with the activation thresholds adjusted by inhibition from the ET sector. This notion suggests that the JA and PAD4 sectors may be pushed toward one of four rather qualitative states, “only JA on”, “only PAD4 on”, “both on”, or “neither on,” i.e., a tetra-stable switch (Figure 7B). The case with mock treatment represents the “neither on” state, the cases with chitosan and elf18 represent the “only JA on” state, and the case with flg22 represents the “both on” state (Figures 5 and S5). The “only PAD4 on” state might be caused by treatment with MAMPs not included in our study. An alternative, tantalizing possibility is that the “only PAD4 on” state might be related to effector-triggered immunity (ETI). ETI triggered by the P. syringae effector AvrRpt2 (AvrRpt2-ETI) is largely dependent on the signaling network defined by the four signaling sectors, and the AvrRpt2-ETI level is largely intact in dde2/ein2/sid2 (i.e., only PAD4 is wild type) (Tsuda et al., 2009). These observations suggest that a different state of the same invariant signaling network obtained by modeling PTI signaling may explain AvrRpt2-ETI signaling and that the response mediated by the PAD4 sector is crucial for AvrRpt2-ETI.
Figure 7.
A static summary of the model suggests a JA-PAD4 dichotomy and tetra-stable network states. (A) A static summary of signal flows in the sector activity model shown in Figure 2A. (B) A schematic representation of tetra-stable states of the signaling network. The “only JA on”, “both on”, “only PAD4 on”, and “neither on” states may correspond to lower energy states of the network.
A dichotomic view that the responses mediated by the JA sector and the SA sector are important for immunity against necrotrophic pathogens and immunity against biotrophic and hemibiotrophic pathogens, respectively, is generally accepted (Glazebrook, 2005; Spoel et al., 2007). However, the symmetric roles of the JA and PAD4 sectors in our network model raise a question: is it the SA sector per se that is important for immunity against biotrophs and hemibiotrophs or is the main role of the SA sector to activate the PAD4 sector which mediates more effective responses against these pathogens? Our observation that the (SA-signaling-independent) PAD4 sector's effect on Pto and Pma immunity is stronger than that of the SA sector (Figure 2A) is consistent with the latter. The high orders of network perturbations utilized in this study will allow rigorous testing of these hypotheses.
Conclusions
Teasing out mechanistic models from complex networks is a difficult but critical task of systems biology. Our success was enabled by inclusion of several highly interacting signaling sectors, high orders of network perturbation regarding the sectors, multiple defined inputs, and measurement of the activities at the perturbation points across multiple time points. Our model revealed how the robustness of the network output against network perturbations and the tunability of the network response are achieved in a single invariant network for plant immune signaling under PTI conditions. Furthermore, analysis of the network structure led to testable hypotheses of a tetera-stable switch and of alternative roles for the PAD4 and SA sectors. Modeling signal flows in a complex network via network sector reconstitution is a powerful strategy to elucidate the mechanisms behind network properties.
Experimental Procedures
Plant materials and growth conditions
Arabidopsis thaliana accession Col-0 was the background of the 16 combinatorial genotypes (Tsuda et al., 2009) and fls2 (SAIL_691C4) (Zipfel et al., 2004). Plants were grown in a controlled environment at 22°C with a 12h/12h photoperiod and 75% relative humidity. Leaves of four-week old plants were used.
Sector marker gene expression level measurements and data preprocessing
Selection of the sector marker genes, At3g50280, At2g41230, At5g46960, and At2g14610 (PR1) for the JA, ET, PAD4, and SA sectors, and the normalization gene At4g29480 is described in Supplemental Information. Leaves were harvested 3 or 9 hours after infiltration with mock (H2O), 1 μM flg22, 1 μM elf18, or 100 μg/ml chitosan using a needleless syringe. RNA extraction and mRNA quantification by qRT-PCR with the primers listed in Table S4 were performed as previously described (Tsuda et al., 2008). From three independent experiments, the Ct values for the sector marker genes were subjected to between-samples normalization, mutant-adjustment, and non-linear transformation for homogenous SD within and between sectors to obtain the sector activity values, as detailed in Supplementary Information.
Bacterial count measurements
At 24 hpt with a MAMP or mock, the same leaves were infiltrated with a suspension of Pto or Pma at OD600 = 0.0001. Two days after inoculation the bacterial titer in the leaves was measured as previously described (Tsuda et al., 2009).
SA and JA measurements and data analyses
Leaves were flash frozen with liquid N2, macerated to powder and freeze-dried at 9 hpt with flg22 and at 0 hpt (untreated). Extraction and determination of SA and JA from Arabidopsis were performed with an UPLC-MS/MS (AQITY UPLC™ System/Quattro Premier XE; Waters) with an ODS column (AQUITY UPLC BEH C18, 1.7 μm, 2.1 × 100 mm, Waters) as described previously (Kojima et al., 2009; Kojima and Sakakibara, 2012). The measurements were made in three independent experiments. A mixed linear model with genotype:time fixed effects and experiment random effects was fit to the log2-transformed SA or JA level (pmol/g dry weight of tissue) data. The mean estimates and their standard errors obtained from the model were used to perform two-sided t-tests for the comparisons of interest.
Multiple regression models
The starting multiple regression models were fitted with L1-norm (Lasso) regularization (Friedman et al., 2010), formulated via:
where p is the total number of initial parameters excluding an intercept, N is the total number of cases covering all possible combinatorial conditions, β0 is an intercept, and β is the parameter vector to be estimated (i.e., the links in Figure S1E). The explanatory variable xi consists of either binary indicators for treatment-specific variables or continuous variables corresponding to the sector activity. is the response, which is either an actual activity value for sector m or an actual log10-transformed count of bacterial strain m. λ is the penalty factor balancing the prediction error and the model complexity, which was searched in (0.001,1.5).
For each λ, the starting model was fit to each of 1000 datasets generated by bootstrapping the treatment:genotype combinations from the full dataset. Each of the 1000 obtained models was used to predict the sector activities and the immunity levels for the treatment:genotype combinations held out from the bootstrapped training dataset, and the median of the predictions was chosen as the prediction for each treatment:genotype:time:sector activity or each treatment:genotype:strain immunity level (a bagging approach (Hastie et al., 2009)). Based on the PCC between the observed data and the predictions, the largest λ that yielded a PCC within the 95 % confidence interval of the best PCCs across all λ values was selected (Friedman et al., 2010). The model structure for the selected λ was refit to the full dataset using least squares to obtain the parameter value estimates (Figure 2A). See Supplementary Information for details and evaluation of the modeling approach and analysis of the model.
Supplementary Material
Highlights.
A predictive, dynamic PTI signaling network model was built.
Inhibition of the JA sector by the ET sector was central to network robustness.
MAMP-specific patterns of multiple inputs can tune the network response.
The symmetrically positioned JA and PAD4 sectors may form a tetra-stable switch.
Acknowledgments
We thank Mikiko Kojima for hormone analysis and Jane Glazebrook for critical reading of the manuscript. This work was supported by grants MCB-0918908 (FK and CLM), IOS-1121425 (FK), and DBI-0953881 (CLM) from the National Science Foundation, a grant from Ajinomoto Co. (FK), and the Max Planck Society (KT). RAH was partially supported by the University of Minnesota's NIH/NIGMS training grant 2T32GM008347-21A1.
References
- Alonso JM, Hirayama T, Roman G, Nourizadeh S, Ecker JR. EIN2, a bifunctional transducer of ethylene and stress responses in Arabidopsis. Science. 1999;284:2148–2152. doi: 10.1126/science.284.5423.2148. [DOI] [PubMed] [Google Scholar]
- Boller T, Felix G. A Renaissance of Elicitors: Perception of Microbe-Associated Molecular Patterns and Danger Signals by Pattern-Recognition Receptors. Annu Rev Plant Biol. 2009;60:379–406. doi: 10.1146/annurev.arplant.57.032905.105346. [DOI] [PubMed] [Google Scholar]
- Chinchilla D, Bauer Z, Regenass M, Boller T, Felix G. The Arabidopsis receptor kinase FLS2 binds flg22 and determines the specificity of flagellin perception. The Plant Cell. 2006;18:465–476. doi: 10.1105/tpc.105.036574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidsson PR, Kariola T, Niemi O, Palva ET. Pathogenicity of and plant immunity to soft rot pectobacteria. Frontiers in Plant Science. 2013;4:191. doi: 10.3389/fpls.2013.00191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jonge R, van Esse HP, Kombrink A, Shinya T, Desaki Y, Bours R, van der Krol S, Shibuya N, Joosten MH, Thomma BP. Conserved fungal LysM effector Ecp6 prevents chitin-triggered immunity in plants. Science. 2010;329:953–955. doi: 10.1126/science.1190859. [DOI] [PubMed] [Google Scholar]
- Dodds PN, Rathjen JP. Plant immunity: towards an integrated view of plant-pathogen interactions. Nat Rev Genet. 2010;11:539–548. doi: 10.1038/nrg2812. [DOI] [PubMed] [Google Scholar]
- Ferrell JE, Xiong W. Bistability in cell signaling: How to make continuous processes discontinuous, and reversible processes irreversible. Chaos. 2001;11:227–236. doi: 10.1063/1.1349894. [DOI] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J Stat Softw. 2010;33:1–22. [PMC free article] [PubMed] [Google Scholar]
- Glazebrook J. Contrasting mechanisms of defense against biotrophic and necrotrophic pathogens. Annu Rev Phytopathol. 2005;43:205–227. doi: 10.1146/annurev.phyto.43.040204.135923. [DOI] [PubMed] [Google Scholar]
- Glazebrook J, Chen W, Estes B, Chang HS, Nawrath C, Metraux JP, Zhu T, Katagiri F. Topology of the network integrating salicylate and jasmonate signal transduction derived from global expression phenotyping. Plant J. 2003;34:217–228. doi: 10.1046/j.1365-313x.2003.01717.x. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Second. Springer; 2009. [Google Scholar]
- Jirage D, Tootle TL, Reuber TL, Frost LN, Feys BJ, Parker JE, Ausubel FM, Glazebrook J. Arabidopsis thaliana PAD4 encodes a lipase-like gene that is important for salicylic acid signaling. Proc Natl Acad Sci U S A. 1999;96:13583–13588. doi: 10.1073/pnas.96.23.13583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones JD, Dangl JL. The plant immune system. Nature. 2006;444:323–329. doi: 10.1038/nature05286. [DOI] [PubMed] [Google Scholar]
- Katagiri F, Tsuda K. Understanding the Plant Immune System. Mol Plant Microbe Interact. 2010;23:1531–1536. doi: 10.1094/MPMI-04-10-0099. [DOI] [PubMed] [Google Scholar]
- Kojima M, Kamada-Nobusada T, Komatsu H, Takei K, Kuroha T, Mizutani M, Ashikari M, Ueguchi-Tanaka M, Matsuoka M, Suzuki K, et al. Highly Sensitive and High-Throughput Analysis of Plant Hormones Using MS-Probe Modification and Liquid Chromatography Tandem Mass Spectrometry: An Application for Hormone Profiling in Oryza sativa. Plant Cell Physiol. 2009;50:1201–1214. doi: 10.1093/pcp/pcp057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima M, Sakakibara H. Highly sensitive high-throughput profiling of six phytohormones using MS-probe modification and liquid chromatography-tandem mass spectrometry. Methods Mol Biol. 2012;918:151–164. doi: 10.1007/978-1-61779-995-2_11. [DOI] [PubMed] [Google Scholar]
- Lacombe S, Rougon-Cardoso A, Sherwood E, Peeters N, Dahlbeck D, van Esse HP, Smoker M, Rallapalli G, Thomma BP, Staskawicz B, et al. Interfamily transfer of a plant pattern-recognition receptor confers broad-spectrum bacterial resistance. Nat Biotechnol. 2010;28:365–369. doi: 10.1038/nbt.1613. [DOI] [PubMed] [Google Scholar]
- Lindeberg M, Cunnac S, Collmer A. Pseudomonas syringae type III effector repertoires: last words in endless arguments. Trends Microbiol. 2012;20:199–208. doi: 10.1016/j.tim.2012.01.003. [DOI] [PubMed] [Google Scholar]
- Miya A, Albert P, Shinya T, Desaki Y, Ichimura K, Shirasu K, Narusaka Y, Kawakami N, Kaku H, Shibuya N. CERK1, a LysM receptor kinase, is essential for chitin elicitor signaling in Arabidopsis. Proc Natl Acad Sci USA. 2007;104:19613–19618. doi: 10.1073/pnas.0705147104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park JH, Halitschke R, Kim HB, Baldwin IT, Feldmann KA, Feyereisen R. A knock-out mutation in allene oxide synthase results in male sterility and defective wound signal transduction in Arabidopsis due to a block in jasmonic acid biosynthesis. Plant J. 2002;31:1–12. doi: 10.1046/j.1365-313x.2002.01328.x. [DOI] [PubMed] [Google Scholar]
- Saijo Y, Tintor N, Lu X, Rauf P, Pajerowska-Mukhtar K, Haweker H, Dong X, Robatzek S, Schulze-Lefert P. Receptor quality control in the endoplasmic reticulum for plant innate immunity. EMBO J. 2009;28:3439–3449. doi: 10.1038/emboj.2009.263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Tsuda K, Wang L, Coller J, Watanabe Y, Glazebrook J, Katagiri F. Network Modeling Reveals Prevalent Negative Regulatory Relationships between Signaling Sectors in Arabidopsis Immune Signaling. PLoS Pathog. 2010;6:e1001011. doi: 10.1371/journal.ppat.1001011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah J. The salicylic acid loop in plant defense. Curr Opin Plant Biol. 2003;6:365–371. doi: 10.1016/s1369-5266(03)00058-x. [DOI] [PubMed] [Google Scholar]
- Silipo A, Erbs G, Shinya T, Dow JM, Parrilli M, Lanzetta R, Shibuya N, Newman MA, Molinaro A. Glyco-conjugates as elicitors or suppressors of plant innate immunity. Glycobiology. 2010;20:406–419. doi: 10.1093/glycob/cwp201. [DOI] [PubMed] [Google Scholar]
- Spoel SH, Johnson JS, Dong X. Regulation of tradeoffs between plant defenses against pathogens with different lifestyles. Proc Natl Acad Sci U S A. 2007;104:18842–18847. doi: 10.1073/pnas.0708139104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuda K, Katagiri F. Comparing signaling mechanisms engaged in pattern-triggered and effector-triggered immunity. Curr Opin Plant Biol. 2010;13:459–465. doi: 10.1016/j.pbi.2010.04.006. [DOI] [PubMed] [Google Scholar]
- Tsuda K, Sato M, Glazebrook J, Cohen JD, Katagiri F. Interplay between MAMP-triggered and SA-mediated defense responses. Plant J. 2008;53:763–775. doi: 10.1111/j.1365-313X.2007.03369.x. [DOI] [PubMed] [Google Scholar]
- Tsuda K, Sato M, Stoddard T, Glazebrook J, Katagiri F. Network Properties of Robust Immunity in Plants. PLoS Genet. 2009;5:e1000772. doi: 10.1371/journal.pgen.1000772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Does D, Leon-Reyes A, Koornneef A, Van Verk MC, Rodenburg N, Pauwels L, Goossens A, Korbes AP, Memelink J, Ritsema T, et al. Salicylic acid suppresses jasmonic acid signaling downstream of SCFCOI1-JAZ by targeting GCC promoter motifs via transcription factor ORA59. The Plant Cell. 2013;25:744–761. doi: 10.1105/tpc.112.108548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlot AC, Dempsey DA, Klessig DF. Salicylic Acid, a Multifaceted Hormone to Combat Disease. Annu Rev Phytopathol. 2009;47:177–206. doi: 10.1146/annurev.phyto.050908.135202. [DOI] [PubMed] [Google Scholar]
- Wan JR, Zhang XC, Neece D, Ramonell KM, Clough S, Kim SY, Stacey MG, Stacey G. A LysM receptor-like kinase plays a critical role in chitin signaling and fungal resistance in Arabidopsis. The Plant Cell. 2008;20:471–481. doi: 10.1105/tpc.107.056754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiermer M, Feys BJ, Parker JE. Plant immunity: the EDS1 regulatory node. Curr Opin Plant Biol. 2005;8:383–389. doi: 10.1016/j.pbi.2005.05.010. [DOI] [PubMed] [Google Scholar]
- Wildermuth M, Dewdney J, Wu G, Ausubel F. Isochorismate synthase is required to synthesize salicylic acid for plant defence. Nature. 2001;414:562–565. doi: 10.1038/35107108. [DOI] [PubMed] [Google Scholar]
- Willmann R, Lajunen HM, Erbs G, Newman MA, Kolb D, Tsuda K, Katagiri F, Fliegmann J, Bono JJ, Cullimore JV, et al. Arabidopsis lysin-motif proteins LYM1 LYM3 CERK1 mediate bacterial peptidoglycan sensing and immunity to bacterial infection. Proc Natl Acad Sci USA. 2011;108:19824–19829. doi: 10.1073/pnas.1112862108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zipfel C, Kunze G, Chinchilla D, Caniard A, Jones J, Boller T, Felix G. Perception of the bacterial PAMP EF-Tu by the receptor EFR restricts Agrobacterium-mediated transformation. Cell. 2006;125:749–760. doi: 10.1016/j.cell.2006.03.037. [DOI] [PubMed] [Google Scholar]
- Zipfel C, Robatzek S, Navarro L, Oakeley EJ, Jones JD, Felix G, Boller T. Bacterial disease resistance in Arabidopsis through flagellin perception. Nature. 2004;428:764–767. doi: 10.1038/nature02485. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.