Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms

Abstract

We introduce Sailfish, a computational method for quantifying the abundance of previously annotated RNA isoforms from RNA-seq data. Because Sailfish entirely avoids mapping reads, a time-consuming step in all current methods, it provides quantification estimates much faster than do existing approaches (typically 20 times faster) without loss of accuracy. By facilitating frequent reanalysis of data and reducing the need to optimize parameters, Sailfish exemplifies the potential of lightweight algorithms for efficiently processing sequencing reads.

RNA-seq has become the de facto standard technique to measure gene expression, and it is commonly the first step in an analysis of differential expression among multiple samples¹. However, the throughput of technologies used to generate transcriptomic sequencing reads is accelerating faster than the speed of the computers used to analyze these data. The growing repository of data from archived experiments invites reanalysis in the light of new discoveries, but existing methods are too time-consuming to allow frequent reanalysis. The divide between data-acquisition and data-analysis capabilities will only increase as RNA-seq is adopted for clinical use². Finally, the sensitivity of existing methods to parameter choices can affect analysis time and accuracy and can make a priori selection of the appropriate parameters difficult. We must develop efficient, lightweight algorithms with few parameters that minimize unnecessary computation.

Existing approaches to abundance estimation first use read-mapping tools, such as Bowtie³, to determine potential locations from which the RNA-seq reads originated. Mapping the reads can require substantial computational resources and often leads to complicated models that try to account for read bias and error during inference, further adding to the time spent on analysis. Finally, some reads, known as multireads^4,5, can map to multiple, sometimes many, different transcripts. This ambiguity complicates the estimation of transcript abundances. Given read alignments, some of the most accurate transcript quantification tools estimate relative abundance using expectation-maximization (EM) procedures^5,6,7, where reads are first assigned to transcripts, and these assignments are then used to estimate transcript abundances, and these steps are repeated until convergence. In practice, both steps can be time consuming. Even when exploiting the parallel nature of the problem, mapping the reads from a reasonably sized RNA-seq experiment can take hours.

Recent tools, such as eXpress⁷, aim to reduce the computational burden of isoform quantification by substantially altering the EM algorithm. Even for such advanced approaches, performing read alignment and processing the large number of alignments that result from ambiguously mapped reads remains a bottleneck and fundamentally limits the scalability of these approaches. Read-mapping is a complex problem, and the results of existing approaches depend on a host of parameters that affect how errors, gaps, and mismatches are tolerated. These parameters are not always easily interpretable, and they can affect both the resources required for alignment and the results of downstream analysis.

Sailfish, our software for isoform quantification from RNA-seq data, is based on the philosophy of lightweight algorithms, which make frugal use of data, respect constant factors and effectively use concurrent hardware by working with small units of data where possible. Sailfish avoids mapping reads entirely (Fig. 1), resulting in large savings in time and space, and substantially reducing parametric complexity. A key technical contribution behind our approach is the observation that transcript coverage can be accurately estimated using counts of k-mers occurring in reads instead of alignments of reads. This results in the ability to obtain accurate estimates more than an order of magnitude faster than existing approaches, often in minutes instead of hours. For example, for the data described in Figure 2, Sailfish is > 25 times faster than the next fastest method while providing estimates of equal accuracy. This accuracy is possible, despite independent counting and assignment of k-mers, because of an expectation maximization procedure that introduces a statistical coupling between k-mers.

Figure 1.

Overview of the Sailfish pipeline. Sailfish consists of an indexing phase (a) that is invoked via the command `sailfish index' and a quantification phase (b) invoked via the command `sailfish quant'. The Sailfish index has four components: (1) a perfect hash function mapping each k-mer in the transcript set to a unique integer between 0 and N – 1, where N is the number of unique k-mers in the set of transcripts; (2) an array recording the number of times each k-mer occurs in the reference set; (3) an index mapping each transcript to the multiset of k-mers that it contains; (4) an index mapping each k-mer to the set of transcripts in which it appears. The quantification phase consists of counting the indexed k-mers in the set of reads and then applying an expectation-maximization procedure to determine the maximum-likelihood estimates of relative transcript abundance.

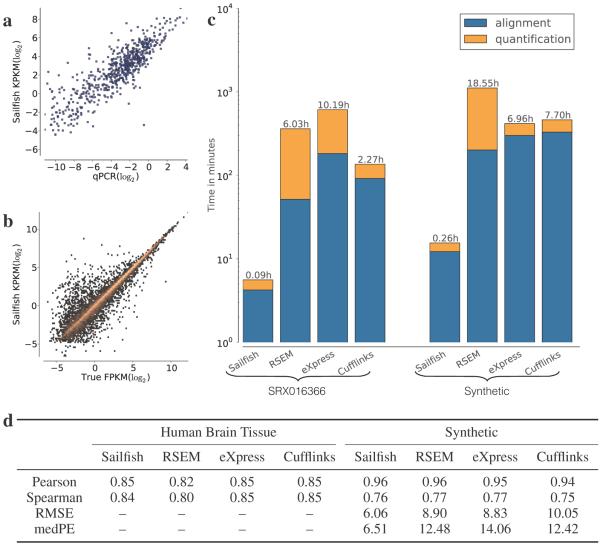
Figure 2.

Speed and accuracy of Sailfish. (a) The correlation between qPCR estimates of gene abundance (x-axis) and the estimates of Sailfish. The qPCR results are taken from the microarray quality control study (MAQC)¹⁵. The results shown here are for the human brain tissue and the RNA-seq based estimates were computed using the reads from SRA accession SRX016366 (81,250,481 35bp single-end reads). The set of transcripts used in this experiment were the curated RefSeq¹⁶ transcripts (accession prefix NM) from hg18 (31,148 transcripts). (b) The correlation between the ground truth FPKM in a simulated dataset (x-axis) and the abundance estimates of Sailfish. The quantification in this experiment was performed on a set of 96,520 transcript sequences taken from Ensembl¹⁷ GRCh37.73. (c) The total time taken by each method, Sailfish, RSEM, eXpress and Cufflinks, to estimate isoform abundance on each dataset. The total time taken by a method is the height of the corresponding bar, and the total is further broken down into the time taken to perform read-alignment (for Sailfish, we instead measured the time taken to count the k-mers in the read set) and the time taken to quantify abundance given the aligned reads (or k-mer counts). All tools were run in multi-threaded mode (where applicable) and were allowed to use up to 16 threads. (d) Accuracy of each of the methods on human brain tissue and a synthetic dataset. Accuracy is measured by the Pearson (log-transformed) and Spearman correlation coefficients between estimated abundance values and MAQC qPCR data (for human brain tissue) or ground truth (for simulated data). Root-mean-square error (RMSE) and median percentage error (medPE) are calculated as described in the Online Methods.

Although the use of k-mers for the purpose of transcript quantification has not been reported previously, recent work⁸ has shown that using k-mers directly for other RNA-seq-based tasks can be as or more effective than traditional approaches. By working with k-mers, we can replace computationally intensive read mapping with the much faster and simpler process of k-mer counting. We also avoid any dependence on read-mapping parameters. Yet, our approach is still able to handle sequencing errors because only the k-mers that overlap the erroneous bases will be discarded or mis-assigned, whereas the rest of the read can be processed as if it were error-free. One can view the k-mer counting mechanism as a proportional assignment of a read to a set of potential loci, with the strength of the assignment varying with the number of k-mers in the read that match the locus. Sailfish has only a single explicit parameter, the k-mer length. Longer k-mers may result in less ambiguity, which makes resolving their origin easier, but may be more affected by errors in the reads (Supplementary Fig. 1). Further, many of our data structures can be represented as arrays of atomic integers (Online Methods). This allows our software to be concurrent and lock-free where possible, leading to an approach that scales well with the number of available CPUs (Supplementary Fig. 2). Additional benefits of the Sailfish approach are discussed in Supplementary Note 1.

Sailfish works in two phases: indexing and quantification (Fig. 1). A Sailfish index is built from a particular set of reference transcripts (a FASTA sequence file) and a specific choice of k-mer length, k. The index consists of data structures that make counting k-mers in a set of reads and resolving their potential origin in the set of transcripts efficient (Online Methods). The most important data structure in the index is the minimal perfect hash function⁹ that maps each k-mer in the reference transcripts to an integer identifier such that no two k-mers share an identifier. Pairing the minimum perfect hash function with an atomically updateable array of k-mer counts allows k-mers to be counted even faster than with existing advanced lock-free hashes such as that used in Jellyfish¹⁰. The index also contains a pair of look-up tables that allow fast access to the k-mers appearing in a specific transcript as well as the transcripts in which a particular k-mer appears, both in amortized constant time. The index only needs to be rebuilt when the set of reference transcripts or the choice of k changes.

The quantification phase of Sailfish takes as input the above index and a set of RNA-seq reads and produces an estimate of the relative abundance of each transcript in the reference, measured in Reads Per Kilobase per Million mapped reads (RPKM), K-mers Per Kilobase per Million mapped k-mers (KPKM), and Transcripts Per Million (TPM); see Online Methods for the definitions of these measures. First, Sailfish counts the number of times each indexed k-mer occurs in the set of reads. Owing to the index, this process is efficient and scalable (Supplementary Fig. 2). Sailfish then applies an expectation-maximization (EM) procedure to determine maximum likelihood estimates for the relative abundance of each transcript. Conceptually, this procedure is similar to the EM algorithm used by RSEM⁶, except that k-mers rather than fragments are probabilistically assigned to transcripts, and a two-step variant of EM is used to speed up convergence. The estimation procedure first assigns k-mers proportionally to their occurrence in the transcripts. These initial allocations are then used to estimate the expected coverage for each transcript (Online Methods, Eqn. 3). In turn, these expected coverage values alter the assignment probabilities of k-mers to transcripts (Online Methods, Eqn. 1). Using these basic EM steps as a building block, we apply a globally convergent EM acceleration method, SQUAREM¹¹, that substantially increases the convergence rate of the estimation procedure by modifying the parameter update step based on the current solution path and the estimated distance from the fixed point (Online Methods, Alg. 2).

Algorithm 2.

A SQUAREM iteration. One iteration updates the relative abundance estimates according to an accelerated EM procedure whose update direction and magnitude are dynamically computed¹¹.

We reduce the number of variables that need to be fit by the EM procedure by collapsing k-mers into equivalence classes, where two k-mers are equivalent if they occur in the same set of transcript sequences with the same rate (Online Methods). The idea of data reduction by equivalence classes has been explored in the context of reads^12,13. Using k-mer equivalence classes has the added benefit that the classes can be computed based solely on the reference transcriptome without considering the read data. This reduction in variables substantially reduces the computational requirements of the EM procedure (Supplementary Note 1).

Once the EM procedure converges, the estimated abundances are corrected for systematic errors due to sequence composition bias and transcript length using a regression approach similar to a previous method¹⁴, though using random forest regression instead of a generalized additive model. This correction is applied after initial estimates have been produced rather than at a read mapping or fragment assignment stage, requiring fewer variables to be fit during bias correction.

We compared Sailfish to RSEM⁶, eXpress⁷ and Cufflinks⁵ using both real and synthetic data. Accuracy on real data was quantified by the agreement between RNA-seq–based expression estimates computed by each piece of software and qPCR measurements for the same sample (human brain tissue (HBR) in Fig. 2 and Supplementary Fig. 3, and universal human reference tissue (UHR) in Supplementary Fig. 4). The qPCR measurements for these samples were performed as part of the Microarray Quality Control Study¹⁵; RNA-seq experiments were later performed on the same samples²³. Abundance measurements for qPCR are given at the resolution of genes. To compare these measurements with the transcript-level estimates, we summed the estimates for all isoforms belonging to a gene. We compare predicted abundances using correlation coefficients and, on the synthetic data, root-mean-square error (RMSE) and median percentage error (medPE) (Supplementary Note 2). Taken together, these results show that the speed of Sailfish does not sacrifice accuracy (Fig. 2).

To show that Sailfish is accurate at the isoform level, we generated synthetic data using the Flux Simulator¹⁸, which allows versatile modeling of various RNA-seq protocols (Supplementary Note 3). Unlike synthetic data used in previous work^6,7, the procedure used by the Flux Simulator is not based on the generative model underlying our estimation procedure. Sailfish remains accurate at the isoform level (Fig. 2, Supplementary Figs. 5 and 6). We also find that Sailfish is robust to differences in the underlying set of reference transcripts used for quantification (Supplementary Fig. 7), and that it remains accurate when applied to a collection of highly similar genes (Supplementary Table 8).

Sailfish applies the idea of lightweight algorithms to the problem of isoform quantification from RNA-seq reads and in doing so achieves a breakthrough in terms of speed. By eliminating read mapping from the expression estimation pipeline, we improve the speed of the process and also simplify it considerably, eliminating the burden of choosing all but a single parameter from the user. Sailfish can be used in a de-novo setting for non-model organisms, along with other reference-free tools^19,20, where some or all of the transcripts are assembled directly from the RNA-seq reads. The memory usage of Sailfish is similar to that of other tools, using 2–6 Gb of RAM during isoform quantification for the experiments reported here. As the size and number of RNA-seq experiments grow, we expect Sailfish and its paradigm to remain efficient for isoform quantification because the memory footprint is bounded by the size and complexity of the target transcripts not the number of reads and the only computation that grows explicitly in the number of reads — k-mer counting — has been designed to effectively exploit many CPU cores.

Sailfish is free and open-source software and is available as Supplementary Data and at http://www.cs.cmu.edu/~ckingsf/software/sailfish.

Online Methods

Indexing

The first step in the Sailfish pipeline is building an index from the set of reference transcripts T. Given a k-mer length k, we compute an index I_k(T) containing four components. The first component is a minimum perfect hash function h on the set of k-mers kmers(T) contained in T. A minimum perfect hash function is a bijection between kmers(T) and the set of integers {0,1,…, |kmers(T)| - 1}. Sailfish uses the BDZ minimum perfect hash function⁹. The second component of the index is an array C containing a count C(s_i) for every s_i∈ kmers(T). Finally, the index contains a lookup table mapping each transcript to the multiset of k-mers that it contains, and a reverse lookup table mapping each k-mer to the set of transcripts in which it appears. The index is a product only of the reference transcripts and the choice of k, and thus needs only to be recomputed when either of these changes.

Quantification

The second step in the Sailfish pipeline is the quantification of relative transcript abundance; this requires the Sailfish index I_k(T) for the reference transcripts T as well as a set of RNA-seq reads $\mathfrak{R}$. First, we count the number of occurrences of each $s_i\in \mathbf{kmers}\left(T\right)\cap \mathbf{kmers}\left(\mathfrak{R}\right)$. Since we know exactly the set of k-mers that need to be counted and already have a perfect hash function h for this set, we can perform this counting in a particularly efficient manner, even faster than efficient hash-based approaches. For example, performing concurrent 20-mer lookups using 8 threads, Jellyfish¹⁰ requires an average of 0.35 μs/key while the minimal perfect hash requires an average of 0.1 μs/key. We maintain an array $C_{\mathfrak{R}}$ of the appropriate size |kmers(T)|, where $C_{\mathfrak{R}}\left(h\right(s_i\left)\right)$ contains the number of times we have thus far observed s_i in $\mathfrak{R}$.

In an unstranded protocol, sequencing reads, and hence the k-mers they contain, may originate from transcripts in either the forward or reverse direction. To account for both possibilities, we check both the forward and reverse-complement k-mers from each read and use a majority-rule heuristic to determine which of the k-mers to increment in the final array of counts $C_{\mathfrak{R}}$. If the number of k-mers appearing in h from the forward direction of the read is greater than the number of reverse-complement k-mers, then we only increment the counts for k-mers appearing in this read in the forward direction. Otherwise, only counts for k-mers appearing in the reverse-complement of this read are incremented in the array of counts. Ties are broken in favor of the forward directed reads. In a stranded RNA-seq protocol, the reads have a known orientation. Reads provided to Sailfish can be specified as originating from unstranded, forward strand or reverse strand reads, and the appropriate k-mers are counted in each case. By taking advantage of atomic integers and the compare-and-swap (CAS) operation provided by modern processors, which allows many hardware threads to efficiently update the value of a memory location without the need for explicit locking, we can stream through and update the counts in $C_{\mathfrak{R}}$ in parallel while sustaining very little resource contention.

We then apply an expectation-maximization algorithm to obtain estimates of the relative abundance of each transcript. We define a k-mer equivalence class as the set of all k-mers that appear in the same set of transcripts with the same frequency. In other words, let X(s) be a vector such that entry t of X(s) gives how many times k-mer s appears in transcript t∈T. Then the equivalence class of a k-mer s_i is given by [s_i] = {s_j ∈kmers(T) : X(s_j) = X(s_i)}. When performing the EM procedure, we will allocate counts to transcripts according to the set of equivalence classes rather than the full set of k-mers. We will let

$$\mathrm{L}\left(s_i\right)=\sum _{s_j\in \left[s_i\right]}{C}_{\mathfrak{R}}\left(h\left(s_j\right)\right)$$ (1)

denote the total count of k-mers in $\mathfrak{R}$ that originate from equivalence class [s_i]. We say that transcript t contains equivalence class [s] if [s] is a subset of the multiset of k-mers of t and denote this by [s] ⊆ t.

Estimating abundances via an EM algorithm

The EM algorithm (Algo. 1) alternates between estimating the fraction of counts of each observed k-mer that originates from each transcript (E-step) and estimating the relative abundances of all transcripts given this allocation (M-step). We initially allocate k-mers to transcripts proportional to their occurrences in the transcript (i.e. if a transcript is the only potential origin for a particular k-mer, then all observations of that k-mer are attributed to this transcript, whereas for a k-mer that appears once in each of n different transcripts and occurs m times in the set of reads, m/n observations are attributed to each potential transcript of origin).

Algorithm 1.

An EM iteration. One iteration of the expectation-maximization procedure that updates the estimated k-mer allocations α(·,·) and computes new estimates of relative transcript abundance μ′′ based on the current estimates of relative transcript abundance μ′.

The E-step of the EM algorithm computes the fraction of each k-mer equivalence class' total count that is allocated to each transcript. For equivalence class [s_j] and transcript t_i, this value is computed by

$$\alpha (j,i)=\frac{{\mu }_i^{\prime }\mathrm{L}\left(s_j\right)}{\sum _{t\supseteq \left[s_j\right]}{\mu }_t^{\prime }},$$ (2)

where μ′_i is the currently estimated relative abundance of transcript i. These allocations are then used in the M-step of the algorithm to compute the relative abundance of each transcript. The relative abundance of transcript i is estimated by

$${\mu }_i^{\prime }=\frac{{\mu }_i}{\sum _{t_j\in T}{\mu }_j},$$ (3)

where μ_i is

$${\mu }_i=\frac{\sum _{\left[s_j\right]\subseteq t_i}\alpha (j,i)}{l_i^{\prime }}.$$ (4)

The variable l_i′ denotes the adjusted length of transcript i and is simply l′_i = ℓ_i – k + 1 where ℓ_i is the length of transcript i in nucleotides.

However, rather than perform the standard EM update steps, we perform updates according to the SQUAREM procedure¹¹ described in Algo. 2, where μ′ = 〈μ′₀, …,μ′_|T|〉 is a vector of relative abundance maximum-likelihood estimates, and EM(·) is a standard iteration of the expectation-maximization procedure as outlined in Algo. 1. For a detailed explanation of the SQUAREM procedure and its proof of convergence, see¹¹. Intuitively, the SQUAREM procedure builds an approximation of the Jacobian of μ′ from 3 successive steps along the EM solution path, and uses the magnitude of the differences between these solutions to determine a step size ɣ by which to update the estimates according to the update rule (line 7). The procedure is then capable of making relatively large updates to the μ′ parameters, which substantially improves the speed of convergence. In Sailfish, the iterative SQUAREM procedure is repeated until a specified convergence criterion is met (by default, the procedure terminates when no transcript with a relative abundance greater than 10⁻⁷ has a relative change greater than half of a percent between consecutive iterations). Additionally, a user may specify either a fixed number of iterations to perform or a required minimum relative change, ε, in transcript abundance estimates between SQUAREM iterations; if no relative change in transcript abundance exceeds ε, then the procedure is considered to have converged and the estimation procedure terminates.

Bias Correction

The bias correction procedure implemented in Sailfish is based on the model introduced by Zheng et al.¹⁴ Briefly, it performs a regression analysis on a set of potential bias factors where the response variables are the estimated transcript abundances (KPKMs). Sailfish automatically considers transcript length, GC content and dinucleotide frequencies as potential bias factors, as this specific set of features were suggested by Zheng et al.¹⁴ For each transcript, the prediction of the regression model represents the contribution of the bias factors to this transcript's estimated abundance. Hence, these regression estimates (which may be positive or negative) are subtracted from the original estimates to obtain bias-corrected KPKMs. For further details on this bias correction procedure, see¹⁴. The original method used a generalized additive model for regression; Sailfish implements the approach using random forest regression to leverage high-performance implementations of this technique. The key idea here is to do the bias correction after abundance estimation rather than earlier in the pipeline. The bias correction of Sailfish can be disabled with the --no–bias–correction command line option. Finally, we note that it is possible to include other potential features, like normalized coverage plots that can encode positional bias, into the bias correction phase. However, in the current version of Sailfish, we have not implemented or tested bias correction for these features.

Computing KPKM, RPKM and TPM

Sailfish outputs K-mers Per Kilobase per Million mapped k-mers (KPKM), Reads Per Kilobase per Million mapped reads (RPKM) and Transcripts Per Million (TPM) as quantities predicting the relative abundance of different isoforms. The RPKM estimate is the most commonly used, and is ideally 10⁹ times the rate at which reads are observed at a given position, but the TPM estimate has also become somewhat common⁶. For Sailfish, the KPKM measure is more natural than RPKM, since the k-mer is the basic unit of transcript coverage; however, the two measures are proportional. Given the relative transcript abundances estimated by the EM procedure described above, the TPM for transcript i is given by

$${\text{TPM}}_i={10}^6{\mu }_i^{\prime }.$$ (5)

Let C_i be the number of k-mers mapped to transcript i. Then, the KPKM is given by

$${\text{KPKM}}_i=\frac{\frac{C_i}{li∕{10}^3}}{N∕{10}^6}=\frac{{10}^9\frac{C_i}{l_i}}{N}\approx \frac{{10}^9{\mu }_i}{N},$$ (6)

where N is the total count of mapped (i.e. hashable) k–mers and the final equality is approximate only because we replace l_i with l_i′. The KPKM is proportional to the RPKM, which can be estimated by replacing C_i with the estimated number of reads mapped to transcript i, and N with the estimated number of mapped reads; these can be calculated from the mapped k-mer counts and the average read length. The Fragments Per Kilobase per Million mapped fragments (FPKM) measure is also proportional to the K/RPKM, but is meant to denote that fragments rather than reads are mapped — for single end data, the reads and fragments coincide, for paired-end data, each concordant read pair is considered a single fragment.

Accuracy Metrics

For all experiments, the Pearson correlation metric was computed between estimates of abundance that were log transformed. As in previous work⁶, this was done to prevent the most abundant transcripts from dominating the correlations, but it necessitates discarding samples that have either a true or estimated abundance of 0. Spearman correlations were computed on estimates that were not log transformed. For the synthetic data, we additionally compute the Root Mean Squared Error (RMSE) and median Percentage Error. Given the vectors x = 〈x₁, x₂, …, x_n〉 of ground-truth abundances and y = 〈y₁, y₂, …, y_n〉 of estimated abundances, the RMSE is defined as

$$\text{RMSE}(\mathbf{x},\mathbf{y})=\sqrt{\frac{\sum _{i=1}^n{(x_i-y_i)}^2}{n}}.$$ (7)

The percentage error (PE) between a true abundance x_i and the corresponding estimate y_i is defined as

$$\mathrm{PE}(x_i,y_i)=100\times \frac{\mid x_i-y_i\mid }{x_i}.$$ (8)

Unlike the definition presented in other work¹², we do not define division by 0 when computing the percentage error. We then define the medPE as the median of the percentage error for all transcripts that have a true abundance greater than 0 (i.e. the median of the values PE(x_i, y_i) for all 1 ≤ i ≤ n where x_i ≠ 0).

When comparing against the qPCR-based abundances, we used the KPKM estimates produced by Sailfish and FPKM estimates produced by RSEM, Cufflinks and eXpress directly. The FluxSimulator records the number of reads that were actually generated by each transcript during the simulated sequencing experiment. These read counts and the transcript lengths were used to compute the ground truth FPKMs directly using Equation 6. However, we found that the FPKM estimates computed by RSEM, eXpress and Cufflinks appeared, for a number of transcripts, to be systematically inflated with respect to the ground truth FPKMs (this inflation persisted even when estimates were compared directly to ground truth relative transcript fractions). This appears to be due to the effective-length normalization procedures employed by these methods. Indeed, when Cufflinks was run with ––no–effective–length–correction, the RMSE and medPE decreased significantly, while the correlations with ground truth FPKMs increased marginally as well. Thus, for the synthetic tests, all Cufflinks results were computed with the ––no–effective–length–correction flag enabled. Though RSEM and eXpress do not expose such a flag directly, we computed FPKM estimates without effective-length corrections for these methods by using the estimated read counts (output directly by both methods) and the true transcript lengths using Equation 6. Using FPKMs computed in this manner reduced the RMSE from 2083.04 to 8.83 and medPE from 19.03 to 14.06 for eXpress and reduced the RMSE from 18.77 to 8.90 and the medPE from 17.90 to 12.48 for RSEM. Sailfish computes the estimated k-mer counts and KPKMs in a consistent manner directly from the underlying transcript abundances, so there is no difference between the KPKMs provided by Sailfish and those that would be computed using the estimated k-mer counts directly.

Simulated Data

The simulated Homo sapiens RNA-seq data was generated by the Flux Simulator¹⁸ v1.2.1 with the parameters listed in Supplementary Note 3. This resulted in a dataset of 75M 76bp × 2 paired-end reads. The reads produced by the Flux Simulator are grouped by their origin (i.e. reads originating from the same genomic locus appear together in the read file). However, this synthetic artifact violates the assumption made by eXpress that reads are produced in a random order. Thus, we post-process the reads generated by the Flux Simulator and shuffle them (while keeping mates appropriately paired) into a random order. The shuffled, mate-pair reads are then split into separate files. To ensure a sufficient mapping rate under the parameters used to produce alignments for eXpress and Cufflinks (–v 3 for Bowtie and –N 3 for TopHat²¹), the synthetic reads were quality trimmed using SICKLE (https://github.com/najoshi/sickle) with the default parameters. Untrimmed reads are more appropriate for RSEM's default parameters, and so RSEM was provided with untrimmed reads. While mapping rates increased significantly for the trimmed reads, the overall accuracy of the methods depended little on whether trimmed or untrimmed reads were used. RSEM, eXpress and Cufflinks were all given paired-end alignments since they make special use of this data. TopHat²¹ was provided with the option ––mate–inner–dist 200, to adjust the expected mate-pair inner-distance to the simulated average, and Bowtie was given the option –X 800 to ensure that paired-end reads originating from all valid fragments would be considered. The untrimmed synthetic read files were provided directly to Sailfish without any extra information since the same quantification procedure is used whether single or paired-end reads are provided.

Software Comparisons

For eXpress, all reads were aligned with Bowtie³ v0.12.9 using the parameters –a and –v 3, as suggested in the eXpress manuscript, which allows up to three mismatches per read and reports all alignments. All alignments for RSEM were computed with default parameters using the rsem–calculate–expression command, which used Bowtie v0.12.9 as the underlying aligner. To prepare alignments for Cufflinks, TopHat was run using Bowtie v0.12.9 (––bowtie1) and with options –N 3 and ––read–edit–dist 3 to allow up to three mismatches per read. For RSEM, eXpress and Cufflinks, the reported times are the sum of the times required for alignment and the times required for quantification. The time required for each method is further decomposed into the times for the alignment and quantification steps in Fig. 2.

Choice of Software Options and Effect on Runtime

Most expression estimation software, including RSEM, eXpress and Cufflinks, provides a myriad of program options to the user which allow for trade-offs between various desiderata. For example, the total time required by TopHat and Cufflinks is lower when Cufflinks is run without bias correction (e.g. 1.92h as opposed to 2.27h with bias correction on the SRX016366 data). However, without bias correction, Cufflinks yields slightly lower accuracy (Pearson σ = 0.82, Spearman ρ = 0.81) than the other methods, while still taking 16 times longer to run than Sailfish. Similarly, although aligned reads can be streamed directly into eXpress via Bowtie, we empirically observed lower overall runtimes when aligning reads and quantifying expressions separately (and in serial), so these times were reported. Finally, when we provided RSEM with the alignments used by eXpress (as was done in previous work⁷), we observed substantially increased runtime on the qPCR datasets (46.5 hours with the alignments generated from SRX016366 and 35.6 hours with the alignments generated from SRX016367), since RSEM does not appear to handle the large number of multiple alignments that can be generated by short reads when allowing many mismatches; instead, we report timings for RSEM when the alignment is performed using its own default parameters. In general, we attempted to run each piece of software with options that would be common in a standard usage scenario. However, despite the inherent difficulty of comparing a set of tools parameterized on an array of potential options, the core thesis that Sailfish can provide accurate expression estimates much faster than any existing tool remains true, as the fastest performing alternatives, when even when sacrificing accuracy for speed, were over an order of magnitude slower than Sailfish.

Sailfish version 0.6.3 was used for all experiments, and all analyses were performed with a k-mer size of k = 20 and using 16 concurrent threads (–p 16). In all experiments involving the real but not simulated data, Sailfish was run with the ––polya option, which discards k-mers consisting of k consecutive As or Ts, and bias correction was enabled. The KPKM values reported by Sailfish were used as transcript abundance estimates.

RSEM⁶ version 1.2.3 was run with the ––no–bam–output flag, and with –p 16. In the experiments involving the real data, rsem–prepare–reference was used to prepare a reference index that appended poly-A tails to all transcripts, and the quantification was performed with the ––estimate-rspd flag. For the synthetic data, RSEM was given the ––paired–end option to produce paired-end alignments from the reads. Apart from these options, RSEM was run with the default parameters for all experiments.

eXpress⁷ version 1.3.1 was used for all experiments. It was run with default parameters on the MACQ data, and without bias correction (––no–bias–correct) on the synthetic data. For the synthetic test, Bowtie was given the appropriate –1 and –2 options to compute paired-end alignments.

Cufflinks⁵ version 2.1.1 was used for experiments and was run with bias correction (–b) and multi-read recovery (–u) on the MACQ data, and with multi-read recovery (–u) and no effective-length correction (––no–effective–length–correction) on the synthetic data. For all tests, both Cufflinks and TopHat were run with with the –p 16 option to take advantage of up to 16 concurrent threads of execution.

All experiments were run on a computer with 8 AMD Opteron™ 6220 processors (4 cores each) and 256Gb of RAM. For all experiments, the wall time was measured using the built-in bash time command.

Implementation of Sailfish

Sailfish has two basic sub-commands, index and quant. The index command initially builds a hash of all k-mers in the set of reference transcripts using the Jellyfish¹⁰ software. This hash is then used to build the minimum perfect hash, count array, and look-up tables described above. The index command takes as input a k-mer size via the –k option and a set of reference transcripts in FASTA format via the –t parameter. It produces the Sailfish index described above, and it can optionally take advantage of multiple threads with the target number of threads being provided via a –p option.

The quant sub-command estimates the relative abundance of transcripts given a set of reads. The quant command takes as input a Sailfish index (computed via the index command described above and provided via the –i parameter). Additionally, it requires the set of reads, provided as a list of FASTA or FASTQ files. Finally, just as can the index command, the quant command can take advantage of multiple processors, the target number of which is provided via the –p option.

Sailfish is implemented in C++11 and takes advantage of several C++11 language and library features. In particular, Sailfish makes heavy use of built-in atomic data types. Parallelization across multiple threads in Sailfish is accomplished via a combination of the standard library's thread facilities and the Intel Threading Building Blocks (TBB) library²². Sailfish is available as an open-source program under the GPLv3 license, and has been developed and tested on Linux and Macintosh OS X.