Assessing multivariate gene-metabolome associations with rare variants using Bayesian reduced rank regression

Abstract

Motivation: A typical genome-wide association study searches for associations between single nucleotide polymorphisms (SNPs) and a univariate phenotype. However, there is a growing interest to investigate associations between genomics data and multivariate phenotypes, for example, in gene expression or metabolomics studies. A common approach is to perform a univariate test between each genotype–phenotype pair, and then to apply a stringent significance cutoff to account for the large number of tests performed. However, this approach has limited ability to uncover dependencies involving multiple variables. Another trend in the current genetics is the investigation of the impact of rare variants on the phenotype, where the standard methods often fail owing to lack of power when the minor allele is present in only a limited number of individuals.

Results: We propose a new statistical approach based on Bayesian reduced rank regression to assess the impact of multiple SNPs on a high-dimensional phenotype. Because of the method’s ability to combine information over multiple SNPs and phenotypes, it is particularly suitable for detecting associations involving rare variants. We demonstrate the potential of our method and compare it with alternatives using the Northern Finland Birth Cohort with 4702 individuals, for whom genome-wide SNP data along with lipoprotein profiles comprising 74 traits are available. We discovered two genes (XRCC4 and MTHFD2L) without previously reported associations, which replicated in a combined analysis of two additional cohorts: 2390 individuals from the Cardiovascular Risk in Young Finns study and 3659 individuals from the FINRISK study.

Availability and implementation: R-code freely available for download at http://users.ics.aalto.fi/pemartti/gene_metabolome/.

Contact: samuli.ripatti@helsinki.fi; samuel.kaski@aalto.fi

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Concentrations of human metabolites are associated with risk of many common diseases; for example, low- and high-density lipoprotein cholesterol (LDL and HDL) levels are associated with coronary artery disease. For this reason, human metabolism has been under intensive investigation and over the past few years several genome-wide association studies have successfully uncovered a part of its genetic basis (Kettunen et al., 2012; Sabatti et al., 2008; Suhre et al., 2011; Teslovich et al., 2010). For example, a large meta-analysis (Teslovich et al., 2010) identified 95 loci influencing the levels of total cholesterol, LDL, HDL and triglycerides. More recent studies used finer subclassifications of metabolites and discovered dozens of novel loci (Kettunen et al., 2012; Suhre et al., 2011). Despite these advances, the variance explained by all reported single nucleotide polymorphisms (SNPs) falls far below the suggested heritability of the common metabolites, as estimated either from twin studies (Kettunen et al., 2012) or from more distantly related individuals (Vattikuti et al., 2012). This motivates us to develop new approaches for association testing that could better use all information available to us.

The present-day cohort studies often come with a rich set of phenotypic features. Examples in addition to metabolomics (Kettunen et al., 2012; Soininen et al., 2009; Suhre et al., 2011) include studies of gene expression (Ackermann et al., 2013) and 3D-facial imaging (Hammond and Suttie, 2012). As a consequence, we need statistical methods that increase the power to uncover genotype–phenotype dependencies by combining information over several related phenotypes (Ferreira and Purcell, 2009; Inouye et al., 2012; O’Reilly et al., 2012). The underlying idea is that if a genetic variant affects a trait, then it is likely to affect other traits that are related to the first one and, by testing for association with the two traits jointly, power may be increased. This reasoning can be taken a step further by testing all traits in high-dimensional omics data simultaneously, for example, all metabolites in comprehensive metabolomic profiles. A comparison of different statistical methods available for joint testing of complete metabolomics profiles was recently conducted (Marttinen et al., 2013).

Besides testing several phenotypes simultaneously, the ability to detect certain kinds of associations may be boosted by combining statistical evidence over several SNPs. Usually this is done in a supervised manner, such that SNPs related by location or function, for example, are tested simultaneously. Combining information over multiple SNPs is particularly crucial with rare variants, i.e. SNPs where the minor allele is present in a small proportion of the population. Testing such SNPs individually is unlikely to yield significant findings because of limited power. Most approaches for handling rare variants are based on collapsing several rare SNPs into a single variable (Bansal et al., 2010). For example, one can simply collapse several rare variants into a single indicator, telling whether any of the rare variants is present in the individual (Morgenthaler and Thilly, 2007) or to count the number of rare variants present in the individual (Morris and Zeggini, 2010). The problem with the collapsing methods is the implicit assumption that the effects are in the same (or a predefined) direction. A more sophisticated variance component method avoiding this assumption is able to investigate the impact of several rare variants on a univariate trait (Wu et al., 2011).

Even if there exists a large number of methods for analyzing rare variants, none of those has been tailored for multivariate phenotypes. On the other hand, standard methods for multivariate phenotypes (Ferreira and Purcell, 2009) have not been thoroughly investigated in the context of rare variants, and we will see later in the text that severe overfitting may occur. In summary, methods for dealing with rare variants in the context of multivariate phenotypes are clearly lacking.

In this article, we derive a novel formulation of the Bayesian reduced rank regression model (Geweke, 1996) to detect multivariate associations between predefined groups of SNPs and a high-dimensional phenotype. In particular, our approach is suitable for analyzing both common and rare variants. Our formulation incorporates prior knowledge about effect sizes to increase the power to detect associations. Furthermore, it is capable of correcting for the number of SNPs considered, which is important when testing a large number of SNP groups of different sizes. We validate our method by assessing associations between SNPs in all human genes, one gene at a time, and metabolic profiles comprising fine-scale lipoprotein measurements for 4702 individuals from the Northern Finland Birth Cohort 1966 (Rantakallio, 1969; Sabatti et al., 2008). Among the top-scoring genes without known associations to the traits studied, two genes (XRCC4 and MTHFD2L) replicated in a combined analysis of 2390 individuals from the Cardiovascular Risk in Young Finns study (YFS; Raitakari et al., 2008) and 3659 individuals from the FINRISK study (Vartiainen et al., 2010). Additional analyses of the same data confirmed that alternative methods discovered only one of these associations and did not identify any further associations that were not known before.

2 METHODS

2.1 Model

To build our model, we assume that the phenotypes may be affected by three kinds of variables, (i) known factors, such as age, sex or population structure, (ii) unknown factors, such as experimental conditions and other batch effects, and (iii) SNPs under consideration, as schematically presented in Figure 1. In contrast to standard regression, where each SNP–phenotype pair has a parameter representing the effect of the SNP on the phenotype, here we assume that a combination of several SNPs is influencing several phenotypes through some unknown factors. This assumption is compactly expressed in terms of the reduced rank regression, where the SNPs are first projected onto a low-dimensional subspace, and the projections are then used as regressors when predicting the phenotypes. The reduced rank regression formulation immediately implies some structural assumptions deemed sensible in the current setting: first, if a SNP has an effect on a phenotype, then the SNP is likely to have an effect on other phenotypes; second, if a phenotype is affected by a SNP, then the phenotype is more likely to be affected by other related SNPs as well.

Fig. 1.

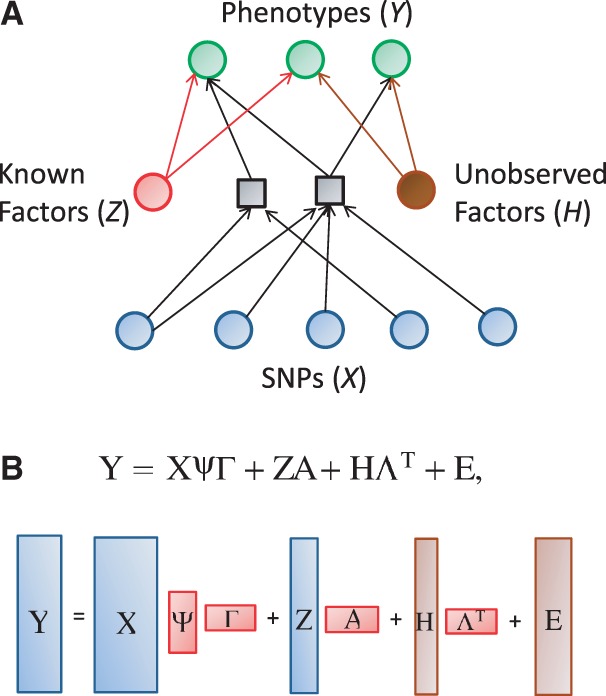
Graphical illustration of the model. (A) The variables and dependencies between them. The phenotypes Y are assumed to be affected by known factors, such as age or sex, unknown factors, such as batch effects caused by varying experimental conditions, and the SNPs. The influence of the SNPs is mediated by unknown combinations of the original SNPs, represented by black squares. (B) The same model using matrix notation. Matrices containing the observed variables, Y (the phenotypes), X (the SNPs) and Z (known factors), are blue. The regression coefficient matrices are red. Note that the coefficient matrix for the SNP effects is written as a product of two matrices, 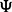and Γ, corresponding to a low-rank approximation to an unconstrained coefficient matrix. The brown matrices comprise unobserved variables, H (unknown factors) and E (noise terms)

Let N denote the number of individuals, S the number of SNPs, P the number of phenotypes and C the number of other covariates. Formally, we consider the Bayesian reduced rank regression model

(1)

where 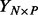contains the phenotypes, 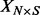contains the SNPs, 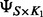and 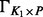represent a low-rank approximation for the regression coefficient matrix 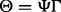, 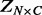represents other covariates with the corresponding coefficient matrix 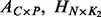contains hidden confounding factors with the corresponding coefficient matrix 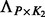and 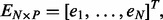with 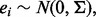where 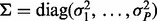. Note that by integrating over the hidden factors H, the model is equivalent to

(2)

where it is assumed that the factors have independent standard normal prior distributions. Therefore, we see that having the latent variable part 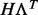in the model corresponds to assuming a low-rank approximation to the full covariance matrix, which is important when analyzing high-dimensional datasets.

For computational reasons, we restrict the rank of the regression model, K₁, to unity in our genome-wide analysis (w.l.o.g. in the detection task, see below) and show results with 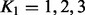for a few representative examples. However, here we present a general infinite-dimensional framework available in our implementation, which does not necessitate the selection of a fixed rank. In general, to use the Bayesian reduced rank regression model, the rank of the model, K₁, and the rank of the low-rank approximation for the covariance matrix, K₂, must be selected. A recent Bayesian infinite sparse factor analysis model (Bhattacharya and Dunson, 2011) circumvents the selection of a fixed rank for K₂ by assuming in principle an infinite number of columns in the Λ matrix; however, the columns shrink progressively such that only the first ranks are influential in practice. We assume this prior formulation for our noise model 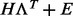. We exploit the idea further by allowing also the rank K₁ to be infinite in principle, and enforcing the low-rank nature by shrinking the columns of 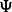and the rows of Γ increasingly as the column/row index grows. In practice, one needs to specify upper bounds for K₁ and K₂. We select the upper bound for K₂ using the adaptive procedure of Bhattacharya and Dunson (2011), and we have implemented an analogous method for learning the upper bound for K₁. In practice, we wanted to minimize the model complexity to maximize the power to detect associations and speed up the computations. Therefore, we decided to run the genome-wide analysis (see Section 3.1) using a fixed rank 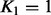. The model with 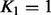is sufficient for our purposes of detecting whether a gene is unrelated to the phenotypes (in which case, rank zero would already be sufficient), although for prediction a higher rank might be more suitable. We experimented with a selected set of known genes with upper bounds 2 and 3 (see below) and noticed that the effect of increasing the upper bound from unity had only a small impact on the amount of variation that is explained by the model. From the biological perspective, this means that the influence of a gene on the phenotypes can mostly be described in terms of a single latent factor mediating the effect. A detailed model description is given in Supplementary Section 1.

The model is related to many published methods, and a thorough comparison can be found in Supplementary Section 2. Correction for unknown factors has recently been considered with the standard regression model, typically for just one SNP at a time (Fusi et al., 2012; Stegle et al., 2010). The difference to the original Bayesian reduced rank regression formulation (Geweke, 1996) is that our model uses low-rank approximation to the covariance matrix, making it more suitable for high-dimensional phenotypes, and informative prior distributions accommodating problem-specific knowledge. Furthermore, we use the model in a new way, as described in the subsequent sections. The Bayesian infinite sparse factor analysis model has been used for high-dimensional data (Bhattacharya and Dunson, 2011); here, we use it to represent the multivariate noise. Canonical correlation analysis (CCA) is a classical tool for modeling multivariate dependencies that have recently been introduced in the association study context (Ferreira and Purcell, 2009; Hotelling, 1936). Sparse CCA (Parkhomenko et al., 2009; Waaijenborg et al., 2008; Witten and Tibshirani, 2009) is more suitable to high-dimensional datasets; however, introducing prior distributions for CCA that would be intuitive in the association study context does not seem straightforward.

2.2 Proportion of total variation explained

A commonly used measure of the impact of multiple SNPs, say , on a univariate trait y is the proportion of variance explained (PVE) by the SNPs:

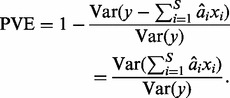Here, 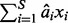is a linear prediction for the phenotype y, given the SNPs. Analogously, as a measure of the overall impact of multiple SNPs on a high-dimensional phenotype, we propose to use the proportion of total variation of the phenotypes explained (PTVE) by the model, namely

(3)

where 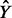is a prediction for a high-dimensional phenotype Y from the model and Tr denotes the trace, i.e. the sum of the diagonal elements of the matrix. In (3) and in general, the total variation of a multivariate random variable is defined as the trace of the covariance matrix, i.e.the sum of the variances of the individual variables. Therefore, PTVE measures the joint impact of the SNPs on several phenotypes and hence is expected to yield high scores to such dependencies in which many phenotypes are affected by the SNPs, even if none of the effects is large by itself.

In the Bayesian statistical framework, the inferences are based on posterior probability distributions of the quantities of interest (Gelman et al., 2004). With the Bayesian reduced rank regression model, samples from the posterior distribution of the PTVE can be obtained from

(4)

where 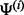and 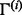are samples from the posterior distribution of the parameters 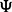and Γ. It is similarly straightforward to estimate the posterior distribution for the proportion of variation explained by the rare variants, by dividing the variation of the prediction into two components, one corresponding to the rare variants, the other to the common variants. The score obtained in this way is referred to as PTVE-rare in the sequel and its exact definition is given in Supplementary Section 3. In practice, we approximate the posterior distribution by using a mode-based point estimate for one of the parameters, Γ, and estimating the joint distribution of the other parameters using an Markov chain Monte Carlo (MCMC) algorithm, as described thoroughly in Supplementary Sections 4 and 5.

2.3 Informative prior

In the Bayesian analysis, external background knowledge may be incorporated in the statistical analysis through prior probability distributions. As our analysis is focused on estimating the posterior distribution of PTVE, a sensible prior is obtained by making the prior distribution of the PTVE represent our true beliefs about this quantity. The prior distribution of the PTVE appears not to be available in a closed form; however, in Supplementary Section 6, we derive results that show how the distribution of the mean of the PTVE, 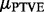, depends on model hyperparameters. Using these results, we set the prior distributions to satisfy the following properties:

(5)

and

(6)

Equation (5) means that the prior median of 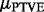is close to zero, as we expect most of the genes to be unrelated to the phenotypes. Equation (6) says that with a small probability, here equal to 0.01, the gene may explain >0.1% of the total variation, a value deemed resonable based on the background knowledge. The resulting prior distribution for the PTVE is obtained by integrating over the distribtion of 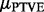, and we used Monte Carlo simulation to investigate the distribution. Figure 2 shows PTVE values sampled from the prior distribution. The following desirable characteristics can be seen: first, a peak close to zero, shrinking the coefficients when no effect is present; second, a long tail, corresponding to the genes with a non-negligible impact on the phenotypes, without imposing strong beliefs about the actual size of these non-zero effects.

Fig. 2.

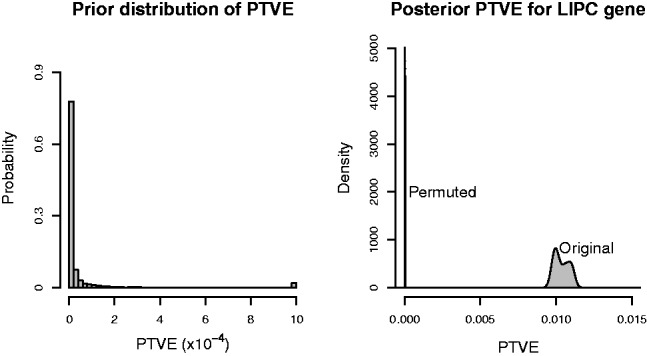
Prior and posterior distributions for the proportion of total variation explained (PTVE) by the model. The panel on the left shows the prior distribution imposed on the proportion of total variation of the phenotypes explained by the SNPs under consideration (here, the SNPs from the LIPC gene). The median of the prior distribution is located at ∼4e-6. The characteristic features of the prior distribution include the peak at values close to zero, effectively removing noise unless there is strong evidence about a possible association, and the long tail allowing a small percentage of genes to explain larger proportions of the phenotype variation. The rightmost bin on the x-axis contains the total probability of values exceeding the maximum value on the axis. The panel on the right shows the posterior distribution of the PTVE for the same SNPs. Two posterior densities are shown, one showing the distribution for the original data, the other showing the distribution for data in which the rows of the phenotype matrix have been permuted. Notice the differing scales on the x-axes of the two panels

Another important property that follows from using the informative prior is that the number of SNPs under consideration can be accounted for. Detailed examination of Corollary 1 in Supplementary Section 6 reveals that with fixed hyperparameters, the expected PTVE is proportional to 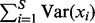, i.e. the total variation of the SNPs. Roughly, this means that if the number of SNPs doubles, the expected PTVE doubles as well, if the hyperparameters are kept fixed. Using the Corollaries 1 and 2 in Supplementary Section 6, it is straightforward to modify the hyperparameter distributions to assert the prior conditions (5) and (6), implying in our setting that all genes are expected to explain the same amount of the variation of the phenotypes, regardless of how many SNPs they contain.

2.4 Data

As a dataset for detecting associations, we consider a sample of 4702 individuals from the Northern Finland Birth Cohort 1966 (NFBC1966), a birth cohort study of children born in 1966 in the two northernmost provinces of Finland (Rantakallio, 1969). The blood samples for the DNA extraction and phenotype data were collected at a follow-up visit when the participants were 31 years of age. For replication, we consider two cohorts. The YFS is a population-based prospective cohort study (Raitakari et al., 2008) conducted in Finland, the purpose of which was to investigate the levels of cardiovascular risk factors in children and adolescents in different parts of the country. The FINRISK study comprises cross-sectional population surveys that have been carried out every 5 years since 1972, to assess the risk factors of chronic diseases, with emphasis on cardiovascular risk factors (Vartiainen et al., 2010). The individuals analyzed in this study belong to the sample from the year 1997. The blood samples for the two replication cohorts were collected when the participants were 30–45 and 25–71 years of age, respectively. The study protocols of all datasets have been approved by the local ethics committees.

The samples were genotyped with Illumina arrays (Illumina, Inc. San Diego, CA, USA) and imputed with IMPUTE 2 (Howie et al., 2009, 2011) using a 1000 Genomes Project reference panel (The 1000 Genomes Project Consortium, 2012). Of the resulting good-quality autosomal SNPs (info >0.4), we extracted SNPs in 24 025 human genes by adding 50 kb flanking regions on both sides of the endpoints of the genes given in NCBI gene database (genome assembly GRCh37.p10, NCBI annotation 104, November 2012). As a preprocessing step, we reduced the genotype space within each gene to the most promising 200 SNPs (at most) that had the highest canonical correlation test score (Ferreira and Purcell, 2009) with the metabolites; however, to prevent overfitting, the priors were specified as described above using the unpruned SNP set. In preliminary experiments, decreasing the number of SNPs in this way from 800 to 200 had no visible effect on the results. Finally, the SNPs were scaled to have unit variance.

Phenotype data came from the serum NMR metabolomics platform described earlier (Soininen et al., 2009). As a preprocessing step, the traits were quantile-normalized to have standard normal distribution. Individuals with 20% missing values were removed and the remaining missing values were imputed by sampling them from the multivariate normal distribution. In this work, we analyzed a subset of 74 lipoprotein subclass measures (Supplementary Table S3). The empirical correlation matrix of the traits is shown in Supplementary Figure S1. Linear regression was used to correct the phenotypes for age, sex and population structure using 10 principal components (Price et al., 2006).

3 RESULTS

3.1 Genome-wide analysis of NFBC1966 data

We computed the PTVE and PTVE-rare scores for each of the 24 025 human genes in the NFBC1966 data, one gene at a time, using the Bayesian reduced rank regression. Table 1(a) shows the top five genes with the highest PTVE scores, all of which are well-known lipid-associated loci. More generally, all 43 top-scoring genes were located within 1 Mb from previously reported genome-wide significant lipid associations (Kettunen et al., 2012; Teslovich et al., 2010; The Global Lipids Genetics Consortium, 2013), and detailed listing of the top genes is given in Supplementary Table S4. Furthermore, of the top 100 genes, which correspond to ∼0.2 false discovery rate (FDR) (see the next section), 73 genes had known associations. Together, these findings serve as a validation of the method and its implementation.

Table 1.

Summary of results from the genome-wide analysis of the real data

Chr	Locus	PTVE (SD)	Rare	P-value	Gene rank
					PTVE	Pairwise	S-CCA	CCA-single
(a)
15	LIPC	0.01 (5e-04)	0.015	5e-19	1	1	1	132
19	APOC1	0.0046 (3e-04)	0.017	1.4e-26	2	8	18	275
19	PVRL2	0.0045 (1e-04)	0.0015	7e-35	3	9	14	276
2	APOB	0.0044 (3e-04)	0.017	1.1e-17	4	45	41	3244
11	APOA5	0.0043 (2e-04)	0.021	5e-10	5	26	33	2433
(b)
16	SPIRE2a	0.0015 (9e-05)	0.89	0.00091b	5 (rare)	8344	5490	4973
5	XRCC4	0.0024 (2e-04)	0.55	0.0016	6 (rare)	2706	5163	2155
(c)
2	DTNBa	0.0015 (2e-04)	0.15	2.6e-04c	138	4715	338	7652
4	MTHFD2L	0.0015 (2e-04)	0.019	7e-06	163	102	1444	1552

Note: (a) Reference results for genes with five highest PTVE scores. (b) Replicated genes from the PTVE-rare score (of six genes tested for replication). (c) Replicated genes from the PTVE score (of 167 genes). Five other replicated genes (PPBP, CXCL5, CXCL2, PF4 and CXCL3) are not shown as they were located within 1 Mb from MTHFD2L, which had the strongest effect. Column PTVE (SD) shows the proportion of total variation explained and its SD, rare specifies the proportion of the variation explained by the gene attributed to the rare variants, P-value specifies the P-value pooled over YFS and FINRISK replication datasets (unless stated otherwise) and the last four columns specify the ranking of the gene among all genes with different methods. ^aDenotes genes that replicated significantly in only one of the two replication datasets. ^b/cReplication P-value in FINRISK/YFS.

To illustrate the effect of the model rank on the results, we carried out a detailed analysis for three known lipid genes: LIPC, APOB and PLTP, with rank 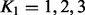. The genes were selected such that they were located in different chromosomes and had dissimilar association profiles [APOB associated most strongly to VLDL, IDL and LDL, PLTP to HDL and LIPC to VLDL, IDL and HDL (Tukiainen et al., 2012)]. In addition to considering the genes separately, we repeated a joint analysis for all three possible pairwise gene combinations. 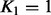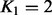The results are shown in Supplementary Figure S2 and are summarized as follows: (i) the rank of the model had a minor effect on the results for a single gene, (ii) increasing the rank from to increased the variance explained in all joint pairwise analyses, and the increase was significant in two of the three cases, (iii) a combination of two genes always had a larger effect than either gene individually; however, the sum of the individual effects was slightly larger than the effect of the combination. We attribute this difference mainly to the stronger shrinkage in the second than the first genotype component. (iv) The first component of a joint model was always strongly correlated with the single-gene model with the larger effect, the second component with the single-gene model with the smaller effect. This is as expected, as the prior distribution was designed to identify the strongest associations using the first genotype component.

To check whether novel associations could be detected by any method, we carried out a replication experiment with the YFS and FINRISK datasets for the most promising genes, after excluding genes located within 1 Mb from previously reported associations. We considered from each method all genes with FDR <0.4 as promising. For the PTVE-rare score, six genes were tested, none of which had previously reported associations to lipids. For the PTVE score, 305 genes had FDR <0.4; however, only 167 were not located close to known associations, and these 167 genes were selected for replication.

For the purposes of replication, the multivariate dependency between the multiple SNPs and phenotypes was reduced into a univariate test by using parameters estimated in the NFBC1966 data to construct univariate genotype and phenotype combinations (see Supplementary Section 7 for further details). Then, the standard linear model was used to test for positive correlation between the genotype and phenotype combinations. A pooled linear regression coefficient combining YFS and FINRISK datasets was formed using a fixed effect model over the two datasets (Thompson et al., 2011), and the P-value was obtained by relating the pooled estimate to its SD. A one-tailed test was used,as we were only interested in findings in which the effects were in the same direction in the replication datasets as in the NFBC1966 data. Bonferroni correction was used to account for the number of genes tested with each method, such that corrected P-value threshold corresponding to the nominal 0.05 level of significance was equal to 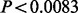for the six putative novel genes from PTVE-rare score and 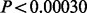for the 167 putative genes from PTVE score.

We considered a replication significant if the test was nominally significant (P < 0.05) in both replication datasets, and the P-value for the pooled estimate was significant after correcting for the multiple tests. Information about genes that replicated significantly is provided in Table 1(b) and (c) and in Figure 3. One gene with PTVE-rare and six genes with PTVE were detected, corresponding to two independent genes: XRCC4 and MTHFD2L. MTHFD2L is located within 1 Mb from two SNPs (rs2168889 and rs16850360) associated with ‘metabolic networks’ containing some lipoprotein traits from our data (Inouye et al., 2012). However, the top metabolite in the associations was Albumin, and when we repeated the multivariate test with the lipoprotein traits considered here, these associations were no longer genome-wide significant (P = 2.5e-4 and P = 6.4e-7). In addition, two genes, SPIRE2 and DTNB, replicated significantly (after the multiple testing correction) in one, but not in the other replication dataset. Table 1 also presents the rankings of these genes by alternative methods (see below). We see that XRCC4, SPIRE2 and DTNB were completely missed by the other methods. Supplementary Table S1 shows the SNPs contributing to the reported associations. We see that with XRCC4, SPIRE2 and DTNB, many SNPs, some of which are rare, are required to represent the overall association. This explains why these genes did not receive any signal from the standard testing with the pairwise linear model. Supplementary Figure S3 shows graphically how the phenotypes are affected by the significant genes and the known LIPC gene. We see that in neither of the new genes is the effect focused on any single trait, but rather a small effect is seen on many lipoprotein measures. This is not surprising, as the PTVE score is expected to give high scores to precisely this kind of association. Supplementary Figure S4 shows the estimated SNP coefficients for the genes and demonstrates the usefulness of analyzing all SNPs in a gene simultaneously to reduce noise resulting from the correlation between the SNPs. Further background information on these genes is presented in Supplementary Table S2; however, a more thorough biological interpretation of the genes remains for future work.

Fig. 3.

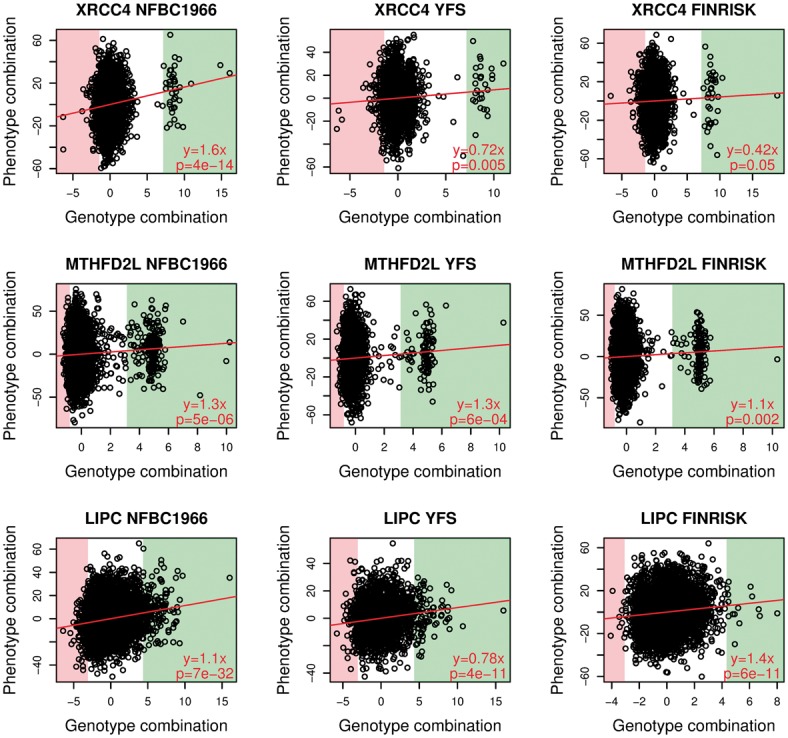
Results for genes with significant replication in both test sets: XRCC4 and MTHFD2L; for reference, the well-known LIPC lipid locus is also shown. Each panel shows the identified phenotype combination plotted against the genotype combination. The left column shows results in the NFBC1966 dataset, in which the associations were detected. The center and right columns show results with the YFS and FINRISK datasets, where coefficient matrices learned with the NFBC1966 data were used to form the variable combinations. The green and red background colorings mark the individuals with the highest/lowest genotype combination values, and the phenotype values in these extreme groups are investigated in more detail in Supplementary Figure S3

Finally, we repeated a similar analysis with three alternative methods: (i) exhaustive pairwise search with a linear model, where the minus logarithm of the smallest pairwise P-value over all SNPs in the gene and metabolites was taken as the test score for the gene, (ii) CCA, applied to a single SNP versus all metabolites at a time as by Ferreira and Purcell (2009) and Inouye et al. (2012) and (iii) sparse CCA, which was used to compute the canonical correlation between all SNPs in a gene and all phenotypes (Parkhomenko et al., 2009). The methods (ii) and (iii) were found to be the most powerful in a recent comparison of approaches for a multivariate metabolomics phenotype (Marttinen et al., 2013); however, here the SNPs were not pruned using the minor allele frequency before applying the methods as by Marttinen et al. (2013) because here the focus is in the rare variant setting. Similarly to PTVE and PTVE-rare methods, we tried to replicate the top-scoring genes up to FDR = 0.4. The last column in Table 2 shows the numbers of genes included in the replication with detailed listings given in Supplementary Tables S4–S8. The association in MTHFD2L was confirmed to be genome-wide significant using the standard pairwise linear regression (SNP rs185567543, trait S.LDL.P, P = 2.5e-15, where the P-value is pooled over all three datasets). All other replicated associations were located within 1 Mb of this or previously known associations, thus yielding no additional novel detections.

Table 2.

Power comparison of the different methods

Method	FDR = 0	FDR = 0.1	FDR = 0.2	FDR = 0.4	Novel
PTVE	36	55	103	305	167
PTVE-rare	3	3	3	6	6
Pairwise	103	176	243	651	300
CCA, single SNP	7	7	7	11	11
Sparse CCA	37	50	66	117	51

Note: The table shows the numbers of gene-metabolome associations that had false discovery rate below the specified threshold. The last column shows the number of putative novel associations within genes with FDR = 0.4 after removing the known associations as described in the main text.

3.2 Power comparison

To investigate the power of the introduced method and compare it with alternative methods, we estimated FDR corresponding to different thresholds d for declaring a gene as detected. FDR estimates were obtained by permuting the rows of the phenotype matrix and analyzing the permuted data in exactly the same way as the original data (Benjamini and Hochberg, 1995; Storey and Tibshirani, 2003; Xie et al., 2005). In detail, we computed the average number of genes in the permuted datasets with scores exceeding a given threshold d (false-positive rates, 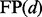), the number of genes in the original data with scores exceeding the same threshold d (total positive rates, 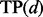) and considered the ratio of the two

Because of computational burden, only one permutation was used with the Bayesian reduced rank regression. With the other methods, three permutations were used. Therefore, the FDR estimates are approximate, which we consider to be sufficient for our purposes, especially because the most extreme quantiles are not considered.

The numbers of genes declared detected with different FDR thresholds are presented in Table 2, and the overall concordance of the scores from different methods is shown in Supplementary Figure S5. In summary, the results show that the method with which most associations were found was exhaustive pairwise search and the second-most powerful method was the Bayesian reduced rank regression with PTVE as the test score. These two methods also had the highest agreement in scoring genes. CCA applied to test for association between individual SNPs and the multivariate phenotype performed badly. These results are somewhat different from what has been reported before by us and others (Inouye et al., 2012; Marttinen et al., 2013). In particular, the CCA applied to individual SNPs performed much worse that the pairwise testing, although previously it has been reported to have clearly higher power. The explanation is that here we applied the methods to all SNPs, including the rare variants. Specifically, the single-SNP-CCA starts to overfit when applied to rare variants. For example, when we investigated the results more carefully, we discovered SNPs in which the minor allele was present in few individuals, and such individuals could be almost perfectly identified by a seemingly random combination of phenotypes, leading to a large spurious canonical correlation test score (or, equivalently, a highly significant P-value). Bayesian reduced rank regression and sparse CCA were less affected by the overfitting because they exploit ways to control the complexity of the model, the former using the informative priors, the latter using the cross-validation.

Combining information over several SNPs using CCA or related methods has recently been demonstrated to improve power to detect associations under certain conditions (Marttinen et al., 2013; Tang and Ferreira, 2012; Zhang et al., 2011). Here we see that the sparse CCA and also the Bayesian reduced rank regression, which use multi-SNP information, have lower power in the genome-wide analysis than the simple pairwise testing. The difference from the earlier experiments is that here the methods are applied to genotype data with a much higher SNP density, as obtained through careful imputation. The conclusion is that if the multi-SNP information has already been used within the imputation protocol, the power to detect associations cannot, in general, be expected to improve by using multi-SNP models.

For a more detailed comparison between the Bayesian reduced rank regression and the exhaustive pairwise testing, Supplementary Figure S6 shows a Q-Q plot of the scores (both PTVE and PTVE-rare) against the expected scores that have been obtained by permutation. The Supplementary Figure S6 also shows genes detectable by the simple exhaustive pairwise search. Both Q-Q plots, but PTVE in particular, indicate an excess of large test scores, reflecting the fact that at least some true associations are detected by the model. We further see that although with PTVE-rare score fewer genes can be detected than with PTVE, none of the top-scoring genes from PTVE-rare are flagged by the pairwise approach, making PTVE-rare an attractive score for mining associations that might be missed by the standard method.

4 DISCUSSION

We have presented a new statistical method for investigating associations in Genome-wide association study (GWAS) datasets with multivariate phenotypes. The method can combine information over multiple SNPs, making it particularly suitable for studying rare variants in the high-dimensional phenotype setting. For this setup, no methods known to the authors have been presented before. Our method is based on estimating the proportion of total variance of the phenotypes that is explained by the SNPs under consideration. For this purpose, we have derived a Bayesian formulation of the reduced rank regression model, which enables us to incorporate our knowledge of the expected effects sizes in the analysis.

We used the new method to analyze a real GWAS dataset with a multivariate lipoprotein phenotype. Two novel loci not previously associated with the phenotype were discovered and replicated in an analysis combining two additional datasets. Furthermore, two more loci were found that replicated significantly in one but not in the other test dataset. Possible reasons for the lack of success in replicating the findings in both the datasets include the following: (i) the associations were false positive in the first place, (ii) the associations involved rare variants that were not present in sufficient numbers to see the effects, (iii) the imputation accuracy of the rare variants was not sufficient in all datasets, (iv) the phenotype data, although preprocessed in exactly the same way with all the datasets, have not been fully equivalent. For example, the scaling of the phenotypes during preprocessing has been done using factors not exactly equal, and the parameters learned in one data may thus not represent the effects adequately in another data. Only further studies will help to distinguish between the alternative explanations.

For doing inference with the model, the current implementation uses MCMC sampling, the computation time of which is approximately half an hour per gene on a 2.3 GHz processor. Thus, analyzing all human genes requires a cluster computer to parallelize the computations over the genes. Analytical approximations, such as the variational or Laplace approximations, e.g. Bishop (2006), could be used to speed up the computations and, based on our experiments with the current method, are worth doing in the future. Alternative ways to use the model might also be considered. For example, focusing the analysis on variants with a predicted function could improve power to detect associations and lessen the computational burden. As another example, we have used 0.01 as the threshold for defining the rare variants when computing their impact on the phenotypes. Results based on different thresholds could readily be extracted from the output of a single MCMC run and are likely to highlight different sets of genes.

Funding: A complete list of funding is given in the Supplementary Material.

Conflict of Interest: none declared.