TroX: a new method to learn about the genesis of aneuploidy from trisomic products of conception

Abstract

Motivation: An estimated 10–30% of clinically recognized conceptions are aneuploid, leading to spontaneous miscarriages, in vitro fertilization failures and, when viable, severe developmental disabilities. With the ongoing reduction in the cost of genotyping and DNA sequencing, the use of high-density single nucleotide polymorphism (SNP) markers for clinical diagnosis of aneuploidy and biomedical research into its causes is becoming common practice. A reliable, flexible and computationally feasible method for inferring the sources of aneuploidy is thus crucial.

Results: We propose a new method, TroX, for analyzing human trisomy data using high density SNP markers from a trisomic individual or product of conception and one parent. Using a hidden Markov model, we infer the stage of the meiotic error (I or II) and the individual in which non-disjunction event occurred, as well as the crossover locations on the trisomic chromosome. A novel and important feature of the method is its reliance on data from the proband and only one parent, reducing the experimental cost by a third and enabling a larger set of data to be used. We evaluate our method by applying it to simulated trio data as well as to genotype data for 282 trios that include a child trisomic for chromosome 21. The analyses show the method to be highly reliable even when data from only one parent are available. With the increasing availability of DNA samples from mother and fetus, application of approaches such as ours should yield unprecedented insights into the genetic risk factors for aneuploidy.

Availability and implementation: An R package implementing TroX is available for download at http://przeworski.uchicago.edu/

Contact: kermany@uchicago.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A fundamental step in meiosis is the segregation of chromosomes to create haploid egg and sperm cells. In humans, this process is highly error-prone: 10–30% of clinically recognized pregnancies are thought to be aneuploid, i.e. to carry an abnormal number of chromosomes (Hassold et al., 1996; Jacobs et al., 1992). The vast majority of aneuploid pregnancies result in spontaneous miscarriages or lead to severe developmental disabilities in the child when not embryonic lethal (Hassold and Hunt, 2001). Conversely, aneuploidy underlies more than a third of spontaneous miscarriages (Nagaoka et al., 2012).

Aneuploidy results from the improper segregation of chromosomes to daughter cells (termed non-disjunction) and can in principle occur in either male or female and in mitosis or meiosis. In practice, in humans, the vast majority of non-disjunction events (∼90–95%) are of maternal origin (Hassold and Hunt, 2001). Meiotic non-disjunction can further originate in meiosis I (MI), if homologous chromosomes fail to disjoin, or in meiosis II (MII), if sister chromatids do not segregate properly (Fig. 1). Errors in MI are thought to be more common, though the proportions vary across chromosomes [e.g. MII is more common for chromosome 18 (Hassold et al., 1993)].

Fig. 1.

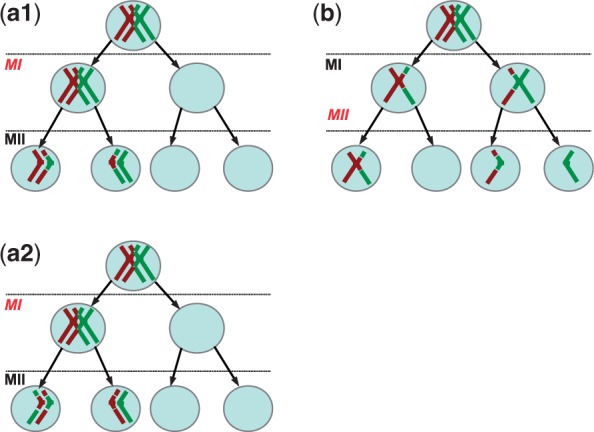
Stages at which non-disjunction can occur. In this cartoon, we consider the tetrad for one chromosome and do not represent the other 22. (a1) MI non-disjunction results in two daughter cells with two chromatids and two with zero chromatids. Alleles near the centromere are not identical by descent (NIBD), so may be heterozygous. In this case, a recombinant chromatid and a non-recombinant chromatid are transmitted, so the crossovers can be detected from proband and parental data. (a2) In contrast, arecombinant crossover cannot be detected if both recombinant (or non-recombinant) chromatids are transmitted. (b) MII non-disjunction results in one daughter cell with two chromatids, one with zero chromatid and two normal cells with one chromatid each. Alleles near the centromere are identical by descent (IBD), so are homozygous. The pattern near the centromere is therefore informative about the stage of meiosis at which non-disjunction events occurred

Among known risk factors for aneuploidy are maternal age, with rates of trisomies increasing exponentially after the age of approximately 35 (Hassold and Hunt, 2001; Penrose, 1933), and errors in recombination. In humans, as in most sexually reproducing organisms, there is an obligate crossover per chromosome to ensure proper disjunction (see Fledel-Alon et al., 2009, and references therein). If no crossover occurs (and in the absence of a backup mechanism for achiasmatic segregation), chromatids are distributed randomly into daughter cells and thus are expected to result in aneuploidy in half the cases. Accordingly, the genetic map of chromosomes that experience non-disjunction in MI is shorter than seen in proper disjunctions (Sherman et al., 1991). In addition to too few crossovers, an abnormal placement of crossovers (e.g. events unusually close to the centromere) has been associated with chromosome 16 and 21 trisomies (Lamb et al., 1996; Sherman et al., 1994; also see Hassold and Hunt, 2001 and references therein). Beyond these features, little is known about the risk factors for non-disjunction. In particular, it remains unclear how much the locations of crossovers overlap between transmissions with proper disjunction and transmissions that lead to aneuploidy.

The analysis of genetic data from trisomic children or trisomic products of conceptions (POC; henceforth referred to as ‘probands’) and their parents allows one to identify the stage (MI or MII) in which the non-disjunction occurred and the origin (maternal or paternal). In a subset of cases, it also allows one to infer the locations of a subset of crossover events that occurred on the tetrad of the chromosome that did not disjoin properly (Jacobs et al., 1988). Thus, as genotyping and sequencing methods become much more accessible and as non-invasive methods to sample fetal DNA from maternal blood become widespread (Fan et al., 2008, 2012; Palomaki et al., 2012), there is an unprecedented opportunity to gain a better understanding of genetic risk factors for non-disjunction.

There exist a number of methods to infer the stage of meiosis at which non-disjunction occurred and to identify crossovers. All are based on the same basic idea: to look for chromosome segments in which the trisomic chromosome has retained the paternal or maternal heterozygosity (Jacobs et al., 1988). Whether this segment surrounds the centromere is indicative of the stage of meiosis in which non-disjunction occurred, and the switches between retained heterozygosity and homozygosity point to the location of crossovers (Fig. 2). Existing methods suffer from important limitations, however. Some rely on few highly polymorphic markers such as microsatellites (Feingold et al., 2000; Li et al., 2001) and are not computationally feasible for high-density markers, so do not allow recombination events to be precisely localized. Others can handle single nucleotide polymorphism (SNP) genotype data, but require data from both parents (Gabriel et al., 2011), as well as complete triploid genotype calls for the proband (requiring that, for example, ATT be distinguished from AAT instead of simply read as heterozygous; Oliver et al., 2012). None of the existing methods have an explicit error model; instead, they rely on post hoc filtering to identify crossovers, potentially leading to errors and inconsistencies among studies. Finally, and perhaps most importantly from a practical standpoint, none of the computationally feasible methods can accommodate missing data from the male, when collecting samples from both male and female is often prohibitive.

Fig. 2.

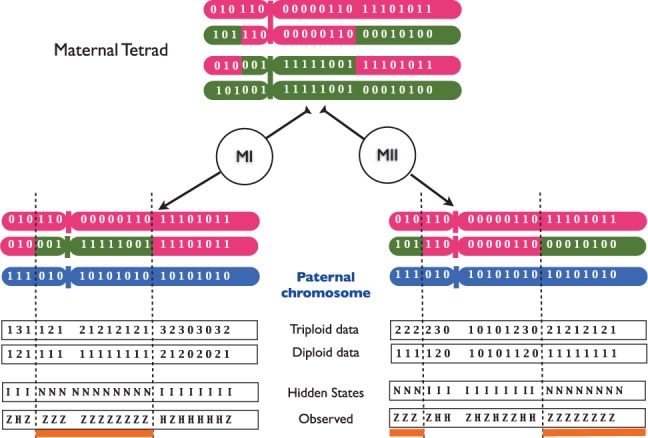
Representation of the genetic pattern indicative of MI and MII non-disjunction errors and where crossovers took place. Shown on the figure are the positions that are heterozygous in the mother, here the origin of the non-disjunction event. The difference between non-disjunction occurring at MI (left panel) and at MII (right panel) lies in the location of the tracts that are NIBD, which are associated with a retention of heterozygosity (underlined in orange). Complete genotypes (triploid) represent the number of alternative alleles to the reference genome carried by the proband, while incomplete genotypes (diploid) correspond to homozygous (0 or 2) or heterozygous (1) sites in the proband. In the HMM, the hidden states are the states of the tracts: IBD (I) or not (N), and the observed values are the genotypes of the proband: heterozygous (Z) or homozygous (H). Transitions between states depend on the recombination rate r

Motivated by these considerations, we developed a new method, TroX (trisomy crossover), and made the software available online as an R package. It uses a hidden Markov model (HMM) to identify the parent and stage of meiosis in which non-disjunction occurred and calls crossover locations on the chromosome involved in non-disjunction from dense SNP data. The method can be used on trio data or data from only the proband and one parent, and takes into account genotyping errors and missing data. Moreover, our method can be applied to diploid genotype data from the trisomic chromosome (i.e. where ATT and AAT are both simply considered heterozygous). We assessed the performance of our method using simulated trisomic sequences based on individuals from the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2012) and, to evaluate how well the method performed when the father is masked, we applied the method to 282 trios with trisomy 21 previously analyzed by Oliver et al. (2012).

2 METHODS

As a consequence of a MI non-disjunction event, alleles at the centromeres of the disomic gamete are descended from distinct homologous chromosomes, i.e. they are not identical by descent (NIBD). In contrast, in the case of a MII non-disjunction event, alleles at the centromere come from the same sister chromatids and therefore are identical by descent (IBD). In the absence of recombination, all alleles are NIBD on MI trisomic chromosomes, whereas all alleles are IBD in the case of MII trisomic chromosomes. As shown in Figure 1, a crossover on the premeiotic tetrad may cause a switch from IBD to NIBD in the disomic gamete transmitted to the proband, or vice versa. Whether it does depends on which chromatids are involved in the crossovers and which two are transmitted to the proband (Fig. 1a2 and Supplementary Material).

As a result of NIBD, heterozygosity of the non-disjoining parent (NDJP) is retained in the proband. Therefore, heterozygosity levels can be used to infer whether the region is IBD or NIBD and estimate the location of a subset of crossovers that occurred on the tetrad. In turn, the meiotic stage of non-disjunction can be inferred from the IBD state at the centromere (Chakravarti and Slaugenhaupt, 1987). Although in principle the stage can always be determined, regardless of whether all crossovers are observable, in practice, the first marker will not be at the centromere but at some genetic distance away, and if there is a crossover between them, the stage may be misclassified. Thus, in practice, the misclassification rate will be approximately equal to the distance between the first marker and the centromere (lower for metacentric chromosomes, in which both arms are informative).

Motivated by these considerations, we used an HMM in which the hidden states are the IBD status of a given locus in the proband and the transition between states depends on the recombination rate. The method assumes that the trisomic chromosome has been independently identified. We note that if this were not the case, the trisomic chromosome could be identified by an increase in the average sequencing read depth (see Fan et al., 2008, and references therein) or from the raw genotype intensities (e.g. Gabriel et al., 2011). The emission probabilities are calculated based on the error model and Mendelian inheritance laws. We incorporated the missing data for a given position (or the whole sequence in the male) and possible diploid genotype of the proband as part of the error model. Considering two alternative models (i.e. the mother versus the father as the NDJP), we used the Forward algorithm to calculate the probability of the proband’s genotype data, D, given each model. We used these probabilities to calculate the Bayes factor, 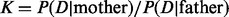, which is then used to calculate the posterior odds ratio (OR) 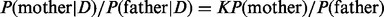. A posterior OR >1 indicates that the mother is more likely to be the NDJP. The prior probabilities [i.e. 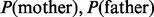] can be specified based on previous studies of trisomies for the chromosome of interest. Having determined the individual in which non-disjunction occurred, we then used the Viterbi algorithm to find the most likely path and estimate the locations of crossovers. Our method is similar to the one developed by Feingold et al. (2000), but applicable to a much larger number of markers; it also differs in considering an explicit error model and in its treatment of missing parental data.

We note that it is not feasible to identify all crossovers that have occurred on the tetrad, as a subset will not generate a discernible change from IBD to NIBD (or vice versa) in the proband. By direct consideration of all possible crossovers between chromatids and possible segregation patterns in MI and MII, we constructed a matrix showing the proportions of observable crossovers (c′) for a given number of crossovers on the tetrad (c), for c = 1, 2, 3 and 4. These proportions are given by the following two matrices, in which rows correspond to c and columns correspond to :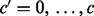

(1)

for MI, and

(2)

for MII errors. For example, if there are four crossovers on the tetrad and an error occurs during MI, in only 6% of cases will all these crossovers be detected; were the error to occur in MII instead, all four crossovers can be detected in 25% of cases.

2.1 The error model

In this section, we present an error model for genotyping data. An alternative error model, more appropriate for next-generation sequencing data, can be found in the Supplementary Material. Both models incorporate genotyping errors in parental data as well as in the trisomic POC. For a given locus, we represent individual genotypes by the number of alternative alleles to the reference genome. Taking into account the possibility of genotyping errors, we distinguish between the observed and the true genotypes of the parents and the proband. Without loss of generality, suppose that the mother is the NDJP. Let i, 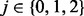and 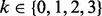denote the actual genotypes of the mother (NDJP), the father and the proband, respectively. Similarly, let 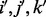denote the corresponding observed genotypes. When triploid data from the proband are available, we have 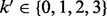, whereas for the diploid case, 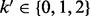. We extend our definition of observed genotypes for the parent to include the missing data, i.e. 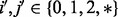, where ‘*’ represents the missing genotype at a given position.

We consider symmetric genotyping error [e.g. 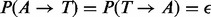] and make the realistic assumption that the probability of an error is given by 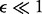. Let 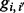be the conditional probability of observing genotype 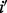in the father or the mother given that the actual value is i, i.e. 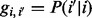. We represent the probability of missing data by c. As shown in the next section, the choice of the value of c does not affect our calculations for the emission probabilities.

The error model for the diploid sequences of the parents is given by a 3 × 4 matrix with the convention that the fourth column corresponds to missing genotypes. Ignoring terms of 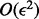, we have

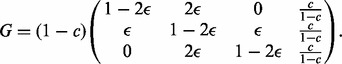(3)

Depending on whether we have diploid or triploid data from the proband, we need to consider either a one-layer or a two-layer error model. Let E denote the 4 × 4 error matrix for the trisomic sequence. We assume that the sites with missing data in the proband have been filtered out. Under similar assumptions as for constructing G, we obtain

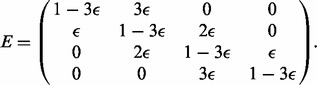(4)

We assume that when only diploid data for the proband are available, genotype values 1, 2 (e.g. 110,001) are more likely to be represented as heterozygous (01), while 0, 3 are always represented as homozygous for the reference and the alternative alleles, respectively. Therefore, for the case of diploid data, we consider 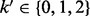and the error matrix is given by a 4 × 3 matrix H

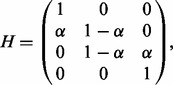(5)

with 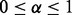. An entry 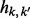of this matrix denotes the conditional probability of observing the diploid genotype 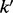given complete triploid genotype k. As an example, consider 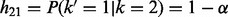. This means that 110 (or 101,011, etc.) is mapped to 11 with probability α, while it is mapped to 10 with probability 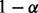. Thus, α can be considered as an error in deciding whether a trisomic locus is heterozygous or homozygous. Finally, the error matrix for the case of diploid data can be computed by multiplying E and H, which, ignoring terms of order 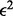, is

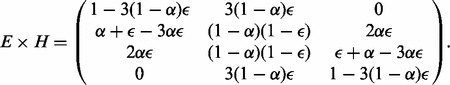(6)

This matrix defines the mapping from triploid data to diploid data. We observe that, for 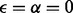, the second and the third row of the matrix (corresponding to mapping 100 and 110 to 01) become identical, reflecting the lack of discriminatory ability between these two cases.

3 IMPLEMENTATION

We approximate the transition process between IBD and NIBD in the two chromosomes transmitted to the proband by the NDJP by a non-homogeneous Markov chain. Let X_n denote the underlying hidden state at position n, with possible values IBD (I) and NIBD (N).

The transition probability matrix can be written as

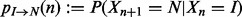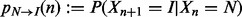where and , given by

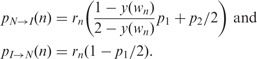In these equations, r_n denotes the probability of a crossover between marker n and n + 1 on the tetrad, w_n is the map distance between the 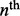marker and the centromere, p₁ and p₂ are the prior probabilities of MI and MII errors, respectively, and y(w_n) is the linkage parameter determining the probability that the two copies of the nth marker on sister chromatids are NIBD (see Chakravarti and Slaugenhaupt (1987) and the Supplementary Material). The value of y, assuming no interference, is related to the map distance by

(Barratt et al., 1954; Chakravarti and Slaugenhaupt, 1987; Mather, 1938), where w is the map distance in Morgans.

We assume that the loci under study are located on the long arm of the chromosome and the first position in the observed trisomic sequence corresponds to the most centromeric locus. The probability of the initial state of the chain is given by

(7)

in which p₁ (corresponding to the NIBD state) and p₂ (IBD state) are based on our prior knowledge regarding the probabilities of MI or MII errors. For metacentric chromosomes, the method can be applied to each arm of the chromosome independently.

We note that, in principle, a different meiotic stage could be inferred from each arm of the chromosome. This could reflect error in the method, or the rare case where there is a crossover between the centromere and the first marker on one of the arms.

To derive the emission probabilities, we condition on the maternal and paternal genotype sequence (including missing genotypes). Let M, F and O represent the observed sequences of the mother, father and the (trisomic) proband, respectively. For a given step n, let 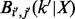to denote the probability of observing 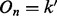given the hidden state X, with observed genotypic values 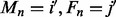for the mother (here, the NDJP) and the father, respectively, i.e.

for some 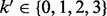and 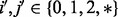. Then we have

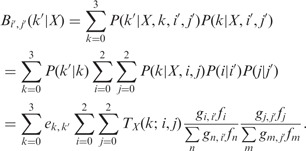(8)

The values of 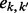are given by E in Equation (4) (in the case of triploid data) and E × H in Equation (6) (for the case of diploid data), and 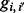values are given by G in Equation (3). f_i denotes the frequency of genotype i in the parent’s population of origin. If individuals are from two different populations, we use different sets of values for the vector f = (f₀, f₁, f₂) for each parent. Assuming Hardy–Weinberg equilibrium within a population, genotype frequencies can be calculated based on allele frequencies. T_X(k; i, j) denotes the probability of the proband’s genotypic value being k, conditional on the mother (assumed to be the NDJP) having genotype i, the father j and the hidden state X at a given locus. Values of T_X(k; i, j) can be calculated based on Mendelian inheritance laws and are given in Table 1.

Table 1.

Probabilities of the proband having genotype k (defined as the number of non-reference alleles), given the parental genotype (left column) and depending on whether the locus under consideration is in an IBD or NIBD region

genotype pairs	IBD				NIBD
	k				k
(i, j)	0	1	2	3	0	1	2	3
(0, 0)	1	0	0	0	1	0	0	0
(0, 1)	1/2	1/2	0	0	1/2	1/2	0	0
(0, 2)	0	1	0	0	0	1	0	0
(1, 0)	1/2	0	1/2	0	0	1	0	0
(1, 1)	1/4	1/4	1/4	1/4	0	1/2	1/2	0
(1, 2)	0	1/2	0	1/2	0	0	1	0
(2, 0)	0	0	1	0	0	0	1	0
(2, 1)	0	0	1/2	1/2	0	0	1/2	1/2
(2, 2)	0	0	0	1	0	0	0	1

(i, j) represents ordered genotype pairs for NDJP and the other parent, respectively.

As an example, suppose that we have triploid genotype data from the proband and 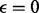. Thus, 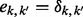, where 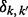is the Kronecker Delta. Assuming no missing genotype values, we have 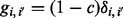. It is then easy to show that 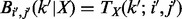. Assuming that the paternal genotype value at a given locus is missing (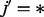), we obtain 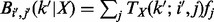. For the case of diploid genotype, with no missing data and 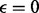, we have

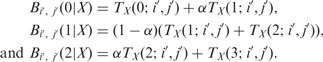(9)

3.1 Simulations

We used data from the 1000 Genomes project (The 1000 Genomes Project Consortium, 2012) to simulate trisomy 21 samples, assuming that both parents belong to the same population. To roughly mimic a genotyping array, we selected at random ∼2500 SNPs with minor allele frequency >1% from the long arm of chromosome 21. An exact simulation of the process would consist in a simulation of all four chromatids, where a pair is chosen at random for each crossover, then non-disjunction occurs in MI or MII. Only a subset of such crossovers will be observable in the chromatids transmitted to the proband, however, and so most of the simulations would be uninformative about the performance of the method in that regard. We instead simulated observable crossovers by modeling crossovers on the disomic gamete. We verified that taking this approach instead makes no difference by comparing it with the full treatment (data not shown).

Specifically, for a given number of observable crossovers 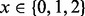for each possible NDJP (mother or father) and for each possible meiotic stage of non-disjunction (MI or MII), we simulated 1000 trisomic samples, choosing the parents at random from a pool of 200 individuals, for two different sets of populations. The first set consists of individuals of African ancestry (15 ASW, 97 LWK and 88 YRI), which we denote AFR, and the second set consists of individuals of European ancestry (4 CEU, 93 FIN, 89 GBR and 14 IBS), which we refer to as EUR. In these simulations, we ignored crossover interference, and we placed 0, 1 or 2 crossovers at random between some pair of markers to simulate the NDJP’s disomic gamete [we did not consider more events because the occurrence of three or more crossovers is rare even in proper disjunctions, e.g. Fledel-Alon et al. (2009)]. Subsequently, we generated errors based on the error models presented in the previous section, assuming 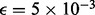(Oliphant et al., 2002) and 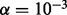. We ran the program for four possible scenarios, i.e. with triploid or diploid genotypes and with or without the paternal genotypes. We also applied the method on simulated trisomy 16 trios and obtained the same qualitative results (data not shown).

4 RESULTS

We applied TroX to simulated trio data where either the mother or the father is the source of non-disjunction and MI and MII are equally likely. We assumed that the recombination rate between adjacent markers is constant and given by 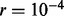(i.e. roughly the sex-averaged recombination rate per base pair, given that the average distance between each pair is 10 kb). We also tried using the sex-averaged HapMap genetic map instead, and results were similar (not shown). We note that neither choice is expected to represent the map in trisomies, which remains unknown, but the results suggest that with dense markers, it should not matter much.

We calculated the OR for the mother versus the father as the source of non-disjunction, using prior odds of 50/50. As shown in Figure 3 (for triploid data) and Supplementary Figure S2 (for diploid data), the distributions of the log ORs are non-overlapping, so maternal and paternal origin can be distinguished in all cases, even when the paternal data are missing, enabling us to detect the NDJP with high reliability. The one exception is when the non-disjunction event arose in MII, 0 crossovers occurred and we have only diploid genotype data (see Supplementary Figure S3). The reason can be understood as follows: in this scenario, the sister chromatids are IBD throughout. Consider an informative locus with maternal genotype 10, paternal genotype 11 and proband genotype 001. If we have triploid data and no genotyping errors (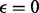), we would observe the proband as 001 and conclude that the mother is the NDJP. However, if we only have diploid data from the proband and there is no bias in mapping triploid to diploid data (α = 0), we observe the proband as 01, which contains no information regarding the parent of origin [i.e. the emission probabilities under both models are equal in this case; see Equation (10) and Table 1]. Counter-intuitively, errors in mapping triploid to diploid data (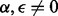) retain some information regarding the parental origin (Supplementary Figure S2). This is because, with mapping errors, the symmetry in emission probabilities breaks down [see Equation (9) and Table 1].

Fig. 3.

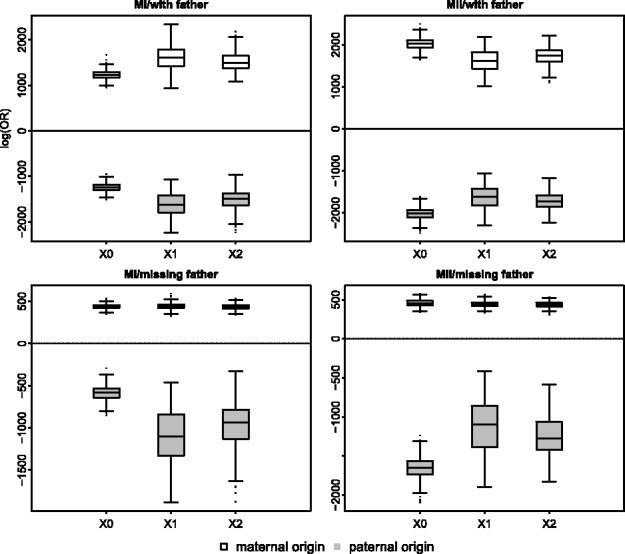
Boxplots of the log OR [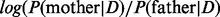] using triploid data from the proband and using data from EUR. Each panel represents one of four possible simulated cases: disjunction occurring at MI or MII, with or without available data for the father. The number of crossovers is shown on the x-axis

Our results further suggest that the method performs well in estimating the meiotic stage of the error (Fig. 4). In at least 98% of cases with triploid genotypes, the correct stage is inferred, irrespective of whether data from the father are available, and a minimum of 94% of cases are called correctly only with diploid data.

Fig. 4.

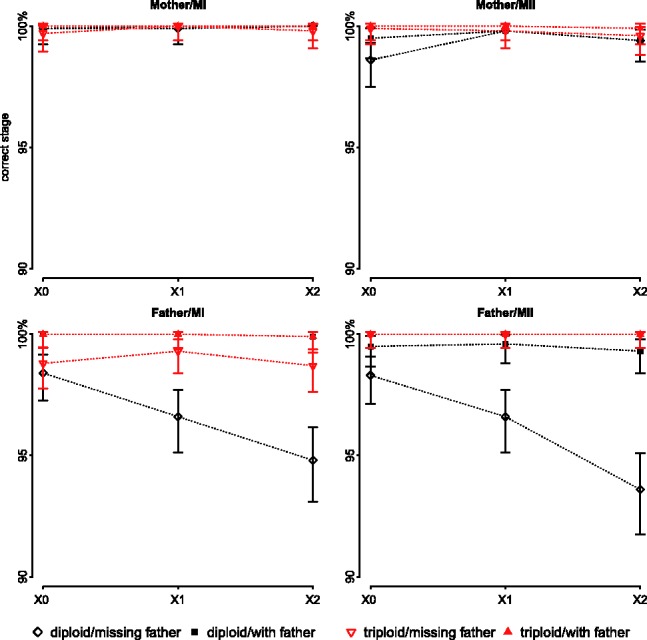
Percentages of cases in which the meiotic stage was correctly identified for each of four possible simulated scenarios (disjunction occurring in the father or the mother, during MI or MII), assuming equal prior odds for MI versus MII. The error bars represent the 95% confidence intervals. The number of observable crossovers is shown on the x-axis. Note that the y-axis is truncated

The method also performs well in estimating the number of crossovers when we have data for the parent of origin of non-disjunction (Fig. 5). As expected, however, when the father is NDJP and yet his data are not available, the proportion of cases in which the number of crossovers is correctly identified decreases somewhat (down to 70% in the worst case). In practice, though, most non-disjunction events are of maternal origin and DNA from the mother is easier to obtain, so this does not represent an important limitation.

Fig. 5.

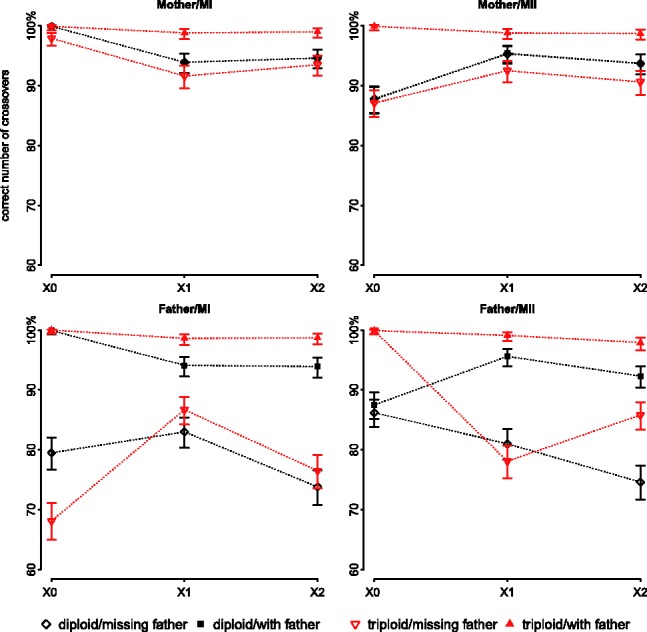
Percentages of observable crossovers that are correctly identified for each of four possible simulated cases (disjunction occurring in the father or the mother, during MI or MII), assuming equal prior odds for MI versus MII. The error bars represent the 95% confidence intervals. The true number of observable crossovers is indicated on the x axis. We emphasize that only a subset of crossovers that occurred on the tetrad is observable, [Equations (1) and (2)]

In most of the cases where the estimated number of crossovers is incorrect, the method detects spurious double crossovers that are close to each other. For example, for the case of MI/missing paternal data applied on triploid genotypes with one true crossover, 8% of cases had an incorrect estimate of the number of crossovers, and 60% of those were within 1 cM of another crossover. Because double crossovers in close proximity are highly unlikely to be real, it is therefore possible to filter them out. We also observe that in some cases when the father’s data are not available, the method performs better in estimating the number of crossovers when only diploid data are available (Fig. 5). This counter-intuitive finding may reflect the fact that, when the father’s data are missing, the emission probabilities are more sensitive to allele frequencies when using triploid rather than diploid data.

Next, we consider the accuracy with which we infer crossover locations. As shown in Figure 6 (for CEU) and Supplementary Figure S4 (for AFR), in most of the cases, the inferred location of the crossover is within 200 kb of the true position (i.e. 20 SNPs on average). As expected, having more information increases the precision of the method in locating crossovers.

Fig. 6.

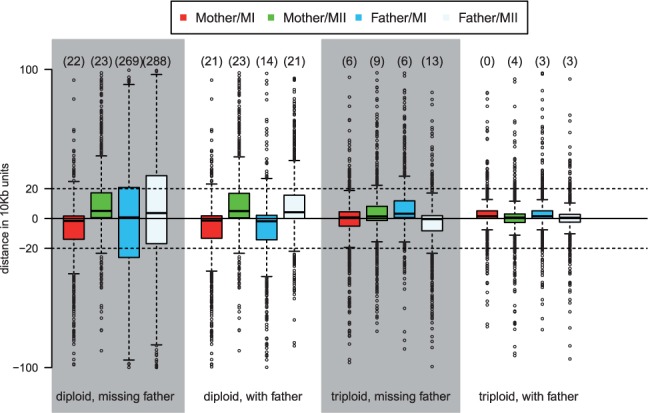
Distance between inferred and true crossover locations in EUR simulations with one crossover, conditional on inferring the right number of crossovers. On the y axis is the distance in units of 10 kb (the average distance between adjacent SNPs). The numbers on top of each box represent the number of outliers outside of the plotted range (−100, 100)

4.1 Application of the method to trisomy 21 samples

To further evaluate the performance of the method and in particular the impact of not having data from the father, we analyzed 282 trios with an offspring trisomic for chromosome 21, in which an average of ∼1270 SNPs were genotyped. Triploid genotypes were called using a clustering method described in Lin et al. (2008). The data are a subset of those described in Oliver et al. (2012). For our prior on recombination rates, we used the sex-averaged fine-scale genetic map for proper disjunctions, inferred from HapMap data (The International HapMap Consortium, 2007). Information regarding the ancestry of the individuals was available for 137 families (103 European/Hispanic–American, 29 African–American and 5 Asian–American, based on self-reporting). For those, we used allele frequencies from the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2012) from European ancestry (CEU), Yoruban ancestry (YRI) as well as Japanese and Chinese ancestries (ASN). For trios without self-reported ancestry, we used CEU allele frequencies. To infer the NDJP, we assumed that the prior odds of the mother being NDJP are 9:1, based on prior studies of chromosome 21 non-disjunction (e.g. Hassold et al. (1996)). We identified the parent of origin as the one with an OR of 10:1 in his/her favor and considered the parent undecided otherwise (thus requiring the likelihood of the father to be >100 times that of the mother to call the father as NDJP).

We compared our results with those of a previous analysis on the same data (Oliver et al., 2012), which looked at retention of heterozygosity of SNPs and Short Tandem Repeats (STR) to infer the source and stage of non-disjunction as well as the locations of crossovers, using the data from both parents (see Oliver et al. (2008, 2012) for more information). Their method does not have an error model and hence markers were filtered for quality. However, in our analysis, we used all SNPs, including those judged to be of lower quality, and an error rate of 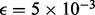(Oliphant et al., 2002).

In making the comparison, we created a set of crossover calls that we believe to be most reliable. Notably, we excluded cases where crossover events were supported by fewer than five SNPs on one side to minimize artifacts due to chromosome edges [e.g. Fledel-Alon et al. (2009); Kong et al.,(2004)]. We further excluded double crossovers within 2 cm, which are highly unlikely to be real (Fledel-Alon et al., 2009), but arise at non-negligible rates in simulations (e.g. 1.3% among 1000 cases of triploid data with paternal data). Application of both filters affected two of the confirmed calls made by the previous method, five made by TroX with the paternal data and nine made by TroX without paternal data.

As in the Oliver et al. (2012) analysis, TroX identifies all but two non-disjunction events as maternal (the two paternal cases are MI and have no crossovers). With paternal data, we find 79% to be due to errors in MI, whereas Oliver et al. (2012) infer 76%; without paternal data, we estimate that fraction to be 78%. Our results regarding the stage and the number of crossovers are also in close agreement with the previous analysis, even though we do not filter out low-quality genotypes (but instead use an error model; Fig. 7). With paternal data, our estimates of the number of crossovers and the stage of the error are identical to the ones made by the previous method in 262 cases (93%). This number reduces only slightly, to 259 (92%) when we mask the paternal data. The only effect of masking the father’s data appears to be an overestimation of the instances of three crossovers in MII (in two cases; Fig. 7).

Fig. 7.

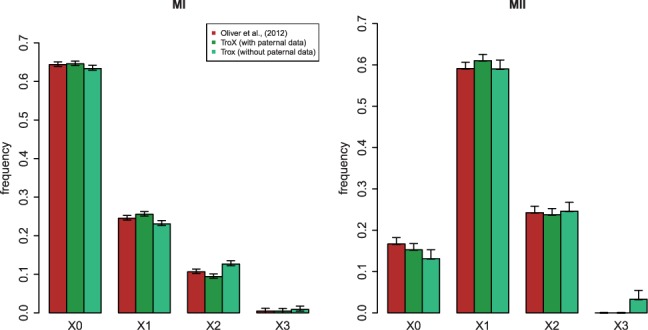
Distribution of crossover numbers among 282 trisomy 21 cases. The TroX analyses were obtained by applying the method to triploid proband data with and without using paternal genotype data. The Oliver et al. (2012) results come from the application of a method outlined in their paper to the same data, using paternal genotype data. Left panel: MI non-disjunction. Right panel: MII non-disjunction. The error bars represent the 95% confidence intervals

5 DISCUSSION

Existing methods for analyzing human trisomies using dense SNP data rely on the availability of DNA samples from both the mother and the father. However, it is often impractical to obtain a sample from the father, which in turn causes in a drastic reduction of full trios for study. For example, in a prospective study of recurrent miscarriages, paternal DNA was not available in ∼80% of the cases (Z. Williams, personal communication). By requiring only the sequence from the mother and the proband, our method overcomes this limitation.

Importantly, our results suggest that even with diploid data, missing data from the male do not affect our estimates of the number of crossovers and stage of the error, unless the father is the NDJP. In this case, estimates of crossover locations become less reliable. However, this scenario should constitutes <10% of all cases [assuming that in 80% of the cases the data from the father are not available and a ∼10% chance that the father is the NDJP (Hassold and Hunt, 2001)]. Thus, for most practical purposes, a sample from the father is unnecessary for these inferences, and therefore, our method allows one to reduce experimental costs by a third. A further advantage of our method is that, by incorporating an explicit error model, it bypasses the need to filter markers somewhat arbitrarily in ways that could introduce differences among studies. In addition, the method allows for missing parental data at a given site, increasing the number of markers that can be used.

Our simulations further indicate that, without paternal data, the method performs better in estimating the number of crossovers when applied to AFR populations as compared with CEU populations (Supplementary Figures S5). One explanation is that in our model, we ignore linkage disequilibrium (LD) among sites and because LD levels are higher in EUR population, this assumption may be more problematic. We examined this hypothesis by applying the method on simulated sequences with no LD, and indeed, the method performs better in this case (data not shown). If precise resolution of crossovers is not important to the specific study, one solution might then be to thin the markers so to minimize LD among them, or alternatively to thin the markers to call crossovers and then localize them using all the data.

One limitation of our method is that it relies on accurate knowledge about the ancestry of the parent whose data are missing. To assess the effect of using incorrect ancestry information, we switched population labels between CEU and AFR in the trisomy 21 samples, and reanalyzed the data. Our results suggest that the reliability of inference about the parent of origin remains the same and in 97% of the cases, estimates of the meiotic stage of the error are unaffected. In contrast, estimates of the number of crossovers become less reliable, with 23% of cases showing a different number than with the correct ancestry (13% after application of our filters). A related problem is what would happen if the parent whose data are missing is admixed. Both problems could be overcome either by extending this approach to consider the ancestries as additional parameters to be inferred by the method or by using methods such as principal component analysis (e.g. Patterson et al., 2006; Novembre et al., 2008) to infer the ancestry of the missing parent from the proband and maternal genotype data.

In conclusion, the rapid decrease in genotyping and sequencing costs, in combination with the advent of non-invasive approaches to sample fetal DNA from a maternal blood sample (Fan et al., 2008, 2012; Palomaki et al., 2012), allow the genomes of mother and fetus to be readily surveyed. Among these will be a substantial fraction of cases in which the fetus is trisomic. Application of our method and related approaches to such data should yield unprecedented insight into recombination profiles that underlie non-disjunction and ultimately help to identify risk factors of aneuploidy in humans.

An open source R package implementing our approach is available at http://przeworski.uchicago.edu/. Users can choose one of our error models or specify their own.