Improving MEME via a two-tiered significance analysis

Abstract

Motivation: With over 9000 unique users recorded in the first half of 2013, MEME is one of the most popular motif-finding tools available. Reliable estimates of the statistical significance of motifs can greatly increase the usefulness of any motif finder. By analogy, it is difficult to imagine evaluating a BLAST result without its accompanying E-value. Currently MEME evaluates its EM-generated candidate motifs using an extension of BLAST’s E-value to the motif-finding context. Although we previously indicated the drawbacks of MEME’s current significance evaluation, we did not offer a practical substitute suited for its needs, especially because MEME also relies on the E-value internally to rank competing candidate motifs.

Results: Here we offer a two-tiered significance analysis that can replace the E-value in selecting the best candidate motif and in evaluating its overall statistical significance. We show that our new approach could substantially improve MEME’s motif-finding performance and would also provide the user with a reliable significance analysis. In addition, for large input sets, our new approach is in fact faster than the currently implemented E-value analysis.

Contact: uri.keich@sydney.edu.au or emi.tanaka@sydney.edu.au

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Motif finding is an essential tool for bioinformatics research. The identification of transcription factor binding sites, and more generally of cis-regulatory elements, often serves as a stepping stone for understanding the regulation of gene expression. Thus, it is not surprising that for the past 20+ years many motif-finding tools have been described that can find short sequence motifs given only an input set of sequences (GuhaThakurta, 2006).

One such particularly popular finder is MEME (Bailey and Elkan, 1994), which relies on expectation maximization (EM) (Dempster et al., 1977) in its search for the ‘most significant motif’ that is present in the input set of sequences. More specifically, MEME evaluates and ranks the candidate motifs returned by each EM run in terms of their E-value. The latter term was initially introduced by the immensely popular BLAST similarity search tool (Altschul et al., 1990, 1997). BLAST’s E-value is successfully used to assess the significance of a reported alignment by estimating the expected number of alignments that will score at least as high as the observed score, assuming the query is independent of the database.

The E-value notion was later incorporated into the motif-finding literature by Hertz and Stormo (1999) who defined it as the expected number of alignments (motifs) of the same dimension and with a score at least as high as the reported one, assuming the input set is random. More precisely, the score of a motif here is the information content/log likelihood ratio (llr)/relative entropy [Stormo, 2000, or Equation (1) in the Supplementary Material], and a random input set is generated using an independent and identically distributed (iid) process. The latter definition of the E-value was adopted by MEME as well, albeit using a different E-value approximation scheme than the one originally suggested by Hertz and Stormo (1999). More details on the E-value and how it is evaluated in MEME are available in Supplementary Section S1.1.2.

Although relying on the BLAST approach seemed like a reasonable idea, it turns out there are multiple issues with it. First, as we pointed out, in practice MEME’s approximation of the E-value can be overly conservative, so real motifs may be rejected (Nagarajan et al., 2005). Moreover, ignoring the problematic approximation, even an accurately computed E-value can be highly conservative as explained later in the text (Ng et al., 2006).

There are two factors that combine to explain how the latter statement can be reconciled with the proven utility of the E-value in the BLAST context. First, using Altschul’s own words: ‘The BLAST programs report E-value rather than P-values because it is easier to understand the difference between, for example, E-value of 5 and 10 than P-values of 0.993 and 0.99995. However, when, P-values and E-value are nearly identical’ (Altschul, 2013). This statement is valid for the pairwise alignment problem where the number of high-scoring random alignments has a Poisson distribution. However, it can be shown that the number of high-scoring alignments in the motif finder context follows a different distribution, and hence, Altschul’s statement does not apply in MEME’s context where the E-value can be as large as 5 or 10 while the P-value is still significant. The second factor is the inherent algorithmic difference between the two tools: BLAST almost invariably finds the optimal alignment, while this is generally not the case for MEME (which is reasonable given the differences between the underlying problems). Thus, when assigning significance to BLAST’s output, we can restrict attention to the theoretical problem of the maximally scoring local alignment between two independently drawn sequences, whereas in the case of MEME, or any other motif finder, we need to evaluate the output relative to its capability or the significance estimate will be overly conservative (Ng et al., 2006).

Therefore, in spite of its immense popularity (MEME and MEME-ChIP had >13 000 unique users in 2012 and >9000 unique users through the first half of 2013), MEME’s significance evaluation leaves room for improvement.

In previous work, we described a computationally intensive alternative to the E-value that takes into account the finder’s performance and avoids the above problems with E-values (Ng and Keich, 2008a,b). Specifically, for some motif finders including MEME, the null distribution of the score of the reported motif seems to be well approximated by the 3-parameter Gamma [The distribution function of a 3-parameter Gamma with 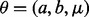is given by 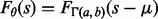, where 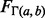is the Gamma distribution with it usual shape and scale parameters, and 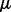is the location parameter (Johnson et al., 1994)], or 3-Gamma, family of distributions (Ng et al., 2006). Relying on this empirical observation, we designed a parametric test that returns a point estimator of, as well as a conservative confidence bound on, the significance of the reported motif (Keich and Ng, 2007).

Having demonstrated the effectiveness of the 3-Gamma significance evaluation scheme (Ng and Keich, 2008a), and having bundled it with a Gibbs sampling finder (Ng and Keich, 2008b), we considered adopting it for MEME in lieu of the E-value. However, in addition to conveying to the user an overall measure of the statistical significance, the E-value is also used internally in MEME to rank competing candidate motifs of which often only the highest scoring one is reported. Although the 3-Gamma approach can be used, for example, to choose among competing motifs of different widths (Ng and Keich, 2008a), it then becomes forbiddingly computationally intensive for assigning an overall significance as well. This motivated our design of a two-tiered significance analysis that we introduce and explore in the remainder of this article. The first tier consists of statistical tests that replace the E-value in selecting the best candidate among competing motifs. The second tier consists of applying the 3-Gamma scheme to assign an overall statistical significance. The results we present indicate that we will be able to improve both motif quality and the accuracy of motif significance estimates while allowing MEME to handle larger datasets in reasonable time.

2 CHOOSING THE BEST CANDIDATE MOTIF

Although MEME relies on EM to converge on a candidate motif, it uses multiple runs of EM (the prefix ME in MEME stands for multiple EM) with different initial values when exploring the space of possible motifs. For example, in the OOPS (one occurrence per sequence) mode, when faced with a range of possible motif widths, MEME runs multiple EMs using several different widths in the specified range. Each EM run yields a candidate motif, and MEME reports the motif with the lowest E-value. In ZOOPS (zero or one occurrence per sequence) mode, MEME needs to address the additional freedom of choosing the sequences that contain an instance of the motif. Therefore, for a given width, MEME starts multiple EMs, assuming a different number of motif instances and the motifs obtained following some further processing are then compared based again on their E-values.

In seeking to replace the E-value–based selection, we were influenced by the discriminative approach that is used to address essentially the same problem in several tools including Amadeus (Linhart et al., 2008) and DREME (Bailey, 2011). The idea is to evaluate a motif by comparing the number of occurrences of the motif in the original input set with the number of occurrences in a background set that can be a reference genome or a randomly drawn set of sequences modeled after the input set. The significance of the observed difference is then essentially assessed in those tools using the hypergeometric distribution as explained in more detail later in the text.

2.1 The minimal hypergeometric score

DREME’s discriminative motif score first uses Fisher’s exact test to evaluate the difference between the number of motif occurrences in the input set and in the background set (by default a random shuffle of the input set). It then adjusts the result, taking into account that the number of motifs it considers grows with the width of the motif: the motif score is the product of the Fisher exact test and the number of motifs tested at the given width.

Although DREME’s selection strategy has been shown to be effective, it cannot be applied as is in MEME’s context. DREME models a motif using a regular expression, and therefore, an occurrence of the motif is well defined, as is the number of possible motifs of a given width. MEME, however, models a motif using a position weight matrix (PWM) so an occurrence of a motif instance is threshold-dependent and the number of possible motifs is infinite.

Amadeus also uses the PWM model and the solution its authors adopted was the same one used in Barash et al. (2001) and Eden et al. (2007), which is to set the site score threshold so that the significance of the difference between the number of sites in the input set and in the background set (a genomic reference set in Amadeus’ case) would be maximized. As this threshold-dependent significance is evaluated using the hypergeometric distribution, the resulting minimal P-value is referred to in Linhart et al. (2008) as the hypergeometric enrichment score.

Here we adopted DREME’s strategy of using a randomly drawn background set of sequences of the same number and lengths as the original input set. In DREME, these sequences are drawn using shuffling of the original input set, whereas here we draw the sequences from genomic sequences with a similar A-T composition (see Supplementary Section S1.1.4 for details). We refer to Amadeus’ discriminative hypergeometric enrichment score in our context as the minimal hypergeometric score, or MHG score for short. The term MHG score was introduced in Eden et al. (2007) and later used in Steinfeld et al. (2008) and Eden et al. (2009) in a more general context. However, as we show in Supplementary Section S1.1.8, our specific usage here is consistent with the more general framework.

We stress that although the MHG score is defined in terms of some P-value, it should be viewed as a discriminative score rather than a P-value per se. As the evaluated PWM is optimized relative to the input set of sequences and is truly independent of the randomly drawn set of sequences, the null hypothesis of the hypergeometric/Fisher exact test is blatantly violated.

As our discriminative score is supposed to help us, among other things, pick the best among competing motifs of varying widths, it is desirable that it be unbiased. That is, the score better not have a tendency to prefer, for example, longer motifs over shorter ones. Unfortunately, longer motifs tend to be more discriminative than shorter ones, and hence, it is not surprising that we found that the MHG score exhibits a fairly strong bias toward longer motifs (Fig. 1a). However, this bias is measured when the input set itself is randomly drawn, and in this context it is harmless: we do not care which random motif MEME will select when there are no ‘real’ motifs to be found. An arguably more important issue is how well our discriminative score does at picking up the right motif when the data does contain one.

Fig. 1.

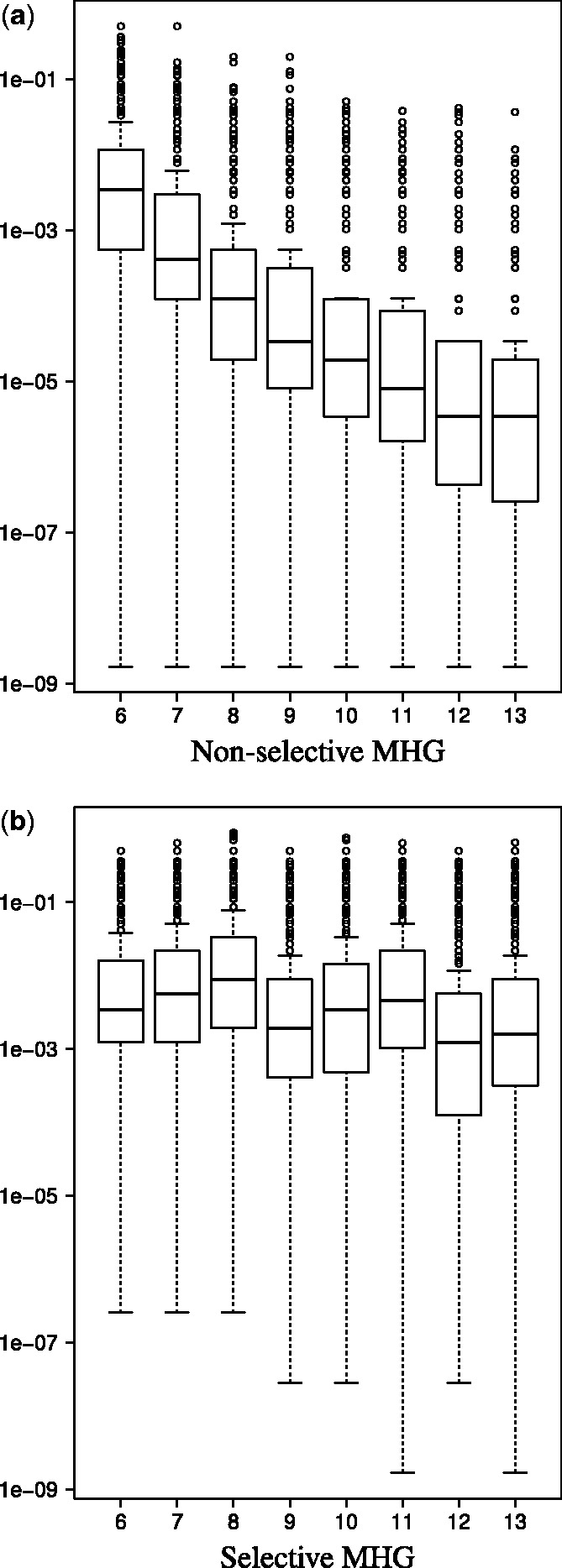
Null distribution of motif scores. The figure shows the boxplots constructed from 10 000 observations of non-selective (a) and selective (b) versions of the MHG scores for each motif width (ranged from 6 to 13). The scores were generated by applying MEME to randomly drawn input set of sequences of a fixed dimension (number of sequences and their lengths). See Supplementary Section S1.2 for details

We therefore designed a set of experiments to test the ‘power’ of a motif score, or its ability to select the correct motif. In the experiments described in detail in the Supplementary Section S1.3, we looked at the number of times each score is able to select a motif that is ‘sufficiently similar’ to the implanted one. The input sequences were randomly drawn from a set of intergenic genomic sequences and instances of one of 100 motifs were implanted into these otherwise unrelated genomic sequences. Those 100 motifs (of width 6–23) were selected so as to form a ‘minimal spanning set’ of a much larger set of 510 motifs: they were chosen so as to cover the motif space while minimizing the similarities between them as much as possible (Supplementary Section S1.3.1). Special care was also given so that the motif-finding problem presented to MEME would be at the right difficulty level: not too easy nor too difficult. This was accomplished by iteratively modifying the dimensions of the randomly drawn input sets resulting in sets with varying length and number of sequences: sequence length ranged from 100 to a maximum of 10 000 (median of set-average length 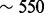), and the number of sequences ranged from a minimum of 5 to a maximum of 100 (median 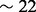) (see Supplementary Section S1.3.2 for details).

MEME was then applied several times to each input set using the same set of several parameter settings. Each application produced a competing putative motif representing a different section of the candidate motifs space. This was done in such a way that MEME’s E-value did not affect the final motif. For example, in the OOPS mode, each MEME run was given a different motif width in the range 6–13, whereas in ZOOPS mode, we varied the specified number of sites MEME looks for (-nsites) as well as covarying this number of sites and the width of the motif. The scoring function, in this case either the E-value or the MHG score, was used to select the best candidate motif suggested by MEME. Finally, Tomtom (Gupta et al., 2007; Tanaka et al., 2011) was used to determine whether the selected motif was sufficiently similar to the implanted motif (specifically a Tomtom P-value cutoff of 0.05 was used), in which case the motif was considered correctly discovered. See Supplementary Section S1.3.4 for more details.

We found that in the OOPS mode, the MHG-based selection yields ∼10% more correct motif identifications than the E-value–based selection. This difference is deemed statistically significant using a sign test (Supplementary Table S1b and Supplementary Sections S1.3.5). In the ZOOPS mode, when varying both the width and the number of sites MEME looks for (-nsites), we notice an even more substantial improvement of 32% additional correct identifications, which is again statistically significant (Fig. 2). Fixing the width and varying only MEME’s -nsites parameter in ZOOPS mode, the MHG score shows consistent improvement over the E-value, albeit the number of additional motifs discovered varies from a substantial 42% (width 6) to a modest 6.8% (width 13, see Supplementary Table S4). Thus, in spite of the strong bias it exhibits on null sets, the MHG score is more powerful than the E-value at selecting the correct motif when such a motif is present.

Fig. 2.

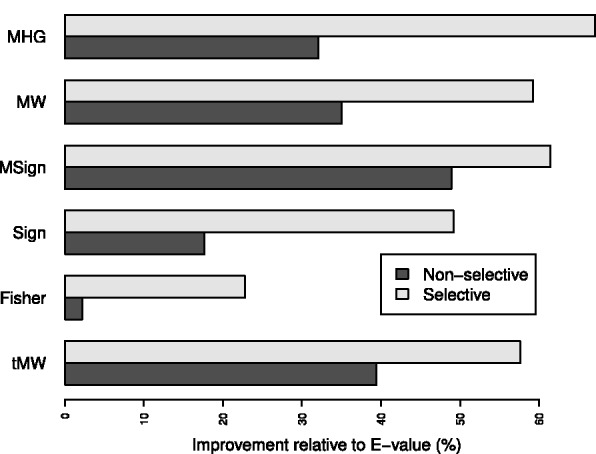
Relative improvement over the E-value. For each scoring method (defined in Section 2 and in Supplementary Section S1), we give the percentage of improvement in its success rate in the ZOOPS mode relative to the E-value’s success rate in the same mode (Supplementary Section S1.3.4). Data are taken from Supplementary Table S3a

Interestingly, although the E-value shows little bias on null sets (Supplementary Fig. S1c), in real terms, not only is it less accurate than the biased MHG score, in the OOPS mode it is slightly less accurate at choosing the best motif than a strategy of always choosing the shortest motif (width 6) would be: 495 versus 503 correctly discovered motifs (out of 1000, Supplementary Table S1). Be that as it may, it stands to reason that if we can somehow adjust the MHG score so it will be less biased, then its power will increase even further. We next propose a heuristic that in practice reduced the bias significantly.

2.2 The selective MHG score

It is intuitively clear that the bias exhibited by the MHG score will be reduced if we truncate the longer motifs when evaluating them. At the same time, it is clear that such a procrustean approach would diminish the power of the score to identify real longer motifs. We therefore adopted a compromise: first, rather than truncating, we choose the best columns of each candidate motif, or, more precisely, we replace the lowest entropy columns with rigid gaps. Second, the number of columns we choose increases with the width of the motif according to the intuitively derived formula

(1)

where w is the width of the motif and 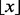denotes the floor function. So, for example, for 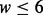the motif is taken as is, whereas in a motif of width 7, we substitute the lowest entropy column of the PWM with a (rigid) gap. Similarly, for motif of width 9, we replace the two weakest columns by two rigid gaps, etc.

The rest of the procedure, which we refer to as the ‘selective MHG’ score because we select the motif columns, remains the same as the non-selective MHG procedure outlined above. Specifically, the gapped PWM is used to assign scores to each site in the input as well as in the randomly drawn sequences, and the best site score in each sequence is noted. Each observed score is then considered as a site if it is greater than or equal to a predetermined threshold, and we compute the hypergeometric P-value of observing that many more sites in the input set than in the null set. The minimal P-value overall possible thresholds is the selective MHG score.

Looking at Figure 1b we see that the above heuristic has considerably diminished the bias exhibited by the non-selective MHG score. More importantly, the selective MHG is consistently more accurate at choosing the correct (most similar) motif from among the candidates (Supplementary Tables S1a and S3a). In the OOPS mode, we see 11% more correct identifications (608 versus 546) when using the selective version, giving 23% more correct identifications (608 versus 495) than when using the E-value. Both of these improvements are statistically significant using a sign test (Supplementary Table S1a and b). In the ZOOPS mode, when varying both the width and the number of sites MEME looks for, we see 27% more correct identifications using the selective version (615 versus 486), giving 67% more correct identifications than when using the E-value (615 versus 368, Fig. 2). Again, both improvements are statistically significant (Supplementary Table S3a and b).

By fixing the motif width that MEME searches for and varying only its -nsites parameter in ZOOPS mode, the selective MHG score is consistently more accurate at selecting the best motif candidate (Supplementary Table S4), albeit the percentage of additional candidate motifs correctly selected varies from an insignificant increase of <1% (536 versus 535, searched motif width 7) to a statistically significant increase of 32% (416 versus 314, searched motif width 13). In the same experiments, the selective MHG has 33–52% more correct identifications than the E-value has, and the relative improvement is particularly pronounced for wider motifs (536 versus 402 and 519 versus 342 for implanted motifs of widths 7 and 11, respectively).

Thus, our selective MHG score improves MEME by allowing a more judicious selection of the best among several EM generated candidate motifs. The cost of computing this score is linear in the size of the input set (with a small constant) and therefore should not be considered a computational burden.

2.3 Alternative motif scores

Using the same setup that we used above to compare the E-value with the non-selective and the selective MHG scores, we studied the power of several other motif scores to discern between random and real motifs:

• The “Mann–Whitney” (MW) score is defined by applying the MW test to compare the set of motif scores from the input set of sequences with the set of scores from the null generated set of sequences (see Supplementary Section S1 for details). As with the MHG score, we consider the MW P-value as a discriminative score rather than carrying a (false) probabilistic interpretation, as the null assumption of the original statistical test is again clearly violated.

• A selective version of the MW score, which, like the selective MHG score, replaces a few of the low entropy scoring columns in the PWM with rigid gaps.

• A thresholded version of the MW (tMW) score applies the MW test to the same lists as originally, only with all low scoring sites removed. Similarly, we looked at a selective version of the thresholded MW. These two scores depend on a site-threshold, that is, the site is only considered if its PWM score exceeds a per-dataset threshold.

• The Fisher exact test (Fisher) compares the number of site-bearing sequences in the input set with the same number in the null generated set as does the selective version of the Fisher exact test (removing a few of the low-entropy scoring columns from the PWM). These two scores also depend on a per-dataset threshold on sites.

• The ‘sign score’ (Sign) is defined by applying the sign test to compare the number of input sequences whose best site score is higher than the best scoring site in the corresponding null generated sequence with the number of sequences for which the reversed statement held (the best null-sequence score is higher than the best input-sequence score). Again, a selective version of this score was also considered.

• The ‘minimal sign score’ (MSign) is defined similarly to the sign score except we applied the sign test only to pairs of input-null sequences for which the maximal score exceeded a site-threshold. We then varied the threshold so that the score would be most significant (minimal sign test p-value). A selective variant of this score was also looked at.

None of the site-threshold–dependent variants (the Fisher exact test and the thresholded MW variants) outperformed the selective MHG score in a statistically significant way, and all performed significantly worse in at least some of the tests (Supplementary Tables S1–S3). In light of these results and because finding the per-data threshold increases the computational cost of the score, we see no reason to prefer any of the site-dependent scores over the selective MHG score.

The selective versions of all the motif scores performed better than their non-selective counterparts, which confirms the benefit of reducing the motif width bias. The benefit of using the selective variants increases with the searched motif width (Supplementary Table S4), but we suspect this phenomenon is only partially explained by the reduction of bias. Real motifs often contain short stretches of uninformative columns (Xing and Karp, 2004), and hence, we are potentially adding noise when these uninformative columns form an integral part of the PWM. In contrast, the selective versions of our scores filter out some of the uninformative columns, thereby increasing the signal to noise ratio. This side effect of the heuristic used by the selective versions of the motif scores may be partially responsible for their higher accuracies.

The selective MW score performed slightly better than the selective MHG score in the OOPS set of experiments (Supplementary Table S1), suggesting that the optimal motif score could be different when running MEME in ZOOPS versus OOPS mode. Although this is possible, it is not clear that the added design complexity is merited by the performance difference, which was not deemed statistically significant in our experiments. At the same time, the advantage of the selective MHG score over the selective MW score in the ZOOPS setting was also not deemed statistically significant (Supplementary Table S3b), and so in terms of their power, these two discriminative scores are fairly comparable in our experimental setup.

The selective sign-test variants are simple to calculate and perform similarly to the selective MHG and MW scores but lose to both scores in a statistically significant way in the OOPS setting (Supplementary Table S1).

Finally, we were curious to find out how well the 3-Gamma–estimated P-value would do in selecting the most promising motif (Supplementary Section S1.1.12). Because of the intensive computational nature of the 3-Gamma score, we only looked at the OOPS test set, and the 3-Gamma motif score was slightly less accurate than the selective MHG score at choosing the best candidate motif (599 versus 608, Supplementary Table S1a), but this difference is not statistically significant (Supplementary Table S1b). So, again, we see that inherent calibration (as the 3-Gamma score has by definition, see Supplementary Fig. S1d) does not necessarily mean superior performance in picking the best motif. Regardless, note that using the 3-Gamma approach for selecting the best motif is not a practical option if the latter is also to be used to assign an overall significance: the resulting procedure is computationally forbiddingly demanding. Rather this experiment should be taken as further validating the power of the selective MW and MHG scores.

3 ASSESSING THE STATISTICAL SIGNIFICANCE OF THE REPORTED MOTIF

As we pointed out above, the selective MHG and MW scores are discriminative ones and cannot be used to directly assign an overall statistical significance to the selected motif. For that, we suggest using our computationally intensive 3-Gamma parametric scheme. The protocol we adopted here is essentially the same as described in Ng and Keich (2008a, b): the input set is used as a template to generate n independently drawn null sets (we suggest n = 50), and MEME is applied to the null sets in exactly the same way as it is applied to the original set of sequences. In particular, our protocol uses the selective MHG (or MW) score to select the best motif in each of the null drawn sets, i.e. an additional random (background) set is generated for every one of the n null sets and the discriminative score is computed relative to these two null sets.

The score assigned to the input set of sequences, as well as to each of the n null drawn sets, is minus the log of the selective MHG (MW) P-value of the chosen motif, i.e. it is minus the log of the smallest selective MHG (MW) P-value among all candidate motifs.

The 3-Gamma P-value of the motif selected from the input set of sequences is estimated using the scores from the null drawn sets as described in Supplementary Section S1.1.12 except that the current score is used instead of the MEME-reported llr score: the maximum likelihood estimate is estimated from the n null scores and then plugged into the 3-Gamma distribution function to yield the 3-Gamma P-value.

We found support to the assumption that the null distribution of the motif score can be approximated to a 3-Gamma distribution empirically by considering the probability plot of 100 000 null selective MHG scores and the fitted 3-Gamma curve in Figure 3 (see Supplementary Fig. S4 for the probability plot of null selective MW scores). Linhart et al. (2008) used a similar approach to assign the significance of the motif to their hypergeometric enrichment score, but they fit a normal distribution. In Figure 3, we show that the fit to the normal distribution substantially deviates from the observed null MHG scores at the tails, highlighting the advantage of our choice of the 3-Gamma distribution. Further empirical support for the validity of the 3-Gamma approximation comes from the fact that it seems to produce a well-calibrated score (Section 5).

Fig. 3.

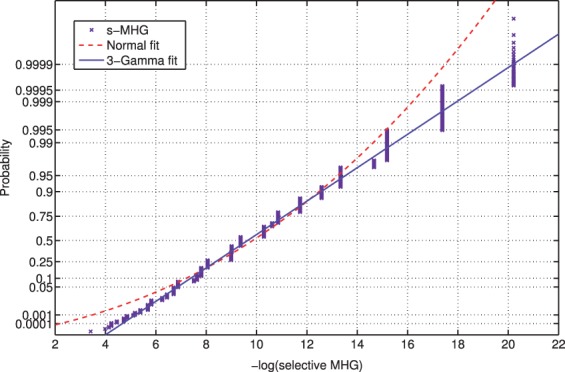
Probability plot of the null selective MHG score with normal and 3-Gamma parametric fits. This probability plot compares the empirical null distribution of the minimum selective MHG score with the optimal normal as well as 3-Gamma parametric fits. The empirical distribution was generated using 100 000 observations, and the parametric fits were estimated using maximum likelihood (see Supplementary Section S1.4 for details)

4 TWO-TIERED SIGNIFICANCE ANALYSIS

Our two-tiered significance analysis offers an alternative to MEME’s current motif selection and significance analysis procedures, both of which are currently based on the E-value. The proposed motif selection step uses our selective MHG or MW scores, and the significance is provided through our 3-Gamma estimation scheme.

We compared our two-tiered analysis with the E-value–based analysis currently implemented in MEME by examining how well they do in correctly discovering the implanted motif. Again, our test set consists of sets of sequences that are randomly sampled from a genome and then implanted with instances of our spanning set of real motifs. The motif is selected from a pool of candidate motifs generated by applying MEME with different settings varying either the width in OOPS mode or the width and the -nsites parameter in ZOOPS mode. The selection is guided by either the E-value or the selective MW or MHG scores. The motif is considered correctly discovered (P or positive) if the Tomtom assigned P-value to the match between the reported motif and the implanted one is 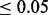. Otherwise, the motif is assigned the label N (for negative, or failure, see Supplementary Section S1.3.4 for more details).

We plot the number of true positives (TPs) versus the number of false positives (FPs) at any given significance threshold. In this case, the P/N labels of a given dataset might differ, as they are assigned to different motifs: the motif selected by E-value would often differ from the one selected by the selective MHG or the MW score. Had the P/N labels been the same, the curve would have been equivalent to the ROC curve, which plots the true-positive rate versus the false-positive rate.

Figure 4 shows that in the ZOOPS mode, our two-tiered analysis, based on either the selective MHG or MW scores, completely dominates the E-value: there are considerably more TPs (correctly identified motifs) for any given number of FPs (incorrectly identified motifs). The differences are particularly striking in the arguably more important section of the graph where the FP count is low. See Supplementary Figure S5 for the corresponding OOPS mode figure.

Fig. 4.

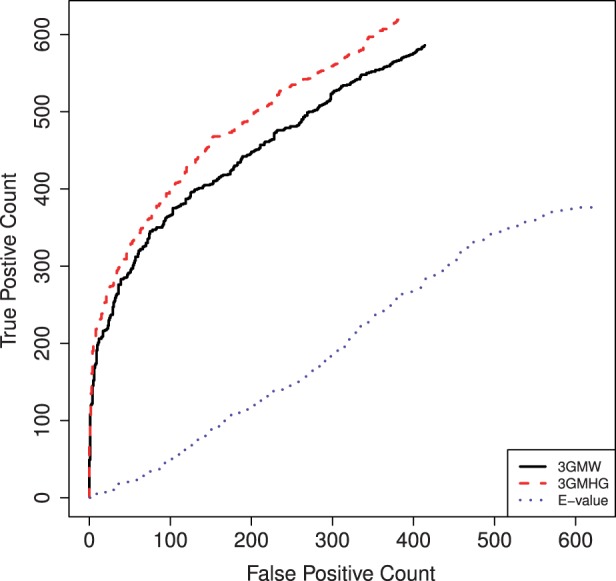
ROC-like plots of two-tiered versus E-value motif scores in ZOOPS mode. An optimal motif is selected in each set using the E-value, selective MHG (3GMHG) or selective MW (3GMW). If the Tomtom assigned P-value to the match between each selected motif and the implanted one is 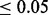, we label the selected motif as positive otherwise as negative. Varying the significance threshold, we plot the number of positive motifs that are deemed significant (TP) versus the number of negative motifs that are called significant at that level (FP). The significance is determined either by the E-value or by the 3-Gamma point estimate of the P-value (3GMW, 3GMHG). As the optimal motif might vary with the method, we plot FP versus TP counts rather than the usual ROC curve

The same overall picture is shown from a slightly different perspective in Supplementary Table S5, which gives the number of TPs and FPs for a few commonly used significance thresholds. It is particularly striking how poorly the E-value is performing as a measure of motif significance in the ZOOPS case: for a significance threshold of 0.05, the E-value–derived motifs have ∼7 times more FPs and less than half the number of TPs compared with our two-tiered analysis based on either the MHG or the MW scores.

The poor performance of the E-value in the above analysis is mostly an indictment against the E-value’s utility as a calibrated measurement of the statistical significance. To show this, in an additional analysis we used the E-value to choose the best candidate motif, but then sorted the selected motifs according to either the E-value or the significance assigned by applying the 3-Gamma procedure to the selective MW (3GMW) or MHG (3GMHG) scores of the E-value–selected motif. Unlike in the previously described experiments, here the same motif is selected by all the methods, and thus, we can compare them using the standard ROC curve (TP rate versus FP rate). The area under the ROC curve (aROC) of the 3GMW or 3GMHG (0.839 and 0.821, respectively) is much larger than that of the E-value (0.530), which is about what you expect from a random classifier (Supplementary Table S7). Thus, the E-value is markedly less accurate as a measure of statistical significance than our two-tiered method. However, for small datasets, the E-value computation is ∼50 times faster than the 3-Gamma significance evaluation.

5 SCORE CALIBRATION

The main goal of the 3-Gamma analysis is to provide the user with a usable significance analysis. Such analysis should, by definition, be calibrated. That is, the more significant the score is, the more likely the motif is not an artifact. On the other hand, a score can be well calibrated even if it fails to convey statistical significance.

We compared the calibration level of the selective MHG and MW scores by comparing their classification power against that of the two-tiered scheme. Specifically we asked whether the ROC curve obtained by using each of these two discriminative scores on their own is improved by using the 3-Gamma–assigned P-value instead of the discriminative score (Supplementary Fig. S6).

It was rather surprising to see that, in terms of calibration, the 3-Gamma–derived analysis adds little to the fairly well-calibrated selective MHG and MW scores. Still, it was reassuring to find that the aROC is slightly higher when we further calibrate those scores using the 3-Gamma–estimated P-values (see Supplementary Table S6).

It remains to be seen whether our selective discriminative scores are well calibrated in a larger setting, where, for example, we might have thousands of input sequences. However, if they are well calibrated, then we could assign the 3-Gamma significance at no additional computational cost. If the score is perfectly calibrated, then a unique universal 3-Gamma distribution applies to all input sets. While it is clear that some accuracy will be lost this way—the discriminative scores are not perfectly calibrated as we see from the fact that the aROC is slightly lower than when using the 3-Gamma P-value—the trade-off in terms of significantly reduced runtime might be deemed favorable to some of the users.

In contrast with the well-calibrated discriminative scores, we noted that the E-value is poorly calibrated. This is further illustrated in Supplementary Figure S7, where the actual motif selection is guided by the E-value but the overall significance is assessed by either the E-value or by our two-tiered analysis applied to the motif selected by the E-value. We note that even though the motif of each input set is selected by the E-value, our two-tiered analysis is doing a much better job in ranking the selected motifs.

6 ANALYSIS OF REAL DATA

The results presented so far were derived from datasets that were synthesized using real motifs implanted in real, though unrelated, sequences. The advantage of using synthetic data is that you have control over the degree of difficulty of the motif-finding problem as well as a well-defined ‘correct’ outcome. As such we find it optimal for comparison between methods. Still, one might ask whether the differences we observe in our synthetic sets are at all relevant to ‘real’ biological data.

To address this question, we analyzed a dataset curated by Narlikar et al. (2007), which consists of 156 sequence sets derived from the Harbison ChIP-chip experiments using 80 transcription factors (Harbison et al., 2004). We found that, as in the case of the synthetic data, MEME performs significantly better when the motif selection is guided by either our selective MHG or MW scores than when guided by MEME’s E-value: 26–29% more correct identification, and both improvements are statistically significant (Supplementary Section S8). Both non-selective versions of the MW and MHG scores give a more modest 14% improvement over the E-value; however, this improvement is not deemed statistically significant.

Similarly, our complete two-tiered analysis is doing a much better job than the E-value in discerning between correct and incorrect motif identifications. For example, using 3GMHG, which is the 3-Gamma analysis based on the selective MHG score, we find 40 correct identifications and 15 incorrect ones at the traditional 0.05 significance threshold. In contrast, using MEME’s E-value, we find 30 correct and 41 incorrect identifications at the same nominal level of 0.05 (Supplementary Table S9). More generally, comparing the FP versus TP counts, we see a similar picture to the one we saw with the synthetic data: the two-tiered analysis completely dominates the E-value–based analysis with a particularly striking difference in the critical region of low-FP count (Supplementary Fig. S8).

Given that we analyzed 156 sequence sets, even the 15 incorrect identifications that our 3GMHG score reports are more than what we would like to see at the 0.05 significance level. However, in classifying a reported motif as an incorrectly identified one, we are not necessarily claiming that the found motif is insignificant. These are real datasets that might contain binding sites of auxiliary motifs. If such motifs are reported, they would be classified as incorrect identifications; yet, they are not insignificant random motifs. Thus, it is not surprising that we find more incorrect identifications than we expect assuming those motifs are truly random. The latter can only be guaranteed using synthetic data.

7 DISCUSSION

We propose a two-tiered significance analysis to replace the E-value currently used in MEME to select the best among competing EM-generated motifs as well as to assign an overall statistical significance. We showed that our selective MHG or MW discriminative scores substantially increase the percentage of correct motif identifications by simply applying a more judicious selection criterion to choose the best of MEME’s several EM generated PWMs—no change in the search strategy is involved.

As the complexity of our selection procedure is linear in the size of the input set (with a small constant), it can be integrated into MEME at a marginal computational cost. As the currently implemented computation of the E-value in MEME is cubic in the number of sequences, our selective MHG and MW schemes compare favorably against the E-value on that account as well, especially with ChIP-seq data with thousands of sequences in mind.

The second part of our two-tiered analysis is associated with a substantial computational cost, as it requires running MEME on n randomly generated images of the input set (we recommend n = 50). Our 3-Gamma significance analysis then uses these n runs to provide a parametric approximation to the P-value of the observed motif. Again we note that although a factor of 50 is a substantial runtime penalty, the current computation of the E-value in MEME incurs an even greater penalty when studying thousands of sequences.

In summary, our two-tiered analysis offers a substantial improvement in finding the correct motif without requiring any change to MEME’s underlying EM motif search strategy. The difference between the signal to noise ratio (TP to FP) of the two-tiered approach and of the E-value approach is particularly striking in the more important region of low noise.

We also showed that the E-value as currently implemented in MEME is not particularly well suited for selecting motifs of competing width: it did worse than the single best width. Also, it is not a good measurement of an overall significance: as a classifier comparing motifs from multiple datasets, it performed about as good as a random one. Taken together, we expect our two-tiered analysis will significantly improve the performance of MEME. Given MEME’s popularity, this improvement can make a substantial practical impact on bioinformatics research.

MEME assumes its input set is uniformly weighted. In cases where one can assign different weights to the input sequences, for example, the binding intensity of a probe, other methods that use such data might yield even better results (Leibovich and Yakhini, 2013).

We stress that although our two-tiered analysis was demonstrated in the context of MEME, it should be applicable more broadly. Certainly, the selective MHG or MW scores could in principle be applied to selecting one of several candidate motifs. Moreover, the associated computational cost is only linear in the size of the input set. The wider applicability of our 3-Gamma scheme is more tentative. It is important to understand that it is an approximation, and so, at the end of the day the question is whether there are better alternatives. Our experience shows that the 3-Gamma family is better than the normal and even the extreme value distributions at approximating the null distribution of the optimal motif score in the examples we considered (Ng and Keich, 2008a, b, and Fig. 3). Whether this applies to the user’s choice of scoring function, motif finder and null model is something that can be looked at empirically.

Although, Amadeus (Linhart et al., 2008) also allows the user to apply an essentially two-tiered analysis through its bootstrap option, there are several differences between it and our proposed solution. First, Amadeus uses the MHG score to choose the best motif, which, as we saw, can be substantially inferior to the selective MHG score we propose. Second, when using the bootstrap option, Amadeus reports an overall significance using a normal approximation, which as we showed can substantially overestimate the true significance of the motif (Fig. 3 and Supplementary Fig. S4).

Whether one should choose to use the selective MW or the selective MHG score seems to depend on the problem: in the OOPS context, the MW had the advantage, while in the ZOOPS experiments, the MHG did better. None of these advantages was deemed statistically significant. The MHG score has one advantage over the MW score: in the ZOOPS mode, it can be used to determine which sequences contain a site, whereas with the MW score, some other method should be used for that purpose.

Our future plans are to determine whether we can estimate a universal 3-Gamma distributions for DNA and protein motifs before incorporating our two-tiered approach into MEME. If this is not possible, we will incorporate the proposed two-tier approach as is, which is how we will incorporate it into GIMSAN (Ng and Keich, 2008b).

Finally we note that the formula for the number of selected columns [Equation (1)] in the selective variants of the scores was not optimized, leaving the door open for potential improvement through optimization of this selection criterion.