Emitters of N-photon bundles

Abstract

Controlling the ouput of a light emitter is one of the basic tasks of photonics, with landmarks such as the laser and single-photon sources. The development of quantum applications makes it increasingly important to diversify the available quantum sources. Here, we propose a cavity QED scheme to realize emitters that release their energy in groups, or “bundles” of N photons, for integer N. Close to 100% of two-photon emission and 90% of three-photon emission is shown to be within reach of state of the art samples. The emission can be tuned with system parameters so that the device behaves as a laser or as a N-photon gun. The theoretical formalism to characterize such emitters is developed, with the bundle statistics arising as an extension of the fundamental correlation functions of quantum optics. These emitters will be useful for quantum information processing and for medical applications.

The photon is the building block of light. Every state of the electromagnetic field comes as a superposition of photons, even classical states, which are Poisson distributions. Particular combinations of photons—from more stringent distributions to entangled superpositions—are required to power quantum technology. A privileged platform to sculpt desirable states of light is Cavity Quantum Electrodynamics (cQED)¹. These laboratories of the extreme allow the control of the interaction of light with matter at the ultimate quantum limit. We show here how they can be used to realize a family of N-photon emitters, i.e., sources that release their energy exclusively in groups, or bundles, of N photons (for integer N) and in effect provide us with light made up from building blocks that are not single photons anymore. This ability to substitute the quantum of light by a bundle has unforeseeable consequences for both applications and fundamental physics. For instance, this renormalizes the link between the energy of the fundamental unit of excitation to its frequency through a magnified Planck constant: E = Nhv. The type of emission can be varied with system parameters to realize both N-photon lasers and photon guns² at the N-photon level. Such highly non-classical emitters should boost new generations of light sources^3,4, be useful to produce NOON states⁵, for quantum lithography and metrology⁶, and also for medical applications, allowing for higher penetration lengths and increased resolution with minimum harm to the tissues^7,8. The recent demonstration that biological photoreceptors are sensitive to photon statistics⁹ may also render such sources highly relevant for studies of biological photosystems and, potentially, of quantum biology¹⁰.

Transition from Jaynes–Cummings to Mollow dynamics

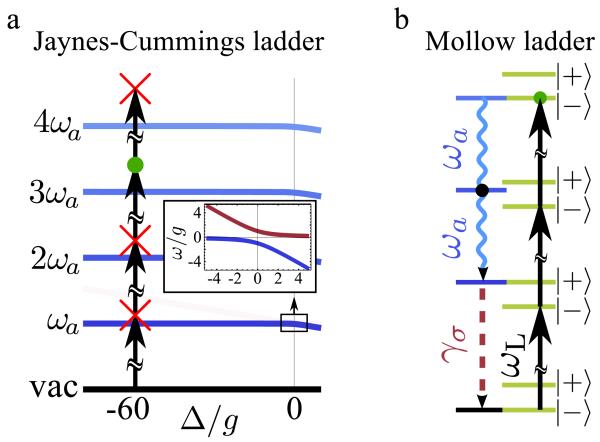
Our scheme relies on the paradigm of cQED: one two-level system in a cavity (Fig. 1). This is realized in a wealth of physical systems, ranging from atoms in optical cavities¹¹ to superconducting qubits in microwave resonators¹² and quantum dots in microcavities¹³. The dynamics is described by the Jaynes–Cummings Hamiltonian H₀ = ω_aa^†a+ω_σσ^†σ+g(a^†σ+σ^†a) with a and σ the second quantization lowering operators of the light field (boson statistics) and the Quantum Emitter (QE, two-level system), respectively, with corresponding free energies ω_a andω_σ and coupling strength g¹⁴. The configuration under study is the resonant excitation by an external laser of the QE^15-17 far in the dispersive regime with the cavity $(\mid {\omega }_a-{\omega }_{\sigma }\mid ⪢g\sqrt{N+1})$^18-20. The energy structure of H₀ is shown in Fig. 2a with the QE at Δ/g = −60 (Δ = ω_a−ω_σ), in which case the states are essentially the bare ones. The laser of frequency ω_L and pumping intensity Ω is included by adding Ω(e^−iωLtσ^† + e^iωLtσ) to H₀. We assume the rotating wave approximation, whose validity is justified in the Supplementary Information. At pumping low enough not to distort the level structure, one can excite selectively a state with N photon(s) in the cavity at the (N + 1)th rung by adjusting the laser frequency to

$${\omega }_N\approx {\omega }_a+\frac{\sqrt{4(N+1)g^2+{\Delta }^2}-\Delta }{2(N+1)},$$ (1)

with N ∈ N²¹. This is shown in Fig. 2a for the case N = 2, corresponding to the excitation of the third rung, with a photon-blockade^{22, 23} at all other rungs (above and below)^24,25. The positions of the resonances are shown in Fig. 3b. In the absence of dissipation, exciting a resonance leads to the generation of an exotic brand of maximally entangled polaritons, of the type $(\mid 0g\rangle \pm \mid Ne\rangle )∕\sqrt{2}$ rather than the usual case $(\mid 0e\rangle +\mid 1g\rangle )∕\sqrt{2}$. The dynamics of the system for the case N = 2 is presented in Fig. 4a. Strikingly, full amplitude Rabi oscillations between the |0g〉 and |Ne〉 states are observed. Further characterization of these remarkable quantum states is provided in the Supplementary Information. We proceed towards the configuration that will bring such resonances to fruition in terms of applications.

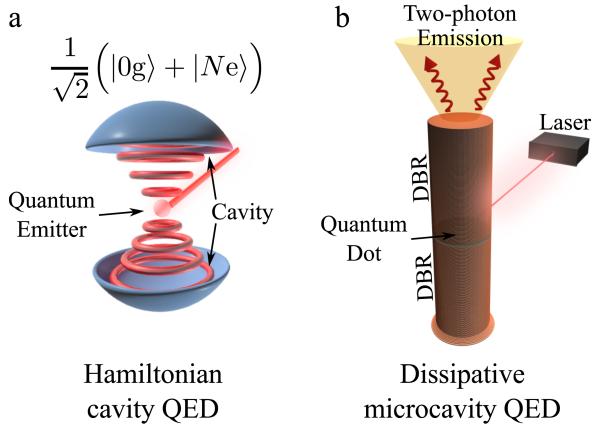
FIG. 1.

a, cQED allows to bring Quantum Electrodynamics—the theory of light-matter interaction—under prolonged scrutiny at the level of a few photons and in the presence of a quantum emitter. An external laser can be shined on the emitter to drive its dynamics. We show in this text how peculiar quantum superpositions can thus be realized and the emission subsequently forced to take place exclusively in bundles of N-photons. b, A possible solid state implementation of our proposal places a quantum dot in a micropillar: exciting on the side with a conventional laser, one can collect in the cavity emission the output from a quantum laser or a quantum gun, depending on the system parameters.

FIG. 2.

Energy levels of the two limiting cases of excitation: a, In the low excitation regime, the Jaynes–Cummings ladder (anticrossing magnified in inset) is probed by resonantly exciting a given rung of the ladder, with photon blockade at all others. b, In the high excitation regime: the laser dresses the QE while the cavity Purcell-enhances a N-photon transition from |−〉 to |+〉 (here for N = 2). A subsequent emission from the QE brings the system back to a |−〉 state.

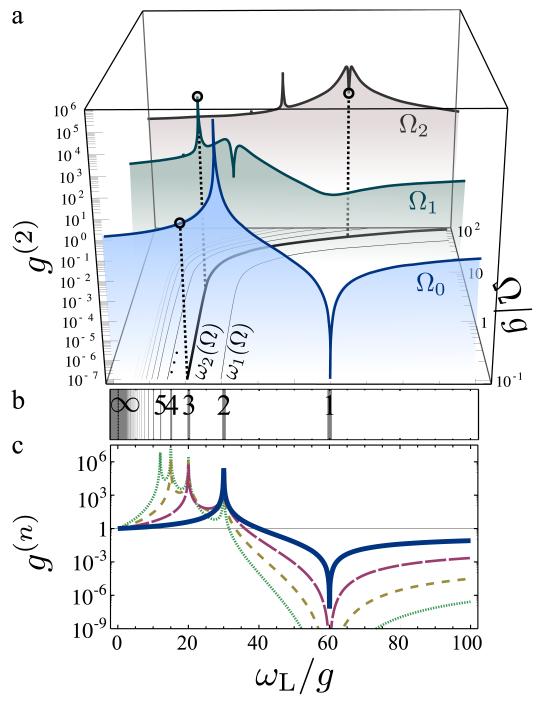
FIG. 3.

a, g⁽²⁾ as a function of ω_L for pumping Ω₀ ≈ 10⁻²g, Ω₁ ≈ 4g and Ω₂ ≈ 32g. The resonances ω_N(Ω) are shown in the plane (ω_L, Ω). Open circles are the projection of ω₂ on g⁽²⁾. b, Resonant energies to excite the nth rung of the ladder. c, g⁽ⁿ⁾ for n = 2 (solid), 3 (long dash), 4 (short dash) and 5 (dotted) at vanishing pumping with n − 1 bunching resonances matching those in b. Δ/g = −60 in all the panels.

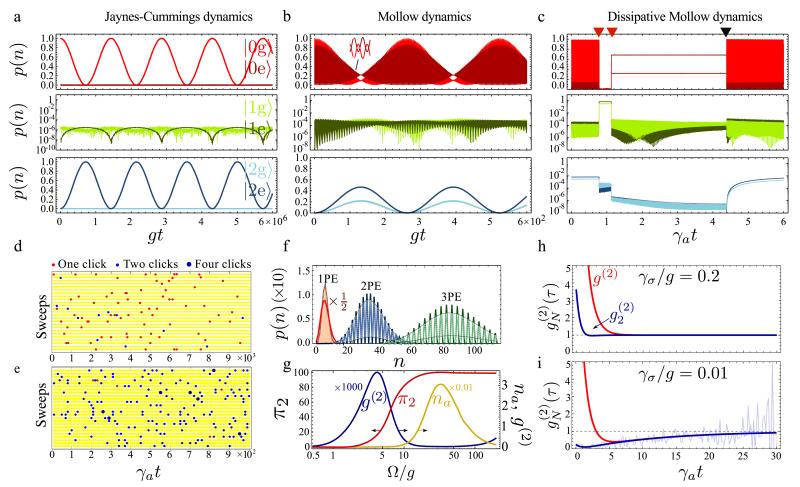
FIG. 4.

Upper row: Wavefunction evolution at the two-photon resonance pictured through the probability of the system to be in any of the states |ng/e〉. a, Hamiltonian evolution in the Jaynes-Cummings regime (low pumping). b, Hamiltonian evolution in the Mollow regime (high pumping). c, Quantum trajectory during a two-photon emission in the same regime as in b, but in the presence of dissipation. d–e, Cavity-photon clicks as they would be recorded by a streak camera (25 sweeps shown) for the pumping values Ω₁ in d and Ω₂ in e atω₂. In d the emission is highly bunched although it largely consists of single clicks, g⁽²⁾ = 3649 and π₂ = 16%, while in e, g⁽²⁾ = 17 with π₂ = 98.8%. f, Ideal NPE (N-Photon Emission) in thick lines and 99% NPE in translucid lines with an envelope to guide the eye. g, Pumping dependence of, left axis, π₂ and, right axis, g⁽²⁾ (from 0 to 3 649) and n_a (from 0 to 0.03) following ω₂. h–i, Second order photon correlations at the N = 1 (red) and N = 2 (blue) level, from Eq. (6) (smooth curve) and from Monte Carlo clicks (data).

When increasing pumping, resonances in the amplitude of the Rabi oscillations persist but are blueshifted due to the dressing of the states by the laser. The level structure becomes that of a dressed atom²⁶ strongly detuned from a cavity mode²⁷, bridging the Jaynes–Cummings dynamics with another fundamental model of light-matter interaction, namely, the Mollow physics of resonance fluorescence²⁸. The strong coupling that was previously dominated by the interaction between the QE and a cavity-photon, and probed by the laser, is now dominated by the interaction of the QE with the laser-photons, and is probed by the cavity. This elegant transition between the two pillars of nonlinear quantum optics brings the resonances in Eq. (1) to the corresponding form:

$${\omega }_N\left(\Omega \right)\approx {\omega }_a+\frac{\sqrt{4(N^2-1){\Omega }^2+N^2{\Delta }^2}+\Delta }{N^2-1}.$$ (2)

Equation (2) is realized when the energy of N cavity-photons match the N-photon transition between the |−〉 and |+〉 levels of the dressed atom²⁹, as sketched in Fig. 2b for the case N = 2. In the indeterminate case N = 1, Eq. (2) should be taken in the limit N → 1, yielding ω_L = ω_a − (2Ω² + Δ²/2)/Δ (in the dispersive regime, Δ ≠ = 0). All the dynamics discussed so far correspond to systems that are Hamiltonian in nature, such as atomic cQED realizations³⁰.

Dissipation as a trigger of quantum emission

Strong dissipation, e.g., in semiconductor cQED, is not always detrimental to quantum effects^31,32. On the contrary, Purcell enhancement of the Hamiltonian resonances just reported may give rise to giant photon correlations in the statistics of the field detected outside the cavity instead of Rabi oscillations^{33, 34}. The corresponding zero-delay photon correlations³⁵ g⁽ⁿ⁾ = 〈 a^†naⁿ〉/〈a^†a〉ⁿ are shown in the limit of vanishing pumping in Fig. 3c. An antibunching dip is observed for each g⁽ⁿ⁾ when exciting resonantly the emitter, followed by a series of N − 1 huge bunching peaks that match the resonances in Eq. (1), plotted in Fig. 3b. In these calculations, the Hamiltonian has been supplemented with superoperators in the Lindblad form to describe dissipation of the cavity (resp. QE) at a rate γ_a (resp. γ_σ)³⁶ (see Methods). Parameters used are γ_a/g = 0.1 and γ_σ/g = 0.01. Details of the formalism, as well as its extension to describe decoherence, are given in the Supplementary Information. As pumping is increased, resonances in g⁽ⁿ⁾ shift along curves ω_N(Ω) in the (ω_L, Ω) space defined by Eq. (2). This is shown for g⁽²⁾ in Fig. 3a for three values of pumping (and animated in the Supplementary Video), starting with Ω₀ = 10⁻¹g, close to the vanishing pumping case shown in Fig. 3c. Following g⁽²⁾ along the ω₂ resonance shows that a new peak emerges out of a uniform background, reaching a maximum g⁽²⁾ ≈ 3649 at the pumping Ω₁ ≈ 4g (middle trace) before a depletion of the resonance forms for higher pumping, reaching its minimum along ω₂ of g⁽²⁾ ≈ 17 at Ω₂ ≈ 32g (background trace). We have thus, so far, transferred some attributes of the remarkable quantum states produced by the cQED system to the outside world. We now proceed to show in which regimes and in which sense this transfer can actually be used for applications.

Strong correlations do not guarantee useful emission

The resonances in g⁽ⁿ⁾ are indicative of strong correlations but not in an intuitive way nor in a particularly useful one for applications. Indeed, g⁽²⁾ (we discuss the case n = 2 with no loss of generality), is unbounded and cannot be interpreted in terms of probability of two-photon emission. Other quantities to measure correlations, such as the differential correlation function³⁷ or the surge³⁸, present the same problem. To gain insights into the dissipative context, we turn to a quantum Monte Carlo approach³⁹, where one follows individual trajectories of the system and records photon clicks whenever the system undergoes a quantum jump. A tiny fraction of such a trajectory is presented in Figs. 4c (a larger fraction is provided in the Supplementary Information). This shows the probabilities of the system to be in the states |ng/e〉 for n up to 2 (probabilities in higher rungs are included in the numerical simulation).

Until time t ≈ 0.8 (in units of 1/γ_a), the QE essentially undergoes fast Rabi flopping (in an empty cavity) under the action of the laser, corresponding to the Mollow regime. At the same time, the driving of the third rung makes the probability to have two photons in the cavity sizable, as seen in bottom panel of Fig. 4c where the combined probability reaches over 1%, while the probability to have one photon is more than one order of magnitude smaller. This relatively high probability of the two-photon state, given the time available to realize it, eventually results in its occurrence. This causes the emission of a first cavity photon (indicated by a red triangle at the top of the figure) that collapses the wavefunction into the one-photon state, which is now the state with almost unit probability. The system is now expected to emit a second photon within the cavity lifetime (second red triangle in Fig. 4c). There is a jitter in the emission of the two-photon state due to the cavity, but this does not destroy their correlation. After the two-photon emission, the system is left in a vacuum state but without Rabi flopping, that is restored after a direct emission from the QE (black triangle) and a two-photon state is again constructed, preparing for the next emission of a correlated photon pair. The system is then brought back to its starting point. Although one photon coming from the QE decay is emitted per two-photon emission cycle, it is at another frequency and in a different solid angle. The two-photon emission is through the cavity mode, being therefore unspoiled and strongly focused.

Figures 4d–e present a series of detection events such as they would be recorded by a streak camera photodetector⁴⁰ for the pumping values Ω₁ and Ω₂ of Fig. 3a atω₂(Ω). The horizontal axis represents time and each point denotes a detection event as the detection spot is raster scanned across the image. The strong bunching at Ω₁ in Fig. 3a conveys that the number of correlated two-photon events (blue points) in Fig. 4d is much larger than would be expected for a coherent source. The emission remains nevertheless predominantly in terms of single photons (red points). Whilst the resonances in statistics are strong, they are therefore not meaningful for applications. On the other hand, at Ω₂, when the g⁽²⁾ resonance is depleted, the emission now consists almost exclusively of correlated photon pairs, as can be seen by the dominance of blue points in Fig. 4e.

Definition of a purity of N-photon emission

Since the standard correlation functions g⁽ⁿ⁾ do not correspond to actual N-photon emission, the problem poses itself how to describe what is in fact the most important feature of such an emitter: the amount of N-photon emission. Photon-counting^41-43 is a convenient way to do so in practical terms, since an ideal N-photon emitter never produces a number of photons which is not a multiple of N⁴⁴. We observe that for time windows T larger than the coherence time, counting of the photon bundles becomes Poisson distributed, as short time correlations are lost⁴⁵. This distribution is shown in Fig. 4f for the cases of ideal two-photon (2PE) and three-photon (3PE) emission. However, a non-ideal N-photon emitter occasionally emits single photons that spoil these distributions. If bundle events are given by the Poisson parameter λ_N and single events are given by λ₁, one finds (see Methods) that the distribution to count n photons in the time window T is:

$$P_N\left(n\right)=e^{-({\lambda }_1+{\lambda }_N)T}\sum _{k=0}^n\frac{n!{\left({\lambda }_{1}T\right)}^{n-Nk}{\left({\lambda }_{N}T\right)}^k}{k!(n-Nk)!}.$$ (3)

When the suppression of photon emission that is not a multiple of N is efficient, these parameters are related to the cavity population n_a through λ_N = γ_an_a/N. The λ parameters being independent of the time window T, we can define the purity of N-photon emission π_N as:

$${\pi }_N={\lambda }_N∕({\lambda }_1+{\lambda }_N).$$ (4)

This ratio represents the percentage of the emission that comes as N-photon bundles, that can now be contrasted with g^(N), as shown in Fig. 4g for N = 2. Here we find the remarkable result that g⁽²⁾, often described as the probability for two-photon emission, is in fact anticorrelated with π₂, the actual such probability: when g⁽²⁾ reaches its maximum, π₂ is starting to grow and when π₂ is maximum, g⁽²⁾ is locally minimum, although still larger than one.

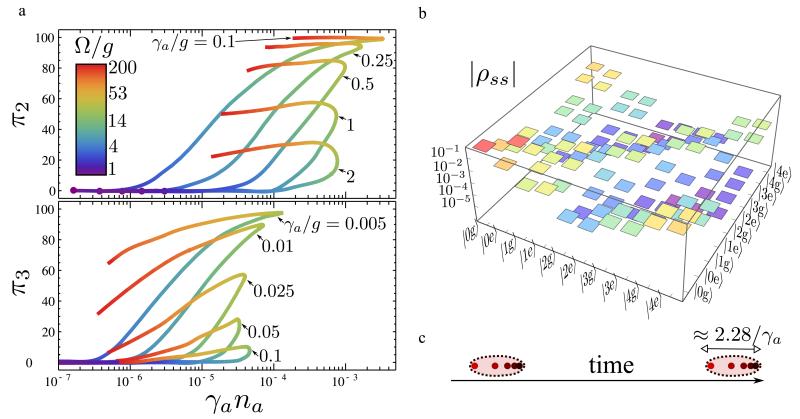
We characterize the efficiency of N-photon emission by plotting the purity and emission together, in Fig. 5a, for π₂ and π₃. Since N-photon emission is a (N + 1)th order process, it is more easily overcome by dissipation as N increases. However, almost pure two-photon and three-photon emission is already feasible with state of the art cQED systems: ≈ 85% of two-photon emission can already be obtained with current semiconductor samples (γ_a/g ≈ 0.5, g ≈ 12 GHz)^{46, 47} with a rate over 10⁷ counts per second (cps), while circuit QED systems (γ_a/g ≈ 0.01, g ≈ 50 MHz)⁴⁸ can even reach ≈ 90% of three-photon emission with a rate of 10³ cps. N-photon emission takes place when the coupling is large enough for the cavity to stop acting as a mere filter and actually Purcell enhance the corresponding multi-photon transitions⁴⁹. These results are extremely robust against dephasing, thanks to the short time window in which a bundle is generated and emitted, as is shown in the Supplementary Information.

FIG. 5.

a, Figures of merit for two- and three-photon emission in the space of purity/emission intensity. Almost pure two-photon and three-photon emission can be achieved with state of the art cQED samples: γ_σ/g = 0.01 for π₂ and 0.001 for π₃. b, Full density matrix of the system in the regime of four-photon emission, showing the predominance of the vacuum and the strong coherence between the 2 × 2 sub-blocks of 0 and 4 photons, and the 1/n cascade along the diagonal. c, Sketch of two five-photon bundles. Each bundle is composed of photons that pile up together upfront in time, due to the mechanism of their production. This structure is not described by the state |5〉.

Relation between the bundle and a Fock state

We have described the emission of our system in terms of “bundles” of photons, introducing a terminology that needs to be justified. In quantum theory, a state of the field with exactly N quanta of excitation is a Fock state |N〉 and it is natural to question whether our device is not precisely an “Emitter of Fock states |N〉”.

There are subtle links and departures between the two concepts. The Fock state |N〉 is a well-defined state that can be prepared and maintained exactly. It has no further structure and each of the N photons that compose it is fully indistinguishable from the others. The bundle, on the other hand, arises in a dynamical process of emission, describing the energy released from the cavity QED setup to the outside world. The cavity itself is not in the Fock state |N〉, being, to begin with, in the vacuum most of the time, and only in very short temporal windows does it undergo a cascade that sees in rapid successions the field transit through the various Fock states |n〉, with 0 ≤ n ≤ N, for a time γ_an in each of them. Since the system has a small probability to be in the state |N〉 before the emission and probability close to one to transit through each of the intermediate states during the cascade, one obtains the steady state probability:

$$p\left(n\right)=\frac{n_a}{N}\frac{1}{n},\text{for}1\le n\le N.$$ (5)

A snapshot of the full density matrix in the regime of four-photon emission is given in Fig. 5b. This shows the breakdown of the matrix into clusters of 2 × 2 blocks corresponding to the subspaces of the QE with n-photons. The vacuum largely predominates (the probabilities are shown in log-scale), followed by the blocks on the diagonal which provide p(n) as given by Eq. (5), and blocks of coherence between the various manifolds, which are small although nonzero, except the coherence elements |0μ〉 〈4ν with μ,ν ∈ {g,e} which are large. This confirms the direct manifestation, also in the dissipative regime, of the quantum superposition of the type $(\mid 0e\rangle \pm \mid Ne\rangle )∕\sqrt{2}$.

There remains a trace of this intra-cavity dynamics in the photodetection. The bundles are strongly correlated in two senses: first extrinsically, the emission comes in groups of N photons, suppressing the release of packets with other numbers of photons. Second, intrinsically, with different time intervals separating successive photons: the first photon is more closely followed by the second one than the second is by the third, and so on till the last photon that comes within 1/α_a of the penultimate (see Fig. 5c). Clearly, the bundle is a strongly-correlated group of closely-spaced photons that has a structure which is not described by the abstract object |N〉 alone. However, regardless of the internal structure of the bundle, it would appear as a Fock state in a measurement integrated over a small time window. Further discussion through the Wigner function can be found in the Supplementary Information.

Regimes of N-photon emission: guns and lasers

Now that we have engineered N-photon emitters, we have to ask the same questions than those put by Glauber³⁵ at the dawn of quantum optics, on the nature of quantum optical coherence for these sources. The answer is as simple as it is beautiful: N-photon emitters are the exact counterpart of conventional emitters with the provision of replacing the unit of emission—the photon—by a bundle of N of them. We now show that our class of emitters can operate in the same regimes, lasing or photon guns, but with bundles. To do so, we describe the statistics of the bundles when considered as single entities, by introducing the generalized correlation functions $g_N^{\left(n\right)}$:

$$g_N^{\left(n\right)}(t_1{,}_{\cdots },t_n)=\frac{\langle \mathcal{T}-\left\{\prod _{i=1}^n{a}^{†N}\right(t_i\left)\right\}\mathcal{T}+\left\{\prod _{i=1}^n{a}^N\right(t_i\left)\right\}\rangle }{\prod _{i=1}^n\langle a^{†N}{a}^N\rangle \left(t_i\right)}$$ (6)

with ${\mathcal{T}}_{\pm }$ the time ordering operators. This upgrades the concept of the nth order correlation function for isolated photons to bundles of N photons. The case N = 1 recovers the definition of the standard g⁽ⁿ⁾, but for N ≥ 2, the normalization to the bundle density makes Eq. (6) essentially different from the standard correlation functions g^{(n × N)}. Similarly to the single-photon case, the two-bundle statistics $g_N^{\left(2\right)}\left(\tau \right)=\frac{\langle a^{†N}\left(0\right)a^{†N}\left(\tau \right)a^N\left(\tau \right)a^N\left(0\right)\rangle }{\langle \left(a^{†N}{a}^N\right)\left(0\right)\rangle \langle \left(a^{†N}{a}^N\right)\left(\tau \right)\rangle }$ is the most important one. The validity of this definition for $g_2^{\left(2\right)}$ is confirmed in Figs. 4h-i, where it is plotted (smooth curve) along with direct coincidences between clicks from the Monte Carlo simulation (data). Such $g_2^{\left(2\right)}$ correlations can be measured directly thanks to recent developments in two-photon detection⁵⁰. For the Monte Carlo computation, all events are considered as single photons for the standard g⁽²⁾ calculation (red curve in Fig. 4h-i), and only two-photon events are considered as the basic unit of emission for $g_2^{\left(2\right)}$ (blue curve). Except in the small jitter window of width 1/γ_a in which they cannot be defined, photon pairs exhibit antibunching for long-lived QE, while they are Poisson distributed for short-lived QE. In the latter case, one can check that $g_2^{\left(3\right)}({\tau }_1,{\tau }_2)=1$ except from the aforementioned jitter window (Supplementary Information). The emitter therefore behaves respectively as a two-photon gun, and—according to Glauber³⁵—as a laser, but at the two-photon level. The effect the QE lifetime has on the statistics of the bundles can be understood as a consequence of the key role the QE emission plays to restore the construction of a N-photon state. At the single-photon level, the standard g⁽²⁾(τ) fails to capture this fundamental dynamics of emission. All this confirms the emergence of a new physics at the two-photon level. The same behaviours hold for higher N.

METHODS

System dynamics

In order to describe dissipation in addition to the Hamiltonian dynamics, we resort to a master equation in the Lindblad form³⁶:

$$\stackrel{.}{\rho }=-i[H,\rho ]+\left[\frac{{\gamma }_a}{2}{\mathcal{L}}_a+\frac{{\gamma }_{\sigma }}{2}{\mathcal{L}}_{\sigma }\right]\rho ,$$ (7)

expressed in terms of the Liouvillian super-operator ${\mathcal{L}}_c\rho =2c\rho c^{†}-c^{†}c\rho -\rho c^{†}c$, with γ_a and γ_σ the decay rates of the cavity and the quantum emitter, respectively. By arranging the elements of the density matrix in a vectorial form, we can express this equation as $\dot{\overrightarrow{\rho }}=M\overrightarrow{\rho }$ from which the steady-state density matrix ${\overrightarrow{\rho }}_{\mathrm{SS}}$ is obtained as the null space of the matrix M. A more general expression that takes into account additional dephasing terms is provided and investigated in the Supplementary Information.

For photon counting calculations, we solve the same problem using the Monte Carlo method of quantum trajectories, which allows to use a wavefunction picture in a dissipative context. In this approach, one uses an evolution operator constructed with a non-Hermitian Hamiltonian $H_{\mathrm{eff}}=H-i\frac{{\gamma }_a}{2}{a}^{†}a-i\frac{{\gamma }_{\sigma }}{2}{\sigma }^{†}\sigma$, whose resulting dynamics can be interrupted in each time step δt by a quantum jump acting on the wavefunction as cψ|〉/〈ψ|c^†c|ψ〉 (c ∈ {a, σ}) with probability p_c = δt γc〈ψ|c^†c|ψ〉. These jump events are then recorded as photon emissions coming from the cavity or the QE.

Photon counting distribution for the imperfect N-photon emitter

In the limit in which the counting of N-photon bundles becomes Poisson distributed, the random variable X_N that counts them in a time window T follows the distribution P(X_N = k) = exp(−λ_NT)(λ_NT)^k/N/(k/N)! if k is a multiple of N, and is zero otherwise, with a generating function Π_XN (s) = 〈s^X_N〉 = e^{−λ_N(1−sN)}. A non-ideal N-photon emitter emits in addition single photons that spoil these distributions. Photon counting then results from the sum of two random variables X₁ + X_N where X₁ is a conventional Poisson process. The generating function of the imperfect N-photon emitter is ${\prod }_{X_1+X_N}={\prod }_{X_1}{\prod }_{X_N}$, where ${\prod }_1=e^{-{\lambda }_1(1-s)}$ is the generating function of a Poissonian distribution. The closed-form expression provided in the text is straightforwardly derived as $P_N\left(n\right)={\partial }^{\left(n\right)}{\prod }_{X_1+X_N}∕\partial s{\mid }_s=0$.