Abstract
We have recently completed a full re-architecturing of the Rosetta molecular modeling program, generalizing and expanding its existing functionality. The new architecture enables the rapid prototyping of novel protocols by providing easy to use interfaces to powerful tools for molecular modeling. The source code of this rearchitecturing has been released as Rosetta3 and is freely available for academic use. At the time of its release, it contained 470,000 lines of code. Counting currently unpublished protocols at the time of this writing, the source includes 1,285,000 lines. Its rapid growth is a testament to its ease of use. This document describes the requirements for our new architecture, justifies the design decisions, sketches out central classes, and highlights a few of the common tasks that the new software can perform.
1 Introduction
The Rosetta molecular modeling suite has proven useful in solving a wide variety of problems in structural biology (Das & Baker, 2008, Kaufmann et al., 2010) (Table 1). Rosetta was initially written in Fortran77 as two separate programs for protein structure prediction (Simons et al., 1997.) and for protein design (Kuhlman & Baker, 2000), merged, mechanically ported to C++, and refactored for several years thereafter. The code base has been in upheaval through the majority of its existence. Three years ago, we began a complete rewrite to recenter the program using modern software design principles. The final product, like its predecessor, remains in a state of flux; however, several core modules have solidified to provide a reliable foundation on which to build new protocols for macromolecular modeling. This document attempts to describe these central modules in the way one might describe industrial software: in terms of requirements, design decisions, and architecture. It provides the necessary background for constructing new modeling simulations using these library modules. We close the chapter with a concrete example of one such simulation.
Table 1.
Some representative applications available within the Rosetta molecular modeling suite.
| Application Name | Brief Description |
|---|---|
| AbinitioRelax | predict the structure of a protein from its sequence(Simons et al., 1997., Bonneau et al., 2001, Bonneau et al., 2002, Bradley et al., 2005, Das et al., 2007, Raman et al., 2009) |
| enzdes | design a protein active site to catalyze a chemical reaction (Zanghellini et al., 2006, Rothlisberger et al., 2008, Jiang et al., 2008) |
| FixedBBProteinDesign | redesign the amino acids on a fixed protein backbone (Kuhlman & Baker, 2000, Dantas et al., 2003, Kortemme et al. 2004) |
| protein_docking | predict the docked conformation of two proteins with known structure (Gray et al., 2003, Wang et al., 2005) |
| ligand_docking | predict the orientation that a small molecule binds to a protein (Meiler & Baker, 2006, , Kaufmann et al., 2008, , Davis & Baker, 2009) |
| loop_modeling | predict the conformation of a set of protein loops (Rohl et al., 2004, Mandell et al., 2009). |
| rna_denovo | predict the folded structure of an RNA molecule given its sequence (Das & Baker, 2007) |
| rna_design | Design a new sequence for an RNA molecule (Das et al., 2010) |
The new architecture has enabled a rapid expansion in Rosetta’s functionality. In addition to providing a solid foundation on which many new protocols have been built, the new architecture has enabled functionality that would have been virtually impossible in Rosetta2, including Python bindings for all Rosetta classes (Chaudhury et al., 2010) and an interactive game, Foldit, that challenges users to predict a protein’s structure (Cooper et al., 2010).
2 Requirements
The driving requirements for our reimplementation of Rosetta can be categorized into four major groups. Our new code should preserve the existing functionality. It should generalize that functionality to enable expansion. It should adhere to certain code-quality standards to enable new execution pathways. Finally, it should be fast.
2.1 Preserving Existing Functionality
Our new implementation needed to recreate the existing Rosetta functionality. In particular, we required the new implementation to faithfully reproduce the terms in Rosetta’s score function (Rohl et al., 2004). We required that it reproduce the central algorithms: gradient-based minimization, rotamer packing/protein design, Monte Carlo conformational search, and Rosetta’s efficient reuse of scores when rescoring a structure that has changed very little. It needed to update a structure’s Cartesian coordinates following changes to its internal degrees of freedom (e.g. to a protein’s backbone dihedral angles). Finally, it had to allow for user-defined restraints (a.k.a. “constraints” in Rosetta jargon) between arbitrary groups of atoms.
2.2 Generality Requirements
Beyond ensuring that Rosetta3 was capable of performing the same functions as Rosetta2, we required that it be more general on several levels so that it could be applied to new challenges in computational structural biology. 1) It should be able to represent new chemical moieties. 2) It should be amenable to the addition of new energy terms. 3) It should encourage the development of new algorithms. The implementation for these three aspects of the code should be as loosely coupled as possible to minimize the amount of work necessary to expand in one direction; adding a new term to the score function should require no updates to the chemical representation of structures, or the algorithms used to evaluate that term on structures (Figure 1).
Figure 1.
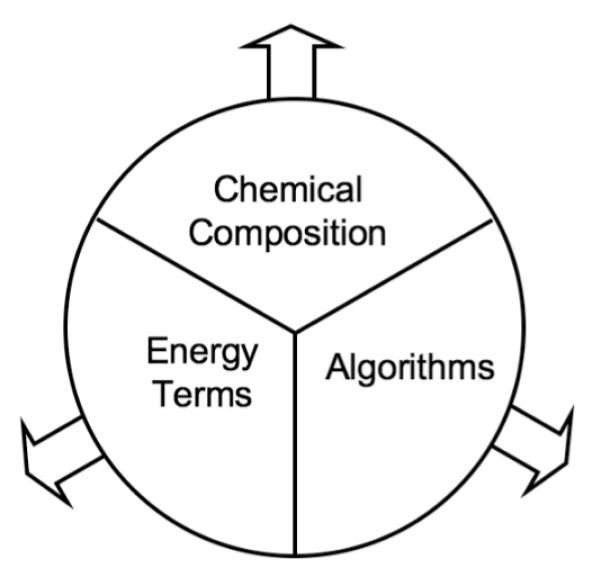
Generality Wheel. Expanding Rosetta’s functionality in one area (Energy Terms, Chemical Composition, or Algorithms) should not require an expansion to the other areas. The areas should be protected from each other through the use of generic interfaces.
We required that the system be allowed to change its chemical composition at any point during a simulation; the new software could make no assumptions that the sequence composition or length be fixed. We further required generality within protocols such that they be nestable within each other. Moreover, we wanted to decouple job distribution from protocols themselves so that protocols could be run in any one of several job-management environments (e.g., desktop computer, commodity cluster, distributed computing environment, and supercomputer).
2.3 Code Quality Requirements
In addition to requiring the new code to perform new computational tasks and broach new problems in macromolecular modeling, we also required that we be able to perform these tasks in novel ways. We wanted to ensure Rosetta could be executed in a multithreaded environment where multiple threads could execute simultaneously working with separate structures and score functions without corrupting each other’s data. As a consequence, Rosetta could not rely on non-constant shared data (e.g., a global array containing the coordinates of the current structure, or a global score function).
Furthermore, we were interested in enforcing code-quality requirements for the purpose of ensuring the greatest reusability of our code. Consider a piece of code, P, written to perform some task, T, in some context, C; P’s reusability can be measured as the number of other contexts besides C in which P can perform T. While it is impossible to list all the alternate contexts in which a piece of code should be able to function, reusable code contains certain identifiable features, and so we imposed requirements on our code that it should contain these features. In particular: Reusable code is clearly written with descriptive variable names and function names, and comments describing the behavior of the classes and functions, so that users would understand what will happen when invoking a particular function. Reusable code is factored into its component pieces, resulting in short functions and small classes with well defined responsibilities, so that users can pick out just the pieces of functionality they are interested in reusing. Reusable code is easy to use, and hard to misuse because code that frustrates developers does not get reused.
2.4 Speed Requirements
To ensure that our code was absolutely as fast as it could be, we required certain specific features of our algorithms and code. Score function evaluation: Scoring an N residue structure, assuming there are no long-range energy terms, should proceeded in O(N) time. Scoring a long-range energy term defined over M pairs of atoms should proceed in O(MlgM) time; i.e. if  O(N), then long-range energy evaluation should be only logarithmically more expensive than short-range energy evaluation. Kinematics: The number of coordinate update operations should be minimal and should be transparent – the user should never be allowed to access out-of-date coordinate data. Together, these requirements suggest using a just-in-time (lazy) coordinate update algorithm. Furthermore, updating the coordinates for k atoms following a set of changes to m internal degrees of freedom (DOFs) should take O(k+m) time. General: Energy and coordinate calculations should be performed at double precision since our gradient-based minimization techniques converge after fewer score-function evaluations at higher precision. Calls to new and delete should be avoided in performance-sensitive code. Finally, function calls in inner-most loops should be inlined to the greatest extent possible.
O(N), then long-range energy evaluation should be only logarithmically more expensive than short-range energy evaluation. Kinematics: The number of coordinate update operations should be minimal and should be transparent – the user should never be allowed to access out-of-date coordinate data. Together, these requirements suggest using a just-in-time (lazy) coordinate update algorithm. Furthermore, updating the coordinates for k atoms following a set of changes to m internal degrees of freedom (DOFs) should take O(k+m) time. General: Energy and coordinate calculations should be performed at double precision since our gradient-based minimization techniques converge after fewer score-function evaluations at higher precision. Calls to new and delete should be avoided in performance-sensitive code. Finally, function calls in inner-most loops should be inlined to the greatest extent possible.
3 Design Decisions
In response to the requirements for our new software, we made a series of decisions that shaped its design. This section lays out the rationale for some of the most important decisions, connecting these decisions to the requirements they were meant to address.
3.1 Object-oriented Architecture
Our earliest design decision was that we would follow object-oriented design principles in the creation of our new software. There are two prominent features of object-oriented programs that we sought to take advantage of: the encapsulation of data within classes, and the pairing of data and algorithms through polymorphic lookup (virtual functions). Data encapsulation is arguably the most important advance in software design since the advent of high level programming languages. Classes encapsulate data through a compiler-provided mechanism of privacy: code that is outside of a class is unable to read from or write to private data inside of a class. Instead, classes gate access to private data through public function calls. The use of gating functions allows a class to enforce data-integrity rules that might otherwise be broken if external code were able to change the class’s data without its knowledge. The fact that classes assume responsibility for their data frees the remaining code in the program from the responsibility of maintaining that data. Global variables, in contrast, inflict their integrity-maintenance requirements on the entire program. Every new line of code has to be aware of and respect the data integrity requirements stemming from the program’s global variables. The more global variables a program contains, the more complicated extending that program becomes. Global variables restrict the alternate contexts in which a working piece of code could be harnessed, they make code hard to use and easy to misuse. Indeed, Rosetta2’s reliance on global variables motivated our rearchitecturing more than any other factor. Finally, it should be mentioned that multithreaded applications are significantly easier to write when data is held in classes instead of global variables.
In addition to pursuing an object-oriented architecture, we also decided to impose “const-correctness” requirements of the classes we created. C++ compilers enforce an idea that, if an instance of a class is const, then its non-const functions may not be called, and that the data inside the instance may not be modified. The primary benefit of const-correct code is speed. Class A holding an instance of class B can provide read-only access to B by delivering a “B const &” instead of delivering a copy of B (which would be slow). As a secondary benefit, const-correctness makes code hard to misuse, as the const status of an object conveys what function calls are appropriate and which are not.
3.2 Residue centrality
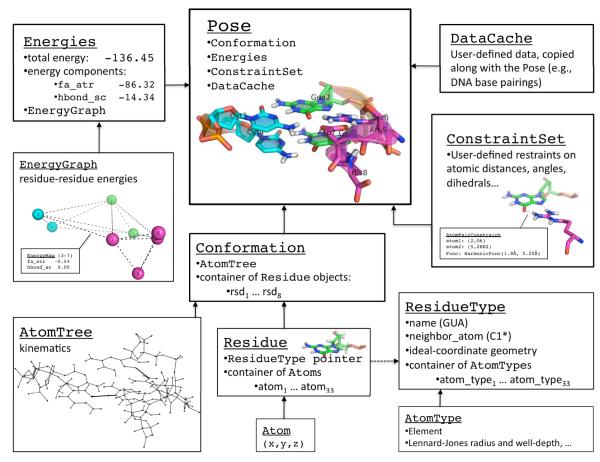
Two requirements – the preservation of Rosetta’s protein design functionality, and the desire to easily incorporate new chemical moieties – quickly led to an early design decision that shaped much of our new implementation: Rosetta3 would be “residue centric.” This decision manifested in two ways: all atoms in a molecular system would be represented within residues (Figure 2), and residues would be the unit for scoring. To justify this design decision, the remainder of this section introduces the fundamental concepts behind Rosetta’s protein-design module, the packer.
Figure 2.
Pose architecture. The components of the Pose class are illustrated for the case of a simple eight-residue system consisting of a two base-pair DNA duplex (residues 1-4) and a protein segment (residues 5-8). Conformational and chemical information are stored within the Conformation class as Residue objects (coordinates) with pointers to ResidueTypes (chemistry); the AtomTree class records the kinematic connectivity (the mapping between internal and Cartesian coordinates). Energies from the most recent evaluation of the scoring function are stored in the Energies class, which holds residue-residue interactions in the EnergyGraph. Finally, user-defined coordinate restraints are stored in the ConstraintSet, and additional Pose-associated data can be stored in the DataCache, where it will be copied along with the Pose during simulations.
In the packer, the task of designing a new sequence is accomplished by building new amino acids onto a fixed-protein-backbone scaffold. Each design task is modeled as a combinatorial optimization problem where the optimal solution is the sequence and structure of side chains built upon the scaffold that minimizes the score function. At each residue, i, the algorithm considers a set of rotamers (Ponder & Richards, 1987), Si, which represent one or more amino acid types. The algorithm then searches for the vector assignment of rotamers to the backbone, s, where the assignment to residue i, si ∈ Si. The rotamer-vector search space is the Cartesian product of the individual rotamer spaces: S = ∏iSi. This problem is NP-complete (Pierce & Winfree, 2002). Rosetta’s design algorithm searches for a low-energy (if sub-optimal) rotamer assignment using a Monte Carlo with simulated annealing approach (Kuhlman & Baker, 2000). Starting from a particular rotamer vector s, it computes the change in the score, ΔE, induced by substituting the rotamer at residue i, a = si with a new rotamer b ∈ Si. The computed ΔE is then fed to the Metropolis Criterion leading either to the acceptance or rejection of the rotamer substitution. For a typical design simulation, several million rotamer substitutions are considered. At the conclusion of simulated annealing, the design algorithm replaces residues from the input structure with the new rotamers it had selected.
The task of computing ΔE for a given rotamer substitution suggests the utility of a residue-centric design. Design software that relies on a pairwise-decomposable energy function (as almost all design software does (Hellinga et al., 1991, Desmet et al., 1992, Dahiyat & Mayo, 1996, Chowdry et al., 2007)) typically pretabulates rotamer-pair-interaction energies: that is, the interaction energies for rotamers on residue i and the rotamers on residue j are computed before rotamer search begins and stored in a table Eij of size ∣Si∣×∣Sj∣. When computing ΔE for replacing rotamer a on residue i with rotamer b, the interaction energy for both a and b may be looked up from the set of tables holding residue i’s interactions with i’s neighbors. If residues were the unit of scoring, then residue-pair energies could easily be pretabulated.
Moreover, we required the new code to be sufficiently general to perform fixed-backbone-like design on nucleic acids and small molecules in addition to proteins. The analogy from designing protein residues to designing nucleic acid residues is so straight forward that it barely qualifies as an analogy; instead of building amino-acid rotamers at the design positions, the algorithm would build nucleic-acid rotamers. Each down stream step in the design process (energy pretabulation, simulated annealing and residue replacement) could be identical. Design of RNA using Rosetta3 has already been tested (Das et al., 2010). The analogy from designing protein residues to designing small molecules is similar: the algorithm would need to build small-molecule rotamers, whatever they might look like. For the design algorithm to handle amino acids, nucleic acids, and small molecules uniformly, it is best to represent each class of molecule in the same fashion: ergo, we would represent all chemical entities with residues.
3.3 Pose
Following the residue-centrality decision, we sought to define the complete state of a molecular system within a single container class, termed a Pose. The Pose would be responsible for holding a set of residues and the result of a score-function evaluation on those residues (class Pose (Sec. 4.5) would hold a Conformation object (Sec. 4.4) and an Energies object (Sec. 4.6.3); see Figure 2). By storing the scores with the structure, it would be possible to reuse certain scores from the last score-function evaluation when rescoring a structure. In addition to holding a structure and its energies, class Pose would also be responsible for holding generic data for presently-unforeseen purposes; as a generic container, this would allow protocol developers to pair information relevant for a particular structure with that structure. Then, when copying a Pose, all the information that is relevant for that Pose, would be copied with it. To recreate Rosetta2’s Monte Carlo mechanism, we would thus rely on Pose copy operations – the history of how a particular structure came into being could be recorded in a Pose during the course of its trajectory, and would be automatically copied along with the structural and energetic information.
3.4 Scoring
With the residue-centrality design decision (Sec. 3.2), residues would be the unit of scoring in Rosetta. We extended this idea slightly by imposing a decomposition of the score-function terms into those which are defined on residues, those which are defined on residue pairs, and those which are defined on entire structures, and by representing this decomposition through a class hierarchy (Sec. 4.6.2). To include a new term in Rosetta requires finding the appropriate base class from which to derive and implementing the interface to that class. As a consequence, once a new term was incorporated into this class hierarchy, it could be used in scoring, packing and minimizing and in any future algorithm that relies only on the class interfaces. This class hierarchy separates energy terms from algorithms that use those terms, making it easy to add new terms and new algorithms. Rosetta developers are currently experimenting with 174 terms, proving that adding new terms is quite easy.
4 Architecture
The remainder of this paper describes the layout of Rosetta’s classes and further sketches the rationale for the way we have organized data and algorithms.
At its highest level, Rosetta is composed of three sets of libraries: a) a core library that defines structures, and supports structure I/O, scoring, packing and minimization, b) a protocols library that consists of common structural modifications one might wish to make to a structure, and a means to control the distribution of jobs, and c) several utility libraries which collect common data structures (a 1-indexed container, an owning pointer class, an optimized graph class) and numeric subroutines (vector and matrix classes, random number generators). Individual executables link against these libraries allowing a protocol writer to rapidly prototype by creating a new executable rather than modifying the single monolithic executable, a design flaw in Rosetta2.
Code is organized so that libraries and namespaces (C++ namespaces provide a mechanism for grouping related class and function names) mirror the directory structure thus making it easy to find code. The top-level directory src/ (source) contains directories utility/, numeric/, core/, protocols/, and devel/, each corresponding to their own library. It also contains an apps/ directory, in which executables with main() functions live; apps is not linked as a library. Each library corresponds to a top-level namespace. Any subdirectory of a library directory corresponds to a nested namespace. Classes are generally declared and defined in files with the same name and a .hh and .cc extension. For example, class ScoreFunction is declared in src/core/scoring/ScoreFunction.hh and defined in src/core/scoring/-ScoreFunction.cc. It lives in namespace core::scoring. Dividing up code into namespaces allows class writers to communicate their purpose by association, and avoids problems of name-collision that are common in large software projects.
4.1 core Library
Namespace core contains data structures and algorithms for describing macromolecules chemically (Sec. 4.2) and structurally (Sec 4.3), for scoring macromolecular conformations (Sec. 4.6), and for optimizing these conformations with two common techniques: minimizing (Sec. 4.7) and packing (Sec. 4.8).
4.2 core::chemical
The main class housed in the chemical namespace is ResidueType. A ResidueType class describes the chemical connectivity of a single, abstract residue type. Every instance of alanine in a single structure will point to the alanine ResidueType; this ensures a minimal memory footprint by avoiding redundant representations. Class ResidueType lists the set of atoms, their names, their elements, their atom type, their set of intra-residue chemical bonds, and notes which atoms are able to form inter-residue chemical bonds. Each atom in a ResidueType must have a unique name. Two residue types are different if they have different chemical bonds; this means the two tautomers of histidine (where either ND1 or NE2 is protonated) are represented by two different ResidueTypes. To change the tautomerization state of a structure is to change its chemical identity. Similarly, the N- and C-terminal variants on each of the 20 amino acids must be represented by separate ResidueTypes from the “mid” variants since they have different atom counts, and different inter-residue connection capacities. To avoid defining by hand each of the 60 additional variants for the 20 amino acids (the N-terminal variant, the C-terminal variant, and the free-amino-acid variant), we have implemented a system for patching residue types similar to the one used by CHARMM (Brooks et al., 2009).
ResidueType is also responsible for defining two features that are used to determine “neighborness” of residue pairs: it nominates one of its atoms as its “neighbor atom,” the coordinate of which is used in neighbor detection; and it defines a “neighbor radius” measured as the longest distance possible from the neighbor atom to all other heavy-atoms in the residue under all possible assignments of dihedral angles. Neighbor detection is discussed further in Sections 4.6.2 and 4.6.3.
To hold the set of ResidueTypes, the chemical namespace also houses class ResidueTypeSet; each Residue-Type must have a unique name among the other ResidueTypes belonging to the same ResidueTypeSet. Rosetta protocols often rely on multiple residue type sets, with the most common being the “centroid,” or low-resolution, residue type set and the “fullatom” residue type set. The protein design subroutines (Sec. 4.8) consider alternate ResidueTypes for an existing residue by requesting the list of all available ResidueTypes from the ResidueTypeSet of the existing residue. Because the fullatom and centroid residue type sets are both represented with a single class, the design subroutines are capable of performing both full-atom and centroid design.
4.3 core::kinematics
Rosetta uses an internal-coordinate representation of a molecular system when performing updates to the conformation. Thus the primary degrees of freedom during Monte Carlo perturbations and gradient-based minimization are dihedral angles about rotatable bonds and rigid-body transformations between subunits, rather than the xyz coordinates of individual atoms common in molecular dynamics simulations (bond lengths and angles can also be included but are typically held fixed). The internal coordinate representation makes possible a dramatic reduction in the number of degrees of freedom, permitting efficient exploration of conformational space. At the same time, it introduces a complication into the process of specifying a molecular system, namely that one must explicitly define the path by which internal coordinate changes propagate through the system. In the case of flexible-backbone protein docking, for example, the kinematics can be specified by the choice of an anchor residue in each partner. Changes to the six rigid-body degrees of freedom modify the relative orientation of these two anchor residues; changes to the dihedral angles of the monomers preserve the relative orientation of the anchors while the coordinates of the monomers are updated by folding the chains outward from the anchor points.
In general, the kinematic connectivity of any molecular system can be specified by defining a tree (connected, acyclic graph) whose nodes correspond to the atoms in the system, and whose edges represent kinematic connections. We generate Cartesian coordinates for the system by starting at a defined root node and traversing outward (downstream) to the leaves. The internal coordinates of the system are mapped onto the individual atoms, with most atoms storing a bond length, bond angle, and dihedral angle relative to a reference frame defined by three upstream atoms. Where rigid-body connections between subunits are needed, a second flavor of atom is introduced which stores a full rigid-body rotation and translation between reference frames defined on the two partners. This kinematic tree of atoms is referred to as an AtomTree (Abagyan et al., 1994). To simplify the process of specifying the AtomTree, a user can define a residue-level tree of kinematic connectivity, termed the FoldTree, in which nodes correspond to individual residues rather than atoms. The AtomTree can be built automatically from the FoldTree.
For efficient scoring, the AtomTree tracks which DOFs have changed since the last score function evaluation; if two residues have not moved with respect to each other, then some of their interaction energies from the last score function evaluation may be reused (Sec. 4.6.2). To communicate which residues have moved, the AtomTree creates a “coloring” of the residues in the structure (wherein each residue is assigned an integer) through a recursive traversal of the tree; if two residues have not moved with respect to each other, they are assigned the same color in this traversal. If a residue has undergone a change to its internal degrees of freedom, then it is assigned the color zero, signaling to the scoring machinery that none of its old energies may be reused in the next score evaluation. The data structure for holding the coloring is called the DomainMap.
4.4 core::conformation
The conformation layer describes the physical instantiation of a macromolecule; its main class, class Residue, contains the coordinate information (both Cartesian and internal) for a single residue. It contains none of the chemical information needed to describe the residue, but rather, keeps a pointer to the ResidueType (Sec. 4.2) that it is an instance of. Class Residue also holds all the information about the inter-residue chemical bonds that it forms to other residues. Such information would not be appropriately held in the chemical layer.
A full structure is represented by a Conformation object, which is composed of a set of Residues and an AtomTree. As mentioned in Section 2.4, the user should never be able to access out-of-date coordinate information. The Conformation handles this responsibility by controlling access to the Residues it contains: it provides a set of mutator methods for setting Cartesian and internal coordinates so that it can shuttle these changes between the Residue objects and the AtomTree nodes efficiently, and it allows efficient read access (const access) to its Residues. By disallowing non-const access to its Residue objects, it ensures data integrity; only the Conformation has the permission to modify its Residues. The central classes of the chemical, conformation, and kinematic namespaces and their relationships are illustrated in Figure 2.
4.5 core::pose
Class Pose, as described in Section 3.3, represents the complete state for a molecular system; it stores a Conformation object, an Energies object (Sec. 4.6.3), a ConstraintSet (Sec. 4.6.5), and a generic DataCache container (Figure 2).). When a user copies a Pose, they copy all relevant information for that structure. The MonteCarlo object (Sec. 4.10) relies on the Pose’s copy operations to keep track of the best scoring structure encountered in a trajectory.
We have two levels of observers for Pose objects: active and passive observers. The passive observers deliver just-in-time information about a Pose; these are the PoseMetrics classes. A PoseMetric will report a certain property of a Pose that is pertinent for decision making about the structure, but which may be slow to compute, e.g. its solvent accessible surface area. The PoseMetric observes the Pose so that, if the Pose has not changed since the last time the property was calculated, then the PoseMetric can report the previously-calculated value.
We have a second set of active observers that respond immediately to particular events, e.g. residue insertion or deletion events. Such observers are commonly used to maintain residue mapping information when a Pose is undergoing a series of residue insertions or deletions. For example, a Constraint (Sec. 4.6.5) between residue 5 and residue 50 needs to be remapped when residue 39 is deleted so that it applies to residue 5 and residue 49. These active observers allow protocol writers to perform residue insertions and deletions without having to provide an additional residue-remapping interface; and it allows users to rely on these protocols even when they would like to maintain application-specific residue-mapping information.
4.6 core::scoring
Namespace core::scoring contains the many classes that define and evaluate Rosetta’s score function. The key classes in this namespace are ScoreFunction, EnergyMethod, and Energies.
4.6.1 ScoreFunction as a container
The score for a structure is the weighted sum of the component energies. A ScoreFunction object holds a set of weights and a set of classes (EnergyMethods) that are able to evaluate the energies and derivatives for the components with non-zero weight. A score function may be evaluated on a Pose, and will return its score:
core::scoring::ScoreFunction sfxn;
core::pose::Pose p;
... // initialization
double the_score = sfxn( p );
The ScoreFunction acts as a container making it easy to pass the active components into subroutines that require a score function to guide their behavior (e.g. packing or minimizing) but that are indifferent to which components are active. The ScoreFunction holds its EnergyMethods in seven lists (one for each of the direct base classes in Figure 3), and when scoring a Pose, iterates across each list to request each EnergyMethod evaluate the energies for certain residues and/or residue pairs in the Pose. Unlike Rosetta2, there is not a singular (global) score function that is active. Separate threads will instantiate separate ScoreFunction instances; subroutines and classes that rely on computing the score will be given ScoreFunction objects to use.
Figure 3.
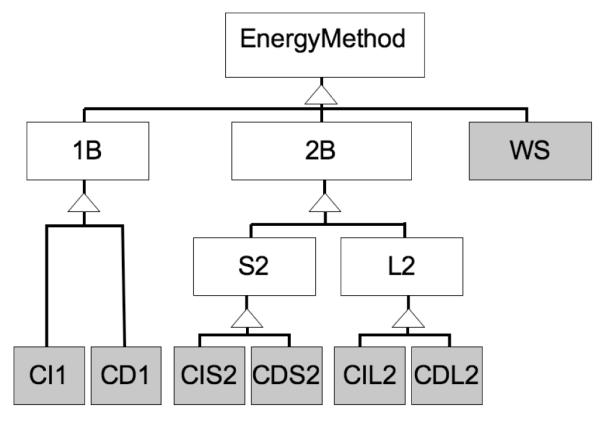
EnergyMethod class hierarchy. The first level divides the one-body (1B), two-body (2B) and whole-structure (WS) energies. The second level divides the two body energies into short-ranged (S2) and long-ranged (L2). The final level divides context dependent (CD) from context independent (CI) energy methods. The seven classes in gray are the direct base classes for concrete energy methods; e.g. the HydrogenBondEnergy derives from the CDS2 class, as it is context-dependent, short ranged, and two-body.
The terms available in Rosetta’s score function are listed in the ScoreType enumeration. Each element in this enumeration corresponds to one term. EnergyMethods are allowed to compute more than one term at a time; they place the scores they calculate into an object of type EnergyMap, which contains an array with one double for each element in the ScoreType enumeration. The ScoreFunction and its EnergyMethods communicate through EnergyMaps. The total score is simply the dot product between the unweighted-energies vector and the weights vector.
To activate a term in a ScoreFunction, a user needs merely to set the weight for that component to a non-zero value. For example, the call to sfxn.set_weight(fa_atr,0.8) would trigger the activation of the attractive portion of the Lennard-Jones energy. Behind the scenes, the ScoreFunction fetches an instance of the EnergyMethod that is responsible for evaluating the fa_atr ScoreType and stores that EnergyMethod. The class responsible for doling out EnergyMethods to ScoreFunctions is the ScoringManager; the ScoringManager maintains a map from ScoreTypes to EnergyMethodCreators, each of which is responsible for instantiating a particular EnergyMethod. EnergyMethodCreators register with the ScoringManager at load time – not compile time – thereby allowing definition of EnergyMethods outside of core (e.g. in protocols or devel).
4.6.2 Energy Method Class Hierarchy
There are twelve abstract EnergyMethod classes, seven of which are intended for deriving concrete energy methods (Figure 3). The ScoreFunction treats each of the seven classes differently when it comes to score evaluation and bookkeeping. At the top of the hierarchy is the EnergyMethod class. Three classes derive from it directly: OneBodyEnergy, TwoBodyEnergy, and WholeStructureEnergy. These classes represent energy functions that are defined on single residues, on residue pairs, or on entire structures. Derived OneBodyEnergy classes implement a method:
void
residue_energy(
conformation::Residue const & res,
pose::Pose const & p,
ScoreFunction const & sfxn,
EnergyMap & emap
) const;
and derived TwoBodyEnergy classes implement a method
void
residue_pair_energy
conformation::Residue const & res1,
conformation::Residue const & res2,
pose::Pose const & p,
ScoreFunction const & sfxn,
EnergyMap & emap,
) const;
The presence of a Pose in the interfaces allows context-dependent EnergyMethods to use the Pose for context (see below). The presence of the ScoreFunction in the interface allows for EnergyMethods to alter their behavior in the presence of other EnergyMethods; e.g. the Lennard-Jones term changes the way it counts the interaction energies for atom pairs separated by either three or four bonds when the CHARMM torsion term (mm_twist) is active in the score function. WholeStructureEnergy classes perform all of their work in the final stage of scoring (Sec. 4.6.4) in the call to their finalize_total_energy method. For example, the radius-of-gyration score is implemented as a WholeStructureEnergy.
Two classes derive from the TwoBodyEnergy class: ShortRangeTwoBodyEnergy and LongRangeTwoBodyEnergy. The “short range” property of ShortRangeTwoBodyEnergy classes lies in the fact that they define some distance cutoff, d, beyond which any heavy-atom pair interaction is guaranteed to be zero. The ScoreFunction uses the maximum cutoff of its short-ranged two-body energy instances and the neighbor-radii (Sec. 4.2) to define a sparse graph representing residue-neighbor relationships, an EnergyGraph, described in the next section. ShortRangeTwoBodyEnergy classes are not responsible for determining which pairs of residues to evaluate during scoring; rather, the ScoreFunction directs the short-ranged energy methods to evaluate particular residue-pair-interaction energies using the EnergyGraph.
Long-range energy terms do not define a cutoff distance and so they cannot rely on the ScoreFunction to determine their neighbor relationships for them. Instead, they must provide their own data structure for directing the residue pairs over which they should be evaluated and for storing those energies once computed: a LongRangeEnergyContainer. This data structure may be as sparse or dense as the EnergyMethod requires. Truly long-ranged energy functions, such as the Generalized Born solvation model (Onufriev et al., 2004), provide upper triangles of N×N tables to store all residue pair interactions, but sparse non-local energy functions provide graphs (graphs are introduced in the next section). User-defined constraints (Sec. 4.6.5) are treated as long-ranged since a constraint score should be evaluated regardless of how far apart two residues become in a structure. Once a user has input their desired constraints, the ConstraintsEnergy (see below) creates a sparse graph representing their relationships. Thus, the cost to evaluate M constraints costs O(MlgM) time. Similarly the DisulfideEnergy is defined as long range so that it can control which pairs of residues it is evaluated on; for one, most interacting residue pairs are not disulfide bonded, but more importantly, the disulfide bond-stretch term should be applied regardless of the distance separating two disulfide-bonded residues.
The final split in the EnergyMethod hierarchy is between context-dependency and context-independency. The short- and long-range two-body energy methods both split, as does the one-body energy method, defining six of the seven abstract classes meant for direct inheritance from by concrete classes. Context-dependent terms are those where the context for a residue (or for a residue pair) influences the score; e.g. many terms in Rosetta depend on the number of neighbors within 10 Å. The centroid “environment” term depends on the number of neighbors, as do the fullatom hydrogen-bond terms. The Lennard-Jones term, in contrast, does not depend on the context, and is thus implemented as a context-independent term. Context-dependency is a crucial attribute in determining whether stored residue-pair energies may be reused: the Lennard-Jones interaction energy between two residues is unchanged provided that their relative orientation has not changed since the last energy evaluation, whereas the environment of a hydrogen bond (and hence its strength) may change even if the relative orientation of the interacting atoms does not.
4.6.3 class Energies and class EnergyGraph
The Pose stores the results of its most recent score function evaluation in an Energies object. Class Energies stores the total weighted energy, the unweighted component energies, the per-residue and per-residue-pair unweighted component energies, and the LongRangeEnergyContainers. It holds its per-residue-pair unweighted energies from ShortRangeTwoBodyEnergy classes in a “sparse graph” data structure, class EnergyGraph. The key to the EnergyGraph data structure is that it stores energies for pairs of residues without the O(N2) cost associated with N×N tables. In this section, we show that the memory use for the EnergyGraph is O(N); this means that when copying a Pose, the expense of copying its EnergyGraph is O(N). It also means that the expense of traversing the graph during scoring is O(N) (Sec 4.6.4).
The concept of a graph comes from computer science: a graph is a set of vertices and edges; G = {V, E}. A vertex, v ∈ V, represents an object; an edge, e = {u,v} ∈ E, represents a relationship between two objects, u and v. In sparse graphs, the number of edges, ∣E∣, is bound by a linear function of the number of vertices; ∣E∣ ∈ O(V). In our graph implementation, edge addition and deletion costs O(1) time; this feature is necessary for the O(N) complexity bound for scoring a Pose. Edge addition and deletion in our graph data structures is further sped up by the use of “pool” data structures (Cleary, 2004) which reduce the number of calls to new and delete.
Each vertex in the EnergyGraph represents a residue in the Pose. Each edge in the EnergyGraph represents a short-range interaction between two residues (Figure 2). Contained on each edge is an array used to store the unweighted energies for the active short-range two-body-energy components. If there are five active two-body components, then exactly five elements are allocated for each array on each edge.
The EnergyGraph contains O(N) edges: the EnergyGraph contains an edge between residues i and j if the distance between the neighbor atoms of i and j is less than the sum of the neighbor radius of i and j, (ri and rj), (Sec. 4.2), and the ScoreFunction’s maximum short-range distance cutoff, d, (Sec 4.6.2). Under the assumption that our simulations never exceed some residue-density maximum, ρ, (e.g. by collapsing all residues on top of each other) then each residue has fewer than neighbors, and thus the EnergyGraph contains O(N) edges.
4.6.4 Score Function Evaluation
To expedite score function evaluation, the ScoreFunction reuses previously computed interaction energies where possible. Here, we present the logic for rescoring a Pose. The Pose, to communicate its structural changes since the previous score function evaluation, hands a DomainMap (Sec. 4.3) to the ScoreFunction at the beginning of scoring.
(Re)Scoring a Pose proceeds in eight stages:
The ScoreFunction iterates across all edges in the EnergyGraph (whose edges reflected the interactions present at the last score-function evaluation) and deletes out-of-date edges – edges whose nodes have a different color or are color 0 (O(N)),
it detects residue neighbors (with an STL map in O(NlgN) time or quite rapidly with a 3D grid in O(N3) time),
it iterates across all residue neighbors, and for any pair of residues with non-matching colors, adds new edges to the EnergyGraph (O(N)),
it calls a function setup_for_scoring on each of its EnergyMethods (O(N)*),
it evaluates the one-body energies, reusing context-independent energies for residues with a non-zero color (O(N)),
it iterates across all edges in the EnergyGraph and evaluates the short-range two-body energies for each neighboring residue pair, reusing the context-independent energies for residue pairs with the same non-zero color, (O(N))
it iterates across all long-range two-body energies and iterates across the corresponding long-range two-body-energy containers to evaluate the requisite two-body energies, again reusing context-independent energies for those residue pairs assigned the same non-zero color, (O(N2)) ,
finally it calls finalize_total_energy on each of its EnergyMethods (O(N)*). WholeStructureEnergy classes perform all of their work during the finalize stage.
*These steps are O(N) assuming that the EnergyMethods perform only O(N) work in these steps.
Discounting the neighbor-detection expense and the presence of long-range energy terms, score function evaluation is an O(N) operation. During minimization (Sec 4.7), we assume the neighbor relationships will remain fixed, and avoid the neighbor-detection and graph update steps (steps 1,2, and 3) during score function evaluation.
4.6.5 core::scoring::constraints
Constraints are used in Rosetta protocols either to bias conformational sampling toward regions where the user thinks their solution lies, or to force the conformation into a high-energy state in order to study that state (e.g. to design an active site around the transition state geometry for a reaction). Constraints are used to bias sampling with homology information, or experimentally derived data. Their prominent role in so many protocols earns them a place directly in a Pose; each Pose contains a ConstraintSet object. The ConstraintSet holds the collection of Constraints and manages their assignment into 1-body, 2-body, and multi-body terms; it creates a graph, the ConstraintGraph, as the LongRangeEnergyContainer for the ConstraintsEnergy class.
The constraint system makes extensive use of polymorphism to provide tremendous expressibility. Class Constraint is the abstract base class for the various constraint forms in use in Rosetta: e.g. an AtomPairConstraint will compute a score and its derivative based on the distance of two particular atoms; AngleConstraints and DihedralConstraints operate on atom triple and atom quadruples. The actual score that is computed for most Constraints comes from a generic Func class; the interface for class Func is simply two functions, func(x) and dfunc(x), that report the value and the derivative for some value x (x can be a distance, an angle, or a dihedral). Example concrete Func classes include the HarmonicFunc, the CircularHarmonicFunc, the PeriodicFunc, and the SquareWellFunc.
Evaluating the score for a Constraint requires that it be provided access to coordinates, but each Constraint requires a different number of coordinates. To provide a uniform interface for all constraints, we pass coordinates in to a Constraint via an XYZFunc whose job is to return a coordinate given an atom identifier. There are three concrete XYZFunc classes; the ResidueXYZFunc, the ResiduePairXYZFunc, and the ConformationXYZFunc, which are used to evaluate 1-body, 2-body, and multi-body constraints. The same AngleConstraint class can be used for either intra-residue or inter-residue constraints, and can be used with a wide variety of functional forms.
4.7 core::optimization
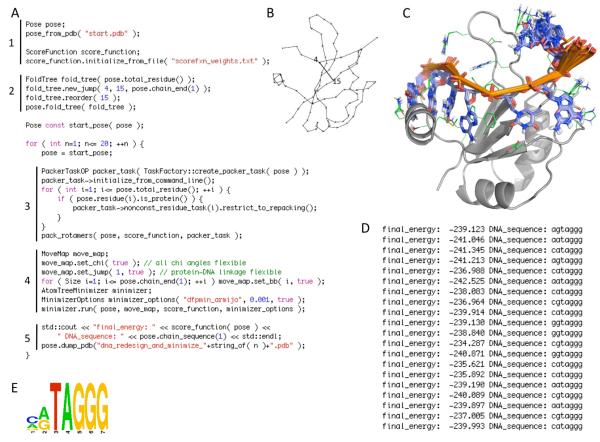
The classes in core::optimization provide the functionality for gradient-based minimization of arbitrary degrees of freedom. The most commonly used class is AtomTreeMinimizer. This class is specialized for the degrees of freedom of interest to molecular modelers, although it depends upon more general minimization classes described below. The run method of the AtomTreeMinimizer takes as input a Pose, a MoveMap, a ScoreFunction, and a MinimizerOptions object. The MoveMap provides a detailed selection of the AtomTree-defined degrees of freedom to vary. The MinimizerOptions provides a description of the desired minimization algorithm, and control parameters such as required tolerances in objective function and maximum iterations before termination (Fig. 4A, section 4).
Figure 4.
Simple Rosetta3 protocol for performing a binding specificity calculation on a protein-single-stranded-DNA complex. The simulation code (A) is broken into 5 segments: (1) initialization of the molecular system from a PDB file and the scoring function from a text file containing the energy terms and weights; (2) setup of the kinematic connectivity via a FoldTree (illustrated in B) with a long-range rigid-body connection between residue 4 in the DNA and residue 15 in the protein; (3) redesign of the DNA sequence and simultaneous optimization of the protein sidechain conformations using a PackerTask object to direct the operation of Rosetta’s packing subroutine pack_rotamers; (4) gradient-based minimization of the resulting Pose with flexibility of all chi angles (including glycosidic dihedrals in the DNA), the rigid-body linkage between the protein and the DNA, and the DNA backbone dihedrals (the MoveMap object communicates the allowed flexibility to the minimizer); (5) output of the final optimized structures (superimposed in C) and sequence and score information (text output shown in D, sequences summarized by a sequence logo representation in E, which can be compared with the DNA sequence in the starting PDB file: GTTAGGG). This simulation code could be compiled into a free-standing C++ executable by linking against the Rosetta libraries.
The low-level class for implementing gradient-based minimization is Minimizer. This class is configured with Multifunc and MinimizerOptions objects at construction. The Multifunc class is an abstract class that calculates the objective function and the derivative of the objective function for a given set of degrees of freedom. The AtomTreeMultifunc is the most commonly used subclass of Multifunc. In fact, one of the major tasks of the AtomTreeMinimizer is to construct a suitable AtomTreeMultifunc from the input MoveMap and ScoreFunction, and to enforce the correspondence between the degrees of freedom expected by the AtomTreeMultifunc object and the degrees of freedom manipulated by the Minimizer object. The AtomTreeMultifunc is responsible for converting the Cartesian derivative vectors into derivatives for the torsional degrees of freedom (Abe et al., 1984).
The minimization-algorithm options are split into the direction-determining and line-minimization options. Currently, the only direction-determining option is a variable metric method using a Broyden-Fletcher-Goldfarb-Shanno (BFGS) update (Nocedal & Wright, 2006). The available line minimization algorithms are an inexact method using the Armijo back-tracking acceptance criterion (Nocedal & Wright, 2006), a similar but “non-monotone” method that allows the minimization trajectory to temporarily move uphill in energy, and a more exact method due to Brent (Brent, 1973). The termination criterion for the minimization is specified by a tolerance, which may be absolute or relative to the current value for the objective function.
4.8 core::pack
Namespace core::pack houses the classes associated with two commonly used subroutines in Rosetta protocols, pack_rotamers and rotamer_trials, which optimize rotamer placement. The packer builds a set of rotamers at each of several residues, computes their interaction energies, and, in the case of pack_rotamers, performs simulated annealing to find low energy rotamer placements. In rotamer_trials, the best rotamer is chosen at each residue, where each residue is optimized one at a time in a random order. Both subroutines take as input a Pose, a ScoreFunction, and a PackerTask.
In previous versions of Rosetta, the most complicated portion of the packer was in how it decomposed the score function into rotamer-one-body energies and rotamer-pair energies. The packer had to be aware of all the score function components, their nature, and their interface. This knowledge was duplicated in several places as packer functionality expanded, making the incorporation of new terms difficult and error prone. With the EnergyMethod hierarchy, the ScoreFunction is pre-decomposed; once an EnergyMethod can be incorporated as a one- or two-body energy into score-function evaluation, it can be included in packing.
Namespace core::pack::task houses a class whose sole purpose is to let users control the packer’s behavior: PackerTask. The PackerTask communicates rotamer-building instructions, simulated annealing parameters, and other data between the various classes and subroutines of the packer. The PackerTask contains a host of options, many of which are configurable on the per-residue level (see Figure 4A, section 3 for a packing example).
Namespace rotamer_set holds class RotamerSet, which builds the set of rotamers for a particular position in the structure (e.g. residue 10). It represents each rotamer with a single Residue object. Class RotamerSet also stores trie data structures for EnergyMethods that are able to take advantage of the trie-vs-trie algorithm (Leaver-Fay et al., 2005b).
Namespace interaction_graph houses several “interaction graph” classes (Leaver-Fay et al., 2005a) that store tables of rotamer-pair energies (or compute them on-the-fly (Leaver-Fay et al., 2008)) on edges between neighboring residues. The InteractionGraph abstraction serves also as an interface to the simulated annealing algorithms. Due to their ease of use, protocols that create and store their own InteractionGraph for use in multiple annealing trajectories have flourished.
Namespace annealer houses the last components of the packer, the annealers, which search for low-energy rotamer assignments by considering rotamer substitutions and deciding whether each substitution should be accepted or rejected. There are currently three annealers available; the first two differ mainly in their temperature schedule, the third, for DNA design, makes simultaneous base substitutions to preserve Watson-Crick base pairing.
4.9 protocols Library
The protocols library contains code representing protocols for specific purposes (e.g. protein/protein docking), whereas the core library contains code with more general purposes that the protocols rely on. This paper does not detail all the protocols contained within this library (and which are published separately), but rather, highlights a few classes and algorithms which are common to various protocols and could be useful for developers interested in writing their own protocols.
4.10 protocols::moves
Namespace protocols::moves houses the class responsible for recapitulating Rosetta’s classic Monte Carlo technique, class MonteCarlo. In particular, this class keeps track of two Poses: the best scoring Pose it has ever encountered, and the most-recently-accepted Pose. After the class is initialized (with a starting Pose and a ScoreFunction), a protocol writer can invoke its boltzmann( core::pose::Pose & p ) method passing in a structurally perturbed Pose, p for evaluation. The MonteCarlo object scores p, and will then accept or reject p either by copying p into the most-recently-accepted Pose, or by copying the most-recently-accepted Pose back into p, thereby undoing whatever structural perturbation had just been applied. The MonteCarlo object also keeps track of how frequently structural perturbations are rejected, and can optionally increases its temperature if it has been too long since the last acceptance.
Namespace protocols::moves also contains an important base class that makes Rosetta3 protocols nestable. On one level, protocols are nestable simply because protocols are represented by classes; one could create an instance of a protocol, or one could have two instances of a protocol and arrange the second instance to be invoked from within the first. Our protocols are generically nestable because our protocols all derive from a common base class: Mover. Mover defines an interface method
virtual
apply( core::pose::Pose & p ) = 0;
which takes a non-const Pose reference where the Mover is meant to change the input Pose. A Mover can model an entire protocol (e.g. docking) which can be seen as taking an input Pose and producing an output Pose. Rosetta’s job distribution system, described in the next section, relies on this premise. The TrialMover exemplifies the way in which this generic nestability is so powerful. A TrialMover (itself derived from Mover) is constructed from an instance of another Mover and a MonteCarlo object. In its apply method, it invokes the Mover’s apply method and follows up by invoking the MonteCarlo’s boltzmann method. A portion of a protocol might be written succinctly as a series of TrialMover applications.
A final class housed in namespace protocols::moves worth mentioning is the abstract base class, Filter. Filter defines a single function virtual bool apply( Pose const & p ) const = 0; which will return “true” if Pose p meets some quality standard, and “false” otherwise. Classes Mover and Filter both play an important role in Rosetta3’s scripting language, described in Section 4.13 below.
4.11 JobDistributor
Due to the vast size of conformation space, and the ruggedness of the energy landscape, most protocols require the simulation of thousands of trajectories to produce reliable predictions. The job distributor layer is responsible for abstracting the details of structure I/O and the allocation of computational resources away from the task of writing protocols. If a protocol is written to interface with the job distributor classes, then it can be run on any kind of cluster supported by our job distribution framework.
The main task for a job distributor is to execute a pair of nested for loops: one outer loop over all input structures, and one inner loop over all trajectories required for each input structure. Inside the inner loop, the job distributor generates a Pose from input, runs the intended protocol (by invoking a Mover’s apply method) on that Pose, and then writes the results to disk. These central loops are implemented in the base JobDistributor class. A series of derived classes inherit from this base, and provide the logic for how to farm out the jobs across the available resources. As of this writing, the choices include one job distributor for distributed computing within the BOINC framework (Anderson, 2004), one for use with one or more processes that communicate via the file system, and four MPI variants. The MPI variants run as nearly-independent processes (that are “embarrassingly parallel”), where interprocess communication is limited to signaling which jobs have completed and managing disk access.
Besides managing the assignment of jobs to processors, the JobDistributor has two extra responsibilities: determining which jobs exist and writing output at their conclusion. These tasks are handled by the JobInputter and JobOutputter classes. Derived members of these classes specialize for particular types of input and output. The JobInputter informs the JobDistributor what jobs are present from command line inputs and also turns the information for those jobs into Pose objects. The major JobInputters handle standard PDBs and silent files (compressed output files in which a structure is described by its internal DOFs, only). There are also JobInputters specialized for ab initio folding (which has no starting structure) and other purposes. The JobOutputter is responsible for outputting the final Pose from a trajectory, usually to disk. Again, the standard output methods are PDBs and silent files, with more exotic choices available. The JobOutputter class is also responsible for determining what trajectories have already been finished; if Rosetta is interrupted and later restarted, it can resume the last job it was processing by examining the set of outputs that have already been generated.
4.12 protocols::loops
Loop modelling is heavily utilized during protein homology modelling and refinement as well as during flexible-backbone protein design. Loops are defined by a Loop class that stores the start and end residues for the loop, as well as a “cutpoint” residue position at which a chainbreak is introduced into the AtomTree (Wang et al. 2007). This chainbreak allows kinematic perturbations to propagate inwards from the loop endpoints toward the cutpoint residue so that regions outside the loop are unmodified by dihedral angle changes within the loop.
Loop modeling in Rosetta3 can be used for de novo prediction of protein loop conformations (loop reconstruction), or for refinement of given loop structures. Loop refinement protocols derive from the class LoopMover and may alter the conformation of any loops in the Pose. Protocols that reconstruct only a single loop derive from the class IndependentLoopMover. A typical loop building task starts with a centroid representation of the loop followed by an all-atom refinement.
Two main algorithms for loop building are implemented in Rosetta. The first algorithm uses rounds of fragment insertion to modify the loop conformations where a “chainbreak” term is included in the score function to keep the two cutpoint residues close together, followed by cyclic-coordinate descent (Canutescu & Dunbrack, 2003) to close the chain. This algorithm is fast and is used in homology modeling to construct the gap regions of a sequence alignment. The second type uses an algorithm called kinematic closure (KIC) (Coutsias et al., 2004, Mandell et al., 2009). KIC uses inverse kinematics to solve analytically for assignments to six torsional degrees of freedom that close the loop exactly, while sampling all other phi/psi angles in the loop region from Ramachandran space. The KIC method provides enhanced high-resolution sampling and can be used for de novo prediction of loop conformations, high-resolution refinement of protein structures following low-resolution rebuilding, and remodeling of defined regions of proteins such as during protein design procedures.
4.13 Protocols from text files
Most Rosetta protocols can be abstracted into a series of steps where each step either changes the structure being operated on (the Pose) or decides that the trajectory should be restarted. The classes Mover and Filter introduced above (Sec. 4.10) provide the building blocks for such an abstraction. We have leveraged these two classes to generate a framework for writing protocols in a user-friendly, XML scripting language that can be read by a Rosetta application called RosettaScripts. RosettaScripts programs are written as text files and are converted into a sequence of Movers and Filters at runtime. Each Mover and Filter accessible within RosettaScripts implements an initialization function, parse_my_tag, which allows the script writer to control various features of each class; however, great care has been taken to make the default behavior for each Mover or Filter as robust and intuitive as possible.
There are several advantages of this scripting functionality. First, it allows users to rapidly create and tune protocols without having to recompile C++ source code. This is especially useful for Rosetta@home (Chivian et al., 2003) where distributing a new executable is expensive both in labor and in server load. Second, the ability to pass parameters to RosettaScripts Movers through the XML input file helps eliminate command-line flags, which, as global variables, frustrate code reuse. Third, RosettaScripts protocols are self contained and written to work within the standard job-distribution framework (Sec. 4.11), making RosettaScripts protocols as easy to deploy on a given cluster as any other Rosetta application. Finally, RosettaScripts is just as fast as any hard-coded protocol it might replace, since the underlying Movers and Filters it relies upon are fully compiled C++ classes.
5 Conclusion
Our new architecture has greatly advanced the functional capacity of Rosetta. It has allowed users to rapidly develop new protocols, to model a wider set of chemical structures, and to easily experiment with new scoring terms. As a concrete example, Figure 4 illustrates a simple Rosetta3 simulation for predicting protein-single-stranded-DNA binding specificity using DNA redesign followed by gradient-based minimization. The new architecture has allowed the creation of a multithreaded, interactive game where players are given access to Rosetta’s minimization, packing, and loop modeling routines to compete for the best protein structure predictions (Cooper et al., 2010). It has enabled the creation of PyRosetta (Chaudhury et al., 2010), that allows command-line interactivity with Rosetta classes and functions from within the Python interpreter which in turn promotes even faster protocol prototyping. With an object-oriented approach toward protocol development, we are able to construct arbitrarily complicated protocols from component Mover classes using a simple XML scripting language. It is our optimistic hope that this rearchitecturing will be a lasting foundation for the code base so that the tumult of another complete rewrite may be avoided for the next decade if not longer.
Acknowledgements
This work was funded by NIH and HHMI. OFL was funded by the Human Frontier Science Program.
References
- Abe H, Braun W, Noguti T, Go N. Rapid calculation of first and second derivatives of conformational energy with respect to dihedral angles for proteins. General recurrent equations. Computers & Chemistry. 1984;8:239–247. [Google Scholar]
- Abagyan R, Totrov MM, Kuznetsov DN. ICM – a new method for protein modeling and design: applications to docking and structure prediction from the distorted native conformation. J. Comput. Chem. 1994;15:488–506. [Google Scholar]
- Anderson DP. BOINC: A System for Public-Resource Computing and Storage. Pages 4-10 of the 5th IEEE/ACM International Conference on Grid Computing. IEEE Computer Society; Pittsburg PA: 2004. [Google Scholar]
- Bonneau R, Tsai J, Ruczinski I, Chivian D, Rohl C, Strauss CE, Baker D. Rosetta in CASP4: Progress in ab initio protein structure prediction. Proteins. 2001;5:119–126. doi: 10.1002/prot.1170. [DOI] [PubMed] [Google Scholar]
- Bonneau R, Strauss CE, Rohl CA, Chivian D, Bradley P, Malmstrom L, Robertson T, Baker D. De novo prediction of three-dimensional structures for major protein families. J. Mol. Biol. 2002;322:65–78. doi: 10.1016/s0022-2836(02)00698-8. [DOI] [PubMed] [Google Scholar]
- Bradley P, Malmstrom L, Qian B, Schonbrun J, Chivian D, Kim DE, Meiler J, Misura KM, Baker D. Free modeling with Rosetta in CASP6. Proteins. 2005:1. doi: 10.1002/prot.20729. [DOI] [PubMed] [Google Scholar]
- Brent RP. Algorithms for minimization without derivatives. Prentice Hall; Englewood Cliffs, NJ: 1973. [Google Scholar]
- Brooks BR, III, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Caflisch S. Boresch A., Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: The Biomolecular simulation Program. J. Comput. Chem. 2009;30:1545–1615. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canutescu AA, Dunbrack RL., Jr. Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci. 2003;12:963–972. doi: 10.1110/ps.0242703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhury S, Lyskov S, Gray JJ. PyRosetta: a script-based interface for implementing molecular modeling algorithms using Rosetta. Bioinformatics. 2010;26:689–691. doi: 10.1093/bioinformatics/btq007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chivian D, Kim DE, Malmstrom L, Bradley P, Robertson T, Murphy P, Strauss CE, Bonneau R, Rohl CA, Baker D. Automated prediction of CASP-5 structures using the Robetta server. Proteins. 2003;53 Suppl 6:524–533. doi: 10.1002/prot.10529. [DOI] [PubMed] [Google Scholar]
- Chowdry AB, Reynolds KA, Hanes MS, Voorhies M, Pokala N, Handel TM. An Object-Oriented Library for Computational Protein Design. J. Comput. Chem. 2007;28:2378–2388. doi: 10.1002/jcc.20727. [DOI] [PubMed] [Google Scholar]
- Cleary S. The Boost Pool Library. 2001 www.boost.org/libs/pool.
- Cooper S, Khatib F, Treuille A, Barbero J, Lee J, Beenen M, Leaver-Fay A, Baker D, Popović Z. Predicting protein structures with a multiplayer online game. Accepted. 2010 doi: 10.1038/nature09304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutsias EA, Seok C, Jacobson MP, Dill KA. A kinematic view of loop closure. J. Comput. Chem. 2004;25:510–528. doi: 10.1002/jcc.10416. [DOI] [PubMed] [Google Scholar]
- Dahiyat BI, Mayo SL. Protein design automation. Protein Sci. 1996;5:895–903. doi: 10.1002/pro.5560050511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dantas G, Kuhlman B, Callender D, Wong M, Baker D. A large scale test of computational protein design: folding and stability of nine completely redesigned globular proteins. J. Mol. Biol. 2003;332:449–460. doi: 10.1016/s0022-2836(03)00888-x. [DOI] [PubMed] [Google Scholar]
- Das R, Baker D. Macromolecular modeling with Rosetta. Annu. Rev. Biochem. 2008;77:363–382. doi: 10.1146/annurev.biochem.77.062906.171838. [DOI] [PubMed] [Google Scholar]
- Das R, Qian B, Raman S, Vernon R, Thompson J, Bradley P, Khare S, Tyka MD, Bhat D, Kim DE, Sheffler WH, Malmstrom L, Wollacott AM, Wang C, Andre I, Baker D. Structure prediction for CASP7 targets using extensive all-atom refinement with Rosetta@home. Proteins. 2007;106:18978–18983. doi: 10.1002/prot.21636. [DOI] [PubMed] [Google Scholar]
- Das R, Karanicolas J, Baker D. Atomic accuracy in predicting and designing noncanonical RNA structure. Nat. Methods. 2010;7:291–294. doi: 10.1038/nmeth.1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R, Baker D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. U. S. A., USA. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis IW, Baker D. RosettaLigand docking with full ligand and receptor flexibility. J. Mol. Biol. 2009;385:381–392. doi: 10.1016/j.jmb.2008.11.010. [DOI] [PubMed] [Google Scholar]
- Desmet J, De Maeyer M, Hazes B, Lasters I. The dead-end elimination theorem and its use in protein side-chain positioning. Nature. 1992;356:539–541. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]
- Gray JJ, Moughon S, Wang C, Schueler-Furman O, Kuhlman B, Rohl CA, Baker D. Protein–Protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- Hellinga HW, Caradonna JP, Richards FM. Construction of new ligand binding sites in proteins of known structure. II. Grafting of a buried transition metal binding site into Escherichia coli thioredoxin. J. Mol. Biol. 1991;222:787–803. doi: 10.1016/0022-2836(91)90511-4. [DOI] [PubMed] [Google Scholar]
- Jiang L, Althoff EA, Clemente FR, Doyle L, Rothlisberger D, Zanghellini A, Gallaher JL, Betker JL, Tanaka F, Barbas CF, Hilvert D, Houk KN, Stoddard BL, Baker D. De novo computational design of retro-aldol enzymes. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann K, Glab K, Mueller R, Meiler J. Small molecule rotamers enable simultaneous optimization of small molecule and protein degrees of freedom in ROSETTALIGAND docking. In: Beyer A, Schroeder M, editors. German Conference on Bioinformatics. 2008. pp. 148–157. [Google Scholar]
- Kaufmann KW, Lemmon GH, DeLuca SL, Sheehan JH, Meiler J. Practically Useful: What the Rosetta protein modeling suite can do for you. Biochemistry. 2010:1. doi: 10.1021/bi902153g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kortemme T, Joachimiak LA, Bullock AN, Schuler AD, Stoddard BL, Baker D. Computational redesign of protein-protein interaction specificity. Nat. Struct. Mol. Biol. 2004;11:371–379. doi: 10.1038/nsmb749. [DOI] [PubMed] [Google Scholar]
- Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. U. S. A., USA. 2000;97:10383–8. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leaver-Fay A, Kuhlman B, Snoeyink JS. Pages 17–28 of: Pacific Symposium on Biocomputing, 2005. World Scientific; The Big Island, HI: 2005. An Adaptive Dynamic Programming Algorithm for The Side Chain Placement Problem. [PubMed] [Google Scholar]
- Leaver-Fay A, Kuhlman B, Snoeyink JS. Rotamer-Pair Energy Calculations using a Trie Data Structure. Pages 500–511 of: Workshop on Algorithms in Bioinformatics (WABI) 2005 [Google Scholar]
- Leaver-Fay A, Snoeyink JS, Kuhlman B. On-The-Fly Rotamer Pair Energy Evaluation in Protein Design. Pages 343–354 of: The 4th International Symposium on Bioinformatics Reasearch and Applications (ISBRA 2008) 2008 [Google Scholar]
- Mandell DJ, Coutsias EA, Kortemme T. Sub-angstrom accuracy in protein loop reconstruction by robotics-inspired conformational sampling. Nat. Methods. 2009;6:551–552. doi: 10.1038/nmeth0809-551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meiler J, Baker D. ROSETTALIGAND: Protein-small molecule docking with full side chain flexibility. Proteins: Structure Function and Genetics. 2006;65:538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
- Nocedal Jorge, Wright Stephen J. Numerical Optimization. 2nd edn Springer; 2006. [Google Scholar]
- Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–94. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Pierce NA, Winfree E. Protein design is NP-hard. Protein Engineering. 2002;15:779–82. doi: 10.1093/protein/15.10.779. [DOI] [PubMed] [Google Scholar]
- Ponder JW, Richards FM. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J. Mol. Biol. 1987;193:775–791. doi: 10.1016/0022-2836(87)90358-5. [DOI] [PubMed] [Google Scholar]
- Raman S, Vernon R, Thompson J, Tyka M, Sadreyev R, Pei J, Kim D, Kellogg E, Dimaio F, Lange O, Kinch L, Sheffler W, Kim BH, Das R, Grishin NV, Baker D. Structure prediction for CASP8 with all-atom refinement using Rosetta. Poteins. 2009;77:89–99. doi: 10.1002/prot.22540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl CA, Strauss CE, Chivian D, Baker D. Modeling structurally variable regions in homologous proteins with Rosetta. Proteins. 2004;55:656–677. doi: 10.1002/prot.10629. [DOI] [PubMed] [Google Scholar]
- Rothlisberger D, Khersonsky O, Wollacott AM, Jiang L, DeChancie J, Betker J, Gallaher JL, Althoff EA, Zanghellini A, Dym O, Albeck S, Houk KN, Tawfik DS, Baker D. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453:190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- Simons KT, Kooperberg C, Huang E, Baker D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol. 1997;268:209–225. doi: 10.1006/jmbi.1997.0959. [DOI] [PubMed] [Google Scholar]
- Stepanov A, Lee M. The Standard Template Library. WG21/N0482, ISO Programming Language C++ Project. 2005 [Google Scholar]
- Wang C, Schueler-Furman O, Baker D. Improved Side Chain Modeling for Protein–Protein Docking. Protein Sci. 2005;14:1328–1339. doi: 10.1110/ps.041222905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Bradley P, Baker D. Protein-protein docking with backbone flexibility. J. Mol. Biol. 2007;373:503–519. doi: 10.1016/j.jmb.2007.07.050. [DOI] [PubMed] [Google Scholar]
- Zanghellini A, Jiang L, Wollacott AM, Cheng G, Meiler J, Althoff EA, Rothlisberger D, Baker D. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15:2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]