A Novel Haplotype-Sharing Approach for Genome-Wide Case-Control Association Studies Implicates the Calpastatin Gene in Parkinson’s Disease

Abstract

The large number of markers considered in a genome-wide association study (GWAS) has resulted in a simplification of analyses conducted. Most studies are analyzed one marker at a time using simple tests like the trend test. Methods that account for the special features of genetic association studies, yet remain computationally feasible for genome-wide analysis, are desirable as they may lead to increased power to detect associations. Haplotype sharing attempts to translate between population genetics and genetic epidemiology. Near a recent mutation that increases disease risk, haplotypes of case participants should be more similar to each other than haplotypes of control participants; conversely, the opposite pattern may be found near a recent mutation that lowers disease risk. We give computationally simple association tests based on haplotype sharing that can be easily applied to GWASs while allowing use of fast (but not likelihood-based) haplotyping algorithms and properly accounting for the uncertainty introduced by using inferred haplotypes. We also give haplotype-sharing analyses that adjust for population stratification. Applying our methods to a GWAS of Parkinson’s disease, we find a genome-wide significant signal in the CAST gene that is not found by single-SNP methods. Further, a missing-data artifact that causes a spurious single-SNP association on chromosome 9 does not impact our test.

INTRODUCTION

The large number of markers tested in a genome-wide association study (GWAS) has forced a simplification of analytic approaches. While sophisticated methodology may be used to adjust for multiple comparisons, the sheer number of tests in a GWAS requires that each test be fairly simple; currently, most studies are analyzed by computing a simple test such as the Cochran-Armitage trend test at each locus. Even when fairly sophisticated methods are used to determine associations with alleles at untyped loci, these associations are typically tested using the trend test. Although computationally intensive fully Bayesian methods [Wellcome Trust Case Control Consortium, 2007; Marchini et al., 2007] are a notable exception, the GWAS era has in some sense forced a simplification in testing methodology. Methods that account for the special features of genetic association studies, yet remain computationally feasible for genome-wide analysis, are desirable as they may lead to increased power to detect associations.

Haplotype sharing is a simple concept that attempts to translate between population genetics and genetic epidemiology [van der Meulen and te Meerman, 1997; Bourgain et al., 2000]. For recent mutations that influence the risk of disease, we would expect to see a difference between the amount of similarity among the haplotypes of case participants and the amount of similarity among the haplotypes of control participants. For example, near a mutation that increases disease risk, we would expect that haplotypes of case participants would be more similar to each other in the immediate region of a mutation than they would be to the haplotypes of control participants [van der Meulen and te Meerman, 1997]. Haplotypes of control participants may be more similar to each other than are those of case participants near a mutation that decreases risk. The analysis is carried out without specifying the underlying evolutionary history that may have given rise to this sharing pattern, by using an ad hoc definition of sharing between two haplotypes such as the number of loci up- and down-stream from a test locus that are identical by state (IBS). Because we do not actually assume an underlying population genetics model, our approach can detect differences between case- and control-haplotype sharing that arise from any source. A number of empirical haplotype-sharing approaches have been developed since the idea was first proposed [Tzeng et al., 2003; Allen and Satten, 2007a,b; Nolte et al., 2007].

In this paper, we seek to develop computationally simple association tests based on haplotype sharing that can be easily applied to case-control studies on the genome-wide scale. We give tests that allow for the use of fast (but not likelihood-based) haplotyping algorithms such as 2SNP [Brinza and Zelikovsky, 2008] or ent [Gusev et al., 2008], while properly accounting for the statistical uncertainty introduced by using inferred or imputed haplotypes. Many GWAS analyses are adjusted for the potentially confounding effects of population stratification. Hence, we also provide simple stratified haplotype-sharing tests that adjust for confounding.

We performed a haplotype sharing-based genome-wide association scan on data from a study of Parkinson’s disease obtained from dbGaP (database of genotype and phenotype) to illustrate our approach. These data have been analyzed using single-locus tests [Fung et al., 2006] but no associations were reported that were genome-wide significant. Using our approach, we find a strong genome-wide significant signal in the calpastatin (CAST [MIM ^*114090]) gene. This finding is biologically plausible as the calpain-calpastatin system is thought to play a role in neuronal death [Shukla et al., 2006; Camins et al., 2006] and has been previously implicated in Parkinson’s disease [Mouatt-Prigent et al., 1996; Crocker, 2003] (see discussion). Further, a single-locus association that is spurious [and not reported by Fung et al. 2006 but reported in online analyses found on dbGaP, accession numbers pha000003.1 and pha000004.1] shows no sign of association using our approach. These results suggest that haplotype-based methods that can be applied genome-wide may be useful for association studies.

HAPLOTYPE SHARING AND HAPLOTYPE REGRESSION

Initially, assume that haplotype phase is known. Let h =(h₁, h₂) be the diplotype that comprises haplotypes h₁ and h₂ and let S_k(h₁, h₂) be some measure of haplotype similarity between haplotypes h₁ and h₂ at locus k. For example, S_k(h₁, h₂) may be the maximum information length criterion (MILC) that counts the number of loci that are IBS up- and down-stream from locus k. For case-control data, the original haplotype-sharing statistic [van der Meulen and te Meerman, 1997] has numerator

$$\begin{array}{l}{T}_k\propto \frac{1}{2n_1(2n_1-1)}\times \sum _{i,i^{\prime }}\sum _{j,j^{\prime }=1}^2{S}_k(h_{ij},h_{i^{\prime }{j}^{\prime }})I(d_i=1)\{1-I[i=i^{\prime },j=j^{\prime }]\}\\ -\frac{1}{2n_0(2n_0-1)}\times \sum _{i,i^{\prime }}\sum _{j,j^{\prime }=1}^2{S}_k(h_{ij},h_{i^{\prime }{j}^{\prime }})I(d_i=0)\{1-I[i=i^{\prime },j=j^{\prime }]\}\end{array}$$ (1)

where i indexes study participants, D_i = 1 for case participants and D_i = 0 for control participants, and n₁ (n₀) is the number of case (control) participants in the study. Equation (1) has the form of a U-statistic which makes variance estimation more difficult. If we restrict attention to haplotypes of fixed length L then there are only 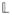= 2^L possible haplotypes to consider. We can form an 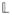-dimensional vector ρ̂_k(π_k) whose jth component is the observed proportion of haplotype j found among case (control) participants. Specifically, let

$$\mathcal{I}(h)=\frac{1}{2}\left(\begin{array}{c}I(h_1=1)+I(h_2=1)\\ I(h_1=2)+I(h_2=2)\\ ⋮\\ I(h_1=\mathbb{L})+I(h_2=\mathbb{L})\end{array}\right);$$ (2a)

then

$${\widehat{\mathrm{\rho }}}_k=\frac{1}{n_1}\sum _{i}I(d_i=1)\mathcal{I}(h_i),$$ (2b)

and

$${\widehat{\mathrm{\pi }}}_k=\frac{1}{n_0}\sum _{i}I(d_i=0)\mathcal{I}(h_i),$$ (2c)

where n_d = Σ_i I(d_i = d) is the number of case (d =1) or control (d =0) participants. We also define the (symmetric) 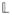× 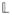matrix 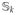whose (j,j′) element is the sharing between the jth and j′th haplotypes. Then (1) can be re-written as

$$T_k\propto {\widehat{\mathrm{\rho }}}_k^{\mathrm{T}}{\mathbb{S}}_k{\widehat{\mathrm{\rho }}}_k-{\widehat{\mathrm{\pi }}}_k^{\mathrm{T}}{\mathbb{S}}_k{\widehat{\mathrm{\pi }}}_k={({\widehat{\mathrm{\rho }}}_k+{\widehat{\mathrm{\pi }}}_k)}^{\mathrm{T}}{\mathbb{S}}_k({\widehat{\mathrm{\rho }}}_k-{\widehat{\mathrm{\pi }}}_k).$$ (3)

The form of (3) motivates us to seek test statistics that are proportional to

$$U_k(\underset{\_}{h};{\mathrm{\gamma }}_k)={\mathrm{\gamma }}_k^{\mathrm{T}}{\mathbb{S}}_k({\widehat{\mathrm{\rho }}}_k-{\widehat{\mathrm{\pi }}}_k),$$ (4)

where γ_k is some fixed vector and h denotes the full set of diplotypes in the study. Once the distribution of U_k(h ; γ) is found, Slutsky’s theorem [Serfling, 1980] assures that the distribution of U_k(h; γ̂_k) is the same as long as γ̂_k ↛ 0 where → denotes convergence in probability.

When phase is uncertain, we must assume a model for the distribution of diplotypes given multilocus genotypes. Let ϕ(h|g) denote the probability of diplotype h given multilocus genotype g for some assumed model. Then, we may replace ρ̂_k and π̂_k by

$${\stackrel{\sim }{\mathrm{\rho }}}_k=\frac{1}{n_1}\sum _{i}I(d_i=1){\stackrel{\sim }{p}}_{i,k}$$ (5a)

and

$${\stackrel{\sim }{\mathrm{\pi }}}_k=\frac{1}{n_0}\sum _{i}I(d_i=0){\stackrel{\sim }{p}}_{i,k},$$ (5b)

respectively, where

$${\stackrel{\sim }{p}}_{i,k}=\sum _{h\in \mathcal{H}(g_i)}\mathcal{I}(h)\mathrm{\varphi }(h\mid g_i),$$ (5c)

and where 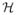(g) is the set of diplotypes that are consistent with multilocus genotype g. The vector p̃_i,k has jth component equal to the expected number of haplotypes of type j in the ith study subject based on the model ϕ(h|g). Thus, for phase uncertain data we seek a test statistic that is proportional to

$$U_k(\underset{\_}{g},;{\mathrm{\gamma }}_k)={\mathrm{\gamma }}_k^{\mathrm{T}}{\mathbb{S}}_k({\stackrel{\sim }{\mathrm{\rho }}}_k-{\stackrel{\sim }{\mathrm{\pi }}}_k),$$ (6)

where g is the set of multilocus genotypes for all study participants. As before, U_k(g, ; γ̂_k)will have the same distribution as U_k(g, ; γ̂_k) as long as γ̂_k ↛ 0. Here, we consider three choices for γ̂_k. The first is

$${\widehat{\mathrm{\gamma }}}_k=\frac{n_1}{n}{\stackrel{\sim }{\mathrm{\rho }}}_k+\frac{n_0}{n}{\stackrel{\sim }{\mathrm{\pi }}}_k\equiv {\widehat{p}}_k.$$

The resulting test, which we call the p test, is asymptotically equivalent to the test obtained by choosing

$${\widehat{\mathrm{\gamma }}}_k=\frac{1}{2}{\stackrel{\sim }{\mathrm{\rho }}}_k+\frac{1}{2}{\stackrel{\sim }{\mathrm{\pi }}}_k,$$

which yields $U_k(\underset{\_}{g};{\mathrm{\gamma }}_k)\propto {\stackrel{\sim }{\mathrm{\rho }}}_k^{\mathrm{T}}{\mathbb{S}}_k{\stackrel{\sim }{\mathrm{\rho }}}_k-{\stackrel{\sim }{\mathrm{\pi }}}_k^{\mathrm{T}}{\mathbb{S}}_k{\stackrel{\sim }{\mathrm{\pi }}}_k$, the original haplotype-sharing statistic. The second choice is to take γ̂_k to be the first principal component (pc) of the variance-covariance matrix of the p̃_i, which we call the pc test. Finally, we consider γ̂_k = ρ̃_k − π̃_k corresponding to the cross statistic [Nolte et al., 2007]. Note that for the cross statistic, γ_k → 0 under the null hypothesis of no association; for this case, the distribution of U_k(g, ; γ̂_k) is a mixture of χ² distributions (see below for detailed discussion).

For stratified data, we may wish to consider a weighted sum of haplotype-sharing statistics of the form (6) for 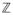strata. Thus, when phase information is available, we seek a test statistic that is proportional to

$$U_k(\underset{\_}{h},{\underset{\_}{w}}_k;{\underset{\_}{\mathrm{\gamma }}}_k)=\sum _{z=1}^{\mathbb{Z}}{w}_{z,k}{\mathrm{\gamma }}_{z,k}^{\mathrm{T}}{\mathbb{S}}_{z,k}({\widehat{\mathrm{\rho }}}_{z,k}-{\widehat{\mathrm{\pi }}}_{z,k});$$ (7a)

when only multilocus genotypes are available, we seek a test statistic proportional to

$$U_k(\underset{\_}{g},{\underset{\_}{w}}_k;{\underset{\_}{\mathrm{\gamma }}}_k)=\sum _{z=1}^{\mathbb{Z}}{w}_{z,k}{\mathrm{\gamma }}_{z,k}^{\mathrm{T}}{\mathbb{S}}_{z,k}({\stackrel{\sim }{\mathrm{\rho }}}_{z,k}-{\stackrel{\sim }{\mathrm{\pi }}}_{z,k}),$$ (7b)

where w_z,k is the weight given to stratum z at locus k, w_k = {w_z,k, z = 1, …, 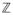}, γ_k = {γ_z,k, z = 1, · · ·, 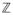} and all other quantities are as defined previously except restricted to stratum z. Although (7) is written in full generality, we expect most applications will use the same sharing matrix 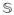in each stratum. Similarly, we anticipate most applications will use the same weights at each locus. In our implementation, we use the number of study participants in the zth stratum as w_z,k for each locus k.

We now show that (4), (6) and (7) are score functions for logistic regression models in which stratum and haplotype determine risk of disease. This connection allows us to determine the distribution of test statistics like U_k(g, w_k ; γ̂_k) when γ_z,k ↛ 0 for every z. We consider the case where γ̂ → 0 later.

For simplicity of notation in what follows, we will drop the subscript k in subsequent expressions, although it should be understood that all calculations are conducted at each locus k. Consider the model

$$ln\frac{\text{Pr}[D=1\mid H=h,Z=z]}{\text{Pr}[D=0\mid H=h,Z=z]}\equiv ln{\mathrm{\theta }}_{h,z}={\mathrm{\eta }}_z+\mathrm{\beta }X(h,z),$$ (8)

where the scalar function X(h₁,h₂,z) is given by

$$X(h,z)=\frac{n_{0,z}+n_{1,z}}{n_{0,z}{n}_{1,z}}{w}_z{\mathrm{\gamma }}_z^{\mathrm{T}}·{\mathbb{S}}_z·\mathcal{I}(h).$$ (9)

When phase information is available, inference on parameters in (8) can be made using the prospective case-control likelihood

$${\mathcal{L}}_{p,h}=\prod _i\frac{{\mathrm{\theta }}_{h_i,z_i}^{d_i}}{1+{\mathrm{\theta }}_{h_i,z_i}}.$$ (10)

We show in Appendix A that (7a) is the score function for parameter β when β =0. This connection allows us to make statements about (stratified) haplotype-sharing analyses of case-control data using the simpler properties of logistic regression of case-control data. When only multilocus genotype data are available, inference on parameters in (8) can be made using the likelihood

$${\mathcal{L}}_{p,g}=\prod _i\left[\sum _{h\in \mathcal{H}(g_i)}\frac{{\mathrm{\theta }}_{h,z_i}^{d_i}}{1+{\mathrm{\theta }}_{h,z_i}}\mathrm{\varphi }(h\mid g_i)\right].$$ (11)

Since (7a) is the score function for likelihood (10), it follows from standard missing-data model theory that (7b) is the score function for likelihood (11) when β =0.

PHASE UNCERTAINTY AND THE EFFICIENT SCORE

The dependence of inference on the model ϕ(h|g) in (5), (7b), and (11) raises two questions. First, what is the consequence of a poor model choice for ϕ(h|g) on inference? Recall that ϕ(h|g) is not identified from data without additional model assumptions such as Hardy-Weinberg equilibrium (HWE) that cannot be evaluated using multilocus genotype data. Second, if ϕ(h|g) contains nuisance parameters that are estimated from the case-control sample, how do we account for the sampling variability in the nuisance parameters when calculating the variance of the score function? For example, if we use a maximum likelihood estimator (MLE) for haplotype frequencies assuming HWE, we could base variance estimators on the joint information matrix for model and nuisance parameters. However, computing the MLE is too slow for genome-wide analysis. It is unclear how to proceed when ad hoc models for ϕ(h|g) are used.

Allen and Satten [2008] considered inference based on (11) and showed that when β = 0, the observed-data score function is the efficient score for a model in which we assume a saturated model for ϕ(h|g). Although this model is not identifiable, Allen and Satten [2008] show that when constructing hypothesis tests, this property implies that misspecification of ϕ(h|g) only affects power, not test validity. As a result, we can use any “working” model for ϕ(h|g) that is identifiable. In particular, it is not necessary to use an MLE when estimating parameters in ϕ(h|g). In our calculations, we use the software package ent [Gusev et al., 2008] to estimate ϕ(h|g) by first allowing ent to impute a single diplotype for each study participant, then using the empirical distribution of these imputed haplotypes to construct ϕ(h|g).

Because U(g, w; γ) is an efficient score, we can estimate its variance by rewriting it as a sum of iid terms and using the empirical variance of these terms. This empirical variance is valid without further adjustment for any variability introduced by estimating parameters in the working model for ϕ(h|g), because the efficient score is orthogonal to these sources of variation. We can write U(g, w; γ) as a sum of iid terms by noting that

$$U(g,w;\mathrm{\gamma })=\sum _i\frac{w_{z_i}}{n_{d_i,z_i}}{\mathrm{\gamma }}_{z_i}^{\mathrm{T}}·{\mathbb{S}}_{z_i}·{\stackrel{\sim }{p}}_i[I(d_i=1)-I(d_i=0)],$$ (12)

hence, the variance of U(g, w; γ) is given by

$$V(g,z;\mathrm{\gamma })=\sum _i{\left(\frac{w_{z_i}}{h_{d_i,z_i}}{\mathrm{\gamma }}_{z_i}^{\mathrm{T}}·{\mathbb{S}}_{z_i}·{\stackrel{\sim }{p}}_i\right)}^2.$$

A test of excess haplotype sharing at a locus can be constructed using the statistic

$$T(g,w;\widehat{\mathrm{\gamma }})=\frac{U{(g,w;\widehat{\mathrm{\gamma }})}^2}{V(g,w;\widehat{\mathrm{\gamma }})},$$ (13)

which has an asymptotic ${\mathrm{\chi }}_1^2$ distribution as long as γ̂ ↛ 0 (so that Slutsky’s theorem holds).

We now consider the asymptotic distribution of the cross statistic, for which γ̂ = ρ̂ − π̂ → 0 under the null hypothesis. For simplicity, we consider a single stratum; the argument for a multiple strata is outlined below. The cross statistic is given by

$$U(g,\stackrel{\sim }{\mathrm{\rho }}-\stackrel{\sim }{\mathrm{\pi }})={(\stackrel{\sim }{\mathrm{\rho }}-\stackrel{\sim }{\mathrm{\pi }})}^{\mathrm{T}}{\mathbb{S}}_k(\stackrel{\sim }{\mathrm{\rho }}-\stackrel{\sim }{\mathrm{\pi }}).$$

In Appendix A we show that (ρ̃ − π̃) is itself an efficient score within the class of models considered by Allen and Satten [2008]. It follows that under the null hypothesis (ρ̃ − π̃) is normally distributed with mean zero and that the variance-covariance matrix can be consistently estimated by

$$\begin{array}{l}\widehat{\mathrm{\sum }}=\sum _i({\stackrel{\sim }{\mathrm{\rho }}}_i-{\stackrel{\sim }{\mathrm{\pi }}}_i){({\stackrel{\sim }{\mathrm{\rho }}}_i-{\stackrel{\sim }{\mathrm{\pi }}}_i)}^{\mathrm{T}}\\ =\sum _i\frac{1}{n_{d_i}^2}{\stackrel{\sim }{\mathrm{\rho }}}_i{\stackrel{\sim }{\mathrm{\rho }}}_i^{\mathrm{T}}.\end{array}$$ (14)

Hence, the theory of quadratic forms in normal variables [Sheffe, 1957] shows that U(g, ρ̃ − π̃) is distributed as a mixture of independent χ² variates with weights given by the eigenvalues of Σ̂ 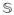. We approximate this distribution using a 3 moment approximation [Imhoff, 1961], which has the computational advantage of only depending on the trace of (Σ̂ 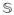)^m for m = 1, 2, 3.

When considering the distribution of the stratified cross statistic the same basic argument applies. First, we stack the vectors ρ̃_z − π̃_z for z = 1, …, 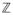into a single vector and form a block diagonal matrix containing stratum specific sharing matrices in each block. Since each (ρ̃_z − π̃_z) is normally distributed with mean zero, and variance-covariance Σ̂_z calculated as in (14) but restricted to data from the zth stratum, the stratified cross statistic is again a quadratic form which is distributed as a mixture of independent χ² variates with weights given by the eigenvalues of {w_zΣ̂_z 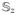, z = 1, …, }.

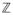When assessing genome-wide significance of results based on (13) it is necessary to account for multiple testing. Although a Bonferroni correction can be used, it may be worthwhile to use a more powerful Monte-Carlo approach that properly accounts for the dependence between tests. For unstratified data, permutation tests that randomize phenotype give a simple way to achieve this goal. For stratified data, permutations must be carried out within strata. For sharing statistics in which γ̂ is not affected by permutation (e.g., p and pc), the form of (12) gives a particularly simple way to conduct permutation tests. For each locus, let

$${\mathrm{\psi }}_i=w_{z_i}({\mathrm{\gamma }}_{z_i}^{\mathrm{T}}·{\mathbb{S}}_{z_i}·{\stackrel{\sim }{p}}_i),$$

for the qth permutation and let $r_i^q$ be a permutation of the disease indicators d_i that preserves stratum. Then, the score function for the qth permutation data set can be written as

$$U(g,w;\mathrm{\gamma })=\sum _i{\mathrm{\psi }}_i\frac{I(r_i^q=1)-I(r_i^q=0)}{n_{r_i^q,z_i}}.$$

Note that ψ_i can be calculated for each locus using the original data and remains unchanged for each permutation data set. Hence, permutation tests can be constructed by storing a scalar quantity for each individual at each locus. For the cross statistic, ψ_i is not invariant to permutation, thus for each locus and each pair of individuals i, j we define

$${\mathrm{\lambda }}_{ij}=w_{z_i}({\stackrel{\sim }{p}}_j^{\mathrm{T}}·{\mathbb{S}}_{z_i}·{\stackrel{\sim }{p}}_i),$$

and express the cross score function for the qth permutation data as

$$U(g,w;\mathrm{\gamma })=\sum _i\sum _j{\mathrm{\lambda }}_{ij}\left[\frac{I(r_i^q=1)-I(r_i^q=0)}{n_{r_j^q,z_j}}\right]\times \left[\frac{I(r_i^q=1)-I(r_i^q=0)}{n_{r_i^q,z_i}}\right].$$

Once again λ_ij can be calculated using the original data and remains unchanged for each permutation data set. However, the storage requirements are significantly greater in this case. In our application, we chose instead to store $r_i^q$ for all permutations q and all individuals i and then, at each locus compute U for each of these permuted datasets. Minimum p-values were then computed across all loci for each permutation.

THE EFFECT OF THE WINDOW SIZE

We have assumed haplotypes of length 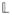when formulating our approach. The value of 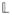affects computational efficiency (the effort required to calculate p̃ increases with 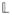) and the ability to distinguish differences in sharing among haplotypes that share many loci IBS. Specifically, a larger value of 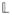allows differentiation between haplotypes that share up to 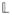loci IBS. Haplotypes that share more than 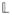loci IBS cannot be differentiated. Thus, increasing 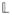increases the resolution of the sharing test. However, once 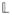is large enough that it is unlikely that two haplotypes will share 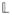loci IBS, the effect of increasing 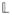will diminish. Note that the distribution of the p and pc tests do not depend on the dimension of 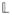, as these tests always have one degree of freedom. The effect on the cross statistic is less clear, although the argument that increasing 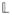only affects the resolution of sharing at very long lengths suggests that the effect of increasing 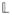on the distribution of the cross test will also level off. This suggests using the largest window size computationally feasible. We discuss this further in the context of the Parkinson’s disease data below.

APPLICATION TO NINDS PARKINSON’S DISEASE DATA

We applied our proposed haplotype-sharing methodology to the National Institute of Neurological Disorders and Stroke (NINDS) Parkinson’s disease data set that we obtained through dbGaP (dbGaP accession number phs000089). This data set contains genotypes of 269 patients with Parkinson’s disease and 266 neurologically normal controls at over 408,000 unique SNPs. The NINDS Parkinson’s disease data set and an initial genome-wide association scan have been described in detail [Fung et al., 2006]. Here, we give a brief overview beginning with a description of case/control assessment. All cases were evaluated by a neurologist and found to have Parkinson’s by either the Gelb et al. [1999] or UK Brain Bank [Hughes et al., 1992] criteria. Those with three or more relatives with Parkinsonism, or apparent Mendelian inheritance of neurodegenerative disease, were excluded. The age at onset of patients in the case sample ranged from 55 to 84 years. Each control underwent a detailed medical history interview and had no family history on specific query of Alzheimer’s disease, amyotrophic lateral sclerosis, ataxia, autism, bipolar disorder, brain aneurysm, dementia, dystonia or Parkinson’s disease. Folstein mini-mental state examination scores among the controls ranged from 26–30. Controls were further interviewed for detailed family history and had no first degree relative with any of the following: amyotrophic lateral sclerosis, ataxia, autism, brain aneurysm, dystonia, Parkinson’s disease and schizophrenia. The mean age of controls in the sample was 68 (range 55–88 years).

GENOTYPES, HAPLOTYPES AND QUALITY CONTROL

The NINDS data consist of genotypes at 109,365 genecentric SNPs obtained using the Illumina Infinium I assay and 317,511 haplotype tagging SNPs obtained using the Illumina HumanHap300 assay. Because there are 18,073 SNPs in common between these two assays, the total number of unique SNPs genotyped was 408,803. Following Fellay et al. [2007], we excluded data from SNPs that had extensive missingness (missingness >10%), deviations from HWE (P-value <0.001 in controls), and low minor allele frequency (<0.2%). We found that the majority of SNPs (606 out of 646) in the psuedo-autosomal region of the X chromosome failed the screen for HWE, throwing some doubt on the quality of these data. For this reason we decided to exclude the sex chromosomes from our analysis. After this quality control (QC) filtering, 391,787 autosomal SNPs remained. Using the software package PLINK [Purcell et al., 2007] we found one pair of individuals (ND00197 and ND00198) who were estimated to share over 20% of SNPs identical by descent. One of these cryptically related individuals (ND00198) was chosen at random to be excluded from subsequent analyses. Using data on self-reported race, the one African American (ND05016) and two Hispanic (ND01060 and ND04404) participants were excluded from subsequent analyses. In addition the two participants (ND05146 and ND05841) reported by Fung et al. [2006] to have been mistakenly included in the panel and not included in their analyses were excluded from our analyses as well. No individuals were excluded for missingness (NINDS had already excluded several individuals with a large proportion of failed genotypes from the dbGaP data set).

We used a computationally efficient estimator of the distribution of haplotypes given the observed genotype data ϕ(h|g). The phasing program ent [Gusev et al., 2008] was used to impute a single diplotype for each chromosome of each study participant. For a given window, the empirical distribution of the imputed haplotypes comprised of SNPs in the window was used as the “working” model for ϕ (h|g). As discussed above, misspecification of ϕ (h|g) will not affect the validity of the haplotype-sharing tests.

ADJUSTMENT FOR CONFOUNDING DUE TO POPULATION STRATIFICATION

We used the stratification score [Epstein et al., 2007] to adjust our analyses for confounding due to population stratification. In Epstein et al. [2007], partial least squares (PLS) were used to estimate the stratification score. Here, we used a modified principal component (PC) approach [Fellay et al., 2007] in place of PLS. This modified PC approach captures the large-scale genetic variation in the data by minimizing the influence of a few high LD regions that would otherwise dominate the first few PCs. This is accomplished by excluding SNPs from the PC analysis that reside in regions of known high LD and then further pruning the PC SNP set to minimize the LD between the remaining SNPs [Fellay et al., 2007]. Using the first few PCs, one individual (ND02579) was found to be a significant outlier, suggesting appreciable non-European ancestry. This individual was excluded from subsequent analyses and when the PC analysis was repeated, no further outliers were identified. The first 10 PCs were then used in a logistic model of disease to estimate each individual’s stratification score—their predicted probability of being a case given the genomic information contained in the PCs. Five strata were then formed based on the quartiles of the stratification scores, for use in a stratified haplotype-sharing analysis. For each locus k, we used the sample size in the zth stratum as the weight function w_k,z in equation (7).

GENOME-WIDE HAPLOTYPE-SHARING ANALYSIS

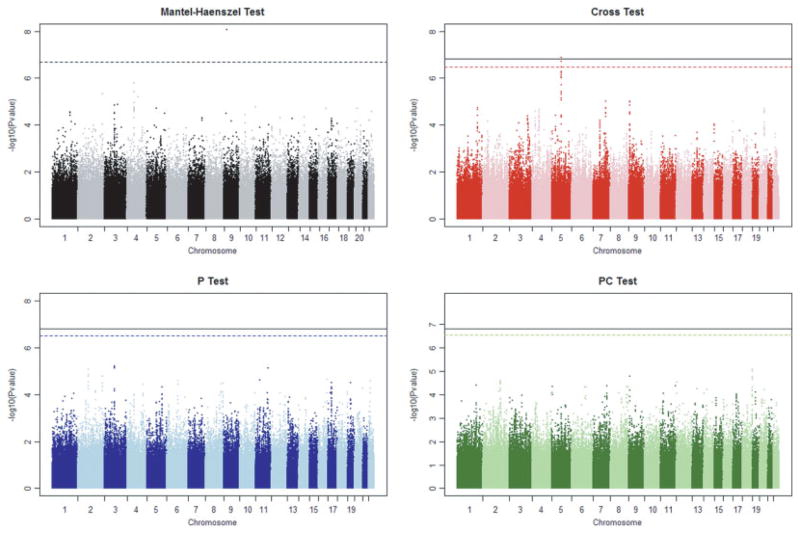
The final analysis data set consisted of genotypes at the 391,787 SNPs that passed QC from 264 case participants with Parkinson’s disease and 264 neurologically normal control participants. To this data set we applied three, stratified, haplotype-sharing tests: the cross test, the p test and the pc test. Each test was calculated using a sliding window of 15 SNPs. All tests used the MILC sharing metric. We measured inflation of test statistics due to residual population stratification by variance inflation factors (median of ratio of observed and expected χ² statistics across the genome; 1.0 signifies no inflation) and q-q plots (see supplemental Figs. 1–3). Variance inflation factors were very close to 1.0 (p test 1.00, pc test 1.00, cross test 1.02), suggesting that residual stratification was not an issue in these analyses. The variance inflation factor for the cross test was calculated by quantile-transforming p-values to a χ² distribution with 1 degree of freedom. Permutation tests were conducted by randomly permuting case/control labels within each stratum and then capturing the minimum P-value of each statistic across the genome for each permutation. We estimated genome-wide significance by comparing the observed P-values to this permutation distribution. The results of these genome-wide analyses, as well as a stratified single-locus (Mantel-Haenszel, MH) test are presented in Figure 1.

Fig. 1.

Genome-wide analyses of NINDS Parkinson’s disease data. Dashed horizontal line represents the permutation-based 0.05 genome-wide threshold for each statistic (black—Mantel-Haenszel; red—Cross; blue—P; green—PC). Solid black horizontal line represents permutation-based 0.05 genome-wide threshold accounting for all three haplotype-sharing tests (computed from minimum P-value of all three statistics). NINDS, National Institute of Neurological Disorders and Stroke.

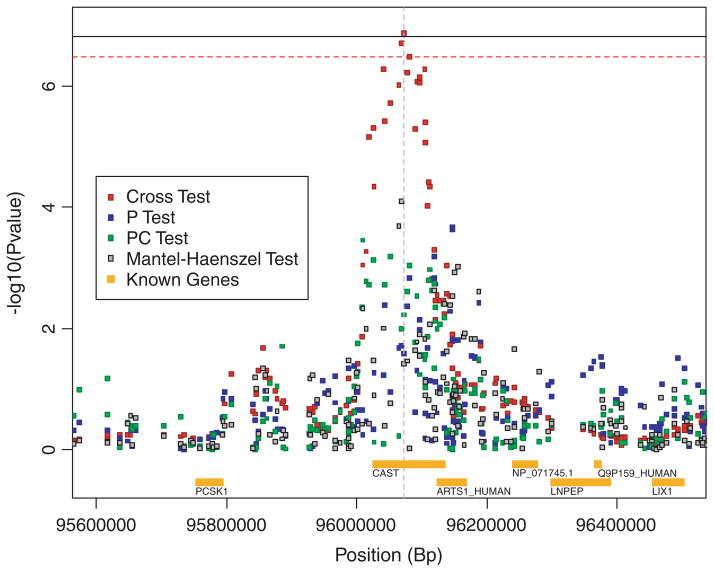
Two genomic regions are suggested by the results shown in Figure 1. The cross statistic suggests a region on chromosome 5 (5q15), while the MH test suggests a SNP on chromosome 9 (9p22). The novel region on chromosome 5 (5q15) suggested by the cross statistic is shown in Figure 2. The maximum signal (6.88) centered on SNP rs27852 exceeds the 0.05 genome-wide significance threshold both for the cross test (6.49) as well as the 0.05 significance threshold when one considers all three haplotype-sharing tests jointly (6.81). The second largest signal, centered on SNP rs10053056, has a value (6.71) that also exceeds the cross statistic’s genome-wide significance threshold. Both of these SNPs map to introns within the Calpastatin (CAST) gene. In fact, the 17 largest values of the cross statistic correspond to windows centered at SNPs that lie within CAST. None of the SNPs in this region (or, in fact, any SNPs on this chromosome) were listed among the top SNPs by Fung et al. [2006].

Fig. 2.

Test results and known genes within a region of chromosome 5 identified by the cross statistic. The solid black horizontal line represents permutation-based 0.05 genome-wide threshold accounting for all three haplotype-sharing tests (computed from minimum P-value of all three statistics). The dashed red horizontal line represents the permutation-based 0.05 genome-wide threshold for the cross statistic. The gray dashed vertical line represents location of maximal cross statistic and locus at which asymptotic approximation is evaluated. Known genes in the region include (left to right): PCSK1, CAST, ARTS1_HUMAN, NP_071745.1, LNPEP, Q9P159_HUMAN, and LIX1.

We investigated agreement between asymptotic and (marginal) permutation P-values at the locus having the smallest (asymptotic) P-value for association using the cross statistic (indicated by dashed vertical gray line in Fig. 2). We permuted case/control status (within strata) 10,000 times and recomputed all statistics at this locus for each permuted data set. We then compute the frequency with which the asymptotic P-values (computed for each permuted data set) are less than or equal to the nominal α levels. The results of this analysis are presented in Table I. The close agreement between permutation P-values and nominal α levels in Table I indicates a good asymptotic approximation. Note that the quality of the asymptotic approximation is important as it has been used to convert test statistics to P-values in order to make tests at different loci comparable.

TABLE I.

Evaluation of asymptotic approximation

	α	Empirical P-value
Cross	0.10	0.096
	0.05	0.046
	0.01	0.009
p	0.10	0.099
	0.05	0.048
	0.01	0.009
pc	0.10	0.099
	0.05	0.049
	0.01	0.007

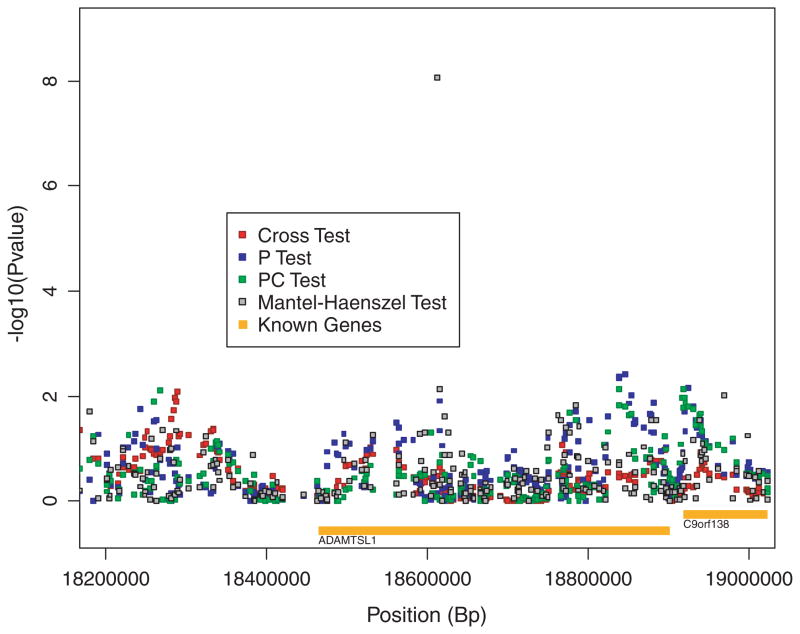
The single-locus MH test yields one genome-wide significant result (rs10963676; asymptotic P-value =2.2 × 10⁻⁸; permutation-based genome-wide adjusted P-value =0.006). This is an intronic SNP within the ADAMTSL1 (MIM ^*609198) gene found on the p arm of chromosome 9 (band 22). We noted a disparity between the asymptotic P-value at this locus and the (marginal) P-value calculated from the permutation distribution of P-values at this locus (marginal permutation P-value = 0.002), suggesting that the asymptotic approximation is poor and may explain why this SNP was not identified by Fung et al. [2006]. Still, the significant genome-wide adjusted P-value would suggest this SNP is an interesting candidate for follow-up. However, further investigation uncovered differential missingness between cases and controls at this locus. Four (1.5%) control individuals have missing genotypes at this marker while 40 (15%) cases have missing genotypes. A test of differential missingness between cases and controls was highly significant (P-value =4.6 × 10⁻⁹). A nearby SNP (rs7027296) was reported to be in complete LD with rs10963676 (r² =1.0) in the hapmap CEU sample. This SNP, which has no missing values in the Parkinson’s disease data, shows a far weaker association with Parkinson’s disease (asymptotic P-value =0.007; marginal permutation P-value =0.024 permutation-based genome-wide adjusted P-value =1) suggesting that the apparent association between Parkinson’s and rs10963676 is most likely an artifact. Interestingly, the haplotype-sharing tests are not affected by this artifact: none of the haplotype-sharing statistics are elevated in this region (see Fig. 3) and the marginal permutation P-values are in good agreement with their asymptotic counterparts. (Results for 15 SNP window centered at rs10963676: p test 0.012 asymptotic, 0.010 permutation; pc test 0.909 asymptotic, 0.908 permutation; cross test 0.189 asymptotic, 0.186 permutation.)

Fig. 3.

Test results and known genes within a region of chromosome 9 identified by the Mantel-Haenszel statistic. Known genes in the region include (left to right): ADAMTSL1 and C9orf138.

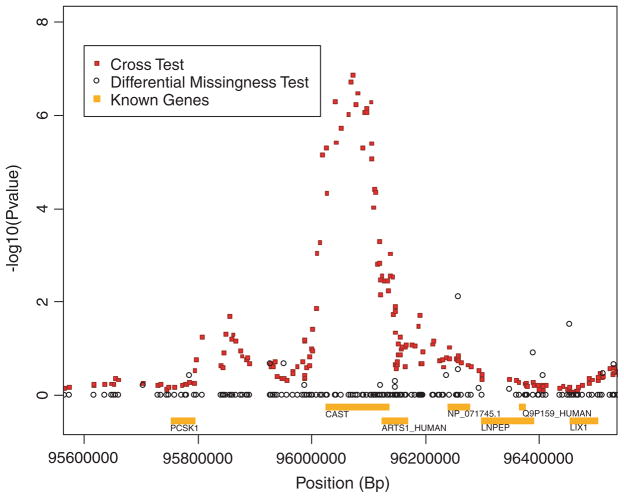
Given the existence of differential missingness at at least one locus in this data set and its apparent role in generating a spurious association with disease, we investigated differential missingness among the SNPs in the region highlighted in Figure 2. For each SNP in this region we tested whether genotype missingness rates differ between cases and controls. The results of this analysis are presented in Figure 4, along with the values of the cross statistic in this region. The lack of loci exhibiting differential missingness and the apparent lack of correlation between the cross statistic and the test statistic for differential missingness suggest that differential missingness plays no role in the associations found in this region.

Fig. 4.

Test of differential missingness (between cases and controls) for each SNP within a region of chromosome 5 identified by the cross statistic.

In the computation of the haplotype-sharing statistics, windows of 15 SNPs were used. This window size was chosen primarily for computational convenience (increasing window size leads to increased computational burden). Table II presents the maximum −log₁₀(P value) of the cross statistic over the region of chromosome 5 highlighted in Figure 3 based on a number of different window sizes used to compute the statistics. The values increase steadily with increasing window sizes up to a window of 31 SNPs, after which, the values seem to level off. Thus, there is some evidence that sharing extends beyond 15 SNPs in this region, i.e., that the 15-SNP window we used results in a truncation of sharing lengths. Increasing window size also seems to lead to a decrease in the genome-wide threshold (3 SNP window, 6.70; 15 SNP window, 6.49; 21 SNP window, 6.43). Ostensibly, this is due to the increased correlation between adjoining windows (more SNPs in common between tests) leading to a reduction in the effective number of tests conducted.

TABLE II.

Peak cross statistic as a function of window size

Size of window (#SNPs)	−log10(P-value)
3	5.85
7	6.23
11	6.57
15	6.88
17	6.97
21	7.09
31	7.20
41	7.16

DISCUSSION

The haplotype-sharing methods we have presented here are simple enough to implement that they can be used for GWASs. By using the efficient score [Allen and Satten, 2008], we can construct computationally simple association tests based on haplotype sharing that allows use of fast (but not likelihood-based) haplotyping algorithms while properly accounting for the uncertainty introduced by using inferred haplotypes. We also give haplotype-sharing analyses that adjust for population stratification.

Our analysis of the NINDS Parkinson’s disease data set implicates a genomic region containing the calpastatin (CAST) gene. Calpastatin is an inhibitor of calpain: a calcium-dependent protease involved in a number of physiologic processes [Goll et al., 2003]. Calpains have been implicated in a number of diseases [Huang and Wang, 2001; Zatz and Starling 2005] including neurodegenerative disorders such as multiple sclerosis, Alzheimer’s and Parkinson’s disease [Saito et al., 1993; Mouatt-Prigent et al., 1996; Tsuji et al., 1998; Shields et al., 1999; Adamec et al., 2002; Raynaud and Marcilhac, 2006]. Increased levels of calpain have been found in the midbrains of Parkinson’s patients [Mouatt-Prigent et al., 1996] and calpain overexpression has been suggested to play a role in neuronal death [Shukla et al., 2006; Camins et al., 2006]. Animal models of Parkinson’s demonstrate that calpain inhibition prevents neuronal and behavioral deficits [Crocker et al., 2003]. Thus, variation in calpastatin expression leading to a lack of calpain inhibition provides a plausible mechanism for CAST’s role in the development of Parkinson’s disease.

For computational simplicity, we used a 15-SNP window for our analyses of the NINDS Parkinson’s disease data. However, there are reasons for thinking that one should use the largest window size possible. Larger window sizes would allow for measuring sharing over greater genomic sequences, which could, in turn, lead to more powerful statistics. Thus, one would expect, in a neighborhood of a disease locus, that the haplotype-sharing statistics would increase in magnitude as the window size used increases, up to the point that the window size approximates the extent of sharing in the data. Once the window size is as large or larger than the extent of sharing, the magnitude of the haplotype-sharing statistics should then level off. This pattern is, in fact, observed in the Parkinson’s disease data. Moreover, this increase in the statistic with window size translates into a real increase in power as the genome-wide significance threshold decreases with increasing window size. This decrease in the cutoff for genome-wide significance is, ostensibly, due to the increasing correlation between tests at adjacent loci as these tests include more and more SNPs in common as the window size increases.

In our calculations reported here, we constructed haplotype-sharing tests at each locus in the genome. Because there is substantial overlap for adjacent windows, it should be possible to avoid calculating a haplotype-sharing statistic at each locus. We are investigating a procedure in which the number of loci between adjacent test statistics is determined adaptively, with tests at every locus when such tests are “large,” but at lower density when the tests are “small.” This could lead to far fewer tests being conducted across the genome and, in turn, a lower significance threshold. The overall significance would be determined by permutation.

The largest single-SNP result found in these data (rs10963676) is likely to be spurious due to substantial differential missingness between cases and controls at this locus. It is interesting that the haplotype-sharing statistics were not affected by this artifact. This is perhaps to be expected as it is unlikely for one aberrant SNP to radically change the sharing pattern in a region, suggesting that haplotype-sharing statistics are less susceptible than single-SNP methods to artifacts affecting a single SNP.

In this study, we chose not to analyze the sex chromosomes in our genome scan. This was largely because the majority of SNPs in the pseudo-autosomal region of chromosome X showed significant deviation from HWE. However, there is no reason a haplotype-sharing analysis could not be applied to the sex chromosomes. One way this could be done would be to consider each male to be homozygous at each X-linked SNP and then conducting an analysis that was stratified by gender.

Although the motivation for haplotype sharing is detection of recent mutations that predispose to disease, our sharing-based approach can detect differences in sharing patterns whether it is the case or control haplotypes that have excess sharing. Under the right circumstances, a recent protective mutation can result in excess sharing among control haplotypes. Recently introduced protective alleles could also be detected if “case” status is defined by an advantageous condition (such as extreme long life), or in situations where case and control participants are extreme samples (e.g., persons with very high or very low cholesterol).

Our approach found a genome-wide significant signal at the CAST gene that was not seen in single-locus tests. This suggests that haplotype-based methods should have a role in the analysis of GWAS. The current approach of single-locus tests possibly followed by a small-scale application of haplotype methods in candidate regions or regions where the single-SNP results are significant or almost-significant may miss regions where a haplotype-based approach would find a signal. As a general point, we note that the strategy of evaluating haplotype methods by looking at their performance in regions implicated by single-SNP methods may result in the false impression that single-SNP methods out-perform haplotype-based methods.

APPENDIX A

Stratified haplotype sharing statistic as score function of

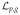
The log-likelihood corresponding to 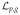(10) is

$$\ell =\sum _i{d}_i[{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)]-ln(1+{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)}).$$

The score vector for β is

$$\frac{\partial \ell }{\partial \mathrm{\beta }}=\sum _i\left(d_i-\frac{{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)}}{1+{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)}}\right)X(h_i,z_i).$$

The score function for each η_z is

$$\frac{\partial \ell }{\partial {\mathrm{\eta }}_z}=\sum _i\left(d_i-\frac{{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)}}{1+{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}+\mathrm{\beta }X(h_i,z_i)}}\right)I[z_i=z],$$

when β = 0, we find that η̂_z solves

$$0=\sum _i\left(d_i-\frac{{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}}}{1+{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}}}\right)I[z_i=z]=n_{1,z}-(n_{0,z}+n_{1,z})\frac{{\mathrm{e}}^{{\mathrm{\eta }}_z}}{1+{\mathrm{e}}^{{\mathrm{\eta }}_z}},$$

where n_d,z = Σ_i I[d_i = d, z_i = z] and hence

$$\frac{{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}}}{1+{\mathrm{e}}^{{\mathrm{\eta }}_{z_i}}}=\frac{n_{1,z_i}}{n_{0,z}+n_{1,z}}.$$

Thus, we find that

$$\frac{\partial \ell }{\partial \mathrm{\beta }}{\mid }_{\mathrm{\beta }=0}=\sum _i\left(d_i-\frac{n_{1,z_i}}{n_{0,z_i}+n_{1,z_i}}\right)X(h_i,z_i).$$ (A1)

Rewriting and using (9) we have

$$\begin{array}{l}\frac{\partial \ell }{\partial \mathrm{\beta }}{\mid }_{\mathrm{\beta }=0}=\sum _i\frac{n_{1-d_i,z_i}}{n_{0,z_i}+n_{1,z_i}}\left[\frac{n_{0,z_i}+n_{1,z_i}}{n_{0,z_i}{n}_{1,z_i}}{w}_{z_i}{\mathrm{\gamma }}_{z_i}^{\mathrm{T}}·{\mathbb{S}}_{z_i}·\mathcal{I}(h_i)\right]\times [I(d_i=1)-I(d_i=0)]\\ =\sum _i\frac{1}{n_{d_i,z_i}}{w}_{z_i}{\mathrm{\gamma }}_{z_i}^{\mathrm{T}}·{\mathbb{S}}_{z_i}·\mathcal{I}(h_i)[I(d_i=1)-I(d_i=0)].\end{array}$$ (A2)

Summing over i and using (2b) and (2c) we have immediately that

$$U(\underset{\_}{h},\underset{\_}{w};\mathrm{\gamma })=\sum _z{w}_z{\mathrm{\gamma }}_z^{\mathrm{T}}·{\mathbb{S}}_z·({\widehat{\mathrm{\rho }}}_z-{\widehat{\mathrm{\pi }}}_z).$$

The score function for likelihood 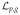(11) is given by

$$U(\underset{\_}{g},\underset{\_}{w};\mathrm{\gamma })=E[U(\underset{\_}{h},\underset{\_}{w};\mathrm{\gamma })\mid g].$$

Examination of (A2) and use of (5a), (5b) and (5c) gives

$$U(\underset{\_}{g},\underset{\_}{w};\mathrm{\gamma })=\sum _z{w}_z{\mathrm{\gamma }}_z^{\mathrm{T}}·{\mathbb{S}}_z·({\stackrel{\sim }{\mathrm{\rho }}}_z-{\stackrel{\sim }{\mathrm{\pi }}}_z).$$

as desired.

(ρ̃ − π̃) as score function of

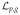
For unstratified data, we show that (ρ̃ − π̃) is the score function for a logistic model of the class considered by Allen and Satten. Let

$$log({\mathrm{\theta }}_h)=\mathrm{\eta }+{\mathrm{\beta }}^{\mathrm{T}}\mathcal{I}(h),$$

where 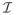(h) is given in (2a) and β is a 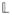-dimensional parameter vector. Using this model in the logistic likelihood (10) but restricting to a single stratum, we find that

$${\frac{\partial log({\mathcal{L}}_{p,h})}{\partial \mathrm{\beta }}|}_{\mathrm{\beta }=0}\propto \sum _i\frac{1}{n_{d_i}}\mathcal{I}(h_i)[I(d_i=1)-I(d_i=0)]$$

for phase-certain data. Using (5a), (5b) and (5c), standard missing data theory then shows that

$${\frac{\partial log({\mathcal{L}}_{p,g})}{\partial \mathrm{\beta }}|}_{\mathrm{\beta }=0}\propto \sum _i\frac{1}{n_{d_i}}{\stackrel{\sim }{p}}_i[I(d_i=1)-I(d_i=0)]=\stackrel{\sim }{\mathrm{\rho }}-\stackrel{\sim }{\mathrm{\pi }}.$$

Applying this reasoning to the independent data in each stratum yields the desired result for stratified tests.