The Past, Present, and Future of Real-Time Control in Cellular Electrophysiology

Abstract

For over 60 years, real-time control has been an important technique in the study of excitable cells. Two such control-based technologies are reviewed here. First, voltage-clamp methods revolutionized the study of excitable cells. In this family of techniques, membrane potential is controlled, allowing one to parameterize a powerful class of models that describe the voltage-current relationship of cell membranes simply, flexibly, and accurately. Second, dynamic-clamp methods allow the addition of new, ‘virtual’ membrane mechanisms to living cells. Dynamic clamp allows researchers unprecedented ways of testing computationally based hypotheses in biological preparations. The review ends with predictions of how control-based technologies will be improved and adapted for new uses in the near future.

I. Introduction

The goal of this work is to review important advances in the use of control-based approaches in the study of excitable cells, especially neurons. In Section II, we review voltage-clamp techniques, used for the last 60+ years to develop models of voltage-sensitive behavior in excitable cells. In Section III, we describe more recent dynamic-clamp techniques, which are used to build model-based hypotheses into electrophysiological experiments. Section IV describes needed advances in dynamic clamp, and Section V describes other emerging uses of real-time control in electrophysiology and in the clinic. Although the focus of the article is on cellular neurophysiology, we discuss several examples from cardiac electrophysiology and other applications.

II. Voltage-Clamp Techniques

Although the field of neural electrophysiology is nearly 500 years old [1], it was not until the middle of the 20^th century that the mechanistic underpinnings of neuronal excitability were determined. The technological driver of these advances was the voltage-clamp method, an early and extremely influential form of real-time control in electrophysiology. In this section, we briefly review the voltage-clamp technique as a necessary introduction to several key topics. More extensive coverage of this material can be found elsewhere [2]–[7].

Two key findings set the stage for developing a quantitative theory that could account for generation of action potentials. First, Cole and Curtis [8] demonstrated that the action potential involves an increase in membrane permeability to ions. Second, Hodgkin and Huxley [9] demonstrated, via intracellular recordings, that membrane potential overshoots 0 mV during the action potential. Together, these findings suggested a model in which membrane permeability to specific ions changed dynamically to generate the action potential.

The necessary next step in this process was to develop a more precise hypothesis, along with an appropriately controlled experiment to test it. Hypothesizing that membrane potential drives changes in membrane permeability [2], Hodgkin and Huxley adopted two techniques from Cole [10] and Marmont [11]: the voltage-clamp and space-clamp methods.

The voltage-clamp technique involves using a feedback system to “clamp” membrane potential at a controllable value. The Hodgkin-Huxley-Katz [12] form of this technology (Fig. 1A) uses two intracellular electrodes. Via the first electrode, a high-impedance “follower” circuit measures membrane potential with unity gain. This signal is passed to a high-gain feedback amplifier, designed to minimize the difference between the measured voltage and a desired voltage “command” signal, schematized in Fig. 1A as a square pulse from an external voltage source. This circuit passes current into the cell via a second electrode, thus closing the feedback loop. Under perfect voltage clamp, the time-dependent current generated by the feedback amplifier exactly counterbalances the current flowing through the membrane from biological sources. Consequently, one can in theory measure voltage-controlled membrane currents simply by monitoring the output current of the feedback amplifier.

Fig. 1.

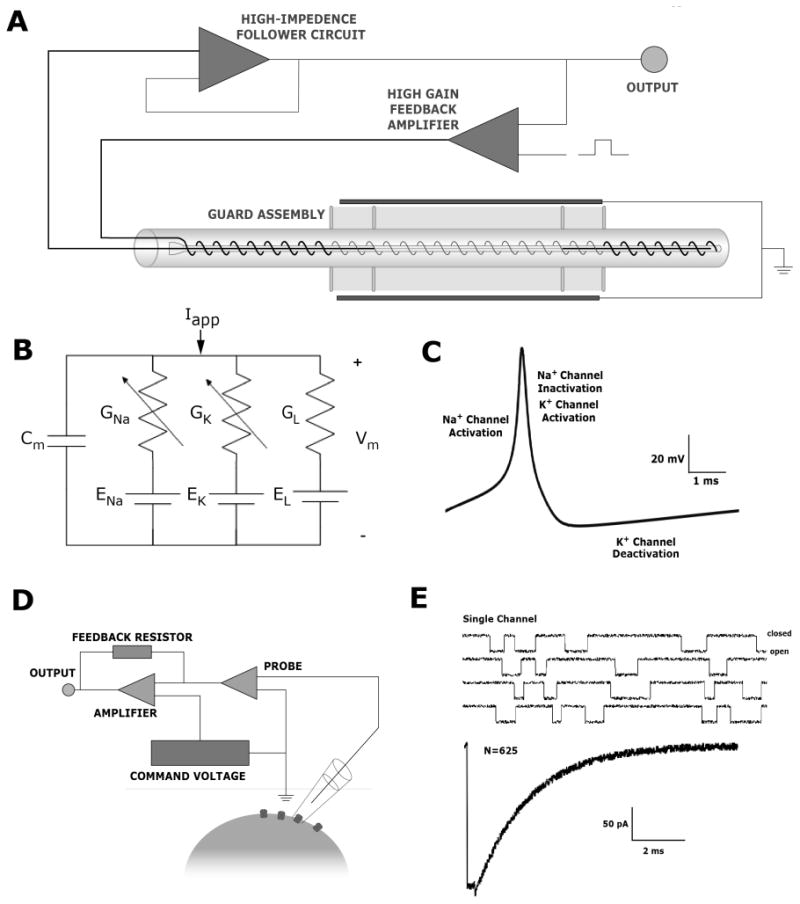
A.) Axial voltage clamp assembly indicating internal and external electrodes as well as simplified circuitry for reading membrane voltage and injecting desired output current. The fine wire threaded down the long axis of the isolated axon assures that the interior is isopotential (“space clamped”). B.) Circuit diagram of the space-clamped cell membrane as described by Hodgkin and Huxley. C.) Neuronal action potential with channel kinetic labels as described by Hodgkin and Huxley. D.) Schematized experimental instrumentation for patch clamp The glass pipette has a smooth tip and a typical inner diameter of 1-3 mm The crucial factor for high-quality patch-clamp recordings is a high (> 1 GΩ) resistance seal between the pipette tip and the cell membrane Circuitry is an elaboration of that used for traditional voltage clamp. E.) Simulated data showing how summed stochastic binary currents generated by single channels give rise to smooth currents of the Hodgkin-Huxley form.

To conduct a well-controlled voltage-clamp experiment, one must also ensure that the interior space of the cell under study is isopotential, or spaced-clamped. Without adequate space clamp, the value of membrane potential at regions of the cell distant from the voltage-measuring electrode are not controlled. Membrane currents from these unclamped regions can flow to the current-passing site and distort voltage-clamp measurements severely [13]. Hodgkin, Huxley, and Katz [12] achieved space clamp by winding the voltage-measuring and current-passing electrodes in a double helix around a very thin glass filament (Fig. 1A).

Using voltage-clamp data collected under space-clamped conditions, Hodgkin and Huxley [14] developed a simple, powerful model of the unmyelinated axon. Figure 1B shows this model in the form of an electrical circuit. The model includes the capacitance of the lipid bilayer (C_m) in parallel with three conductances. The nonlinear (voltage-dependent) conductances G_Na and G_K are placed in series with the Nernst potentials for Na⁺ and K⁺ ions, reflecting the fact that these conductances are modeled as passing only Na⁺ and K⁺, respectively. The linear conductance G_L is in series with an empirically determined battery E_L. This conductance represents the weighted contributions of all voltage-independent conductances in the axon. The current source I_app signifies current injected via the electrode. The first of the Hodgkin-Huxley equations simply represents conservation of charge in this circuit:

$$C_m\frac{d{V}_m}{\mathit{\text{dt}}}=-\left[G_{\mathit{\text{Na}}}\left(V_m-E_{\mathit{\text{Na}}}\right)+G_K\left(V_m-E_K\right)+G_L\left(V_m-E_L\right)\right]+I_{\mathit{\text{app}}}$$

Much of the beauty of the Hodgkin-Huxley model comes from the simple way in which the nonlinear conductances are described. Each nonlinear conductance is described by one or two gating variables, which represent (e.g.) the proportion of its maximal value that the conductance has attained. Hodgkin-Huxley gating variables are each described by first-order, nonlinear differential equation of the form:

$$\frac{\mathit{\text{dx}}}{\mathit{\text{dt}}}=\frac{x_{\infty }\left(V_m\right)-x}{{\tau }_x\left(V_m\right)}$$ (1)

In Eq. 1, the voltage-dependent function x_∞(V_m) represents the steady-state value of x at a given value of membrane potential V_m, and τ_x(V_m) represents the time constant with which x approaches that steady-state value. In the case of ideal voltage-clamp of a space-clamped cell, Eq. 1 reduces to a first-order differential equation with a simple exponential course from its initial value x₀ to its asymptotic value x_∞:

$$x(t)=x_{\infty }-\left(x_{\infty }-x_0\right)e^{-t/{\tau }_x}$$

Hodgkin-Huxley-style equations are readily solvable under a number of conditions, including the absence of either space or voltage clamp. In their original modeling paper [14], Hodgkin and Huxley showed that their equations could replicate accurately the action potential at a point in space (Fig. 1C) and, more impressively, that the model accounted accurately for the propagation speed of the action potential. These successful predictions are often credited as the crucial factors that led to the 1963 Nobel Prize in Medicine or Physiology for this team.

Left unknown by this wonderful work was the fundamental source of voltage-gated and ligand-gated conductances in excitable cells. Early research suggested that ligand-gated conductance changes are generated as the sum of discrete events of size 10-100 nS, giving rise (with typical driving forces < 100 mV) to discrete changes in membrane current that are less than 10 pA in amplitude [15]. Because cellular input resistances are typically relatively small (∼10-100 MO), measurement of 10-pA events is prevented in most whole-cell preparations by thermal (Johnson-Nyquist) noise, which is inversely proportional to the input impedance of the source [16], [17].

To reduce levels of thermal noise and thus measure discrete changes in membrane conductance, Nobel-Prizewinners Sakmann and Neher reasoned correctly that a very small conductance source with correspondingly high input resistance is required [18]. To this end, they developed so-called patch-clamp methods (Fig. 1D), in which a glass pipette of diameter 3-5 μm is lowered to the cell surface and forms an extremely high (GΩ) resistance “seal” with the plasma membrane. The underlying membrane can then be pulled off the cell surface to create a current source with very high input resistance and, experience has shown, a small number of underlying ion channels. Using the patch-clamp technique, along with improvements in amplifier technology [19], allowed the group of Sakmann and Neher to demonstrate that the cellular-level currents, measurable via previously developed voltage-clamp techniques, can be ascribed to the summed activity of hundreds or thousands of individual ion channels (Fig. 1E). Each of these channels flickers stochastically between open and closed states. The voltage-dependent rate constants measurable at the whole-cell level reflect the rates of transition between these open and closed states [4], [7].

The techniques pioneered by these two Nobel-Prize-winning groups have become standard techniques in cellular electrophysiology. Particularly widely used are two more recent variants of these techniques:

1. In whole-cell patch clamp, the researcher creates the GΩ seal as described by Sakmann and Neher, but then applies suction to break through the cell membrane and give access to the cell as a whole. The whole-cell technique does not allow observation of currents from single channels, but it is a straightforward method to obtain high-quality intracellular recordings from cells, even in the living animal.

2. In single-electrode voltage clamp, one electrode is used for the distinct purposes of measuring membrane potential V_m and passing current in order to control V_m. This technique is experimentally valuable but has the down side that measurement of V_m is distorted when passing current through the tip of the pipette, which has non-zero series resistance. A variety of clever techniques have been developed to mitigate this and other problems associated with real-world intracellular recordings [20].

Without question, the “commoditization” of voltage-clamp techniques has been invaluable for our understanding of how excitable cells function in health and disease [3], [21]. However, it is important to realize that all data are not of equal quality. Compensation for electrode resistances and sources of stray capacitance is necessarily incomplete for reasons related to electrical stability of recorded signals [20]. This becomes more of a problem as researchers record from deeper structures (increasing capacitance problems) with smaller (and thus higher-resistance) pipettes (e.g., [22], [23]). Additionally, the whole-cell patch-clamp does not allow the researcher to establish space clamp. To a degree, this problem can be mitigated by using pharmacological blockers to increase membrane resistance and thus make the cell electrically more “compact” [24]. However, because this approach does not by any means guarantee good space clamp, voltage-clamp data from such preparations should be expected to be significantly distorted [13].

III. Dynamic Clamp

Voltage-clamp techniques are a particularly valuable form of control in cellular physiology, because they allow the researcher to control (clamp) membrane potential V_m, usually in a step-wise fashion. With V_m held at a fixed value, the Hodgkin-Huxley gating equation (Eq.1) is linear and gives rise to a simple exponential solution. Newer, more complex forms of control, developed in the last 25 years, have allowed ever-more sophisticated forms of hypothesis testing in electrically excitable cells and circuits. In the cellular electrophysiology literature, these techniques are generally referred to as dynamic conductance injection or, more commonly, dynamic clamp.

The goal of dynamic clamp techniques is to better study the roles of quantitatively specified conductances, synaptic inputs, and network structures on excitable cells. This objective is accomplished by constructing a system that can read instantaneous values of membrane potential V_m, and operate on them to generate virtual currents to be delivered at appropriately high update rates. Between the “reading” of V_m and the “writing” of applied current is an algorithm that represents any of a number of membrane mechanisms and other factors. Dynamic clamp is not a typical control method, because it does not impose a particular behavior on the cell. Instead, dynamic clamp is a method of studying the interactions between excitable cells and a user-specified computational model in an experimental setting. Dynamic clamp can, for example, replicate the actions of modeled voltage-gated ion channels in excitable cells, or immerse those cells in virtual-reality-inspired neuronal networks. Thus, dynamic clamp allows the researcher to test computationally rigorous hypotheses in living cells.

Dynamic-clamp-like techniques were first used for simple linear-resistive-coupling experiments in recordings from cardiomyocytes [25], [26] and neurons [27]. In 1993, two groups launched more sophisticated dynamic-clamp technologies. The system of Robinson and Kawai [28] relied upon digital-signal-processing hardware to generate artificial synaptic inputs. An MS-DOS-based system from the groups of Abbott and Marder [29] was software-based, substantially expanding the number of potential applications. However, because this system was programmed in assembly language, it was challenging for other groups to adapt for new purposes.

In the 1990s, a number of approaches were taken to develop ever-more-powerful dynamic-clamp systems. Masson, et. al., designed both a very large scale integration (VLSI) circuit and a Digital Signal Processor (DSP) based system capable of imitating any type of membrane channel [30]. The VLSI model was implemented using a customized application specific integrated circuit (ASIC) consisting of 45 CMOS and 75 bipolar transistors to simulate the activation and inactivation gating curves for sodium from the Hodgkin Huxley model. The DSP-based system efficiently processed numerical data, but required a microcomputer for acquisition and storage of conductance values as well as the DSP board [30]. Like previous circuit-based implementations [26], [27], the analog VLSI model neurons and DSP-based systems also had the advantage of operating without significant delays despite their complexity. However, such circuits were only able to remain programmable and allow model changes through specialized construction, which increased the required number of components and system cost. In 1996, Wilder et al. [31] developed the first MS-DOS system based around a higher-level language (Pascal). Through a series of clever simplifications, they were able to use their system to study 2-cell networks consisting of one biological and one simulated cardiomyocyte [32].

By the year 2000, personal computers were powerful enough to support dynamic clamp systems written in somewhat human-friendly programming languages on multi-tasking operating systems. Pinto et. al., produced a Windows implementation which required only a computer capable of running Windows and a ADC/DAC interface for recording membrane potential and injecting current [33]. Similar Windows-based systems have followed [34]–[36]. However, the use of multitasking operating systems like Windows for dynamic clamp raises the possibility of the disruption of the timing of dynamic-clamp operations [37], [38].

The ideal, software-based dynamic clamp system would allow “hard” real-time performance (i.e., consistent real-time performance on each cycle of input and output) with the conveniences of a multi-tasking operating system. Responding to this need, our group [39], along with those of David Christini (Weill Cornell, ref. [40]) and Robert Butera (Georgia Tech, ref. [41]) developed dynamic-clamp systems based on real-time versions of the Linux operating system. Recognizing that the strengths of our three systems were complementary, we subsequently merged them into a system we call the Real Time eXperiment Interface (RTXI; www.rtxi.org). RTXI (Fig. 2A) takes advantage of modified versions of the Linux operating system that allow uninterruptible real-time (RT) threads (processes) to be to created and run alongside a non-real-time (NRT) thread [42]. The RT thread performs all the time-sensitive data movement and mathematical operations, and communicates with the data-acquisition (DAQ) board. The DAQ, in turn, communicates with a current-clamp amplifier, digitizing measured membrane potential at a fixed frequency (usually 10-75 kHz) and at the same frequency delivering a signal that is converted by the amplifier to current injected into the cell via the recording electrode, typically under whole-cell patch-clamp. For a given computer, the RT thread must run fast enough to “read” the value of membrane potential and update the applied current within one clock cycle of the DAQ card.

Fig. 2.

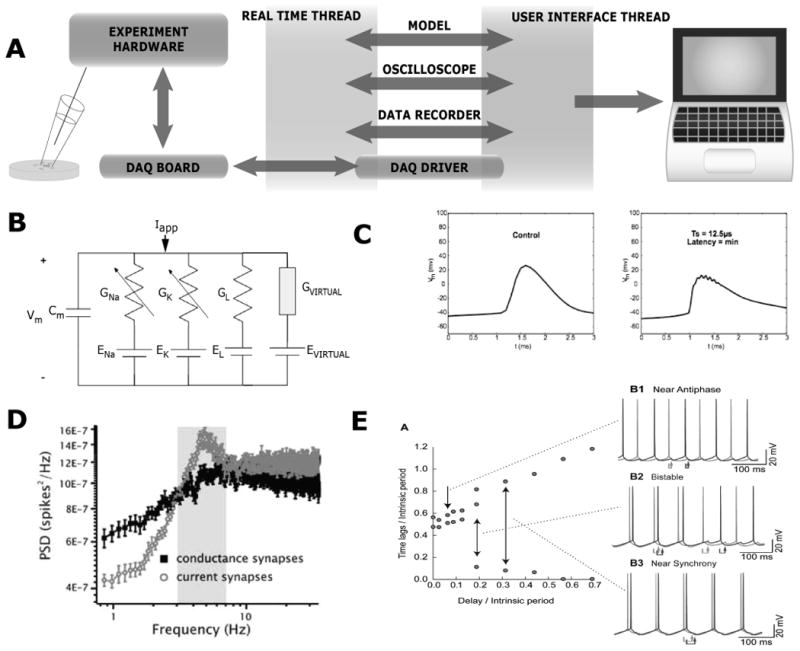
A.) General setup for RTXI [42], an open-source system for dynamic clamp and other control-based experimental protocols. Arrows indicate transfer of information. The real-time thread is uninterruptable to ensure real-time performance. B.) Dynamic clamp is often used to introduce a virtual conductance source into a cell membrane at the location of the electrode. This conductance is injected as a current and may be modeled as a series conductance and reversal potential, connected in parallel with existing biological membrane conductances at the site of the electrode. C.) Left panel: A neuronal action potential, recorded intracellularly under control conditions. Right Panel: With time steps of 12.5 μs, RTXI is fast enough to replicate, with reasonable accuracy, the actions of previously blocked, fast-inactivating Na⁺ channels in generating action potentials [66]. D.) Power spectral densities of spike trains show that 3-8 Hz interspike intervals are eliminated with the use of conductance-based synaptic activity delivered with dynamic clamp, but preserved with current-based inputs [58]. E.) A hybrid model/neuron circuit moves between antiphase (y-axis value near 0.5) and synchrony (y-axis value near 0 and 1) with changing conduction delay between two neurons that have been connected via virtual synapses (dark and light gray traces in the right panels) [63].

The NRT thread represents the processes that operate on slower time scales. A graphical user interface allows the user to update model parameters. Changes made in the non-real time thread are sent to the real time thread where they are incorporated into the thread on the next data acquisition board trigger [42]. RTXI includes several standard features or plug-ins, as well as the ability to incorporate any additional user made plug-ins (Fig. 2A). Dynamic data obtained by the RT thread from the cell or calculated in real time from cellular data may be passed from the real time thread to the NRT thread. They are sent to first in first out (FIFO) queues which allowed the data to be recorded or displayed using the virtual oscilloscope or data recorder features. Additional features included a System Control Panel designed to configure data acquisition devices and a Connector used to make connections between user written plug-ins and the data acquisition device. RTXI is able to interface with multiple DAQs and dynamically link any user-written plug-ins at run time [42].

As noted above, dynamic clamp has been used for many applications [37], [38]. One common use involves injecting voltage-dependent conductances into the patched area of the cell (Fig. 2C). In this case, the dynamic clamp system reads membrane voltage V_m, calculates the associated value of conductance from Hodgkin-Huxley-style equations, and multiplies conductance by the potential difference V_m-E_rev, where E_rev is the reversal potential of the modeled conductance. This current is then injected into the cell, creating a serial conductance-reversal potential network which combines in parallel with the conductances already present within the cell (Fig. 2B). This approach allows users to temporarily embed virtual ion channels in the cell membrane, and record the response. Virtual ion channels can be of the Hodgkin-Huxley type, or can take more complex forms that include stochastic channel flicker [43]. Such experiments allow the researcher to evaluate the relationship between channel properties and emergent cellular outputs with much greater speed and flexibility than is allowed with traditional molecular biological approaches.

In a complementary approach, dynamic clamp can be used to subtract a voltage-dependent conductance. In this case, negative-conductance channels are added to counteract the presence of biological channels in the membrane [44]–[46]. In this kind of experiment, particular care is required. It is not a trivial matter to effectively cancel a biological nonlinear conductance, and control experiments must be performed to ensure that the results are correct.

Dynamic clamp also provides the user with unique ways to quantify input-output relationships in response to user-defined inputs [47]–[57]. In one such example, Fernandez and White [58] used dynamic clamp to compare the responses of suspected oscillatory neurons (entorhinal stellate cells) to artificial synaptic stimuli of two kinds. For current-based stimuli, the stimulus waveform was independent of membrane potential. For more realistic, conductance-based stimuli, input scaled instantaneously with membrane potential as described in the previous paragraph. Use of conductance-based synaptic inputs substantially altered the power spectrum of the resulting output spike train (Fig. 2D), arguing against the common hypothesis that stellate cells serve as pacemakers for prominent synchronized in vivo activity at 4-12 Hz [58]. Other recent work from our group show that stellate cells are better poised to serve as amplifiers of synchronized activity that is received from other neuronal populations [59]–[61].

Dynamic clamp can also be used to couple biological cells together via artificial, and thus user-controllable, synapses. Such hybrid networks can in principle contain a fair number of biological cells – the number is limited by intracellular recording capabilities – along with an arbitrary number of simulated virtual neurons. In early work of this kind, analog circuitry was used to artificially connect excitable myocytes or neurons [26], [27]. Since then, a number of flexible hardware- and software-based systems have been developed for such studies [28], [29], [33], [39], [41], [42], [62]. In one hybrid-network example, Wang and colleagues built hybrid networks to study the effects of conduction delay on neuronal synchronization [63]. Using dynamic clamp to alter the apparent conduction delay between recorded neurons, they found that biologically relevant delays can have profound effects on the stability of oscillatory synchrony. An example of this effect is shown in Fig. 2E, which shows results from a hybrid network of two biological neurons, connected via virtual inhibition. The plot shows the time lag between action potentials for the two cells, normalized by their firing periods, plotted vs. normalized time delay. For small delays, the two cells fire in near-antiphase (normalized time lag near 0.5). For larger delays, the cells switch into near-synchronous firing (normalized time lag near 0 or 1) [63].

A particularly imaginative example of dynamic-clamp technology comes from the work of Berecki and colleagues [64]. They simultaneously recorded from two cells: a ventricular myocyte and a human embryonic kidney (HEK) cell. In their experiments, membrane potential from the myocyte was recorded and used as a variable voltage-clamp input to the HEK cell, which had been transfected to express a particular variant of K⁺ channels in either wild-type or mutated form. The current generated by the K⁺ channels was recorded and injected back into the myocyte. In effect, the transfected HEK cell was used as a biological element to solve the associated Hodgkin-Huxley-style gating differential equation (Eq. 1). This approach allowed the authors to assess the effects of channel mutations on myocyte physiology without the intermediate step of constructing the differential equation-based model.

Like most experimental techniques, the dynamic clamp method has potential weaknesses. Some of these weaknesses apply only to specific platforms. For example:

• Hardware-based dynamic clamp systems are very fast but relatively limited in their programmability.

• As noted above, some software-based systems do not ensure “hard” real-time performance.

• All software-based systems running on traditional PCs face several design limitations. First, software-based systems require non-zero time steps in order to perform the real-time calculations. Second, there is small (∼5 μs) but measurable jitter (variability) in the time step, generated by the computer bus [39], [41]. Third, within each time step, there is some latency between the operation of “reading” membrane potential and “writing” applied current. Fourth, the number of bits in A/D and D/A conversion can limit system dynamic range to a degree that degrades performance [41]. In most cases, RTXI and other software-based systems run fast enough to make the effects of these issues negligible [39], [65]. However, in demanding applications, the effects of time step, jitter, and latency can be important [41], [66], [67].

Some of the more vexing issues that one must consider in designing, performing, and interpreting dynamic clamp experiments are common to all platforms:

• Model error is inevitable and leads to inexact outcomes. For example, in Fig. 2C, the mimicked action potential (right) is measurably different from the control version (left). Some of this discrepancy is surely caused by inaccuracies in the real-time gating equations.

• Another source of model error is perhaps more important: unless the cell is space-clamped, and thus isopotential, it is impossible to use a point source to represent voltage- or ligand-gated channels that are widely distributed on the cell membrane. This factor is no doubt an additional source of error in the right panel of Fig. 2C.

• In most cases, dynamic clamp is performed using a single electrode to measure membrane potential V_m and inject calculated current I_app. As noted earlier, the use of a single electrode gives rise to unavoidable inaccuracies, due to imperfect compensation for the electrode series resistance and capacitance. These imperfections place significant limits on dynamic-clamp performance [67]. This problem is particularly acute under two extremes of recording conditions: recording from very small cells or processes, with correspondingly small-diameter patch electrodes; and recording from very large cells, for which so much current is needed that electrode or amplifier properties can be limiting.

• In dynamic clamp, charge is passed to the recorded cell via the electrode. The chemical identities of the mimicked ions are not respected. For this reason, dynamic clamp cannot replicate the effects of ions like calcium on second-messenger systems.

IV. Emerging Advances in Dynamic Clamp

Control-based approaches have been important in cellular electrophysiology for 60+ years. Two examples were discussed here: voltage-clamp techniques, which revolutionized our understanding of cellular electrophysiology, and much more recent dynamic-clamp approaches, which have allowed virtual-reality-inspired techniques to understand cells and networks. However, as described at the end of the previous section, many challenges remain. Here, we discuss methods to mitigate these issues, in the same order:

• Model error is a reasonably tractable problem if two conditions are met. First, there must be control data, so that the model can be optimized to fit the control case. Second, the membrane mechanism should be electronically very near the location of the electrode. Given the speed of modern computers, and the relatively small number of free parameters for most models of membrane mechanisms, one could “tune” the model to better-match the control data in relatively short order.

• Distributed virtual conductances present a major problem. One can attempt to overcome this error source by building a model that includes “virtual” extensions (e.g., dendrites or axons in neurons) and spatially distributed sources [36], [45]. Inaccuracies in these virtual extensions can in principle be corrected via optimization, given a sufficiently constrained model.

• Compensation for electrode properties can be performed in software, under the assumption that the electrode has linear properties [68]. Because this compensation involves deconvolution to remove the low-pass effects of uncompensated resistance and capacitance, it is challenging but tractable to perform in practice. Such deconvolution methods make it feasible to introduce artificial membrane mechanisms at locations other than the neuronal cell body.

• Idoux and Mertz [69] pioneered a method to “clamp” calcium, using a feedback-controlled laser to release chemically-bound calcium that had been previously introduced to the cell. Although the fidelity of measurement and uncaging techniques make this approach challenging, we see this as an extremely promising research path, given the importance of the spatiotemporal signature of the calcium transient for cellular metabolism in both myocytes and neurons (e.g., [70]–[72]).

V. Future Directions

Although we have focused on cellular electrophysiology, mainly in the realm of neurophysiology, it bears mentioning that feedback-based techniques are useful in many other realms of biomedical engineering. Feedback-based devices are emerging as an important frontier for systems-level applications like seizure control [73], [74], deep brain stimulation [75], [76], and cardiac arrhythmias [77], [78]. Some, but not all, of these applications can make use of the sub-millisecond timing necessary for dynamic clamp. Real-time control is also emerging as an important topic in automated, optimized experimental design [79] and in the particularly challenging field of virtual acoustic realities [80]. In the decades to come, we anticipate that feedback-based experimental design will become ubiquitous in basic and applied studies of many stripes.