Estimation of the number of fluorescent end-members for quantitative analysis of multispectral FLIM data

Abstract

Multispectral fluorescence lifetime imaging (m-FLIM) can potentially allow identifying the endogenous fluorophores present in biological tissue. Quantitative description of such data requires estimating the number of components in the sample, their characteristic fluorescent decays, and their relative contributions or abundances. Unfortunately, this inverse problem usually requires prior knowledge about the data, which is seldom available in biomedical applications. This work presents a new methodology to estimate the number of potential endogenous fluorophores present in biological tissue samples from time-domain m-FLIM data. Furthermore, a completely blind linear unmixing algorithm is proposed. The method was validated using both synthetic and experimental m-FLIM data. The experimental m-FLIM data include in-vivo measurements from healthy and cancerous hamster cheek-pouch epithelial tissue, and ex-vivo measurements from human coronary atherosclerotic plaques. The analysis of m-FLIM data from in-vivo hamster oral mucosa identified healthy from precancerous lesions, based on the relative concentration of their characteristic fluorophores. The algorithm also provided a better description of atherosclerotic plaques in term of their endogenous fluorophores. These results demonstrate the potential of this methodology to provide quantitative description of tissue biochemical composition.

1. Introduction

Fluorescence lifetime imaging (FLIM) is a powerful tool in biological and clinical sciences for characterization of tissue samples. Despite several studies showing the potential of multi-spectral FLIM (m-FLIM) as a promising clinical optical imaging modality, its utility has not yet fully demonstrated [1–4]. One of the main reasons for this is the element of subjectivity involved in interpreting multispectral FLIM images, which is based on qualitative comparison of spectral intensity and lifetime values obtained from sample fluorescence time-resolved measurements with those of known fluorophores. Such comparison-based interpretation of FLIM images is satisfactory only when the fluorescence decay recorded at a pixel in a FLIM image can be attributed to a single fluorophore. However, in most practical applications, there are often more than one fluorescing species contributing to the bulk fluorescence signal. In such cases, it becomes imperative to develop a method that can quantitatively identify the number, the type and the relative abundance of fluorophores present in the sample.

The number of components present in a sample, their identification and relative concentration or abundance are three major problems, whose solutions are needed to provide meaningful descriptions for m-FLIM data. These problems are also present in other fields of application, such as in remote sensing where they are known as unmixing problems [5]. Different unmixing schemes have been applied with spectral fluorescence data [6, 7], frequency resolved FLIM data [8], and more recently with time-resolved m-FLIM data [9, 10]. The assumption that the number of components is known a priori is a common approach [5], however this estimation is complicated by the presence of outliers and experimental noise.

From the remote sensing literature, three distinct approaches for the estimation of the number of components can be distinguished: methods based on information theoretic criteria [14, 15], eigenvalue based algorithms [11–13], and more recently geometry based strategies [16–18]. Methods based on information theoretic criteria usually select a model, or families of probability density functions, that best fits the data according to a cost function. Some of these algorithms were first employed in passive sensor array processing [14, 15]. Other approaches are based on the eigenvalue decomposition of the observed data. These techniques also reduces the dimensionality of the problem and the computational cost. The method by Harsanyi et al. (1993) [11] introduced the use of Neyman-Pearson (NP) detection theory to make a decision based on a fixed probability of false alarm. The virtual dimensionality (VD) [12] method is based on the difference between the eigenvalues of the correlation and covariance matrix. This technique detects a noise component when the difference between the eigenvalues have similar magnitudes, and a signal source when the difference is significant. Another popular methodology is hyperspectral signal identification by minimum error (HySime) [13], which estimates the subspace of the eigenvectors that best contains the data according to a least squares criteria.

Geometry-based approaches are a recent trend, which is providing important advances in remote sensing. Hyperspectral intrinsic dimensionality estimation with nearest-neighbour distance ratios (HIDENN) [16] measures two geometrical properties from the data to estimate the fractal dimension of a manifold that contains the data. The intrinsic dimensionality of this manifold is then employed to estimate the effective dimensionality of the data. Outlier detection method (ODM) [17] characterizes data as outliers of noise in a principal component space. The noise components are spherically symmetric, while data signals are expected to present higher radius, in a hyper-ellipsoid fashion. These differences are measured by using an outlier detector based on inter-quartile ranges. The methods proposed by Ambikapathi et al. (2013) [18] are based on convex geometry. The constraints imposed on the abundances in a linear mixture model provide information to decide if the measured data should lie inside a convex hull (Gene-CH). In addition, if the end-members are linear independent they also lie inside an affine hull (Gene-AH). In both cases, the end-members are the vertex of the hulls. An NP detector is employed to validate the end-members.

It should be noted that the problem of estimating the number of components in the context of m-FLIM data has never been attacked before. Hence the technical contribution of this work relies on a new method for estimating the number of components in time-domain m-FLIM data by proposing two simultaneous NP tests to evaluate temporal and spatial consistency among the estimated end-members. These two tests are required mainly since the end-members are highly overlapped in m-FLIM data, compared with remote sensing applications. The first NP test evaluates temporal consistency by the linear independence of the resulting end-members (the estimated fluorescence time-decays), without using dimensionality reductions as in [18]. The second NP detector checks the spatial consistency by the abundances or fractional contributions of the end-members in the data sample. Only those end-members with significant abundance levels are considered as original components; otherwise, they could be produced by experimental noise or outliers. By employing our previous contributions in [9, 10], the new method implements a complete solution for the blind linear unmixing problem for m-FLIM data. That is, without prior information, our proposal thus estimates simultaneously the number of end-members, their time-domain fluorescence profiles and their relative abundances. Synthetic data was employed to measure quantitatively the performance of the algorithm. In addition, the algorithm was further validated using experimental m-FLIM data measured from in vivo samples of hamster pouches with induced oral carcinoma, and ex-vivo human atherosclerotic plaques.

The paper is organized as follows: Section 2 describes the linear unmixing model employed in the decomposition of m-FLIM data. In Section 3, the proposed NP detectors for linear independence and spatial coherence are presented in detail. Also, the BEAE is briefly introduced, and the final algorithm for estimating the number of components, the end-members and their abundances is detailed at the end of this section. The experiments and their results for the synthetic and experimental m-FLIM datasets are shown in Sections 4 and 5, respectively. Section 6 introduces a discussion on the results, and the final remarks are presented in Section 7.

2. Linear unmixing of m-FLIM data

The linear mixture model [19–21] assumes that every measurement is a linear combination of the end-members. In the case of time-domain m-FLIM data [9], the measurements and the end-members are fluorescence intensity decays measured in different spectral bands simultaneously, which can be concatenated as shown in Fig. 1(a). The fluorescence decays y_k = [y_k,1,..., y_k,L]^⊤ ∈ ℝ^L recorded at K positions k ∈ [1, K] are a combination of the end-members p_j ∈ ℝ^L for all j ∈ [1, N] with their respective concentrations α_k,j, which are usually referred as abundances in remote sensing literature. This linear mixture is given by

$$y_k=\sum _{j=1}^N{p}_j{\alpha }_{k,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k\in [1,K]$$ (1)

The mixture model can be rewritten in matrix form to include all the K measurements available. For this purpose, the end-members matrix P^N = [p₁,..., p_N] ∈ ℝ^L×N gathers the time-domain fluorescence profiles of the N components, and the abundances are grouped in vectors α_k = [α_k,1,...,α_k,N]^⊤ at each spatial location k. Using these definitions, the mixture model can be written as

$$Y=P^N{𝒜}^N$$ (2)

where Y ∈ ℝ^L×K contains the available m-FLIM measurements, and the abundance matrix 𝒜^N ∈ ℝ^N×K is defined as 𝒜^N = [α₁,...,α_K]. This model considers the following two constraints for the abundances at each spatial location k [5], since these parameters represent the proportional concentration of the end-members:

$${\mathbf{1}}_N^{\top }{\alpha }_k=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k\in [1,K]$$ (3)

$${\alpha }_k\ge 0,$$ (4)

where 1_N represents a vector with unitary entries of dimension N, and the inequality ≥ is interpreted component-wise. Furthermore, the linear mixture model in (1) subject to the constrains in (3) and (4) can have a geometrical interpretation: the set of mixture samples 𝒴 = {y₁,..., y_K} should be a subset of a convex hull [22], where the end-members p_n represent its vertices. The corresponding convex hull can be written as

$${\mathrm{\Omega }}_p^N\triangleq \text{conv}\{p_1,\dots ,p_N\}=\left\{\mathbf{y}\in {ℝ}^L|\mathbf{y}=\sum _{j=1}^N{p}_j{\omega }_n\hspace{0.17em}\hspace{0.17em}\text{s}.\text{t}.\sum _{j=1}^N{\omega }_j=1,\hspace{0.17em}\hspace{0.17em}{\omega }_j\ge 0\forall j\in [1,N]\right\}$$ (5)

Moreover, our formulation requires that the end-members {p₁,..., p_N} are linearly independent [23], and as a consequence ${\mathrm{\Omega }}_p^N$ is a simplex of size N − 1. A notable difference between linear unmixing for mFLIM data and remote sensing information is the incorporation of constraints in the estimation of end-members [10]. The fluorescence intensity time decays are strictly positive, and they are usually normalized in order to minimize intensity artifact problems [19, 24]. Therefore, in our application, there are two additional constraints for the end-members with respect to the linear unmixing model

$${\mathbf{1}}_L^{\top }{p}_j=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j\in [1,N]$$ (6)

$${\mathbf{p}}_j\ge 0.$$ (7)

Fig. 1.

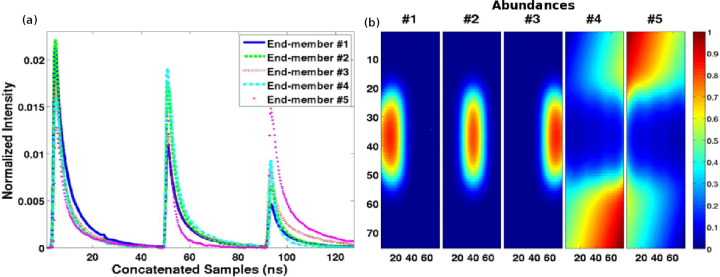
The 5 synthetic end-members (a) and their abundance maps (b), with purity level ρ = 1, employed in the synthetic evaluation. The end-members of 510 samples represent the concatenated fluorescence intensity time-decays at three different wavelength bands. The x and y positions (75 × 75) in (b) correspond to spatial coordinates in the sample, while the color depicts the quantitative abundance values.

3. Estimating the number of components

The accurate estimation of end-members P^N and their abundances 𝒜^N rely on a correct knowledge of the number of components N in the m-FLIM data, which by itself represents a difficult task due to the presence of noise and outliers [5]. Outliers are generated by measurement errors or components with very low occurrence in the sample. The proposed algorithm is based on our previous methodology for blind unmixing or BEAE [10] that requires a linear independence property of the end-members. BEAE relies on alternating least squares (ALS) [25] and restricted quadratic optimization to compute the end-members and their abundances in the sample [9]. For this new challenge, we propose an iterative methodology to increase gradually the estimation of the number of components, if at each step the resulting end-members satisfy a joint coherence test to validate their independence and their spatial interpretation. Once all candidates are good estimations of the fluorescent components present in the sample, the set of end-members will satisfy the following criteria:

• Linear Independence: The convex hull (5) is a simplex and the set of end-members should be affinely independent [18,23].

• Spatial Coherence: Each end-member has a significant relative abundance, since it is contributing to the sample fluorescence signal.

These criteria are evaluated by using NP tests [26], as detailed in the following subsections.

3.1. Linear independence criterion

In the BEAE methodology [10], we perform the linear unmixing of the m-FLIM samples while estimating a set of candidate end-members:

$${𝒫}_{\widehat{N}}\triangleq \{p_1,\dots ,p_{\widehat{N}}\}$$ (8)

where N̂ > 0 is the estimated number of components. After an iteration, we add one more candidate to the set (8) and increase our estimation of the number of end-members to N̂ = N̂ +1. As long as the number of candidates N̂ is lower or equal to the real number of components N, i.e. N̂ ≤ N, the set of end-members (8) will be affinely independent and ${\mathrm{\Omega }}_p^{\widehat{N}}$ will be a simplex. To detect if the j-th candidate end-member p_j is a linear combination of the rest, we propose the following approach based on the methodology by Ambikapathi et al. (2013) [18]. For each candidate p_j ∈ 𝒫_N̂, its projection into the closed-subspace spanned by {p₁,..., p_j−1, p_j+1,..., p_N̂} is calculated as

$${\widehat{p}}_j=P_j{\beta }_j$$ (9)

where P_j = [p₁,..., p_j−1, p_j+1,..., p_N̂] ∈ ℝ^L×(N̂−1) and β_j = [β_j,1,..., β_j,N̂−1]^⊤∈ ℝ^N̂−1. The optimal projection is estimated by a quadratic criterion as

$${\beta }_j=\text{arg}\underset{\beta }{\text{min}}{\Vert p_j-P_j\beta \Vert }_2^2$$ (10)

subject to ${\mathbf{1}}_{\widehat{N}-1}^{\top }\beta =1$ and β ≥ 0, where ‖ · ‖² denotes the Euclidean norm. A direct solution for (10) can be obtained by using the methodology of Gutierrez-Navarro et al. (2014) [9]. In our formulation, we consider that the estimation of the end-members is not perfect, and there is some additive uncertainty which is represented by a zero-mean Gaussian vector w_j ∈ ℝ^L with covariance Σ > 0, i.e.

$$p_j=p_j^o+w_j\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j\in [1,\widehat{N}],$$

where $p_j^o$ denotes the true j-th end-member. In order to detect fake end-members, we define the j-th error vector

$$e_j=p_j-P_j{\beta }_j\in {ℝ}^L,$$ (11)

$$=\left[\underset{{\mu }_j}{\underbrace{p_j^o-P_j^o{\beta }_j}}\right]+\left[\underset{v_j}{\underbrace{w_j-W_j^o{\beta }_j}}\right],$$ (12)

where $P_j^o=\left[p_1^o,\cdots ,p_{j-1}^o,p_{j+1}^o,\cdots ,p_{\widehat{N}}^o\right]$ and W_j = [w₁,..., w_j−1, w_j+1,..., w_N̂] ∈ ℝ^L×(N̂−1). Note that the new uncertainty term v_j is still a zero-mean Gaussian vector, but with covariance κΣ > 0, where

$$\kappa =1+\sum _{i=1}^{\widehat{N}-1}{\beta }_{j,i}^2.$$ (13)

Therefore, in our evaluation, there are only two possible cases:

• The candidate p_j is a linear combination {p₁,..., p_j−1, p_j+1,..., p_N̂}, which implies that μ_j = 0 since the j-th end-member $p_j^o$ can be represented exactly by $P_j^o{\beta }_j$, ${\mathrm{\Omega }}_p^{\widehat{N}}$ is not a simplex and therefore N̂ > N, i.e. the error vector e_j is only affected by the additive uncertainty v_j:

  $$e_j~𝒩(0,\kappa \mathrm{\Sigma }).$$ (14)

  where 𝒩 (a, B) denotes a Gaussian distribution with mean a and covariance B.
• The set in (8) is linearly independent and p_j is a valid end-member, and as a consequence μ_j ≠ 0, i.e. the error vector e_j is affected by a constant term μ_j plus the additive uncertainty v_j:

  $$e_j~𝒩\left({\mu }_j,\kappa \mathrm{\Sigma }\right).$$ (15)

The noise covariance matrix of the extracted end-members Σ is estimated by using the methodology from Bioucas-Dias and Nascimento (2008) [13]. Hence, from our previous analysis, we are facing a binary hypothesis test, where the observation (error vector) in (11) presents a Gaussian distribution. Therefore, to simplify the evaluation, a quadratic decision variable $r_j^I$ is constructed by the weighted Euclidean norm of the error vector:

$$r_j^I=e_j^{\top }{\left(\kappa \mathrm{\Sigma }\right)}^{-1}{e}_j\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j\in [1,\widehat{N}]$$ (16)

where the inverse of the resulting covariance in the error (κΣ)⁻¹ is employed to normalize $r_j^I$. Since the error vector e_j is Gaussian, then the new variable r_j will have a χ²-distribution. In this way, a binary hypothesis testing problem [26] is defined as:

$$H_0:r_j^I~{\chi }^2(L-1)$$ (17)

$$H_1:r_j^I~{\chi }^2(L-1,{\mu }_j)$$ (18)

where L − 1 are the degrees of freedom in the distribution associated to the length of the error vector e_j, χ² (L − 1) denotes a central χ² distribution, and χ² (L − 1, μ_j) the non-central one with noncentrality parameter μ_j. The expression in (18) cannot be evaluated since μ_j is unknown. However, we can employ the NP approach [26] to overcome this limitation. This method distinguishes between the null H₀ and alternative H₁ hypotheses by fixing the false alarm probability for this test to a predefined value $P_{FA}^I$, i.e.

$$P_{FA}^I={\int }_{{\eta }_j}^{\infty }{f}_{\chi }(x,L-1)\hspace{0.17em}\hspace{0.17em}\text{d}x$$ (19)

where η_j is a constant that satisfies (19), and f_χ (x, L − 1) is the χ²-probability distribution with respect to H₀. Thus the decision can be made based only on a criterion that employs the distribution of the null hypothesis H₀ for j-th end-member, as

$$\begin{array}{lll}\text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_0^I\hfill & \text{if}\hfill & r_j^I<{\eta }_j\hfill \\ \text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_1^I\hfill & \text{if}\hfill & r_j^I>{\eta }_j\hfill \end{array}$$ (20)

and we can define the decision rule for our problem as

$$\begin{array}{lll}\text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_0^I\hfill & \text{if}\hfill & \underset{r_j}{\overset{\infty }{\int }}{f}_{\chi }(x,L-1)\hspace{0.17em}\hspace{0.17em}\text{d}x>P_{FA}^I\hfill \\ \text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_1^I\hfill & \text{if}\hfill & \underset{r_j}{\overset{\infty }{\int }}{f}_{\chi }(x,L-1)\hspace{0.17em}\hspace{0.17em}\text{d}x<P_{FA}^I\hfill \end{array}$$ (21)

Since $r_j^I$ is the sum of L squared independent random variables with finite mean and unit variance, we can further simplify our decision rule. By the central limit theorem, for a large value of L, the variable $r_j^I$ is close to a normal distribution. In the case of m-FLIM data, L is usually several hundreds. Hence, we propose to simplify the calculations by using a linear mapping of r_j to normalize and obtain a new decision variable:

$$d_j^I=\frac{r_j^I-(L-1)}{\sqrt{2(L-1)}}~𝒩(0,1).$$ (22)

Our decision problem for the linear independence criteria is finally stated as

$$\begin{array}{lll}\text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_0^I\hfill & \text{if}\hfill & \frac{1}{\sqrt{2\pi }}\underset{d_j^I}{\overset{\infty }{\int }}{e}^{-x^2/2}\hspace{0.17em}\hspace{0.17em}\text{d}x>P_{FA}^I\hfill \\ \text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_1^I\hfill & \text{if}\hfill & \frac{1}{\sqrt{2\pi }}\underset{d_j^I}{\overset{\infty }{\int }}{e}^{-x^2/2}\hspace{0.17em}\hspace{0.17em}\text{d}x<P_{FA}^I\hfill \end{array}$$ (23)

3.2. Spatial coherence criterion

In the BEAE methodology [10], if the number of components is higher than the real value, the extra end-members will be a linear combination of the real ones. However, low signal-to-noise ratios and the presence of outliers may lead to evaluate an end-member that could deceive the linear independence criteria. On the other hand, end-members with high abundance throughout the m-FLIM sample are responsible for most of the fluorescence intensity. Even components with a localized abundance could present high concentration levels, which could be the case for some dyes or molecules of interest. Hence, end-members that represent real components in the sample data should not only be linearly independent but also have a significant spatial contribution, which is quantified by their abundances. Under this hypothesis, we need to discard end-members with a low relative abundance throughout the m-FLIM data, since they will not have spatial coherence. The abundance information of the end-members at each spatial location of the sample is provided by the BEAE algorithm in matrix 𝒜^N.

To evaluate the spatial coherence, for j-th end-member, its abundance is extracted from matrix 𝒜^N by the j-th row, and an histogram h_j ∈ ℝ^B is constructed with B bins or levels, defined by the vector b ∈ ℝ^B. Therefore, the i-th element h_j,i in h_j represents the number of occurrences where the abundance belonged to the range (b_i−1, b_i] with b₋₁ = 0 for j-th end-member. As a result, each histogram satisfies ${\mathbf{1}}_B^{\top }{h}_j=K$ for all j ∈ [1, N̂], and we define an spatial coherence descriptor s_j = [s_j,1,..., s_j,B]^⊤ with binary components:

$$s_{j,i}=\{\begin{array}{lll}1\hfill & \text{if}\hfill & h_{j,i}\ge \theta \hfill \\ 0\hfill & \text{if}\hfill & h_{j,i}<\theta \hfill \end{array}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i\in [1,B]$$ (24)

where θ is the minimum number of occurrences for an abundance bin to be considered significant, and h_j = [h_j,1,..., h_j,B]^⊤. In this work, we fixed the threshold θ = 0.005K, i.e. 0.5% of the total spatial sample. End-members with significant abundance values throughout the m-FLIM sample will present mostly spatial coherence descriptors s_j in (24) with all unitary entries. On the contrary, the descriptor obtained from a bad candidate will be zero in entries related to low abundances. Therefore, to evaluate the presence of bad end-member candidates, which present only low-valued abundances, we can use the information provided by the spatial coherence descriptor s_j. With this information at hand, we propose a new decision variable $r_j^{II}\in {ℝ}^B$ to evaluate the spatial coherence of j-th end-member

$$r_j^{II}=\frac{b^{\top }{s}_j}{{\mathbf{1}}_B^{\top }{s}_j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j\in [1,\widehat{N}].$$ (25)

As a result, $r_j^{II}$ is an indicator of the mean value of the abundances with significant contributions throughout the m-FLIM data sample. Once again, a binary hypothesis test [26] will be faced:

• $H_0^{II}$: The decision variable $r_j^{II}$ has a low value since it represents an end-member with a low-valued abundance, with the following observation model:

  $$r_j^{II}~𝒰(0,{\omega }_1)$$ (26)

  where 𝒰 (0, ω₁) represents a uniform distribution in the interval [0, ω₁], and ω₁ ∈ (0, 1].
• $H_1^{II}$: If the j-th end-member does have a significant contribution in the m-FLIM sample then

  $$r_j^{II}~𝒰(0,{\omega }_2)$$ (27)

  where ω₂ ∈ (0, 1] and ω₂ > ω₁.

Since it is not possible to characterize the decision variable $r_j^{II}$ for $H_1^{II}$ defined by the upper bound ω₂, as in the linear independence criterion, we propose another NP test based on the spatial coherence descriptor:

$$\begin{array}{lll}\text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_0^{II}\hfill & \text{if}\hfill & \underset{r_j^{II}}{\overset{\infty }{\int }}{f}_{𝒰}^{[0,{\omega }_1]}(x)\hspace{0.17em}\hspace{0.17em}\text{d}x>P_{FA}^{II}\hfill \\ \text{Decide}\hspace{0.17em}\hspace{0.17em}{H}_1^{II}\hfill & \text{if}\hfill & \underset{r_j^{II}}{\overset{\infty }{\int }}{f}_{𝒰}^{[0,{\omega }_1]}(x)\hspace{0.17em}\hspace{0.17em}\text{d}x<P_{FA}^{II}\hfill \end{array}$$ (28)

where $f_{𝒰}^{[0,{\omega }_1]}(\cdot )$ denotes the uniform probability distribution in the interval [0, ω₁], and $P_{FA}^{II}$ the probability of false alarm for the spatial coherence test. As a result, the key parameter in the spatial coherence criterion is ω₁.

3.3. Blind end-member and abundance extraction algorithm

Our proposal is based on an ALS procedure [10] which minimizes the quadratic cost function

$$\underset{P^N,{𝒜}^N}{\text{min}}L(P^N,{𝒜}^N)=\underset{P^N,{𝒜}^N}{\text{min}}\frac{1}{2}{\Vert Y-P^N{𝒜}^N\Vert }_F^2+\xi \sum _{i=1}^{N-1}\sum _{j=i+1}^N{\Vert p_i-p_j\Vert }_2^2$$ (29)

subject to constraints (4), (3), (6) and (7), where ‖·‖_F denotes the Frobenius norm for matrices, and ξ > 0 is a weight parameter related to the regularization term. The complete algorithm employed in this paper is described in Algorithm 1.

Algorithm 1.

Estimation of the Number of Components and Linear Unmixing of m-FLIM Data.

4. Experiments

4.1. Synthetic experiments

The performance of Algorithm 1 was first evaluated by using computer simulations. Synthetic m-FLIM data was created by considering the five synthetic end-members P⁵ depicted in Fig. 1(a). The end-members were generated using the stretched exponential model [27], and designed to be linearly independent. In multispectral time-domain fluorescence techniques [28,29], the statistical noise in the photodetector follows a Poisson distribution. However, when there is a large photon count, this stochastic term approaches a Normal distribution with zero mean [30], whose standard deviation is proportional to the square root of the fluorescence intensity. As a result, the noise components have a variable variance that depends on the actual fluorescence intensity. Hence, the synthetic data was produced according to the following model:

$$Y=P^5{𝒜}^5+ℰ$$ (31)

where ℰ ∈ ℝ^L×K is a noise matrix defined as ℰ = [e₁,..., e_K]. The noise components e_k = [e_k,1,..., e_k,L]^⊤ ∈ ℝ^L at position k are proportional to the square root of the intensity at that location and time instant, $e_{k,i}={\delta }_{k,i}\sqrt{y_{k,i}}$ for all k ∈ [1, K] and i ∈ [1, L], where δ_k,i ∼ 𝒩 (0, σ²). In this way, the standard deviation of the noise component at k location and i time instant will be equal to $\sigma \sqrt{y_{k,i}}$. Since the equivalent signal-to-noise ratios will be time-varying at each spatial sample, the values of σ were selected to satisfy a Peak Signal-to-Noise (PSNR) ratio of 15, 20 and 25 dB according to

$$\mathit{PSNR}=10{\text{log}}_{10}\left(\frac{{\text{max}}_{i\in [1,L]}{y}_{k,i}}{{\sigma }^2}\right).$$ (32)

for all spatial locations k in the sample. The matrices of synthetic abundances 𝒜⁵ were selected to assign purity levels [18] ρ equal to 1.0, 0.9 and 0.8, see Fig. 1(b). The purity level ρ is a measure of the presence of pure samples in the data. The value of ρ for the j-th end-member is defined by its spatial abundance as

$$\rho =\underset{k\in [1,K]}{\text{max}}{\Vert {\alpha }_{k,j}\Vert }_2$$ (33)

A value ρ = 1 indicates the presence of pure samples of the j-th component in the synthetic data. In fact, a ρ value lower than 1 makes the linear unmixing decomposition more difficult [5, 22]. We analysed the influence of P_FA and the upper bound on the distribution of the descriptor ω₁ of the spatial coherence test in the NP evaluations. The probabilities of false alarm were set to the same value for both tests $P_{FA}^I=P_{FA}^{II}=P_{FA}$, and the number of bins B was fixed to 30 bins. This value of B balanced a compromise between accuracy and complexity in our evaluations. The size of each m-FLIM dataset was 75×75×510, where the first two dimensions correspond to the spatial plane of the sample (the same dimension of the abundance maps in Fig. 1(b), and the third dimension is time, as shown in Fig. 1(a). A total of 50 synthetic data sets were employed for each PSNR level.

4.2. In-vivo experimentation with hamster pouches

We employed in-vivo m-FLIM data taken from the cheek pouches of a golden Syrian hamster. The data was obtained from Jabbour et al. (2013) [29], where the protocol employed to treat the hamster and the tissue extraction are detailed. One dataset corresponds to the left pouch, which was left untreated for control purposes. The right pouch was treated with 7, 12-dimethylbenz[α]anthracene (DMBA) to induce oral carcinogenesis. Both tissue samples have an approximate area of 16 × 16 cm², and they were imaged using a 400 × 400 × 1200 m-FLIM dataset. The first two dimensions correspond to the X-Y plane of the tissue sample. The third dimension corresponds to time-domain fluorescence intensity decays measured with a temporal resolution of 160 ps in three wavelength bands: 390 nm, 452 nm, and >500 nm.

The m-FLIM samples were processed together to estimate their common end-members and abundances. Measurements over the edges of both samples were discarded to reduce border effects. For the estimation of the end-members and due to computational limitations, the size of the initial m-FLIM dataset was reduced in the X–Y plane to 300 × 300 × 1200, but afterwards the complete m-FLIM dataset was processed to estimate the abundances in the original X–Y plane 400 × 400 measurements. Since in the experimental data a high PSNR is considered, the parameters employed in the NP tests were ω₁ = 0.2, B = 30 bins and the threshold for the minimum number of significant measurements θ was set to 225 positions.

4.3. Ex-vivo experimentation with atherosclerotic plaques

The proposed methodology was also tested with m-FLIM data from ex-vivo human coronary arteries. The samples were obtained from Park et al. (2011) [28]. The temporal resolution of the measurements was 250 ps, and they were recorded in the wavelength bands: 390 ± 20 nm, 452 ± 22.5 nm and 550 ± 20 nm. The datasets were classified by an expert [28] using histopathology analysis. Two samples were labeled as Low-Collagen/Lipids (LCL), two datasets were identified as having High-Collagen (HC), and another two as High-Lipids (HL), while the last three samples were classified as Mixtures (Mix), since none component was dominant. Nine individual datasets with a field of view 2 × 2 mm² (60 × 60 × 510) were analysed jointly with Algorithm 1 to estimate the number of components and estimate their quantitative descriptions. The same configuration of parameters employed in section 4.2 were used for these experiments.

5. Results

5.1. Synthetic validation

The performance of Algorithm 1 to estimate the number of end-members was evaluated first using the synthetic datasets, see Fig. 1. The results obtained for each noise level (PSNR) and parameters configurations (ω₁, P_FA, ρ) are shown in Table 1. Note that these results allow to identify separately the effect of each parameter (ω₁, P_FA, ρ) in the estimated number of end-members for the subsequent experimental validation.

Table 1.

Average number of end-members estimated ± the standard deviation from 50 simulations for each experiment using different PSNR levels. The real number of end-members present in the mixture samples is 5.

ω	PFA	ρ = 1.0			ρ = 0.9			ρ = 0.8
		PSNR			PSNR			PSNR
		15 dB	20 dB	25 dB	15 dB	20 dB	25 dB	15 dB	20 dB	25 dB
0.1	1.00e-03	3.96±0.20	5.08±0.34	5.00±0.00	3.88±0.33	4.98±0.32	5.00±0.00	3.12±0.33	4.76±0.48	5.00±0.00
	1.00e-04	3.94±0.24	5.08±0.34	5.00±0.00	3.80±0.40	4.98±0.32	5.00±0.00	3.06±0.24	4.74±0.49	5.00±0.00
	1.00e-05	3.92±0.27	5.08±0.34	5.00±0.00	3.78±0.42	4.94±0.24	5.00±0.00	3.04±0.20	4.72±0.50	5.00±0.00
	1.00e-06	3.90±0.30	5.04±0.28	5.00±0.00	3.74±0.44	4.94±0.24	5.00±0.00	3.00±0.00	4.70±0.51	5.00±0.00
0.2	1.00e-03	3.00±0.00	3.00±0.00	4.96±0.20	3.00±0.00	3.00±0.00	4.98±0.14	2.46±0.50	2.96±0.20	4.96±0.20
	1.00e-04	3.00±0.00	3.00±0.00	4.96±0.20	3.00±0.00	3.00±0.00	4.98±0.14	2.46±0.50	2.96±0.20	4.96±0.20
	1.00e-05	3.00±0.00	3.00±0.00	4.96±0.20	3.00±0.00	3.00±0.00	4.98±0.14	2.46±0.50	2.96±0.20	4.96±0.20
	1.00e-06	3.00±0.00	3.00±0.00	4.96±0.20	3.00±0.00	3.00±0.00	4.98±0.14	2.46±0.50	2.96±0.20	4.96±0.20
0.3	1.00e-03	2.00±0.00	2.00±0.00	3.00±0.00	2.00±0.00	2.00±0.00	2.18±0.39	2.00±0.00	2.00±0.00	2.74±0.44
	1.00e-04	2.00±0.00	2.00±0.00	3.00±0.00	2.00±0.00	2.00±0.00	2.18±0.39	2.00±0.00	2.00±0.00	2.74±0.44
	1.00e-05	2.00±0.00	2.00±0.00	3.00±0.00	2.00±0.00	2.00±0.00	2.18±0.39	2.00±0.00	2.00±0.00	2.74±0.44
	1.00e-06	2.00±0.00	2.00±0.00	3.00±0.00	2.00±0.00	2.00±0.00	2.18±0.39	2.00±0.00	2.00±0.00	2.74±0.44

5.2. Oral carcinogenesis in hamster pouches

Three end-members were detected (N̂ = 3) when solving the hamster m-FLIM datasets simultaneously. By recalling that j-th end-members p_j, represents the concatenated response at three wavelengths ( $p_j^{{\lambda }_1},p_j^{{\lambda }_2},p_j^{{\lambda }_3}$), i.e. $p_j={\left[{\left(p_j^{{\lambda }_1}\right)}^{\top }{\left(p_j^{{\lambda }_2}\right)}^{\top }{\left(p_j^{{\lambda }_3}\right)}^{\top }\right]}^{\top }$, we can evaluate the accuracy and interpretation of the estimated end-members by the resulting average lifetime and normalized intensity at each frequency band [31]. For this purpose, we compute in discrete-time the average lifetime for each j-th end-member at wavelenght band λ_i:

$${\tau }_j^{{\lambda }_i}=\frac{t^{\top }{\widehat{p}}_j^{{\lambda }_i}}{{\mathbf{1}}_L^{\top }{\widehat{p}}_j^{{\lambda }_i}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i,j\in [1,3]$$ (34)

where ${\widehat{p}}_j^{{\lambda }_i}$ represents the end-member $p_j^{{\lambda }_i}$ after performing the time-deconvolution [31] with the instrument response, and t is the time vector associated to the periodic sampling during the experiment. The normalized intensity for each wavelength band λ_i and j-th end-member is expressed as

$$I_j^{{\lambda }_i}=\frac{1_L^{\top }{\widehat{p}}_j^{{\lambda }_i}}{{\sum }_{i=1}^3{\mathbf{1}}_L^{\top }{\widehat{p}}_j^{{\lambda }_i}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i,j\in [1,3]$$ (35)

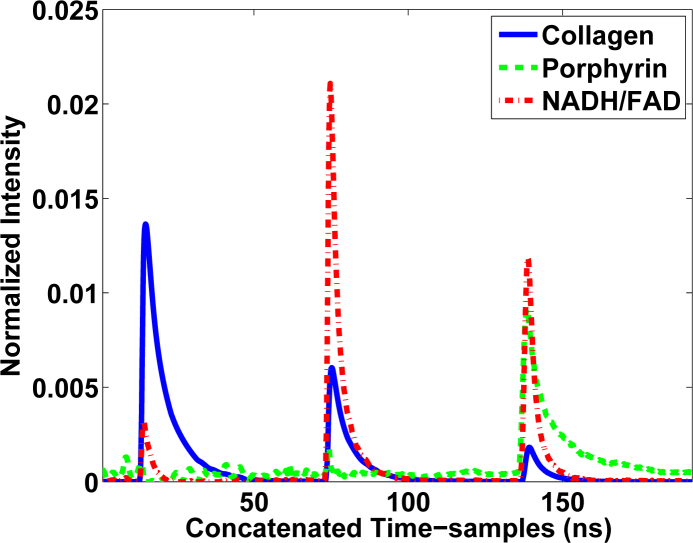
The average lifetimes and normalized intensities are shown in Table 2. Based on this information, the end-members were identified as Collagen, Porphyrin and NADH/FAD. The end-members calculated are depicted in Fig. 2. The abundance maps obtained from 400 × 400 measurements of the m-FLIM dataset are shown in Fig. 3.

Table 2.

Average lifetimes and normalized intensities of the end-members extracted from the m-FLIM datasets of hamster pouches. The 2nd end-member presented no response in the first and second wavelength band.

Wavelength λ	Lifetime			Normalized Intensity
Component j	390 nm ${\tau }_j^{{\lambda }_1}$	452 nm ${\tau }_j^{{\lambda }_2}$	>500 nm ${\tau }_j^{{\lambda }_3}$	390 nm $I_j^{{\lambda }_1}$	452 nm $I_j^{{\lambda }_2}$	>500 nm $I_j^{{\lambda }_3}$
1	6.1249 ns	5.289 ns	4.3854 ns	0.6611	0.2689	0.0700
2	N/A	N/A	8.6284 ns	N/A	N/A	1.000
3	1.6201 ns	3.5216 ns	2.8461 ns	0.0665	0.6046	0.3289

Fig. 2.

End-members extracted from the m-FLIM datasets of hamster pouches. The second end-member presents practically no emission fluorescence signal on the first two bands. The end-members were identified as Collagen, Porphyrin and NADH/FAD according to the lifetimes calculated in Table 2.

Fig. 3.

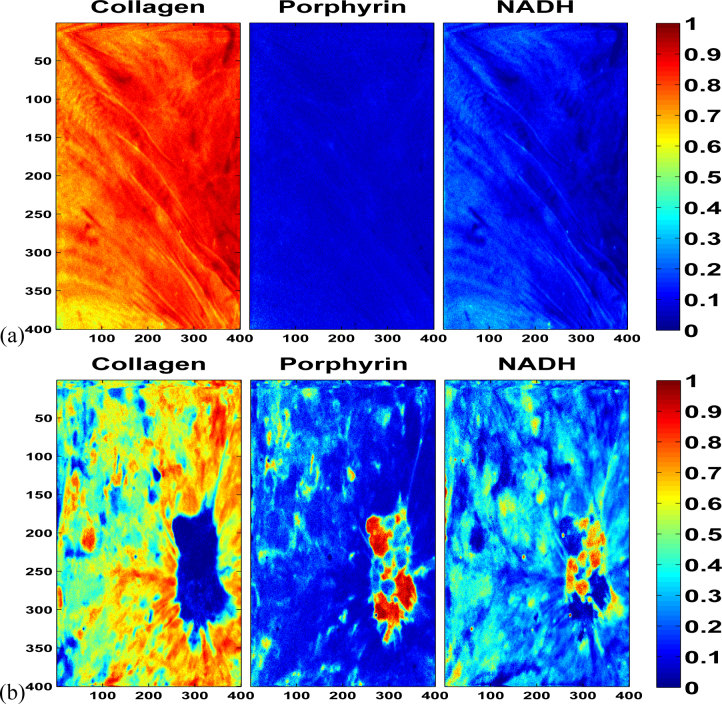
Abundance maps (400 × 400) corresponding to the end-members in Fig. 2 detected in the m-FLIM datasets of hamster pouches. The abundance maps shown in row (a) correspond to the quantitative description obtained from the healthy hamster pouch. Meanwhile, the diseased tissue produced the abundance maps shown in row (b).

5.3. Atherosclerotic plaques

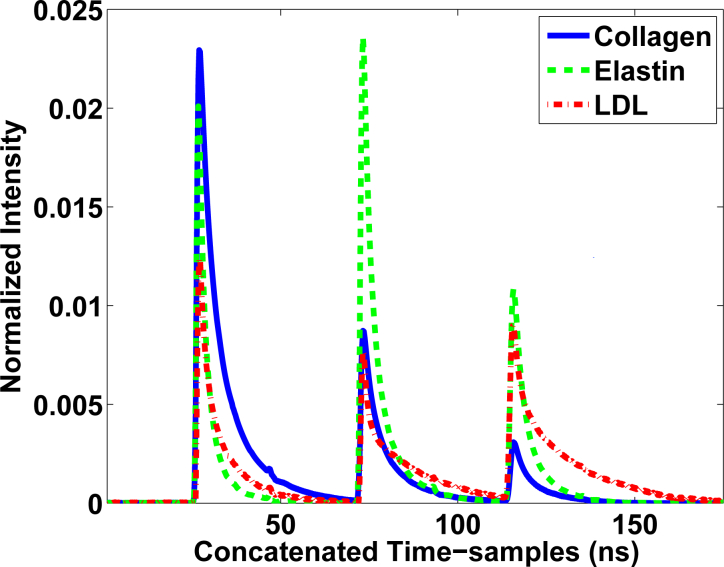
M-FLIM samples from ex-vivo atherosclerotic plaques were analysed using the methodology in Algorithm 1. Three wavelengths were also considered in the m-FLIM measurements: 390 nm, 452 nm, and 550 nm. Once more, three components were detected (N̂ = 3) and their deconvoluted lifetimes were also calculated according to eq. (34). The average lifetimes are shown in Table 3, where now the end-members were identified as Collagen, Elastin and Low Density Lipoproteins (LDL). The end-members and their abundances are shown in Figs. 4 and 5, respectively.

Table 3.

Average Lifetime and Normalized Intensities of the end-members extracted from m-FLIM datasets of atherosclerotic plaques.

Wavelength λ	Lifetime			Normalized Intensity
Component #	390 ± 20 nm ${\tau }_j^{{\lambda }_1}$	452 ± 22.5 nm ${\tau }_j^{{\lambda }_2}$	550 ± 20 nm ${\tau }_j^{{\lambda }_3}$	390 ± 20 nm $I_j^{{\lambda }_1}$	452 ± 22.5 nm $I_j^{{\lambda }_2}$	550 ± 20 nm $I_j^{{\lambda }_3}$
1	5.9946 ns	6.8429 ns	5.9085 ns	0.6594	0.2530	0.0876
2	1.9527 ns	3.9044 ns	4.4292 ns	0.2658	0.4754	0.2588
3	4.8496 ns	9.9976 ns	11.3631 ns	0.2787	0.2860	0.4353

Fig. 4.

End-members extracted from the m-FLIM datasets of atherosclerotic plaques, which were identified as Collagen, Elastin and LDL.

Fig. 5.

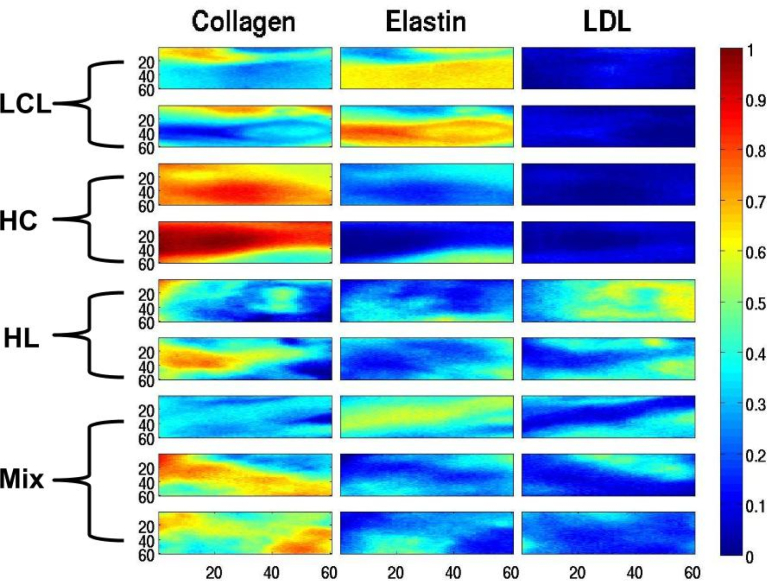
Abundance maps (60 × 60) for the m-FLIM datasets of atherosclerotic plaques, where each row correspond to a quantitative description. The m-FLIM datasets were identified through histopathology analysis as LCL, HC, HL and Mix, as indicated in the picture.

6. Discussion

Blind linear unmixing of m-FLIM data allows to obtain a quantitative description of the biochemical composition of the biological samples, which is easy to interpret and validate. Usually, the interpretation and validation is difficult without prior knowledge of the number of components in the sample, and their characteristic signatures. This task is even more difficult when unreliable or partial information is available, as is usually the case when working with biomedical data. The method proposed in this paper performs the linear decomposition of time-domain m-FLIM data, while it evaluates the accuracy of the solution by the linear independence and spatial coherence NP tests. As a result, our proposal takes a decision based on the quality of the end-members and their abundances obtained in an iterative fashion. The iteration stops once the current solution is not able to satisfy the linear independence criterion among the end-members, and the spatial coherence related to their abundances. To the best of the authors’ knowledge, this is the first completely blind algorithm tailored for linear unmixing of time-domain m-FLIM data. In the literature, there are some approaches targeted for remote sensing applications [5], however, there are intrinsic differences. First, satellite imagery usually contains a high number of end-members (> 30), while the number of endogenous fluorophores present in an m-FLIM sample is usually low. This property could be seen as an advantage, but in m-FLIM data, the end-members are highly overlapped which complicates the linear unmixing problem. Furthermore, the BEAE method [10] takes advantage of the non-negativity nature of fluorescence, which is translated into a normalization of the end-members that helps to constraint the solution space [23,32], and reduce the signal variability in the data [10].

In the evaluation process, experimentation with synthetic data is the only way to quantitatively measure the performance of the proposal, since it is difficult to estimate the exact and localized abundance of biological samples without destroying them. These experiments are also useful to determine the best parameter configuration in the proposed methodology. According to the results obtained in Table 1, the proposed algorithm presented good performance in estimating the number of components in the synthetic m-FLIM data at PSNR levels of at least 20 dB, independently of P_FA and ρ. For PSNR = 20 dB, ω₁ = 0.1 performed the best, while for PSNR = 25 dB either ω₁ = 0.1 or ω₁ = 0.2 performed similarly well.

The processing of the m-FLIM data of hamster pouches determined the presence of three components. Using their estimated lifetime values and relative normalized intensities for each measured emission band, we could identify the first one as Collagen, whose fluorescence has a peak emission at ≈ 400 nm and lifetime values in the order of 4–6 ns. The second end-member was identified as Porphyrin, whose fluorescence has not emission below 500 nm and lifetime values longer than 7–8 ns [29]. The third end-member presented lifetimes that did not match any expected end-member found in hamsters oral mucosa. The lifetime of this third end-member in the 390 nm wavelength band alone matched the description of NADH, however, the lifetime is too long in the wavelengths bands 450 nm and > 500 nm. These lifetimes actually seem to match the description of FAD, which is another of the expected primary endogenous fluorophores [29]. This is the reason why the third end-member was labelled as a mixture of NADH and FAD. We believe that m-FLIM data presented no pure samples of NADH and FAD, which is why they could not be separated. The third end-member profile was characterized by a peak emission at the 450 nm channel, and lifetime values between ≈1.5–3.5 ns. These fluorescence characteristics can be associated to NADH, whose fluorescence emission also peaks at ≈450 nm with lifetime values between ≈0.5–3 ns, depending whether it is in a free or bound state. On the other hand, FAD has a peak emission ≈510 nm and similar lifetime values. Since the third end-member profile also has significant contribution in the 500 nm band, it could be possible that this end-member reflects the contribution of both NADH and FAD. The fact that these two molecules are usually co-localized within the cell cytoplasm further support this hypothesis. Thus, the third end-member was attributed to a combined contribution of both NADH and FAD.

The healthy pouch, depicted in Fig. 3(a) presented a high relative concentration of Collagen, with some NADH/FAD contribution in the lower left section, and practically no Porphyrin through the imaged area. On the contrary, the right pouch presents a tumour which is visible in the lower right section of the abundance maps, as shown on Fig. 3(b). The resulting abundances reveal that the tissue surrounding the tumour contains high levels of Collagen and lower levels of Porphyrin, in a similar fashion to the healthy tissue in Fig. 3(a). The tumour area presents high abundance of Porphyrin, reaching relative concentration values of 100% in some areas. The relative concentration of NADH/FAD was also high in the tumor region, and has relative high presence throughout the entire imaged are of the DMBA treated cheek pouch. The quantitative results obtained in the hamster m-FLIM samples matches the qualitative description provided by Jabbour et al. (2013) [29]. The detection of Porphyrin and NADH/FAD could play an important part in the detection of precancerous lesions, which is of great interest in clinical diagnosis of oral carcinoma.

The method was also tested with m-FLIM samples of ex-vivo human coronary atherosclerotic plaques. We were able to find the principal endogenous fluorescent biomarkers in atherosclerotic plaques [33], and estimate their relative concentrations quantitatively. The computed lifetimes allowed the identification of estimated end-members as Collagen, Elastin and LDL without ambiguity, see Table 3. The time profiles of the end-members and their abundances are shown in Figs. 4 and 5, respectively. The results were contrasted against the visual description provided from histopathology analysis previously reported [28]. The samples labeled as LCL, rows 1 and 2 from Fig. 5, actually contained some Collagen and high levels of Elastin, which is consistent with the previous results reported in [9]. The samples labelled as HC and HL were consistent with the quantitative results in rows 3 and 4 from Fig. 5. High levels of Collagen were also detected in the samples labeled as HL (rows 5 and 6 in Fig. 5). The samples classified as mixtures are described in the last three rows of Fig. 5, an provide a quantitative description of the mixed components in the sample.

Algorithm 1 was implemented in Matlab under a Windows 64 bits operative system. No code optimization or hardware acceleration methods, such as parallel programming, were employed. The experiments were performed on a Core i7 4770 CPU with 12 GB in RAM. The linear unmixing of each synthetic dataset of 75 × 75 × 510 took around 47.48 seconds. Due to a high PSNR in the experimental data, the laboratory evaluation used the following parameters: ω₁ = 0.2, θ = 0.005K and P_FA = 10⁻³. The quantitative description of an m-FLIM dataset of both hamster pouches 400 × 800 × 1200 was obtained in around 18.60 minutes. Meanwhile, the linear unmixing for the complete nine artery datasets of 60×540×510 from subsection 4.3 was estimated in approximately 2.49 minutes.

7. Conclusions

In this paper, a new methodology to estimate the number of components in time-domain m-FLIM data was presented. The proposal departs from a blind end-member and abundance extraction algorithm for linear unmixing. This algorithm does not require a priori information and could be used with minimal intervention from the users. The method was validated with both synthetic and experimental data. Compared to previous approaches in the literature, this proposal provides quantitative results for an intuitive description and interpretation of the biological samples. Future work will focus on developing more efficient methods for blind linear unmixing, as well as, a CUDA implementation of Algorithm 1 to reduce computational time.