Abstract
Syndromic and virological data are routinely collected by many countries and are often the only information available in real time. The analysis of surveillance data poses many statistical challenges that have not yet been addressed. For instance, the fraction of cases that seek healthcare and are thus detected is often unknown. Here, we propose a general statistical framework that explicitly takes into account the way the surveillance data are generated. Our approach couples a deterministic mathematical model with a statistical description of the reporting process and is applied to surveillance data collected in Italy during the 2009–2010 A/H1N1 influenza pandemic. We estimate that the reproduction number R was initially into the range 1.2 – 1.4 and that case detection in children was significantly higher than in adults. According to the best fit models, we estimate that school-age children experienced the highest infection rate overall. In terms of both estimated peak-incidence and overall attack rate, according to the Susceptibility and Immunity models the 5–14 years age-class was about 5 times more infected than the 65+ years old age-group and about twice more than the 15 – 64 years age-class. The multiplying factors are doubled using the Baseline model. Overall, the estimated attack rate was about 16% according to the Baseline model and 30% according to the Susceptibility and Immunity models.
Keywords: SEIR model, epidemic modelling, Markov Chain Monte Carlo methods, Bayesian inference, reporting process
1 Introduction
The detection and control of existing, newly emerging or re-emerging infections in the human population often relies on the analysis of syndromic and virological surveillance data. Such data are routinely collected in most developed and many developing countries, and are key for analysis of epidemics in real-time to inform public health decision making. During the 2009–2010 A/H1N1 influenza pandemic, syndromic and virological surveillance data were routinely collected by most European countries and made available in real time. Since the emergence of the novel H1N1pdm influenza virus, many studies have been published on the epidemiological characteristics of the disease and its transmission potential [1, 2, 3, 4, 5, 6], on the optimisation and assessment of the possible intervention strategies [7, 8, 9] and on the investigation of the natural history and characterisation of infection at the individual level [10, 11]. Moreover, a variety of different methods have been proposed to estimate the epidemic infection rates on the basis of serological (cross-sectional and cohort) studies [10, 12, 13, 14, 15] and syndromic and virological data [9, 15, 16, 17]. These latter studies rely on assumptions or estimates (mainly obtained through health-seeking behavioural studies) of the reporting rates. The analysis of syndromic and virological data poses many statistical challenges that have not yet been fully addressed. Only a proportion of syndromic cases in the community seek healthcare and are therefore eligible for detection by sentinel surveillance systems. The size of the population that is monitored by primary-care based surveillance also tends to change over time. Last, only a fraction of syndromic cases who are detected by the surveillance system have really been infected by the aetiological agent of interest (e.g. H1N1pdm virus, in the past 2009–2010 influenza pandemic), with the remainder of cases being due to other causes. These problems are usually either ignored or corrected by scaling the epidemic curve with multiplicative factors [9], something which is expected to bias the variance of the estimates. Here we present a general framework to tackle these issues and analyse syndromic and virological data by taking stochasticity in the surveillance system explicitly into account. We couple a deterministic model of transmission dynamics with a statistical description of how the surveillance data is generated. To our knowledge this is one of the first studies that rigorously integrates syndromic and virological data and the main novelty is in the observational model, where we aim at modelling the stochasticity existing in the reporting process. Furthermore, the method proposed in this study only requires standard syndromic and virological surveillance data and is therefore potentially applicable to a broad range of countries for a variety of diseases.
Estimation of epidemiological parameters such as the reproduction number R, age-dependent reporting rates and susceptibility is then performed via Bayesian Markov Chain Monte-Carlo (MCMC) sampling [18]. The approach is applied to surveillance data collected in Italy during the 2009–2010 A/H1N1 influenza pandemic.
2 Data
2.1 Influenza-like-illness and virology
For over ten years, influenza surveillance in Italy has been based on a sentinel system called INFLUNET [19, 20]. The number of practitioners involved in the surveillance system during the 2009–2010 H1N1 pandemic influenza season was on average 1094 (minimum 561, maximum 1165), covering on average 1.4 million people (2.3% of the Italian population). Data collected by INFLUNET on the weekly size of the monitored patients population and on the weekly number of observed influenza-like illness (ILI) cases, aggregated by age groups (0–4 years, 5–14 years, 15–64 years and 65+ years) are available online on the INFLUNET website (http://www.iss.it/iflu/).
Virological surveillance during the 2009 pandemic in Italy was conducted by the Ministry of Health, which coordinated the collection and testing of nasal swabs through hospitals, laboratories operating within the national health service, sentinel GPs and paediatricians. Weekly reports are available online on the Italian Ministry of Health website under “sorveglianza virologica” (http://www.salute.gov.it/influenza/influenza.jsp).
We analyse ILI and virological data from week 38 of 2009 (corresponding to mid September 2009, when the schools re-opened after the summer vacation) to week 7 of year 2010 (corresponding to the end of February, when the epidemic had clearly died out).
2.2 Social contact data
There is evidence that the number and structure of the contacts within an age-structured population significantly vary over time, in particular between holiday/week-end days and working days [21, 22]. For this reason, using raw data from the Italian arm of the POLYMOD survey (a diary-based survey of daily contacts in eight European countries) [23], we compute the daily mean number of contacts among the considered age classes during working days and holiday/week-end days. Finally, we use Italian demographic data for year 2008 which can be found on the Italian National Statistical Institute website (http://www.istat.it/).
The methodology we adopted to compute the contact matrices is very similar to those used in [23]. Starting from the raw data of the POLYMOD survey [23], we computed contact matrices for the Italian population separately for working days and week-ends. As the Italian POLYMOD survey was conducted between May 17th 2006 and June 1st 2006, a period during which no official holidays occurred, we were not able to explicitly estimate contact rates in holidays, so instead used the weekend estimates.
Since the age distribution of the survey population does not match the Italian population age distribution, we standardise the estimates. First, we calculate the average number of contacts per participant in each age class with every other age class. We then multiply these averages by the sizes of the corresponding participant age classes in the Italian population, to get a matrix of estimated total contacts between any two age classes in the Italian population. Since the number contacts of class i with class j should be the same as the number of contacts between j and i, we symmetrize the obtained matrix substituting each of the corresponding off-diagonal pairs of elements with their arithmetic mean. We then divide each matrix element by the size of the participant age class for that element, obtaining Tables SI-1 and SI-2 (see the Supplementary Information), which represent the symmetric individual-level contact matrices.
3 Model Formulation
3.1 Transmission model
We use an age-structured deterministic transmission model, where individuals move from being susceptible, to exposed (but not yet infectious), to infectious before recovering (i.e. a SEIR model). Five age classes are used (0–4, 5–14, 15–24, 25–64, 65+ years). The latent period (i.e. the duration of the exposed state) and the infectious period are assumed to be Gamma distributed (this is achieved by splitting each of the exposed and infectious states in 2 sub-compartments). The disaggregation of the 15–64 INFLUNET age-class into 15–24 and 25–64 age-classes allows a better representation of observed heterogeneity in contacts among the younger age-groups which were particularly affected by the H1N1pdm virus.
The model is defined by the following differential equations
| (1) |
where i, j = 1, …, 5 index the five age-classes 0–4, 5–14, 15–24, 25–64, 65+years. The rates of loss of latency ν and infectiousness γ are assumed not to depend on the age class. The force of infection λi is given by
| (2) |
where σi represents the susceptibility of age-class i, cij indicates the mean number of contacts between an individual of age class i with individuals of age class j, Nj represents the (constant in time) size of age group j (with i, j = 1, …, 5), p is for the probability of getting infected upon a contact with an infectious individual and h1 and h2 represent the infectivity of the two infectious stages I1 and I2 respectively.
If we assume that at the beginning of the epidemic the whole population is completely susceptible, the mean number of secondary infections generated by a single infective of age class j in age class i is given by
| (3) |
where A(τ) denotes the infectivity function at time τ after infection. The entries given in (3) define the next generation matrix K and following [24] we define the basic reproduction number R0 as the spectral radius s(K) of the next generation matrix
| (4) |
It turns out (see the SI for the whole computation) that the basic reproduction number is given by
| (5) |
The effective reproduction number R is the expected number of cases generated by a single infective when a fraction of the population is protected against infection. If we assume that at the beginning of the epidemic the whole population is susceptible and that susceptibility σi varies across the age-classes i = 1, …, 5, the expected number of cases generated by a ‘typical’ infective is given by
| (6) |
and the effective reproduction number R is
| (7) |
with matrix M given by
| (8) |
If we assume that at the early stages of the epidemic only a fraction Si(0)/N of the population is completely susceptible (Si(0) represents the number of fully susceptible individuals in age-class i at the beginning of the epidemic and N = ∑i Ni is the total size of the population) and the remaining part is fully immune, the effective reproduction number R is still defined by (7) with M given by
| (9) |
The reproduction number R is clearly proportional to p, the probability of infection given an infectious contact. We used R as a parameter and calculated p as a function of R.
The mean generation time, defined as the mean duration between time of infection of a secondary infectee and the time of infection of its primary infector [25], is given by
| (10) |
We assume a latency period (2/ν) of 1 day and fix Tg = 2.6 days, compatible with estimates obtained from 2009 H1N1 pandemic [4, 5, 9, 26]. We assigned the infectiousness parameters values by fitting the infectiousness profile (infectiousness as a function of time from infection) from the SEIR model to data on time-dependent viral shedding in experimental infection studies [27], giving h1 = 16.1 and h2 = 9.6.
The model was coded in C and numerically solved using the Runge-Kutta algorithm with variable step size [28]. The transmission model outputs , the number of A/H1N1 infections in week t and age-class i (i = 1, …, 5) in the Italian population. By scaling down to the size of the monitored population (i.e. that covered by INFLUNET ILI sentinel surveillance), we obtain , the expected number of A/H1N1 infections generated within class i during week t in the monitored population.
3.2 Statistical model
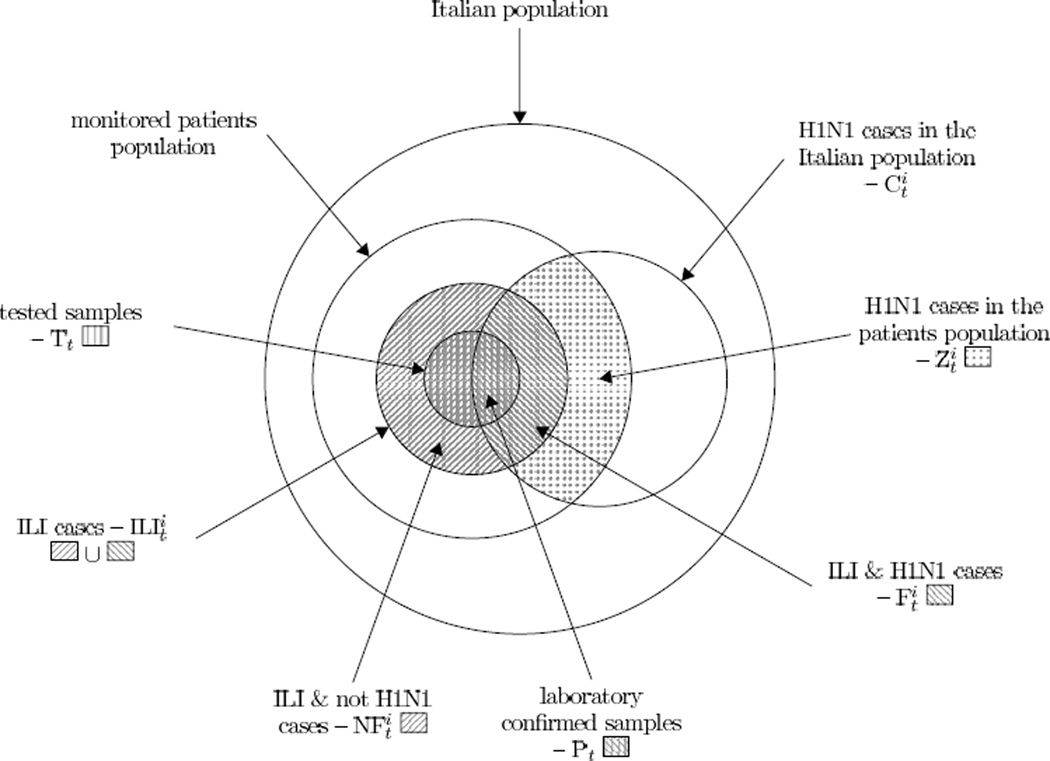
In what follows we adopt the notation graphically represented on Figure 1 for the purpose of clarity. Except for the variable , which represents the age-structured weekly number of A/H1N1 cases in the Italian population, all the other variables are defined at the monitored population level. We assume sentinel GP reports are all independent samples of the same population (thus GPs are exchangeable and the absence of a GP report from a particular week’s data is a random process). This almost underestimates true variability (e.g. due to spatial heterogeneity), which is one reason we explore models with overdispersion below.
Figure 1.
Graphical representation of the populations taken into account and notation adopted in the work. The Italian population is considered constant over the whole study period while the monitored patients population changes every week. Index i denotes the age-class and t denotes the week.
It should be noted that no information on patient age was provided for the virological data, so we assume that πt, the probability that a person with ILI in week t is in fact infected with H1N1pdm (and therefore would test positive), does not vary across the age-groups.
We divide the presentation of the derivation of the likelihood function L for the ILI and virological data in two parts. We first consider a case where we assume that the weekly number of H1N1pdm infections in the monitored population in the i-th age class (represented by ) is subject to no sampling variability (or dynamical stochasticity) and is equal to , the solution of the deterministic transmission model. Then, we extend our model to the situation when can be over-dispersed. In this latter case we assume that the distribution of is Negative Binomial. The Negative Binomial model has been chosen as an alternative to the Poisson distribution to allow the sample variance to exceed the sample mean, which is still fixed at , the solution of the deterministic transmission model. The additional random variation given by the over-dispersed model is meant to reflect the clustered sampling, which occurs by monitoring only a sample of GPs, whose patients will have specific spatial and social features. Furthermore, assuming an over-dispersed model is a heuristic method to allow for fluctuations of the number of infected individuals due to dynamical stochasticity (i.e. away from the predictions of a deterministic model).
3.2.1 No overdispersion
Since we lack information about the precise timing of collection of the swabs, we assume that samples tested on week t had been collected from individuals who were symptomatic in week t − 1. Given πt and the number of tested swabs Tt, the number of positive swabs Pt follows the binomial distribution
| (11) |
Let represent the number of ILI cases in the monitored population of age-class i and week t, and be the number of individuals with H1N1pdm infection in age-class i that report ILI symptoms in week t (Figure 1). Hence, if ρi represents the probability that a person infected with H1N1pdm reports ILI symptoms, the distribution of is given by the Binomial model with parameters and ρi
| (12) |
Let represent the number of ILI cases (in the monitored population) that are not infected with the A/H1N1 virus. Given , we model as the number of H1N1pdm-negative individuals one gets in a sequence of Bernoulli trials before obtaining the positive individual. This is an approximation as in theory total can exceed the size of the corresponding monitored population, and in addition it gives a higher variance to non-H1N1 ILI than a binomial model would. However, its use here significantly simplifies the later analysis.
Hence, given and πt, we assume that has a negative binomial distribution with parameters and 1 − πt
| (13) |
Hence
and the probability distribution of is explicitly given by
| (14) |
If , then the whole set is uninfected with H1N1pdm, that is
| (15) |
Using conditional probability and assumptions (13),(14) and (15), the probability of the data given the model is hence given by
| (16) |
Notice that, at this stage, the likelihood is a function of πt. The explicit estimation of πt would be time consuming, challenging (there is one such parameter for each week) and goes beyond the scopes of this work.
For these reasons we assign a prior distribution P(πt) to πt and integrate over πt, thus obtaining
| (17) |
Typically the integral over the πt would not be analytically tractable, meaning these parameters would need to be explicitly estimated via MCMC along with the transmission parameters of the model. However, by assuming a prior Beta distribution for πt,
| (18) |
where α and β are shape parameters, and then substituting (11), (12), (14), (15) and (18) into (17), we can obtain (see the SI for the complete computation) the following explicit evaluation of the integral over πt:
| (19) |
Using θ to denote the parameter vector, the Bayesian model is defined by:
| (20) |
where P(θ) is the prior distribution.
3.2.2 With overdispersion
Instead of taking as being fixed (and equal to ), we can account for variability in the reporting (or infection) process by assuming that is drawn from a negative binomial distribution [29, 30, 31, 32, 33]
| (21) |
where r is the dispersion. Decreasing values of r correspond to increasing levels of overdispersion. The expected value is still , but the variance is . Under this assumption, it can be proved (see the SI) that
| (22) |
The probability of the data given the model is in this case given by (up to a normalising constant):
| (23) |
where for simplicity of notation we set . Expression (23) is been obtained substituting (11), (22), (14), (15) and (18) into formula
| (24) |
If we denote the parameter vector by θ, the Bayesian model is defined by (20) with (23) in place of (19).
4 Models variants and parameterisation
4.1 Model variants examined
From early on in the 2009 pandemic, it was noticed that the children were particularly affected [3, 4]. There are two age-dependent parameters in our model which might explain this pattern: susceptibility (i.e. the probability of getting infected given a contact with an infectious individual) and reporting rate (i.e. the probability that someone infected with H1N1pdm in the monitored population reports ILI symptoms). Since the age distribution of cases effectively only provides information on the product of susceptibility and reporting rates by age, it is not possible to make inference on both parameters at the same time and one has to fix one of the two and make inference on the other. We therefore explore 3 model variants in this paper:
Baseline model– here we assume that at the beginning of the epidemic the whole population is at least partially susceptible (i.e. no fraction of the population is immune) and estimate the susceptibility of each age group prior to the pandemic (fixing the susceptibility of adults at 1.0, to avoid over-parameterisation) and a reporting rate which is the same for all age groups (i.e. ρ1 = ⋯ = ρ5).
Susceptibility model – here we fix values of the age-specific susceptibility parameters and fit reporting rates (see below). We assume that at the beginning of the epidemic the whole population is at least partially susceptible (i.e. no fraction of the population is immune) and assign an age-specific susceptibility to the different age-classes
Immunity model – here we assume that at the beginning of the epidemic a fraction of the population in each age-class is completely immune but that the susceptible population is completely and equally susceptible to H1N1pdm (σ1 = ⋯ = σ5 = 1.0). As for the Susceptibility model, we fit the reporting rate as an age-dependent parameter.
Pre-existing immunity is modelled here (as in previous works [9, 32, 34, 35]) in two different ways: either by assuming that a proportion of the population is partially protected against infection (Baseline and Susceptibility models) or by assuming that a fraction of the population is completely immune (Immunity model). When assigning either the average susceptibility of an age group (Susceptibility model) or the pre-pandemic proportion of an age group who were immune (Immunity model) we used pre-pandemic cross-sectional serological data from the UK [10]. For the Immunity model, the proportion of an age group assumed to be immune is fixed at the average of the proportion of baseline (pre-pandemic) samples showing microneutralization titre at or above the cut-off value of 1:40 and haemagglutination inhibition assay titre at or above 1:32. For the Susceptibility model, the susceptibility of an age group is fixed at 1 minus the same average. The values of susceptibility used for the Susceptibility model and the proportion of an age group assumed to be fully susceptible in the Immunity model are given in Table 1.
Table 1.
Summary of model parameter values (excluding contact rates).
| Parameter | Value | |
|---|---|---|
| η | latency rate | 2.0/day or est. |
| γ | infectious rate | 0.833/day |
| σ1 | susceptibility of age-class 0 – 4 years | 0.98 or est. |
| σ2 | susceptibility of age-class 5 – 14 years | 0.96 or est. |
| σ3 | susceptibility of age-class 15 – 24 years | 0.85 or est. |
| σ4 | susceptibility of age-class 25 – 64 years | 0.87 or est. |
| σ5 | susceptibility of age-class 65+ years | 0.73 or est. |
| S1(0)/N | frac. susceptible individuals 0 – 4 years at baseline | 0.98 or 1.0 |
| S2(0)/N | frac. susceptible individuals 5 – 14 years at baseline | 0.96 or 1.0 |
| S3(0)/N | frac. susceptible individuals 15 – 24 years at baseline | 0.85 or 1.0 |
| S4(0)/N | frac. susceptible individuals 25 –64 years at baseline | 0.87 or 1.0 |
| S5(0)/N | frac. susceptible individuals 65+ years at baseline | 0.73 or 1.0 |
| h1 | infectivity of the infectious stage I1 | 16.1 |
| h2 | infectivity of the infectious stage I2 | 9.6 |
| α, β | shape parameters of the Beta distribution in Eq. (18) | 1.0 |
| R | effective reproduction number | est. |
| I0 | number of H1N1 cases at week 31 | est. |
| ρ1 | ILI reporting rate of H1N1 cases of age-class 0 – 4 years | est. |
| ρ2 | ILI reporting rate of H1N1 cases of age-class 5 – 24 years | est. |
| ρ3 | ILI reporting rate of H1N1 cases of age-class 25 – 64 years | est. |
| ρ4 | ILI reporting rate of H1N1 cases of age-class 65+ years | est. |
| a, b | parameters defining the time dependent reporting see Eq. (25) | est. |
Abbreviations: est.=estimated, frac.=fraction. See main text for a description of how parameter values were assigned or estimated.
For both the Immunity and Susceptibility models we define Basic (same reporting rate for all age-groups (i.e. ρ1 = ⋯ = ρ5) and constant over time), Age-Dependent Reporting (ADR - reporting rate, ρi, fitted separately for each age group, but assumed constant over time) and Time-Varying Reporting (TVR - reporting rate fitted separately for each age group and can vary over time) model variants. For the latter, we assume that the age-dependent reporting rate changes over time t (weeks) as given by a piecewise linear function
| (25) |
where g(38) = 1, g(45) = a, g(52) = b, and g is linear in the intervals before and after week 45. We estimate a, b and ρi with i = 1, …, 4. We also examine the Basic and TVR variants for the Baseline model (with reporting rates always being the same for all age groups).
We fit each of these model variants using the likelihood defined above with and without over-dispersion.
4.2 Infection seeding and school holidays
We seed an initial number of A/H1N1 cases, I0, on week 31 (mid August 2009) and fit the model to the surveillance data in the time window between week 38 of year 2009 and week 7 of 2010. The initial number of cases I0 is distributed among the age classes proportionally to the vector (5%, 10%, 45%, 35%, 5%) which is comparable to the age distribution of reported cases over the summer [36]. Model results are not sensitive to this choice of assignment.
In Italy schools re-opened after the summer vacation in 2009 on September 15th (week 38). Up until that time, we assign weekend contact rates to all those contact matrix elements that involve school-aged children (5 – 14 years). To reproduce Christmas holidays (December 23rd 2009–January 7th 2010) we assign weekend contacts to the whole population, reflecting the fact that most adults are off work for much of the Christmas holiday, but not necessarily the summer holiday.
4.3 Parameter estimation
In a Bayesian setting, we make inference on the parameters which are summarised in Table 1. Given the likelihood function L and chosen a (in our case uniform) prior distribution of the parameters, the (target) posterior distribution is known up to a normalising constant. MCMC methods construct Markov chains whose stationary distribution is the distribution of interest, when it cannot be directly simulated. We implemented the classical Metropolis-Hastings algorithm [18, 37, 38, 39] and, starting from arbitrary initial values in the parameter space, generated sequences of draws from the unknown (target) probability distribution of the parameters. We assume a flat prior distribution for πt, thus setting the shape parameters α and β of equation (18) equal to 1.0. A log scale was used for sampling as the parameters were all positive definite and were expected to potentially vary by orders of magnitude. We checked convergence by assigning different starting values in the parameter space (also far from the posterior mean) and by visual inspection of the trace plots. The algorithm was iterated for 500,000 times and we fixed a burn-in period of 100,000 steps. By tuning the variance of the proposal distribution, we adjusted the mixing of the chains and attempted to reach a rate of acceptance (number of accepted moves/number of proposed points) as closest as possible to the ‘golden’ acceptance rate for the Random Walk Metropolis Hastings of 23% [40]. As expected, we found some correlations between certain parameters (for example, R0 and I0).
In addition to the log-likelihood, we use the Deviance Information Criterion (DIC) for model comparison and selection, for which the preferred model is the one showing the lowest DIC [41].
4.4 Model Validation
For each model we draw 500 (sets of) parameters from the relative joint posterior distribution and with each set we numerically solve the SEIR model in the Italian population. After rescaling the solution to the patient population (thus obtaining , the number of patients infected by the A/H1N1 virus), in the models without overdispersion we apply the binomial model given in equation (12) and draw 100 realisations of , the number of flu (H1N1pdm) cases within the patients population. For the models with overdispersion, we sample 100 realisations of from equation (21) and for each of these we draw from equation (22). We hence obtain the simulated H1N1 incidence curve to be compared with the observed data.
5 Results
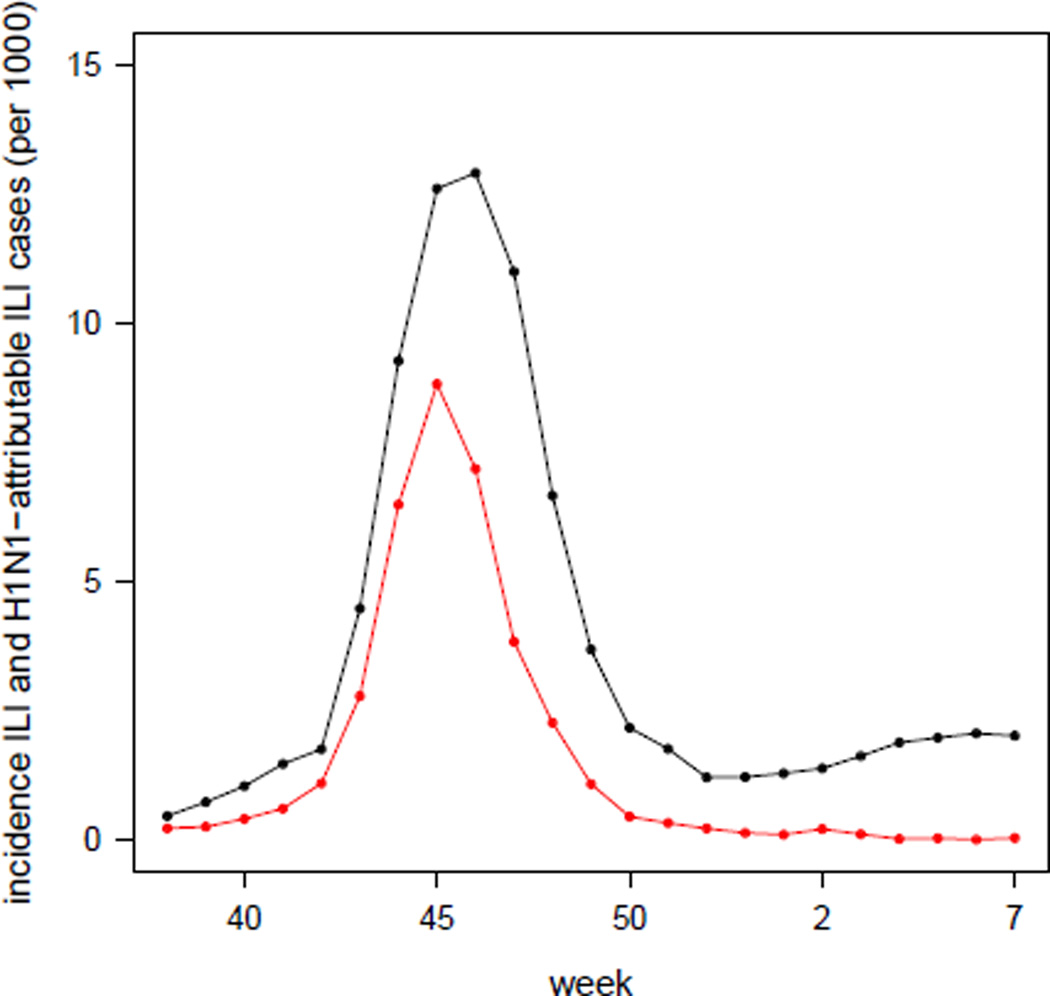
The ILI incidence curve peaked on week 46 (mid November), decreased over the next 6 weeks and then slowly increased again during the first weeks of 2010 (see Figure 2). The H1N1-attributable ILI-incidence curve (red dots) in Figure 2 has been simply obtained by multiplying the ILI incidence times the proportion of positive swabs collected in that week, under the assumption that the samples tested on week t had been collected during week t − 1.
Figure 2.
Incidence (per 1000) of the total number of reported ILI cases (black) and of the number of reported H1N1-attributable ILI-cases (red), obtained by multiplying the weekly ILI datum by the proportion of positive samples on the corresponding week.
We summarise the estimates (in terms of mean and 95% credible interval) obtained for all the examined variants of the Baseline model in Table 2. If we rescale the susceptibility estimates reported in Table 2 to the values we estimated from serological data [10] shown in Table 1, we find that susceptibility drops with age more sharply than the serological data would suggest (the rescaled mean estimates obtained in the basic no-overdispersion variant are σ1 = 2.9, σ2 = 2.0, σ3 = 0.86, σ4 = 0.6). Table 3 summarises the estimates obtained for the Susceptibility and Immunity models with over-dispersion for the ADR and TVR variants. Tables SI-3, SI-4, SI-5 in the Supplementary Information report the estimates for the other model variants. Looking across all these model variants, estimates of R are in the range 1.27–1.42. Models with overdispersion show slightly lower estimates of R than those without overdispersion.
Table 2.
Baseline model: mean and, in brackets, equal-tailed 95% credible interval of the marginal posterior distribution of the parameters for each specified model. Basic: reporting rates constant in time and across the age groups. TVR: Time-Varying Reporting, i.e. age-specific and time-dependent reporting rates as defined by the piecewise linear function given in Eq. (25).
| Baseline model | ||||
|---|---|---|---|---|
| no-overdispersion | with-overdispersion | |||
| basic | TVR | basic | TVR | |
| DIC | 2778.4 | 2614.5 | 1463.1 | 1455.7 |
| log-likelihood | −1386.9 | −1304.4 | −728.2 | −725.8 |
| (−1384.4, −1391.1) | (−1301.1, −1309.4) | (−725.5, −732.7) | (−722.6, −731.1) | |
| R | 1.417 | 1.379 | 1.321 | 1.315 |
| (1.411, 1.424) | (1.371, 1.389) | (1.299, 1.343) | (1.282, 1.350) | |
| I0 | 2123 | 3174 | 7626 | 6249 |
| (1794, 2502) | (2586, 3803) | (3982, 9850) | (2081, 9747) | |
| σ1 | 3.401 | 3.227 | 3.787 | 3.516 |
| (3.296, 3.506) | (3.131, 3.328) | (3.009, 4.652) | (2.844, 4.289) | |
| σ2 | 2.308 | 2.174 | 2.040 | 1.999 |
| (2.264, 2.349) | (2.128, 2.220) | (1.757, 2.347) | (1.704, 2.355) | |
| σ3 | fixed at 1 | fixed at 1 | fixed at 1 | fixed at 1 |
| σ4 | 0.688 | 0.690 | 0.981 | 0.985 |
| (0.646, 0.731) | (0.649, 0.733) | (0.725, 1.306) | (0.737, 1.303) | |
| ρ1 = ⋯ = ρ4 | 0.178 | 0.217 | 0.175 | 0.311 |
| (0.174, 0.183) | (0.205, 0.237) | (0.148, 0.206) | (0.191, 0.556) | |
| a | - | 0.952 | - | 0.603 |
| - | (0.852, 0.998) | - | (0.257, 0.955) | |
| b | - | 0.220 | - | 0.300 |
| - | (0.150, 0.302) | - | (0.094, 0.682) | |
| r | - | - | 8.092 | 8.776 |
| - | - | (5.170, 11.794) | (5.476, 13.070) | |
Table 3.
ADR and TVR with-overdispersion models (Susceptibility and Immunity variants): mean and, in brackets, equal-tailed 95% credible interval of the marginal posterior distribution of the parameters for each specified model. ADR: Age-Dependent Reporting, i.e. reporting rates constant in time and age-specific. TVR: Time-Varying Reporting, i.e. age-specific and time-dependent reporting rates as defined by the piecewise linear function given in Eq. (25).
| With-overdispersion | ||||
|---|---|---|---|---|
| Susceptibility model | Immunity model | |||
| ADR | TVR | ADR | TVR | |
| DIC | 1473.0 | 1453.0 | 1471.5 | 1455.2 |
| log-likelihood | −733.0 | −730.7 | −732.3 | −730.4 |
| (−730.1, −737.9) | (−727.4, −736.0) | (−729.4, −737.2) | (−727.1, −735.6) | |
| R | 1.297 | 1.276 | 1.296 | 1.274 |
| (1.275, 1.318) | (1.236, 1.322) | (1.274, 1.316) | (1.234, 1.317) | |
| I0 | 2431 | 3197 | 2251 | 3150 |
| (1394, 4043) | (639, 8227) | (1287, 3702) | (706, 8122) | |
| ρ1 | 0.246 | 0.361 | 0.267 | 0.365 |
| (0.197, 0.305) | (0.167, 0.735) | (0.215, 0.332) | (0.177, 0.708) | |
| ρ2 | 0.165 | 0.228 | 0.177 | 0.227 |
| (0.134, 0.204) | (0.106, 0.464) | (0.143, 0.218) | (0.109, 0.441) | |
| ρ3 | 0.073 | 0.108 | 0.082 | 0.112 |
| (0.059, 0.091) | (0.050, 0.221) | (0.067, 0.101) | (0.054, 0.217) | |
| ρ4 | 0.069 | 0.105 | 0.078 | 0.109 |
| (0.055, 0.088) | (0.048, 0.217) | (0.062, 0.099) | (0.052, 0.214) | |
| a | - | 0.971 | - | 1.032 |
| - | (0.284, 2.140) | - | (0.336, 2.228) | |
| b | - | 0.345 | - | 0.387 |
| - | (0.082, 0.888) | - | (0.101, 0.965) | |
| r | 6.741 | 7.292 | 6.925 | 7.403 |
| (4.280, 9.906) | (4.600, 10.728) | (4.400, 10.197) | (4.660, 10.983) | |
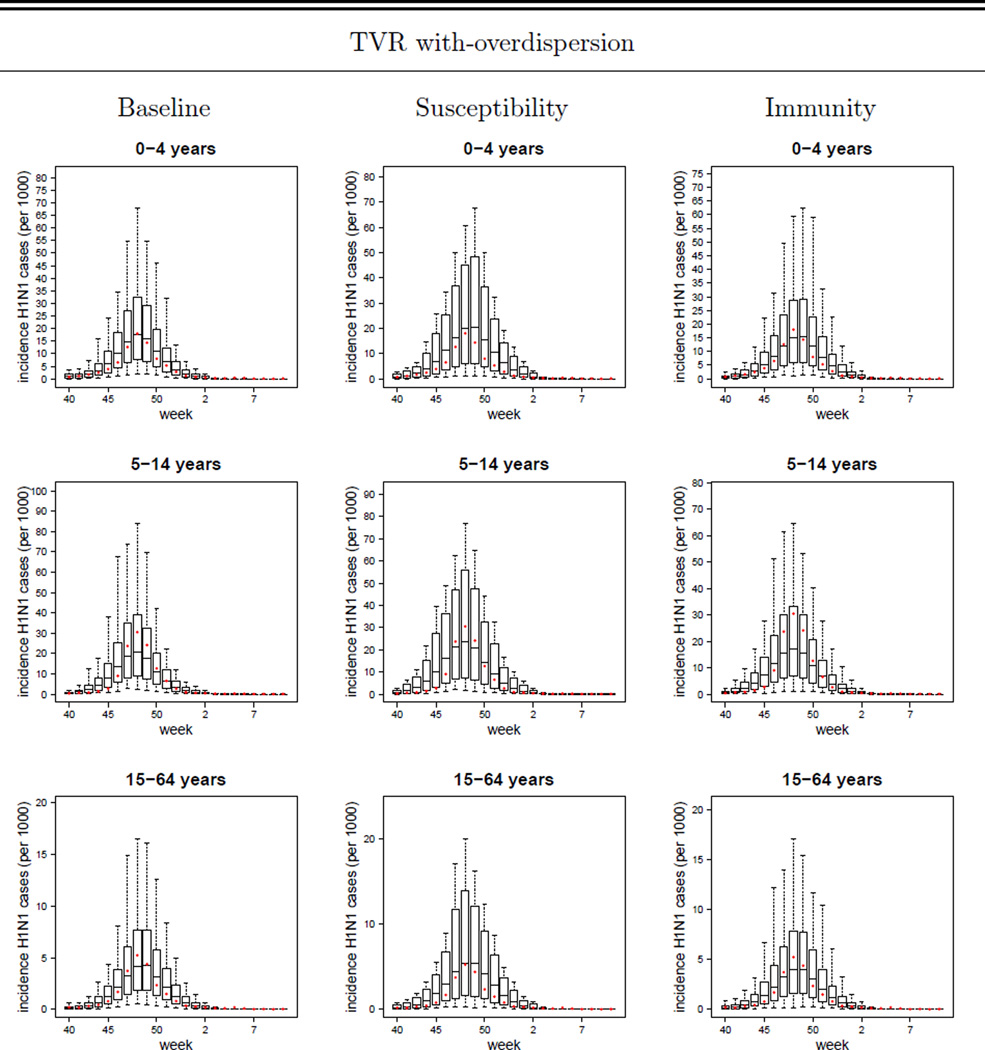
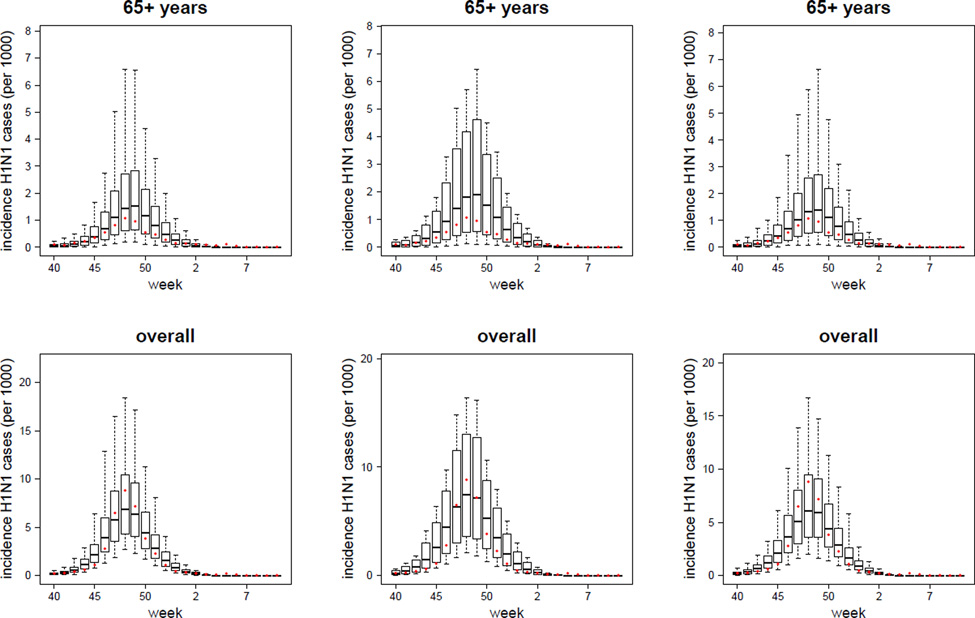
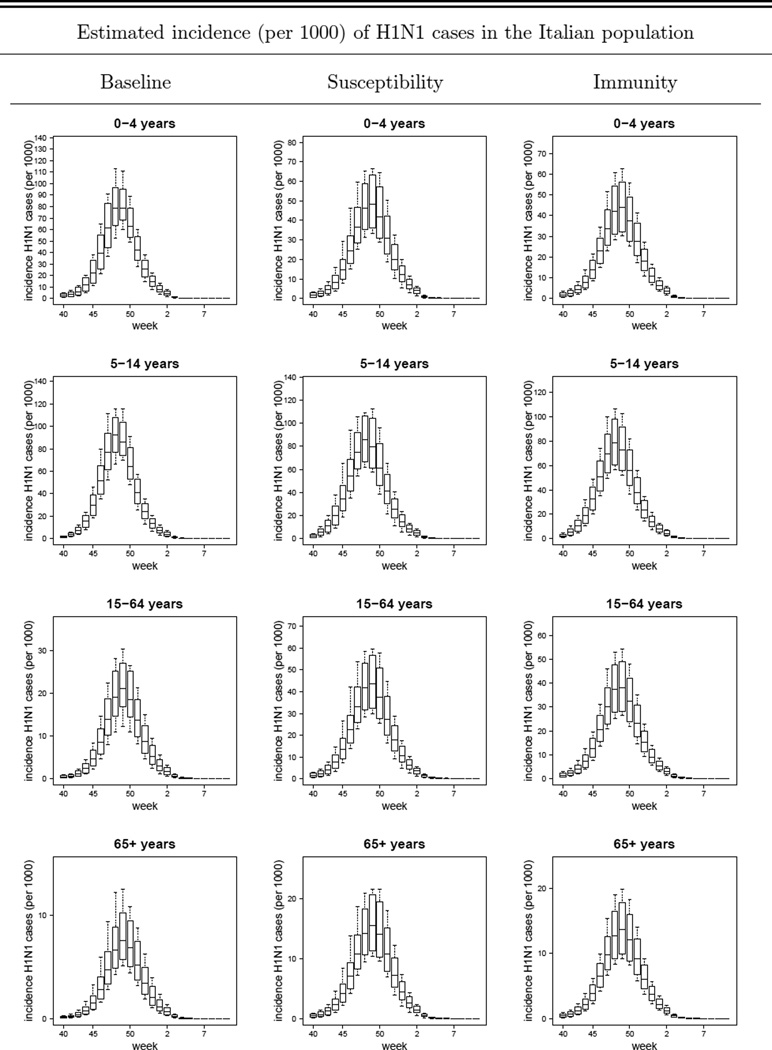
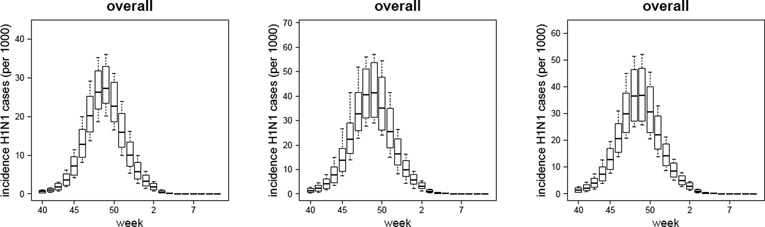
In Figure 3 we plot the simulated H1N1 reported case incidence curves (replicating the sample sizes of the data) obtained with the TVR variants of the Baseline, Susceptibility and Immunity models with overdispersion, together with the observed H1N1-attributable ILI incidence data. Comparable plots for other model variants are given in Figures SI-1, SI-2, SI-3, SI-4 and SI-5. The box-plots are generated as described in the ‘Model Validation’ section.
Figure 3.
TVR with-overdispersion models (Baseline, Susceptibility and Immunity variants): plot of the mean, 95%CI, maximum and minimum simulated weekly reported incidences (per 1000) of symptomatic H1N1 cases (i.e. ILI & H1N1 cases) in the 0 – 4, 5 – 14, 15 – 64, 65+ years age-classes and in the overall population. The dots represent the observed data (i.e. the H1N1-attributable ILI incidence curve). TVR: Time-Varying Reporting, i.e. age-specific and time-dependent reporting rates as defined by the piecewise linear function given in Eq. (25).
As expected, the models with overdispersion show much higher likelihoods (and lower DIC values) together with wider credible intervals around parameter and incidence estimates than the respective no-overdispersion variants. While we discuss the limitations of using a negative binomial model to describe unexplained variation later, we take the models with over-dispersion as being preferred over those without. However, to what extent can we distinguish between the different mechanistic model variants? The basic version of the Susceptibility and Immunity models clearly fit the data worse than the respective ADR and TVR variants (see Table SI-3 and Figure SI-1). Comparing the ADR versions of the Susceptibility and Immunity models with the basic version of the Baseline model, all have identical numbers of fitted parameters (7), but the Baseline model has the best fit from a comparison of the mean posterior log-likelihood or DIC values of each model. However, the posterior log-likelihood credible intervals overlap substantially. The TVR model variants fit 2 additional parameters, and achieve a better fit as measured by DIC, though the log-likelihood posterior distribution overlaps with that of the non-time varying variants for all three models. It is difficult to distinguish the fit quality between the TVR variants of the Baseline, Susceptibility and Immunity models (which each fit 9 parameters), given the huge overlap in the posterior distributions of the log likelihood and the very limited difference in DIC values. The Baseline TVR model’s mean log-likelihood is approximately 5 units higher than the other two models, while the Susceptibility model has a marginally better DIC. Given this, and that the Immunity TVR model is the best fitting of the models without overdispersion, we do not feel it is possible to firmly choose one model over the other in terms of model fit alone.
Biologically, the equally good fit of all three models (and very similar estimates of R) means that the observed age distribution of cases can be nearly equally well explained by either substantial age-dependence in susceptibility to infection (Baseline model), or by substantial age-dependence in reporting rates (Susceptibility and Immunity models) - supporting our previous statement that age-dependent reporting cannot be distinguished from age-dependent prior immunity.
Table 4 therefore reports the peak-incidence (the highest weekly incidence, occurring at the peak) and the cumulative attack rate (final size of the epidemic) for the TVR, with-overdispersion versions of all three models, while Figure 4 shows the corresponding infection (as compared with reported case) incidence over time. The cumulative attack rate has been computed over the whole study period (from week 31 of 2009 to week 7 of 2010). We find that school-age children led and sustained the epidemic, followed by younger children and young adults, while older adults were less affected.
Table 4.
Estimated age-specific peak-incidence (peak-inc.) (per 1000) and cumulative attack rate (AR) (%) of H1N1 infections in the Italian population obtained with the TVR with-overdispersion models (Baseline, Susceptibility and Immunity variants). The attack rate is computed on the time period starting from week 31–2009 to week 7–2010. Mean and, in brackets, 5 to 95 percentile interval.
| Estimates at the Italian population level | ||||||
|---|---|---|---|---|---|---|
| Baseline | Susceptibility | Immunity | ||||
| peak-inc. | AR | peak-inc. | AR | peak-inc. | AR | |
| 0–4 years | 80.7 | 47.3 | 48.8 | 30.8 | 44.2 | 28.1 |
| (68.6, 97.0) | (40.5, 55.2) | (36.4, 63.3) | (26.6, 35.2) | (32.0, 56.1) | (24.1, 31.9) | |
| 5–14 years | 92.9 | 52.5 | 86.1 | 52.9 | 79.2 | 49.0 |
| (76.8, 108.6) | (47.9, 56.6) | (66.8, 107.0) | (47.5, 58.2) | (60.4, 98.4) | (43.6, 53.7) | |
| 15–64 years | 21.1 | 12.5 | 43.9 | 27.8 | 38.7 | 24.7 |
| (16.7, 27.2) | (9.8, 16.0) | (32.8, 56.8) | (24.0, 31.6) | (28.1, 48.9) | (21.3, 27.8) | |
| 65+ years | 7.6 | 4.5 | 15.6 | 9.9 | 13.7 | 8.7 |
| (5.7, 10.3) | (3.4, 6.0) | (11.3, 20.6) | (8.3, 11.6) | (9.8, 17.8) | (7.4, 10.1) | |
| overall | 27.4 | 16.3 | 42.1 | 26.7 | 37.5 | 23.9 |
| (23.4, 33.1) | (14.3, 18.9) | (31.5, 54.0) | (23.2, 30.2) | (27.5, 47.2) | (20.7, 26.9) | |
Figure 4.
Estimated mean, 95%CI, maximum and minimum weekly incidences of H1N1 cases in the Italian population in the 0 – 4, 5 – 14, 15 – 64, 65+ years age-classes and in the overall population obtained using the TVR, with-overdispersion model in its Baseline, Susceptibility and Immunity variants. Best fit models are defined according to the DIC score.
The absolute level of incidence varies markedly by model variant, however. At the community level the estimated peak-incidence is 27.4 (23.4, 33.1) per 1000 for the Baseline model, 42.1 (31.5, 54.0) per 1000 for the Susceptibility model and of 37.5 (27.5, 47.2) per 1000 for the Immunity model. Corresponding cumulative infection attack rates were 16.3% (14.3%, 18.9%), 26.7% (23.2%, 30.2%) and 23.9% (20.7%, 26.0%) respectively for those three models variants. As expected, the Baseline model - which allows for much greater variation in susceptibility to infection with age than the other two - give much lower infection attack rates (and higher reporting rates). There is some consistency in the relative magnitude of age-specific attack rates obtained with the Susceptibility and Immunity models, with the the 0 – 4 and 5 – 14 years age-classes being respectively about 3 and 5 times more affected than the 65+ years old age-group. The estimated attack rate in the 5 – 14 years age-class obtained with the Baseline model is consistent with the estimates obtained using the Susceptibility and Immunity models. Due to lower attack rates in the 15– 64 and 65+ years old age-classes than those obtained with the Susceptibility and Immunity models, the relative magnitude of age-specific attack rates obtained with the Baseline model is amplified, with the the 5 – 14 years age-class being about 11 times more affected than the 65+ years old age-group.
6 Discussion
In this work we propose a general and rigorous statistical framework which explicitly takes into account the way surveillance data are generated. Our methodology allows to fit a transmission model to virological and ILI data simultaneously, by taking into account the uncertainty existing in the data. Let us consider parameters πt, the weekly probability that a swab tests positive. In the absence of any ILI data, the maximum likelihood estimate of πt is simply Pt/Tt, where Tt represents the weekly number of individuals (showing ILI symptoms in the monitored population) who are virologically tested and Pt is the number who test positive for H1N1 infection (Figure 1). The relatively few number of individuals who are virologically tested means that estimates of πt typically have considerable uncertainty. This uncertainty needs to be taken into account when ILI data are available and we want to correctly estimate the parameters of interest (i.e. transmission parameters and reporting rates). Rather than just multiplying ILI incidence with our naive estimate of πt = Pt/Tt [9], we estimate here the likelihood of the observed counts of positive samples and overall ILI simultaneously.
The introduction of a negative binomial distribution as a model for variation in underlying infection incidence () is a heuristic mechanism for allowing for over-dispersion in incidence count data [32, 33]. The estimated values of the dispersion parameter r (1.7 – 13.1) are in the range already used by other authors, but resulted in rather wide credible intervals for the expected number of infections in any given week (see for instance Figure 3).
Overall, judging which model is preferred in this study is challenging. Clearly the models with overdispersion have much lower DIC values, but at the cost of introducing dynamically unconstrained levels of variation in the model. Comparing the models with and without overdispersion clearly indicates that the assumption that the epidemic process is deterministic and spatially homogeneous across Italy is a poor one. But the assumption that incidence is negatively binomially distributed is also crude, and almost certainly over-estimates the degree of variation (for instance, by not allowing for any temporal correlation in the noise introduced). Reality almost certainly lies between the two. That said, the magnitude of difference in log likelihood and DIC models between the models with and without overdispersion leads us to focus on presenting results from models in the presence of overdispersion.
Comparison of measures of model fit does not allow us to convincingly choose between the Baseline, Susceptibility and Immunity model variants with fitted age-specific susceptibility or reporting rates, however. Including time-varying reporting rates improves model fit somewhat (though visually it is hard to see the difference on incidence plots, and the posterior log-likelihood distributions heavily overlapped with the models without TVR), but all three TVR models (with over-dispersion) had identical numbers of fitted parameters, very similar DIC values, and overlapping posterior log-likelihood distributions. In choosing between models we therefore have to rely on biological plausibility and comparison with data collected in other countries.
We found that the estimates of the reproduction number R varied depending on the model but all fell in the range 1.2 – 1.4, with 1.3 being the value preferred by the best fit model variants. These estimates are consistent with those of [42] derived from the exponential growth phase of the ILI number of cases and [43] on the same dataset. They also agree with recent estimates for the fall pandemic wave in Mexico [44, 45], for the initial transmission in Ontario province (Canada) [46] and with the lower bound of the basic reproduction number estimates obtained from the early spread of pandemic H1N1 in La Gloria (Mexico) [3] and in the United States [47].
The results obtained using the Baseline model confirm a substantially lower susceptibility to H1N1 in adults compared with children, with a larger difference than would have been expected from baseline (pre-pandemic) UK serological data [10]. However, the equally-well fitting Susceptibility and Immunity models explain the same trends equally by allowing reporting rates to vary with age. It is likely both susceptibility and reporting rates were higher in children and lower in adults, but the exact age-dependence of each is difficult to resolve without additional data. Post-pandemic serology data now available from a number of countries [49, 50, 51, 52] shows age-specific seroconversion rates more compatible with estimates from the Baseline model than from the other two models (which produce much higher infection attack rate estimates in adults), suggesting that variation in susceptibility to infection with the H1N1pdm virus was more extreme than suggested from serological testing of pre-pandemic samples.
Our estimates of time-varying reporting rates suggest a declining reporting rate late in the pandemic, perhaps reflecting decreased concern. Some model variants show an increase in reporting rate close to the peak of the pandemic [33], perhaps reflecting greater worry and awareness of the pandemic in the general population when incidence was high [48]. Studies to quantify changes in health-care seeking behaviour over time would be desirable in future pandemics [48, 53].
Our analysis would benefit from the availability of more detailed information on the criteria adopted for the collection of the swabs. For instance, information on the day of collection of the swab or, alternatively, on the average delay between collection and testing of the samples would give us more accurate data and hence more accurate and reliable results. Delays in the laboratory confirmation of the swabs can potentially have biased our estimates. Information on the eventual changes occurred in the collection process during an epidemic are also essential, as these changes are potentially another source of bias of the data. We assumed that the swabs selected for testing were a random sample of all ILI cases while in reality a sizeable proportion were collected outside the normal virological surveillance system - presumably in hospitals and GPs for clinical reasons, potentially biasing the results from this surveillance source. Unfortunately, the available data do not allow us to disaggregate swab results by source, which would be another important information.
Finally, this type of study would clearly have benefited from the availability of age-specific virological data, ideally stratified according to the age-classes used by the syndromic surveillance system (or to a compatible age-stratification). If age-specific virological data had been available, we would have been able to distinguish better between model variants and therefore produced more reliable estimates of age-specific infection rates.
There are some minor systematic deviations between model estimates and the data (for instance, the predicted incidence in the first few fitted weeks of the epidemic are systematically lower than the observed data in the 0–4 age-class and systematically higher than the observed data in the 5–14 age-class). Clearly this aspect of model fit might be improved by increasing model complexity, for instance by making the modelled proportion of ILI cases which test positive for H1N1pdm influenza age-dependent. However, the cost of increased model complexity is poorer parameter identifiability (and greater computational requirements). Overall, we feel the relatively simple model we used here gives an adequate description of the trends seen in the surveillance data, and is at the limit of acceptable complexity in terms of being able to be rigorously fitted to the available data.
The general modelling framework proposed in this work can be rapidly applied to the analysis of other influenza surveillance data (both pandemic and seasonal), provided that epidemiological and virological data are available. As such, the methodology developed in this work is a potentially powerful tool for providing real-time epidemiological estimates to public health officials and policy-makers.
Supplementary Material
Acknowledgements
All authors thank the EU FP7 FluModCont and EMPERIE projects and the UK Medical Research Council for support. SC thanks Research Councils UK for fellowship funding. We also thank Antonella Lunelli for providing the infectivity estimates of the infectious stages we used in our model, Gianpaolo Scalia Tomba for the useful notes on the methodology adopted to compute the contact matrices in the POLYMOD project, Caterina Rizzo and Antonino Bella for providing information on the Italian surveillance system and the two anonymous reviewers for their useful comments and suggestions on a previous version of this manuscript.
Footnotes
Conflicts of interest
SC received consulting fees by Sanofi Pasteur MSD on a project on the modelling of the transmission of Varicella Zoster Virus.
References
- 1.Boёlle P, Bernillon P, Desenclos J. A preliminary estimation of the reproduction ratio for new influenza A(H1N1) from the outbreak in Mexico, March–April 2009. Euro Surveill. 2009;14(19) doi: 10.2807/ese.14.19.19205-en. [DOI] [PubMed] [Google Scholar]
- 2.Flahault A, Vergu E, Boёlle P. Potential for a global dynamic of influenza A (H1N1) BMC Infectious Diseases. 2009;9:129. doi: 10.1186/1471-2334-9-129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fraser C, Donnelly CA, Cauchemez S, et al. Pandemic potential of a strain of influenza A (H1N1): Early findings. Science. 2009 Jun;324(no. 5934):1557–1561. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ghani A, Baguelin M, Griffin J, et al. The early transmission dynamics of H1N1pdm influenza in the United Kingdom. PLoS Curr Influenza. 2009;RRN1130 doi: 10.1371/currents.RRN1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cauchemez S, Donnelly CA, Reed C, et al. Household transmission of 2009 pandemic influenza A (H1N1) virus in the United States. New England Journal of Medicine. 2009 Dec;361(no. 27):2619–2627. doi: 10.1056/NEJMoa0905498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Merler S, Ajelli M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proceedings of the Royal Society B: Biological Sciences. 2010 Feb;277(no. 1681):557–565. doi: 10.1098/rspb.2009.1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lee V, Lye D, Wilder-Smith A. Combination strategies for pandemic influenza response - a systematic review of mathematical modeling studies. BMC Medicine. 2009;7(no. 1):76. doi: 10.1186/1741-7015-7-76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang Y, Halloran ME, Longini IMJ. A bayesian model for evaluating influenza antiviral efficacy in household studies with asymptomatic infections. Biostat. 2009;10(no. 2):390–403. doi: 10.1093/biostatistics/kxn045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Baguelin M, Hoek AJV, Jit M, et al. Vaccination against pandemic influenza A/H1N1v in England: A real-time economic evaluation. Vaccine. 2010 Mar;28(no. 12):2370–2384. doi: 10.1016/j.vaccine.2010.01.002. [DOI] [PubMed] [Google Scholar]
- 10.Miller E, Hoschler K, Hardelid P, et al. Incidence of 2009 pandemic influenza A H1N1 infection in England: a cross-sectional serological study. The Lancet. 2010 Mar;375(no. 9720):1100–1108. doi: 10.1016/S0140-6736(09)62126-7. [DOI] [PubMed] [Google Scholar]
- 11.Ross T, Zimmer S, Burke D, et al. Seroprevalence following the second wave of pandemic 2009 H1N1 influenza. PLoS Curr Influenza. 2010 doi: 10.1371/currents.RRN1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Allwinn R, Geiler J, Berger A, et al. Determination of serum antibodies against swine-origin influenza a virus H1N1/09 by immunofluorescence, haemagglutination inhibition, and by neutralization tests: how is the prevalence rate of protecting antibodies in humans? Medical Microbiology and Immunology. 2010 May 01;199(no. 2):117–121. doi: 10.1007/s00430-010-0143-4. [DOI] [PubMed] [Google Scholar]
- 13.Chen MIC, Lee VJM, Lim W-Y, et al. 2009 influenza A(H1N1) seroconversion rates and risk factors among distinct adult cohorts in Singapore. JAMA: The Journal of the American Medical Association. 2010;303(no. 14):1383–1391. doi: 10.1001/jama.2010.404. [DOI] [PubMed] [Google Scholar]
- 14.Baguelin M, Hoschler K, Stanford E, et al. Age-Specific Incidence of A/H1N1 2009 Influenza Infection in England from Sequential Antibody Prevalence Data Using Likelihood-Based Estimation. PLoS ONE. 2011;6(no. 2):e17074. doi: 10.1371/journal.pone.0017074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee VJ, Chen MI, Yap J, et al. Comparability of different methods for estimating influenza infection rates over a single epidemic wave. American Journal of Epidemiology. 2011;174(no. 4):468–478. doi: 10.1093/aje/kwr113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Presanis AM, De Angelis D, Hagy A, et al. The severity of pandemic H1N1 influenza in the United States, from April to July 2009: a Bayesian analysis. PLoS Med. 2009 Dec;6(no. 12):e1 000 207. doi: 10.1371/journal.pmed.1000207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.D’Ortenzio E, Renault P, Jaffar-Bandjee MC, et al. A review of the dynamics and severity of the pandemic A(H1N1) influenza virus on Réunion Island, 2009. Clinical Microbiology and Infection. 2010;16(no. 4):309–316. doi: 10.1111/j.1469-0691.2010.03171.x. [DOI] [PubMed] [Google Scholar]
- 18.Gilks W, Richardson S, Spiegelhalter D. Markov Chain Monte Carlo in Practice. Chapman & Hall/CRC; 1996. [Google Scholar]
- 19.Salmaso S, Donatelli I, Crovari P and collaborative groups for influenza surveillance. The Italian network for surveillance of influenza 1999–2000. Journal of Preventive Medicine and Hygiene. 2000;41:59–61. [Google Scholar]
- 20.Surveillance group for New Influenza A/H1N1 Virus Investigation in Italy. Virological surveillance of human cases of influenza A/H1N1v virus in Italy: preliminary results. Eurosurveillance. 2009;14(24):1–5. doi: 10.2807/ese.14.24.19247-en. [DOI] [PubMed] [Google Scholar]
- 21.Hens N, Goeyvaerts N, Aerts M, et al. Mining social mixing patterns for infectious disease models based on a two-day population survey in Belgium. BMC Infectious Diseases. 2009;9(no. 1):5. doi: 10.1186/1471-2334-9-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hens N, Ayele G, Goeyvaerts N, et al. Estimating the impact of school closure on social mixing behaviour and the transmission of close contact infections in eight European countries. BMC Infectious Diseases. 2009;9(no. 1):187. doi: 10.1186/1471-2334-9-187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mossong J, Hens N, Jit M, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLOS Medicine. 2008;5:381–391. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Diekmann O, Heesterbeek J. Mathematical Epidemiology of Infectious Diseases. Chichester, New York: Wiley; 2000. [Google Scholar]
- 25.Wallinga J, Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences. 2007;274(no. 1609):599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lessler J, Reich NG, Cummings DA. Outbreak of 2009 pandemic influenza A (H1N1) at a New York City school. New England Journal of Medicine. 2009 Dec;361(no. 27):2628–2636. doi: 10.1056/NEJMoa0906089. [DOI] [PubMed] [Google Scholar]
- 27.Baccam P, Beauchemin C, Macken CA, et al. Kinetics of influenza A virus infection in humans. J. Virol. 2006;80(no. 15):7590–7599. doi: 10.1128/JVI.01623-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Press W, Teukolsky S, Vetterling W, Flannery B. Numerical Recipes in C++, The Art of Scientific Computing. Cambridge University Press; 2002. [Google Scholar]
- 29.Alexander N, Moyeed R, Stander J. Spatial modelling of individual-level parasite counts using the negative binomial distribution. Biostatistics. 2000 Dec;1(no. 4):453–463. doi: 10.1093/biostatistics/1.4.453. [DOI] [PubMed] [Google Scholar]
- 30.Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. NATURE. 2005 Nov;438(no. 7066):355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lloyd-Smith JO. Maximum likelihood estimation of the negative binomial dispersion parameter for highly overdispersed data, with applications to infectious diseases. PLoS ONE. 2007;2(no. 2):e180. doi: 10.1371/journal.pone.0000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mathews JD, McCaw CT, McVernon J, et al. A biological model for influenza transmission: Pandemic planning implications of asymptomatic infection and immunity. PLoS ONE. 2007 Nov;2(no. 11):e1220. doi: 10.1371/journal.pone.0001220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cauchemez S, Ferguson NM. Likelihood-based estimation of continuous-time epidemic models from time-series data: application to measles transmission in London. Journal of The Royal Society Interface. 2008;5(no. 25):885–897. doi: 10.1098/rsif.2007.1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gojovic MZ, Sander B, Fisman D, et al. Modelling mitigation strategies for pandemic (H1N1) 2009. Canadian Medical Association Journal. 2009;181(no. 10):673–680. doi: 10.1503/cmaj.091641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mathews J, McBryde E, McVernon J, et al. Prior immunity helps to explain wave-like behaviour of pandemic influenza in 1918-9. BMC Infectious Diseases. 2010;10(no. 1):128. doi: 10.1186/1471-2334-10-128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rizzo C, Declich S, Bella A, et al. Enhanced epidemiological surveillance of influenza A(H1N1)v in Italy. Euro Surveill. 2009;9(27) doi: 10.2807/ese.14.27.19266-en. 14. [DOI] [PubMed] [Google Scholar]
- 37.Tierney L. Markov chains for exploring posterior distributions. The Annals of Statistics. 1994 Dec;22(no. 4):1701–1728. [Google Scholar]
- 38.Walsh B. Markov chain monte carlo and gibbs sampling. Lecture Notes for EEB 581. 2004 [Google Scholar]
- 39.O’Neill PD. A tutorial introduction to bayesian inference for stochastic epidemic models using Markov chain Monte Carlo methods. Math. Biosci. 2002;180:103–114. doi: 10.1016/s0025-5564(02)00109-8. [DOI] [PubMed] [Google Scholar]
- 40.Roberts GO, Gelman A, Gilks WR. Weak convergence and optimal scaling of random walk metropolis algorithms. The Annals of Applied Probability. 1997 Feb;7(no. 1):110–120. [Google Scholar]
- 41.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. Journal Of The Royal Statistical Society Series B. 2002;64(no. 4):583–639. [Google Scholar]
- 42.Ajelli M, Merler S, Pugliese A, Rizzo C. Model predictions and evaluation of possible control strategies for the 2009 A/H1N1v influenza pandemic in Italy. Epidemiol Infect. 2011;139(no. 1):68–79. doi: 10.1017/S0950268810001317. [DOI] [PubMed] [Google Scholar]
- 43.Poletti P, Ajelli M, Merler S. The Effect of Risk Perception on the 2009 H1N1 Pandemic Influenza Dynamics. PLoS ONE. 2011;6(no. 2):e16460. doi: 10.1371/journal.pone.0016460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chowell G, Echevarría-Zuno S, Viboud C, et al. Characterizing the epidemiology of the 2009 influenza A/H1N1 pandemic in Mexico. PLoS Med. 2011;8(no. 5):e1000436. doi: 10.1371/journal.pmed.1000436. 05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pourbohloul B, Ahued A, Davoudi B, et al. Initial human transmission dynamics of the pandemic (H1N1) 2009 virus in North America. Influenza and Other Respiratory Viruses. 2009;3(no. 5):215–222. doi: 10.1111/j.1750-2659.2009.00100.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tuite AR, Greer AL, Whelan M, et al. Estimated epidemiologic parameters and morbidity associated with pandemic H1N1 influenza. Canadian Medical Association Journal. 2010;182(no. 2):131–136. doi: 10.1503/cmaj.091807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yang Y, Sugimoto JD, Halloran ME, et al. The transmissibility and control of pandemic influenza A (H1N1) virus. Science. 2009 Oct;326(no. 5953):729–733. doi: 10.1126/science.1177373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rubin G, Potts H, Michie S. The impact of communications about swine flu (influenza A H1N1v) on public responses to the outbreak: results from 36 national telephone surveys in the UK. Health Technol. Assess. 2010;14(34):183–266. doi: 10.3310/hta14340-03. [DOI] [PubMed] [Google Scholar]
- 49.Hardelid P, Andrews NJ, Hoschler K, et al. Assessment of baseline age-specific antibody prevalence and incidence of infection to novel influenza AH1N1 2009. Health Technol. Assess. 2010;14(55):115–192. doi: 10.3310/hta14550-03. [DOI] [PubMed] [Google Scholar]
- 50.Wu JT, Ma ESK, Lee CK, et al. The Infection Attack Rate and Severity of 2009 Pandemic H1N1 Influenza in Hong Kong. Clin. Infect. Dis. 2010;51(10):1184–1191. doi: 10.1086/656740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xu C, Bai T, Iuliano AD, et al. The Seroprevalence of Pandemic Influenza H1N1 (2009) Virus in China. PLoS One. 2011;6(4) doi: 10.1371/journal.pone.0017919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tandale BV, Pawar SD, Gurav YK, et al. Seroepidemiology of pandemic influenza A (H1N1) 2009 virus infections in Pune, India. MC Infect Dis. 2010;10:255. doi: 10.1186/1471-2334-10-255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jones JH, Salathé M. Early Assessment of Anxiety and Behavioral Response to Novel Swine-Origin Influenza A(H1N1) PLoS ONE. 2009;4(no. 12):e8032. doi: 10.1371/journal.pone.0008032. 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rizzo C, Rota MC, Bella A, et al. Cross-reactive antibody responses to the 2009 A/H1N1v influenza virus in the Italian population in the pre-pandemic period. Vaccine. 2010 Apr;28(no. 20):3558–3562. doi: 10.1016/j.vaccine.2010.03.006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.