Abstract
DNA methylation is an important epigenetic mechanism that has been linked to complex disease and is of great interest to researchers as a potential link between genome, environment, and disease. As the scale of DNA methylation association studies approaches that of genome-wide association studies (GWAS), issues such as population stratification will need to be addressed. It is well-documented that failure to adjust for population stratification can lead to false positives in genetic association studies, but population stratification is often unaccounted for in DNA methylation studies. Here, we propose several approaches to correct for population stratification using principal components from different subsets of genome-wide methylation data. We first illustrate the potential for confounding due to population stratification by demonstrating widespread associations between DNA methylation and race in 388 individuals (365 African American and 23 Caucasian). We subsequently evaluate the performance of our principal-components approaches and other methods in adjusting for confounding due to population stratification. Our simulations show that 1) all of the methods considered are effective at removing inflation due to population stratification, and 2) maximum power can be obtained with SNP-based principal components, followed by methylation-based principal components, which out-perform both surrogate variable analysis and genomic control. Among our different approaches to computing methylation-based principal components, we find that principal components based on CpG sites chosen for their potential to proxy nearby SNPs can provide a powerful and computationally efficient approach to adjustment for population stratification in DNA methylation studies when genome-wide SNP data are unavailable.
Introduction
DNA methylation is an epigenetic mechanism that typically involves the addition of a methyl group to a cytosine base pair followed by a guanine (cytosine-phosphate-guanine, or CpG site). Advances in technology and rapidly decreasing costs of data generation have led to an increased focus on large-scale studies of DNA methylation in human subjects. Through these studies, altered DNA methylation has been linked to diseases such as cancer, autism, and lupus in addition to environmental stressors such as smoking and age [Alisch, et al. 2012; Breitling, et al. 2011; Christensen, et al. 2009; Cicek, et al. 2013; Coit, et al. 2013; Numata, et al. 2012; Rakyan, et al. 2010; Selamat, et al. 2012; Sun, et al. 2013; Teschendorff, et al. 2010; Wong, et al. 2013].
Recently, several DNA methylation studies have identified CpG sites where methylation levels differed by race or ethnicity [Adkins, et al. 2011; Heyn, et al. 2013; Kwabi-Addo, et al. 2010; Liu, et al. 2010; Nielsen, et al. 2010; Terry, et al. 2008]. These differences could arise from epigenetic inheritance [Pembrey, et al. 2006; Richards 2008] or population-specific environmental factors, but most are likely due to the presence of 1) between-population differences in single nucleotide polymorphism (SNP) allele frequencies [Cavalli-Sforza and Edwards 1967; Cavalli-Sforza, et al. 1994; Price, et al. 2006; The International HapMap 3 Consortium, et al. 2010] and 2) allele-specific DNA methylation or methylation quantitative trait loci (mQTLs) [Bell, et al. 2011; Boks, et al. 2009; Heijmans, et al. 2007; Kerkel, et al. 2008; Schalkwyk, et al. 2010; Zhang, et al. 2010]. Regardless of the mechanisms behind the observed differences in DNA methylation across populations, there are no established methods to account for population stratification in methylation studies. Population stratification is a well-known confounder in genome-wide association studies (GWAS) [Cavalli-Sforza and Edwards 1967; Cavalli-Sforza, et al. 1994; Price, et al. 2006; The International HapMap 3 Consortium, et al. 2010], and is likely to present a similar problem in DNA methylation studies. Methods to account for population stratification in GWAS include the use of genomic control to correct inflated test statistics [Bacanu, et al. 2000; Devlin and Roeder 1999; Devlin, et al. 2001a] and inclusion of the top principal components (PCs) of genome-wide genotype data as covariates in association tests to serve as proxies for individual ancestry [Price, et al. 2006]. These methods may be extended to address population stratification in DNA methylation studies, though the lack of available GWAS data presents a complication in many studies. PCs computed from methylation data present one possible solution to this problem, though the efficacy of these approaches has not been explored. In particular, the use of methylation-based PCs may present additional complications, since in contrast with genetic variation, genomic patterns of DNA methylation are known to vary with many factors beyond ancestry, including technical factors, age [Alisch, et al. 2012; Christensen, et al. 2009; Numata, et al. 2012; Rakyan, et al. 2010; Teschendorff, et al. 2010], and cellular composition [Houseman, et al. 2012; Reinius, et al. 2012]. In this manuscript, we develop several methylation-based principal component approaches and assess their ability to account for population stratification in DNA methylation studies when GWAS data may not be available.
Methods
For this study, we sought to 1) assess the potential for confounding due to population stratification in DNA methylation analyses, and 2) compare the ability of different approaches to account for population stratification. We first examined the potential for confounding in a typical methylation dataset by testing >469K autosomal CpG sites for association with self-reported race among 388 individuals self-identifying as African-American or Caucasian. We next assessed the ability of approaches based on PCs from genomic methylation or SNP data to adjust for population stratification based on the reduction in the number of CpG sites significantly associated with race after these PCs were included as covariates in the analysis. For each approach we then performed simulations to obtain estimates of type I error and power with or without population stratification. Finally, we examined our ability to replicate published results in our data using each of these approaches to adjust for population stratification.
Data
The data used in this study were collected as part of a larger study investigating the roles of genetic and environmental factors in predicting response to stressful life events [Gillespie, et al. 2009]. Individuals were recruited from the waiting rooms of a public hospital in Atlanta, GA, and those providing informed consent participated in a verbal interview and provided salivary and/or blood samples. All procedures in this study were approved by the Institutional Review Boards of Emory University School of Medicine and Grady Memorial Hospital.
To assess DNA methylation, we extracted DNA from whole blood at the Max Planck Institute in Munich using the Gentra Puregene Kit (Qiagen). Genomic DNA was then bisulfite converted using the Zymo EZ-96 DNA Methylation Kit (Zymo Research). We assessed DNA methylation for 393 individuals at >480,000 CpG sites using Illumina HumanMethylation450 BeadChip arrays, with hybridization and processing performed according to the instructions of the manufacturer. For each CpG site and individual, we collected two data points: M (the total methylated signal), and U (the total unmethylated signal). We set to missing data points with 1) a detection p-value greater than 0.001 or 2) a combined signal less than 25% of the total median signal and less than both the median unmethylated and median methylated signal. We removed individual samples from analysis if they had 1) a mean total signal less than half of the median of the overall mean signal or 2000 arbitrary units, or 2) a missingness rate above 5%. Similarly, we removed from analysis CpG sites with a missingness rate above 10%. We then quantile-normalized the signal data to remove systematic differences across individuals in overall signal distribution (Supplementary Methods). Using the normalized signals, we then computed β-values for each individual at each CpG site as the total methylated signal divided by the total signal:
For genotyping, we extracted DNA either from saliva (Oragene DNA, DNA Genotek, Kanata, Ontario, Canada) or whole blood at Emory University. We used Illumina Omni-Quad 1M and Omni-Express arrays with 200 ng (blood) or 400 ng (saliva) of DNA to genotype 639,053 SNPs for the same 393 individuals at the Max Planck Institute. We called genotypes using Illumina's GenomeStudio software and used PLINK [Purcell, et al. 2007] to perform quality control analyses, removing individuals with > 2% missing data and SNPs with less than a 99% call rate or MAF<5%. We also identified and removed related individuals by using PLINK to estimate the proportion of identity by descent (IBD) for each pair of individuals [Purcell, et al. 2007]. Among pairs of individuals with IBD proportion > 0.1 (indicating cousins or a closer relation), we removed the individual in each pair with the higher rate of missing genotype data. After quality control, 589,375 autosomal SNPs, 469,142 autosomal CpG sites, and 393 individuals were eligible for further analyses.
Principal Component Analysis
Principal component analysis of genome-wide SNP data
Prior to principal component analysis, we used PLINK [Purcell, et al. 2007] to prune the data in windows of 50 bp (base pairs), removing one SNP from each pair of SNPs with r2>0.05. 54,616 SNPs remained after pruning. We next standardized the allele counts as suggested in [Patterson, et al. 2006], such that if C is a matrix of allele counts, with each row representing an individual, the matrix of standardized allele counts is:
where
We then calculated the PCs of M. To adjust for population stratification, we considered two sets of PCs: the set that were significant according to a Tracey-Widom test [Patterson, et al. 2006] (PCGWAS_TW) and the top ten PCs of M (PCGWAS).
Principal component analysis of genome-wide DNA methylation data
When adjusting for population stratification in GWAS, it is common to work with a roughly independent set of SNPs that have been pruned to remove highly correlated SNPs, as described above. We took a similar approach for the methylation data, although to account for differences in the correlation structure of methylation data compared to SNP data, we performed more extensive correlation-based pruning than typically used for SNPs (Supplementary Methods). As potential corrections for population stratification, we considered the top ten PCs based on: the complete unpruned data (PCunpruned), data pruned to keep only CpG sites with r2 < 0.25 (PCr2<0.25), or data pruned to keep only CpG sites with r2 < 0.1 (PCr2<0.1).
In addition to the correlation-based pruning, we also devised a method of location-based pruning to take advantage of information on the proximity of SNP variants to the methylation probes by incorporating data on genetic variation from the 1000 Genomes Project [1000 Genomes Project Consortium 2010]. For each CpG site we identified the closest genetic variant with MAF>.01 in the 1000 Genomes Project, based on all samples in the updated Phase I release. We then created seven pruned datasets that included only CpG sites within a certain distance (0, 1, 2, 5, 10, 50, or 100 bp) of a genetic variant (lists of CpG sites available at http://genetics.emory.edu/conneely). The purpose of this location-based pruning was to focus on CpG sites that may proxy for SNP genotypes in situations where SNP data may not be available. We hypothesized that the PCs from these CpG sites could pick up on population differences in allele frequency of the genetic variants and thus may provide an appropriate adjustment for population stratification when genome-wide SNP data are not available. Thus, we tested an additional seven sets of the top ten PCs based on CpG sites located: directly on a genetic variant (PC0bp), within one (PC1bp), two (PC2bp), five (PC5bp), ten (PC10bp), fifty (PC50bp), or one hundred base pairs (PC100bp) of a genetic variant.
Assessing the Potential for Population Stratification in Methylation Data
To assess the potential for population stratification in our methylation data, we tested for associations between methylation and self-reported race in all individuals who self-reported as African-American (N=365) or Caucasian (N=23) in our data. We used the R package CpGassoc [Barfield, et al. 2012] to perform a genome-wide methylation association study to identify CpG sites that associated significantly with race. Analyzing each CpG site separately, we performed a multivariate linear regression that modeled either the β-values or M-values (the logit-transformed β-values log(β/(1- β)) described by [Du, et al. 2010]) on an indicator for self-reported race (African-American vs. Caucasian) and included covariates for sex, age, chip, and row on chip to adjust for age- and sex-dependent methylation along with potential technical effects of chip and location on chip. To assess significance while accounting for multiple testing we used the Benjamini-Hochberg FDR procedure and the Holm method (a step down Bonferroni procedure) [Benjamini and Hochberg 1995; Holm 1979].
We next assessed the effectiveness of each set of PCs described above as proxies for self-reported race in our data, since the goal of PC-based adjustment for population stratification is to construct covariates that proxy for ancestry. For each set of PCs, we re-ran our CpGassoc analysis including the top PCs (generally the top ten PCs, except with PCGWAS_TW) as covariates in the model. When working with M-values, we computed principal components based on M-values instead of the untransformed β-values. To assess the potential of each set of PCs as proxies for ancestry, we considered the number of CpG sites significantly associated with race before and after adjustment. For comparison, we also applied the method of genomic control (GC) to adjust the test statistics by an estimated inflation factor statistics [Bacanu, et al. 2000; Devlin and Roeder 1999; Devlin, et al. 2001a]. To estimate the GC inflation factor, we first computed tmed, the median t-statistic from the unadjusted model. Since the squared t-statistics are approximately distributed as λχ21 [Devlin, et al. 2001b], where λ represents an unknown inflation factor, we computed the GC inflation factor as λGC = t2med /.4549, where .4549 is the median of the χ21 distribution. We then divided each of the test statistics by before calculating p-values.
Simulations
To assess rates of type I error and power for the proposed adjustments, we performed a series of simulations. Because of the difficulty of simulating realistic genome-wide methylation and SNP data, we based our simulations on the genome-wide genotypes and epigenotypes of randomly drawn subsets of individuals from the data described above. In each simulation, we randomly sampled 100 of the 365 African American individuals and included all 23 Caucasian individuals; this strategy was used because of the scarcity of Caucasian individuals in our data. For each sample of 123 individuals, we then simulated either a continuous or dichotomous variable that had a different mean for Caucasians and African Americans.
To estimate type I error rates for the continuous case, we simulated a variable Yi so that:
where α is a constant term, εi ~ N(0,1), and I(Caucasian) is an indicator variable that is 1 for Caucasian and 0 for African-American individuals. We performed two sets of 5,000 simulations each: one where γ=0 (no population stratification) and one where γ>0 (population stratification is present). To test the ability of each method to control experiment-wide type I error at the appropriate level (0.05), we used CpGassoc to perform a genome-wide analysis for association between methylation and the simulated continuous variable in each simulated dataset. CpGassoc fits a linear model for each CpG site that models either the β- or M-value as a linear function of covariates. Our covariates included the simulated continuous variable as well as age, sex, chip, and location on chip. In each simulation, we next attempted to adjust for population stratification using each of the methods described above, as well as GC [Bacanu, et al. 2000; Devlin and Roeder 1999; Devlin, et al. 2001a] and Leek and Storey's surrogate variable analysis (SVA) method [Leek, et al. 2012; Leek and Storey 2007; Leek and Storey 2008]. To avoid excessive computational burden, each set of PCs was computed for the entire sample of individuals in the simulation study (N=388) prior to performing simulations, rather than computing a separate set for each simulation. To perform SVA we used the SVA R package to estimate the surrogate variables via iteratively re-weighted surrogate variable analysis [Buja A 1992; Leek and Storey 2007; Leek and Storey 2008] and to select the number of surrogate variables to include in the analysis via permutation testing [Buja A 1992]. As with the PCs, we then included the surrogate variables as additional covariates in the model. SVA typically failed for a small number of simulations; for T1E simulations we assumed for the sake of comparison that those unsuccessful runs would not have returned false positives, while for power simulations we simply computed power based on the successful simulations. The resulting estimate of type I error in each set of simulations was the proportion of simulations with one or more Holm-significant CpG sites.
To estimate power, we simulated the continuous variable such that its mean depended on both race and the methylation of a specific CpG site. The variable was simulated according to a linear model where:
where α is a constant term, δ>0 is a constant slope term, εi ~ N(0,1), and βi represents the β-value or M-value at the chosen CpG site. Here we performed two sets of 1,000 simulations each: one where γ=0 (no population stratification) and one where γ>0 (population stratification is present). We then used CpGassoc to test each CpG site for association as described above. Estimated power for each set of simulations was then the proportion of simulations that correctly identified the chosen CpG site as Bonferroni-significant.
For the binary case, we performed similar simulations using a logit model. For each individual, we simulated the probability of disease pi such that:
and simulated disease status as a Bernoulli(pi) random variable. To estimate type I error rates, we created 5,000 simulated datasets where disease status was simulated with δ=0 and either γ=0 (population stratification present) or γ>0 (population stratification present). We then used CpGassoc to test each CpG site for association by fitting linear regressions that modeled β-values as a linear function of disease status as well as age, sex, chip, and location on chip, and tried adjusting for population stratification via all of the methods described above. As above, we estimated type I error in each set of simulations as the proportion of simulations with one or more Holm-significant CpG sites. To estimate power, we performed 1,000 simulations where δ>0, and proceeded in the same way as above.
Replication of previously published results
To compare the above methods in a real-world setting we attempted to replicate two sets of previously published results: the top eight CpG sites from a study of methylation and age [Teschendorff, et al. 2010] and a CpG site that has shown strong association with smoking in several studies [Breitling, et al. 2012; Breitling, et al. 2011; Shenker, et al. 2013; Sun, et al. 2013; Wan, et al. 2012].
We first analyzed eight CpG sites that we selected by taking the five CpG sites most significantly associated with age in each of Supplementary Tables 3 and 5 in [Teschendorff, et al. 2010]. For these analyses, we used our original data plus five additional individuals who were not included in the simulations because they did not self-report as African-American or Caucasian (four reported as mixed race and one as “other”), raising our sample size to 393. We then recalculated all the PCs. We used CpGassoc to model β-values as a linear function of age, with covariates for sex, chip, and location on chip. We then refit the model including one of the sets of PCs described above as additional covariates, or used genomic control or SVA [Leek, et al. 2012; Leek and Storey 2007]. As a gold standard, we also ran the model including self-reported race for comparison (coded as categorical based on self-reported race).
We next analyzed CpG site cg19859270, which has demonstrated strong association with smoking across several studies [Breitling, et al. 2012; Breitling, et al. 2011; Shenker, et al. 2013; Sun, et al. 2013; Wan, et al. 2012], including a previous analysis in a subset of our data (239 African American subjects with useable smoking data) as a replication sample in Sun et al. [Sun, et al. 2013]. Here we modeled β-values as a function of the total current KMSK (Kreek-McHugh-Schluger-Kellogg) score with the usual covariates for age, sex, chip, and location (row) on chip. We then refit the model several times including each set of PCs as covariates. Our analysis included 255 individuals for whom KMSK was available, including 239 self-identifying as African American, 13 as Caucasian, 2 as mixed, and 1 as “other”.
For these analyses and others, we also performed secondary analyses adjusting for estimated cell type proportions. We estimated the proportions of 6 cell types (monocytes, granulocytes, CD8+ T-cells, CD4+ T-cells, NK cells, and B cells) for each individual from their genome-wide methylation signatures, using the method of [Houseman, et al. 2012] to infer proportions based on an external reference sample of cell-specific methylation profiles [Reinius, et al. 2012]. We then performed secondary analyses where we included these estimated cell type proportions as additional covariates in our replication studies of age and smoking. For all regressions we standardized the cell type proportions to sum to exactly 1 for each individual, and then included 5 of the 6 proportions as covariates in our regression. We also used these estimated proportions to investigate the ability of the top ten methylation-based PCs to pick up on cell type heterogeneity (Supplementary Table 2).
Results
Our dataset included 365 African American and 23 Caucasian individuals, according to self-report. The mean age was 41.5 (range 18-77), with 279 females and 109 males. For the preliminary tests of genome-wide association between methylation β- or M-values and self- reported race, we analyzed 469,142 autosomal CpG sites. 912 sites were associated with race according to the conservative Holm method of adjustment for multiple testing, and 12,827 sites were associated at FDR<.05 (first row of Table I), suggesting that population stratification is a potential confounder in DNA methylation studies as well as in GWAS.
Table I.
Total number of sites associated with race, before and after correction for population stratification
| Correction method used | # markers used to compute PCs | # FDR-significant CpG sites | # Holm-significant CpG sites | λ GC |
|---|---|---|---|---|
| No correction | - | 12827 | 912 | 2.09 |
| GC | - | 578 | 90 | 1 |
| PCgwas | 54,610 | 13 | 3 | 1 |
| PCGWAS TW | 54,610 | 19 | 4 | 1 |
| PCunpruned | 469,142 | 1 | 1 | 1.08 |
| PCr2<0.25 | 225,440 | 0 | 0 | 1.06 |
| PCr2<0.1 | 121,855 | 0 | 0 | 1.11 |
| PC0bp | 7,326 | 0 | 0 | 1.16 |
| PC1bp | 17,105 | 1 | 1 | 1.18 |
| PC2bp | 20,336 | 1 | 1 | 1.18 |
| PC5bp | 31,178 | 1 | 1 | 1.12 |
| PC10bp | 48,998 | 1 | 1 | 1.10 |
| PC50bp | 174,510 | 1 | 1 | 1.02 |
| PC100bp | 271,877 | 1 | 1 | 1.05 |
We next performed similar analyses that included each set of PCs as additional covariates to adjust for population stratification, and observed a substantial reduction in the number of sites that significantly associated with race (Table I). Although 90 sites remained associated with race after GC adjustment, inclusion of PCs from GWAS or methylation data generally resulted in 0 or 1 Holm-significant sites. PCS based on genome-wide SNP data (PCGWAS and PCGWAS_TW) were the most successful at removing inflation (λGC =1) but several sites remained significantly associated with race after these corrections. In contrast, slight genomic inflation remained after adjustment via methylation-based PCs (1.02<λGC<1.18).but fewer FDR-significant sites remained. When we performed the analysis using M-values instead of β-values (Supplementary Table I), we observed a similar pattern except that the GWAS-based PCs appeared to fully correct for population stratification, and the methylation-based PCs (now computed based on M-values) performed somewhat worse in terms of genomic inflation and numbers of FDR-significant sites.
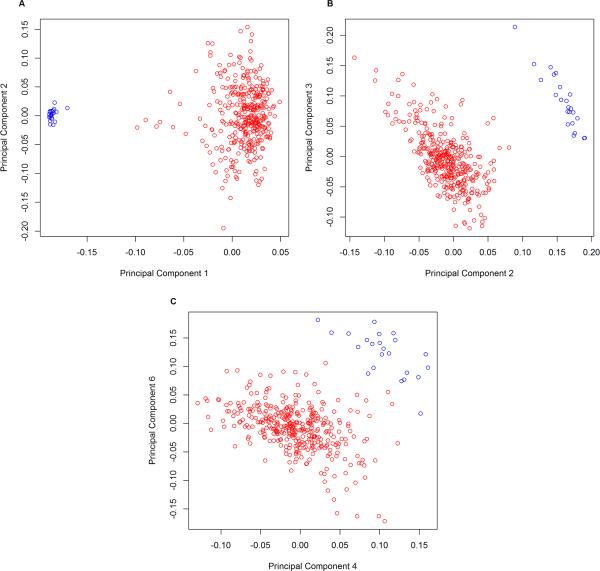
Table I suggests that both GWAS- and methylation-based PCs successfully proxied for self-reported race, including sets based only on DNA methylation data. It is well-established that population structure can generally be represented with the top PCs from GWAS data, but no such pattern has been established for DNA methylation data. In our data, we observe that in contrast to GWAS-based PCs (Figure 1A), the first methylation-based PC generally does not represent variation due to population structure, suggesting that variation in methylation data may be less influenced by population structure and more influenced by other factors. This is unsurprising considering that DNA methylation may be influenced by technical factors, individual age, or cell type composition of individual samples. For example, when examining the first ten components from most sets of methylation-based PCs, we found top principal components to be significantly associated not only with race, but with age, chip, row on chip, and cell type proportions estimated via the method of Houseman et al. [2012] (Supplementary Table II). Figure 1 shows that in our data self-reported race associates with the first PC of PCGWAS (Figure 1A) but with the 2nd and 3rd PCs of PC0bp (Figure 1B) and the 4th and 6th PCs of PC50bp (Figure 1C). The difference between Figures 1B and 1C is consistent with the idea that principal components based only on CpG sites harboring a SNP (PC0bp) may provide the best proxy for SNP-based principal components when genome-wide SNP data are unavailable. Supplementary Table II demonstrates a similar pattern for the other methylation-based PCs, in which race correlates with higher-order PCs when PCs are computed for CpG sites within ≤10 bp of SNPs.
Figure 1. Principal components by self-reported race.
A) 1st and 2nd PC from PCGWAS B) 2nd and 3rd PC from PC0bp C) 4th and 6th PC from PC50bp. Red points = African American individuals; blue points = Caucasian individuals.
To estimate type I error rates for the different approaches, we performed 5,000 simulations as described in Methods, and fit the model using each of the proposed adjustments. To provide a “gold standard” for our comparisons, we also fit the model adjusting for self-reported race as a covariate. Results are presented in the first two columns of Table II (β-values modeled as a function of a continuous phenotype), Supplementary Table III (M-values modeled as a function of a continuous phenotype) and Table III (β-values modeled as a function of a dichotomous phenotype). Prior to correction, the type I error rate was inflated in the presence of population stratification (first row of Tables II and III and Supplementary Table III). For continuous phenotypes, all of the proposed adjustments achieved or came close to the targeted type I error of 0.05 both in the presence and absence of population stratification (Table II and Supplementary Table III). For simulations based on a dichotomous phenotype this was true in the absence of population stratification, but in the presence of population stratification we observed mild inflation of the type I error rate, which ranged from .0534 to .0718 after PC-based corrections. For all analyses, the most conservative control of type I error was typically obtained with genomic control, with one exception (Supplementary Table III).
Table II.
Type I error rate and power for analysis of a continuous trait, by method of correction for population stratification
| Rate of type I error |
Power |
|||
|---|---|---|---|---|
| Correction method | No population stratification | Stratification present | No population Stratification | stratification present |
| No correction | 0.0364 | 0.2690 | 0.964 | --- |
| Race included as covariate | 0.0344 | 0.0344 | 0.963 | 0.963 |
| GC | 0.0116 | 0 | 0.908 | 0.662 |
| PCgwas | 0.0348 | 0.0326 | 0.879 | 0.871 |
| PCGWAS_TW | 0.0340 | 0.0322 | 0.962 | 0.951 |
| PCunpruned | 0.0466 | 0.0478 | 0.885 | 0.860 |
| PCr2<0.25 | 0.0464 | 0.0514 | 0.888 | 0.861 |
| PCr2<0.1 | 0.0448 | 0.0500 | 0.893 | 0.857 |
| PC0bp | 0.0418 | 0.0412 | 0.832 | 0.828 |
| PC1bp | 0.0380 | 0.0374 | 0.880 | 0.858 |
| PC2bp | 0.0390 | 0.0376 | 0.887 | 0.852 |
| PC5bp | 0.0382 | 0.0436 | 0.888 | 0.856 |
| PC10bp | 0.0404 | 0.0430 | 0.893 | 0.860 |
| PC50bp | 0.0496 | 0.0462 | 0.894 | 0.869 |
| PC100bp | 0.0464 | 0.0450 | 0.884 | 0.860 |
| SVA | 0.0460 | 0.0506 | 0.881 | 0.839 |
Table III.
Type I error rate and power for analysis of a dichotomous trait, by method of correction for population stratification
| Rate of type I error |
Power |
|||
|---|---|---|---|---|
| Correction method | No population stratification | Stratification present | No population stratification | Stratification present |
| No correction | 0.0304 | 0.1354 | 0.948 | --- |
| Race included as covariate | 0.0290 | 0.0692 | 0.945 | 0.885 |
| GC | 0.0084 | 0.0488 | 0.903 | 0.801 |
| PCgwas | 0.0304 | 0.0534 | 0.869 | 0.794 |
| PCGWAS_TW | 0.0290 | 0.0712 | 0.946 | 0.883 |
| PCunpruned | 0.0402 | 0.0694 | 0.880 | 0.802 |
| PCr2<0.25 | 0.0370 | 0.0704 | 0.885 | 0.807 |
| PCr2<0.1 | 0.0356 | 0.0676 | 0.885 | 0.800 |
| PC0bp | 0.0398 | 0.0650 | 0.840 | 0.749 |
| PC1bp | 0.0392 | 0.0678 | 0.871 | 0.789 |
| PC2bp | 0.0398 | 0.0708 | 0.874 | 0.792 |
| PC5bp | 0.0410 | 0.0708 | 0.875 | 0.795 |
| PC10bp | 0.0392 | 0.0718 | 0.880 | 0.797 |
| PC50bp | 0.0390 | 0.0700 | 0.884 | 0.804 |
| PC100bp | 0.0382 | 0.0718 | 0.883 | 0.806 |
| SVA | 0.0358 | 0.0794 | 0.790 | 0.689 |
Results from the power simulations are presented in the third and fourth columns of Table II, Supplementary Table III and Table III. The most powerful approaches in all cases were those that added only one additional covariate to the model (PCGWAS_TW and inclusion of race as a covariate, with power ranging from 0.883 - 0.963, though we note that power cannot be directly compared across the different models presented in the three tables). Compared to these single-covariate approaches, adjustments involving the inclusion of 10 principal components showed somewhat lower power that ranged from 0.832 - 0.894 when no population stratification was present, and from 0.749 - 0.871 in the presence of population stratification. Among the adjustments based on 10 PCs, the correlation-based pruning approaches that led to the largest reduction in race-associated sites in Table I (PCunpruned, PCr2<0.25 and PCr2<0.1) were among the most powerful methylation-based approaches when population stratification was present, but some of the location-based pruning approaches performed as well or better. Interestingly, PCs based on CpG sites within ≤10bp of SNPs were among the less powerful approaches, which is surprising given the associations with race demonstrated by these sets of PCs (Supplementary Table II). We generally observed slightly lower power for surrogate variable analysis than for the PC-based methods. Finally, the genomic control method performed well when there was no population stratification, but in the presence of stratification it performed the worst of all methods considered for continuous traits, with 0.662 power to detect an association in Table II and power of .656 in Supplementary Table III.
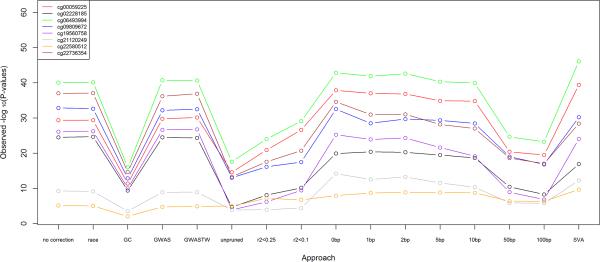
We next attempted to replicate the top eight methylation-age associations reported by Teschendorff et al. [Teschendorff, et al. 2010]. Figure 2 shows that for all eight CpG sites, we successfully replicated the association with age in our data. Interestingly, correction with PCs based on larger sets of CpG sites (PCr2<0.25, PCr2<0.1, PCunpruned, PC50bp, PC100bp) led to the least significant results in the replicated age-association results (Figure 2). This may be due to the greater association of these principal components with age (Supplementary Table II). While genotype data is static, DNA methylation is dynamic and it is thus likely that its principal components may vary with dynamic traits like age, as demonstrated in Supplementary Table II. In contrast, adjustment via principal components based on genetic variants (PCGWAS, PCGWAS_TW) or proxies for genetic variants within ≤10bp (PC0bp, ..., PC10bp) led to stronger age-methylation associations, which makes sense given that genetic variation is independent of age and those sets of PCs are less associated with age than the other sets of methylation-based PCs (Supplementary Table II). SVA also led to stronger associations, which makes sense given its goal to account for unmeasured factors that are independent of the variable of interest [Leek, et al. 2012; Leek and Storey 2007]. Finally, genomic control appeared to perform poorly in this context, likely because the large inflation factor (λGC=3.07) was in part due to a widespread genomic pattern of association between age and methylation. Notably, the inflation factor remained large even after correcting for population stratification with GWAS-based principal components (λGC=3.13), suggesting that the observed inflation was indeed due to factors other than population stratification, and that genomic control may not be an appropriate correction in this case.
Figure 2. Replication of aging results.
Replication of the top eight CpG sites associated with aging [Teschendorff, et al. 2010], using 16 different approaches to adjust for population stratification.
Because cell type heterogeneity is a potential confounder between methylation and age, we refit the above models including covariates for estimated cell type proportions, as described in Methods. Supplementary Figure 1 compares the –log10 p-values for cell-type-corrected analyses vs. unadjusted analyses, and Supplementary Figure 2 summarizes the associations with age after cell type adjustment. Notably, for all eight CpG sites the associations with age become more significant upon adjustment for cell type for the models not adjusted for population stratification (“no correction”) or those adjusted via GWAS or inclusion of race as a covariate. For the models adjusted for population stratification with methylation-based PCs, the pattern is less consistent, and it is important to note that here we have introduced a large amount of collinearity to the model through the inclusion of both estimated cell type proportions and the top ten methylation PCs. Supplementary Table II demonstrates extremely high correlation between estimated cell type proportions and the top methylation-based PCs; thus, by including the top 10 PCs in the model we are already adjusting for cell type to some extent. In Supplementary Figure 1, adjustment for population stratification via SVA or PCs based on CpG sites within ≤10 bp of a SNP typically yields cell-type-unadjusted p-values that are similar to the cell-type-adjusted p-values for the “no correction” or GWAS-based approaches, suggesting that these approaches may do the best job of accounting for cellular heterogeneity as well as population stratification.
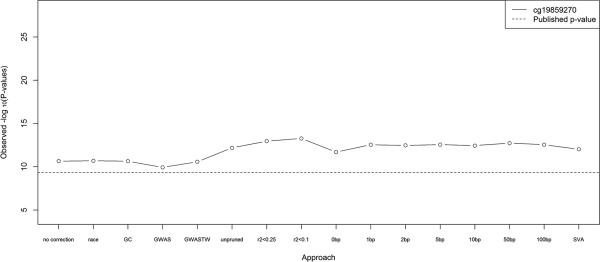
We next attempted to replicate a previously reported association between methylation and smoking [Breitling, et al. 2012; Breitling, et al. 2011; Shenker, et al. 2013; Sun, et al. 2013; Wan, et al. 2012]. This result has already been replicated in the African-Americans in our dataset with available smoking data (N = 239; [Sun, et al. 2013]), but as a proof-of-principle we re-performed the analysis including individuals self-reporting as Caucasian, mixed race, and other (N = 255). Comparing to the replication results from Sun et al. [Sun, et al. 2013] (Figure 3, dotted line), we observe stronger associations between smoking and cg19859270 regardless of which method is used to adjust for population stratification. This may result partially from the slight increase in sample size, but notably there was not much increase in significance when no correction for population stratification was performed (leftmost point on Figure 3). Upon adjustment for cell type proportions, results were similar for the methods based on GWAS PCs, inclusion of race as a covariate, or no correction, but less significant when methylation-based PCs were included; as above, this is consistent with high collinearity between estimated cell type proportions and methylation-based PCs.
Figure 3. Replication of smoking results.
Replication of the top CpG site associated with smoking in [Breitling, et al. 2012; Breitling, et al. 2011; Shenker, et al. 2013; Sun, et al. 2013; Wan, et al. 2012], using 16 different approaches to adjust for population stratification. The dotted line indicates the p-value from a previous replication based on 239 African Americans from our sample [Sun, et al. 2013].
In contrast to the age replication, in the methylation-smoking analysis all of the methylation-based PC methods led to more significant associations than the GWAS-based PC methods (Figure 3). Adjustment for population stratification via PCr2<0.1 led to the most significant association between cg19859270 and smoking (p=5.3×10−14), followed by the PC methods using correlation-based pruning. The difference between Figures 2 and 3 is consistent with the idea that unlike GWAS-based principal components, the top ten methylation-based principal components pick up some age-associated methylation (10−26 < p < 10−7, Supplementary Table II), and their inclusion as covariates can thus reduce power to detect association with age. Sets of principal components that are based on CpG sites close to SNPs may be better proxies for genetic variation and thus somewhat less associated with age (as demonstrated in Supplementary Table II), and methods such as SVA will avoid this issue entirely; this is consistent with the pattern shown in Figure 2. In contrast, because only a few CpG sites associate with smoking, the principal components do not proxy for association between methylation and smoking (p>.005 for all PCs tested); in this case all of the methylation-based principal-component based methods perform similarly well, as in Figure 3. Similarly, adjustment via genomic control led to somewhat reduced significance in the smoking analysis (Figure 3), but not the large reduction observed in the age analysis (Figure 2); this is likely because thousands of CpG sites across the genome have been shown to associate with age [Alisch, et al. 2012; Christensen, et al. 2009; Numata, et al. 2012; Rakyan, et al. 2010; Teschendorff, et al. 2010], while only a handful have been associated with smoking [Breitling, et al. 2012; Breitling, et al. 2011; Shenker, et al. 2013; Sun, et al. 2013; Wan, et al. 2012].
Discussion
Our study is the first to address population stratification in studies of DNA methylation and to propose and compare approaches to correct for population stratification. When adjusting for population stratification, an important distinction between classic GWAS and genome-wide studies of DNA methylation is that the top principal components of methylation data generally proxy for many factors beyond ancestry, including technical artifacts such as batch effects, cell type heterogeneity, and sample age. Thus, adjustment with methylation-based PCs typically requires the inclusion of a greater number of PCs and may potentially lead to power loss if the principal components from DNA methylation proxy for the variables of interest, as exemplified in the replication of methylation-age associations in Figure 2. However, sample age is a confounder rather than a variable of interest in most studies, as are cellular heterogeneity and technical factors. Thus, the ability of principal components approaches and SVA to proxy for these factors in addition to ancestry can generally be considered an advantage of such methods. Cellular composition is in a sense an analogous problem to population stratification: just as individual genetic background reflects a mixture of different ancestries, individual blood samples reflect a mixture of different cell types. The association of both race and estimated cell type proportions with top methylation PCs (Supplementary Table II) does suggest that methylation-based approaches could adjust for both of these factors at once. Our analyses in Supplementary Figures 1-3 suggested that methylation-based PC and SVA approaches do adjust for cellular heterogeneity to some extent, and that including both the estimated cell type proportions and the top ten principal components in the same model may lead to collinearity and reduced power. However, our study was designed to focus on population stratification, and our results do not provide sufficient evidence to assess whether these methods will fully control for other confounding factors such as cellular heterogeneity; further work will be needed to address this interesting problem.
Our proposed approach to compute the principal components of sets of CpG sites near SNPs can help narrow the focus to variation in methylation that reflects genetic variation and compute PCs that are better proxies for ancestry. Restricting to CpG sites within 0-50 bp of genetic variants will enrich for CpG sites that may proxy for genetic variation due to the possibility of a SNP influencing probe binding specificity, rather than those that proxy for genetic variation due to the influence of mQTLs. Given inter-tissue differences in methylation patterns [e.g. Byun, et al. 2009], and emerging evidence that mQTLs and eQTLs are in part tissue-specific [Nica, et al. 2011; Smith et al. 2013], computation of principal components based on sets of CpG sites within 50 bp of SNPs may provide an adjustment strategy that is robust regardless of what tissue type is studied. Another advantage of this approach is its computational simplicity compared to pruning based on correlation. To facilitate the use of this approach by other groups, we have made available our lists of CpG sites from the Illumina 450K that are located within 0-100bp of 1000 Genomes Project variants with minor allele frequency>.01, along with R code to compute the principal components (http://genetics.emory.edu/conneely). Variations of this approach such as focusing on CpG sites near ancestry informative markers could also be useful, although this approach would require knowledge about the underlying populations potentially driving stratification as well as pre-identified set of thousands of ancestry-informative markers.
In conclusion, we have proposed and made available a simple approach to adjust for population stratification in studies of DNA methylation that does not require the collection of SNP genotype data. Potential limitations of our study included the focus on two self-reported race categories and the small number of Caucasians in our data, and future studies should seek to generalize our results in larger samples from other populations. However, even with this limited dataset we have demonstrated the potential of population stratification to inflate type I error rates in DNA methylation association studies. Our simulations show that our approach appropriately effectively removes this inflation while remaining nearly as powerful as using the top principal components from genome-wide SNP data, thus providing an effective way to adjust for population stratification in DNA methylation studies when genome-wide SNP data are unavailable.
Supplementary Material
Acknowledgments
This work was primarily supported by National Institutes of Mental Health (MH071537 and MH096764). Epigenotyping was supported in part by the Max-Planck Society, and we thank Anne Löschner for excellent technical assistance. Salary support was provided by MH085806 (for AKS) and HG007508 (for MPE and RD). Simulations were performed on Emory's high-powered computing cluster, which is supported by the National Center for Advancing Translational Sciences of the National Institutes of Health under Award UL1TR000454. We would also like to thank the participants who made this work possible, as well as the staff of the Grady Trauma Project. Finally, we thank two anonymous reviewers whose comments have led to substantial improvements in our manuscript.
References
- 1000 Genomes Project Consortium AG. Altshuler D, Auton A, Brooks LD, Durbin RM, Gibbs RA, Hurles ME, McVean GA. A map of human genome variation from population-scale sequencing. Nature. 2010;467(7319):1061–73. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adkins RM, Krushkal J, Tylavsky FA, Thomas F. Racial differences in gene-specific DNA methylation levels are present at birth. Birth Defects Res A Clin Mol Teratol. 2011;91(8):728–36. doi: 10.1002/bdra.20770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alisch RS, Barwick BG, Chopra P, Myrick LK, Satten GA, Conneely KN, Warren ST. Age-associated DNA methylation in pediatric populations. Genome research. 2012;22(4):623–32. doi: 10.1101/gr.125187.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacanu SA, Devlin B, Roeder K. The power of genomic control. Am J Hum Genet. 2000;66(6):1933–44. doi: 10.1086/302929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barfield RT, Kilaru V, Smith AK, Conneely KN. CpGassoc: an R function for analysis of DNA methylation microarray data. Bioinformatics. 2012 doi: 10.1093/bioinformatics/bts124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell JT, Pai AA, Pickrell JK, Gaffney DJ, Pique-Regi R, Degner JF, Gilad Y, Pritchard JK. DNA methylation patterns associate with genetic and gene expression variation in HapMap cell lines. Genome Biol. 2011;12(1):R10. doi: 10.1186/gb-2011-12-1-r10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995;57(1):289–300. [Google Scholar]
- Boks MP, Derks EM, Weisenberger DJ, Strengman E, Janson E, Sommer IE, Kahn RS, Ophoff RA. The relationship of DNA methylation with age, gender and genotype in twins and healthy controls. PLoS One. 2009;4(8):e6767. doi: 10.1371/journal.pone.0006767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breitling LP, Salzmann K, Rothenbacher D, Burwinkel B, Brenner H. Smoking, F2RL3 methylation, and prognosis in stable coronary heart disease. European heart journal. 2012;33(22):2841–8. doi: 10.1093/eurheartj/ehs091. [DOI] [PubMed] [Google Scholar]
- Breitling LP, Yang R, Korn B, Burwinkel B, Brenner H. Tobacco-smoking-related differential DNA methylation: 27K discovery and replication. American journal of human genetics. 2011;88(4):450–7. doi: 10.1016/j.ajhg.2011.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buja AEN. Remarks on parallel analysis. Multivariate Behavioral Research. 1992;27:509–540. doi: 10.1207/s15327906mbr2704_2. [DOI] [PubMed] [Google Scholar]
- Byun HM, Siegmund KD, Pan F, Weisenberger DJ, Kanel G, Laird PW, Yang AS. Epigenetic profiling of somatic tissues from human autopsy specimens identifies tissue- and individual-specific DNA methylation patterns. Human molecular genetics. 2009;18(24):4808–17. doi: 10.1093/hmg/ddp445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Edwards AW. Phylogenetic analysis. Models and estimation procedures. Am J Hum Genet. 1967;19(3 Pt 1):233–57. [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Menozzi P, Piazza A. The history and geography of human genes. Princeton University Press; Princeton, N.J.: 1994. [Google Scholar]
- Christensen BC, Houseman EA, Marsit CJ, Zheng S, Wrensch MR, Wiemels JL, Nelson HH, Karagas MR, Padbury JF, Bueno R. Aging and environmental exposures alter tissue-specific DNA methylation dependent upon CpG island context. PLoS genetics. 2009;5(8):e1000602. doi: 10.1371/journal.pgen.1000602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cicek MS, Koestler DC, Fridley BL, Kalli KR, Armasu SM, Larson MC, Wang C, Winham SJ, Vierkant RA, Rider DN. Epigenome-wide ovarian cancer analysis identifies a methylation profile differentiating clear-cell histology with epigenetic silencing of the HERG K+ channel. Human molecular genetics. 2013;22(15):3038–47. doi: 10.1093/hmg/ddt160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coit P, Jeffries M, Altorok N, Dozmorov MG, Koelsch KA, Wren JD, Merrill JT, McCune WJ, Sawalha AH. Genome-wide DNA methylation study suggests epigenetic accessibility and transcriptional poising of interferon-regulated genes in naive CD4+ T cells from lupus patients. Journal of autoimmunity. 2013;43:78–84. doi: 10.1016/j.jaut.2013.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55(4):997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K, Bacanu SA. Unbiased methods for population-based association studies. Genet Epidemiol. 2001a;21(4):273–84. doi: 10.1002/gepi.1034. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K, Wasserman L. Genomic control, a new approach to genetic-based association studies. Theoretical population biology. 2001b;60(3):155–66. doi: 10.1006/tpbi.2001.1542. [DOI] [PubMed] [Google Scholar]
- Du P, Zhang X, Huang CC, Jafari N, Kibbe WA, Hou L, Lin SM. Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC bioinformatics. 2010;11:587. doi: 10.1186/1471-2105-11-587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie CF, Bradley B, Mercer K, Smith AK, Conneely K, Gapen M, Weiss T, Schwartz AC, Cubells JF, Ressler KJ. Trauma exposure and stress-related disorders in inner city primary care patients. General hospital psychiatry. 2009;31(6):505–14. doi: 10.1016/j.genhosppsych.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heijmans BT, Kremer D, Tobi EW, Boomsma DI, Slagboom PE. Heritable rather than age-related environmental and stochastic factors dominate variation in DNA methylation of the human IGF2/H19 locus. Hum Mol Genet. 2007;16(5):547–54. doi: 10.1093/hmg/ddm010. [DOI] [PubMed] [Google Scholar]
- Heyn H, Moran S, Hernando-Herraez I, Sayols S, Gomez A, Sandoval J, Monk D, Hata K, Marques-Bonet T, Wang L. DNA methylation contributes to natural human variation. Genome research. 2013;23:1363–1372. doi: 10.1101/gr.154187.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6(2):65–70. [Google Scholar]
- Houseman EA, Accomando WP, Koestler DC, Christensen BC, Marsit CJ, Nelson HH, Wiencke JK, Kelsey KT. DNA methylation arrays as surrogate measures of cell mixture distribution. BMC bioinformatics. 2012;13:86. doi: 10.1186/1471-2105-13-86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerkel K, Spadola A, Yuan E, Kosek J, Jiang L, Hod E, Li K, Murty VV, Schupf N, Vilain E. Genomic surveys by methylation-sensitive SNP analysis identify sequence-dependent allele-specific DNA methylation. Nat Genet. 2008;40(7):904–8. doi: 10.1038/ng.174. [DOI] [PubMed] [Google Scholar]
- Kwabi-Addo B, Wang S, Chung W, Jelinek J, Patierno SR, Wang BD, Andrawis R, Lee NH, Apprey V, Issa JP. Identification of differentially methylated genes in normal prostate tissues from African American and Caucasian men. Clin Cancer Res. 2010;16(14):3539–47. doi: 10.1158/1078-0432.CCR-09-3342. [DOI] [PubMed] [Google Scholar]
- Leek JT, Johnson WE, Parker HS, Jaffe AE, Storey JD. The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics. 2012;28(6):882–3. doi: 10.1093/bioinformatics/bts034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Storey JD. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 2007;3(9):1724–35. doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Storey JD. A general framework for multiple testing dependence. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(48):18718–23. doi: 10.1073/pnas.0808709105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Hutchison K, Perrone-Bizzozero N, Morgan M, Sui J, Calhoun V. Identification of genetic and epigenetic marks involved in population structure. PLoS One. 2010;5(10):e13209. doi: 10.1371/journal.pone.0013209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nica AC, Parts L, Glass D, Nisbet J, Barrett A, Sekowska M, Travers M, Potter S, Grundberg E, Small K. The architecture of gene regulatory variation across multiple human tissues: the MuTHER study. PLoS genetics. 2011;7(2):e1002003. doi: 10.1371/journal.pgen.1002003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen DA, Hamon S, Yuferov V, Jackson C, Ho A, Ott J, Kreek MJ. Ethnic diversity of DNA methylation in the OPRM1 promoter region in lymphocytes of heroin addicts. Hum Genet. 2010;127(6):639–49. doi: 10.1007/s00439-010-0807-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numata S, Ye T, Hyde TM, Guitart-Navarro X, Tao R, Wininger M, Colantuoni C, Weinberger DR, Kleinman JE, Lipska BK. DNA methylation signatures in development and aging of the human prefrontal cortex. American journal of human genetics. 2012;90(2):260–72. doi: 10.1016/j.ajhg.2011.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genet. 2006;2(12):e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pembrey ME, Bygren LO, Kaati G, Edvinsson S, Northstone K, Sjostrom M, Golding J. Sex-specific, male-line transgenerational responses in humans. Eur J Hum Genet. 2006;14(2):159–66. doi: 10.1038/sj.ejhg.5201538. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–9. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–75. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakyan VK, Down TA, Maslau S, Andrew T, Yang TP, Beyan H, Whittaker P, McCann OT, Finer S, Valdes AM. Human aging-associated DNA hypermethylation occurs preferentially at bivalent chromatin domains. Genome research. 2010;20(4):434–9. doi: 10.1101/gr.103101.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinius LE, Acevedo N, Joerink M, Pershagen G, Dahlen SE, Greco D, Soderhall C, Scheynius A, Kere J. Differential DNA methylation in purified human blood cells: implications for cell lineage and studies on disease susceptibility. PLoS One. 2012;7(7):e41361. doi: 10.1371/journal.pone.0041361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards EJ. Population epigenetics. Curr Opin Genet Dev. 2008;18(2):221–6. doi: 10.1016/j.gde.2008.01.014. [DOI] [PubMed] [Google Scholar]
- Schalkwyk LC, Meaburn EL, Smith R, Dempster EL, Jeffries AR, Davies MN, Plomin R, Mill J. Allelic skewing of DNA methylation is widespread across the genome. Am J Hum Genet. 2010;86(2):196–212. doi: 10.1016/j.ajhg.2010.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selamat SA, Chung BS, Girard L, Zhang W, Zhang Y, Campan M, Siegmund KD, Koss MN, Hagen JA, Lam WL. Genome-scale analysis of DNA methylation in lung adenocarcinoma and integration with mRNA expression. Genome research. 2012;22(7):1197–211. doi: 10.1101/gr.132662.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shenker NS, Polidoro S, van Veldhoven K, Sacerdote C, Ricceri F, Birrell MA, Belvisi MG, Brown R, Vineis P, Flanagan JM. Epigenome-wide association study in the European Prospective Investigation into Cancer and Nutrition (EPIC-Turin) identifies novel genetic loci associated with smoking. Human molecular genetics. 2013;22(5):843–51. doi: 10.1093/hmg/dds488. [DOI] [PubMed] [Google Scholar]
- Smith AKKV, Almli LM, Mercer KB, Ressler KJ, Tylavsky FA, Conneely KN. Methylation quantitative trait loci (meQTLs) are consistently detected across ancestry, developmental stage, and tissue type. 2013. Submitted manuscript. [DOI] [PMC free article] [PubMed]
- Sun YV, Smith AK, Conneely KN, Chang Q, Li W, Lazarus A, Smith JA, Almli LM, Binder EB, Klengel T. Epigenomic association analysis identifies smoking-related DNA methylation sites in African Americans. Human genetics. 2013 doi: 10.1007/s00439-013-1311-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terry MB, Ferris JS, Pilsner R, Flom JD, Tehranifar P, Santella RM, Gamble MV, Susser E. Genomic DNA methylation among women in a multiethnic New York City birth cohort. Cancer Epidemiol Biomarkers Prev. 2008;17(9):2306–10. doi: 10.1158/1055-9965.EPI-08-0312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teschendorff AE, Menon U, Gentry-Maharaj A, Ramus SJ, Weisenberger DJ, Shen H, Campan M, Noushmehr H, Bell CG, Maxwell AP. Age-dependent DNA methylation of genes that are suppressed in stem cells is a hallmark of cancer. Genome Res. 2010;20(4):440–6. doi: 10.1101/gr.103606.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap 3 Consortium. Altshuler DM, Gibbs RA, Peltonen L, Dermitzakis E, Schaffner SF, Yu F, Bonnen PE, de Bakker PI, Deloukas P. Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467(7311):52–8. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan ES, Qiu W, Baccarelli A, Carey VJ, Bacherman H, Rennard SI, Agusti A, Anderson W, Lomas DA, Demeo DL. Cigarette smoking behaviors and time since quitting are associated with differential DNA methylation across the human genome. Human molecular genetics. 2012;21(13):3073–82. doi: 10.1093/hmg/dds135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong CC, Meaburn EL, Ronald A, Price TS, Jeffries AR, Schalkwyk LC, Plomin R, Mill J. Methylomic analysis of monozygotic twins discordant for autism spectrum disorder and related behavioural traits. Molecular psychiatry. 2013 doi: 10.1038/mp.2013.41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Cheng L, Badner JA, Chen C, Chen Q, Luo W, Craig DW, Redman M, Gershon ES, Liu C. Genetic control of individual differences in gene-specific methylation in human brain. Am J Hum Genet. 2010;86(3):411–9. doi: 10.1016/j.ajhg.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.