Point Process Models show Temporal Dependencies of Basal Ganglia Nuclei under Deep Brain Stimulation

Abstract

Deep Brain Stimulation (DBS) is an effective treatment for patients with Parkinsons disease, but its impact on basal ganglia nuclei is not fully understood. DBS applied to the subthalamic nucleus (STN) affects neurons in the Globus Pallidus pars interna (GPi) through direct projections, as well as indirectly through the Globus Pallidus pars externa (GPe). Since traditional statistical analyses of electrophysiological data provide too coarse a view of circuit dynamics, and mesoscopic biophysical dynamic models contain an intractable number of state variables for small populations of neurons, we apply a modular approach and treat each region in the STN-GPe-GPi circuit as a multi-input multi-output point process system. We use microelectrode recordings of a normal primate with DBS applied to STN at 100 and 130 Hz to estimate point process models (PPMs) for recorded regions in GPi. Our PPMs uncovered distinct dependencies between regions of GPe and GPi neurons, separated by the position of the GPi neurons, and showed normal refractory periods, inhibition from projecting neurons in the GPe, and DBS-induced oscillatory effects. The PPMs also showed the relative impact of the above factors, which traditional statistics fail to capture. Our PPM framework suggests a useful approach for understanding dynamics of complex neural circuits.

I. INTRODUCTION

Parkinons disease (PD) is a chronic progressive neurological disorder affecting an estimated 6.5 million people world-wide, with no treatment to stop disease progression. The symptoms, namely tremor, rigidity, and bradykinesia, are aided by a highly promising therapy: deep brain stimulation (DBS). An electrode is surgically implanted sub-cortically and wired to a battery-powered electrical stimulator in order to postoperatively deliver periodic trains of electrical pulses. When appropriately stimulated, patients can regain control of movements. The electrode is implanted in the basal ganglia (BG), a set of sub-cortical nuclei involved in multiple segregated parallel loops (e.g., limbic, prefrontal, motor loop) that modulate cortical activity [1]. Although clinically effective, and despite a growing number of applications [2], [3], the exact effect of the stimulation is still not fully understood, since the neurons in these areas are densely connected in an excitatory and inhibitory manner. This gives rise to a multitude of interrelated outcomes in the cortex [4]. It is important to better understand the effects of DBS to further fine-tune stimulation applied to the basal ganglia, thus leading to more effective therapeutic outcomes. In PD patients, DBS is typically delivered to the subthalamic nucleus (STN), which directly affects the Globus Pallidus pars interna (GPi), one of the output nuclei of the basal ganglia. The effects of STN DBS on GPi mainly stem from direct activation of the subthalamo-pallidal projections, which are both excitatory in nature (direct projection) as well as inhibitory via the Globus Pallidus pars externa (GPe) [1], as seen in Fig.1. The relative impact of these two pathways, however, is still not fully understood. Microelectrode exploration has enabled the collection of large amounts of electrophysiological data in PD patients and primates from the basal ganglia [5], [6], [7], [8]. However, this data is not sufficient to support biophysically detailed modeling of the neural circuits composing BG nuclei [7], [9], [10], forcing neuroscientists to compute first and second-order statistics (eg. rastograms, histograms, power spectra) [8], [11]. Instead, we use a modular approach, treating each nuclear region within the BG as a multi-input, multi-output stochastic system. Probability distributions describing temporal dependencies of neurons in each system are estimated from primate data. The estimated probability distributions parameters also help uncover strengths of interconnections between nuclei. We focus on the STN-GPe-GPi circuit and model each recorded region within the GPi as a point process system whose spike train outputs are influenced by two inputs: the DBS signal applied to STN and the activity from projecting GPe neurons. This can be visualized in Fig.1. A point process model (PPM) generalizes the spike-rate of a Poisson process to one that is time-varying, history dependent, and can characterize the relative contribution of intrinsic factors (e.g. spike history effects of projecting nuclei) and extrinsic factors (e.g. DBS signal) on the probability that a neuron will spike at any given time [12]. Each GPi PPM captures aggregate information about neural activity in the GPi system as it specifies one spike-rate function applicable to all neurons in it. This implies that the stochastic nature of these neurons is governed by the same probability distribution. PPMs provide a way to incorporate the inherent dynamic nature and temporal dependencies in the activity of neurons while under DBS. In this paper, we concentrate on the effect of DBS on the GPi neurons, since these are the neurons that directly project to the thalamus and thus have a more immediate impact on the cortex [1]. Our PPMs gave us information about the connections between neurons in different positions of the GPi and GPe. The PPMs built on these groups of neurons showed us the oscillations and spiking patterns seen by traditional methods of analysis, in addition to quantifying the impact of the GPe neurons and the DBS signal on the dynamics of GPi neurons. Identification of refractory behavior, inhibition due to GPe neurons at a latency of 4–6 ms, and an excitation due to the DBS signal was made using our models.

Fig. 1.

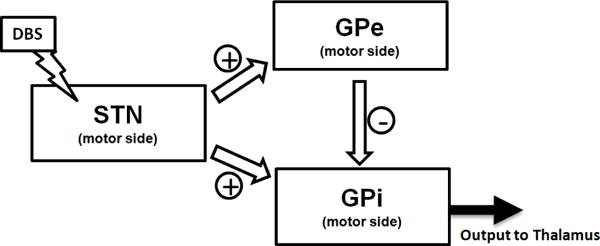
The different pathways for the effects from STN to reach GPi neurons

II. METHODS

A. Data Collection

Recordings from one non-human primate were used in this study. The animal was awake and trained to limit itself to passive movements. Details about surgical procedures and data collection are in [5]. Briefly, the primate (macaca mulatta) was implanted with a recording chamber and received a constant current biphasic square pulse stimulation in the STN via a reduced scale model of the human DBS lead. Stimulation frequencies were 100 and 130 Hz. Microelectrode recordings were alternatively obtained from different sites in the motor side of GPe and GPi during STN DBS (positions later confirmed by histological examination). During each recording session, continuous recordings of neuronal activity were made during 30s under stimulation. Only neurons with an average spiking rate 10 Hz before stimulation were included in this study (Table I).

TABLE I.

Experimental Set Up

Nucleus	Recording Site Label	Frequency	Number of Neurons	Number of Sessions
GPi	p1d1	130Hz	2	6
		100Hz	1	3
	p1d2	130Hz	1	3
		100Hz	2	8
	p1d3	130Hz	1	3
GPe	p1d2	130Hz	3	11
		100Hz	2	6
	p1d1	130Hz	4	15
		100Hz	4	13
	p2d2	130Hz	1	3
	p1d3	130Hz	1	3

B. Point Process Models

Point process methods have been used in the past to analyze the spike train activity for a broad range of neural systems [12], [13], [14]. We formulated point process models to relate the spiking propensity of GPi neurons in each recording site to their own spiking history, the spiking history of the neurons in the GPe sites, and the DBS pattern. We used the model parameters to analyze oscillations and modulations of the GPi spiking due to the DBS signal and the activity of GPe neurons. A neural spike train may be treated as a point process, i.e., a series of random binary events that occur continuously in time [12], [14]. In this case, the 1s correspond to the individual spike times and the 0s are the times at which no spikes occur. A PPM of a neural spike train is completely characterized by considering an observation interval (0,T] and defining its conditional intensity function (CIF), λ(t|H_t):

$$\lambda (t|H_t)=\underset{\mathrm{\Delta }\to 0}{\lim }\frac{P(N(t+\mathrm{\Delta })-N(t)=1|H_t)}{\mathrm{\Delta }},$$ (1)

where N(t) is the number of spikes counted in interval (0,t] for t in (0,T], H_t the history of spikes up to time t, and P the probability [15], [16]. When Δ is small, It follows from (1) that the probability of a single spike in (t,t +Δ] is approximately λ(t|H_t)Δ, which gives the spiking propensity at time t. The CIF generalizes the rate function of a Poisson process to a rate function that is history dependent. Because the CIF completely characterizes a spike train, defining a model for the CIF defines a model for the spike train [17], [18]. For our analyses, we defined one CIF model for each group of GPi neurons (i.e., neurons recorded in the same site under the same stimulation settings) by using generalized linear models (GLM) [19]. The GLM is an extension of the multiple linear regression model in which the variable being predicted, in this case spike times, need not be Gaussian [19]. GLM also provides an efficient computational scheme for model parameter estimation and a likelihood framework for conducting statistical inferences [17]. Instead of estimating the CIF continuously throughout the entire trial, we estimated it at discrete time intervals, each a millisecond in length, for a duration of 30 seconds. Specifically, for each millisecond bin, k, we modeled the CIF for GPi neurons as follows:

$$\log (\lambda (k|H_k))=\alpha +{{\displaystyle \sum }}_{r=1}^T{\beta }_r^{\mathit{\text{GPi}}}{\mathit{dN}}_{k-r}^{\mathit{\text{GPi}}}+{{\displaystyle \sum }}_{j=1}^T{\beta }_j^{\mathit{\text{GPe}}}{\mathit{dN}}_{k-j}^{\mathit{\text{GPe}}}+{{\displaystyle \sum }}_{h=1}^T{\gamma }_h{\mathit{dN}}_{k-h}^{\mathit{\text{DBS}}},$$ (2)

where T is the time window (equivalent to the inter pulse interval in this study, i.e., 10 ms for 100Hz DBS and 8ms for 130Hz DBS), ${\mathit{dN}}_a^b$ the number of spikes observed in the interval [a,a + 1) (in ms) at nucleus b, and ${\mathit{dN}}_a^{\mathit{\text{DBS}}}$ the number of DBS pulses delivered in the same interval. The vector of parameters $\theta =[\alpha ,{\{{\beta }_r^{\mathit{\text{GPi}}}\}}_{r=1}^T,{\{{\beta }_j^{\mathit{\text{GPi}}}\}}_{j=1}^T,{\{{\gamma }_h\}}_{h=1}^T]$ was estimated by maximizing the likelihood of observing the recorded spike trains from GPe and GPi, and quantifies spiking history effects of both groups of neurons on the propensity that neurons in the GPi site will spike. Specifically, α accounts for the history-independent activity of each neuron, β^GPis measure the effect of the neurons own spiking history, β^GPes measure the effect of the spiking of the GPe neurons, and γs measure the time-varying effect of the DBS signal. Establishing the degree of agreement between a point process model and observations of the spike train and associated experimental variables is a prerequisite for using the point process analysis to make scientific inferences. 80% of spike trains were used for model parameter fitting and the last 20% for validation. We used Kolmogorov-Smirov (KS) plots based on the time-rescaling theorem [20] to plot the empirical cumulative distribution function of the transformed spike times versus the cumulative distribution function of a unit rate exponential in order to assess goodness-of-fit for each model. The model is better if its corresponding KS plot lies near the 45 degree line.

C. Connections between Groups of Neurons

Rather than relying on functional models of the basal ganglia loop, we used the data available to uncover the most influential dependencies between groups of GPe and GPi neurons. Specifically, we used PPMs to systematically identify the most significant dependencies between GPe and GPi, i.e., the physiological connections. However, we did not have the data to relate this to anatomical connections in the basal ganglia. We considered 4 groups of neurons in GPe and 3 in GPi (Table 1), separated on the basis of their recording sites (Fig.2A). For each group, we concatenated all spike trains according to several randomized concatenation sequences. For each sequence of concatenated spike trains in GPi, taking as its input each sequence in GPe, we estimated a PPM of the form (2). All the computed vectors of PPM parameters were then collected and segmented via K-means clustering [21]. Silhouette coefficients were computed for each cluster point to measure the intra-cluster homogeneity and cluster-to-cluster heterogeneity [22]. Only clusters with three or more vectors with a silhouette coefficient 0.7 were considered as valid, and new point process models were built based on the information provided by these. A population model taking as inputs spike trains from all the neurons in the GPe and modeling the spiking activity of all the neurons in GPi was also constructed for comparison purposes. The Akaikes criterion (AIC), which is 2*(number of parameters -log likelihood of model), is useful to analyze the efficiency of a likelihood model [23]. When comparing two models with the same number of parameters, a lower AIC value indicates an increase in the likelihood of the model [12]. The AIC number was compared between the population model and the clustered model to gage the increase in efficiency obtained after clustering.

Fig. 2.

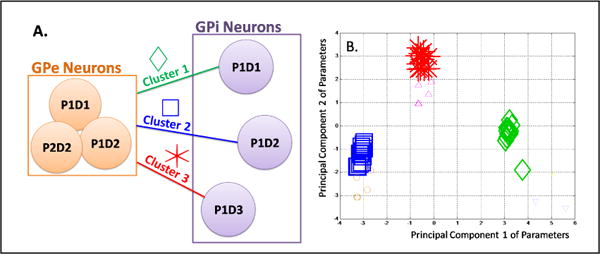
Clustering Analysis. (A) Schematic Diagram of the dependencies between sites in GPe and GPi; (B) Principal Components of the parameter vectors for 100Hz stimulation frequency.

III. RESULTS

PPMs were estimated from data collected over 80 sessions on 15 neurons from different sites in GPe and GPi.

A. Connections between Groups of Neurons

Three strong clusters emerged that mapped connections from all GPe groups to each GPi group, as shown in Fig.2A,B. The factor that separates the clusters is the site of the GPi group, i.e., the same activity by a group of GPe neurons affects each of the GPi neurons differently. This remained consistent for both DBS frequencies 100 and 130Hz. A possible explanation for that comes from the architecture of GPi and GPe: GPi is smaller than GPe in primates, with highly segregated pathways and several projections from GPe. GPe projections have a highly patterned set of collaterals which result in a multifarious effect on the target cells in GPi [24]. The impact of the GPe activity depends therefore on the actual conditions of the target neurons in the GPi. This is also confirmed by the analysis of the parameters of the PPMs (see III-B). The AIC values of the clustered models are also seen to decrease when compared to models estimated from all the GPe and GPi neurons, which suggests an increase in the likelihood of the model as compared to the observed data using the clustered PPMs (for ex. the AIC value is 2344.1 for the population model as opposed to an average of 1604.8 for the clustered models under 100 Hz DBS).

B. Point Process Models

As we just demonstrated, the clustering of PPM parameters is useful for analyzing the most influential connections between the different positions in connected nuclei. Furthermore, the point process models based on these connections increase in precision. Here, we highlight two PPMs fitted on data recorded in the same GPi site under 130 Hz (Fig.3A) and 100 Hz (Fig.3C) DBS respectively. In both cases, we plot the optimal maximum likelihood estimates of each models parameters (bold lines) along with their 95% confidence bounds (shaded regions). The goodness-of-fit of the PPMs is confirmed by the KS-plots (Fig.3B, E), which are within their 95% confidence bounds. The first row plots the single e^α parameter (around 11Hz) with its confidence bounds. The ${\beta }_r^{\mathit{\text{GPi}}}$ estimates (whose exponentials are depicted in Fig.3A, second row, from right to left) show the dependency of GPi spiking propensity on the GPis own history. They suggest that the GPi neurons have a refractory period between 1–6 msec and a prominent oscillation at the stimulation frequency. The peak at ${\beta }_8^{\mathit{\text{GPi}}}$, indeed, suggests that at any time t, the propensity to spike of a GPi neuron is significantly modulated up (factor of 4) if it spiked 8 ms prior to t. The ${\beta }_j^{\mathit{\text{GPe}}}$ parameters (whose exponentials are depicted in Fig.3A, third row) suggest that the neurons in the GPe site have an inhibitory effect on GPi neurons with a delay of approximately 5 ms (minimum for j=5 and ${\mathrm{e}}^{{\beta }_5^{\text{GPe}}}<1$). We also see a slight excitation around j = 7,8 $({\mathrm{e}}^{{\beta }_{7,8}^{\text{GPe}}}>1.5)$ which means that the GPi spiking propensity increases if neurons in the GPe site fired 7–8 ms prior to t, probably showing rebound activity of the GPi neurons. The effect of the DBS stimulation can either appear in the GPi’s own history parameters $({\beta }_r^{\mathit{\text{GPi}}})$, or the DBS signal parameters (γ_h). This can be seen as an indication of the level of entrainment of the neurons to that frequency, i.e. if the stimulation effect is seen in the ${\beta }_r^{\mathit{\text{GPi}}}$ parameters, as in the case of a 130 Hz stimulation frequency, this suggests that the DBS mainly works by fully entraining the GPi neurons in oscillations at the stimulation frequency. This observation is further strengthened by the low value of the γ_h estimates (the exponentials of which are depicted in Fig.3A, fourth row). For the case of 100 Hz stimulation frequency (Fig.3D), DBS modulates the spike propensity of the GPi neurons in a more complicated way. In particular, the propensity of the GPi neurons to spike dramatically increases (e^γ5 > 2.5) at a lag of 5ms after the DBS signal and there is a lack of excitatory influence by the ${\beta }_r^{\mathit{\text{GPi}}}$ parameters, suggesting that neurons being stimulated at lower frequencies are not fully entrained to the stimulation. The refractory behavior of the neurons is seen in the ${\beta }_r^{\mathit{\text{GPi}}}$ parameters, which show inhibition at delays of 1, 2, 4 and 6 ms. A minimal impact is seen by the GPe spiking activity (low values of the ${\beta }_j^{\mathit{\text{GPe}}}$ parameters in Fig.3D), which is mainly due to the dominant role of the GPi’s own history and DBS pattern. It could, however, also be a result of the alignment of a possible GPe inhibition with the DBS excitation. We also see a slight decrease in the parameter α with the stimulation frequency (e^α = 11 Hz for 130 Hz DBS, e^α = 9.5 Hz in case of 100 Hz DBS). The temporal dependencies shown by analyzing the PPM parameters are also consistent with traditional statistics. The Peri Stimulus Time Histograms (PSTHs) in Fig.3C,F confirm that GPi neurons at both frequencies are in effect being stimulated by the DBS. In the case of the stimulation at 130 Hz, the effect of this stimulation masks the effect of the GPe inhibition in the PSTH. However, this effect is uncovered in the GPe covariates as seen in Fig.3A.

Fig. 3.

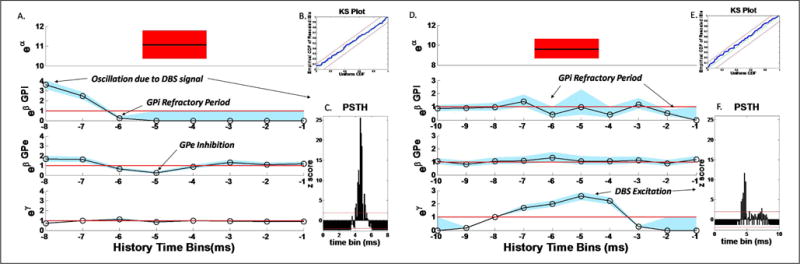
PPM of the group of GPi neurons recorded in site p1d1. Parameters are estimated by using spike trains from the GPe neurons recorded in sites p1d1, p1d2 and p2d2 (where available) as history covariates. A, D) PPM parameters for 130Hz and 100Hz DBS respectively. B, E) KS plots for the PPMs with 95% confidence intervals for the models in A, D respectively. C, F) Z-scores of Peri Stimulus Time Histograms with 95% confidence intervals for the spiking of the GPi neurons used in the models A, D respectively.

IV. CONCLUSIONS AND FUTURE WORK

In this paper, we use a rare experimental setup and a point process modeling framework to investigate the physiological connections between different sites in the GPe and GPi. Our PPMs are consistent with classic statistical analyses. Furthermore, they show the relative impact of GPe spiking activity and DBS inputs on the GPi spiking propensity. Details on comparing PPMs to traditional statistics are given in [25]. We are currently extending our work by increasing the number of primates and neurons included in the study, and investigating the temporal dependencies between GPe and GPi in Parkinsonian-induced primates treated with 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP).