Measurement of the Time-Resolved Reflection Matrix for Enhancing Light Energy Delivery into a Scattering Medium

Abstract

Multiple scatterings occurring in a turbid medium attenuate the intensity of propagating waves. Here, we propose a method to efficiently deliver light energy to the desired target depth in a scattering medium. We measure the time-resolved reflection matrix of a scattering medium using coherent time-gated detection. From this matrix, we derive and experimentally implement an incident wave pattern that optimizes the detected signal corresponding to a specific arrival time. This leads to enhanced light delivery at the target depth. The proposed method will lay a foundation for efficient phototherapy and deep-tissue in vivo imaging in the near future.

Light propagation through disordered media is often treated as a statistical process in which photons diffuse in a random fashion. The wave nature of the light is clearly manifested, however, if it stays coherent during propagation and the structural variations of the medium are negligible over the transit time. Then it is possible to deterministically control the light propagation through disordered media, which even enables us to use the media as useful optical elements. In recent studies, two independent approaches have been introduced for exploiting disordered media as focusing and imaging elements. The first is based on a feedback mechanism where the intensity at a specific position and/or time located at the far side of a medium is maximized by controlling the incident wave front [1–4]. This method has been used to demonstrate point-to-point as well as extended object imaging across a turbid medium via point scanning and the so-called memory effect [5]. The second is recording a transmission matrix of a disordered medium, which relates the complex amplitudes of output free modes to those of input modes. With the transmission matrix, the input wave for a desired output can be determined and vice versa. It permits not only controlling the wave at the far side of the medium [6] but also transmitting extended object information [7–10] and enhanced energy delivery through the disordered media [11].

However, the preceding methods have generally been limited to the transmission geometry, where the signal should be measured at the opposite side of the illumination. This constraint has posed a fundamental limitation on their application to practical situations. For instance, medical applications such as in vivo imaging or phototherapy require reflection-mode detection. A technical advance is, therefore, needed to assess and control light scattering in the reflection geometry. Success in this regime has been limited so far, and only for mild turbidity. For example, by maximizing the fluorescence signal via wave front control, the focus is sharpened in two-photon microscopy for a weakly turbid medium [12]. Alternatively, in a recent study using optical phase conjugation and ultrasound modulation, the latter successfully generated a guide star inside a turbid medium [13,14]. Although the approach allowed fluorescence signal acquisition in reflection mode (with respect to the phase conjugated illumination), the original ultrasound modulated scattered light was collected and recorded in the transmission geometry. The imaging of a fluorescent object behind a thin disordered medium has also been demonstrated in reflection using the feedback approach and the memory effect [15]. However, this is not depth resolved unless it is coupled with confocal detection. We note that the recording of a scattering matrix in reflection can provide extensive information about a turbid medium similar to that in the transmission. In the past, the recording of a reflection matrix has been demonstrated in ultrasound imaging [16]. The possibility of a reflection matrix measurement in the optical regime has also been reported, but time-gated detection was not used [17].

In this Letter, we present the first experimental measurement of the time-resolved reflection matrix (TRRM) of a scattering medium in the optical regime. Unlike the transmission matrix, the TRRM describes the input-output response of a scattering medium at the same port generated by a laser source with low temporal coherence. Therefore, we can extract the response of the medium for a particular arrival time (at the detector) with respect to each input. This information is processed to find the combination of input channels that maximizes the backscattered waves at a specific arrival time. This is distinct from previous studies where feedback optimization was used [1–5]. By experimentally implementing this unique input wave, we have demonstrated enhanced light energy delivery within a scattering medium.

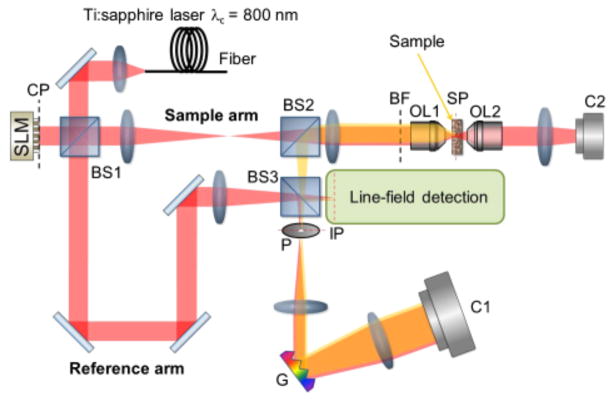
An experimental setup to record a sample’s TRRM is depicted in Fig. 1. A broadband laser with center wavelength λ_c = 800 nm and bandwidth Δλ = 16.7 nm (FWHM) is sampled by a beam splitter (BS1) and subsequently reflected by a spatial light modulator (SLM) operating in a phase-only control mode. The light is then transmitted through the BS1 again and illuminates a scattering medium via an objective lens (OL1). We prepared a scattering medium from Polydimethylsiloxane (PDMS) and 4.5 μm diameter polystyrene beads to be used as a test sample. The mean scattering free path of the sample l_c was measured as 35.9 ± 0.2 μm and the transport mean free path $l_c^{\prime }=394.3\pm 2.0\mu \mathrm{m}$, respectively. The measured sample thickness L was 376.6 μm corresponding to an average 2L/l_c = 21.0 scattering events ( $2L/l_c^{\prime }=1.41$ reduced scattering events) for light reflected from the farthest surface in the sample. The thickest sample used in the experiments had $2L/l_c^{\prime }=4.43$ [18]. The sample thickness is well beyond the ballistic regime. Instead, it is in a quasidiffusive regime ( $1<2L/l_c^{\prime }<10$) for which propagating waves retain only a weak memory of an incident wave [19]. The beam directly transmitted through BS1 is combined with the backscattered light from the sample at BS3 to serve as a reference beam. The interference is measured using a spectrometer comprised of a diffraction grating (G) and a line scan camera (C1). The measured spectral fringe pattern is Fourier transformed to acquire a time-resolved complex field, which carries both the amplitude and phase information of the returning light. The temporal resolution of the spectrometer is Δt = 20.3 fs with a total time span of 12.4 ps. A spatial degree of freedom is constrained by a pinhole (P, ϕ = 50 μm) at a plane conjugate to the sample plane. Thus, the system measures the space-constrained and time-resolved response of a turbid medium. We also implemented a time-resolved line-field detection setup at the second detection port of BS3 to monitor the 1D field distribution of the backscattered light from the sample [see Fig. 4(a) and [18]]. At the opposite side of the sample, an imaging system is positioned to observe the transmitted light through the sample.

FIG. 1.

(color online). Schematic of the coherent time-gated detection system. A line-field detection setup is attached at the second detection port of BS3. SLM: spatial light modulator, BSi: ith beam splitter, OL1 and OL2: objective lens (20X, 0.4NA), C2: 2D camera, P: pinhole, G: diffraction grating, C1: line scan camera (Basler, Sprint L2048-39km), BF: back focal plane of the objective lens OL1, CP: SLM plane conjugated to BF, SP: sample plane, IP: image plane conjugated to SP.

FIG. 4.

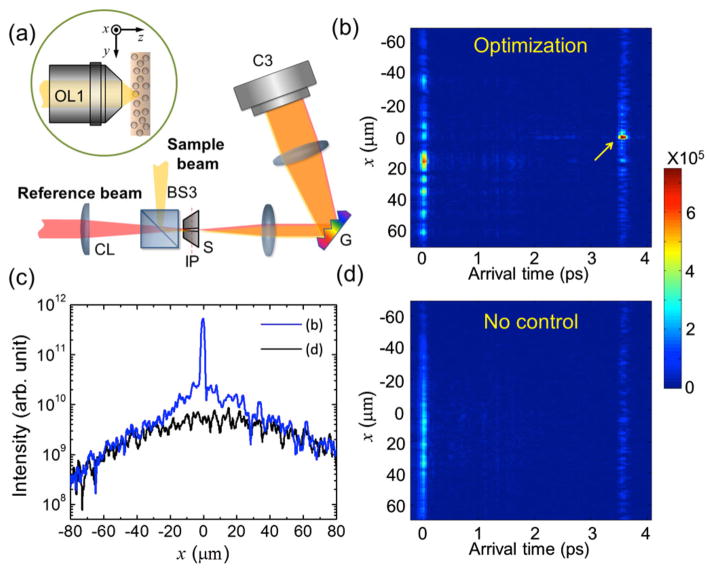
(color online). Spatiotemporal focusing of reflected wave. (a) Schematic of the 1D line-field detection setup. CL: cylindrical lens, S: slit, C3: 2D camera. Inset: spatial coordinates at the sample plane [18]. (b) Representative measured amplitude of the reflected light after optimization with N = 1600. (c) Ensemble averaged intensity profiles along the target arrival time τ = 3.6 ps in (b) and (d). (d) The same as (b), but before the optimization. Color bar: arbitrary units.

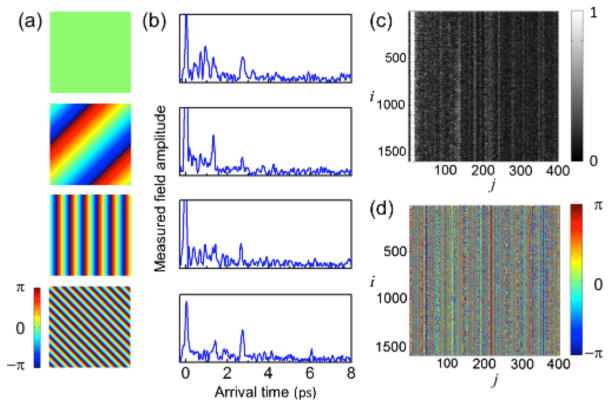
When measuring the sample’s TRRM, we need to transmit light into various independent input channels. Each channel is generated by writing a linear phase ramp on the SLM filling the back aperture of the objective lens. Each phase ramp generates a field E_in(k⃗_i) on the sample plane where k⃗_i is the wave vector for incident light and i the index of the phase ramp. To generate the TRRM, as shown in Fig. 2(a), we apply one phase ramp on the SLM and the measure complex amplitude of the backscattered signal [Fig. 2(b)]. Various arrival times in the time-gated measurements serve as independent detection channels. Next, the complex field is determined for another phase ramp in the set. After measuring reflected fields for all the phase ramps in the basis set, we construct the TRRM, r(k⃗_i, jΔt), where index j represents jth time bin. Figures 2(c) and 2(d) show the amplitude and phase of the measured TRRM.

FIG. 2.

(color online). Measurement of TRRM. (a) Representative phase ramps written on the SLM. (b) Time-resolved reflection amplitude from a turbid medium for each incident channel shown in (a). The arrival time is a round-trip delay of light. Reflection from the first surface of a turbid sample is set as 0. (c) Amplitude part of the constructed TRRM. Indices i and j represent incident channel (phase ramp) and detection channel (time bin), respectively. Color bar: arbitrary units. (d) Phase portion of the TRRM. Color bars: phase in radians.

The incident field that maximizes the backscattered wave at a specific arrival time, t₀ = j₀Δt, can be constructed by a superposition of input channels

$$E_{\text{opt}}(t_0)=\sum _{i=1}^N{a}_i(j_0\mathrm{\Delta }t)E_{\text{in}}(k_i),$$ (1)

where N is the total number of input channels. From the measured TRRM, we can determine the complex amplitude for ith phase ramp,

$$a_i(j_0\mathrm{\Delta }t)=r^{\ast }({\overrightarrow{k}}_i,j_0\mathrm{\Delta }t)/\sum _{i^{\prime }=1}^N{\mid r({\overrightarrow{k}}_{i^{\prime }},j_0\mathrm{\Delta }t)\mid }^2.$$ (2)

In Eq. (2), the denominator is a normalization factor for the conservation of input power. The optimization process aligns the complex phasors of backscattered waves for various input channels each multiplied by a complex weighting factor.

In order to realize this optimization, we implement a superposition of illumination channels satisfying Eq. (1). The insets in Figs. 3(a)–3(c) show the phase patterns applied to the incident light that maximize the backscattered signal at the arrival times indicated as dashed lines in respective figures. Only the phase distribution of the complex superposition is generated with a flat amplitude profile since the SLM is in a phase-only control mode. The blue lines in Figs. 3(a)–3(c) represent the measured reflection signal. Compared with a single channel illumination with no wave front control (black lines), the amplitude is dramatically increased at the target arrival times. When N = 1000, the maximum achievable enhancement of the reflected energy is 335 at the target arrival time and position.

FIG. 3.

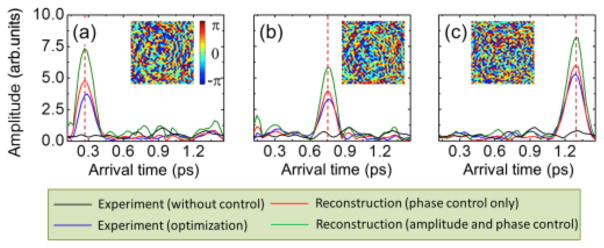
(color online). Optimization of reflected wave at a target arrival time. (a)–(c) Reflected light signals after optimization with N = 1000 for arrival times of (a) 0.27 ps, (b) 0.75 ps, and (c) 1.28 ps, respectively. Insets are phase patterns for optimization. Color bar: phase in radians.

For assessing the accuracy of the optimization, we estimate the reflected wave from the TRRM. For the input wave given by Eqs. (1) and (2), which optimizes the intensity at t₀ = j₀Δt, the backscattered wave at an arbitrary t = jΔt is calculated. The green lines in Fig. 3 show the expected reflected waves, the signals we can obtain if we implemented both amplitude and phase patterns. Therefore, the potential enhancement is higher than that achieved in our experiment. To account for the effect of the phase-only control, we eliminated the amplitude component and used only the phase component of the input wave for calculating the output wave. In doing so, we determined the expected reflected wave for the phase-only control (red lines). The expected signal is now very similar to that observed experimentally. We also investigated the enhanced amplitude at a fixed target arrival time as a function of N, and it is in good agreement with the TRRM reconstruction, especially that using phase-only control [18].

Next, we explore the field distribution of backscattered light from the turbid medium before and after the optimization. The experimental schematic is depicted in Fig. 4(a). After recording the TRRM using 1600 input channels, we chose a specific time bin corresponding to the direct flight to the back surface of the turbid medium, and performed the optimization for the selected time bin. We then measured the time-resolved complex field at the image plane [IP, dashed line in Fig. 4(a)] along the line including the target point using the separate line-field detection setup. The time-resolved reflected waves measured at 15 different positions are averaged to achieve an ensemble average of various realizations of the turbid medium (with the same thickness and scattering properties). Figure 4(b) shows one of the representative amplitude profiles of the backscattered wave from the sample. The optimized spot is clearly visible at the target arrival time (τ = 3.6 ps) and the corresponding pinhole location (x = 0 μm). This result illustrates the spatiotemporal focusing of the returning wave at the pinhole location. For comparison, we applied a flat pattern on the SLM and measured the backscattered wave along the line [Fig. 4(d)] and confirmed that the optimized spot had disappeared. The spatial line profile of the ensemble averaged intensity distribution at the target arrival time is plotted in Fig. 4(c). The peak intensity after the optimization is about 2 orders of magnitude higher than that before the optimization. Moreover, the observed intensity in the region surrounding the target position also increases to a certain extent as well. This background intensity augmentation is known as an effect of single-channel optimization [20]. Furthermore, when we calculate the energy of the reflected light at the target arrival time by assuming the azimuthal symmetry of scattered waves, we observe a 41% increment in reflected energy after the optimization. This indicates the optimization process delivers more light energy to the target arrival time. One important implication of this observation is that the optimization process can enhance light energy delivery to the sample depth associated with the target arrival time. This is most feasible for a medium in a quasidiffusive regime because the arrival time is directly linked to the depth at which light is reflected to a certain extent.

In order to unambiguously support our claim that the optimization of reflected wave corresponding to a specific arrival time enhances light energy delivered to the associated depth, we measure transmitted energy at the far side of the turbid medium after the optimization. The experimental schematic is shown in Fig. 5(a). After optimizing the backscattered wave at the arrival time corresponding to the back surface of the sample, the energy enhancement (η_tr), defined as the ratio of net increased transmission energy after the optimization to the transmission energy under no control, is obtained as a function of N [Fig. 5(b)]. The enhancement increases up to about 20% as N is increased. Since the back surface of the sample serves as a partial reflector, the transmitted energy is proportional to the amount of light delivered to that surface. Therefore, the increase in measured transmission confirms the enhanced energy delivery to the target depth.

FIG. 5.

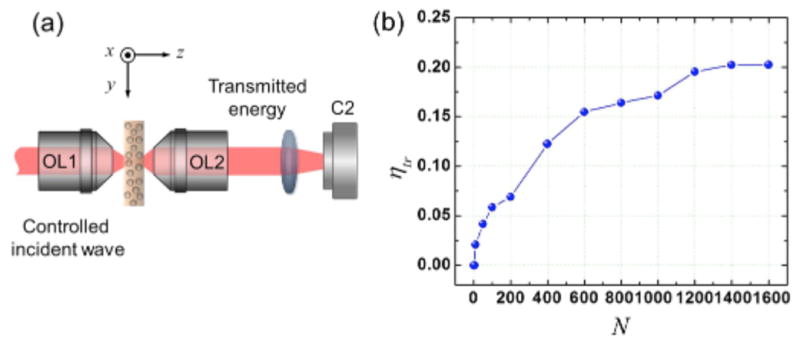
(color online). Transmission enhancement. (a) Experimental schematic. Transmitted energy is measured before and after optimization. (b) The transmission energy enhancement is measured after the optimization as a function of N. It is equal to about half of the reflection enhancement.

For experimental verification, we repeated the same experiment with several samples of different thickness and scattering properties. The number of reduced scattering events, $2L/l_c^{\prime }$, ranges between 0.44 and 4.43, covering ballistic to quasidiffusive regimes. We found that the measured enhancement depends on the sample thickness. For example, with the thinnest sample ( $2L/l_c^{\prime }=0.44$) the reflection enhancement at the target arrival time and the corresponding transmission enhancement were measured to be 100% and 41%, respectively, the best experimental demonstration reported so far (see Fig. S4 in [18]). The enhancement values can be further improved if more input channels are used with improved accuracy for wave front shaping. In an ideal condition where the full solid angle of input channels is covered, our theoretical model predicts more than a fourfold increase in the energy delivery. As the thickness of samples increases, the light energy delivery becomes less efficient [18]. We observed the transmission enhancement till $2L/l_c^{\prime }$ is increased to 4.43, but with a reduced enhancement factor (see more details in [18]). As the sample thickness is increased to several times the transport mean free path, the correlation between arrival time and sample depth is diminished. This limits the effectiveness of our approach. In addition to the nonbiological samples, we have also demonstrated the effectiveness of our method when applied to biological tissues [18]. This confirms that our technique can be extended to a wide range of disordered samples.

The enhancement of reflected energy at the target arrival time by the optimization can be understood by an analogy with the single-channel optimization in the transmission geometry [20,21]. In the transmission case, the optimization of intensity at a single point in the output plane enhances the total energy at the entire output plane. In the reflection configuration, as in our experiment, the optimization for a single point represented by a specific time bin enhances light energy delivered to the entire plane associated with the same time bin, which was evidenced in Fig. 4(c). Since the arrival time and the depth are related to a certain extent in the quasidiffusive regime, the enhancement of light waves with a particular time-of-flight will lead to the enhanced light energy delivery to the corresponding depth.

The single-channel optimization in reflection can be modeled as that of a double-transmission geometry where a fraction of the reflected waves with a specific arrival time can be considered that it travels through the same medium twice, in a forward direction and then a backward direction. As shown in Ref. [21], single-channel optimization in the transmission geometry leads to internal field enhancement of a turbid medium due to constructive interference. This means that the optical power at the center point of the double transmission geometry, corresponding to transmission at the far side of the scattering medium in our experiment, is expected to increase. We have extended random matrix theory to provide quantitative analysis for our experimental results using this double-transmission model (see more details in [18]).

In conclusion, we have measured the space-constrained and time-resolved reflection matrix of a scattering medium in the optical regime and made use of the matrix to experimentally optimize the backscattered wave in time and space. The optimization dramatically enhanced the magnitude of the reflected signal from the target depth, generating a strong spatiotemporal focused distribution. We have quantitatively shown that optimizing the reflected wave enhances delivered energy to the target arrival time and the corresponding depth inside a scattering medium. Since our technique employs a reflection configuration rather than a transmission geometry, it is highly relevant to advancing medical applications such as deep-tissue in vivo imaging [22–24] and efficient light delivery for photodynamic therapy.