An Allometric Relationship between the Genome Length and Virion Volume of Viruses

ABSTRACT

Virions vary in size by at least 4 orders of magnitude, yet the evolutionary forces responsible for this enormous diversity are unknown. We document a significant allometric relationship, with an exponent of approximately 1.5, between the genome length and virion volume of viruses and find that this relationship is not due to geometric constraints. Notably, this allometric relationship holds regardless of genomic nucleic acid, genome structure, or type of virion architecture and therefore represents a powerful scaling law. In contrast, no such relationship is observed at the scale of individual genes. Similarly, after adjusting for genome length, no association is observed between virion volume and the number of proteins, ruling out protein number as the explanation for the relationship between genome and virion sizes. Such a fundamental allometric relationship not only sheds light on the constraints to virus evolution, in that increases in virion size but not necessarily structure are associated with concomitant increases in genome size, but also implies that virion sizes in nature can be broadly predicted from genome sequence data alone.

IMPORTANCE Viruses vary dramatically in both genome and virion sizes, but the factors responsible for this diversity are uncertain. Through a comparative and quantitative investigation of these two fundamental biological parameters across diverse viral taxa, we show that genome length and virion volume conform to a simple allometric scaling law. Notably, this allometric relationship holds regardless of the type of virus, including those with both RNA and DNA genomes, and encompasses viruses that exhibit more than 3 logs of genome size variation. Accordingly, this study helps to reveal the basic rules of virus design.

INTRODUCTION

Although they may superficially appear similar, viruses exhibit a diverse range of morphologies. Mature virus particles (virions) consist of either DNA or RNA molecules, a protein shell (capsid) that coats and protects this genomic nucleic acid, and in some cases an outer envelope that combines virally encoded proteins with lipids derived from the host cell membrane. Despite the similar structural and functional roles played by viral virions, they exhibit a remarkable diversity of forms, including icosahedral, filamentous, rod, and brick shapes. Such diversity is even apparent within smaller taxonomic groupings. For example, negative-sense single-stranded RNA (−ssRNA) viruses of the order Mononegavirales possess similar genome structures and are clearly related in phylogenies based on the RNA-dependent RNA polymerase, yet exhibit virion structures as diverse as bullet shaped, spherical, and filamentous. Virions also vary dramatically in size, whether they possess an envelope or not. For example, icosahedral virions vary in diameter from 17 to 400 nm, while filamentous virions vary in length from 650 to 1,950 nm (1). The evolutionary processes responsible for such a rich diversity of virion sizes are uncertain, but it is essential to understand both the forces that shape viral biodiversity and the evolutionary transition from simplicity to complexity.

As with their virions, viruses exhibit a wide diversity of genome sizes. RNA viruses possess genomes that are universally small, ranging from 1,682 nucleotides (nt) (hepatitis delta virus [Deltavirus]) to 31,526 nt (murine hepatitis virus [Coronaviridae]). In contrast, the genome sizes of DNA viruses range over 3 orders of magnitude, from only 1,758 nt (porcine circovirus [Circoviridae]) to 2,473,870 nt for the recently discovered Pandoravirus salinus (2), although all ssDNA viruses are small, possessing genomes that overlap in size with those of RNA viruses.

It has been suggested that virus genome sizes are constrained by the maximum size of the genetic material that can be packaged within a single virion (3), such that there is a fundamental relationship between genome and virion size. However, the opposite directionality, in which the optimal size of the virion is set by the size of the viral genome, was proposed following the experimental manipulation of genomes of cowpea chlorotic mottle virus (CCMV) (4) and through simulation by predicting the genome-capsid interaction of a number of RNA viruses, including CCMV (5, 6). Some experimental studies also suggest that virion sizes are a function of genome sizes. For example, an in vitro study of the self-assembly of virus-like particles formed by the CCMV capsid showed that packaging genomes of increasing size led to a concomitant increase in capsid size (7), a relationship also observed in experimental manipulations of infectious bursal disease virus (IBDV) (8). Irrespective of whether the evolution of genome size drives that of virion size, or vice versa, the exact relationship between these two fundamental biological parameters has not been quantified.

There are a variety of other factors that can influence the size of virus genomes and virions. For example, it has been proposed that the size of the icosahedral capsid of satellite bacteriophage P4 is not determined by its underlying genome size but rather by the interaction of the product of the size determination (sid) gene with helper phage P2 (9). Similarly, it is likely that biophysical factors, such as the net charge on the peptide arms of capsids, also influence virion size (10). In addition, it is possible that the small genome sizes of RNA viruses are determined in part by the necessity to replicate quickly, such that excessively long genomes are selected against, although this cannot easily explain the enormous range of genome sizes exhibited by double-stranded DNA (dsDNA) viruses that are also likely to be under selection to replicate rapidly (11). The requirement to unwind long regions of dsRNA during replication has likewise been proposed as a factor that caps the sizes of RNA virus genomes (12) and which may have been in part overcome by the evolution of a distinct helicase domain (13).

Those studies undertaken to date have provided only case-specific, qualitative and often contradictory insights into the relationship between genome and virion sizes, without a full evolutionary perspective. However, understanding the nature of the evolutionary relationship between genome and virion sizes is of fundamental importance for revealing the factors that shape viral life history and because the similar structural architectures exhibited by some RNA and DNA viral proteins suggest that they share a deep common ancestry (14, 15). To explore the nature of the relationship between the genome and virion sizes of viruses in a more quantitative manner, we performed a statistical analysis of a diverse set of viruses representing much of the known biodiversity of the virosphere and observed a simple allometric relationship between genome and virion size.

MATERIALS AND METHODS

Virus data.

A total of 88 reference viruses with associated morphological and genomic data were indexed from the Eighth Report of the International Committee on Taxonomy of Viruses (1) and at ViralZone (http://viralzone.expasy.org/) (16) (see Table S1 in the supplemental material) or from the literature. Information on genome length and protein numbers for each viral genome was obtained using the NCBI Genome browser (http://www.ncbi.nlm.nih.gov/genome) (see Table S1) or from relevant publications. All viruses were grouped into six categories based on their genome structure: dsDNA (n = 33), ssDNA (n = 6), reverse-transcribing dsDNA (dsDNA-RT) and ssRNA-RT (n = 3), dsRNA (n = 8), negative-sense ssRNA (−ssRNA) (n = 4), and positive-sense ssRNA (+ssRNA) (n = 34). To understand the relationship between genome and virion sizes, we subdivided these viruses into the following categories: (i) spherical (most of which possess icosahedral virions [n = 65]) and nonspherical (brick, filamentous, ovoid, and rod [n = 23]), (ii) enveloped (n = 28) and nonenveloped (n = 60), (iii) those with linear (n = 77) and those with circular (n = 11) genomes, and (iii) dsDNA viruses (n = 33) and +ssRNA viruses (n = 34). For 13 additional viruses only a range of virion volumes were available. These viruses were excluded from the main analysis but used as a secondary, independent test of the allometric relationship observed (see Results).

Calculation of virion sizes.

The morphology of each virus was characterized using virion diameter (nm) and/or virion length (nm). Due to a lack of precise measurements of the edge length or radius that touches the icosahedron at all vertices, it was not possible to use the standard formula for icosahedron volume to precisely calculate the volume of icosahedral virions. Rather, because icosahedral particles are treated as spherical during electronic observation (1), we instead employed the formula for the calculation of spherical volumes. Accordingly, we calculated virion volume using the following formulae: (i) spherical (including icosahedral) viruses, V = 4/3 × πr³; (ii) ovoid (including lemon-shaped) viruses, V = 4/3 × πa²c; (iii) filamentous (rod) viruses, V = πr² × l; and (iv) brick viruses, h × d × l. In these formulae, V is the virion volume, r is the radius (i.e., semidiameter) of the sphere (or circle), a is the equatorial radius of the spheroid, c is the distance from center to pole along the symmetry axis, l is virion length, h is height, d is depth, and π is a constant. The virion volume for Pandoravirus salinus was taken from the relevant publication (2).

Statistical analysis.

We used a Spearman's rank test to test for the association between genome length and virion volume and linear regression to test for an association between the natural logarithm of genome length and the natural logarithm of virion volume. If a linear relationship exists between the logarithms of two variables, then it can be concluded that the two variables exhibit an allometric relationship with the regression coefficient equal to the power law exponent. For the comparison of medians between groups, we used the Mann-Whitney U test. Analysis of variance was used to test the significance of covariates in multiple linear regression. Because the interfamily evolutionary relationships of DNA and RNA viruses are usually obscure, with extreme distances impeding phylogenetic resolution, we were unable to formally take these into account during the statistical analysis. However, the fact that significant allometric relationships were obtained in all genome-scale comparisons and not in those undertaken at the gene level suggests that our results are not overly biased by any phylogenetic nonindependence in the data. The statistical analysis was performed in R v3.0.2.

RESULTS

Relationship between viral genome and virion sizes.

We calculated the virion sizes (volumes) of 88 viruses, chosen to be as representative as possible of known viral biodiversity (i.e., covering 50 viral families and unassigned taxa) and for which accurate data to calculate virion volumes were also available (1). These viruses were dsDNA (n = 33 viruses), ssDNA (n = 6), reverse-transcribing (RT) (n = 3), dsRNA (n = 8), negative-sense ssRNA (−ssRNA) (n = 4), and positive-sense ssRNA (+ssRNA) viruses (n = 34). These data are summarized in Table 1 and presented fully in Table S1 in the supplemental material. We calculated virion volumes using a number of common structural parameters—namely virion diameter, distance from center to pole, length, height, and depth (1, 16)—or used the volume reported in the original publication.

TABLE 1.

Summary of the viral morphological data utilized in this study

Family or genus	Envelope	Virion type	Virion vol (nm3)	Genome length (kb)
dsDNA viruses
Myoviridae	No	Icosahedral	1.1 × 105–4.3 × 105	33.6–132.6
Siphoviridae	No	Icosahedral	7.8 × 104–2.7 × 105	26.1–121.8
Podoviridae	No	Icosahedral	1.1 × 105–1.8 × 105	39.9–70.2
Corticoviridae	Yes	Icosahedral	9.1 × 104	10.1
Lipothrixviridae	Yes	Filamentous	4.1 × 105–8.8 × 105	20.9–40.9
Poxviridae	Yes	Brick or ovoid	1.0 × 107–1.8 × 107	134.7–288.5
Iridoviridae	Yes	Icosahedral	1.8 × 106–3.1 × 106	105.9–191.1
Adenoviridae	No	Icosahedral	3.8 × 105	35.9
Polyomaviridae	No	Icosahedral	4.8 × 104	5.2
Papillomaviridae	No	Icosahedral	8.7 × 104	7.9
Mimiviridae	No	Icosahedral	3.3 × 107	1,181.6
Pandoravirusa	Yes	Ovoid	7.5 × 107	2,473.9
Salterprovirusa	Yes	Ovoid	8.7 × 104	14.5
ssDNA viruses
Inoviridae	No	Rod	2.7 × 104–7.7 × 104	5.8–7.4
Microviridae	No	Icosahedral	1.4 × 104	5.4
Parvoviridae	No	Icosahedral	5.6 × 103	5.9
Circoviridae	No	Icosahedral	2.6 × 103–8.2 × 103	1.8–2.3
Reverse-transcribing DNA and RNA viruses
Hepadnaviridae	Yes	Icosahedral	3.9 × 104	3.2
Caulimoviridae	No	Icosahedral	6.5 × 104	8.0
Retroviridae	Yes	Spherical	5.2 × 105	13.3
dsRNA viruses
Cystoviridae	Yes	Icosahedral	3.2 × 105	13.4
Reoviridae	No	Icosahedral	6.5 × 104–1.2 × 105	23.2–24.7
Birnaviridae	No	Icosahedral	1.1 × 105	5.9
Totiviridae	No	Icosahedral	1.9 × 104–3.3 × 104	4.6–6.3
Partitiviridae	No	Icosahedral	1.4 × 104	3.7
Negative-sense ssRNA viruses
Filoviridae	Yes	Filamentous	3.3 × 106–4.0 × 106	19.0–19.1
Orthomyxoviridae	Yes	Spherical	5.2 × 105	13.6
Deltavirusa	Yes	Spherical	5.6 × 103	1.7
Positive-sense ssRNA viruses
Leviviridae	No	Icosahedral	9.2 × 103	3.6
Picornaviridae	No	Icosahedral	1.4 × 104	9.7
Marnaviridae	No	Icosahedral	8.2 × 103	8.6
Secoviridae	No	Icosahedral	1.4 × 104	12.2
Potyviridae	No	Filamentous	7.3 × 104–9.0 × 104	8.2–10.9
Caliciviridae	No	Icosahedral	2.2 × 104	7.4
Hepeviridae	No	Icosahedral	1.7 × 104	7.2
Astroviridae	No	Icosahedral	1.1 × 104	7.0
Nodaviridae	No	Icosahedral	1.7 × 104–2.7 × 104	4.5
Tetraviridae	No	Icosahedral	3.3 × 104	6.6
Luteoviridae	No	Icosahedral	6.3 × 103–8.1 × 103	5.7
Tombusviridae	No	Icosahedral	1.1 × 104–2.2 × 104	3.7–4.4
Coronaviridae	Yes	Spherical	9.0 × 105	26.7–31.4
Arteriviridae	Yes	Spherical	1.1 × 105	12.7
Flaviviridae	Yes	Spherical	6.5 × 104	9.7–10.9
Togaviridae	Yes	Spherical	1.8 × 105	11.7
Virgaviridae	No	Rod	7.6 × 104–1.5 × 105	6.4–10.4
Bromoviridae	No	Icosahedral	1.0 × 104–1.4 × 104	8.2–8.6
Tymoviridae	No	Icosahedral	1.4 × 104	6.32
Alphaflexiviridae	No	Filamentous	8.6 × 104–9.0 × 104	7.6–8.8
Sobemovirusa	No	Icosahedral	1.4 × 104	4.1
Idaeovirusa	No	Icosahedral	1.9 × 104	7.7

^aGenus unassigned to a family.

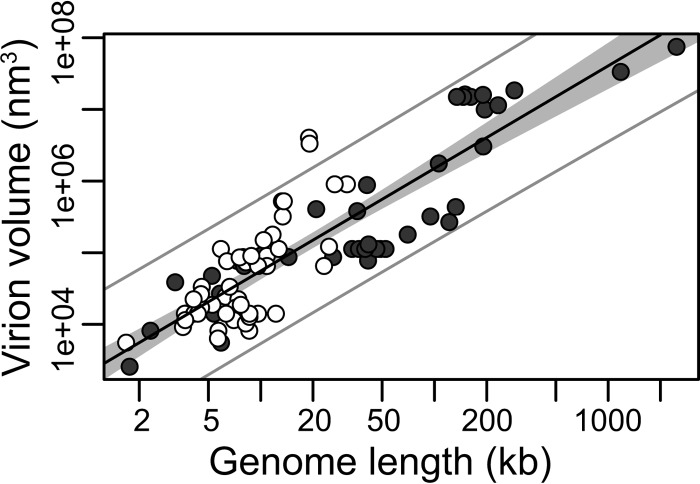
The virion volume of the viruses studied varied by 4 orders of magnitude (Table 1), with the smallest (2.6 × 10³ nm³) recorded in Circovirus (ssDNA virus) and the largest (7.53 × 10⁷ nm³) observed in Pandoravirus (dsDNA virus). The genome lengths of the viruses varied by approximately 3 orders of magnitude, with the smallest (1.68 kb) recorded in Deltavirus (−ssRNA virus) and the largest (2,473.87 kb) in Pandoravirus (dsDNA virus). Across the data set as a whole, we observed a significant positive correlation between genome length and virion volume (P < 0.001). Plotting this on a log-log scale showed a strong positive linear relationship, in which 76% of the variance in the logarithm of virion volume can be accounted for by the logarithm of genome length (P < 0.001, R² = 0.76, slope = 1.43) (Fig. 1). It is striking that all but two viruses—the filoviruses Ebolavirus and Marburgvirus—fall within the 95% prediction interval, which depicts where 95% of virion sizes are expected to lie within for a given genome size (outer gray lines on Fig. 1). Therefore, virion volume has an allometric relationship with genome length, with a mean exponent of 1.43 and with relatively tight confidence intervals (CI) (1.26 to 1.6) (Table 2). That this exponent is significantly greater than 1 (P < 0.001) indicates that an allometric relationship between volume and genome length is a better descriptor than a simple linear relationship. Importantly, the exponent is also significantly lower than 3 (P < 0.001), which is the value of the standard “geometric” relationship between length and volume (i.e., as the units for volume are the units of length to the third power). This indicates that the relationship is not just a product of physical space availability (17) (Table 2).

FIG 1.

Relationship between viral genome and virion sizes. The y axis shows virion sizes displayed as volume (nm³) on a log scale, while the x axis indicates genome length (kb) on a log scale. RNA viruses are shown by open circles and DNA viruses by closed circles. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

TABLE 2.

Allometric relationships between virion volume and genome length

Group	Allometric exponent (95% CI)	Scaling factor (95% CI)
All viruses	1.43 (1.26–1.6)	2,057 (1,185–3,571)
Enveloped	1.37 (1.14–1.6)	7,515 (2,969–19,024)
Nonenveloped	1.06 (0.88–1.23)	3,170 (1,977–5,082)
Linear	1.46 (1.27–1.66)	1,775 (917–3,435)
Circular	1.74 (1.12–2.36)	1,848 (675–5,057)
Spherical	1.17 (0.98–1.36)	2,785 (1,621–4,785)
Nonspherical	1.44 (1.19–1.69)	5,697 (2,088–15,545)
dsDNA	1.52 (1.16–1.87)	1,182 (246–5,675)
dsRNA	0.97 (−0.11–2.05)	6,760 (602–75,960)
Positive-sense ssRNA	1.95 (1.33–2.58)	596 (159–2,238)
Negative-sense ssRNA	2.58 (1.23–3.94)	1,314 (46–37,463)

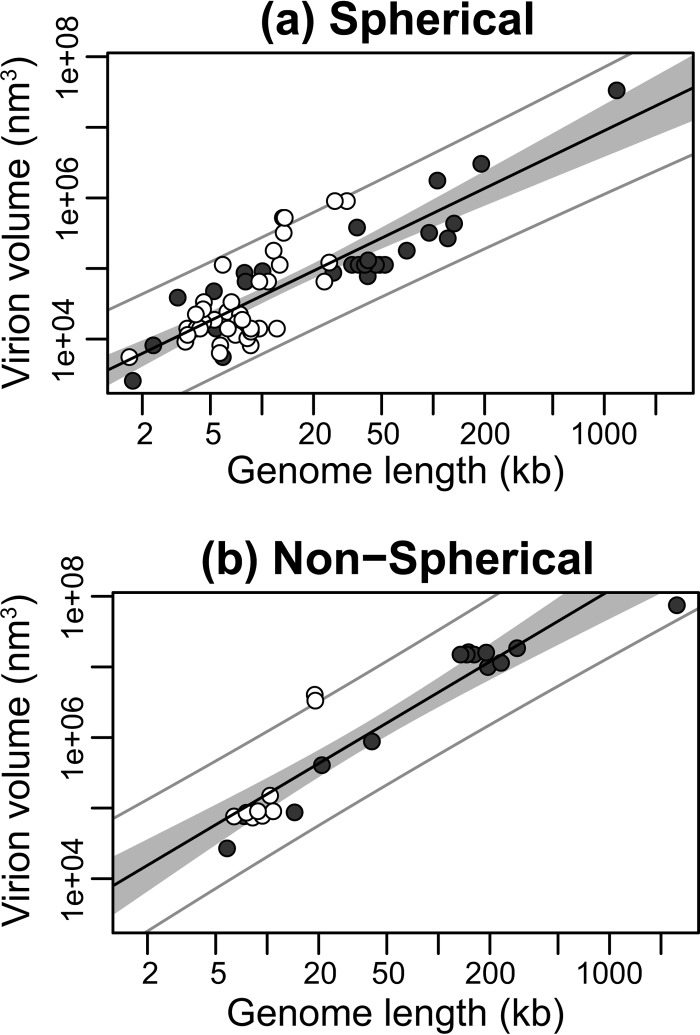
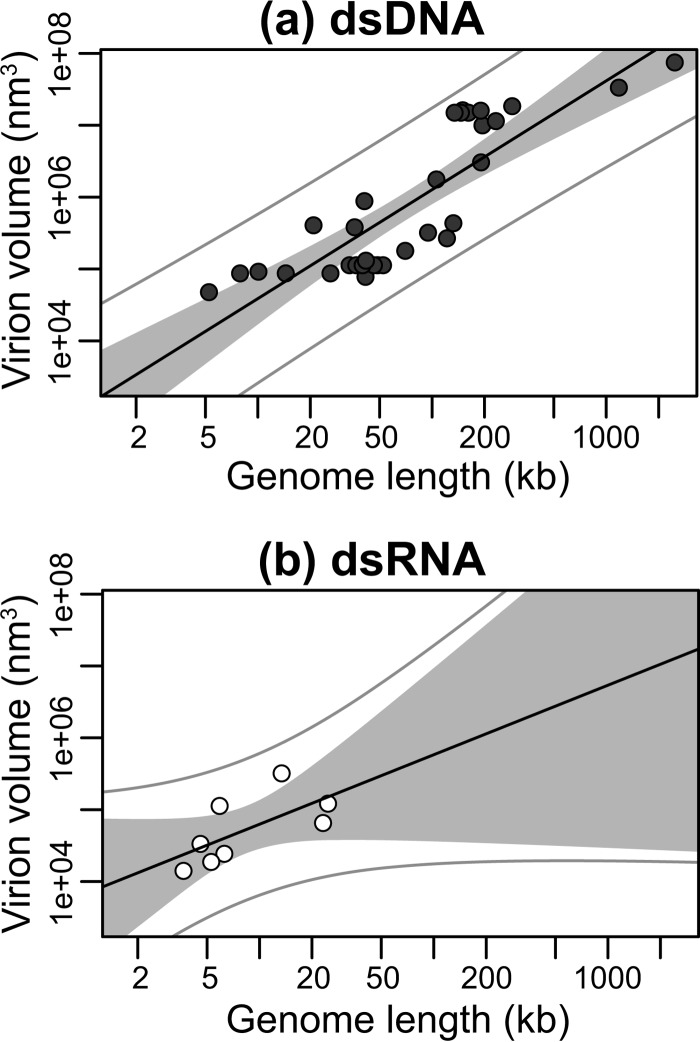
To determine whether the association between volume and genome length holds among viruses of profoundly different types and whether this association is also described by an allometric relationship, we subdivided our data into viruses with spherical (i.e., spherical and icosahedral [n = 65]) and nonspherical (brick, filamentous, ovoid, and rod [n = 23]) virions. Spherical viruses have a median virion volume that is significantly less than those of nonspherical viruses (median volumes, 6.5 × 10⁴ nm³ and 8.8 × 10⁵ nm³ for spherical and nonspherical virions, respectively; P < 0.001). In both groups there was a strong positive correlation between virion volume and genome length (P < 0.001), and the relationship was defined well by a power law. Specifically, the allometric regression results were as follows: spherical, R² = 0.71, P < 0.001, exponent = 1.17; and nonspherical, R² = 0.87, P < 0.001, exponent = 1.44 (Fig. 2; Table 2).

FIG 2.

Relationship between genome and virion sizes among spherical (a) and nonspherical (b) viruses. The y axis shows virion sizes calculated as volume (nm³) on a log scale, while the x axis shows genome length (kb) on a log scale. RNA viruses are shown by open circles and DNA viruses by closed circles. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

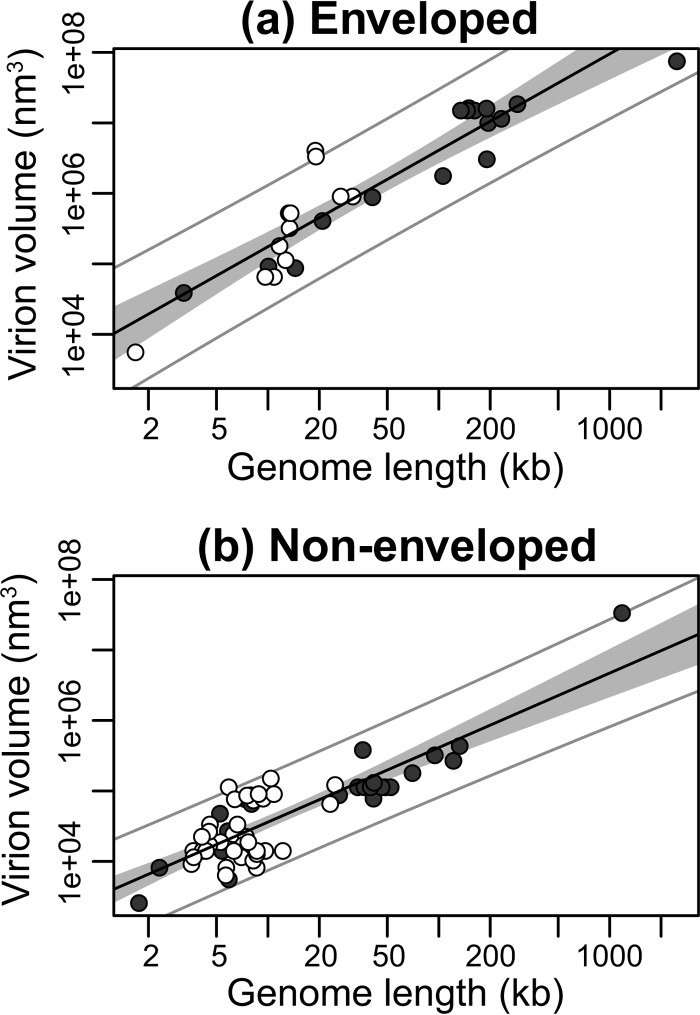
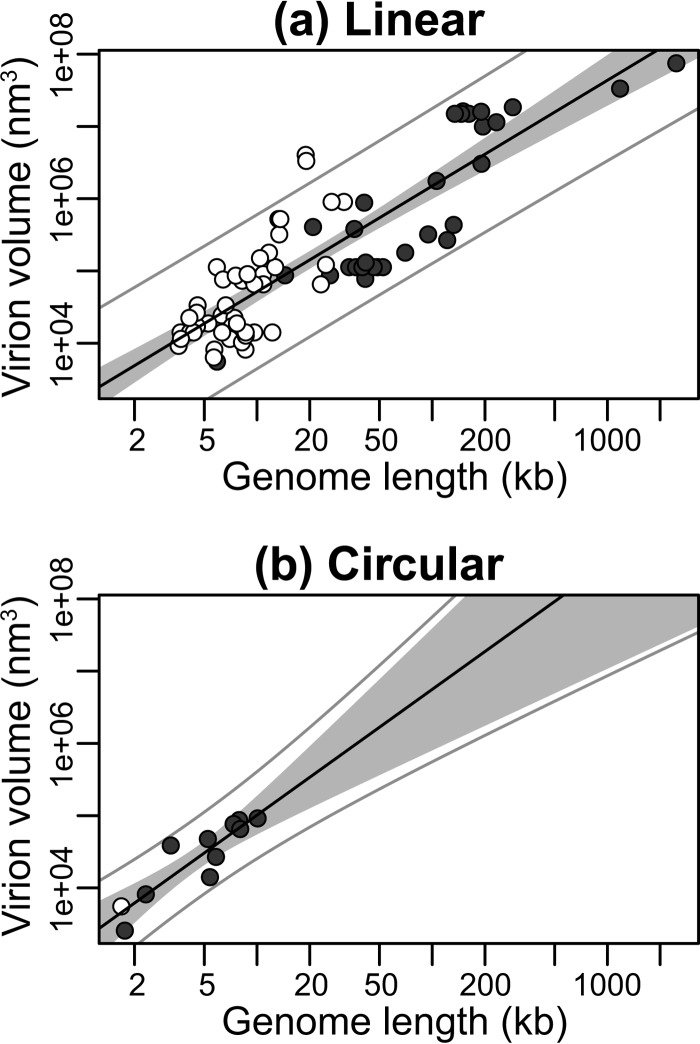
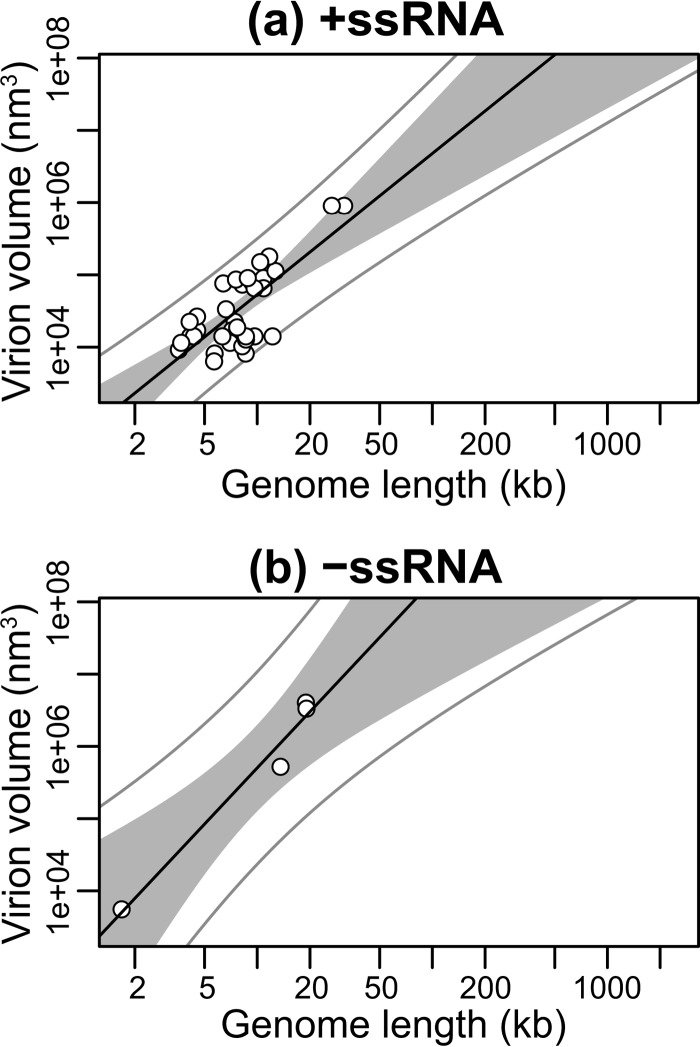
Next, we subdivided our data into enveloped (n = 28) and nonenveloped (n = 60) viral groups. Although viruses with envelopes possess larger genomes (median of 148.21 kb for DNA viruses and 13.32 kb for RNA viruses) compared to nonenveloped viruses (36.72 kb for DNA viruses and 7.00 kb for RNA viruses) (P < 0.001, P = 0.004, and P < 0.001 for all viruses, DNA viruses, and RNA viruses, respectively), both groups exhibited a significant linear relationship between log virion volume and log genome length, indicating a power law relationship between the two: enveloped, R² = 0.85, P < 0.001, exponent = 1.37 (Fig. 3a); nonenveloped, R² = 0.72, P < 0.001, exponent 1.06 (Fig. 3b). Similarly, allometric relationships were observed after subdividing the data (i) into viruses with linear (n = 77, R² = 0.72, P < 0.001, exponent = 1.06) and circular (n = 11, R² = 0.82, P < 0.001, exponent = 1.74) genomes (Fig. 4), (ii) into dsDNA (n = 33, R² = 0.71, P < 0.001, exponent = 1.52) and dsRNA (n = 8, R² = 0.45, P = 0.07, exponent = 0.97) viral groups (Fig. 5), and (iii) into +ssRNA (n = 34, R² = 0.56, P < 0.001, exponent = 1.95) and −ssRNA (n = 4, R² = 0.97, P = 0.01, exponent = 2.58) viral groups (Fig. 6; Table 2). Note, however, that because of the small sample sizes for the dsRNA and −ssRNA viruses, the confidence intervals for the exponent estimate are large in both cases.

FIG 3.

Relationship between genome lengths and virion sizes among enveloped (a) and nonenveloped (b) viruses. The y axis shows the virion sizes calculated as volume (nm³) on a log scale, while genome lengths (kb) are shown on the x axis on a log scale. RNA viruses are shown by open circles and DNA viruses by closed circles. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

FIG 4.

Relationship between genome and virion sizes among linear (a) and circular (b) viruses. The y axis shows virion sizes calculated as volume (nm³) on a log scale, while the x axis shows genome length (kb) on a log scale. RNA viruses are shown by open circles and DNA viruses by closed circles. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

FIG 5.

Relationship between genome and virion sizes among dsDNA viruses (closed circles) (a) and dsRNA viruses (open circles) (b). The y axis shows virion sizes calculated as volume (nm³) on a log scale, while the x axis shows genome length (kb) on a log scale. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

FIG 6.

Relationship between genome and virion sizes among +ssRNA (a) and −ssRNA (b) viruses. The y axis shows virion sizes calculated as volume (nm³) on a log scale, while the x axis shows genome length (kb) on a log scale. The solid black line marks the linear regression between log-log-transformed data. The gray area represents the 95% confidence interval for the linear regression line. The outer gray lines represent the 95% prediction interval, within which we expect 95% of virion sizes to lie for a given genome size.

Finally, although overlapping genes are commonly utilized in RNA viruses and small DNA viruses (18), our results are minimally affected when accounting for overlap by estimating an adjusted genome length (R² = 0.52, P < 0.001, exponent = 1.61).

Hence, overall these data clearly show that for a diverse set of viruses, virion volume and genome length follow a strong power law, V = aL^b, in which V is the volume of the virion, L is the length of the genome in base pairs, a is the scaling factor, and b is the allometric exponent (Table 2).

Relationship between protein numbers, gene lengths, and virion volumes.

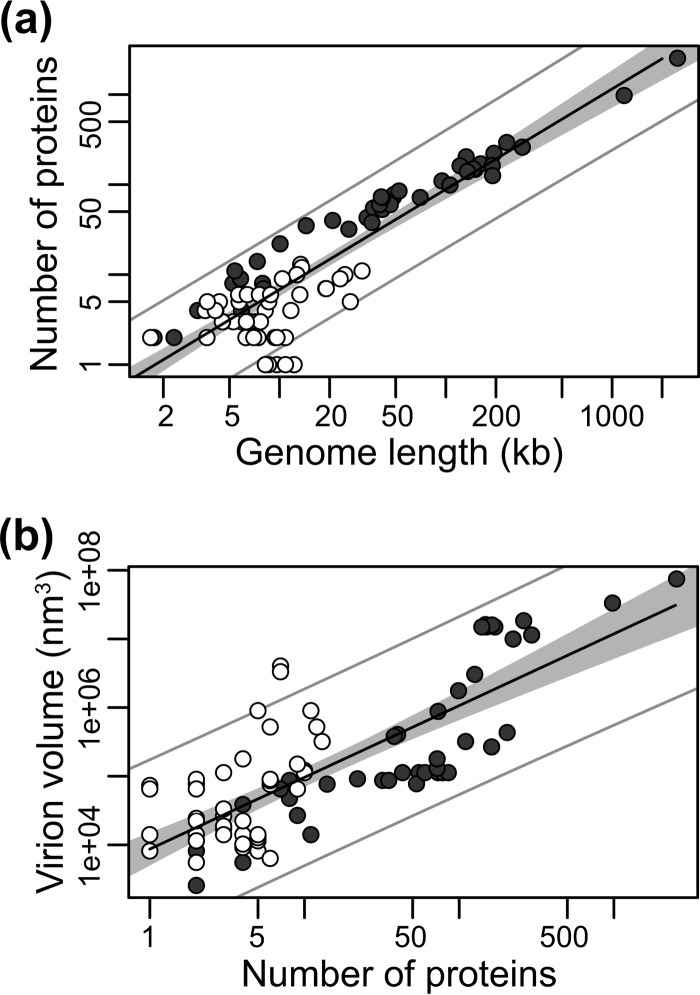
One explanation for the relationship between virion volume and genome length is that viruses with longer genomes produce more proteins, which in turn must be housed in larger virions. We therefore sought to determine if the number of distinct proteins encoded by each virus (see Table S1 in the supplemental material) was associated with virion volume and genome length. As we expected, larger viral genomes harbored significantly greater numbers of proteins, and this relationship was again allometric (Fig. 7a): R² = 0.82, P < 0.001, exponent = 1.11. Additionally, there was a strong correlation between virion volume and number of proteins (Fig. 7b): P < 0.001, R² = 0.61, exponent = 1.05. To investigate this further, we performed a multiple linear regression on the logarithm of virion volume, genome length, and number of proteins. This revealed that genome length was still associated with both virion volume and number of proteins after adjustment of one another (P < 0.001) but that virion volume is only associated with genome length (P < 0.001) and not with the number of proteins (P = 0.71) after adjustment for genome length. As a consequence, the relationship between genome length and virion volume is not a product of the number of proteins encoded.

FIG 7.

Relationship between (a) the number of proteins in a viral genome (y axis, log scale) and its length (kb) (x axis, log scale) and (b) virion volumes (nm³) (y axis, log scale) and protein numbers (x axis, log scale). RNA viruses are shown by open circles and DNA viruses by closed circles. The solid line marks the linear regression on log-log-transformed data.

In marked contrast to the genome-scale associations with virion size, no such correlations were observed at the level of two key individual viral genes (on either the untransformed or log-log-transformed data). In the case of nonenveloped RNA viruses, we found no relationship between the length of the capsid gene, which encodes the structural component of the virus capsid, and the virion volumes: R² = 0.059, P = 0.18 (n = 32). A similar result was observed in the case of the RNA-dependent RNA polymerase gene, which encodes the enzyme responsible for replication of RNA from an RNA template (and hence is common to all RNA viruses): R² = 0.009, P = 0.60 (n = 36). Hence, these results demonstrate that the expansion of virion sizes during evolution is not due to the elongation of these genes but rather is directly linked to the expansion of total genome length.

Testing the allometric relationship between virion volume and genome length.

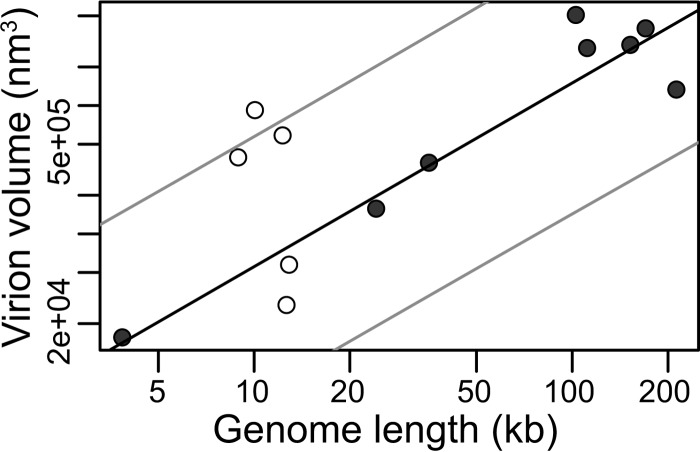
Although our main analysis considered 88 viruses, an additional 13 viruses were excluded as only a range of virion volumes were reported, rather than a specific value (Table 3). For these viruses, we calculated the midpoint of the reported virion volumes and used this to independently test the predictive power of the allometric model calculated in Fig. 1. Importantly, we find that our model accurately predicts virion volume from genome length (Fig. 8).

TABLE 3.

Summary data of the 13 viruses excluded from the main analysis but used to test the allometric relationship^a

Family	Virus species	Virion vol (nm3)	Genome length (kb)
dsDNA viruses
Rudiviridae	Sulfolobus islandicus rod-shaped virus 2	3.4 × 10−5–3.7 × 10−5	35.4
Fuselloviridae	Sulfolobus spindle-shaped virus 1	1.3 × 10−5–1.9 × 10−5	24.2
Asfarviridae	African swine fever virus	2.8 × 10−6–5.2 × 10−6	170.1
Iridoviridae	Invertebrate iridescent virus 6	9.0 × 10−5–1.8 × 10−6	212.5
	Lymphocystis disease virus 1	4.1 × 10−6–6.1 × 10−6	102.6
	Infectious spleen and kidney necrosis virus	1.4 × 10−6–4.2 × 10−6	111.4
Herpesviridae	Human herpesvirus 1	1.8 × 10−6–4.2 × 10−6	152.3
ssDNA viruses
Anelloviridae	Torque teno virus 1	1.4 × 10−4–1.7 × 10−4	3.8
dsRNA viruses
Chrysoviridae	Penicillium chrysogenum virus	2.2 × 10−4–3.3 × 10−4	12.6
Negative-sense ssRNA viruses
Bornaviridae	Borna disease virus	2.7 × 10−5–5.2 × 10−5	8.9
Bunyaviridae	Bunyamwera virus	2.7 × 10−5–9.0 × 10−5	12.3
Arenaviridae	Lymphocytic choriomeningitis virus	7.0 × 10−5–1.1 × 10−6	10.1
Unassigned	Lettuce big-vein associated virus	5.4 × 10−4–6.1 × 10−4	12.9

^aFor details, see Fig. 8.

FIG 8.

Relationship between genome and virion sizes for 13 viruses excluded from the original analysis because only a range of virion volumes were available (Table 3). RNA viruses are shown by open circles and DNA viruses by closed circles. The solid black line marks the prediction line calculated for our original analysis (Fig. 1). The outer gray lines represent the 95% prediction interval for our original analysis, within which we expect 95% of predicted virion sizes to lie.

DISCUSSION

One of the most important, yet understudied, aspects of virus evolution is determining the processes responsible for the diverse array of genome and virion architectures employed by these infectious agents. To this end, we have revealed a simple and significant allometric relationship between genome length and virion volume that broadly applies to all viruses, regardless of their nucleic acid type, genome, or virion structure. We also find that the allometric exponent is consistently less than that predicted by geometric scaling and that the association is independent of the number of proteins encoded by the genome. As such, the relationship between virion volume and genome length is not a product of physical dimension constraints or protein quantity. That the allometric relationship between genome and virion size holds regardless of the specific capsid architecture, or whether the virus in question contains an envelope, indicates that it represents a fundamental aspect of the structural design of viruses. Additional work is needed to determine whether the differences between the exponent values observed in comparisons of different virus groups (with, for example, means of 1.06 in the case of nonenveloped viruses and of 1.95 for +ssRNA viruses) are significant and, if so, the underlying biological reasons.

Our study shows that while there is clearly great flexibility in the shapes exhibited by virus virions, these must conform to a general set of volume constraints. As a case in point, members of the Poxviridae (dsDNA) possess genomes of broadly similar lengths (134.7 to 288.5 kb) and virions of similar sizes (1.0 × 10⁷ to 1.8 × 10⁷ nm³) (Table 1), yet they possess virions with shapes as diverse as brick and ovoid. As there is also a profound inverse relationship between mutation rate and genome size in viruses that covers many orders of magnitude (11, 19, 20), selection for a reduction in mutation rate will in turn result in both larger genomes and virions. We therefore propose that there is an evolutionary cascade that links the frequency of genomic mutations to the size of mature virus particles. However, it is impossible to quantitatively determine the direction of causality—that is, whether genome size evolution drives virion size or vice versa—from these data alone, although this is clearly a subject that merits additional investigation.

Finally, we note that the strength of the relationship between genome and virion sizes, as reflected in the 95% prediction intervals, provides a simple way to broadly estimate the latter from genome sequence data alone, as might be generated by metagenomic surveys in the absence of individual virus isolation (21). Indeed, it is striking that both the giant mimiviruses (22) and pandoraviruses (2) conform to the same scaling law as RNA viruses.