Mapping the architecture of the HIV-lTat circuit: A decision-making circuit that lacks bistability and exploits stochastic noise

Abstract

Upon infection of a CD4⁺ T cell, HIV-l appears to ‘choose’ between two alternate fates: active replication or a long-lived dormant statetermed proviral latency. A transcriptional positive-feedback loop generated by the HIV-l Tat protein appears sufficient to mediate this decision. Here, we describea coupled wet-lab and computational approach that uses mathematical modeling and live-cell time-lapse microscopy to map the architecture of the HIV-l Tat transcriptional regulatorycircuit and generate predictive models of HIV-l latency. This approach provided the first characterization of a ‘decision-making’ circuit that lacks bistability andinstead exploits stochastic fluctuations in cellular molecules (i.e. noise) to generate a decision between an on or off transcriptional state.

1. INTRODUCTION

1.1 Background on quantitative modeling and the need for kinetic data

From chemical engineering to meteorology, ecology and infectious-disease epidemiology, mathematical modeling has long been a vital and accepted tool for interpreting data, deriving mechanism of action, and predicting the behavior of complex systems. Modeling even has a storied past in molecular biology–notably Watson and Crick's seminal 1952 paper on the structure of DNA. During the 1990s, mathematical modeling approaches adopted from ecology were pivotal in determining fundamental kinetic rates of HIV replication and turnover in patients and transformed our understanding of HIV pathogenesis and the evolution of drug resistance (1-6), for a review see (7). These models of HIV were successful largely because high quality time-lapse data was available to ’fit’ the models.

In general, the availability of high-frequency time-resolved data is key for many types of mathematical modeling and this data is essential for the mathematical modeling we focus on here: kinetic modeling with Ordinary Differential Equations (ODEs). Although the term ‘mathematical modeling’ encompasses a wide range of computational approaches, we focus on ODEs (and the stochastic version of ODEs)since this approach has a strong track record of successfully generating accurate, predictive, and testable models of many cellular signaling networks (8-20). Time-lapse data to fit ODE models has been used from a variety of different in vitro experimental modalities including Western Blot, gel-shift assay, RT-PCR, and others—as long as the experimental system can be plotted to generate a kinetic curve of [quantity] versus [time]. The data from time-lapse experiments can potentially lead to a predictive and testable ODE model of the system being studied. During the past 15 years technical advances, such as the invent of fluorescent proteins (e.g. GFP) have allowed very high frequency time-lapse data to be collected from live cells by flow cytometry and live-cell time-lapse microscopy. Here, we describe how a time-lapse imaging approach can be combined with modeling analysis to study the HIV Tat positive-feedback circuit, whichregulates active viral replication and plays a crucial role in regulating the establishment ofproviral latency and viral reactivation. The HIV Tatsystem represents an illustrative example because the network is tractable, many predictions of the model have been validated experimentally, and this model can serve as a ‘module’ that can be adapted and expanded to more complex models of HIV regulation.

The mathematical modeling approach we present here utilizes the computer as a form of model system to run ‘experiments’. The computer experiments make predictions that must then be validated in other experimental model systems such as cell-culture or animal models. This approach is not dissimilar to how other experimental model systems are used: tissue culture actsas a model system that provides data which must eventually be validated in other model systems such asmurine modelsand the data from murine models must in turn be validated in another system. When developing murine models, those models that do not recapitulate physiological realism are usually discarded and more relevant models are developed. Mathematical models, much like in vitro or in vivo models, undergo a cycle of development, testing, and reformation; for example, models that do not recapitulate experimental data from tissue culture, are discarded and new models are developed.

Each experimental model system has inherent benefits and drawbacks with some systems having greaterphysiological relevance and others having greater resolving power to differentiate specific mechanisms. The tradeoff between physiological relevance and resolving power is alwaus a consideration and in this regard mathematical modeling represents a powerful reductionist assay system for resolving between competing models. Specifically, the key benefit of mathematical modeling is that upon ‘discarding’ the athematical model, very specific mechanisms can be negated; each ODE model ideally represents a specific mechanism and when this model cannot fit experimental data from tissue culture, that specific mechanism is eliminated from consideration. Thus, the most informative models are often the models that do not fit the data! In this way, ODE modeling can provide mechanistic and even structural insight.

There is extensive literature on mathematical modeling of HIV-1 intracellular dynamics (21-24), intercellular viral transmission (3, 5, 7, 25), and HIV-1 epidemiology (26).Here, we argue thatthe coupling of mathematical modeling with time-lapse microscopy experiments is a powerful method to differentiate between alternate models and shows that the HIV Tat circuit does not encode a ‘bistable’ circuit architecture. The lack of bistability in the Tat circuit leads to the stochastic model of the HIV Tat circuit where the circuit acts as a monostable ‘timer’ switch which inevitably shuts off (15). Importantly, the HIV Tat circuit was the first characterized decision-making circuit that lacks bistability and the coupled modeling+imaging method we describe provided a predictive model for the establishment of HIV provirallatency.

1.3 The Problem at Hand: HIV-1 proviral latency (a decision-makina circuit)

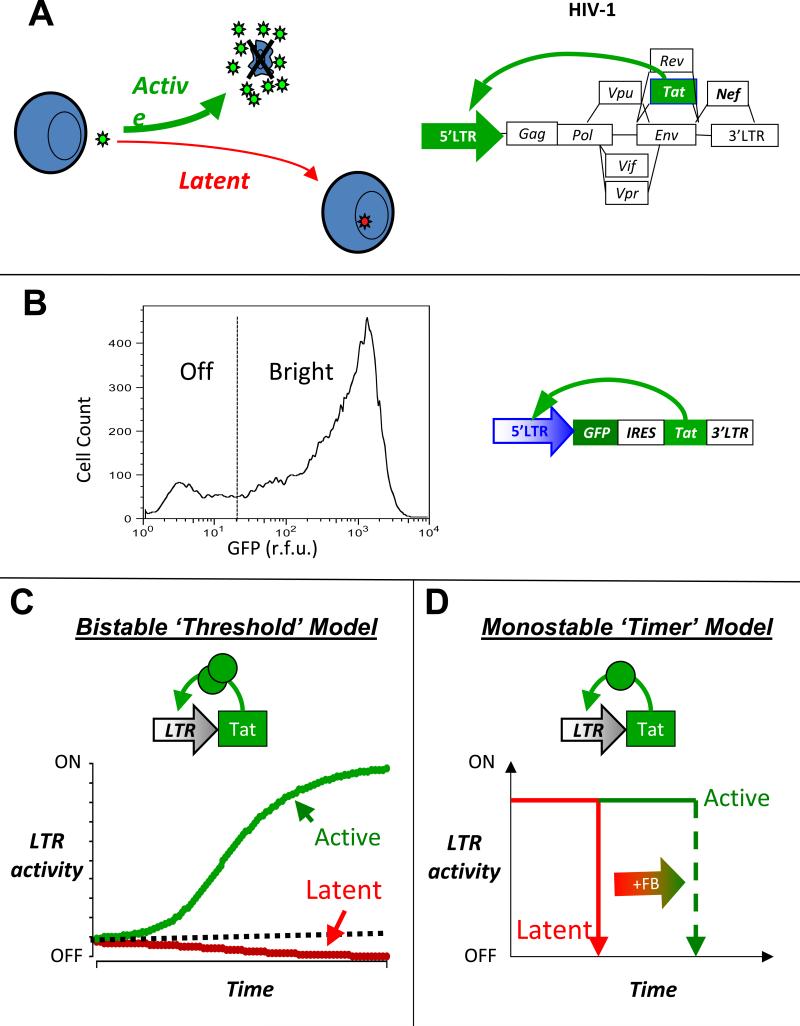
Many viruses appear to have the ability to undergo a developmental ‘bifurcation’ between two lifecycle states. The lysis-lysogeny decisionin bacteriophage-λ is the prototypical example, for a review see (10). Mechanistically, bacteriophage-λ appears to achieve this developmental bifurcation, in part, by encoding bistability (the ability to stably ‘rest’ in two different states) within its master regulator circuit,the λ-operator. Bistability within the bacteriophage-λ circuitry appears to be achieved by means of two competing negative-feedback loops acting on the λ-operator (27, 28). Similar to bacteriophage-λ, HIV-1 can also enter one of two developmental fates: upon infecting a CD4⁺ T lymphocyte, HIV-1 can either enter an active replication state (productive infection) or enter a post-integration/pro viral latent state (an analog of phage lysogeny) (Fig 1A). HIV's ability to enter a proviral latent state in resting CD4 T cells is considered the most significant obstacle thwarting HIV-1 eradication from a patient (29, 30)since latent cells can ‘reactivate’ during interruption of highly active anti-retroviral therapy (HAART) to generate rapid viral rebounds that re-establish pre-treatment HIV-1 levels (31). A substantial body of evidence has confirmed that HIV-1 proviral latent cells are quiescent for viral production and that viral gene expression is shut off during viral latency (3, 32, 33). Entry into proviral latency appears to be multifactorial with many molecular processescontrolling the decision to enter latency including the integration site of virus within repressed chromatin regions(34), transcriptional blocking due to surrounding genes (35), epigenetic silencing of proviral DNA (36-38),a transition from active to memory state of CD4+ T cells during infection (39), or a function attenuating mutation in the necessary HIV-1 transactivator of transcription, Tat (40). Previous work by our group has demonstrated thatthe transcriptional master circuit of HIV-1, the Tat positive-feedback loop,can control the latency decision and appears to be sufficient to drive a ‘decision’ between two states: briaht and off (Fig 1b) (12).

Figure 1. The HIV-1 provirallatency decision oand two potential decision-making mechanisms.

(A) Schematic of HIV-1 infecting a CD4+ T cell and ‘choosing’ between active replication and proviral latency (left) and schematic of the HIV-1 proviral genome where the HIV-1 Tat positive feedback is essential for active replication and entry into proviral latency (right). (B) A minimal Tat circuit LTR-GFP-IRES-Tat (LGIT) can generate a rcation in GFP between two states: Off and Bhght(12). Flow cytometry histogram of a at cell clonal population expressing LGIT from a single locus and exhibiting a developmental bifurcation; despite all cells having the same integration of LGIT, one subpopulation of cells does not express GFP and Tat while another subpopulation of cells does express GFP and Tat. The bifurcation is not consistent with chromatin silencing or position effect variegation but is consistent with stochastic fluctuations in Tat (12). (C) The bistability model for developmental bifurcation. If a transcriptional positive-feedback circuit encodes a self-cooperative threshold (e.g. homodimerizationof the transactivator or multiple DNA binding sites that must all be bound by the transactivator), the circuit can exhibit bistability (the ability to stably rest in two alternate states). If the transactivator levels are above the threshold (dashed line), the circuit self-perpetually transcribes increasing amounts of transactivator and remains stably in an active state (green line). If transactivator levels are below the threshold, feedback regulation cannot be completed and any available transactivator decays away at its intrinsic half-life (red line). (D) An alternate model of kinetic partitioning (or a ‘timer’ switch) for developmental bifurcation. In this model, the positive-feedback loop is not required to encode a self-cooperativity threshold and all trajectories eventually fall to an off state (red) and the strength of positive feedback determines the duration of time that a circuit resides in the on state (green).

Below, we describe how mathematical modeling coupled with flow cytometry and single-cell time-lapse imaging can be used to probe whether the Tat circuit architecture is bistable and switch-like, as in bacteriophage-λ, or whether Tat encodes a different circuit architecture (Fig. 1c-d). The imaging and modeling experiments below demonstrated that the Tat circuit lacks bistability and instead acts as monostable ‘timer’ switch, where the latent state appears to be the only true stable state (15). Finally, we discuss how stochastic modeling approaches demonstrated that the Tat circuit's decision between an on and off state can be accounted for by incorporating noise (i.e. molecular fluctuations) models of Tat gene expression and how noise appears sufficient to control fate determination in the Tat circuit (10,12,13,15).

2. Approach

We present the following schemeto map the architecture of the Tat positive feedback loop and test for bistablility: (i) we develop minimal mathematical models of HIV Tat positive feedbackthat predict specific kinetic behaviors, (ii) we construct simplified HIV-1 based lentiviral vectors that examine Tat positive feedback in isolation from all other viral elements, and (iii) we analyze the kinetic behavior of these vectors using time-lapse fluorescence microscopy to test the various mathematical models. After demonstrating that the experimental single-cell data does not support the bistabilitymodel in the HIV-1 Tat positive-feedback decision-making circuit, we discuss how stochastic models of a monostable Tat positive-feedback circuit can account for HIV-1’ sability to decide between two alternate states.

2.1 Starting Considerations for Generating a Predictive Model

The modeling discipline faces the philosophical dilemma as to whether models should be complex and attempt to fit all known mechanisms or whether models should be simple and attempt to fit only the most essential phenomena. Clearly, what phenomena and characteristics qualify as ‘essential’ is subject to interpretation and debate. However, modeling every molecular detail frequently results in models that are difficult to interpret and have little predictive value, so here we will focus on constructing ‘simple’ minimal models that consider only a skeletal set of processes needed to quantitatively fit a specific set of experimental data. Our approach follows an underlying principle of model development: A model should aim to be predictive rather than descriptive. Modeling every molecular detail frequently results in models that are difficult to interpret and have little predictive value. This simplified model approach has strong precedent: models that simplified much of the known biological and molecular detail were essential for elucidating key molecular mechanisms such as bi-stability in the λ-phage lysis/lysogeny decision (27,28, 41-45), multi-stability and plasticity in the lac operon (46, 47), robustness in the E. coli chemotaxis network (48, 49) as well as many other key molecular mechanisms. Simplified models have been particularly successful for HIV, correctly predicting HIV-1 population dynamics (5, 50-55), HIV-1 viral kinetics in vivo(1, 3, 6, 56), and have also demonstrated how stochastic molecular fluctuations in HIV-1 Tat contribute to viral latency (12). Arguably the best example of the utility of simple models over complex models is in protein folding which appears to be “relatively insensitive to details of the interatomic interactions” where Baker and colleagues established that low-resolution models have far better predictive power than high-resolution thermodynamic models (for a review see (57)). Complex models that account for many of the molecular details are eventually developed but it is very rare for comprehensive models to be constructed de novo. Helpful and comprehensive models must be developed in a stepwise fashion, and we describe the development of the initial models for HIV in a stepwise fashion in sections 3.1-3.3.

2.2 Designing Lentiviral Vectorsand Creatina Cell Lines to Test the Different Models

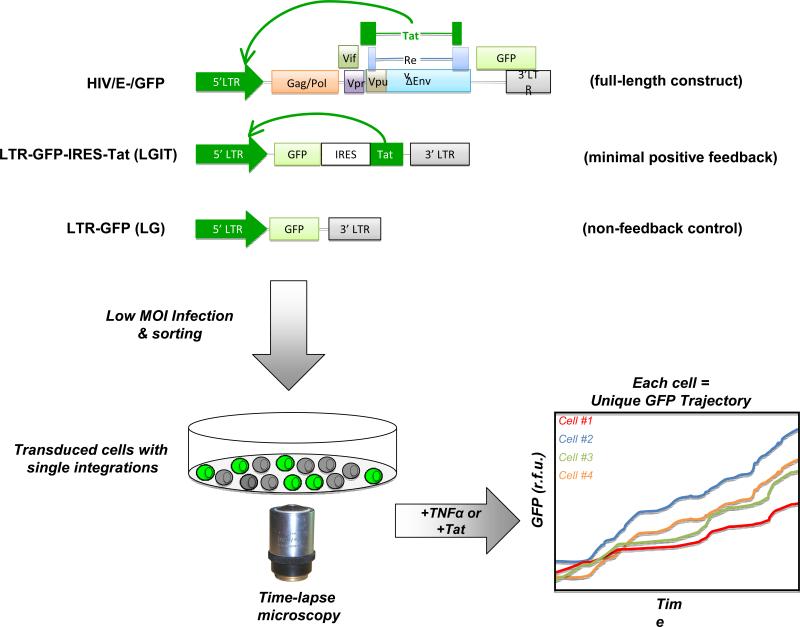
To determine quantitative values for different components of a system and ‘parameterize’ an ODE model, minimal circuit constructs can be used. We present maps for a number of different HIV-1 circuit constructs of increasing circuit complexity in Figure 2 since these maps will provide a helpful guide for the ODE models presented in Figure 3. Each minimal circuit construct is important for differentiating between the different levels of control in HIV-1 gene expression. The LTR-GFP (LG) system contains the HIV-1 5’ long terminal repeat promoter (5’ LTR) driving expression of the green fluorescent protein (GFP) followed by the 3’ LTR. Gene expression from this system depends purely on the integration site of that particular cell, which controls the basal rate of transcription from the 5’ LTR (58). The LG provides a means to estimate basal promoter strength of the LTR and fold activation in response to inducers in the absence of the Tat positive-feedback loop. The LTR-GFP-IRES-Tat (LGIT) construct removes many of the complex regulatory processes present in full-length HIV-1, such as splicing or other feedback components, and just leaves the interactions between Tat and the LTR. The LGIT system has the 5’ LTR driving a single mRNA that contains GFP, an internal ribosomal entry sequence (IRES) (59), and the HIV-1 Trans-Activator of Transcription (Tat), all followed by the 3’ LTR (12, 13, 15). The single mRNA species does not contain any splicing signals, however, the IRES sequence allows for GFP and Tat expression from the same mRNA inrelatedand measureable amounts with the Tat protein being expressed at a 10-100 fold lower level (60). The HIVQEnvsystem is a ‘full-length’ derivative of the HIV-1 pNL 4-3 virus (61)with a point mutation at the start codon of the env gene and GFP in place of nef(34). Like LGIT, HIVΔEnvcan also be used to examine Tat positive-feedbackkineticssince Nef, Tat, and Rev act as alternative-splice variants of one another.

Figure 2. Experimental approachto map HIV-1 Tat circuitarchitectureusingsingle-celltime-lapse imaging.

Various lentiviral vector constructscan be used for analyzing Tat circuitry. The HIVAEnv construct contains the full-length HIV-1 genome, with GFP in place of the nef reading frame, and has a start codon mutation in the env so it does not produce infectious virus(34). Nef and Tat are alternatively spliced, so GFP acts as an ectopic )orter for Tat kinetics. The LTR-GFP-IRES-Tat (LGIT)constructexpresses a single bicistronicmRNA that codes only for GFP (the first cistron) and for Tat (the second cistron) which is translated from an internal ribosomal entry sequence (IRES). Tat positively feeds back onto the 5’ LTR to transactivate it (black arrows). The LTR-GFP (LG)constructcodes only forGFP driven by the HIV-1 5’ long terminal repeat (LTR) promoter. The LG construct is useful as a non-feedback control. Each lentiviral construct can be packaged using standard approaches (62) and Jurkat T cellscan be infected at low multiplicity of infection (MOI), FACS sorted to generate isoclonal (or polyclonal) populations, and then im£ live-cell fluorescence microscope system (15). Single-cell trajectories are extracted from time-lapse imaging moviesand can be analyzed by mathematical models.

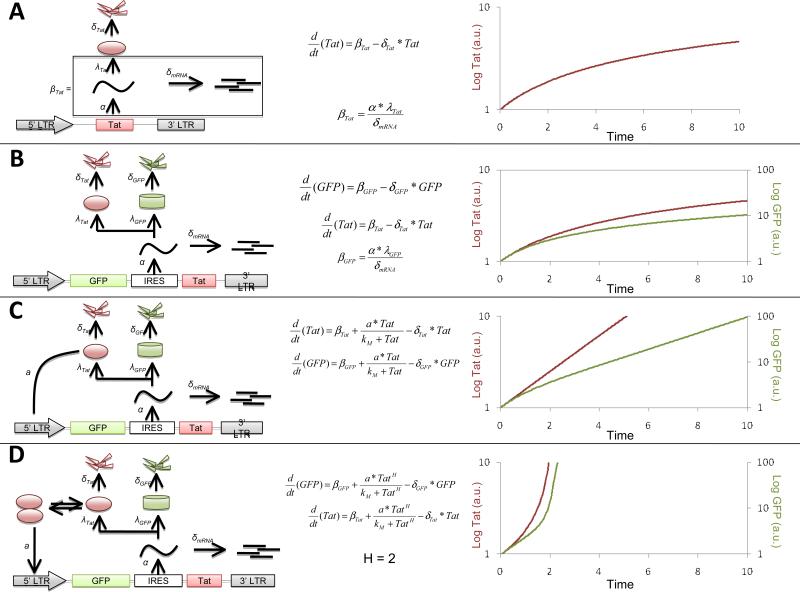
Figure 3. Mathematical models that predictthe behavior of potential feedback architectures underlyingthe HIV-1 Tat circuit.

(A) Schematic, ODE model, and numerical solution of a hypothetical LTR-Tat circuit without any feedback; the basal rate of mRNA transcription, α, the degradation of mRNA, δ_mRNA, translation rate of Tat, λ_Tat, and the degradation rate of Tat, δ_Tat, are considered in the model.The basal rate, β_Tat, of Tat expression can be approximated by lumping the terms (bottom equation) within the black-framed box. The top equation is an ordinary differential equation (ODE) that describes the dynamics of Tat in this circuit. Aplotof Tat versus time (with the log of Tat plotted versus time) shows that Tatapproaches a steady state at a linear rate of increase(i.e. a sub-linear rate of increase on the log-linear plot). For this simulation δ_Tat = 1,β_Tat= 10 and the initial condition is that Tat[0]=0.1. (B) Schematic, ODE model, and numerical solution of the LGIT system without any positive feedback. The production of GFP, β_GFP, was calculated using the approach asused above for Tat.The first(top) equation describes the GFP dynamics, the second (middle) equation is the same as that in panel A. The plot on the right shows that GFP and Tat dynamicsmirror each other and are qualitativelyvery similar. δ_GFP = 0.5,β_GFP= 0.1 (C) Schematic, ODE model, and numerical solution of the LGIT systempositive feedback added. Tat and GFP expression both depend on a positive-feedback term with a Hill coefficient (H) = 1. The positive-feedback strength is described by the parametera, and kM is aMichaelis-like constant that describes the level at which the feedback begins to saturate. This model generatesan exponential rise in Tat and GFP levels (i.e. a linear rise on the log scale). For this simulation α=1,k_M=1, and all other parameters are unchanged from above. (D) Schematic, ODE model, and numerical solution of the LGIT system encoding a positive-feedback loop with nonlinear self-cooperativity (i.e. H > 1).H = 2 can drastically changes the shape of both GFP and Tat dynamics. All parameters are the same as in panel c except that H = 2 in this simulation. All simulations where performed in Mathematica™.

Below, we will focus on the LGIT circuit, since we address the architecture of the feedback circuitry. However, the LG construct ishelpful to probeLTR regulation in the absence of feedback and any other HIV factors and the HIVΔEnvconstruct is helpful to verify the results of studies with LGIT and to probe more complex regulation in HIV-1.

To create cell lines expressing our construct of interest, we use standard lentiviral packaging systems(62)and tranducejurkat T lymphocytes with the packaged lentivirus to create stable cell lines that expresses our genes of interest. We typically infect at low multiplicity of infection (MOI ≈ 0.01-0.1) to ensure that infected cells contain only a single integration. Enrichment of infected-cell populations is then achieved byfluorescence activated cell sorting (FACS) for fluorescent proteins such as GFP. For a complete discussion on the use of lentiviral vectors see(63).

2.3 Choosing Between Different Methods for Obtaining Time Lapse-Data

Data from various experimental methods can be used for ODE modeling including data from qPCR, RT-PCR, Western blot, Western immunoprecipitation (IP), chromatin IP (ChIP), Northern blot, or other methods. If one has the luxury of choosing which experimental method to use to obtain time-lapse data for ODE models, a number of considerations come into play. Most of biochemical assays mentioned above provide only data on the mean of a large population of cells in the culture (hundreds of thousands to millions of cells), which can obscure or complicate analysis if cell behaviors are not well synchronized. Alternative methods include flow cytometery, which presents the advantage of allowing one to assay both population means and distributions, or fluorescence microscopy that provides the unique advantage of tracking individual cells over time. The automated fluorescence microscopeis an ideal tool to collect time-lapse data since data can be captured for thousands of cells in an automated fashion at an exceptionally high frequency (up to once every second) for hours to days. In this way, a vast amount of data is collected and this method has been used to probe dynamicsof gene expression (13, 15, 64, 65), network cascades (66), and many other spatiotemporally regulated systems of the cell (67, 68). Here, we focus primarily on the technique of fluorescence time-lapse microscopy to track gene expression of HIV-1 in single mammalian cells over time. We show how single-cell fluorescence trajectories can be interpreted by mathematical modeling to provide insight into the architecture of the specific gene circuit and how HIV-1 may enter a latent state.

3. Methods

3.1 Developing and Analyzing ODE Models

3.1a ODE Model of Tat expression without feedback

To begin, we normally draw a schematic or cartoon of the system that describes the key interactions to be assessed (20). We consider a set of alternate models forpossible architectures of the Tat feedback circuit(Fig 3) and we predict the output ofeach modelin terms of HIV-1 gene expression. First, in Figure 3A we consider a model without any feedback and we draw the schematic for this model (Fig. 3A. left). Then, we deduce the ODEs that describe thisschematic (Fig 3A. middle), and we simulate the kinetics of Tat and GFP expression (Fig 3A, right). The differential equations that describe this system are: whereα is the basal rate of mRNA expression, δ_mRNAis the per-capita decay rate of the expressed mRNA, λ_Tatis the translation rate of Tat from mRNA, and δ_Tat is the per-capita decay rate of Tat protein. Equations 1 and 2 can be lumped into a simplified version by making the quasi steady-state assumption of mRNA expression off of the LTR. We can solve for the steady-state mRNA levels by setting the left-hand side of Equation 1 to zero. We then obtain similar dynamics because the IRES allows for expression of both GFP and Tatin stoichiometric amounts off of the same mRNA species (59). The log plot shows the same characteristic asymptote for GFP and Tat.

3.1b ODE Model of Tat Positive Feedback loop without potential for bistability (i.e. H=1, no Tat self-cooperativity)

Tat is known to establish a positive-feedback loop (12) via binding to an RNA stem loop within the 5’LTR, termed the TAR loop (TransActivation Responsive loop that extends from -18 to -70 in the 5’LTR) and relieving an elongation stall in RNA Polymerase II (RNAPII) (73-75). There is a rich literature detailing the complex array of molecular interactions involved in Tat transactivation (69-72)but we follow the minimalist philosophy above and by assuming that these molecular processes are non-limiting we ‘lump’ many of these processes into two parameters to generate a minimal model of HIV-1 Tat transactivation (Fig 3C). The resulting minimal model can be described bythe following set of ODEs: 3C)and thus Eq. 4 generates behavior that differs significantly from the linearly increasing rate generated by Eqs. 1-3.

In this system with positive feedback, if the system operates far from saturation (i.e.k_M>>Tat(t)), the middle term is approximately (x/k_M)*Tat(t) which gives an exponential increase. As the system approaches saturation(i.e. the amount of Tat(t)>>k_M) then the positive-feedback terms collapse to x, since Tat(t) + k_M ≈ Tat(t). This equation becomes very similar to the system without any feedback (Fig 3A). Overall, the system displays exponential increase at early times and asymptotes at later times (i.e. linear on a log scale at early times and asymptotes at later times).Below, we will show that the HIV-1 Tat feedback system exhibits this type of exponential increase over time.

3.1c ODE Model of Tat Positive Feedback loop with potential for bistability (i.e. H>1, Tat is self-cooperative)

Here we model the possibility that Tat positive-feedback is nonlinear or operates in a self-cooperative manner. Self-cooperativity in positive-feedback loops can generatemultistability(or the ability to rest in multiple states) andprovide a mechanism forchoosing between alternate fates (46, 76, 77). Self-cooperativity can be modeled by adding a Hill coefficient (H) to the positive feedback term in Eq. 4 to generate: or three Tat binding sites on the LTR that must be bound for transactivation to occur, or (iii) that Tat is multiply phosphorylated in a cooperative manner. The kinetics of GFP and Tat expression in a self-cooperative system (Fig 3D) are qualitatively distinct from the kinetics of GFP expressionin a system without cooperativity (i.e. Eq. 4 and Fig. 3C).Self-cooperative functions grow at rates thatexhibit far greater curvaturethan exponential growth (H=1) or linear growth (H=0). The increased curvature is dueto rates of increase being relatively low below the self-cooperative threshold (because feedback is notactive), and the rate being relatively high and increasing quickly once the self-cooperative threshold is reached.

Notably, the model in Eq. 5 collapses into equation 4 when H=1 (and to Eq3 when H=0) and we will utilize this fact to differentiate between models. The model described by Eq. 5 allows for the possibility that Tat could act as a multistable switch and that HIV-1 may be able to stably rest in multiple states (e.g. active replication or proviral latency). The model described by Eq. 4 does not allow for bistability or multistability in Tat positive feedback. Below, we differentiate between the models in Eqs. 4 and 5 by fitting the data from the single-cell microscopy experimentsto our ODE models to determine the value of H.

3.2 Time-lapse Microscopy

3.2a Preparing Cells for Imaging

Once an appropriate fluorescently-labeled cell line expressing the constructs has been created, the next step in the process is imaging.Jurkat T lymphocytes are non-adherent cells and in order to perform time-lapse microscopy thecells must be immobilized. Nonadherent cells can be immobilized in a confluent monolayer by trapping them within microfluidic or small-chambered devices (78), trapping within a polymer matrix (79), or using a ‘sticky’ film coating on a glass-bottom imaging dish (www.glassbottomdishes.com). The type of sticky substance used can be fibronectin, poly-L-lysine, or other substrates. We have successfully used BD Cell-Tak™ (www.BDBiosciences.com)a formulation of proteins isolated from marine mussels. A thin film of this substance allows for uninterrupted imaging of individual Jurkat cells for up to 30 hours. We use 35mm glass-bottom dishes or glass-bottom 96-well plates on which we ‘stick down’ Jurkat cellsas a monolayer of cells. Once cells are stuck down, the imaging process can begin.

3.2b Imaging Conditions and Image Acquision

For time-lapse imaging of live cells, aninverted fluorescent microscope, with a motorized stage, and environmental incubation chamber (5% CO2, 70-90% humidity, 37°C) is necessary. Software to control the microscope and automate the image acquisition process is essential (an excellent open-source microscope controller software is μManager which is available at: http://valelab.ucsf.edu/~nico/MMweb/overview.php) and microscope hardware and software that can minimize focal drift and maintain the focal plane of the froscope over the course of a multi-hour imaging experiment is also extremely helpful. ensure cell viability during the course of the experiment, we usually monitor and carefully control excitation power, exposure time, humidity, CO₂, and temperature. Typically, 20-30 distinct X-Y positions (or nodes) on a glass-bottom dish are chosen, with a typical exposure time per nodeof 300-500ms, and one image captured every 5-10 minutes.We have determined that this exposure time minimizes photobleaching and phototoxicity in jurkat cells, while still maintaining a high signal-to-noise ratio. It is important that the camera setting be tuned so that the dynamic range of fluorescence increaseor decrease over the course of the experimentdoes not produce saturation or allow the signal to drop into a regime of poor signal-to-noise. The type of objective, gain, and offset settings can also be changed to ensure proper image quality (a number of web-based resources, e.g. Nikon www.microscopyu.com, provide helpful information on microscopy conditions).

After acquiring the time-lapse data series, analysis programs are needed to ‘segment’ the image. There are many options for segmentation programs capable of tracking singlecells, (one commonly used program is CellProfiler(80)) and for an excellent review of single-cell imaging and segmentation see (81). Many labs, including us, utilize custom-writtenMatlab™ programs for automated cell tracking and to quantify GFP fluorescence intensity in individual cells over time (13).

3.2c Sample Trajectories from an Experiment

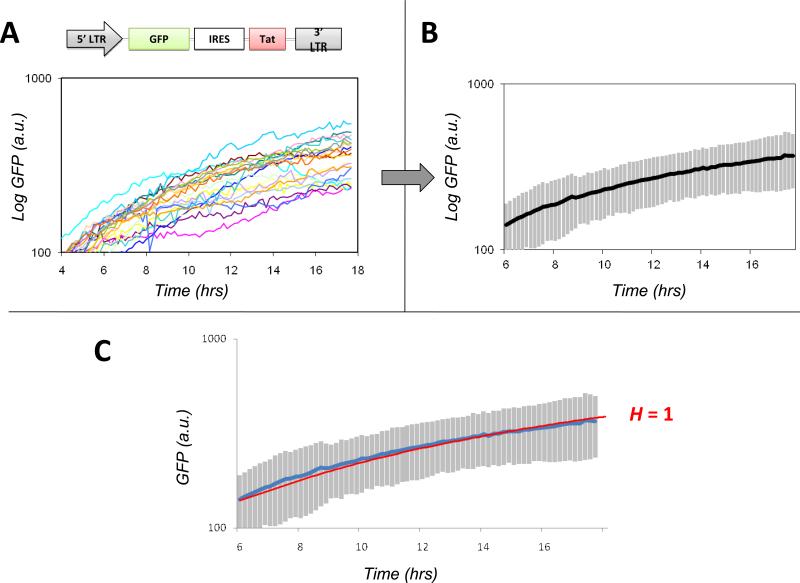
Once the individual cell trajectories have been acquired by ‘image segmentation’ these trajectories must be processedbefore comparison to mathematical models and fitting. We follow a scheme of background subtraction of the segmented trajectories followed by conversion to a log scale (Fig 4). In this experiment, jurkat T Lymphocytes with a stable integration of the LGIT plasmidare stimulated by tumor necrosis factor alpha (TNFα) and our automated in-house Matlab™ softwareextractsand segments raw trajectories for 25 individual cells. Background subtraction is then performed so that the fold-increase in GFP expression over background can be analyzed – we have found that background subtracted data exhibits a fold-increase that agrees with flow cytometery and Western Blot data (15). The individual cell trajectories are extracted from the single-cell movie (Fig 4A), the mean is calculated (Fig, 4B) and then converted to log scale (Fig 4B inset). Conversion to log scale is a typical approach used to fit data since log conversion minimizes the contribution of outlier data points.Although, the exact molecular interactions of Tat and the LTR cannot be deduced from the trajectories in Fig 4C, the GFP expression kinetics do not appear to increase at a rate greater than exponential (i.e. linear on a log scale)(Fig. 4B). The following sections will focus on fitting this time-lapse microscopy data to Eqs. 4 and 5 to determine the value of H.

Figure 4. Time-lapse GFP trajectories from individual LGIT-infected cells show that H = 1 for the Tat positive-feedback circuit.

(A) Plot of raw GFP trajectories versustime obtained after image segmentation of a time-lapse confocal microscopy movie of LGIT Jurkat cells immobilized on a glass slide and imaged live for 18 hours after addition of TNFα. Each trajectory represents an individual cell and each trajectory has been pre-processed by background fluorescence subtraction. (B) Plot of the calculated mean of the individual cell trajectories (blackline). Inset: Log-linear plot of the mean that is used for nonlinear least squares regression fitting to mathematical models. (C) Nonlinear least-squares regression fitting of the single-cell datato the mathematical model in Eq. 5. All parameters in Eq. 5 except Hwere fit to a parallel time-lapse movie of LG + TNFα (data not shown, see (15)) and H was allowed to vary. The green line represents the best fit obtained, which is H ≈ 1.Simulations were also performed by fixing the value of H to 0 (blue), 2 (purple), or 3 (red); none of these simulations generated a trajectory that could fit the data nearly as well as H = 1. (fits were performed on log-converted data to minimize the influence of outlier data points, fits trajectories were then back converted to linear scale)

3.2d Fitting the Single-cell Data to a model

To fit our microscopy data with the ODE model in Eq. 5, any number of different ODE solver softwarepackages can be used (e.g. Matlab™ or Mathematica™). The mean of the 25 ‘segmented’ trajectories is imported into the ODE-solver software package for fitting to Eq. 5. Ideally, parameter values for the basal rate of GFP and Tat expression – as well as the decay rates of GFP and Tat proteins – are determined from parallel experiments (e.g. with the LG construct or similar) but the values of these parameters should not effect the shape of the GFP increase. The only parameter that is essential to fit is the Hill coefficient, H. Fig 4C shows that H = 1 provides the best fit to the single-cell microscopy data for the LGIT construct. This analysis of the single-cell time-lapse data argues strongly that the Tat positive-feedback loop does not encode self-cooperativity and that Tat positive feedback lacks the architecture required for bistability. In support of this finding, parallel dose-response experiments, sorting experiments, and FRET-based analysis confirm that the Tat positive-feedback loop is notbistable(15).

The lack of bistability in Tat positive-feedback raises the question of how this circuit is able to mediate a decision between two states (on vs off) in the absence of bistability. Below, we show how simplified models of Tat positive feedback that consider stochastic fluctuations are sufficient to generate a decision between two different states (on vs off) without requiring H> 1 or bistability.

3.3 Stochastic Models of the Tat p ositive-feedback loop

3.3a Backaround on Stochastic Fluctuations and Stochastic vs ODE Modelina

Stochastic ‘noise’ arises from random thermal fluctuations in the concentration of protein, RNA or other molecules within the cell and is an unavoidable aspect of life at the single-cell level. Even cells in a clonal population (i.e. isogenic background)exhibit considerable cell-to-cell variation in the level of any specific gene product due to stochastic noise(82-84). The origin of this noise isbiochemical: it arises from intracellular processes that are driven by reactant moleculesrandomly diffusing and colliding within the cell. Noise in gene expression can arise from the random timing in individual reactions associated with promoter remodeling, transcription and translation (65, 85, 86) and intercellular differences in the amount of cellular components (for example, RNA polymerase, transcription factors and ribosomes) also cause variations in expression levels. Measurements in live, single cells have shown that gene expression noise can lead to large statistical fluctuations in protein and mRNA levels in both prokaryotes and eukaryotes (87-90). These fluctuations (i.e. noise) can have significant effects on biological function and phenotype.

The ODE models we have considered until now are continuous approximations models consider concentration, a quantity that varies smoothly even when describing the transition between a single molecule and zero molecules). ODE models describe the mean of a population, do not typically consider these molecular fluctuations, and are essentially an approximation for systems where a large number of molecules are present such that molecular fluctuations cancel out (Fig 5a).

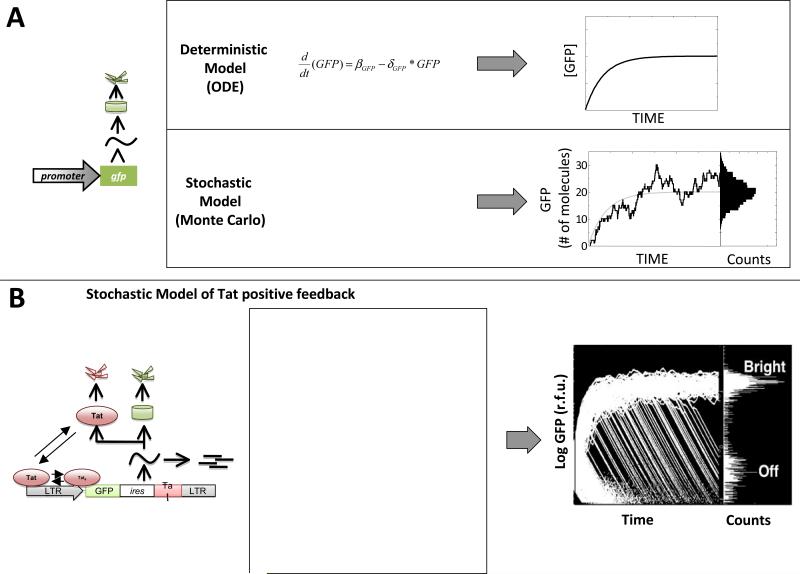
Figure 5. Stochastic fluctuations in the levels of Tat account for the developmental bifurcation of HIV-1.

(A) Deterministic (continuous) ODE models versus stochastic Monte-Carlo models for a simple gene circuit (left). The ODE model (top) generates a single smooth line that approximates the population average of a large population of GFP molecules. The stochastic model (bottom) considers a set of chemical reactions and generates a fluctuating trajectory that represents the number of molecules in the system (e.g. a single cell) over time. When simulated, each trajectory from such a stochastic model will vary and a histogram of GFP can be generated for any point in time.(B) Schematic, reaction scheme, and stochastic simulation results for the LGIT circuit(reproduced from (12)). The reaction scheme models a positive-feedback circuit lacking a bistable threshold (15) and 10,000 individual trajectories (where each trajectory represents a single cell) are shown for simulated time-span of one week to generate the histogram of 10,000 cells at right. The simulated model of Tat positive feedback is sufficient to reproduce the GFP bifurcation from the flow-cytometry data in Figure 1. The initial conditions for this simulation are: all species begin with zero value except LTR (1 copy), Tat (1 - 5 molecules), GFP (25,000 - 125,000 molecules); the parameter values are: k_basai = 10⁻⁸/sec, k_bind= 0.00015/sec, k_unbind= 0.017/sec, k_A = 0.001/sec, k_D = 0.13/sec, k_transact = 0.1/sec, dccay_mRNAn = 0.000048/sec, k_export = 0.00072/sec, k_GFP = 0.5/sec, k_Tat = 0.00132/sec, decay_mRNAc = 0.000048/sec, decay_GFP = 0.00000301/sec, decay_Tat= 0.0000043/sec.

Unlike ODE models, stochastic models describe the state of the system in terms of numbers of molecules and they model discrete numbers of molecules for each species (not continuous values such as concentration). Stochastic models are implemented by writing down a reaction scheme (Fig 5a) where the probability of any reaction going forward is modeled in a ‘Monte-Carlo’ fashion by choosing random numbers from distribution that describe the rate of random collisions between reactant molecules. Thus, the integer numbers of reactants and products fluctuates randomly between any two given simulation runs. In the regime of very large numbers of molecules, the fluctuations begin to overlap :el out such that stochastic models collapse to the ODE model (91). A clear fference between ODE models and stochastic Monte-Carlo models is that in Monte-Carlo models, each simulation trajectory can and will vary from every other simulated trajectory. Thus, by running many simulations we can generate a histogram of the trajectories for a given point in time, compare the simulated histogram to flow cytomteryhistrograms(12), and even use the variation around the mean to quantitatively analyze promoter architecture (9). For a thorough review on analyzing noise in gene circuits see (82). Below, we present a stochastic model of HIV Tat transactivation, and demonstrate how this no bistable model is sufficient to reproduce the HIV-1 decision-making phenotype.

3.3b Moving from an ODE to a Stochastic Model

Much like the setup of the wiring diagram in ODE models, a wiring diagram or ‘cartoon’ of the molecular reactions is helpful in generating a stochastic model. Based on our single-cell analysis (15) and literature studies (92), we can propose the wiring diagram and corresponding set of chemical reactions (Fig 5b). The reaction scheme in Fig 5bis by no means comprehensive and is intended to describe a minimal set ofreactions that are sufficient to generate a ‘decision’ (or bifurcation) in a positive-feedback loop without self-cooperativity(12). Each arrow indicates the direction of the reaction and the speed (or probability) of each reaction is indicated above (or below) each arrow by a parameter constant. As described in the next section, these reactions can be coded into freely available simulation programs such as BioNetS(93) and simulations can then be run to analyze the model of interest.

3.3c Running Stochastic Simulations

A variety of programs allow for stochastic modeling by running Monte-Carlo simulation using an algorithm now referred to as the ‘Gillespie’ algorithm (94, 95). Chemical reaction schemes can be coded for simulation using the Gillespie algorithm in a programming language (e.g. FORTRAN or C++), Matlab™, or a web-based freeware graphical user-interface (GUI) software tool such as BIONETS (93). In Figure 5b, we show a schematic and reaction scheme for the LGIT circuit. The reaction scheme models a positive-feedback circuit lacking a bistable threshold (15) and we present a sample simulation of 10,000 individual trajectories (where each trajectory represents a single cell).

At time=0 (the start of the simulation) each cell contains identical initial conditions, but over time, each cell follows a different (random) path. At any point in time we can analyze all GFP values to generate a histogram. The simulated model of Tat positive feedback is sufficient to reproduce the GFP bifurcation from the flow-cytometry data in Figure 1. From the histogram and simulation we can see that each individual cell has the potential of entering one of two states (Bright or Off). Importantly, in this model, every trajectory will eventually fall into the Off state (the off state is essentially a form of molecular extinction of Tat and acts as a trap from which the LGIT circuit cannot recover). This model coupled with experimental analysis (12, 15) was the first demonstration that a decision-making circuit, which lacked bistability, could generate a developmental bifurcation. Later work went on to demonstrate that the duration of the Tat transient in the bright state controlled entry and exit from HIV-1 proviral latency in full-length HIVAEnv system (13).

4. Conclusions

Here we argue that a coupled single-cell imaging and mathematical modeling approach can differentiate between alternate models of the HIV Tat transcriptional circuit and enables mapping of the architecture of the HIV-1 Tat latency circuit. We demonstrate that the Tat circuit lacks bistability (the ability to stably rest in two alternate states) by measuring the Hill coefficient of Tat feedback in single cells. We also show that a monostable circuit architecture that exploits stochastic noise in gene expression can account for the Tat circuit's ability to ‘choose’ between two alternate states. Importantly, the Tat circuit represents the first example of a natural decision-making circuit shown to lack bistability and utilize stochastic noise to probabilistically ‘choose’ between two alternate states (12, 13, 15).

Abbreviations

ODE

Ordinary Differential Equation

LG

LTR-GFP

LGIT

LTR-GFP-IRES-Tat

FACS

Fluorescence Activated Cell Sorting

Tat

Transactivator of Transcription

LTR

Long Terminal Repeat

GFP

Green Fluorescent Protein

MOI

Multiplicity of Infection

1RES

Internal Ribosomal Entry Sequence

FRET

Forster Resonance Energy Transfer