Loop 2 of myosin is a force-dependent inhibitor of the rigor bond

Abstract

Myosin’s actin-binding loop (loop 2) carries a charge opposite to that of its binding site on actin and is thought to play an important role in ionic interactions between the two molecules during the initial binding step. However, no subsequent role has been identified for loop 2 in actin-myosin binding. We used an optical trap to measure bond formation and bond rupture between actin and rigor heavy meromyosin when loaded perpendicular to the filament axis. We studied HMM with intact or proteolytically cleaved loop 2 at low and physiologic ionic strength. Here we show that the presence of intact loop 2 allows actomyosin bonds to form quickly and that they do so in a short-lived bound state. Increasing tensile load causes the transition to a long-lived state—the distinguishing behavior of a catch bond. When loop 2 was cleaved catch bond behavior was abrogated leaving only a long-lived state. These data suggest that in addition to its role in locating binding sites on actin, loop 2 is also a force-dependent inhibitor of the long-lived actomyosin complex. This may be important for reducing the duty ratio and increasing the shortening velocity of actomyosin at low forces.

Introduction

The initial actin-myosin binding step is thought to occur through long-range electrostatic interactions, creating a weak collision complex that is followed by isomerization to the attached state and a second isomerization to a rigor-like, strong-binding state (Geeves and Conibear 1995). Myosin’s actin-binding pocket is hydrophobic and is neighbored by the positively charged loop 2 (the “actin binding loop”) which is thought to help the myosin head to locate its binding site on actin (Rayment et al. 1993a). Once the initial electrostatic interaction between the loop 2 and actin’s myosin binding site is established, binding can proceed to a strongly-bound state through additional hydrophobic and stereospecific interactions (Geeves and Conibear 1995; Geeves et al. 1984).

Loop 2 connects myosin’s upper and lower 50 K domains (Rayment et al. 1993b). The general function of loop 2 includes the control of actin-activated ATPase activity by altering V_m and actin affinity (Murphy and Spudich 2000). The loop varies in length and sequence (Murphy and Spudich 2000) but is well-conserved among myosins with similar kinetics (Goodson et al. 1999). It is particularly reliant on the presence and sequence of a few key residues rather than its overall charge or length to retain its function in modulating kinetics (Murphy and Spudich 2000).

Because the loop is flexible, it is unresolved in most myosin II structures except for two from Dictyostelium discoideum (Lorenz and Holmes 2010). However, cross-linking and digestion studies have shown loop 2 to be part of the actomyosin binding interface (Mornet et al. 1981; Sutoh 1982). Still, the shape and location of loop 2 after binding is controversial. Molecular dynamics simulations suggest that myosin’s loop 2 takes on a distinct conformation upon actin-myosin binding, but its specific locations and interactions differ between studies (Liu et al. 2006; Lorenz and Holmes 2010). A recent high resolution cryo-EM-based model identifies potential electrostatic interactions between loop 2 on myosin and actin’s N-terminus, putting loop 2 at the center of the actin-myosin interface (Behrmann et al. 2012).

Skeletal muscle actomyosin has been shown to behave as a catch bond in the ADP and rigor states (Guo and Guilford 2006) and in both the presence and absence of the actin regulatory protein tropomyosin (Rao et al. 2011). Catch bonds increase in lifetime with applied force, up to a critical force value beyond which bond lifetime falls. Catch bonds stand in contrast to slip bonds, which decrease in lifetime with increasing load in an intuitively obvious way. Actomyosin catch bond behavior is though to arise from a force dependent transition from a short- to a long-lived bond state, while slip bonds have only a single bound state. In actomyosin the maximum bond lifetime occurs close to the isometric force that is generated by a single myosin molecule (Guo and Guilford 2006) suggesting that catch bond function is tuned to maximize bond lifetime during isometric contractions. Others have suggested that the actomyosin catch bond assists in aggregate formation and initial ordering from disorganized actin and myosin networks (Inoue and Adachi 2013).

Here we tested the hypothesis that myosin’s loop 2 alters the mechanics of rigor actomyosin bond formation and rupture, and specifically that it is involved in catch bond behavior. To do this we used force spectroscopy—the dynamic application of force to single molecules or single intermolecular bonds to reveal energy barriers to unfolding or dissociation. Force spectroscopy can reveal conformational and binding states that cannot be resolved by conventional methods of structural biology (Rao et al. 2011). In this instance an optical trap was used to measure the binding rate and the bond lifetimes between heavy meromyosin (HMM) and actin over a range of compressive and tensile loads applied perpendicular to the filament axis. These measurements were performed at both low and physiologic ionic strength. Measurements of intact HMM were compared to those when loop 2 was enzymatically cleaved in order to determine the contributions of loop 2 to binding and unbinding. Our data suggest that loop 2 is a force-dependent inhibitor of a long-lived bound state of actomyosin.

Methods

Proteins

HMM was purified from rat skeletal muscle as described in Guo and Guilford (2004) with minor modifications. Briefly, 400 mg muscle tissue was homogenized on ice in 2 ml extraction buffer (0.3 M KCl, 0.01 M HEPES, 0.01 M Na₄P₂O₇·10 H₂O, 1 mM MgCl₂, 0.01 M DTT, 1 mM ATP, pH 6.8) with protease inhibitor (SIGMAFAST^™, Sigma-Aldrich, St. Louis, MO). The homogenate was stirred for 30 min on ice, then clarified at 140,000 g for 1 h. Supernatant was diluted with three volumes of 1 mM DTT and left undisturbed on ice for 1 h. Myosin was collected by centrifugation at 15,000×g for 20 min. Precipitated myosin was dissolved in 200 μl storage solution (0.5 M KCl, 0.05 M KH₂PO₄, 2 mM MgCl₂, 0.01 M DTT, pH 6.8). HMM was prepared from fresh myosin by adding α-chymotrypsin (59.3 units/mg protein, Sigma C4129) in 0.001 N HCl to a final concentration of 0.04 mg/ml and incubated at room temperature for 7 min. The reaction was quenched by adding PMSF (Sigma-Aldrich) in ethanol to a final concentration of 0.5 mM and dialyzed overnight against 1 L actin buffer (0.25 M KCl, 0.25 M Imidazole, 1 mM EGTA, 4 mM MgCl₂, pH 7.4) with 2 mM DTT at 4 °C. The dialysis product was clarified at 200,000 g for 30 min and the HMM supernatant was stored in liquid nitrogen in aliquots containing 50 % glycerol.

F-actin was prepared from rat skeletal muscle as described in Pardee and Spudich (1982), biotinylated with N-hydroxysuccinimide biotin according to Rao et al. (2009), and stabilized with phalloidin. Biotinylated actin filaments were coupled to 0.97 μm diameter streptavidin-coated microspheres (Bangs Laboratories, Fishers, IN) by combining a suspension containing ~4 × 10⁸ beads with a 3 μM final concentration of biotinylated actin filaments and allowed to couple with overnight mixing at 4 °C. Beads were washed and resuspended with actin buffer. Actin-coated beads were stored in actin buffer with 10 mM DTT at 4 °C for up to 2 weeks. HMM and actin-coated beads were diluted immediately before use in actin buffer containing either 0.025 M or 0.145 M KCl.

Tryptic proteolysis of HMM loop 2

HMM was selectively digested at the actin-binding loop 2 (cleaved HMM) as described in Bobkov et al. (1996) with minor modifications. Briefly, HMM was dialyzed against 0.02 M KCl, 0.02 M Tris–HCl and 1 mM DTT at pH 7.4. To protect loop 1 from digestion, the ionic strength was increased to 0.5 M KCl and ATP was added to 6 mM (Mocz et al. 1984). TPCK-treated trypsin (proteolytic activity 0.08 BTEE units/mg; Sigma-Aldrich T1426) was added to HMM to a final concentration of 0.05 mg/ml and incubated on ice for 6 min. Digestion was stopped using soybean trypsin inhibitor type 1-S (Sigma-Aldrich T9003) at a molar ratio of 3:1 to trypsin. Cleaved HMM was used within 48 h of digestion, and then discarded.

Digestion was assessed by electrophoresis on NuPAGE 12 % Bis–Tris Gel in MOPS running buffer and gels were stained using SimplyBlue^™ Safe Stain (Invitrogen, Carlsbad, CA). The molecular weight of fragments was determined by comparison to SeeBlue^® Plus2 Protein Standard (Invitrogen) using the AlphaEaseFC (Alpha Innotech Corp., San Leandro, CA) molecular weight tool. As in previous experiments digestion of HMM mainly resulted in two fragments, the N-terminal fragment of S1 and the combined C-terminal region of S1 fragment and S2 (Bálint et al. 1975; Bobkov et al. 1996) (Fig. 1). Other contaminating fragments were present in low amounts.

Fig. 1.

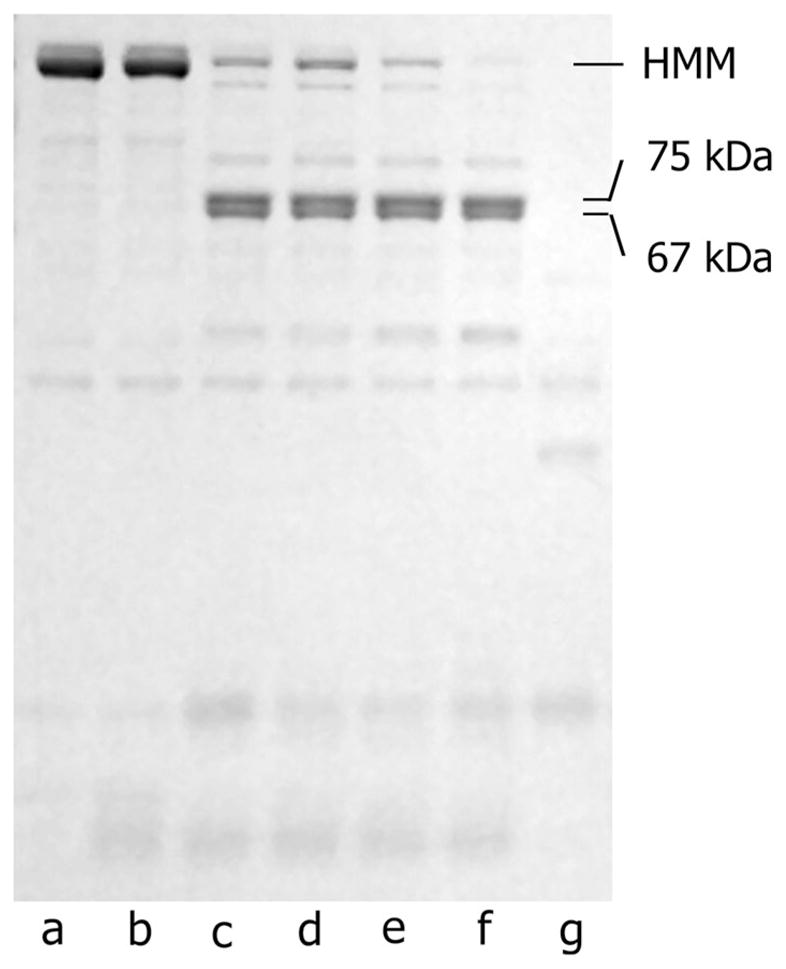
Representative tryptic digestion of HMM. Lanes (a) HMM prepared by chymotryptic digestion of myosin. (b) Soybean trypsin inhibitor and HMM. (c) HMM pre-incubated with soybean trypsin inhibitor before addition of trypsin. Lanes (d–f) show HMM digestion by trypsin quenched with soybean trypsin inhibitor after 2 (d), 4 (e), and 6 (f) min. (g) HMM digestion by trypsin without inhibitor, which was used as a control. Note that all samples were stored on ice overnight following addition of inhibitor

In vitro motility assay

Motility was measured as described by others (Guo and Guilford 2004; Kron et al. 1991; Uyeda et al. 1991; Warshaw et al. 1990) at 30 °C. Briefly, intact, cleaved, or fully digested (no trypsin inhibitor) HMM was applied to a flow cell made of a glass slide and nitrocellulose-coated coverslip separated by mylar shims. After a 1 min incubation, the flow cell was blocked with 1 % BSA (Sigma) in actin buffer with 10 mM DTT for 1 min, followed by addition of TRITC-phalloidin labeled actin filaments. After a 1 min incubation, the flow cell was washed with actin buffer with 10 mM DTT and motility buffer (25 mM KCl, 25 mM Imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT, 1 mM ATP, 0.5 % Methylcellulose, pH 7.4) containing an oxygen scavenger system was applied. The flow cell was incubated for 1 min at 30 °C before imaging. The mean velocities of filaments and the fraction of filaments that move were determined using the tracking algorithm described in Snook et al. (2008).

Laser trap

The laser trap used in these experiments was the same as described in Guilford et al. (2004) with minor modifications. The laser is a 25 W, 1,020 nm fiber laser (SPI Lasers, Santa Clara, CA), and the digital signal processor has been replaced by a field-programmable gate array (National Instruments, Austin, TX) with a user interface created in LabVIEW (National Instruments). Back focal plane interferometry was used to measure the position of a trapped bead relative to the trap center, from which measurements of displacement and force were calculated. The temporal resolution of the detection system is 150 kHz. The sensitivity of the interferometer and the trap stiffness were calibrated by the step response method (Dupuis et al. 1997; Svoboda and Block 1994) and by fits to the power spectral density (Allersma et al. 1998).

Coverslips coated with 3–10 μm glass spheres (targets) and then coated with nitrocellulose were prepared as in Guo and Guilford (2006) and assembled into flow cells. HMM was incubated in the flow cell for 1 min. The flow cell was then blocked with 1 mg/ml BSA in actin buffer for 1 min and washed with actin buffer. A suspension of actin buffer and actin-coated beads was added to the flow cell. An oxygen scavenger system (0.125 mg/ml glucose oxidase, 0.0,225 mg/ml catalase, 2.87 mg/ml glucose) and 0.01 mM DTT were included in the actin buffer and the bead suspension. The flow cell was placed onto a piezoelectric microscope stage (nPoint Inc., Middleton, WI, USA).

All experiments were performed in the absence of nucleotide with intact or cleaved HMM in the presence of 0.025 M KCl (low ionic strength) or 0.145 M KCl (physiologic ionic strength). Actin-coated beads were captured in a laser trap and brought into contact with a HMM-coated target for 1 s. The concentration of HMM used to coat the target depended on the experiment—10 μg/ml HMM for bond rupture experiments, or 80 μg/ml HMM for bond formation experiments. The laser trap was stepped 200 nm away from the target and held there for 1 s before repeating this cycle (Fig. 2). The initial separation between the trapped bead and the target was random, resulting in random compressive and tensile loads. Over a large number of experiments this resulted in a range of random step loads being applied to actin-HMM bonds using the laser trap. Bond formation was accompanied by the trapped bead remaining in contact with the target after the laser trap was stepped away from it. Bond rupture was accompanied by return of the bead to its original position away from the target. Bond lifetime was defined as the time elapsed between stepping the laser away from the HMM-coated target and bond rupture. The tensile load experienced by a bond was calculated from the stiffness of the laser trap and the distance a bead moved to return to the center of the laser trap. Details of individual laser trap experiments, including the determination of loads, are given in the results section.

Fig. 2.

a Experimental set up. A bead coated in actin is captured in the laser trap. The laser is rapidly stepped toward a nitrocellulose-covered glass bead coated in HMM, bringing the molecules within binding range. The actomyosin bond is loaded by rapidly stepping the laser trap away from the HMM-coated target. The load on the bond is directed perpendicular to the axis of the filament. b A representative data trace collected for an intact HMM-coated target. (i) The actin-coated bead was stepped 200 nm toward the stationary HMM-coated target which is visible as a jump in the displacement signal. (ii) The molecules were allowed time to form a bond. (iii) t_b, the time elapsed from when the bead was stepped toward the target and when a bond formed (time to bond formation) was identified by a slight shift in the displacement signal and a decrease in Brownian motion. (iv) The bond was then loaded perpendicular to the axis of the filament by stepping the laser 200 nm away from the HMM-coated target which is seen as a second jump in the displacement signal in the opposite direction of the original shift. In bond rupture measurements, (v) the resulting bond lifetime was measured as (iv) the time from when the laser was stepped away from the target to (vi) the time that the bond ruptured and the bead returned to the center of the laser trap. Bond rupture is characterized by the displacement signal returning to the original baseline accompanied by a return to the original level of Brownian motion in the displacement signal. (vii) The tensile load experienced by a bond was calculated based upon the stiffness of the laser trap and the sensitivity of the quadrant photodiode detector. In bond formation experiments, (vii) the compressive load between the actin-coated bead and the HMM-coated target was calculated as the difference between distance the laser was stepped and the distance the actin-coated bead actually moved, multiplied by the stiffness of the laser. The second y-axis, Force (pN), is the product of the displacement signal (V), the stiffness (pN/nm) and sensitivity (nm/V) calibrations specific to this example data trace. Displacement signal values >0 are not shown because the laser is refracted by the target when the laser is nearby and therefore the stiffness and sensitivity calibrations measured far from the target do not apply in that position. Laser trap stiffness is 0.10 pN/nm for the sample data trace

Loads were applied perpendicular to the axis of the filament. The minimum bond duration that can be measured by our laser trap system is 62 μs, which is the time it takes a bead under a representative 7 pN force to travel the shortest distance at which it would be outside the range of the noise, given a 99 % confidence interval. Bonds shorter than 4 ms were not measured.

Bond lifetimes were divided into 2 pN bins, within any one of which the lifetimes were exponentially distributed. 95 % confidence intervals of the mean of the exponentially distributed bond lifetime data were calculated in each 2 pN force bin using the equation

$$\theta \in \left(\frac{2{\sum }_{i=1}^n{X}_i}{{\mathrm{\chi }}_{\mathrm{\alpha }/2,2n}^2},\frac{2{\sum }_{i=1}^n{X}_i}{{\mathrm{\chi }}_{1-\mathrm{\alpha }/2,2n}^2}\right),$$ (1)

where X_i is an exponentially distributed variable with mean θ of n total measurements and α = 0.05 (Ross 2009).

Bond lifetimes at near-zero load were measured as in Guo et al. (2006) by holding an actin-coated bead adjacent to an HMM-coated target and allowing bonds to form and break under low, semi-random loads. Bond formation was identified by a decrease in Brownian motion accompanied by a small shift in baseline, and bond rupture by a reversal of those changes. Fits to power spectral density were used to calibrate the laser trap stiffness and detector sensitivity.

Control experiments were performed at 0.145 M KCl with blank targets (no HMM) as well as in the presence of 1 mM pyrophosphate in the bead suspension which is thought to be analogous to the prehydrolysis, myosin-ATP state (Gränicher and Portzehl 1964).

Results

Ionic strength has a modest effect on the actomyosin catch bond

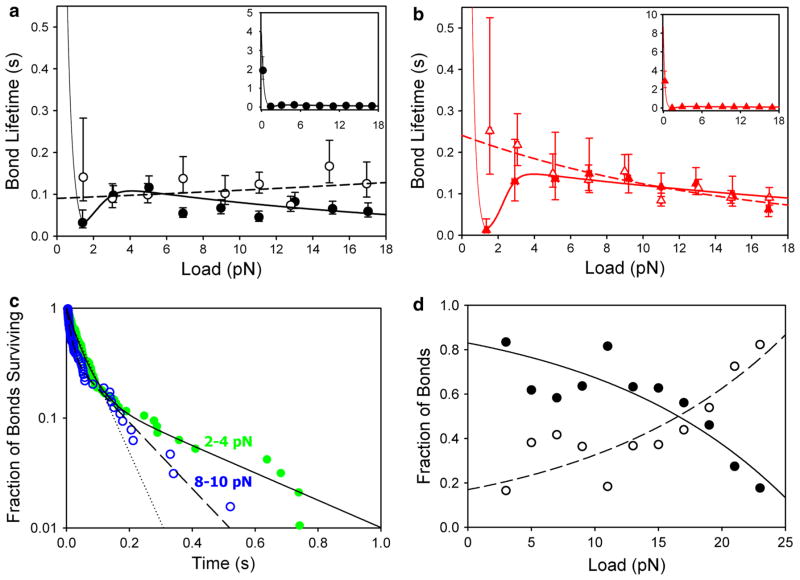
Our data at low (Fig. 3a) and physiologic ionic strength (Fig. 3b) are consistent with previous reports from our lab that found the actin-HMM bond to behave as a catch-slip bond (Guo and Guilford 2006; Rao et al. 2011). The peak bond lifetimes were greater at physiologic ionic strength compared to low ionic strength, 0.15 and 0.11 s, respectively, though this difference is not statistically significant. The critical force (at which peak lifetime occurs) was obtained from the fitted parameters from a two-pathway model (Pereverzev et al. 2005, Eq. 9) and was similar for the two conditions—4.09 and 3.95 pN at low and physiologic ionic strength, respectively. These values are slightly lower than previously reported by us but are well-within the range of forces reported for the isometric force generated by a single myosin molecule (Finer et al. 1994; Guilford et al. 1997; Molloy et al. 1995; Takagi et al. 2006; Tyska et al. 1999), supporting the notion that bond kinetics are closely matched to biomechanical function in myosin (Guo and Guilford 2006).

Fig. 3.

a At low ionic strength the catch bond formed between intact HMM and actin (circle) is abrogated when loop 2 is cleaved (open circle). Catch bond data were fit by the two-pathway model (bold solid line) (Pereverzev et al. 2005). Cleaved HMM exhibited ideal bond behavior. These data were fit by the single-pathway model (dashed line) (Bell 1978). Near zero load data at low ionic strength for intact HMM were fit by an exponential decay (unbold solid line) (Guo and Guilford 2006). Near zero load data points are off the scale of the axis. Inset Same as intact HMM shown in full figure with vertical axis extended to include near zero load data. b At physiologic ionic strength the catch bond formed between intact HMM and actin (red triangle) is abrogated when loop 2 is cleaved (red open triangle). Lines were fitted as in (a). a & b There is a trend toward longer bond lifetimes at physiologic ionic strength though this difference is not statistically significant. Color and symbols are consistent with Fig. 4. The mean number of bonds measured per 2 pN force bin was 58. Horizontal error bars represent the standard error of the mean load for each 2 pN bin and most fall within the symbols. Vertical error bars represent the 95 % confidence intervals of the exponentially distributed data. c The fraction of bonds surviving over time was plotted for two representative force bins, 2–4 pN (green circle, n = 95) and 8–10 pN (black open circle, n = 63) from the low ionic strength condition with 10 μg/ml HMM present. 2–4 pN data were fit with a single (dotted line) and double exponential decay weighted by time (solid line). 8–10 pN data were fit with a double exponential decay weighted by time (dashed line). The two phases of the double exponential decay suggest a short- and a long-lived bond state are present in each population. d The fraction of bonds in a short- (black circle) and long-lived (black open circle) state for each force bin in the low ionic strength condition with 10 μg/ml intact HMM is shown. The population of bonds shifts from a short-lived to a long-lived state with increasing tensile load. Data were fit by a force-dependent Boltzmann distribution. The mean total number of bonds in each 2 pN force bin (short- and long-lived state combined) was 56

As a control, the same measurement was performed at physiologic ionic strength both in the presence of 1 mM Na₄P₂O₇ (pyrophosphate; PPi) as well as in the absence of HMM (a blank target surface). Both control conditions resulted in a flat bond lifetime profile over the range of loads measured, confirming that non-specific bonds are roughly load-independent (Guo and Guilford 2006; Kong et al. 2009). The binding frequency—the fraction of bonds formed per those attempted—was lower for the control than for the experimental measurements. The binding frequency was 2.8 and 3.0 % for HMM with PPi and for blank targets, respectively. This compares to 11.1 and 19.8 % for intact and cleaved HMM at low ionic strength, and 18.8 and 18.5 % for intact and cleaved HMM at physiologic ionic strength. These increased bond frequency and response to load suggest that our bond lifetime measurements are actin-HMM specific.

Solution studies suggest the actomyosin bond lasts for tens to hundreds of seconds in unloaded conditions (Marston 1982), but more recent data (Guo and Guilford 2006) as well as the data we present here show a rapid decrease in bond lifetime with infinitesimal loading. The mean bond lifetimes at loads of only 0.21 ± 0.01 pN for low and physiologic ionic strength were 1.9 ± 0.6 s and 2.9 ± 0.7 s, respectively (p = 0.206). Data were fit using an exponential decay, shown in Fig. 3a, b. This divergence of infinitesimal loads from solution studies (zero load) has also been seen in catch bonds unrelated to actomyosin, such as L- and P-selectin with receptor PSGL-1 (Fritz et al. 1998; Marshall et al. 2003; Phan et al. 2006; Sarangapani et al. 2004). It has been postulated that this rapid decrease is due to loading of the actomyosin bond overcoming the tension of water at the interface between the actomyosin molecules in an aqueous environment (Prezhdo and Pereverzev 2009).

The actomyosin catch bond is the result of allostery

Myosin has been proposed to act as an allosteric catch bond (Rao et al. 2011). The allosteric model describes molecules starting in one of two bound states, each with a different dissociation rate, and the ratio of bonds in these states is dependent upon applied force (Thomas et al. 2006). In other words, it is possible that load applied to the actomyosin complex changes the conformation of the complex from a relatively short-lived state to a relatively long-lived state. To test this hypothesis, the fraction of bonds surviving over time was plotted as a function of applied tensile load (Fig. 3c) and fitted by exponentials.

As previously reported, the bond survival data was significantly better fit by a double- than a single-exponential decay (Rao et al. 2011); this is suggestive of an allosteric catch bond mechanism (Thomas et al. 2006). A closer look at the force-dependent fraction of bonds surviving in the short- and long-lived states shows that with increasing force the proportion of bonds shifts to the long-lived state (Fig. 3d). A force-dependent Boltzmann distribution was used to fit the distribution at steady state between the two hypothetical states as in Snook and Guilford (2010),

$$z_i(f)/z_{\mathit{total}}(f)=exp((-\mathit{\Delta }{E}_i+f{x}_{i\delta })/k_{B}T),$$ (2)

where f is applied load, z is the number of bonds in a particular state i (short- or long-lived), z_total is the total number of bonds, ΔE_i is the energy difference between the two states, x_iδ is the transition state distance between the two states, k_B is the Boltzmann constant, and T is the absolute temperature. This assumes that the redistribution between the states reaches rapid equilibrium as force is applied. When the fit was extended to f = 0, 91 % of bonds were predicted to be in the short-lived state at zero load (analogous to solution studies, but not reflecting the rapid increase in lifetime <2 pN). The fitted value of ΔE = 1.8 ± 0.2 × 10⁻²¹ J. The fit also predicts a conformational change of x_iδ = 2.7 ± 0.5 Å accompanying myosin’s transition to the long-lived state.

Loop 2 is required for catch bond behavior

Catch-bond behavior was abrogated with the cleavage of loop 2, suggesting that an intact actin-binding loop is essential for the force-dependent transition from a short- to a long-lived bond state. The bond between actin and cleaved HMM was best fit with a single dissociation pathway from a single bound state (Bell 1978) at both high and low ionic strength (Fig. 3a, b). Interestingly, the surviving bound state is the long-lived state, suggesting that loop 2 functions to weaken the actomyosin bond.

One might argue that the observed differences between intact and cleaved HMM arose from a population of inactive or aberrant heads present in the cleaved HMM. If so, this would likely be reflected in a change in actin filament motility driven by cleaved HMM. In vitro motility was performed on intact, cleaved, and fully-digested HMM at equal surface densities in the flow cell. The mean velocities of intact and cleaved HMM were 3.7 ± 0.07 μm/s and 4.4 ± 0.10 μm/s respectively. Actin filaments did not bind to fully digested HMM. The mean velocity of intact and cleaved HMM samples displayed a trend opposite to those reported in Bobkov et al. (1996), where they observed a small decrease in velocity in cleaved HMM. However, in their study motility of intact HMM was measured under a different experimental condition (no methylcellulose) than was cleaved HMM. Methylcellulose was used for all motility measurements reported here.

Load dependent 2D on-rates

The load-dependent 2D on-rate (the rate of bond formation) was measured over a range of compressive forces (−4.0–21.7 pN) using a method reported previously by us (Rao et al. 2011) and others (Chen et al. 2008). Intact or cleaved HMM was applied to flow cells at a concentration of 80 μg/ml. The surface density was increased because on-rate experiments require a surface density high enough to overcome the limitations of diffusion in the ligand-receptor interaction, whereas bond lifetime measurements necessitate low site densities to ensure single bond events (Snook and Guilford 2012). An actin-coated bead was brought into contact with an HMM-coated target for 1 s, then rapidly stepped 200 nm away perpendicular to the filament axis for 1 s. This cycle was repeated 30 times.

Bond formation was observed directly in the laser trap. We observe a change in the mean signal magnitude and variance (due to Brownian motion) when the first bond forms between the trapped bead and the target. The time to bond formation (t_b) is the elapsed time between arrival of the bead at the target and the moment of bond formation (Fig. 2b, position iii). 2D on-rate is inversely related to t_b:

$$k_{on}^o={(t_b{m}_r{m}_l{A}_c)}^{-1},$$ (3)

where m_r is the site density of HMM on the nitrocellulose-coated targets (3,300 heads/μm²) (Guo and Guilford 2004), m_l is the density of available myosin binding sites on actin-coated beads (637 sites/μm²), and A_c is the effective contact area between the target and trapped bead (0.14 μm²) as calculated using Eqs. 1 & 2 in Rinko et al. (2004). Specific 2D on-rate data were fit using a “reverse Bell model” as in Snook and Guilford (2010). The perpendicular, compressive force (f_c) between the bead and the target during bond formation was calculated as the difference between the distance the laser was stepped and the distance the bead actually moved after bond rupture, multiplied by the stiffness of the laser trap. Negative f_c values indicate no contact between the bead and the target, resulting in a time-averaged tensile rather than compressive load.

Load-dependent specific 2D on-rates are shown in Fig. 4. With increasing compressive loads the specific 2D on-rates for intact HMM at low ionic strength approached the value reported by Rao et al. (2011) (2.0 × 10⁻⁴ μm²/s) measured under similar conditions but without controlling inward compression. The two ionic strength conditions displayed similar 2D on-rates at low compressive loads but diverged with increasing compressive load. On-rates were lower at physiologic ionic strength. This inverse relationship between ionic strength and 2D on-rate is consistent with previous measurements of association rates using classical methods (Coates et al. 1985; Marston 1982; Taylor 1991; White and Taylor 1976).

Fig. 4.

Intact HMM binds to actin faster at low (solid black circle) and physiologic (solid red triangle) ionic strength than cleaved HMM (open black circle and open red triangle are low and physiologic ionic strength, respectively) over a range of compressive loads. The load-dependence of specific 2D on-rate is reduced when cleaved HMM is forming bonds with actin at physiologic ionic strength. Data were fit by a reverse Bell model (Snook and Guilford 2010). The fitted value for the specific 2D on-rate for cleaved and intact HMM at low and physiologic ionic strength were compared using a z statistic and were not statistically different (p = 0.179 and 0.102). The mean number of bonds per 2 pN force bin is 38. The range of independent beads used per condition is 139–171. Data were divided into 2 pN bins and data points were plotted at the mean force value for each bin

HMM with loop 2 cleaved exhibited lower specific 2D on-rates than intact HMM over the range of forces measured. This is particularly apparent for cleaved HMM at physiologic ionic strength, which additionally exhibited reduced load-dependence in its binding rate. Bonds took ~2 times longer to form at physiologic ionic strength when loop 2 was cleaved (p = 0.102). Botts et al. (1982) found the actin-S1 association constant decreased when S1 loops 1 and 2 were cleaved. Bobkov et al. (1996) similarly observed decreased affinity of HMM for actin when loops 1 and 2 were tryptically cleaved, and to a lesser extent when only loop 2 was cleaved. Our direct measurements of actin-HMM binding confirm that loop 2 cleavage decreases the actomyosin binding rate and show that the reduction is similar at both low and physiologic ionic strength.

Discussion

Our data confirm that loop 2 accelerates actin-myosin binding, but also reveal that loop 2 serves as a force-dependent inhibitor of a long-lived rigor state.

Catch-bond behavior arises from the ability of actomyosin to form a short- or long-lived bound state with the balance between them being force-dependent. One might suppose that these two bound states are the weakly and strongly bound states; however, catch bond behavior remained when the ionic strength was increased almost six fold. Therefore, it is independent of weak binding, and the short- and long-lived states comprising the actomyosin catch bond must arise from two force-dependent strong-binding states of myosin. As our experiments were performed in the absence of nucleotide, these data suggest that myosin has two rigor states, and that force regulates the distribution between them via loop 2. The actomyosin bond will typically form in the short-lived state, and rupture from either the short- or long-lived states as biased by internally and externally applied loads.

Rao et al. (2011 and others have suggested that myosin acts as an allosteric catch bond resulting from movement at one of its hinge regions; Thomas et al. 2008). The present data, however, suggest that a much smaller change in loop 2 or its adjoining domains is responsible for the allosteric change from a short- to a long-lived bond state shown in the scheme in Fig. 5. Removal of either pathway would result in slip-bond behavior, but the bond lifetime at low forces reveals which pathway has been eliminated. Indeed, when loop 2 was cleaved catch bond behavior was eliminated and only the long-lived pathway remained. Fig. 3a, b show that loop 2 cleavage extended bond lifetimes at low forces to durations greater than at the critical force of the catch bond; this is the long-lived pathway.

Fig. 5.

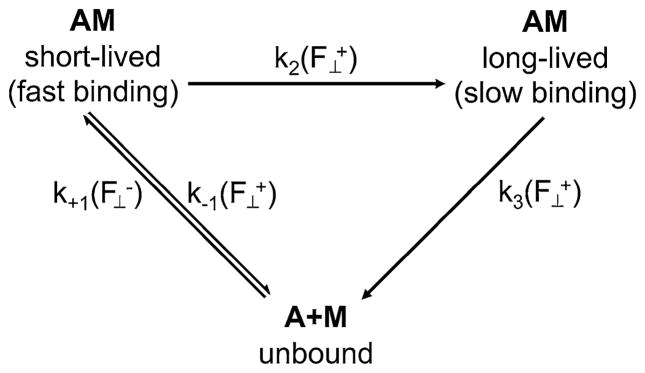
A scheme of the two states in which rigor myosin can bind actin (AM) and unbind (A+M) from actin. Myosin binds at rate $k_{+\mathit{1}}(F_{\perp }^{-})$ in the short-lived state under a compressive load $F_{\perp }^{-}$ applied perpendicular to the filament axis. A perpendicular tensile load $F_{\perp }^{+}$ applied to this short-lived bond will cause the bond either to break at rate $k_{-\mathit{1}}(F_{\perp }^{+})$ or to transition into a long-lived bond state with rate $k_{\mathit{2}}(F_{\perp }^{+})$. Bonds that are in a long-lived bond state rupture at rate $k_{\mathit{3}}(F_{\perp }^{+})$. Bonds form and rupture faster in the short-lived state than in the long-lived state. The majority of bonds form in the short-lived state and transition to a long-lived state instead of forming directly in the long-lived bond state

To understand how the load-dependent rupture of the actomyosin bond could potentially affect a cycling cross-bridge, and the role of loop 2 in particular, we modeled rate of passage of myosin through the crossbridge cycle under the influence of load (Supplementary material 1). Our model predicts the time required for a population of actomyosin bonds starting in the ADP-bound state to dissociate through biochemical (spontaneous or nucleotide-driven dissociation) or biomechanical (load-dependent dissociation) pathways to unbound myosin. Interestingly, our model predicts that skeletal muscle crossbridges are more likely to dissociate because of applied mechanical tension at low loads than by nucleotide binding. The opposite is true above ~2 pN. Therefore, the main impact of the catch bond on the cycling crossbridge in skeletal muscle may be to enable higher unloaded shortening velocities. During shortening, attached crossbridges impose a resistive drag on others that are undergoing power strokes, thus reducing sliding velocity. Hooft et al. (2007) suggested that reducing the bond duration of resistive myosin heads increases the shortening velocity, thereby overtaking ATP binding in limiting shortening velocity.

When a similar model is applied to a slower-cycling phasic smooth muscle, however, the catch bond is predicted to increase the crossbridge dissociation rate and therefore decrease bond duration over a wide range of forces (0–10 pN). This may act as a mechanism to prevent cross-bridges from remaining bound too long. The evolutionary history of class II myosin (Korn 2000) suggests that the loop 2 catch bond function may have developed in smooth and non-muscle myosin, but may have later become vestigial in skeletal muscle myosin where the crossbridge movement accompanying ADP release is small.

Our model relies upon biomechanical dissociation rates that we measured with tension applied perpendicular to the axis of the filament. This loading direction is less physiological than axial loading, but offers a defined direction to the load on the bond. The compliance of the myosin molecule suggests that a tension applied to the actomyosin crossbridge parallel to the filament axis is not pure shear, nor is it purely tensile or compressive.

Though allostery accounts for catch bond behavior in bond rupture, the allosteric model of bond formation does not account for the observed load-dependence of bond formation (Snook and Guilford 2010). Our load-dependent specific 2D on-rate data suggest that in applying a compressive load we are forcing the opposing binding sites together. This has been termed a “reverse Bell model,” in which the energy landscape for bond formation is tilted and therefore activation energy required to form a bond is lowered (Snook and Guilford 2010).

There is not enough evidence to determine whether the observed effects of compressive load on actomyosin binding are physiologically important. As the filaments slide, the bond formation may occur under a compressive force if it does so as the myosin head is approaching its binding site on actin; this is because the continuing motion of the filaments may drive the myosin head into its binding site. Similarly, bond formation may occur under a tensile force if it does so after the myosin head has passed its binding site on actin.

Ionic strength is an important factor in the initial collision complex formation between actin and myosin as well as development of the subsequent attached state in actomyosin binding. (Geeves and Conibear 1995). Because of decreased actin-myosin binding affinity at physiologic ionic strength, classical solution studies (Eisenberg and Moos 1968; White and Taylor 1976) and actin-myosin in vitro motility (Takiguchi et al. 1990) have often been performed in non-physiologic, low ionic strength conditions. The geometric constraints acting on actin and myosin in vivo overcomes the problem of decreased binding affinity. The design of our experiments creates a partially constrained geometry in which the molecules are restricted to approximately planar movement, thereby allowing the actomyosin bond to be examined at physiologic ionic strength.

The data in Fig. 3a, b, and 4 show mirroring effects of ionic strength on bond formation and rupture. That is, physiologic ionic strength gives rise to low rates of bond formation but also gives rise to low rates of bond rupture (i.e. long lifetimes). Similarly, reduced ionic strength gives rise to high rates of bond rupture and also high rates of bond formation. Microscopic reversibility explains this as the same energy barrier being overcome to break a bond as was overcome in forming it. In this instance, ions must be excluded from the binding interface to allow ionic and hydrophobic interactions to form. When the ion concentration is increased, more energy is required to remove the ions from the binding interface. Similarly, there is an increase in energy needed to rescind the hydrophobic interactions between the binding interfaces of the two proteins and to resolvate them when ionic strength is high.

Loop 2 was previously thought to act only in searching out the myosin binding site on actin. Our data suggest that loop 2 also regulates actomyosin crossbridge kinetics in a force-dependent manner through its integral role in catch bond behavior. This introduces loop 2 as an important regulator of the actomyosin rigor bond.