Pitfalls of predicting complex traits from SNPs

Abstract

The success of genome-wide association studies has led to increasing interest in making predictions of complex trait phenotypes including disease from genotype data. Rigorous assessment of the value of predictors is critical before implementation. Here we discuss some of the limitations and pitfalls of prediction analysis and show how naïve implementations can lead to severe bias and misinterpretation of results.

Introduction

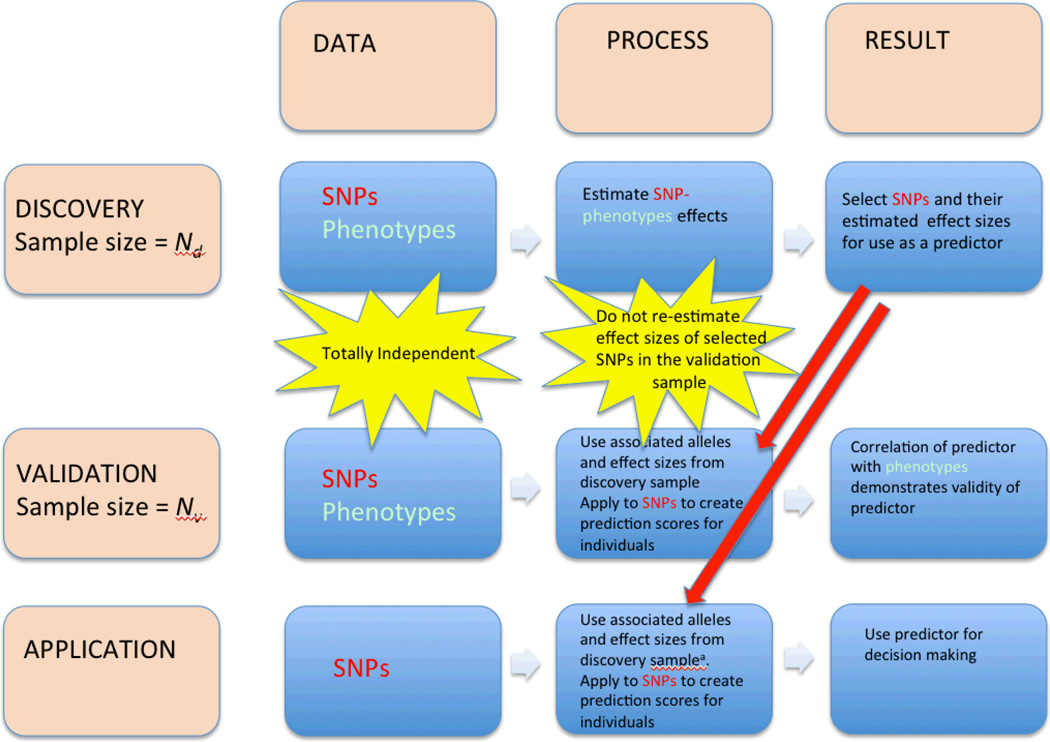
In many species, single nucleotide polymorphism (SNP)-trait associations have been detected through genome-wide association studies (GWASs). In addition to the discovery of trait-associated variants and their biological function, there is increasing interest in making predictions of complex trait phenotypes from genotype data for individuals in plant and animal breeding, experimental organisms and human populations. These predictions are based upon selections of SNPs (or other genomic variants) and estimation of their effects in a discovery sample, followed by validation in an independent sample with known phenotypes, and ultimately application to samples with unknown phenotypes (FIG 1).

Figure 1.

Flowchart of SNP-based prediction analysis. There are three stages for the development of a risk predictor – discovery, validation and application. At each stage data is needed as an input, a process is applied to the data and a result is generated.

^a. At this stage effect sizes estimated from combined discovery and validation samples can be used.

The validation stage of SNP- prediction analysis will be the main focus of this Perspective. Incorrect conclusions at this stage may lead to predictors that will not work as well as inferred or, in the worst case, have no prediction accuracy at all. We organise our Perspective into limitations and common pitfalls of prediction analysis. The limitations are partly inherent given the nature of the trait or the data available. These are factors that users should be aware of but mostly cannot change. The limitations also reflect use of sub-optimal methodology that could be improved upon. The pitfalls are common mistakes in analysis that can lead to over-estimation of the accuracy of a predictor or misinterpretation of results, and we give examples from the literature where these have occurred. We give our opinion on how best to avoid pitfalls in the derivation and application of SNP based predictors for practical applications. There are many aspects of risk prediction that are outside the scope of this article. They include a thorough treatment of the statistical methods that can be used in the discovery phase^1–7, the use of non-genetic sources of information to make predictions or diagnosis, a full discussion about clinical utility of risk prediction in human medicine and a discussion about ethical considerations for applications in human populations⁸.

Limitations of prediction analyses

Limitation 1: Prediction of phenotypes from genetic markers

Variation in complex traits is almost invariably due to a combination of genetic and environmental factors. A useful quantification of the importance of genetic factors is the heritability (h²), i.e. the proportion of phenotypic variation in a trait that is due to genetic factors⁹ (BOX 1). Assuming that the estimated h² is a true reflection of the population parameter, the upper limit of the phenotypic variance explained by a linear predictor (R²) based on DNA markers such as SNPs is h² and a genetic predictor can thus never fully account for all phenotypic variation. This upper limit is only achievable if all genetic variants affecting the trait are known and their effects are estimated without error. In human disease genetics, where ‘personalised medicine’ is actively being pursued, this limitation is not well understood in our opinion and hence we have chosen to highlight it here, even though it has been pointed out before^{10, 11}.

Box 1. Quantifying phenotypic variation explained by SNPs.

Quantitative traits

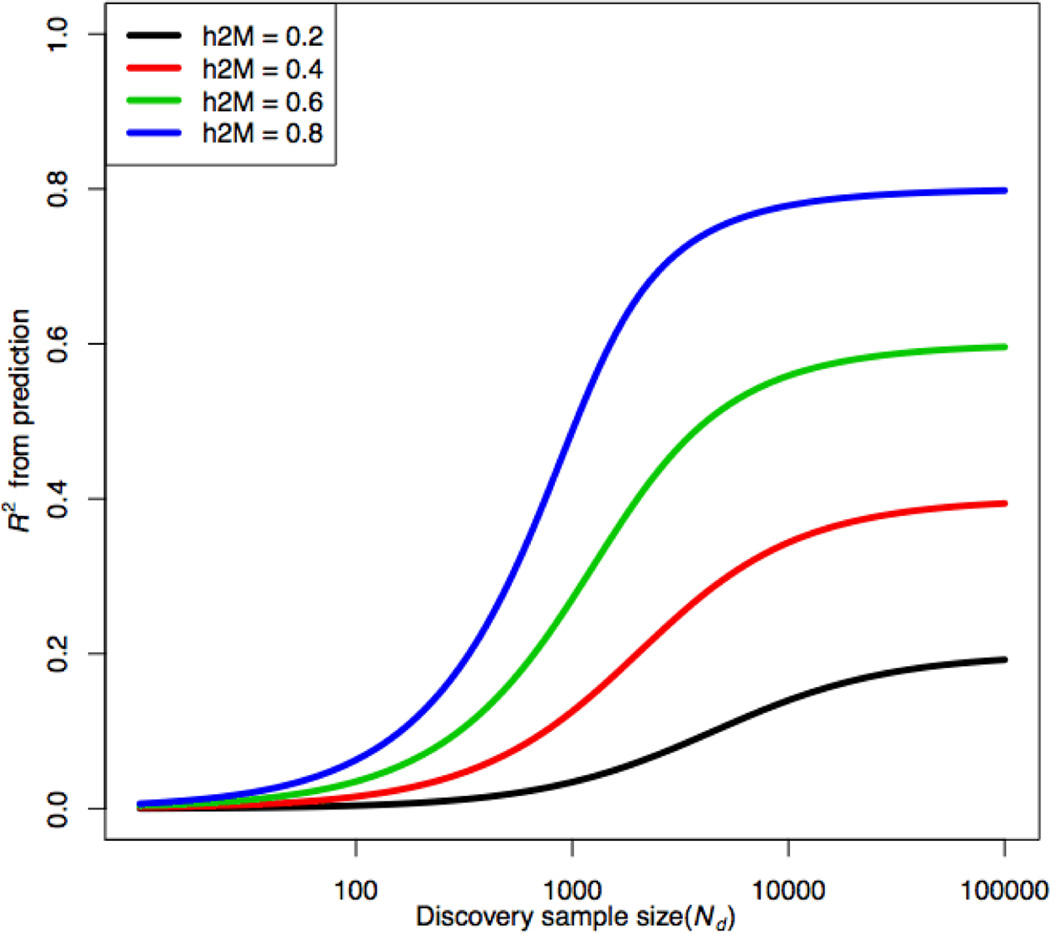
The proportion of phenotypic variance explained (R²) by a predictor of a quantitative trait formed using estimated effects of all markers depends on the number (M) of independent measured genomic variants (e.g., SNPs) associated with the trait, the proportion of the total variance they explain ($h_M^2$), and the sample size in the discovery sample (N_d)^{27, 36, 38}. If all marker effects are assumed to come from the same normal distribution, then approximately

$$R^2=\frac{h_M^2}{1+\frac{M}{N_d{h}_M^2}(1-R^2)}$$ [Equation 1]

Equation 1 holds regardless of the genetic architecture of the trait, but we note that the (least squares) predictor may be far from optimal. $h_M^2$ is usually less than the heritability estimated from family studies and is sometimes called the SNP-heritability or chip-heritability, estimated, for example, using GCTA⁵². Equation 1 is from the supplement of ref³⁸; when R² is small it can be ignored from the denominator, otherwise the quadratic in R² can be solved. The graph below shows that the sample size must be large in order to achieve a high R². If the distribution of marker effects sizes is markedly non-normal, with some large effects and many very small or zero effects, and if knowledge of this distribution is used in estimating SNP effects then higher R² can be achieved⁶¹.

In this article we use R² at the statistic to report efficacy of a predictor or R, the correlation between phenotype and predictor or accuracy. The sign of the correlation is important for interpretation of the predictor. In livestock, genetic predictors have been used for decades (based on pedigree data prior to the availability of genotypic data) and accuracy (R_G,Ĝ) is traditionally used to evaluate utility. R_G,Ĝ is the correlation between true and estimated genetic value (the predictor, which is an estimate of the combined value of all genetic loci). Since $R_{G,\widehat{G}}^2=\frac{R^2}{h^2}$, the R_G,Ĝ statistic quantifies the efficacy of a genetic predictor relative to the best possible genetic predictor.

Disease traits

For disease traits, Nagelkerke’s R² ($R_N^2$) has been used in profile scoring analyses, following Purcell et al²⁹. $R_N^2$ is an R² measure in binary (0–1) outcome data. Application is usually in case-control validation samples, where the proportion of cases is much higher than in the population. Alternatively, the area under the receiver operator curve (AUC) is reported^74–76, a statistic with a long tradition of use in determining the efficacy of clinical predictors. AUC has a desirable property of being independent of the proportion of cases in the validation sample; one definition of AUC is that a randomly selected case is ranked higher by the predictor than a randomly selected control. A new statistic reflecting variance explained on the liability scale ($R_l^2$), which it can be related to other statistics such as $R_N^2$ and AUC¹¹, has been proposed⁷⁷. Like any estimate on the liability scale, calculation of $R_l^2$ requires specification of disease prevalence in the population, but allows direct comparison of the variance explained by the predictor to estimates of heritability from family data and estimates of SNP-heritability from genome-wide SNP data.

Environmental risk factors can be added to the genetic predictor, to make a better predictor of the phenotype. In practice not all environmental factors are identified (and some factors classified as “environment” may simply be stochastic events¹²). For example, combining SNPs and phenotypic predictors, such as body-mass-index and smoking, improved prediction of age-related-macular degeneration, an eye disease in humans where age is a major risk factor¹³. In some circumstances more accurate phenotyping, including the use of repeated measures, can lead to a more heritable trait. In general, expectations need to be adjusted accordingly for the application of phenotype or disease prediction in humans.

Unlike the deterministic genetic tests for fully penetrant Mendelian disorders, genetic predictions for complex traits will be probabilistic and the value may only be incremental in clinical decision making. The value of genetic risk prediction may be at a group level rather than individual level. For example, from a risk predictor for type 1 diabetes (T1D), created from risk variants known up to 2011, a risk group comprising the top ranked 18% of individuals would need to be monitored in order to capture 80% of future cases, yet because T1D is not common (prevalence 0.4%) the probability of disease for individuals in this risk group is still less than 2%¹⁴. Nonetheless, cost-effective public health strategies could result from use of genetic predictors to identify high-risk strata where disease prevention interventions should be focussed^{15, 16}. In agriculture, genetic risk prediction is geared mostly towards selection of breeding stock based on estimates of additive genetic values (‘estimated breeding values’) in the parent generation with the aim of eliciting changes in the phenotype of the of the offspring generation on average. That is, the impact of genetic prediction is naturally at the level of a group rather than an individual.

Limitation 2: Variance explainable by markers

The SNPs included in the genome-wide SNP chips used for identifying SNPs associated with complex traits are typically not the causal variants for a phenotype – more likely they may have an association with the trait because they are in linkage disequilibrium (LD) with one or more causal variants. Since the SNPs on SNP chips are chosen because both their alleles are common they cannot be in complete LD with a causal variant with one rare allele. If the variation generated by the causal variants is completely explained by the genotyped SNPs, then the SNPs potentially can explain all the genetic variation in the trait (i.e. $h_M^2=h^2$, where $h_M^2$ is defined as the genetic variation captured by the SNPs, or markers). Sometimes (e.g.¹⁷) $h_M^2$ is referred to as "narrow-sense heritability", however in our opinion, the term "narrow-sense heritability" should be reserved as the definition of the total additive genetic variance, that is h² (see refs^{9, 18}).

If a genetic variant is associated with fitness, selection will drive one allele to low frequency^19–21. This is the case even for traits without an obvious connection to fitness. The larger the effect of a SNP on a fitness the lower the frequencies of the causal alleles are expected to be^{22, 23}. For example, individual mutations causing severe intellectual disability in humans are rare^{24, 25}. Therefore, in practice, the SNPs identified as associated in the discovery population are unlikely to explain all genetic variation (i.e, $h_M^2$ < h²) since contributions to the variance by rare variants may not be tagged by the genotyped SNPs^26–28. For example, for both height and schizophrenia h² ~ 0.7–0.8 and $h_M^2$ ~ 0.5 for height²⁶ and 0.2–0.3 for schizophrenia^{29, 30}.

The difference between the variance explained by genome-wide significant (GWS) SNPs ($h_{\mathit{\text{GWS}}}^2$) and heritability estimate from family studies (h²) has been called the “missing heritability” and the difference between $h_{\mathit{\text{GWS}}}^2$ and $h_M^2$ the “hidden” heritability, so that the difference between $h_M^2$ is the “still missing heritability”, i.e., $h_{\mathit{\text{GWS}}}^2$ < $h_M^2$ < h². The still missing heritability may simply reflect genomic variants not well tagged by SNPs. In livestock populations, when missing heritability is defined in this way, little is missing with up to 97% of the heritability captured by common SNPs^{31, 32}, probably because the smaller effective population size leads to long range LD and hence even rare alleles can be predicted by a linear combination of SNPs in LD with the causal variant. Even in dairy cattle however, traits that could reasonably be assumed to be under strong natural selection, such as fertility, have greater missing heritability³¹. Moreover, when the SNPs are fitted together with a pedigree as much as half of the genetic variance is explained by the pedigree and not the SNPs³³. The simplest explanation is that in livestock as in humans some causal variants are rare and in poor LD with the SNPs.

With the advances in whole genome sequencing technologies, causative mutations will be present in the data and the proportion of variation that can be captured by the sequence data is expected to approach h². In principle, known rare risk variants, if identified, can be included in the predictor in the same way as common variants; cumulatively their contribution may be important. Their importance can be assessed by the proportion of variation they explain. Both the ability to detect an association between a trait and a SNP, and the value of including the SNP in a predictor, depend on the proportion of variance the SNP explains. For example, a rare variant with a frequency of 1/1000 in the population and a relative risk for a disease of 5 will increase the risk of disease by 5-fold for 1 in 1000 people (so from 1% to 5% for a disease with a prevalence of 1%), but such an increase in risk can also be achieved by the cumulative effect of multiple common variants with smaller effect size. The contribution of rare variants can be included into a predictor by grouping them into defined classes of genes^{31, 32}, or by incorporating prior knowledge of functions³⁴.

Limitation 3. Errors in the estimated effects of the markers

The effects of SNPs on a trait must be estimated from a sample of finite size and so the effects are estimated with some sampling error. If there were only a few loci that affected a trait, it would be possible to estimate their effects quite accurately, but most complex traits are controlled by a very large number of largely unknown loci³⁵. Therefore the discovery stage of estimating the prediction equation may involve a genome-wide panel of millions of SNPs. The true effects of most SNPs are small and so the accuracy with which these effects are estimated is low unless a very large discovery sample is used. The correlation between phenotype and a predictor that uses all SNPs simultaneously in a random mating population can be expressed as a function of effective population size (or the effective number of independent chromosome segments which is a function of effective population size), heritability and the size of the discovery sample (Equation 1, BOX 1)^36–38. Specifically, SNP effects will be better estimated when the sample size of the discovery cohort increases (Figure BOX1); estimated or predicted effect sizes of rare variants will be difficult to verify even with large sample sizes.

Limitation 4: Statistical methods in the discovery sample

The least squares prediction or ‘profile scoring’²⁹ method is commonly used for prediction of genetic risk. Although simple to apply it does not have desirable statistical properties and an arbitrary p-value threshold is used for the selection of SNPs that go in the predictor. Moreover, estimation of SNP effects one at a time is not an optimal approach^{1, 39–44}. This is because SNP effects are correlated and accounting for LD in the profile scoring method requires SNP selection on arbitrary thresholds. Methods that model the distribution of SNP effects⁴⁰ and the correlation between SNPs in the presence of single as well as multiple causal variants will be more accurate^{1, 39–43, 45}. In human applications, sometimes only genome-wide significant SNPs are included in the predictor^{15, 46–49}, yet greater accuracy results from the use of less stringent thresholds^{1, 37, 40} and in animal and plant breeding it is typical to use all available SNPs. Better SNP estimation methods exist and are used in plant and animal breeding^{1, 2, 37, 44, 50} and such methods have been proposed for applications to human data^{1, 43}. They rely on prior assumptions about the distribution of SNP effects in the genome, and use all data simultaneously. Such Bayesian methods have also been applied to other species⁵¹, and related methodologies derived in computer science have been applied to disease data in humans^{4, 52}. Ignorance can’t be bliss in this context and it must be best to use all available genetic and phenotypic information simultaneously. It is outside the scope of this Perspective to discuss these methods in more detail.

Pitfalls of the analysis

Pitfall 1: Validation and discovery sample overlap

If the correlation (R) between a phenotype and a single SNP in the population is zero (that is, the SNP is not associated with the trait), the expected value of the squared correlation (R²) estimated from a sample of size N is 1/(N-1), or approximately 1/N if N is large. Hence, a randomly chosen ‘candidate’ (but not truly associated) SNP explains 1/N of variation in any sample. Usually 1/N is small enough not to worry about. However, a set of m uncorrelated SNPs that have nothing to do with a phenotype of interest would, when fitted together, explain m/N of variation (due to the summing of their effects). For example, a set of 100 independent SNPs when fitted together in a regression analysis in a discovery sample of N_d = 1000 would, on average, explain R² =10% of phenotypic variance in the discovery sample under the null hypothesis of no true association.

When the number of SNPs in the predictor is large and the sample size is small, the discovery R² can be very high by chance and can be a gross over-estimation of the true variance explained by the predictor when applied in an independent sample. Also, the expected R² in the validation sample for a set of SNPs selected from a discovery sample but with the effect sizes of the SNPs re-estimated in the validation sample is ~1/N_v, with N_v the validation sample size. Therefore, to estimate the R² of a prediction in a new sample, a prediction equation is estimated in the discovery sample and is tested, without re-estimating the regression coefficients, in the validation sample (Box 2). Applying the incorrect validation procedure results in over-estimation of the accuracy of the prediction (or over-fitting). An example of where over-fitting occurs is when testing the prediction in the discovery sample, i.e., the same data are used to estimate the effect of SNPs on phenotype and to make predictions^{53, 54} . We illustrate the overlap pitfall with examples in dairy cattle, Drosophila and human populations (FIG 2a-c). . For example, in a GWAS on ~150 sequenced inbred lines of Drosophila⁵⁴ in which this was done the authors concluded that 6–10 SNPs selected from > 1M SNPs together explained 51–72% of variation in the lines (depending on the trait analysed). However, a cross-validated Bayesian prediction analysis using all genetic markers on the same data found that only 6% of phenotypic variation could be explained by the predictor⁵¹.

Box 2. Quantifying prediction accuracy for pitfall 2.

When discovery and validation samples are independent

When m SNPs have been selected from a discovery sample, a simple linear predictor in the validation sample is $\widehat{y}=\sum _{i=1}^m{\widehat{b}}_i{x}_i$, with x_i = 0,1 or 2 reference alleles of a SNP and b̂_i the estimated effect size from the discovery sample. In this article we do not concern ourselves with how b̂_i is estimated – there are simple least squares and more complex Bayesian estimation methods that have been described elsewhere^{1, 41, 42}. We also restrict ourselves to linear (additive) models. Given a multi-SNP predictor (ŷ), the validation step is to quantify how much of the variation in trait y is explained by the predictor ŷ. A regression of y on ŷ fits only a single covariate so the R² expected by chance is only 1/N_v, where N_v is the validation sample size. If the validation sample is drawn from the same population as the discovery sample, then a value of R² > 1/N_v is evidence for real predictive ability of the predictor. (Software tools output an adjusted R² that corrects for the R² expected by chance). Hence the sample size in the validation stage does not have to be large to reject the null hypothesis of no association, H₀: ρ² = 0, where ρ² true value of R² in the population. The standard error (SE) of R is approximately $1/\sqrt{N_v}$ if ρ is very small, and more generally ${(1-\mathrm{\rho })}^2/\sqrt{N_v}$. In terms of R², its SE is approximately $\sqrt{2}/N_v$ with ρ small. A general and a more complicated exact equation was given by Wishart (1931)⁷⁷. Using the exact equations, if ρ² is 1% or 10%, then SE(R²) for N_v = 100 is 1.9% or 5.6% and for N_v = 500 it is 0.8% and 2.5%.

When discovery and validation samples are the same

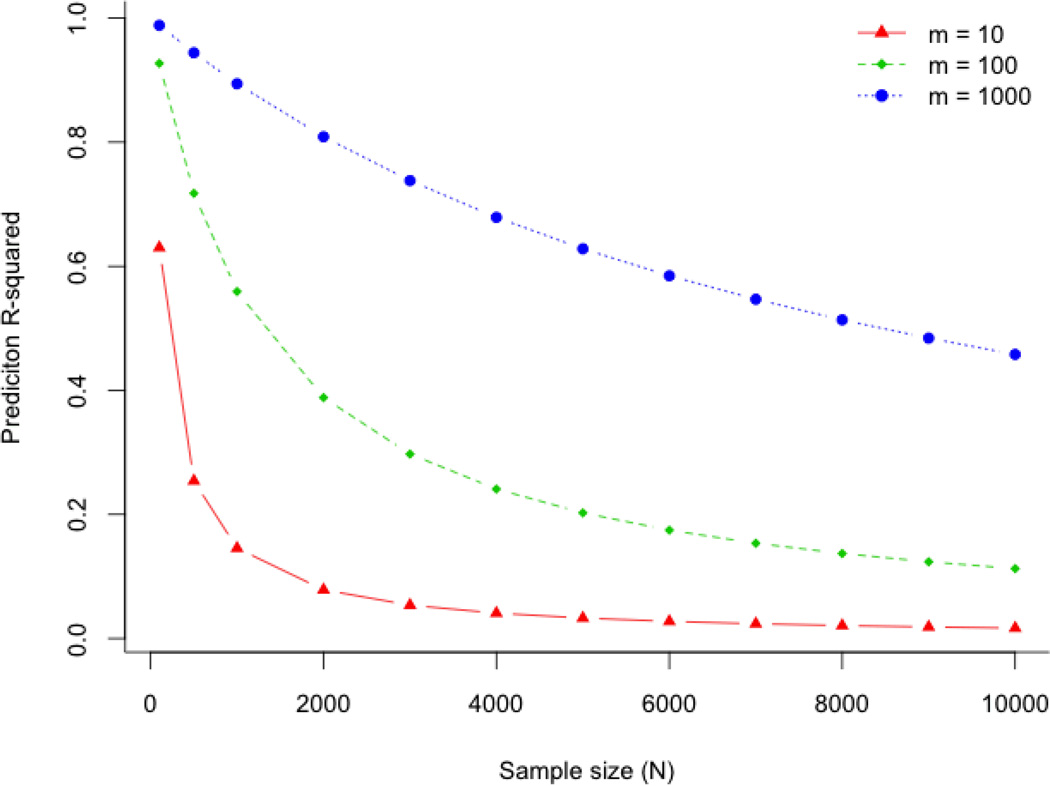
In the supplementary material we derive an approximation of R² (verified by simulation) when there is no correlation in the population between SNPs and phenotypes, but when m “associated” SNPs are identified from the same sample (of size N) in which they are validated as a predictor. The relationship between R² and N, dependent on m and assuming M = 100,000 independent genomic variants associated with the phenotype is plotted below in which m SNPs (m = 10, 100 or 1000) are selected after association analysis of M = 100,000 uncorrelated SNPs in a sample of unrelated individuals and applied as a predictor back into the same sample, when there is no correlation between SNPs and phenotypes. In genome-wide association studies M is large so overestimation of R² occurs even for big sample sizes.

When validation sample overlaps with the discovery sample

If some of the samples in the validation cohort are also in the discovery set then this can create spurious results. For the samples that overlap, the expected R² between predictor and outcome is the same as in the entire discovery sample, because those samples are just a random sample from the discovery cohort. If the proportion of samples in the discovery set that are also in the validation cohort is q, then the expected squared correlation between predictor and outcome in the entire validation cohort is approximately q*R² + (1-q)/N_v, with R² the (spurious) accuracy derived in the supplementary material (see previous section). The important result is that if samples overlap it is not the proportion of those samples in the discovery cohort that matters but it is the proportion of the validation samples that is also in the discovery cohort that determines false accuracy.

Figure 2. Examples of the overlap pitfall: non-independence of discovery and validation samples.

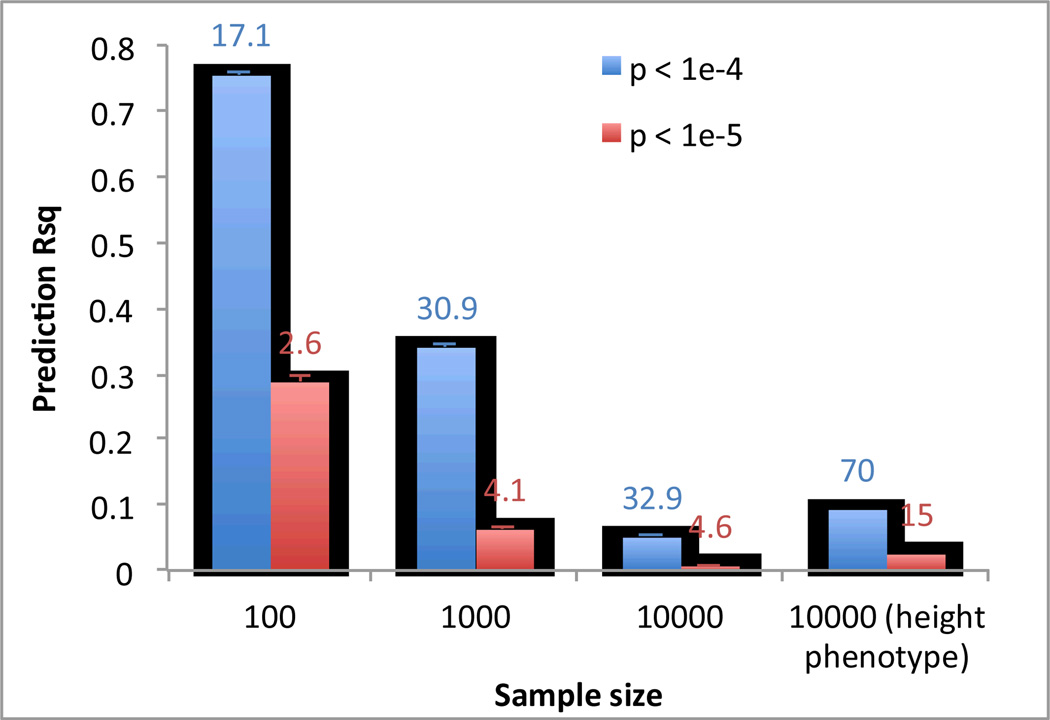
a) Human: High R² can be achieved by chance particularly when sample size is small.

We simulated GWAS data based upon real human genotype data under the null hypothesis of no association. We used data of 11,586 unrelated European Americans genotyped on 563,212 SNPs ^71–73. We randomly sampled N individuals and selected top SNPs for height at p < 10⁻⁵ (red bar) and p < 10⁻⁴ (blue bar) to predict the phenotype in the same data. We also performed association analysis for real height phenotype in 10,000 individuals and selected top SNPs at p < 10⁻⁵ (green bar) and p < 10⁻⁴ (purple bar) to predict height phenotype in the same sample. The graph shows the mean prediction R² over 100 simulation replicates. Error bar: standard error of the mean. The number on top of each column is the mean number of selected SNPs over 100 simulation replicates.

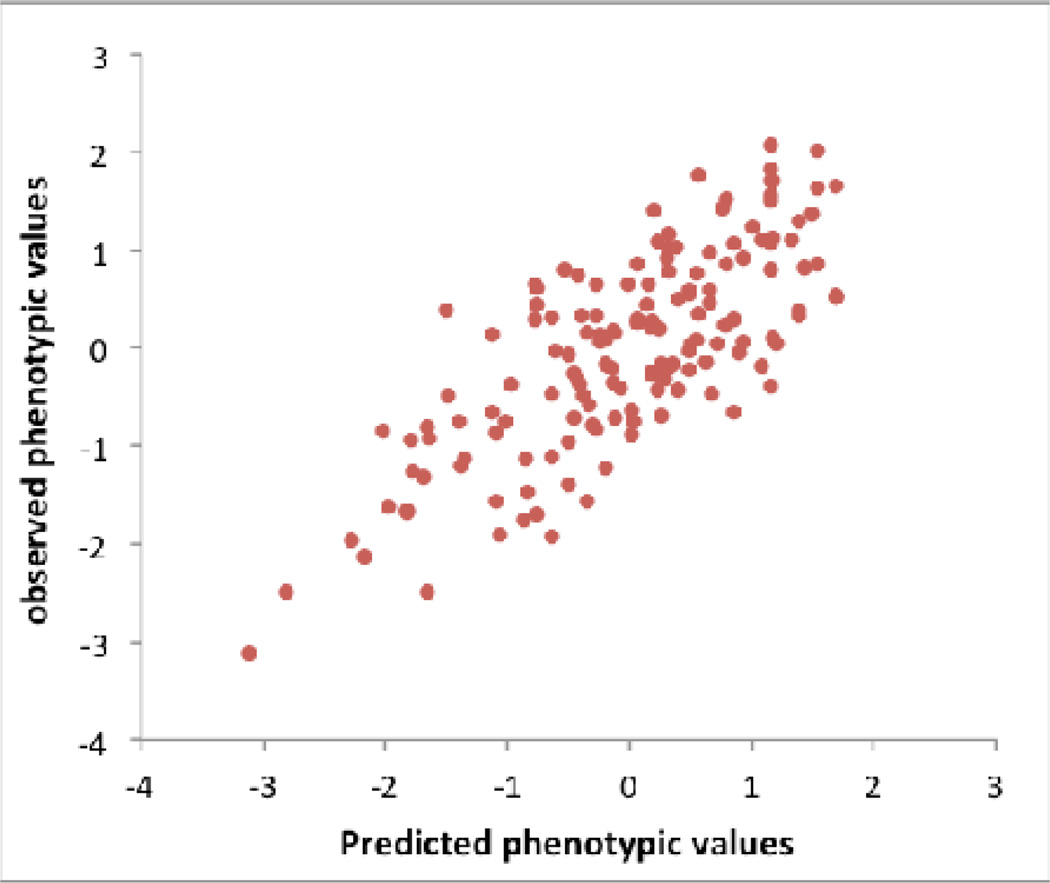
b) Drosophila: An example, illustrating bias when selecting the top SNPs. We downloaded genotype data of the Drosophila Genetics Reference Panel and simulated phenotypes under the null hypothesis, i.e., random association between each of the > 1 million SNPs and phenotype. We repeated the GWAS analysis reported in⁵⁴, selecting the top 10 independently associated SNPs and predicted the phenotypes of the lines using these 10 SNPs. Since in the simulated data there are only random associations between SNP and phenotype any prediction power is false and result of over-fitting. By chance, the top SNPs (in terms of test statistic) explain 57% (R²=57%) of the phenotypic variance between the inbred lines, from a linear regression of phenotype on predictor. Both phenotype and predictor have been standardized to normal distribution z-scores (mean of zero and standard deviation of one).

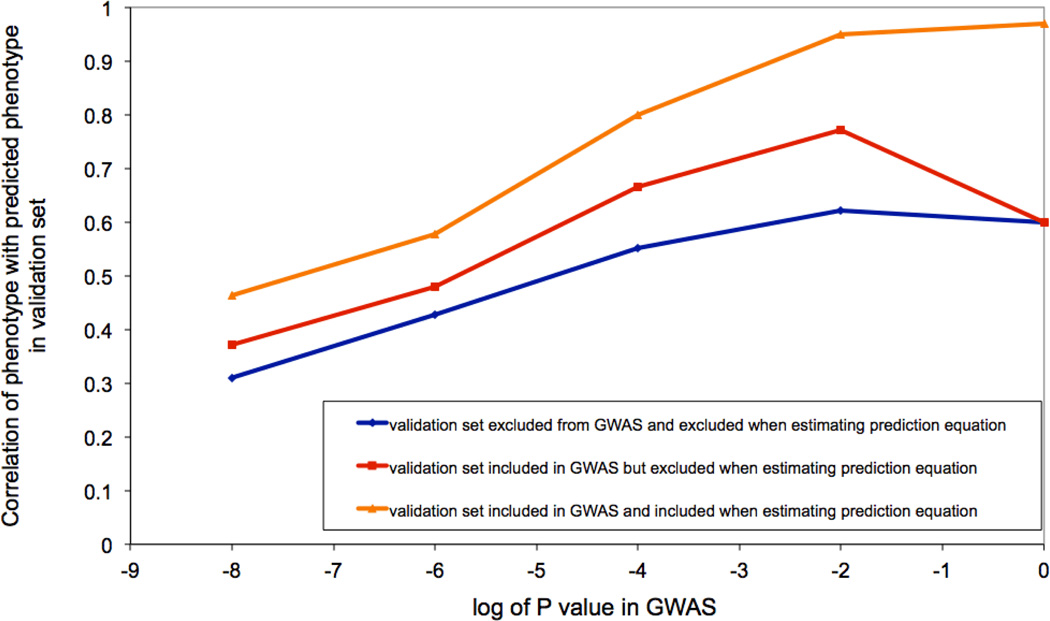
c) Dairy Cattle: The impact of leaving the validation cohort in the discovery set, either at both SNP selection (GWAS) and SNP effect estimation stages, or at the effect size estimation stage only. Data shown are from 2,732 bulls with ~500K SNPs phenotyped for average milk yield of their daughters’ milk production. The bulls were split into a discovery sample (bulls born during or before 2003), N_d = 2,458, and a validation sample (bulls born after 2003) of N_v= 274.

A less obvious mistake is to select the most significantly associated SNPs in the entire sample and to use these to estimate SNP effects and test their prediction accuracy in the discovery and validation sets⁵⁵. In this case the variance explained by the SNPs when applied in the validation sample is inflated. It creates bias and misleading results because the initial selection step of the SNPs is based upon there being a chance correlation between these SNPs and the entire sample, so also between the SNPs and any sub-sample. A prediction equation based on these SNPs will appear to work in the validation sample but not in a genuinely independent sample. Cross-validation analysis after the initial set of SNPs has been selected from the entire sample does not mitigate this bias. The pitfall of SNP selection from discovery and validation samples occurred in a recent study reporting a genetic predictor of autism⁵⁶. SNPs putatively associated with autism in multiple biological pathways were selected based upon p-values from GWAS in the entire data set. Model selection was subsequently applied using cross-validation to narrow down the number of SNPs. The authors did follow up with an independent validation sample, and the prediction accuracy was reduced.

A variation on this pitfall is when a proportion of individuals in the validation sample are also in the discovery sample and then the bias is proportional to the fraction of the validation samples that was also in the discovery set (see BOX 2). In practice it might be difficult to ascertain if any of the validation individuals were also in the discovery set, in particular if there are only summary statistics (i.e., estimates and standard error of SNP effect and allele frequencies) available, particularly from public databases. We use cattle data⁴⁴ to illustrate the inflation in variance explained by a SNP predictor when the validation sample is included in discovery steps (Fig 2c)

The remedy to this pitfall is to use external validation. In some cases independent data sets are not available in which case internal cross-validation is the only option. In cross-validation it is important to avoid the pitfall of updating the predictor based on results derived from the validation sample, hence losing the independence of discovery and validation samples that the strategy has set out to achieve⁵⁷. Overlap in samples can be checked as part of quality control (QC) of the prediction pipeline, by estimating pairwise relatedness using SNP data, but this requires access to full genotype data from both discovery and validation samples. There are many software tools that can do this, including PLINK⁵⁸ and GCTA⁵⁹.

Pitfall 2: The validation sample

If the validation sample is more closely related to the discovery population than to the target population, then the prediction accuracy will be over-estimated. In humans, a polygenic prediction analysis of height in 5,117 individuals from the Framingham Heart Study (FHS; original and offspring cohorts only) reported a prediction R² of 0.25 using 10-fold cross-validation when including all individuals in the analysis⁶⁰. However, because FHS includes many related individuals, the authors repeated the analysis restricting the 10-fold cross-validation samples to individuals with no known close relatives (parent-offspring, sibling, or half-sib) in the data set based on pedigree information. In this restricted analysis, the prediction R² decreased to 0.15. We caution that cryptic relatedness can still inflate prediction accuracy even when known close relatives are excluded. To demonstrate this, we conducted a polygenic prediction analysis of height using 7,434 individuals from the FHS SHARe data⁶¹ (BOX 3). Our results demonstrate that cryptic relatedness, beyond the close relatives inferred from pedigrees, can inflate prediction accuracy relative to the prediction accuracy that could be achieved in an independent validation sample.

Box 3. Using the Framingham Heart Study (FHS) to illustrate pitfalls of validation.

The FHS is a large cohort study of individuals and their family members measured for a wide range of traits (particularly related to cardiovascular disease) and with genome-wide genotypes. A polygenic prediction analysis of height⁶⁰ showed that including known related individuals in the analysis inflated R² (from 0.15 to 0.25) To investigate if genetic relatedness can still inflate prediction accuracy even when known close relatives are excluded, we conducted a polygenic prediction analysis of height using 7,434 individuals from the FHS SHARe data⁶¹. We obtained a prediction R² of 0.13 using 10-fold cross-validation when restricting to individuals with no known close relatives in the data set based on known pedigree information. (We fit markers individually whereas in the original study⁶⁰ markers were fitted simultaneously via a Bayesian random effects model, thus it is expected that a slightly higher R² of 0.15 was reported). We repeated the analysis restricting to individuals with pairwise relatedness estimated from the SNPs of less than 0.40, 0.20, or 0.05, and obtained prediction R² of 0.08, 0.06 and 0.06, respectively, demonstrating the importance of using the genotype data to identify relatives rather than accepting recorded family relationships.

We investigated whether population stratification was inflating prediction accuracy in our FHS analysis, as the prediction R² of 0.06 was much higher than would be expected from theory³⁶ or from empirical data on much larger sample sizes⁶¹. When repeating the analysis using a height phenotype that was adjusted for 10 eigenvectors⁶⁶ of the SNP derived relationship matrix, once again restricting to individuals with pairwise relatedness less than 0.40, 0.20, or 0.05, we obtained prediction R² of 0.06, 0.01 and 0.00, respectively, which were smaller than the prediction R² obtained using unadjusted height. The bulk of the reduction came from correcting for the top eigenvector, representing northwest European vs. southeast European ancestry⁶³, which is strongly correlated to height (R²=0.05 in FHS data, consistent with other studies^{78, 79}). Thus, consistent with theory, polygenic prediction analyses of a few thousand unrelated individuals that do not benefit from population stratification will attain a low prediction R² (<0.01). The results of these analyses are summarised in the graph below.

The remedy of the pitfall described here is to use conventionally unrelated individuals (in discovery and validation stages). Relatedness can be estimated from SNP data^{58, 59} and so close relatives can be excluded based upon observed data. More generally, the validation population should be representative of the population in which the predictor will ultimately be applied. In populations with small effective population size, such as some breeds of livestock, all individuals are related. This does not invalidate the prediction but it does mean that the same prediction accuracy cannot be expected when the prediction equation is applied to another population that is less closely related to the discovery population⁶².

Sometimes the validation population differs from the application (target) population in that it is much more genetically diverse. For example, the validation (and possibly discovery) population might include a diverse set of lines of animals or plants. A prediction equation may work well in this population but less well in an application population that is less diverse such as commercial strains of a crop⁶².

Pitfall 3: Population stratification similarity

Another way in which prediction accuracy can be inflated is if the discovery and validation samples contain similar patterns of population stratification and the eventual target population is not similarly stratified. For example, this could occur if discovery and validation samples are independently sampled from a stratified population such as European Americans⁶³. The question of whether this inflation should be viewed as a pitfall depends on the ultimate goal of the analysis. If the goal is to conduct prediction in European Americans, it is entirely appropriate to leverage ancestry information to the fullest extent possible, and this inflation is not a pitfall (because discovery, validation and target samples are similarly stratified). On the other hand, if the goal is to assess the prediction accuracy that could be achieved using less structured application populations, then this inflation is a pitfall. As an example, we show that population stratification was inflating prediction accuracy in the FHS analysis (See BOX 3 for details). A more serious problem is when there is confounding between ancestry and disease status both in discovery and validation case-control samples, because such spurious association can lead to a predictor of ancestry rather than one of disease. It was recently suggested that the aforementioned predictor of autism⁵⁶ suffers from this pitfall⁶⁴.

A practical remedy to problems associated with population stratification is to fit ancestry principal components in the analysis of discovery samples. We note that differential bias between cases and controls⁶⁵ can also lead to spurious prediction R² if discovery and validation samples exhibit the same differential bias, as could occur when using 10-fold cross-validation. A remedy for differential bias is to perform stringent quality control and/or to validate in a completely independent sample, in lieu of 10-fold cross-validation. One QC step that can be done is to use the genotyped SNPs that are in the predictor and quantify the estimated relatedness between the application sample and the discovery and validation samples, for example in a principal component analysis (PCA)⁶⁶ or related methods⁶⁷. If the application sample is an outlier on the PCA then the prediction accuracy in the target may be less than expected from the validation procedure.

Pitfall 4: Expectation of equality of R² and $h_M^2$

Sometimes called the SNP- or chip-heritability, an unbiased estimate of the variance explained by markers $h_M^2$ is achieved by correlating phenotypic similarity between pairs of individuals with their SNP-based genotypic similarity^{26, 59, 65}. In human populations, the SNP-heritability is broadly between one-third and one-half of total heritability for traits studied to date^{28, 35, 68}. A prediction of phenotype based upon the same set of SNPs would achieve an R² = $h_M^2$ only if the individual SNP effects were estimated without error²⁷. For example, when a multiple-SNP predictor that used the ‘profile scoring’ method was used for height⁶¹, it achieved an R² of 10–15% in out-of-sample predictions. Yet Yang et al (2010)²⁶ estimated that all the SNPs together would explain 40–50% of phenotypic variance if their effects were estimated without error. These results are not inconsistent when the error associated with the estimate of each SNP effect is appreciated.

With ever-larger sample sizes, the size of the error terms in the SNP effect estimates will be reduced, and the two statistics will converge to the same value. However, simulations for human populations suggest that the improvement in trait prediction as sample size increases depends on the genetic architecture of the trait, in particular how many variants there are with tiny effect sizes, and that for most common complex genetic diseases the improvement will be slow and modest even when common SNPs account for a large proportion of heritability of the traits¹⁷. Hence, for applications in human populations to achieve meaningful and accurate predictions, big data are key and sample sizes of hundreds of thousands needed and such data sets are starting to become achievable.

Conclusions

We highlighted what we believe are limitations to genetic risk prediction as well as the most important pitfalls to befall researchers and discussed how these can be avoided. Most problems occur in the validation stage, when data are not fully independent to those in the discovery phase, but care is also needed to ensure that the discovery and validation samples are representative of the population in which the predictor will be applied. Genomic prediction is already having a major impact in livestock selection programmes³⁷ and has great potential for applications in plant breeding, preventative medicine strategies and clinical decision making. However, there are fundamental limitations to the predictive ability of a genetic predictor (see limitations 1 and 2) and so it is important that expectations are realistic and that the accuracy of genetic predictors are fairly evaluated. As sample sizes increase, predictors of genetic risk will have greater clinical utility, particularly in terms of identification of population strata at increased risk of disease as opposed to accurate predictive diagnosis for individuals.

Glossary

Heritability

The proportion of phenotypic variance attributable to additive genetic variation.

Estimated Breeding Value

An estimate of the additive genetic value for a particular trait that an individual will pass on to descendants.

Linkage Disequilibrium

The non-random association of alleles at different loci.

Effective population size

The number of individuals in an idealized population with random mating and no selection that would lead to the same rate of inbreeding as observed in the real population.

Polygenic prediction analysis

Any analysis method that predicts genetic risk or breeding values based on the combined contribution of many loci.

Profile scoring

A polygenic prediction method for prediction of genetic value or risk for each individual (a “profile”) in a validation sample generated from the sum of the alleles they carry weighted by the association effect size estimated in a discovery sample.

Independent SNPs

Independent, uncorrelated SNPs are in linkage equilibrium. Although the effective number of independent markers in standard GWAS chips has sometimes been assumed to as large as 200,000 (e.g. ref¹⁷), we believe that 60,000 is a more appropriate value, as analyses of LD²⁹, genomic inflation factors⁶⁹ and eigenvalues from principal components analysis⁷⁰ have consistently produced estimates close to 60,000 in European populations. Predictions from theory, based upon random mating populations of a given effective size and for given genome length, also come to this number³⁶. Thus the appropriate value for M is approximately 60,000.

Independent sample

In the context of risk prediction an independent sample means a sample from the same population but excluding individuals that are closely related. Necessarily, the individuals in different samples from the same population will share common ancestors, and indeed this distant sharing underpins the efficacy of a risk predictor.

Cross-validation

To test the validity of a prediction in the absence of an independent external validation sample, the sample is divided into k independent subsets (balanced with respect to case-control status in disease data). Each of the k subsets is used in turn as a validation sample for a predictor derived from the remaining k-1 subsets.

Ancestry principal components

Principal components derived from the genome relationship matrix that account for the genetic substructure of the data. In case-control studies these principal components can reflect genotyping artefacts such as plate, batch and genotyping centre that could be confounded with case-control status.

Cryptic relatedness

Cryptic relatedness is when a sample is thought to comprise unrelated individuals based on record pedigree relationships but in fact includes close relatives, for example 2^nd cousin or closer.

Conventionally unrelated

Individuals from that are not closely related, for example more distantly related than 3^rd cousins