Detecting the Molecular Signature of Social Conflict: Theory and a Test with Bacterial Quorum Sensing Genes

Abstract

Extending social evolution theory to the molecular level opens the door to an unparalleled abundance of data and statistical tools for testing alternative hypotheses about the long-term evolutionary dynamics of cooperation and conflict. To this end, we take a collection of known sociality genes (bacterial quorum sensing [QS] genes), model their evolution in terms of patterns that are detectable using gene sequence data, and then test model predictions using available genetic data sets. Specifically, we test two alternative hypotheses of social conflict: (1) the “adaptive” hypothesis that cheaters are maintained in natural populations by frequency-dependent balancing selection as an evolutionarily stable strategy and (2) the “evolutionary null” hypothesis that cheaters are opposed by purifying kin selection yet exist transiently because of their recurrent introduction into populations by mutation (i.e., kin selection-mutation balance). We find that QS genes have elevated within- and among-species sequence variation, nonsignificant signatures of natural selection, and putatively small effect sizes of mutant alleles, all patterns predicted by our evolutionary null model but not by the stable cheater hypothesis. These empirical findings support our theoretical prediction that QS genes experience relaxed selection due to nonclonality of social groups, conditional expression, and the individual-level advantage enjoyed by cheaters. Furthermore, cheaters are evolutionarily transient, persisting in populations because of their recurrent introduction by mutation and not because they enjoy a frequency-dependent fitness advantage.

Introduction

Gene sequences contain a record of the evolutionary history of a population. Some studies have leveraged this rich source of data to test a number of evolutionary hypotheses, including distinguishing among competing theories for the advantage of sex and recombination (Shapiro et al. 2007; Betancourt et al. 2009) and the relative prevalence of positive selection compared with neutral processes in driving evolutionary change (Fay et al. 2002; Smith and Eyre-Walker 2002; Wang et al. 2006; Sabeti et al. 2007). Surprisingly, the study of social evolution, which has an extensive theoretical literature, has yet to fully embrace the use of gene sequence data to test competing hypotheses about the statics and dynamics of cooperation and conflict. This is in part because of a lack of suitable data, but it is also because of a lack of theory that is properly formulated to make predictions at the gene sequence level. The empirical molecular genetics of sociality has been driven by the burgeoning field of sociogenomics, which seeks to identify the genes underlying social traits in order to enhance our understanding of the origin and evolution of sociality (Robinson et al. 2005; Nedelcu and Michod 2006). Evolutionary inferences from this work have been based on comparative phylogenetic methods (Robinson et al. 2005; Nedelcu and Michod 2006) or rates of sequence divergence between closely related species (Hunt et al. 2010; Sucgang et al. 2011). To extend the study of the molecular evolution of sociality, we demonstrate here how with a combination of within- and among-species sequence data, along with properly formulated genetic models of social evolution, we can make use of the vast tool set of molecular population genetics (Kreitman 2000) to test hypotheses about the evolution of genes controlling sociality. This is the extension of “sociogenomics” into “sociomolecular population genetics.”

The two biggest constraints to applying molecular population-genetic approaches to social evolution are (1) the difficulty in identifying sociality genes with a well-understood genotype-to-phenotype mapping (Robinson et al. 2005; Foster et al. 2007; Linksvayer and Wade 2009) and (2) the scarcity of suitable gene sequence data. Bacterial quorum sensing (QS) avoids these two constraints: QS is a widespread social trait in bacteria that has a well-described, simple genetic basis (Miller and Bassler 2001; Lerat and Moran 2004), and multiple population-genetic data sets for these genes are available. In this article we use these data in conjunction with appropriately formulated social-genetic theory to test a central question in the study of social evolution: what are the short- and longterm dynamics of social conflict, and how is conflict maintained within populations?

The potential for conflict in social systems arises when cooperative traits are exploited by social “cheaters,” which are genetic mutants that receive the benefits from cooperators in their social group but do not pay the cost of contributing to the public good. Empirical study of social conflict has typically relied on easily measurable social phenotypes, such as sex ratios (West 2009). Yet, with the recent upsurge in availability of genetic data, there have been a growing number of attempts to use social evolution theory to explain observed patterns at the molecular level (e.g., Greig and Travisano 2004; Diggle et al. 2007a; Eldar 2011; Sucgang et al. 2011). However, these attempts have typically relied on verbal models rather than formal theory, and they have often lacked quantitative estimates of genetic variability, statistical tests for signatures of natural selection, or evolutionary null expectations against which to test alternative, adaptive hypotheses. Indeed, most of these studies have proposed adaptive explanations for observed patterns of social genetic variation without considering what pattern is to be expected in the absence of adaptive evolution. Without comparison to an evolutionary null hypothesis, one risks incorrectly inferring adaptive mechanisms where none exist (Gould and Lewontin 1979; Kimura 1983; Currat et al 2006; Lynch 2007; Van Dyken et al. 2011).

Here we compare a common adaptive hypothesis for the evolutionary dynamics of social conflict with an evolutionary null hypothesis. The adaptive hypothesis that we consider, which we call the “evolutionarily stable cheater” (ESC) hypothesis, argues that cheaters arise and are maintained by selection as an alternative stable strategy. This conforms to a game-theoretic view of polymorphism, where heterogeneity is caused by the coexistence of alternative strategies maintained by frequency-dependent selection at a stable internal equilibrium (Maynard Smith 1982; Doebeli et al. 2004). Frequency-dependent cheating can be mathematically formalized by the “snowdrift” game (also known as “hawk-dove” or “chicken”; Maynard Smith 1982; Doebeli et al. 2004; Doebeli and Hauert 2005). The ESC hypothesis has experimental support in microbes where frequency-dependent cooperation (snowdrift game dynamics) has been measured in the laboratory (Velicer et al. 2000; Greig and Travisano 2004; Gore et al. 2009; Ross-Gillespie et al. 2007; smith et al. 2010). These experiments all have in common the fact that cooperation involved the secretion of public goods in diffusion-limited environments (Driscoll and Pepper 2010; Frank 2010), such that cooperators disproportionately received their own public goods. This allowed cooperation to invade when rare, as rare cooperators receive more of their own benefit than their cheating neighbors even though cooperation is vulnerable to invasion by cheaters when it is common. Stable coexistence may also derive from the ability of individuals to detect and respond conditionally to their social partner’s strategy (Maynard Smith 1982; Werfel and Bar-Yam 2004; Gore et al. 2009), but there is currently no direct empirical evidence for such conditional social expression in these systems. Notably, a number of alternative adaptive hypotheses exist in addition to the ESC. These include an evolutionary “arms race” scenario, where cheaters continually change strategies in order to counter the evolutionary response of cooperators (Greig and Travisano 2004; Sucgang et al. 2011). Another is diversifying selection favoring rapidly changing cooperative signals (Ansaldi and Dubnau 2004) in order to prevent “eaves-dropping” (Brown and Johnstone 2001; Diggle et al. 2007b; Early 2010). Even more elaborate adaptive models have been proposed that involve facultative cheating with perpetual coevolution of cheaters and cheater-immune strains (Eldar 2011). We address these alternatives in “Discussion.”

In order to test adaptive hypotheses using molecular data, one must be able to reject an evolutionary null (i.e., nonadaptive) model (Gould and Lewontin 1979; Kimura 1983; Currat et al 2006; Lynch 2007). That is, are the observed patterns explainable simply via drift, mutation, and purifying selection, or must one invoke adaptive mechanisms? Here we formulate an evolutionary null model for QS gene evolution that is based on the “kin selection-mutation balance” (KSMB) hypothesis (Van Dyken et al. 2011). According to the KSMB hypothesis, polymorphism at a sociality locus with linear social effects (i.e., wherein a group with two altruists has twice the fitness benefit as a group with one altruist) is maintained via recurrent mutation despite purifying kin selection. Under this hypothesis, the level of standing genetic variation in a population is determined by the balance between the rate at which mutation introduces socially deleterious (i.e., defective or impaired) “cheater” alleles and the rate at which kin selection purges these alleles from the population (Van Dyken et al. 2011). This process is directly analogous to traditional mutation-selection balance, which maintains standing polymorphism at nonsocial loci and serves as an evolutionary null hypothesis for nonsocial traits (Kimura 1983; Lynch 2007). As we show, our evolutionary null model predicts that QS genes should experience relaxed selection because of nonclonality, costs of expression, and conditional gene expression, resulting in elevated genetic diversity.

Here we test these competing hypotheses, using models and gene sequence data for bacterial QS. QS is a wide-spread, cooperative signal-response system that is involved in the regulatory control of a number of bacterial social traits, including virulence, antibiotic resistance, plasmid transfer, biofilm formation, and bioluminescence (Miller and Bassler 2001). QS operates via the constitutive production of small, diffusible chemical pheromone signals called “autoinducers” that bind to a gene regulatory protein called the “response regulator” (Fuqua et al. 1994). The response regulator becomes activated when a threshold concentration of the autoinducer is detected in the environment, causing it to respond by up- or downregulating a suite of target genes such as those responsible for bioluminescence or virulence. Autoinducer molecules accumulate in the environment in proportion to cell density, so that genes upregulated by QS are likely to have positive density-dependent benefits (although see Redfield 2002). QS-deficient mutants have been considered to be “social cheaters” because they do not incur the costs of producing the autoinducers or activating the response-regulatory apparatus (Velicer et al. 2000; Diggle et al. 2007a; Foster et al. 2007; Sandoz et al. 2007). Thus, bacterial QS is a social trait with a well-known underlying genetic basis, making it well suited for tests using the tools of molecular population genetics.

Theory

Distinguishing between Hypotheses

The ESC and KSMB hypotheses make distinct predictions about the patterns of polymorphism expected at the molecular level. First, they make different predictions for the “site frequency spectrum” (Ewens 1972; Tajima 1989), that is, the frequency distribution of mutations in a gene sequence. The ESC hypothesis predicts that the polymorphism frequency distribution will deviate from random by having “fat tails,” meaning that there are more intermediate frequency alleles segregating in the population than predicted under neutrality. Frequency-dependent selection creates this skew in the allele frequency spectrum by driving low-frequency cheating mutants to a stable equilibrium at a higher, intermediate frequency, where they are maintained as cheater haplotypes distinct from cooperator haplotypes. Selection prevents either cheaters or cooperators from extinction or fixation, and linked neutral variation surrounding the selected polymorphism allows the detection of haplotype blocks (i.e., a genetic “footprint”) associated with selectively balanced polymorphisms (Kreitman and Di Rienzo 2004; Charlesworth 2006). On the other hand, the KSMB hypothesis predicts “skinny tails” as individual cheater mutations, deleterious to the group, are removed from the population by kin selection faster than neutral mutations are removed by drift. As we shall see, our KSMB model for QS genes predicts that selection against cheaters is weak due to conditional expression, so that a site frequency spectrum close to the neutral expectation is still consistent with the KSMB hypothesis.

The ESC and KSMB hypotheses also make distinct predictions about relative levels of sequence divergence between closely related species. The stable maintenance of cheaters by selection prevents fixed differences from arising between closely related species, because rare mutant advantage prevents any one type from sweeping to fixation (McDonald and Kreitman 1991; Kreitman and Di Rienzo 2004; Charlesworth 2006). Put differently, the active maintenance of polymorphism by selection reduces the rate of gene substitution, not just for the target of selection but also for neighboring neutral variants (base pairs). Furthermore, cheaters of large effect, which are predicted by the ESC hypothesis (see below), cannot fix in a species that is QS+. If a cheater of large effect fixes, then that species will no longer possess functional QS. Thus, as long as both species in our two-species comparisons are QS+, the ESC hypothesis predicts that sequence divergence between species will be significantly lower than polymorphism within species. The statistical significance of this difference can be determined using the McDonald-Kreitman (MK) test (McDonald and Kreitman 1991). Alternatively, kin selection-mutation balance creates transient but not stable polymorphisms (Van Dyken et al. 2011), so that segregating variations may fix stochastically in proportion to the strength of selection and the effective population size. As a consequence, KSMB theory predicts either equal rates of polymorphism within species and divergence between them or, as a result of positive selection favoring better cooperators, greater sequence divergence between species than polymorphism within them. Unlike the ESC hypothesis, superior cooperators are not prevented from sweeping to fixation.

Another difference between the two hypotheses, although one that is perhaps less straightforward to test, is a difference in predictions about the effect sizes of segregating cheater mutations. The ESC hypothesis predicts that cheaters in nature will typically have large fitness effects, as cheaters with the most extreme phenotypes will be favored most strongly when rare. In fact, cheaters used in laboratory experiments are typically complete loss-of-function mutants (Strassmann et al. 2000; Velicer et al. 2000; Foster et al. 2007). Thus, under the ESC hypothesis, we predict that intermediate-frequency cheater variants would be disproportionately characterized by large insertions/deletions (indels), frame shifts, or premature stop codons. On the other hand, the KSMB hypothesis predicts stronger purifying kin selection against such large effect mutations but weaker selection against mutations with small effects. Thus, on average, segregating cheating variants are predicted by the KSMB hypothesis to have small cheating effects, as the frequency obtained by a deleterious mutation is inversely proportional to the strength of selection against it. As we note in “Discussion,” this prediction is difficult to test.

Model

Here we present the KSMB model in order to demonstrate that purifying kin selection and mutation are sufficient to generate high levels of within- and among-species genetic diversity at both the signal and the response loci of QS systems. Expression of the QS phenotype gives a total possible benefit of b_R. The R subscript denotes the fitness benefit contributed by “responder” cells. The expression of the signal comes at a cost c_S, and the expression of the suite of downstream genes regulated by QS comes at a cost c_R.

Because the response regulator is activated only when cells reach a sufficient density, QS is a conditionally expressed trait. We let ϕ be the average proportion of generations over an interval where the QS phenotype is activated, which is approximately equivalent to the proportion of the population in any one generation that expresses QS (Van Dyken and Wade 2010). In the next section, we derive a model for the evolution of the response-regulator and signaling loci of bacterial QS systems. The models are then translated into predictions for levels of sequence polymorphism and divergence at these loci.

The expected level of sequence polymorphism at a locus is defined as

$$\pi \equiv \frac{1}{L}\sum _{l=1}^{L}2{\widehat{q}}_l(1-{\widehat{q}}_l),$$ (1)

(Tajima 1983) where L is the number of nonsynonymous nucleotides at the locus and the sum is taken over all nonsynonymous nucleotides. We are assuming that the population is at equilibrium between mutation and selection, so that q̂ is the equilibrium frequency of the mutant allele in the population at the kin selection-mutation balance.

The fixation process determines the level of sequence divergence among species. The probability of fixation of a mutant allele is given by

$$P=\frac{{\int }_0^{q}G(x)dx}{{\int }_0^{1}G(x)dx},$$ (2)

(Kimura 1962) where G(x) = exp (−∫ 2M/V), M is the mean change in allele frequency over a generation due to directional processes (i.e., selection and mutation), and V is the variance in allele frequency change per generation due to random genetic drift. M is obtained by using standard population-genetic theory for the change in allele frequency in an infinite population due to selection and mutation (see below), while V = pq/N_e, where N_e is the effective population size. For social evolution models, N_e is explicitly a function of population structure. Expressions for N_e have been worked out for a number of different population structures (Whitlock and Barton 1997; Whitlock 2003). For applications of Kimura’s equation to social traits, see studies by Whitlock (2003), Rousset (2006), Demuth and Wade (2007), and Linksvayer and Wade (2009).

Polymorphism and Divergence at the Signaling Locus

We consider two KSMB models of evolution at the signaling locus, one where signal cost is reduced along with signal function (signal cheaters) and the other where signal function is reduced but cost remains unaffected (signal noncheaters). In both models, we assume that the population is fixed for a functional allele at the response locus but is polymorphic at the signaling locus. This assumption greatly simplifies the model but should be relaxed in future investigations.

Model 1: Mutations Reduce Signaling Cost

In model 1, the mutant allele reduces both the functionality of the signaling molecule and the cost of expressing the signal (Diggle et al. 2007a; Sandoz et al 2007). We assume two alleles at the signal locus: S and s. The S genotypes are wild-type cells that constitutively express a fully functional signal, while the s genotypes either do not express the signal or have diminished signal production. The s genotype is a “cheater,” as it does not experience the cost of expressing the signaling molecule (c_S) but nonetheless receives the benefit produced by others. The fitnesses of genotypes S and s are

$$\begin{array}{l}{W}_{S,i}=(1-\varphi )(1-c_{\mathrm{S}})+\varphi (1-c_{\mathrm{S}}+p_{S,i}{b}_{\mathrm{R}}),\\ W_{s,i}=(1-\varphi )(1)+\varphi (1+p_{S,i}{b}_{\mathrm{R}}),\end{array}$$ (3)

where p_{S, i} is the frequency of S genotypes in the ith group (which donate a benefit to both genotypes) and ϕ is the fraction of generations in which the density is sufficiently high that there is a response to the signal and creation of the subsequent benefit, b_R. Note that the S genotype always bears the cost of the signal, whether the benefit is expressed. In the fraction of generations when the group is at low density (1 − ϕ), the response locus is not expressed, and so individuals do not receive the benefit of the response phenotype. Nevertheless, the signaling locus is constitutively expressed, so that its cost is still manifest even at low density. Despite not producing a signal, cheaters nonetheless receive the benefit (b_R) of the expression of the response phenotype from group members in the fraction of generations, ϕ, after the density is sufficient to trigger the response.

Given the fitness model described by equation (3), the change in global allele frequency of the mutant (s) allele at the signaling locus is

$$\mathrm{\Delta }{q}_{\mathrm{S}}=-\frac{q(1-q)(\varphi b_{\mathrm{R}}r-c_{\mathrm{S}})}{\overline{W}}$$ (4)

(see app. A for derivation), where r is the kin selection coefficient of relatedness and W̄ is the global mean fitness. In order for QS to evolve (i.e., in order to prevent cheaters from spreading), the following condition must be satisfied:

$$\varphi b_{\mathrm{R}}r-c_{\mathrm{S}}>0.$$ (5)

Compare this with the condition for the spread of a constitutively altruistic allele, which is given by Hamilton’s rule: br − c > 0 (Hamilton 1964). Equation (5) is more restrictive than this because the conditionality of the expression ϕ < 1 weakens the benefit of acting altruistically (i.e., expressing QS). That is, the group does not experience the benefit in those generations when the gene is not expressed.

Let μ be the per-nucleotide, per-generation rate of one-way mutation from S alleles to s alleles. Then, using equations (1), (3), and (4), we find that the expected level of polymorphism at the signal locus at equilibrium between selection and mutation is approximately (to first order in q)

$${\pi }_{\mathrm{S}}\cong \frac{2\mu }{\varphi b_{\mathrm{R}}r-c_{\mathrm{S}}}$$ (6)

(app. A). Unfortunately, estimates are not available from natural populations for any of the parameters in equation (6). Until these estimates are available, there can be no exact quantitative prediction for levels of standing polymorphism. However, there are clear qualitative predictions relative to other nonsocial genes that can be drawn from equation (6). In particular, note that the level of polymorphism is inflated by the conditional expression ϕ < 1, by interactions in nonclonal groups (r < 1), and by a high cost of signaling (c_S > 0; fig. 1A). These three factors show that, all else being equal, the signaling molecule will have greater sequence polymorphism relative to a constitutively expressed, nonsocial gene with selective advantage b_R (see also Linskvayer and Wade 2009; Van Dyken and Wade 2010; Van Dyken et al. 2011).

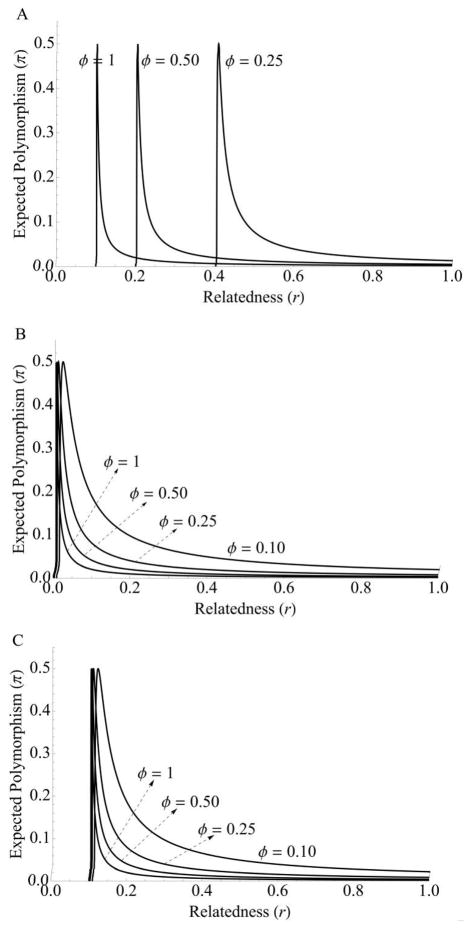
Figure 1.

Expected polymorphism at quorum sensing (QS) loci. Curves represent expected polymorphism as a function of relatedness, r, and frequency of QS expression, ϕ. Note that in every case, polymorphism increases as relatedness and the frequency of expression decrease. The unimodal curve results from the fact that polymorphism has a maximum at π = 0.5. When allele frequency is greater than 0.5, the polymorphism begins to decrease toward 0 (see eq. [1]). The sharp drop in polymorphism at low relatedness after the peak corresponds with fixation of the mutant allele, which eliminates polymorphism and creates a fixed difference between species. Comparison of these plots shows that we would expect greater polymorphism for the signal locus than the response regulator under model 1 but lower polymorphism of signal than the response regulator if model 2 holds. Furthermore, the response regulator can maintain lower mutation load at low frequency of expression, ϕ, than can the signal locus under model 1, where infrequent expression allows cheaters to spread rapidly. Parameter values are as follows: c_R = c_S = 0.01, b_R = 0.10, μ = 10⁻⁴, and N = N_e = 1,000.

We now wish to determine how cheating under the KSMB hypothesis affects the divergence of gene sequences between species. To do so, we must substitute values for M and V into equation (2), which is the equation giving the rate of gene substitution. M is the mean change in the frequency of a mutant allele due to deterministic forces such as selection, which we simply take from equation (4), setting W̄ = 1 because we assume weak selection in a continuous model (Kimura 1962). As stated previously, V is the variance in allele frequency change due to drift, which for haploids equals pq/N_e. By making these substitutions in equation (2) and taking the integral and simplifying, we find that the probability of fixation of the mutant allele at the signal locus under model 1 is

$$P=\frac{1-exp[2N_{\mathrm{e}}{p}_0(\varphi b_{\mathrm{R}}r-c_{\mathrm{S}})]}{1-exp[2N_{\mathrm{e}}(\varphi b_{\mathrm{R}}r-c_{\mathrm{S}})]},$$ (7)

where N_e depends on population structure (Whitlock and Barton 1997; Whitlock 2003) and p₀ is the initial frequency of the mutation in the population (for new mutations p₀ = 1/N, where N is the census size of the population). Just as with polymorphisms, the KSMB hypothesis predicts that divergence at the signaling locus will be inflated by low ϕ and r and high c_S (fig. 2A).

Figure 2.

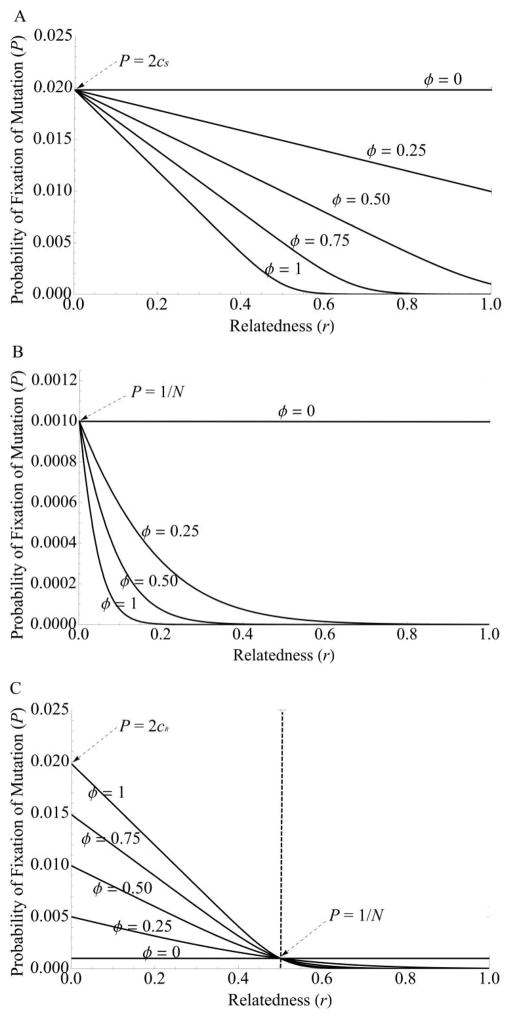
Relatedness can reverse the dynamics of spread of a newly arisen “cheating” mutation. The curve shows the probability of fixation of a newly arisen cheating mutation at the signal locus (under model 1, where signal mutants do not pay the cost of signaling). The dashed vertical line indicates neutrality, that is, the point where the inclusive fitness effect of the cheating mutant equals 0. The probability of fixation at neutrality equals the frequency of the mutant, which is for 1/N a new mutation. The direction of selection depends on relatedness. Cheaters act as deleterious mutants (in which the probability of fixation is less than that for neutral mutations) when relatedness is high but beneficial mutants (in which the probability of fixation is greater than that for neutral mutations) when relatedness is sufficiently high. The curve has a maximum value at r = 0 of P = 2c, corresponding to the fixation probability of a beneficial mutation at a nonsocial locus, where c is the cost of producing the quorum sensing signal. Parameter values are as follows: c = 0.01, b_R = 0.02, N = N_e = 1,000, and ϕ = 1.

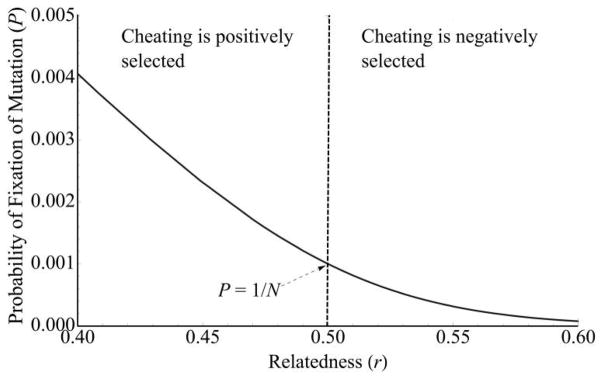
Figures 2 and 3 demonstrate one of the primary consequences of linear fitness for selection on cheating: cheaters behave as deleterious mutations when relatedness is high (greater than the threshold for satisfying Hamilton’s rule) but behave as beneficial mutations when relatedness is low. Cheaters are neutral when the inclusive fitness effect equals 0, such that their probability of fixation equals their initial frequency in the population, p₀ = 1/N. Note that cheaters have a nonzero fixation probability even when relatedness is high, because slightly deleterious mutations can become fixed by random genetic drift in a population (Kimura 1962). Note also that, in the regions of low r where cheater mutations are beneficial, mutations are not guaranteed to fix. For example, when r = 0, cheaters act as beneficial mutations and have a probability of fixation of P ≈ 2c_S, which is the classic result for the probability of fixation of a beneficial mutation at nonsocial loci (Haldane 1927; Kimura 1962).

Figure 3.

Fixation probability of quorum sensing (QS) mutants. Note the sensitivity of fixation probability in all cases to relatedness, r, and the frequency of QS expression, ϕ. A, Signal mutants under model 1 behave as deleterious mutants when r and/or ϕ are high but become advantageous when r and/or ϕ are sufficiently low, peaking at a maximum of P = 2c_S, which is twice the maximal benefit of cheating (see also fig. 2). B, Note the change in scale from model 1, where fixation probabilities are much higher in general. Unlike model 1, the sign of fitness does not change with model 2 (see fig. 2): cheating mutants always act as deleterious mutants in model 2. Infrequent expression and low relatedness relax selection against mutants, increasing their probability of fixation to a maximum at the neutral fixation probability of P = 1/N. C, Fixation probability of mutations at the response-regulator locus. As with signal mutants under model 1, response-regulator mutants can act as either beneficial or deleterious, depending on relatedness. Note that the effect of conditional expression reverses when relatedness reaches the Hamiltonian threshold at neutrality (vertical dashed line), so that rarely expressed mutants (small ϕ) have a lower probability of fixation than frequently expressed mutants (large ϕ) when relatedness is low but a greater fixation probability when relatedness is high. This reversal corresponds to the transition from beneficial (at low relatedness) to deleterious (at high relatedness). The maximum fixation probability occurs at r = 0 and is equal to the standard probability of fixation for a beneficial, nonsocial mutation, P = 2c_R. Parameter values are as follows: c= 0.01, b_R = 0.02, N = N_e = 1,000, and ϕ = 1.

The transition from deleterious to beneficial also occurs by modulating the frequency of the expression of QS, ϕ. When populations undergo many generations before expressing QS-controlled phenotypes (ϕ ≪ 1), cheaters have a greater probability of fixing in the population. This happens because the individual fitness benefit of not expressing the signal (c_S) exceeds the group benefit of the response (ϕb_Rr). Indeed, a QS system can be lost by mutational meltdown if it is too infrequently expressed (see also Van Dyken and Wade 2010).

Note the shape of the fixation curve in figures 2 and 3. The curve is relatively flat and increases slowly in the region where cheaters are deleterious. When cheating becomes beneficial, the curve is steep and quickly approaches the maximum probability of fixation of P = 2c.

Model 2: Mutations Do Not Reduce Signal Cost

In model 2, we assume that mutants at the signal locus impair signal function but not its cost of expression. Unlike in model 1, such mutants are not considered cheaters. We thus have the following fitness model, where both genotypes have the same fitness because both express the signal cost and gain the same benefits when the QS system is activated:

$$\begin{array}{l}{W}_{S,i}=(1-\varphi )(1-c_{\mathrm{S}})+\varphi (1-c_{\mathrm{S}}+p_{S,i}{b}_{\mathrm{R}}),\\ W_{s,i}=(1-\varphi )(1-c_{\mathrm{S}})+\varphi (1-c_{\mathrm{S}}+p_{S,i}{b}_{\mathrm{R}}).\end{array}$$ (8)

The change in frequency of the signal mutant is

$$\mathrm{\Delta }{q}_{\mathrm{S}}=-\frac{q(1-q)\varphi b_{\mathrm{R}}r}{\overline{W}}$$ (9)

(app. A). Interestingly, despite both alleles having the same fitness function (eq. [8]), there is still a response to selection. This is because the s and S alleles experience different expected frequencies of cooperators in their group due to relatedness, so that E[p_{S, i}] will differ for each allele. Relatedness, r, quantifies this difference. The response to selection, then, is entirely among groups, as selection favors groups with a greater proportion of QS-proficient cells. Because mutants experience the same signaling cost as wild-type cells, c_S, mutants are not cheaters, as they gain no relative fitness advantage over cooperators within groups. As long as ϕb_Rr > 0, such a signal mutant will be opposed by kin selection.

The expected level of polymorphism at the signal locus under this model is

$${\pi }_{\mathrm{S}}\cong \frac{2\mu }{\varphi b_{\mathrm{R}}r}.$$ (10)

The value of equation (10) is always less than that of equation (6) for the same parameter values (fig. 1). This is because signal-deficient mutants under model 2 are not cheaters, and so among-group selection against them is not mitigated by an opposing within-group fitness advantage. The net result is that total selection against impaired signalers is stronger than it is against nonsignalers, thus reducing standing variation at the locus at the equilibrium kin-selection-mutation balance.

The probability of fixation of a mutation that impairs signal function under this model is

$$P=\frac{1-exp(2N_{\mathrm{e}}\varphi b_{\mathrm{R}}{rp}_0)}{1-exp(2N_{\mathrm{e}}\varphi b_{\mathrm{R}}r)}.$$ (11)

Unlike in model 1, modifying relatedness does not change the direction of selection. Mutations are uniformly deleterious, and selection against signal-defective mutants simply becomes weaker as relatedness decreases (fig. 2). As relatedness and/or frequency of expression decrease, the probability of fixation of deleterious mutations increases toward a limit at neutrality, where P = 1/N. Thus, the possibility of cheating (model 1) greatly increases the diversity at a sociality locus, particularly when relatedness is high (fig. 1).

Polymorphism and Divergence at the Response-Regulator Locus

Unlike in the cases above, mutations at the response locus always reduce both the functionality of the QS system and the cost of expressing the QS phenotype, so that there is only one model to consider. At the response locus, the genotypic fitnesses are

$$\begin{array}{l}{W}_{B,i}=(1-\varphi )(1)+\varphi (1-c_{\mathrm{R}}+p_{\mathrm{R}}{b}_{\mathrm{R}})-c_{\mathrm{S}},\\ W_{b,i}=(1-\varphi )(1)+\varphi (1+p_{\mathrm{R}}{b}_{\mathrm{R}})-c_{\mathrm{S}}.\end{array}$$ (12)

Note that both alleles experience an equal cost of expressing the QS signal, as we have assumed that both are signal proficient. From this model, we find that the change in allele frequency at the response-regulator locus is

$$\mathrm{\Delta }{q}_{\mathrm{R}}=-\frac{q(1-q)\varphi (b_{\mathrm{R}}r-c_{\mathrm{R}})}{\overline{W}}$$ (13)

(app. A). Note that there are two differences between equation (13) and model 1 of the signaling locus (eq. [4]). First, with our model of the response-regulator locus, both genotypes bear the cost of signaling, so the term c_S does not appear in equation (13) whereas it does in equation (4). Second, with the response-regulator locus, conditional expression (ϕ) weakens total selection and not just the among-group component as with model 1 of the signal locus (eq. [4]). This occurs because both the cost and the benefit of the QS response are expressed only under high density, whereas the cost of producing the signal is expressed under both high and low densities. This means that response-deficient mutants are cheaters whose fitness advantage is conditional: they gain a cheating advantage only in those generations where the QS phenotype is expressed. Signal cheaters, on the other hand, gain a cheating advantage in every generation because the signal is constitutively expressed, regardless of whether there is a response.

For QS to evolve, the following condition must be true:

$$b_{\mathrm{R}}r-c_{\mathrm{R}}>0.$$ (14)

Unlike in model 1 of the signaling locus, conditional expression (ϕ) does not influence the direction of evolution. Following the approach above, we find that the replacement site polymorphism at the response-regulator locus is approximately

$${\pi }_{\mathrm{R}}\cong \frac{2\mu }{\varphi (b_{\mathrm{R}}r-c_{\mathrm{R}})}$$ (15)

(app. A). The level of standing genetic variation at the response-regulator locus is sensitive to the frequency of expression (ϕ). If QS is expressed only half of the time, the sequence diversity (standing polymorphism) doubles; if QS is expressed only a third of the time, the level of sequence diversity triples. In general, polymorphism at the response-regulator locus will increase as the frequency of expression (ϕ) and relatedness (r) decrease and as the cost of expression of the response phenotype (c_R) increases.

The probability of fixation of a mutation at the response locus is

$$P=\frac{1-exp[2N_{\mathrm{e}}\varphi (b_{\mathrm{R}}r-c_{\mathrm{R}})p_0]}{1-exp[2N_{\mathrm{e}}\varphi (b_{\mathrm{R}}r-c_{\mathrm{R}})]}.$$ (16)

Similar to model 1 of the signal locus but unlike model 2, diminution-of-function mutations at the response locus are deleterious at high relatedness but beneficial at low relatedness. However, unlike both models of the signal locus, conditional expression per se does not alter the direction of selection. When the frequency of expression is low (small ϕ), “deleterious” mutants (at high r) have a greater probability of fixation compared with constitutively expressed traits (high ϕ), while “beneficial” mutants (at low r) have a reduced probability of fixation. This makes sense, because response-regulator cheaters gain an advantage only when QS phenotypes are expressed: it is then that they gain a fitness advantage by not experiencing the cost of expressing the response phenotype. Thus, selection against cheaters at high relatedness is weakened, allowing them to accumulate to a higher frequency in the population, while selection favoring cheaters at low relatedness is likewise weakened, impairing their ability to spread.

Which Should Be More Diverse, a Signal or a Response Locus?

A comparison of equations (6) and (15) provides a prediction for the relative diversity of the signaling locus compared with the response locus. For model 1 of the signal locus, we find that, π_R >π_S when ϕc_R > c_S (see also fig. 1). Thus, sequence diversity at the response-regulator locus will be greater than that at the signaling locus when the frequency of expression times the cost of responding (ϕc_R) is greater than the cost of signaling (c_S). Laboratory studies have found that the cost of signaling is typically less than the cost of responding (c_S < c_R) because the signaling molecule is small and relatively inexpensive to synthesize, while the response phenotype is often more complex and likely to be more expensive (Diggle et al. 2007a; Sandoz et al. 2007). However, if the threshold density for expression is high, then ϕ will be small and the response locus will be more diverse than the signaling locus. That is, cost alone is not sufficient to determine the relative diversity of the two loci because the cost of response is mitigated by ϕ, the frequency of expression.

On the other hand, if model 2 is operating—that is, if mutants at the signal locus experience the same cost of expressing the signal as the wild type—then, π_R > π_S when c_R > 0, which is always true by definition. Thus, under model 2, the response locus will always be more diverse than the signal (see fig. 1). Put differently, because of the relationship between polymorphism and gene frequency, we can say that under many conditions, response cheaters will be more common than nonsignaling cheaters.

Empirical Results

With the theory above, we can test the predictions of the ESC and KSMB hypotheses using QS gene sequence data gathered from GenBank. Our data were obtained by searching the PopSet database of GenBank for known QS gene homologues (both signal and response loci) based on those identified by Lerat and Moran (2004). At the time of analysis, this search returned 11 population data sets for known QS genes. We also obtained population sequence data for the Escherichia coli QS homologue sdiA from available fully sequenced E. coli genomes, using a BLAST (Altschul et al. 1997) search of these genomes. No other species with a known QS homologue had enough fully sequenced genomes (eight or more) at the time of analysis to conduct statistical tests.

To estimate within-species sequence polymorphisms, we first controlled for variation in mutation rates and effective population size among genes by taking the ratio of non-synonymous to synonymous site nucleotide diversity (π_A/π_S) as our measure of within-species polymorphism. For comparison with QS genes, polymorphism data for a random sample of bacterial genes were obtained from a study by Hughes (2005). The 149 genes in this data set were sampled randomly with respect to sociality or conditionality of expression. Genes with π_S < 0.10 were eliminated from the analysis in order to reduce the error in the π_A/π_S estimate and to ensure that genes have had time to reach the mutation-selection equilibrium. The resulting data set has N = 65, with a median π_A/π_S of 0.0898 and a mean of 0.1858 (±0.0266 SE). By this criterion, one QS gene was also eliminated from the analysis (agrA in Staphylococcus aureus), giving N = 11 for QS genes with a median π_A/π_S of 0.2514 and mean of 0.3286 (±0.0626 SE). The median and mean levels of polymorphism of the QS genes are significantly higher than those of the random sample of bacterial genes (one-tailed t-test with unequal variances on log-transformed data: P < .001; one-tailed t-test: P = .017).

For gene divergence between species, we take the ratio of nonsynonymous to synonymous site divergence (d_N/d_S) to control for variation in mutation rates and effective population sizes among genes. QS genes had a median divergence of 0.272 and a mean of 0.316 (±0.0898 SE). When conservatively excluding the largest data point because of the high standard error of its estimate, the QS mean is 0.2293 (±0.0316 SE). We used the data set from Ochman et al. (1999) as a representative sample of all bacterial genes. These data were collected randomly with respect to gene identity, except that ribosomal genes were omitted, again making our comparison more conservative, as ribosomal genes have very low divergences. The median d_N/d_S value for this data set is 0.1342 (N = 101). The median divergence for the QS genes is 0.2722, which is more than two times that for the random sample of genes (one-tailed t-test with equal variances on log-transformed data: P = .017). Eleven out of 12 QS genes ranked above the 49th percentile of divergence in the data of Ochman et al. (1999; P < .001).

We tested each QS gene to detect the signature of natural selection. McDonald-Kreitman tests (McDonald and Kreitman 1991) were performed on 11 of the 12 data sets (a BLAST [Altschul et al. 1997] search failed to return a sequence with significant homology for the Lactococcus lactis comX gene, so an MK test could not be conducted for this gene). Of these tested genes, nine of 11 failed to show a significant deviation from neutrality, while two of the 11 showed a weak signature of positive selection (table 1).

Table 1.

Polymorphism, divergence, and selection of quorum sensing genes

Gene	Species	No. SP	No. NP	No. SFD	No. NFD	MK P value	dN/dS	πA/πS	Tajima’s D
ahyI/asaI	Aeromonas hydrophila/Aeromonas salmonicida	78	40	7	0	.096	.134	.178 (.072)	−.975
ahyR/asaR	A. hydrophila/A. salmonicida	…	…	…	…	…	.290	…	…
ahyR/asaR	Aeromonas bestiarium/Aeromonas popoffii	136	71	9	3	.498	.148	.236 (.028)	.981
luxR	Vibrio fischeri/Vibrio parahaemolyticus	71	70	2	5	.253	.294	.251 (.016)	1.891
luxI	V. fischeri/V. parahaemolyticus	27	13	1	0	1.000	.133	.153 (.004)	1.491
sdiA	Escherichia coli/Citrobacter kosseri	24	9	112	66	.272	.133	.095 (.016)	1.164
agrA	Staphylococcus aureus/Staphyolococcus haemoliticus	45	5	91	29	.027*	.082	.017 (.016)	−1.063
agrB	S. aureus/S. haemoliticus	91	65	44	44	.209	.359	.399 (.022)	1.164
agrC	S. aureus/S. haemoliticus	194	121	106	108	.006**	.340	.352 (.026)	1.422
agrD	S. aureus/S. haemoliticus	16	24	10	14	.895	.356	.561 (.026)	1.427
comQ	Bacillus subtilis/Bacillus mojavensis	180	155	27	14	.137	.254	.512 (.283)	−.222
comX	B. subtilis/B. mojavensis	19	33	1	3	.634	1.271	.748 (.156)	−.636
comX	Lactococcus lactis	…	…	…	…	…	…	.131 (.024)	1.009
Pooled MK test		881	606	410	286	.8807

Note: Values in columns 3–6 are the number of synonymous and nonsynonymous polymorphisms (SP and NP, respectively) within species and the number of synonymous and nonsynonymous fixed differences (SFD and NFD, respectively) between species from which individual and pooled MK tests were performed. π_A/π_S and Tajima’s D were calculated for the first species in each two-species comparison. The only significant signatures of selection found positive selection, which is the opposite signature as that produced by balancing selection.

^*P < .05.

^**P < .01.

The signature of positive selection, where divergence is higher than polymorphism, is the opposite of the pattern predicted by the ESC hypothesis, under which within-species polymorphism exceeds between-species divergence owing to frequency-dependent selection. In order to increase the power of our analysis to maximize the chances of seeing a significant deviation from neutrality, an MK test was conducted on the pooled sample of all QS genes. This pooled test failed to reject the null hypothesis of neutral evolution (χ² = 0.023, P = .881, df = 1).

To test the QS genes for departure of the allelic site-frequency spectrum from neutral expectation, we used Tajima’s D test (Tajima 1989). None of the 11 QS genes showed a significant deviation from neutrality, which is consistent with the KSMB model predictions of relaxed selection but inconsistent with the ESC model of frequency dependence (table 1).

We lack the statistical power to determine whether the signal or the response locus has greater variation, and so we are unable to adequately test theoretical predictions on this front. Clearly, more data will allow us to test this and other hypotheses.

Discussion

Understanding the origins, maintenance, and dynamics of social cooperation and conflict in nature is one of the principal aims of the study of social evolution. Here we have shown how kin-selection theory based in population genetics can be extended to make predictions about gene sequence polymorphism and evolutionary divergence (see also Linksvayer and Wade 2009; Van Dyken et al 2011). These predictions can then be tested using the tools of molecular population genetics (e.g., Kreitman 2000; Barker et al. 2005; Cruickshank and Wade 2008).

Stable polymorphisms of cheaters, which arise when there are nonlinear social interactions (Queller 1985; Doebeli et al. 2004; smith et al. 2010), should create a genetic signature of balancing selection typified by inflated polymorphism but diminished among-species sequence divergence and significantly positive Tajima’s D (Mead et al. 2003; Kreitman and Di Rienzo 2004; Charlesworth 2006). We do not see this signature in our data for QS genes. Alternatively, the KSMB model of QS evolution predicts high levels of polymorphism matched by high levels of divergence due to the fact that the selective benefit of QS (b_R) is diluted by low relatedness (Linksvayer and Wade 2009), conditional expression (Van Dyken and Wade 2010), and the within-group fitness benefit gained by “cheater” mutants (Van Dyken et al. 2011; ϕ, r < 1, c > 0). These three factors have been considered independently in previous work (Linksvayer and Wade 2009; Van Dyken and Wade 2010; Van Dyken et al. 2011) but are here united in a single model. Conflict, conditional expression, and nonclonality of social groups all weaken the strength of kin selection, allowing slightly deficient QS mutants to accumulate both within and between populations, enhancing sequence polymorphism and divergence relative to nonsocial, constitutively expressed genes without causing a positive Tajima’s D. These predictions are supported by our QS data.

The fact that our alignments do not show any evidence of segregating total loss-of-function mutations (e.g., premature stop codons, large insertions and/or deletions, frame shifts, etc.) is also consistent with the KSMB prediction that the increased variation found in QS genes is due to the accumulation of point mutations of minor effect. On the other hand, the ESC hypothesis, which predicts that cheating mutants will be of large effect, is inconsistent with our data. However, it is important to recognize that the degree of functionality, and hence the attendant fitness costs and benefits of mutations, cannot be mapped uniquely onto the nature of the mutation. As a consequence, this result is provisional but intriguing nevertheless.

Of course, the failure of the data to reject our null hypothesis is not itself proof that QS cheater dynamics are explained primarily by KSMB theory. In fact, our finding of high within- and among-group variation may also be consistent with an “arms race” scenario (Greig and Travisano 2004; Eldar 2011; Sucgang et al. 2011) or the action of selection favoring rapid diversification of signal and response molecules (Ansaldi and Dubnau 2004). These hypotheses predict rapid genetic diversification within and among species, without stable cheater maintenance. Thus, as currently formulated, their predictions are indistinguishable from those of our evolutionary null hypothesis and so do not currently offer the possibility of a test. One of the goals of our analysis was to demonstrate a much more parsimonious, nonadaptive explanation for observed patterns. Indeed, these hypotheses were proposed post hoc as explanations for observed “high” levels of genetic variation at sociality loci, including QS loci (Ansaldi and Dubnau 2004; Eldar 2011). Rather than considering the possibility that these patterns resulted from nonadaptive processes (namely, relaxed purifying selection due to non-clonality and conditional expression), elaborate adaptive explanations were proposed instead. Because KSMB is a much more parsimonious explanation for the available data, relying, as it does, simply on mutation, drift, and purifying selection, we believe that these adaptive alternatives should be treated with skepticism until they can be shown to make predictions distinguishing them from KSMB and from one another.

Importantly, tests of the site-frequency spectra are subject to bias due to sampling effects, the age of mutations, and population demography (Kreitman and Di Rienzo 2004; Charlesworth 2006). The divergence data are less ambiguous about the importance of balancing selection, as they are less sensitive to sampling and demographic artifacts. Stable polymorphisms increase within-species genetic diversity and diminish the accumulation of fixed differences between species, leading to the phenomenon of “ancient polymorphisms” shared across closely related species (Hittinger et al. 2010). Our data are not consistent with this prediction, as both within- and among-species variation is inflated, consistent with the KSMB models developed above. It is possible that future studies employing more sophisticated statistical tests and sampling protocols designed specifically to detect stable cheating will obtain different conclusions.

In any case, we believe that alternative selective explanations for evolutionary signals at sociality loci should remain in question until the more parsimonious evolutionary null hypothesis (KSMB) is rejected. As it stands, currently available theory and data support the inference that QS “cheaters” are evolutionarily transient and high levels of variation in QS genes result from relaxed selection. Sociomolecular evolution promises to provide a powerful avenue for investigating the action of social evolution in nature. However, before the field can advance further, much more theory and data are required.

APPENDIX A. Derivation of Allele Frequency Recursions and Expected Polymorphism

Here we show how the allele frequency recursions given in the main text can be derived and then how this leads to an expression for the expected level of polymorphism at a locus. We follow the procedures used by Van Dyken (2010) and Van Dyken et al. (2011). With selection in a population structured into social groups, such as bacterial biofilms or host-associated microbial collectives, the change in frequency of an allele over a single generation of selection is given by the multilevel Price equation (Price 1972; Hamilton 1975; Wade 1985; Rice 2004). The multilevel Price equation can be written as

$$\overline{W}\mathrm{\Delta }q=\text{Cov}(W_i,q_i)+\mathrm{E}[\text{Cov}(W_{ij},q_{ij})].$$ (A1)

The first term on the right-hand side is the change in allele frequency over a single generation due to selection among groups, and the second term is change due to selection within groups. Cov( ) denotes covariance, and E[ ] denotes expected value. W_i is the mean fitness of individuals comprising the ith group, while W_ij is the fitness of individual j in group i. Rewriting this equation into its equivalent regression coefficient form (Wade 1985) gives

$$\overline{W}\mathrm{\Delta }q={\beta }_{W_i,q_i}{V}_{\mathrm{b}}+{\beta }_{W_{ij},q_{ij}}{V}_{\mathrm{w}},$$ (A2)

where β_{Wi, qi} and β_{Wij, qij} are the partial regression coefficients of group and individual allele frequency on group and individual fitness, respectively (Wade 1985; Frank 1998; Rice 2004). V_b is the variance in allele frequency among all groups and V_w is the average within-group variance in individual allele frequency (i.e., V_w = E[Var_w (p_ij)]). Values for these variance components are given for neutral alleles by Wright (1951, 1965), and their sum gives the total genetic variance in the population (V_w + V_b = V_t). The ratio of among-group genetic variance to total group variance is, by definition, the kin selection coefficient of relatedness (V_w/V_t = r; Michod and Hamilton 1980; Falconer and Mackay 1996; Frank 1998).

The among-group partial regression coefficient, β_{Wi, qi}, is obtained by first computing the mean fitness of the group, W_i, from the allelic fitness functions provided in the main text (eqq. [3], [8], [12]). For example, the mean fitness for model 1 of the signal locus is obtained by calculating W_i = q_iW_{s, i} + (1 − q_i)W_{S, i}, where W_{s, i} and W_{S, i} come from equation (3). Next, we take the derivative of W_i with respect to q_i, giving β_{Wi, qi}. The within-group partial regression coefficient β_{Wij, qij} is simply the difference in the within-group fitness of each allele (β_{Wij, qij} = (W_{s, i} − W_{S, i}); Rice 2004). By making these substitutions, we obtain equations (4), (9), and (13) in the main text.

To make predictions about sequence polymorphism, we must first find the expected value of the allele frequency at equilibrium between selection and mutation. Mutation introduces variation into the population at a rate equal to the mutation rate m times the frequency of alleles that are subject to mutation (pμ), while selection removes this variation at a rate equal to Δq. At equilibrium, the rate in equals the rate out. The equilibrium allele frequency is found, then, by solving the following equation for q:

$$\mathrm{\Delta }q+(1-q)\mu =0,$$ (A3)

where the expression for Δq is given by equations (4), (9), and (13) in the main text.

Finding the expected polymorphism at a locus requires substituting the solution of equation (A3) into the definition of polymorphism, given as equation (1) in the main text. To simplify the solution, we make a few reasonable assumptions. First, we assume that mutation occurs at an equivalent rate across all L nucleotides of a gene. Second, we assume that the strength of selection is averaged over all nucleotides. Finally, we assume that individual mutant alleles are rare enough that q² is much smaller than q (technically, this is a first-order approximation in q). These assumptions and approximations lead from a solution to equation (A3) to the expressions for expected polymorphism given in the text (eqq. [5], [10], [14]).