Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure

Abstract

A dynamic programming algorithm for prediction of RNA secondary structure has been revised to accommodate folding constraints determined by chemical modification and to include free energy increments for coaxial stacking of helices when they are either adjacent or separated by a single mismatch. Furthermore, free energy parameters are revised to account for recent experimental results for terminal mismatches and hairpin, bulge, internal, and multibranch loops. To demonstrate the applicability of this method, in vivo modification was performed on 5S rRNA in both Escherichia coli and Candida albicans with 1-cyclohexyl-3-(2-morpholinoethyl) carbodiimide metho-p-toluene sulfonate, dimethyl sulfate, and kethoxal. The percentage of known base pairs in the predicted structure increased from 26.3% to 86.8% for the E. coli sequence by using modification constraints. For C. albicans, the accuracy remained 87.5% both with and without modification data. On average, for these sequences and a set of 14 sequences with known secondary structure and chemical modification data taken from the literature, accuracy improves from 67% to 76%. This enhancement primarily reflects improvement for three sequences that are predicted with <40% accuracy on the basis of energetics alone. For these sequences, inclusion of chemical modification constraints improves the average accuracy from 28% to 78%. For the 11 sequences with <6% pseudoknotted base pairs, structures predicted with constraints from chemical modification contain on average 84% of known canonical base pairs.

Recent discoveries have shown that RNA plays a larger role in biology than previously realized, e.g., in posttranscriptional regulation (1), development (2, 3), immunity (4, 5), and peptide bond formation (6, 7). It is necessary to determine the native structures of RNAs to understand their mechanisms of action, and determining secondary structure is a crucial step in this process.

RNA secondary structure can be predicted by free energy minimization with nearest neighbor parameters to evaluate stability (8-18). Previous studies demonstrated that nuclease cleavage data can be used to refine structure prediction and improve accuracy (8, 11). A predicted secondary structure can guide further experiments or comparative sequence analysis (19) and also aid in the design of RNA molecules (20, 21).

Chemical modification is a technique that reveals solvent accessible nucleotides (22). The nucleotides accessible to 1-cyclohexyl-3-(2-morpholinoethyl) carbodiimide metho-p-toluene sulfonate, dimethyl sulfate, and kethoxal are unpaired, in A-U or G-C pairs at helix ends, in G-U pairs anywhere, or adjacent to G-U pairs. This limited specificity differs from that observed with nucleases, and an algorithm allowing constraints from such chemical modification has not been reported. Chemical modification is used extensively to test hypothesized RNA secondary structures (19, 23-28). Chemical modification can also be used to deduce possible tertiary contacts within an RNA (29), to probe RNA bound to protein (25, 26, 30-35), or to follow RNA folding pathways (36-38). The method can map RNA in vivo (39-43), which is not possible with nuclease mapping. This is an important advantage because much is not known about renaturing purified RNA into its native conformation.

In this study, a dynamic programming algorithm for prediction of RNA secondary structure has been revised to use experimentally determined chemical modification constraints. These constraints dramatically improve the accuracy of structure prediction when free energy minimization alone predicts <40% of known base pairs. The nearest-neighbor parameters for free energy are also revised on the basis of recent experiments, and the program rnastructure now includes terms for the free energy of coaxial stacking of helices that are either adjacent or separated by a single mismatch in multibranch and exterior loops.

Methods

Nearest-Neighbor Parameters. Thermodynamic parameters are based on the set of Xia et al. (44-46) and Mathews et al. (8). Hairpin loop parameters (Tables 1 and 2) are revised on the basis of recent experimental results (47, 48) and the previous database of RNA hairpin stabilities (49-55).

Table 1. Free energy parameters for hairpin loop formation.

Parameter (number of nt or sequence)	ΔG°37, kcal/mol
ΔG°37 initiation(3)	5.4 ± 0.2
ΔG°37 initiation(4)	5.6 ± 0.1
ΔG°37 initiation(5)	5.7 ± 0.2
ΔG°37 initiation(6)	5.4 ± 0.1
ΔG°37 initiation(7)	6.0 ± 0.2
ΔG°37 initiation(8)	5.5 ± 0.2
ΔG°37 initiation(9)	6.4 ± 0.2
ΔG°37 bonus(UU or GA first mismatch but not AG)	−0.9 ± 0.1
ΔG°37 bonus(GG first mismatch)	−0.8 ± 0.3
ΔG°37 bonus(special G-U closure)	−2.2 ± 0.2
ΔG°37 penalty(C3 loop)	1.5 ± 0.5
ΔG°37 penalty(Cn loop), A	0.3 ± 0.1
ΔG°37 penalty(Cn loop), B	1.6 ± 0.9

Hairpin loop stabilities are estimated with the equation ΔG°_{37 loop} (n > 3) = ΔG°_{37 initiation}(n) + ΔG°₃₇(first mismatch stacking) + ΔG°_{37 bonus}(UU or GA first mismatch but not AG) + ΔG°_{37 bonus}(GG first mismatch) + ΔG°_{37 bonus}(special G-U closure) + ΔG°_{37 penalty}(oligo-C loops), where n is the number of unpaired nucleotides in the loop. ΔG°₃₇(first mismatch stacking) is derived from studies of terminal mismatch stability as compiled previously (45, 46). Terminal mismatch free energies for UU mismatches on both GU and UG pairs were updated from Dale et al. (47). The special GU closure bonus applies to GU closed hairpins in which a 5′ closing G is preceded by two G residues. The oligo-C penalty applies only to loops composed of all C residues. The penalty for oligo-C loops >3 nt is ΔG°_{37 penalty}(oligo-C loops, n > 3) = An + B. In addition to the terms in the above equation, the AU/GU terminal pair penalty of 0.5 kcal/mol is also applied at the ends of helices closed by hairpin loops (8, 44). Hairpin parameters were derived from linear regression on the database, excluding the stable hairpins ACAGUGCU (where closing pairs are shown and unpaired nucleotides are in bold), ACAGUGAU, ACAGUUCU, ACAGUACU, CUACGG, CUCCGG, and CUUCGG (47, 50, 86). The supporting information contains the complete database of hairpin loops used in the linear regression. Hairpin loops of lengths at 3, 4, and 6 unpaired nt with measured free energies that are either more or less stable by 0.9 kcal/mol when compared to prediction by the above model are included in a separate lookup table (Table 2). Hairpin loops of <3 nt are prohibited. ΔG°₃₇(first mismatch stacking) and terminal mismatch bonuses apply only to hairpin loops >3 unpaired nt. For hairpin loops >9 nt, initiation free energy is approximated (74) by ΔG°_{37 initiation}(n > 9) = ΔG°_{37 initiation}(9) + 1.75RTIn(n/9).

Table 2. Lookup table for unstable triloops and stable tetraloops and hexaloops.

Hairpin	Ref(s).	ΔG°37 loop, kcal/mol
CAACG	87	6.8
GUUAC	87	6.9
CAACGG	48	5.5
CCAAGG	48	3.3
CCACGG	48	3.7
CCCAGG	48	3.4
CCGAGG	48	3.5
CCGCGG	48	3.6
CCUAGG	48	3.7
CCUCGG	48	2.5
CUAAGG	48	3.6
CUACGG	47, 50	2.8
CUCAGG	48	3.7
CUCCGG	47	2.7
CUGCGG	47	2.8
CUUAGG	48	3.5
CUUCGG	47, 50	3.7
ACAGUACU	86	2.8
ACAGUGCU	86	2.9
ACAGUGAU	86	3.6
ACAGUUCU	86	1.8

For extra stable hairpins measured in 0.1 M Na⁺ (48, 87), placement was determined by assuming that the relative stability of loops remains constant between 0.1 and 1 M Na⁺. All values are based on experimental results rather than frequencies of occurrence as used in ref. 8. Unpaired nucleotides are shown in bold.

Thermodynamic parameters for bulge loops of single nucleotides are revised on the basis of measurements by Znosko et al. (56) by using the model

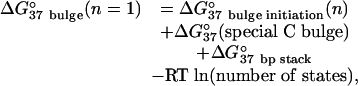where the number of states is the number of secondary structures containing a bulge of identical sequence in slightly different positions because of bulge migration, such as observed by NMR (57). For example, an isoenergetic bulged C in 5′UGU/3′ACCA can occur in two positions. ΔG°₃₇(special C bulge), -0.9 ± 0.3 kcal (1 cal = 4.18 J)/mol, is an empirical bonus applied to bulged C residues adjacent to at least one C. The ΔG°₃₇ bulge initiation for single nucleotide bulges is 3.81 ± 0.08 kcal/mol.

Internal loop free energy parameters are revised on the basis of recent measurements (58-61) and the previously assembled database (8, 45, 46, 62-69). In the program described here, measured values are used when available for 1 × 1, 1 × 2, and 2 × 2 internal loops, but approximations are used for most internal loops. The range of measured free energies differs for different types of internal loops. For example, the range is roughly 2 and 6 kcal/mol for 1 × 3 and 2 × 2 loops, respectively. Evidently, different types of loops require different approximations. Table 3 gives the different approximations used.

Table 3. Approximations for internal loop free energy parameters at 37 °C (in kcal/mol).

Specification			Free energy increments
ΔG°37 initiation(n)	0.5 ± 0.1 (2)	1.6 ± 0.1 (3)	1.1 ± 0.1 (4)	2.1 ± 0.1 (5)	1.9 ± 0.1 (6)	1.9 + 1.08 In(n/6) (>6)
ΔG°37 AU/GU	0.7 ± 0.1	0.7 ± 0.1	0.7 ± 0.1	0.7 ± 0.1	0.7 ± 0.1	0.7 ± 0.1
ΔG°37 asym	0.6 ± 0.1	0.6 ± 0.1	0.6 ± 0.1	0.6 ± 0.1	0.6 ± 0.1	0.6 ± 0.1
Type of loop/first pair:	5′RA/3′YG	5′YA/3′RG	5′RG/3′YA	5′YG/3′RA	GG	UU
1 × 1	NA	NA	NA	NA	−2.6 ± 0.2	−0.4 ± 0.1 if 5′RU/3′YU
1 × 2	0	−1.1 ± 0.2	−1.1 ± 0.2	−1.1 ± 0.2	−1.1 ± 0.2	−0.7 ± 0.2
1 × (n - 1), n > 3	0	0	0	0	0	0
2 × 3	0	−0.5 ± 0.2	−1.2 ± 0.1	−1.1 ± 0.1	−0.8 ± 0.2	−0.4 ± 0.1
Others, except 2 × 2	−0.8 ± 0.1	−0.8 ± 0.1	−1.0 ± 0.1	−1.0 ± 0.1	−1.2 ± 0.1	−0.7 ± 0.1

For ΔG°_{37 initiation}, the total number of nts in the loop is n. Free energy increments for single noncanonical pairs (68, 69), i.e. 1 × 1 loops, are approximated by ΔG°_{37 loop}(1 × 1) = ΔG°_{37 loop initiation}(n = 2) + ΔG°_{37 AU/GU} (per AU or GU closure) + ΔG°_{37 GG} (1 × 1) + ΔG°_{37 5′RU/3′YU} (1 × 1). Here, ΔG°_{37 loop initiation}(n = 2) is the free energy of initiation for a single noncanonical pair with adjacent GC pairs; ΔG°_{37 AU/GU} is the penalty for replacing a closing GC pair with an AU or GU pair and replaces the AU/GU terminal pair penalty used for helices (8, 44), ΔG°_{37 GG}(1 × 1) is a bonus for a GG pair in a 1 × 1 loop; and ΔG°_{37 5′RU/3′YU} (1 × 1) is a bonus for a 5′RU/3′YU stack in a 1 × 1 loop, where R is A or G in an AU or GC pair. Free energy increments for symmetric 2 × 2 loops lacking a measured value are approximated by interpolation of measured increments for loops of similar sequence (supporting information). Increments for nonsymmetric 2 × 2 loops are approximated by ΔG°_{37 loop} (5′PXYS/3′ QWZT) = 0.5 [ΔG°₃₇(5′PXWQ/3′QWXP) + ΔG°₃₇(5′TZYS/3′SYZT)] + Δ_p + ΔG°_37GG(2 × 2). Here, PQ and ST are canonical base pairs and XW and YZ are noncanonical pairs. The Δ_p term (0.6 ± 0.2 kcal/mol) is applied to loops with an AG or GA pair adjacent to a UC, CU, or CC pair and to loops with a UU pair adjacent to an AA pair. The ΔG°_{37 GG}(2 × 2) term (−1.3 ± 0.2 kcal/mol) is applied to loops with a GG pair adjacent to an AA or any noncanonical pair with a pyrimidine. Values for Δ_p and ΔG°_{37 GG} were obtained by linear regression on the 2 × 2 loop database (8, 58, 62, 64, 65, 68). Other internal loops are approximated by ΔG°_{37 loop}(n) = ΔG°_{37 loop initiation}(n) + ΔG°_{37 AU/GU} +|n1 − n2| ΔG°_{37 asym} + ΔG°_{37 first noncanonical pairs}(except for 1 × (n − 1) for n > 3). Here, ΔG°_{37 loop initiation}(n) is the free energy of initiation for a loop of n nucleotides, ΔG°_{37 asym} is a penalty for loops with unequal numbers of nucleotides on each side, with n1 and n2 the number of nucleotides on each side, ΔG°_{37 first noncanonical pairs} (except for 1 × (n − 1) for n > 3) is a parameter for the incremental free energy of the first noncanonical pair on each side of the loop; it is not applied to loops of the form 1 × (n − 1) with n > 3. Values for the parameters were obtained from a set of fits to available data for 1 × 1 (69), 1 × 2 (59, 62, 63), 1 × 3 (59, 62), 2 × 2 (8, 58, 62, 64, 65, 68), 2 × 3 (59, 61, 62), and 3 × 3 (ref. 62 and X. Jiao and D.H.T., unpublished results) loops (supporting information) and from theory (74) for n > 6. NA, not applicable to that type of loop. Identical values for adjacent parameters indicate that they were fit as a single parameter.

The free energy increment for multibranch loop initiation is roughly approximated by

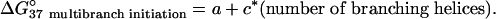On the basis of experiments (20, 70), a better approximation would include another term, b^*(average asymmetry), but this cannot be accommodated in a dynamic programming algorithm. Therefore, asymmetry in the location of unpaired nucleotides in the loop is neglected. The parameters a and c were optimized by finding the best set in the region suggested by the experimental values (70) a = 9.3 ± 0.9 kcal/mol and c = -0.6 ± 0.2 kcal/mol. The maximum accuracy of folding was found for a = 9.3 kcal/mol and c = -0.9 kcal/mol. Accuracy was not highly sensitive to the values of a and c within the region suggested by experiment.

Incorporating Coaxial Stacking in the Dynamic Programming Algorithm. The rnastructure program (8) was extended to include the free energy increments of coaxial stacking for adjacent helices as previously implemented (14) and for helices separated by a single mismatch. The WM array, of size N × 3, introduced to speed the multibranch loop calculation (8), is expanded to N × N, where N is the number of nucleotides in the sequence. At any point in the algorithm where the end of a helix (defined by i and j) is being considered for a multibranch or exterior loop, coaxial stacking of two helices is now considered. This calculation requires a search of k, i < k < j, to divide the region into two helix ends. The supporting information, which is published on the PNAS web site, shows the required recursions.

Constraining Secondary Structure Prediction with Chemical Modification Data. Chemically modified nucleotides are unpaired, in A-U or G-C pairs at helix ends, in G-U pairs anywhere, or adjacent to G-U pairs. The dynamic programming algorithm uses large positive free energies to forbid conformations inconsistent with the data. The supporting information states the recursions.

In Vivo Chemical Modification of 5S rRNA. Modification agents were added to exponentially growing E. coli or C. albicans, OD₅₄₀ 0.4-0.6, at a concentration of 1% vol/vol or wt/vol. At specific times, 10-ml aliquots of the cultures were removed. Cells were isolated by centrifugation and washed three times with sterile water; pellets were immediately placed into a dry ice ethanol bath. Total RNA was isolated from the cells by treatment with Triazol reagent (Invitrogen) supplemented by vortexing the cells with 100 μl of glass beads.

Reverse transcription (RT) was used to determine positions of modification. RT was run by using standard manufacturer's conditions with Na acetate as described (25, 28, 71) with 10 μg of total RNA in each reaction. Two RT primers were used with each RNA. For E. coli 5S rRNA, primer sequences were d(ATGCCTGGCAGTTCCC) and d(CTACCATCGGCGCTACGGCG). For C. albicans 5S rRNA, primer sequences were d(AGATTGCAGCACAATAC) and d(AATTGCAGCACAATAG). Products were separated on a denaturing 8% polyacrylamide gel and quantified with a Molecular Dynamics PhosphorImager and image quant 4.1 software. Each mapping experiment was run in at least triplicate, and modifications are only reported if the nucleotides were modified in each experiment. Strong hits are bands that had at least 10 times the integrated volume of the equivalent band in the control lane, and moderate hits are between 3 and 10 times the volume. Loading was normalized with an RT stop position in each lane that was unchanged by chemical modification.

Availability. rnastructure for Microsoft Windows is available at the Turner laboratory homepage: http://rna.chem.rochester.edu. Source code is available from D.H.M. upon request. Thermodynamic parameters are also available at the Turner laboratory web site.

Results

Nearest-Neighbor Parameters. Nearest neighbor parameters for prediction of RNA conformational free energy at 37°C are revised on the basis of recent experiments on terminal mismatches (47) and hairpin (47, 48), bulge (56), internal (58-61, 72), and multibranch (20, 70) loops. rnastructure for prediction of secondary structures is modified accordingly, and coaxial stacking of helices that are adjacent or separated by a single mismatch has been added. The algorithm remains O(N³) in time and O(N²) in memory. Although slower than without coaxial stacking, the calculation remains rapid. For example, the calculation time for a complete small subunit rRNA, 1,542 nt, is 20 min, and the memory requirement is 47.1 MB on a Pentium 4, 1.6 GHz machine with 512 MB of RAM and Microsoft Windows 2000. The supporting information includes a table of calculation time and memory use for RNA sequences ranging from 77 to 2,904 nt.

The average accuracy of secondary structure prediction is 73% ± 9% of known canonical base pairs for a database (8) of ≈150,000 nt of known RNA structures, divided into domains of <700 nucleotides (supporting information). The single best structure of a set of up to 750 predicted suboptimal structures contains, on average, 87% ± 8% of known base pairs. Finally, 97% ± 3% of known base pairs are found in at least one of the suboptimal structures.

Prior studies took secondary structures generated by a dynamic programming algorithm and revised the free energies with a second program, called EFN2 (8, 73), that added free energy increments for coaxial stacking and a logarithmic dependence for the penalty for the number of unpaired nucleotides in a multibranch loop (74). rnastructure no longer uses EFN2 to revise free energies because coaxial stacking increments are now included in the dynamic programming algorithm. The accuracy of predictions is essentially identical to that obtained previously after EFN2 rearrangement (8).

Chemical Modification Data As Folding Constraints. The dynamic programming algorithm can now incorporate constraints from chemical modification data. Prior versions of the algorithm were unable to use these constraints because chemical modifications occur not just at unpaired nucleotides, but also in A-U or G-C pairs at the ends of helices, G-U pairs anywhere, or adjacent to G-U pairs. Previous studies used modification data by either searching suboptimal structures predicted directly (27, 37) or generated from motifs found in suboptimal structures (19). Neither approach is rigorous, because neither guarantees the lowest free energy structure.

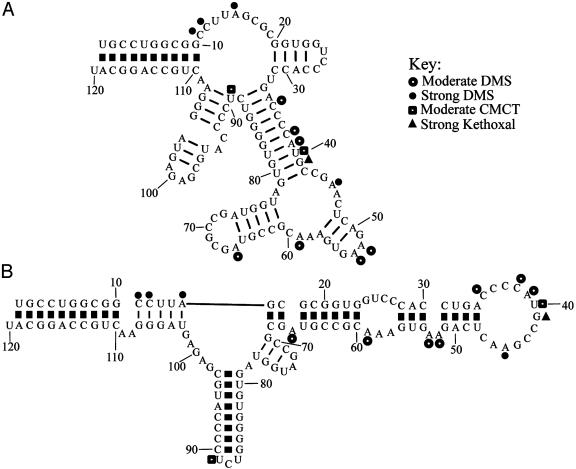
When secondary structure is poorly predicted by free energy minimization alone, accuracy can be significantly improved by adding chemical modification constraints. Fig. 1 shows the secondary structure predicted for the E. coli 5S rRNA with and without constraints determined by chemical mapping in vivo. The accuracy of prediction improves from 26.3% of base pairs correctly predicted to 86.8% (Table 4). The chemical mapping is consistent with the secondary structure determined by comparative sequence analysis (75, 76). Constraints based on in vitro chemical mapping of E. coli 5 S rRNA (29) give identical accuracy.

Fig. 1.

The E. coli 5S rRNA secondary structure predictions and chemical modification. Heavy lines indicate base pairs in the known secondary structure (76, 88). (A) The predicted lowest free energy structure without experimental constraints. (B) The structure predicted with constraints from chemical modification data specified.

Table 4. The average accuracy of structure prediction with and without constraint with chemical modification data expressed as percentage of known canonical base pairs correctly predicted.

			Pseudoknot basepairs, %	Unconstrained		Constrained
RNA type	Ref(s).	Species		LFE	Best	LFE	Best
Signal recognition particle RNA	77, 81	Dog	0.0	18.2	97.7	84.1*	98.9*
5S rRNA in vivo	76	E. coli	0.0	26.3	86.8	86.8	97.4
Small subunit rRNA	25, 78	E. coli	1.6	39.0	49.0	63.3	73.2
RNase P	32, 80	Chromatium vinosum	10.5	53.5	81.6	53.5	81.6
RNase P	31, 80	Bacillus subtilis	7.1	56.3	70.5	56.3	68.8
RNase P	32, 80	E. coli	9.8	58.1†	73.4	64.5†	74.2
RNase P	30, 80	Saccharomyces cerevisiae	7.4	59.3	78.7	58.3	78.7
Telomerase RNA in vivo	43, 82,‡	Tetrahymena thermophila	10.5	65.8	84.2	65.8	84.2
group I bI5	78, 89	S. cerevisiae	5.0	78.2	83.2	81.5	83.2
group I Intron in vivo	43, 78	T. thermophila	4.7	83.0	90.7	83.0	90.7
group II Intron aI5c	27, 79	Yeast	0.0	86.1	89.1	77.7	82.2
group I Intron L-21 Sca I	37, 78	T. thermophila	5.0	86.7	90.0	89.2	90.8
5S rRNA in vivo	76	C. albicans	0.0	90.6†	90.6	90.6†	90.6
Large subunit rRNA (domain 1)	26, 78	E. coli	0.4	88.9	90.5	88.9	91.3
group II Intron	79, 90	Pylaiella littoralis	0.0	90.3†	94.6	90.3†	94.6
5S rRNA	24, 76	Mouse	0.0	94.4	100.0	88.9	94.4
Average				67.2	84.4	76.4	85.9

Accuracies are reported for both the lowest free energy structure (LFE) and best suboptimal structure in a set of up to 750 structures, generated with a window size of zero.

^*Results are reported for protein-bound RNA; when naked RNA chemical modification data are used, the accuracy is 64.8% for the lowest free energy structure and 89.8% for the best suboptimal structure.

^†Best of three or four structures having identical free energies.

^‡ten Dam, E., van Belkum, A. & Pleij, K. (1991) Nucleic Acids Res. 19, 6951.

For C. albicans 5S rRNA, chemical mapping in vivo is consistent with the structure determined by comparative sequence analysis (supporting information). The predicted secondary structure is 90.6% accurate when calculated with or without chemical modification constraints (Table 4).

Table 4 also contains results for 14 RNA sequences of known secondary structure with chemical modification data available in the literature (24-27, 30-32, 37, 43, 76-82, ∥). The average accuracy of secondary structure prediction without and with experimental constraints for the total database is 67% and 76%, respectively. This enhancement primarily reflects improvement for three sequences that are predicted with <40% accuracy on the basis of energetics alone.

The extent of chemical modification is generally graded into strengths. In this study, strong and moderate modifications are used as constraints. In most studies, weakly modified nucleotides can occur buried in helices and therefore are not suitable as constraints for secondary structure prediction. For example, 22 of 251 weak modifications in the small subunit rRNA are inconsistent with the accepted secondary structure (25, 78).

Discussion

Determination of RNA structure is important for understanding structure-function relationships and designing of therapeutics and diagnostics that target RNA. Free energy minimization is an important tool for elucidating RNA secondary structure because it can aid in the determination of a comparative sequence analysis model or suggest possible structures to test by site-directed mutagenesis or other methods. The accuracy of free energy minimization is limited, however, by lack of knowledge of the sequence and salt dependence of energetics and of the effects of tertiary and protein interactions. Constraints from chemical modification (22, 25, 28) can partially compensate for incomplete knowledge of all the factors determining RNA structure. Perhaps of most importance, in vivo studies (39-43) circumvent the difficulties (83) of finding in vitro conditions that mimic the native structure. This feature is an advantage of chemical modification as compared with nuclease mapping (84).

The in vivo chemical modification of E. coli 5S rRNA (Fig. 1) illustrates the impact of chemical modification constraints on secondary structure prediction. The results in Fig. 1 differ from previous in vitro mapping (29), largely because fewer nucleotides are accessible with in vivo mapping, probably because of protein binding. For example, nucleotides 73, 78, 99, and 104, which are accessible to modification in vitro, are not modified in vivo. In addition, the accessible nucleotides in the largest hairpin loop are shifted two nucleotides 5′ in the in vivo mapping so that four consecutive nucleotides are modified starting at position 38 in vivo as opposed to position 40 in vitro. Nevertheless, the chemical modification constraints increase the accuracy of secondary structure prediction from 26.3% to 86.8% (Table 4).

The results for dog signal recognition particle RNA further illustrate how chemical modification data can compensate for factors not included in structure prediction algorithms. The results from chemical modification change when the signal-recognition particle RNA is bound to protein (77). Presumably, the structure deduced by phylogenetic comparison (81) corresponds to the structure with protein bound. Thus, it is encouraging that the predicted structure is closest to the phylogenetic structure when chemical modification data for the RNA-protein complex (84.1%) rather than for the naked RNA (64.8%) are used as constraints (Table 4). Predictions of RNA secondary structure usually provide a number of possible structures with similar predicted free energies (8, 12, 15-18). In some cases, these predictions may reflect conformational switches that can be induced by binding of protein or other perturbations. Chemical modification constraints obtained in the presence and absence of protein and/or under different conditions may help reveal such dynamics.

The results in Table 4 fall into three general classes. Chemical modification constraints dramatically improve predictions of the three sequences that are <40% accurate on the basis of energetics alone. Sequences predicted with between 53% and 66% accuracy when unconstrained all have >7% of their nucleotides in pseudoknots. Pseudoknots are not allowed by the algorithm used in this study, and chemical modification restraints have little effect on the accuracy of prediction for these cases. The third class comprises eight sequences predicted with >78% accuracy on the basis of energetics alone. On average, the chemical modification results decrease the accuracy of predictions for these structures by 1% because of results for the yeast aI5c Group II intron and the mouse 5S rRNA. For the yeast Group II intron, 12 of the 127 moderate modifications violate the assumed rules; i.e., they are buried in helices and not in G-U pairs or adjacent to G-U pairs. This finding suggests that the Group II intron has more than one conformation in the mapping conditions used or that the structure from sequence comparison is not an equilibrium structure for naked RNA. For comparison, the Phalacrocoracidae littoralis Group II intron was mapped with a homogeneous sample and the constraints do not decrease accuracy. On the other hand, for mouse 5S rRNA, the modification data are consistent with the known secondary structure. For this case, a chemical modification is not consistent with the 94.4% accurate structure predicted by energetics alone, and an 88.9% accurate structure with two fewer correct base pairs is the predicted lowest free energy structure consistent with the modification data.

The approach described here for incorporating chemical modification constraints can be applied in essentially any dynamic programming algorithm for prediction of RNA secondary structure. In general, the constraints will reduce the number of structures generated. This should facilitate identification of pseudoknots by programs that allow them (14, 15). The inclusion of coaxial stacking in the dynamic programming algorithm of

rnastructure will also improve applications using dot plots because they now include the effects of coaxial stacking.

One difficulty in predicting RNA secondary structure is that the promiscuity of base pairing and the limited knowledge of the sequence dependence of loop energetics results in a large number of local free energy minima representing different secondary structures. The results presented here show that in vitro and in vivo chemical modification data can be used as constraints to limit predictions to those closely related to the structure of RNA in its true biological context. On average for sequences with <6% of nucleotides in pseudoknots, the structures predicted with constraints from chemical modification contain 84% of the known canonical base pairs. Such an accurate secondary structure model in conjunction with comparative sequence data can then be used to model tertiary contacts and therefore global folds (85). Development of more specific chemical modification reagents would allow tighter constraints and therefore even better deductions of secondary structures.