Origin and Structure of Dynamic Cooperative Networks

Abstract

Societies are built on social interactions among individuals. Cooperation represents the simplest form of a social interaction: one individual provides a benefit to another one at a cost to itself. Social networks represent a dynamical abstraction of social interactions in a society. The behaviour of an individual towards others and of others towards the individual shape the individual's neighbourhood and hence the local structure of the social network. Here we propose a simple theoretical framework to model dynamic social networks by focussing on each individual's actions instead of interactions between individuals. This eliminates the traditional dichotomy between the strategy of individuals and the structure of the population and easily complements empirical studies. As a consequence, altruists, egoists and fair types are naturally determined by the local social structures, while globally egalitarian networks or stratified structures arise. Cooperative interactions drive the emergence and shape the structure of social networks.

Cooperation represents a key organizing principle in evolution because of its potential to turn collectives into superior competitors. The repeated integration of lower level units into higher levels entities includes organizing replicating molecules into DNA, cells into organisms, or individuals into societies¹. In co-operative interactions, cooperators provide a benefit b to their partners at a cost c to themselves (b > c > 0), while defectors provide neither benefits nor incur costs. This represents the most popular form of the prisoner's dilemma. Mutual cooperation is the mutually preferred outcome, but the temptation to increase individual performance results in defection – to the detriment of all. This results in a basic social dilemma, a conflict of interest between individuals and the group. Structured populations help to overcome this dilemma by enabling cooperators to survive and thrive through cluster formation, which generates positive assortment among cooperators²,³,⁴. Social networks represent a dynamical abstraction of social structures in a society based on social ties⁵,⁶,⁷,⁸,⁹. Societies are modelled as graphs where nodes represent individuals and links reflect social interactions.

In traditional evolutionary models, the structures of populations and the strategies of individuals are treated as separate and distinct entities with a focus on the interplay between individual behaviour and population structure²,¹¹,¹². This separation is motivated by spatial extension and limited mobility such that individuals interact only within a local neighbourhood. Spatial clustering enables cooperators to survive under conditions where they would not in unstructured populations. Microorganisms interact mainly with their immediate neighbours through absorption and secretion of extracellular products¹³, while higher animals occupy and defend territories, but in human interactions geographical constraints rapidly decrease in importance. This resulted in a shift of focus towards more general population structures and, in particular, towards scale-free¹⁴ and small-world networks¹⁵, which better reflect structural features of human social networks¹⁶,¹⁷,¹⁸,¹⁹,²⁰. By their very nature, social networks are dynamic, which inspired models and empirical studies where individuals are allowed to adjust their social ties¹⁰,¹¹,²¹,²²,²³. However, as a consequence of the separation of population structures and individual strategies the creation and severing of social ties becomes a challenge and could itself be interpreted as a game²⁴.

Naturally, everyone welcomes cooperators as their neighbours, but no one is interested in interacting with defectors. Thus, a defector establishing a link to a cooperator must either have the means to coerce the cooperator into this interaction or the defector manages to keep its strategy hidden from the cooperator, in which case the connection is expected to be short-lived²¹. Another option is that individuals may employ different strategies towards each neighbour²⁵. Hence, the dynamics of social ties requires careful considerations and further assumptions. Here we propose a simple resolution by removing the dichotomy between strategy and structure.

In order to model dynamic social networks, we propose a framework focussing on the actions of an individual towards others rather than interactions between individuals. Following David Hume's freedom of action²⁶, individuals control their actions and choose their targets – but, whether and how the target individual reacts, lies exclusively in the competence of the target. In structured populations, individuals are represented as nodes on a graph of fixed size N and actions are represented by directed links. If individual i provides a benefit b to another individual j at some cost c then this action is represented by a directed link pointing from node i to node j. Individual j may or may not reciprocate and provide a benefit to individual i – if it does, another directed link points from j to i. We assume that benefits are provided at face value and hence recipients have no reason to refuse and no obligation to pass them on.

This apparently simple change from undirected networks (bi-directional links) to directed networks of actions induces a paradigm shift: the social network now reflects the actual social (inter-)actions and the neighbourhood of an individual encodes its behavioural type. Egoists enjoy the benefits provided by others while providing few or no benefits to their peers, which corresponds to nodes that have few or no outgoing but many incoming links. As an antithesis to egoism the French philosopher and positivist Auguste Comte introduced the term altruism, to live for others²⁷. Hence altruists correspond to nodes with many outgoing but few or no incoming links. In between are the fair players with similar numbers of incoming and outgoing links. The strategy of an individual is given by its number of outgoing links, which can be adjusted by the actor, but their behavioural type is not solely judged based on individuals' actions unto others but in relation to actions of others unto them. As a consequence a natural range of strategies and behavioural types can emerge in the population.

The behavioural type of an individual i can be quantified based on two intuitive measures: its level of altruism, L_i, and activity, A_i, which span the phenotype space L × A. Both quantities are determined by the number of outgoing, k_i, and incoming links, l_i:

The level of altruism, L_i, ranges from pure egoists (L_i = −1, no outgoing links, k_i = 0) via strict fair players (L_i = 0, equal numbers of incoming and outgoing links, k_i = l_i) to pure altruists (L_i = 1, no incoming links, l_i = 0). The activity, A_i, reflects the number of social exchanges the individual engages in as an actor or recipient and ranges from 0 (no interactions) to 1 in the extreme case of a complete graph where every individual is (bi-directionally) connected to every other one (k_i = l_i = N − 1 for all i). Finally, the payoff of individual i is simply P_i = b l_i − c k_i.

The evolutionary dynamics of the social network is driven by individuals aiming to increase their payoff by adjusting their social ties. The structure of the social network is updated by randomly selecting a focal node i to reassess its strategy in two stages. In the first stage, individual i decides whether to reduce its level of altruism through a probabilistic comparison of its performance and strategy with a randomly selected beneficiary m among the k_i recipients of its cooperative actions (Fig. 1-a). Attempting to imitate the strategies of more successful neighbours, individual i is more likely to remove the link to m if individual m has a higher payoff (P_m > P_i) and is less cooperative (k_m < k_i). The link is removed with probability q = f(Δπ) · g(−Δκ) where Δπ = (π_j − π_i)/(π_j + π_i) and Δκ = (k_j − k_i)/(k_j + k_i) represent the normalized differences in payoffs and strategies and f(z), g(z) are properly normalized increasing functions, which we set to f(z) = g(z) = 1/(1 + e^−βz) such that β > 0 represents the selection strength and indicates the weight placed on differences in payoff and strategies. Note that Δπ requires positive payoffs, which is ensured by π_i = 1 + s P_i, π_j = 1 + s P_j with s = 1/((k_i + k_j)c). Both differences, Δπ and Δκ, are normalized to prevent that selection strength scales with network size and density.

Figure 1. Dynamics of social ties: In a sample configuration a focal individual i considers severing its link to a randomly selected beneficiary m and establishing a new link to a randomly chosen member of the population n, who is not already a beneficiary of i's help.

The colour shades indicate the behavioural type of the individuals along with their payoffs (white) prior to any changes to i's links. (a) The beneficiary m is an egoist (red) and more successful than the altruistic focal individual i (blue). Because m is also less cooperative than i, the focal individual is likely to withdraw its help in an attempt to mimic the strategy (fewer outgoing links) of a more successful individual. (b) The individual n is a fair player (green) and more successful. Because n is also more cooperative than i, the focal individual is likely to establish this new link and provide benefits to n, again attempting to mimic the strategy (more outgoing links) of more successful individuals. Benefits can return to the actor either through (I) directed loops (indirect reciprocity) or (II) bi-directional links (direct reciprocity).

In the second stage, individual i considers increasing its level of altruism by establishing a new link to a random member n of the population, which is not already a beneficiary of i's actions (Fig. 1-b). Again, imitating the strategy of more successful individuals, the focal individual is more likely to establish a new link to individual n if it has both a higher payoff (P_n > P_i) and is more cooperative (k_n > k_i). The link is added with probability p = f(Δπ) · g(Δκ).

This framework provides the opportunity to investigate the emergence and structure of social networks arising out of a population of solitary individuals (Fig. 2). The characteristic structure of emerging social networks primarily depends on the selection strength, β, and on the cost-to-benefit ratio of cooperation, c/b, as b can be factored out in the argument of f(z) and be incorporated into β (without loss of generality we set b = 1 and 0 < c < 1). In the absence of selection, β = 0, the costs and benefits are irrelevant and links are added or removed with constant probabilities p = q = 1/4. As a consequence a dense, uncorrelated and relentlessly changing random network emerges (average activity, , see SI). Upon increasing β a phase transition occurs (see SI) and the structure is reduced to a sparse and disconnected network (Fig. 2-a). Even when starting from a complete graph, the network gradually shrinks and decays until it exhibits the same characteristics. Lowering the cost-to-benefit ratio, c/b merely results in a modest increase in density (Fig. 2-b). However, further increases of β result in another phase transition (see SI) and an increasingly dense social network arises. Moreover, altering the cost-to-benefit ratio now induces striking structural changes: high costs promote social stratification of the population such that the welfare of a few is built on the generosity of many (Fig. 2-c), whereas at low costs an egalitarian network of fair players evolves (Fig. 2-d) with a large and tightly connected sub-structure where essentially all links are bi-directional, i.e. most cooperative actions are reciprocated by the beneficiary.

Figure 2. Emergence of social networks: sample snapshots (top row) and the corresponding phenotype distribution (bottom row, log of density) for different costs, c, and selection strengths, β, in a population of N = 500 individuals.

The benefit is set to b = 1 since the cost-to-benefit ratio is the crucial determinant for the success of cooperation. The size of the nodes indicates the individuals activity, A_i, and the colour its behavioural type: altruists (blue, 1/3 < L_i ≤ 1), fair players (green, −1/3 ≤ L_i ≤ 1/3) and egoists (red, −1 ≤ L_i < −1/3). (a) For modest selection, β = 2, a sparse, disconnected network emerges () for large costs of cooperation, c = 0.5, with equal proportions of altruists, egoists, and fair players (only largest connected component with 218 nodes is shown). Because of the low activity, fewer levels of altruism can be realized, which results in extreme values from individuals that have just a single incoming or outgoing link (see SI). (b) Under favourable conditions for cooperation, c = 0.1, the network density slightly increases to and the largest connected component includes 436 nodes. The variance in behavioural types is reduced. (c, d) For strong selection, β = 10, the network density increases while distinct structural characteristics are determined by the cost of cooperation, c. (c) For large costs, c = 0.5, social stratification emerges with more than half the population being egoists (14%) or altruists (45%) as opposed to fair players (40%). Individuals with the highest activity tend to be egoists (average activity, ) whereas the larger fraction of altruistic individuals has low activities (). The activity of fair individuals lies in between (). (d) In contrast, under more favourable conditions, c = 0.1, an even denser (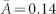) egalitarian network emerges where the all individuals are fair players (99%) with similar activities (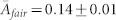), as reflected in a concentrated cluster in phenotype space.

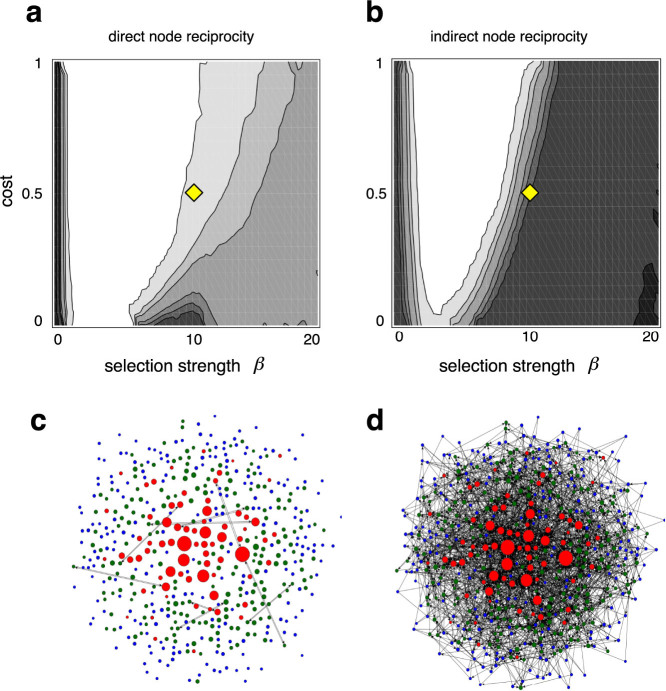
The social network reflects the flux of benefits through the population and, in particular, creates opportunities that benefits may flow back to the providers. A bi-directional link thus represents an instance of direct reciprocity²⁹ following the principle ‘you scratch my back and I scratch yours’, whereas directed loops involving more than two links and individuals represent different degrees of indirect reciprocity²⁸,³⁰,³¹ and follows the principle ‘I scratch your back and someone else scratches mine’ but without time delays and hence without requiring reputation³². We amalgamate the two structural building blocks of reciprocity and quantify their effect as node reciprocity, which measures the average flux of benefits generated by one individual that eventually return to its providers weighted by the length of the loop (Fig. 3-a and SI). The weight decreases as 1/(r − 1) where r denotes the number of links in the directed loop such that bi-directional links contribute a reciprocity of one. In contrast, network reciprocity represents a complimentary measure to quantify the average flux of benefits generated by recipients that eventually return to the individual again weighted by the length of the loop (Fig. 3-b and SI), which also reflects the efficiency of an individuals outgoing links. Thus, node reciprocity indicates the degree to which an individual reciprocates benefits provided by others, whereas network reciprocity indicates to which degree others reciprocate benefits provided by the individual.

Figure 3. Node and network reciprocity - two complementary measures for reciprocity in directed networks.

The focal node f is a fair player with a level of altruism of L = 1/7 because it provides benefits to 4 nodes, i, l, m, and n, and receives benefits from j, k, and l. Shades of grey indicate the strength of reciprocation. White nodes do not reciprocate and pale nodes do not contribute to the respective reciprocity measure. (a) Node reciprocity: the focal node (green) reciprocates provider l directly, j indirectly via i and does not reciprocate k. The direct component, which reduces to the fraction of bi-directional incoming links, is 1/3 and the indirect component amounts to 1/6 (see SI for details). (b) Network reciprocity: the focal node is reciprocated directly by l, indirectly by i via j and no reciprocation by m, n. The direct component (fraction of bi-directional outgoing links) is 1/4 and the indirect component is 1/8. Thus, the node reciprocity is 1/2 and the network reciprocity is 3/8, which means that focal node reciprocates actions of others to a larger extent than others (the network) reciprocate actions of the focal node.

In a hierarchical, socially stratified and tree-like network structure (c.f. Fig. 2-b) node and network reciprocity are both very low because bi-directional links or loops are rare or absent and are maximal on a complete graph. The node reciprocity of egoists is typically low because they tend not to return benefits to their benefactors but their network reciprocity may be high because each of their few outgoing links has potentially a high efficiency and returns benefits through one or several of their more numerous incoming links. Conversely, altruists tend to have higher node reciprocity but lower network reciprocity than egoists. In particular, the network reciprocity of an egoist can exceed one because its few actions (outgoing links) may be associated to the many incoming links and hence the efficiency of each action can get enhanced by the network structure.

The direct reciprocity component of an individuals node reciprocity simply denotes the fraction of incoming links that are reciprocated by the individual (Fig. 4a), whereas for network reciprocity it refers to the fraction of an individuals outgoing links that are directly reciprocated by the recipients (see SI). Similarly, the indirect reciprocity component simply refers to the flux of benefits returned by an individual to its benefactors via other members of the population for node reciprocity (Fig. 4b) and for network reciprocity the flux of benefits created by the beneficiaries of an individual return to the individual via other members of the population (see SI).

Figure 4.

Network Reciprocity: (a) direct and (b) indirect reciprocity components (log scale). Network reciprocity undergoes phase transitions depending on selection strength, β, and costs, c, with b = 1. For β = 0 a dense random network forms (see SI) whereas for moderate selection the network essentially disappears and hence the network reciprocity is close to zero. Only for larger β and/or small c social networks emerge. The socially stratified network (Fig. 2-c, yellow diamond) is decomposed into (c) bi-directional and (d) uni-directional network components. The bi-directional network is completely disconnected and reflects that direct reciprocity is very low. In the egalitarian network (Fig. 2-d) the bi-directional network is connected but the indirect component remains dominant (network components too dense for graphical illustration).

In random networks that emerge in the absence of selection direct reciprocity is unlikely and purely coincidental but due to the density of links indirect reciprocity works through ever changing loops. Similarly, for strong selection direct reciprocity is essentially lacking in stratified populations (Fig. 2-c and Fig. 4-d), whereas in egalitarian networks (Fig. 2-d) direct reciprocity forms the backbone of the society but indirect reciprocity remains the dominant component (Fig. 4), which results in substantial levels of node and network reciprocity (Fig. 4).

The average out-degree, 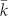, of the egalitarian social network (Fig. 2-d) seems rather high with 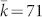(or 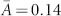) compared to traditional, undirected networks and lattice models, in particular. In undirected networks, increasing connectivity creates conditions that are akin to well-mixed populations and cooperation is expected to get more challenging. More specifically, benefits should exceed the 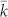-fold costs of cooperation for evolution to favour cooperation³. However, this condition may be relaxed in dynamical networks where higher connectivities have the potential for increased prosperity and welfare but is accompanied by an increased threat of defection, which may result in a decline of the network and can result in a trade-off between stability and prosperity²² and an optimal connectivity around 40 emerges in populations of 100 individuals, which is in line with our model.

Measuring real social networks based on actions and reactions of individuals is notoriously difficult. However, an interesting survey based research on economic networks in 75 rural villages in India³³ tracks lending and borrowing relationships for valuable material goods such as kerosene and rice as well as giving and soliciting (or accepting) advice, a valuable immaterial good, among various other quantities. Both cases are easily mapped onto our framework and each directed link indicates the willingness of one individual to lend rice or kerosene to another one or to provide advice (Fig. 5).

Figure 5. Structure of economic networks in rural India.

Social network based on the willingness (a) to lend (tail node) kerosene or rice and (b) to provide (tail node) advice to someone else (head node). For both networks only the largest connected component is shown (see SI for entire network). Both networks are socially stratified and a majority of altruists supports egoists, which represent the most active individuals (large nodes). (c) Frequency of behavioural types for entire rice/kerosene (solid bars) and advice networks (pale bars). (d) Level of direct (grey bars) and indirect node reciprocity (black bars) for the largest connected component of rice/kerosene and advice networks. The node reciprocity in the advice network is lower because it is more tree-like, which reflects the fact that the flux of advice is more hierarchical and correlates with the age distribution.

In the first case the benefits and costs are obvious whereas in the second the benefits can be equally big but the costs are harder to quantify. However, in both cases selection strength on imitation is expected to be rather weak as other constraints including friendship, age or social status play major roles in shaping connections. Therefore, based on our model we expect neither random networks nor highly dense fair networks but sparse and stratified networks. Both networks are indeed composed of many disconnected components (see SI) with a broad range of behaviour types, with the rice/kerosene network (Fig. 5-a) denser than the advice network (Fig. 5-b). Moreover, reciprocity motives are likely present in the formation of the Indian networks, which is indicated by the pronounced role of direct as opposed to indirect node reciprocity. In real life benefits rarely come without strings attached and donors tend to expect something in return or recipients feel obliged to return the favour, which is a strong promoter of direct reciprocity. Our model deliberately excludes such a bias and focusses on purely success based imitation, which results in a more prominent role of indirect reciprocity (c.f. Fig. 4 and Fig. 5-d).

Social networks based on cooperative actions readily and spontaneously emerge and increase the productivity or welfare of the population provided that individuals are sufficiently careful in targeting promising recipients. Here we focussed on purely success driven imitation where individuals adjust their cooperative actions in reference to the actions of more successful members of the population. Such imitation represents a form of vicarious reciprocity³⁴ because an individual acts towards another, successful member of the population in the same manner as this member towards others and thereby implements a more righteous version of the gospel of Matthew (7:12): ‘do to others what you would have them do to you’ transformed into ‘I do to you what you do to others’. Interestingly, this element of vicarious reciprocity in the imitation process turns out to have a non-trivial role, reducing network density for intermediate selection strength and increasing it for strong selection. In contrast, under misguided reciprocity, where actions are targeted towards a third-party, networks are unlikely to emerge. Our framework easily extends to other imitation rules, which could, for example, acknowledge benefits by initiating reciprocal actions, implement the maxim to counteract unsuccessful behaviour or a combination thereof. Together with the characteristics of potentially different kinds of individual actions – for example cooperation versus spite – this determines the existence and shapes the structure of social networks according to the principle ‘form follows function’.

Author Contributions

L.W. and C.H. designed the model, L.W. analyzed the model and the data, C.H. wrote the manuscript, L.W. prepared the figures. Both authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information