Modeling the specificity of protein-DNA interactions

Abstract

The specificity of protein-DNA interactions is most commonly modeled using position weight matrices (PWMs). First introduced in 1982, they have been adapted to many new types of data and many different approaches have been developed to determine the parameters of the PWM. New high-throughput technologies provide a large amount of data rapidly and offer an unprecedented opportunity to determine accurately the specificities of many transcription factors (TFs). But taking full advantage of the new data requires advanced algorithms that take into account the biophysical processes involved in generating the data. The new large datasets can also aid in determining when the PWM model is inadequate and must be extended to provide accurate predictions of binding sites. This article provides a general mathematical description of a PWM and how it is used to score potential binding sites, a brief history of the approaches that have been developed and the types of data that are used with an emphasis on algorithms that we have developed for analyzing high-throughput datasets from several new technologies. It also describes extensions that can be added when the simple PWM model is inadequate and further enhancements that may be necessary. It briefly describes some applications of PWMs in the discovery and modeling of in vivo regulatory networks.

Introduction

Many transcription factors (TFs), as well as some RNA-binding proteins, bind to DNA (or RNA) in a sequence-specific manner, where the binding affinity depends on the sequence. The earliest, and still a common, representation of the specificity of such TFs is a consensus sequence, a DNA sequence that may include degeneracies. Potential binding sites are predicted based on matches to the consensus sequence, often allowing some number of mismatches. A more general approach, with improved accuracy, is a position weight matrix (PWM, also called just a weight matrix or a position specific scoring matrix, PSSM). In the 30 years since PWMs were introduced as a representation of the specificity of DNA and RNA binding proteins (1), they have become the primary method for representing specificity and for searching genome sequences and predicting binding sites. Although PWMs employ a general mathematical model, a large variety of methods have been developed to assign parameters to the model. Often different methods are used when different types of data are available, but even for the same data different approaches have been used. The accuracy of different PWMs can be assessed in various ways, most effectively when quantitative binding data are available for the TF of interest. There has also been, since the beginning, the realization that PWM models have limitations and may not capture the true specificity of a TF. In fact it is clear that PWMs are approximations to the true specificity and the question to address is how good an approximation it is, which depends on the TF. In many cases PWMs can provide adequate (for the purpose at hand) models of specificity, but for some TFs they do not. Extensions to the basic PWM model can be included that capture important specificity information that may be missing from the PWM.

This article has several purposes. It provides an overview of the primary methods for assigning parameters to PWMs including a brief history of the main innovations. It then focuses on our recent development of algorithms that take advantage of new high-throughput technologies to infer PWM models of specificity. The new datasets provide unprecedented opportunities for improving the accuracies of specificity models, and for determining when PWMs are good representations and when they are not. It also describes extended models for representing specificity when PWMs are inadequate and some further enhancements that may provide more general modeling capabilities. By combining information from many different members of particular TF families it is also possible to develop recognition models that can aid in the design of TFs with novel specificity. This article is not about gene regulation and regulatory networks. Although that is an important reason for studying protein-DNA specificity, the focus here is on models of intrinsic specificity, modeling the differences in binding affinity for different DNA sequences under conditions without any confounding factors. This information can be very useful in modeling in vivo interactions and gene regulation, and in particular on the effects of genetic variations on gene expression, but those applications are mentioned only briefly.

General PWM model

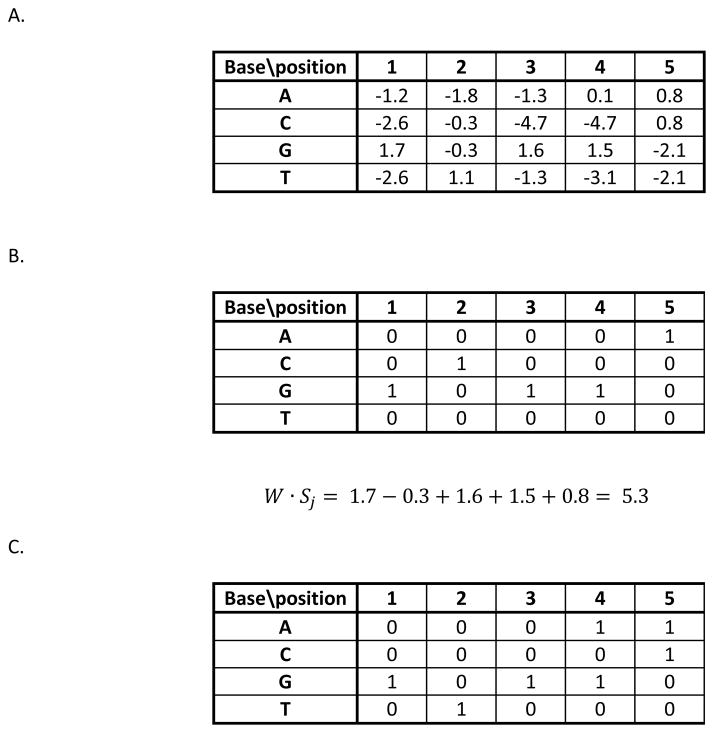
There is some disagreement about the definition of a PWM. In some cases it is used too broadly to cover methods that are really quite distinct. But more often it is defined too narrowly, being tied to a specific method for estimating the parameters of the PWM rather than for the general notion of what a PWM is and how it is used to model specificity. We define a PWM as a matrix, W(b, i), of numbers for each possible base (b = A, C, G or T) at each position (i=1 to L) in an L-long protein binding site (Fig. 1A). Such a matrix provides an additive score for any sequence of length L by summing the elements of W that correspond to the sequence. If we encode the sequence S_j with the same type of matrix, with 1 for the base that occurs at a position and all other elements being 0, the score is the sum of the products of the corresponding elements of the two matrices:

$$\mathit{Score}(S_j\mid W)={\sum }_{b,i}W(b,i)S_j(b,i)$$ (1)

which we can also write as W · S_j, the dot product between the two matrices (Fig. 1B). Obviously all L-long sequences will be encoded in a unique sequence matrix and W will assign a score to each sequence.

Figure 1.

Weight matrices and sequence encoding. A. The weight matrix for a hypothetical transcription factor (YFTF). Scores are provided for each possible base at each position in a five-long binding site. B. The encoding of a particular sequence, GCGGA, with a 1 for the base that occurs at each position and all other elements are 0. The score of the sequence, given the matrix in part A, is shown. C. An alternative weight matrix for the consensus sequence GCGRM (R=A or T, M=A or C). Any sequence that matches the consensus will get a score of 5, allowing one mismatch requires a score of at least 4, etc. This shows how any consensus sequence can be converted into an equivalent weight matrix that will return exactly the same set of sites.

Every sequence-specific DNA binding protein (such as a TF) can be represented by its own W and the challenge is to find one that is a good representation of its specificity, by which we typically mean one that provides a good quantitative prediction of activity for different binding sites or is useful for predicting binding sites in a genome sequence. A PWM is an approximation to the true specificity of a protein, for some proteins it is a good approximation and for others there is no W that provides a good representation. In that case the model can be extended to include additional features of the sequence that increase the accuracy of the representation. A variety of algorithms have been proposed to create the W for a protein and the following section provides a brief history and summary of many methods. In some cases the choice of method depends on the type of data available, but in many cases multiple methods have been applied to the same types of data.

It is important to realize that a PWM is a generalization of the consensus sequence concept. For any consensus sequence, including degeneracies and allowing for mismatches, an equivalent W and threshold score can be created that will return exactly the same set of binding site predictions (Fig. 1C). But a PWM has the advantage that it provides position-specific penalties for deviations from the consensus, rather than treating all mismatches equally. Typically there are some positions that contribute more to the specificity than others, or where particular bases are especially important (either positively or negatively) to the activity of a binding site. A PWM allows those distinctions to be included in a simple, additive manner. Taking the example in Figure 1, if the matrix of Fig. 1A is a true representation of the specificity of the TF, for many choices of thresholds (where one wants to separate all sequences with scores higher than the threshold from those with lower scores) it would be impossible to define a consensus sequence that makes the desired separation. So, although it is possible to represent the specificity of a TF with a consensus sequence, this article focuses solely on PWMs because of their increased potential accuracy (“potential” because it is certainly possible to define a W for a protein that is a very poor representation, worse than a consensus sequence, but that would be due to the method for assigning the parameters to W, not a fundamental limitation of the PWM approach).

It is also important to realize that a PWM does not imply a particular mechanism for the observed specificity. For example, if a T is the preferred base at a particular position that may be due to the specific arrangement of hydrogen bond donors and acceptors in the major groove of an A-T base pair, or it may be due to a strong interaction with the methyl group on the T, or it could be due to the specific shape of the DNA, such as groove width or intrinsic bend, that requires the A-T pair, or even some combination of all of those contributions. The PWM just captures the relative quantitative contribution of different base pairs to functional activity without identifying a specific cause for that preference. On the other hand, given a large number of TFs (especially all from the same TF family so that one can assume they bind to DNA in a very similar manner), each with its own protein sequence and PWM, it is possible to infer some interaction rules, or at least probabilistic models, that allow for prediction of TF specificity based only on the protein sequence. This further facilitates the design of TFs with desired specificity, something that has been most effectively applied to zinc finger proteins (2–5).

Higher order models fit into this paradigm quite easily. W is a vector that weights the features of the sequence to give a score. In a PWM the features are just which base occurs at each position in the site, but one can add more features if they are important. We can still use the notation W · S, but now S encodes the relevant features for the activity and W provides a weight for each of those features. Relevant features might be adjacent bases if the protein interacts with them non-independently, or it could be even more complex. RNA motifs that include structures with internal base-pairs can be included too (6, 7). One thing that is not easily accomplished with W feature vectors are variable lengths, in which case one must go to a different function, such as an HMM (8). Fortunately most TFs interact with fixed-length motifs and can generally be well modeled with a PWM or a slightly more complex function.

Methods for generating PWMs from TF binding data

Various types of data can be used to infer a PWM for a specific TF. The data may be qualitative, simply a list of binding sites (perhaps also negative data, non-binding sites), or quantitative, where each site has an associated value related to its functional activity. In addition one can classify data sets by whether the binding sites are given precisely or if they are embedded in longer segments of DNA without their precise locations being indicated. In the latter case there is a motif discovery aspect to the problem where one must infer both the PWM and the sites simultaneously. The following sections described the most commonly used algorithms for each class of data and include some historical notes about their origins.

Modeling from qualitative binding site data

A large number of specific programs have been written to estimate PWMs based on collections of sites, but they can be broadly classified into three types. When both positive and negative examples exist (sites and non-sites) one can search for discriminant models in which the scores assigned to every (or most) positive sequence are higher than to every (or most) negative sequence. If only positive examples are known a common approach is to use probabilistic modeling, in which the scores provide estimates of the probability of a specific sequence belonging to the set of sites. This approach can also incorporate information about the probability of a sequence belonging to the set of non-sites, the background from which the sites are selected, to provide better discrimination although specific sets of non-sites are not included. A third type of modeling assumes the elements of the PWM represent binding energy contributions of each base at each position which are independent and whose sum determines the binding free energy of any sequence. These different approaches derive from different viewpoints about the data and how best to capture the specificity of the TF, but they are not mutually exclusive. Under some assumptions, the same binding site collection will give rise to the same PWM using both the probabilistic approach and the energy approach, although under different assumptions they can diverge. Some approaches provide implicit discrimination based on assumptions about the non-sites even though specific sets of non-sites are not included.

Discriminant modeling

Given a collection of known binding sites as a positive set, S⁺, and another set of sites that are nonfunctional, S⁻, discriminant modeling searches for a PWM (labeled as W_D for discriminant) that distinguishes the two sets of sites:

$${\mathit{W}}_{\mathit{D}}:W_D\cdot S^{+}>W_D\cdot S^{-}\forall S^{+},S^{-}$$ (2)

This approach was the first use of a PWM (1) in which the sites were E. coli ribosome binding sites and the non-sites were alternative ATGs that did not function as ribosome binding sites. The perceptron algorithm was used in that paper; that is a simple neural network that learns by error correction and is guaranteed to find such a W_D if one exists (the perceptron convergence theorem (9)). Finding a W_D means that the sequence sets are linearly separable with the vector W_D providing the separation function; all positive sequence vectors are closer to W_D (have a smaller angle between them and W_D) than any of the negative set. At the time of that paper all previous efforts at modeling binding site specificities attempted to derive consensus sequences that could be used to predict new binding sites while minimizing false positive predictions; they were focused on deriving maximally discriminant consensus sequences. The fact that a PWM was capable of better discrimination than any of an extensive set of consensus sequences that were developed for comparison (10) demonstrated the value of a linear weighting function. Furthermore a PWM could be an effective method for identifying the relevant features, and their relative importance, in a set of functional sites and as a more precise tool to predict additional sites in genome sequences.

Djordjevic et al (11) also used a form of discriminant modeling. They did not have a set of non-binding sites, but they used quadratic programming to find the smallest W (minimizing |W|, the Euclidian length of W) while requiring that W · S⁺ > c ∀ S⁺ (for any constant c). This puts W in the center of the perimeter of all the S⁺ where it minimizes the number of other sequences that score above the threshold c. In a comparison with a probabilistic model (see next section) they showed that it could greatly reduce the total number of predicted sites, most of which are probably false positives. Of course the real assessment of the accuracy depends on independent predictions, but this approach does provide a means of minimizing the number of predicted sites for any desired level of sensitivity based on only known sites, a goal of the consensus methods described above.

Probabilistic modeling

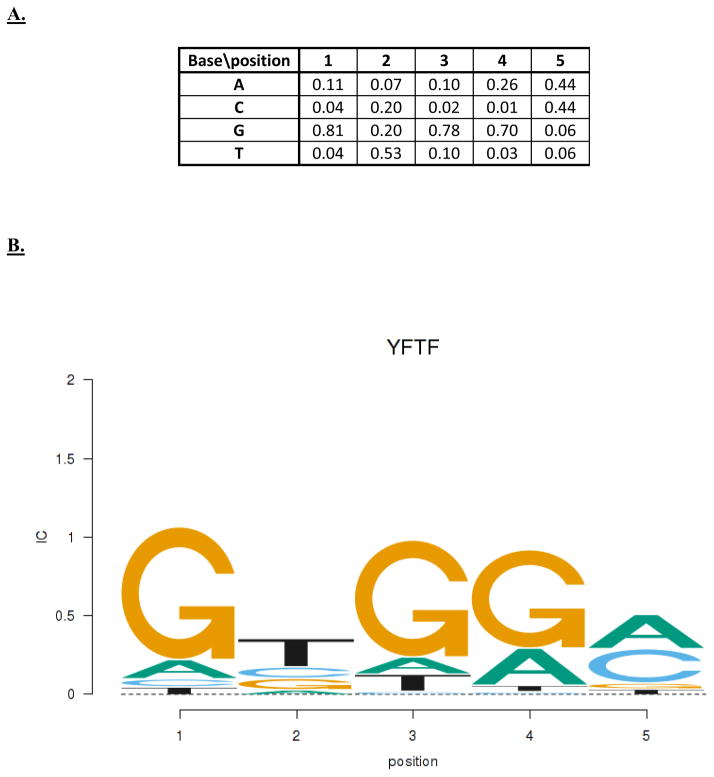
It is more common to have only a set of known functional sites and there have been many algorithms that use such collections to define PWMs for modeling and prediction purposes. Once methods for DNA sequencing were invented (12,13), several groups began identifying the binding sites for specific regulatory factors. The earliest large collections were for E. coli promoters (14–16) and ribosome binding sites (17, 18) and for eukaryotic splice junctions (19). Alignments of those collections of sites were used to generate a position frequency matrix (PFM, Fig. 2A), in which the probability (or frequency) of each base at each position is determined from the alignment. For example, given N sequences encoded in matrices as shown in Fig. 1B, the PFM is:

$$F(b,i)=\frac{1}{N}{\sum }_{j=1}^N{S}_j(b,i)$$ (3)

Figure 2.

Position frequency matrix (PFM) and information content logo. A. The position frequency matrix (PFM) for the YFTF log-odds matrix from Figure 1A. The sum of the base frequencies for each position is 1. B. An information content logo for YFTF based on the PFM of part A. The height of the column at each position is the information content (IC) and the individual base heights are in proportion to their frequencies.

The first use of PFMs directly as a model was for predicting E. coli promoters (20). E. coli promoters have two separate parts, the “−10 region” and the “−35 region”, named for their approximate distances from the transcription start site, but there is variable distance between them. For any given sequence Harr et al. (20) computed the probability given the PFM, including the spacing, and then determined if it was likely to be a promoter based on a threshold score. (They actually used an adjusted probability so that the consensus sequence, the highest scoring site, was assigned 1 and all other sequences were then scored relative to that). This is not a PWM because the function is not additive. In fact one can think of it as providing the score, which is the probability of the sequence given F, as:

$$Pr(S_j\mid F)={\prod }_{b,i}F{(b,i)}^{S_j(b,i)}$$ (4)

This can be converted to a PWM by taking the logarithms of F(b, i):

$${\mathit{W}}_{\mathit{LP}}:W_{LP}(b,i)=logF(b,i)$$ (5)

(“LP” for “log probability”) and then the score of a sequence given W is computed just as in equation (1), but now the score is the log of the probability of the sequence being in the set of functional sites. That is the probabilistic PWM method that Staden published the following year (21) in which he applied it to both E. coli promoters and to eukaryotic splice junctions. The fact that Harr et al. (20) included the probabilities of the different variable spacings means that it was a simplified profile hidden Markov model (8), only allowing gaps in the space between the −10 and −35 regions. Staden’s method did the same, but again using the logarithms of the different spacing probabilities. Harr et al. (20) also suggested that the PFM could be used directly as a PWM, that is W(b, i) = F(b, i) where one adds the base/position frequencies to get the score. They pointed out that would not be a proper probabilistic model, but suggested it might be useful in some cases. That idea, of using the observed frequencies as the PWM, was proposed again later by two other groups (22,23) although instead of using the PFM directly each position was weighted by its information content (see below).

Mulligan et al. (24) also used an alignment of E coli promoters (15) to generate a PWM in which the elements of W were based on the deviation (Z-score) of the observed base frequencies from that expected by chance, and also including a similar score for variable spacings. They called this a “homology score” and they further showed that it was correlated to the activity of any specific promoter sequence.

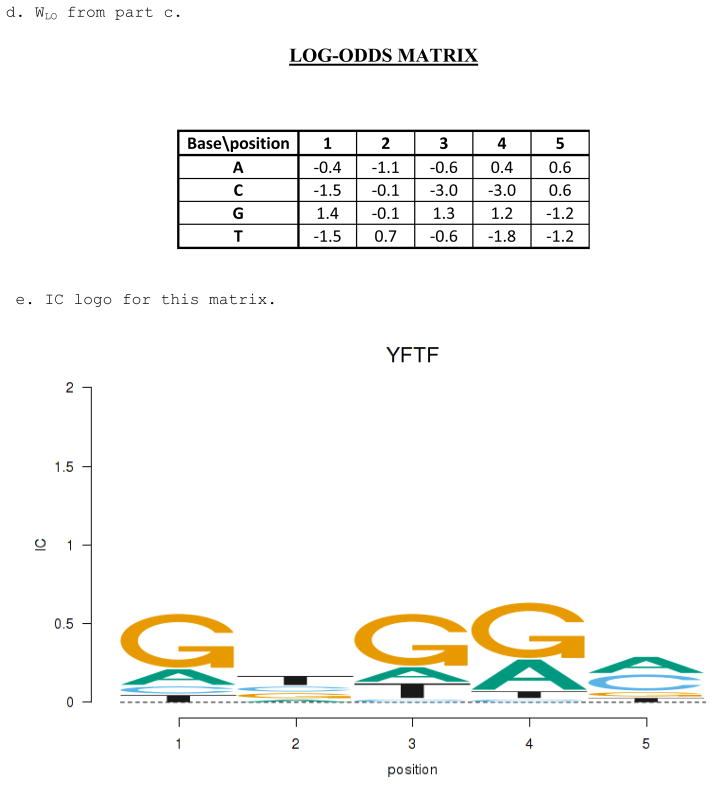
In 1986 Schneider et al. (25) used information theory to analyze binding sites. From F(b, i) of the aligned sites they defined the information content, IC, at each position i as:

$$IC(i)=2+{\sum }_{b}F(b,i){log}_{2}F(b,i)={\sum }_{b}F(b,i){log}_2\frac{F(b,i)}{0.25}$$ (6)

They used log₂ so that the information content is measured in bits. If F(b, i)=0.25 for each base then IC(i)=0 and if F(b, i)=1 for one base and 0 for every other base, then IC(i)=2. Those are the two extreme cases, but 0≤IC(i)≤2 in all cases. The IC of an entire site is the sum over all of the positions. Note that the formula for IC can be rewritten as:

$$IC(i)=2+{\sum }_{b}F(b,i)W_{LP}(b,i)$$ (7)

where W_LP is the probabilistic model given by equation (5). Σ_b,i F(b, i)W_LP (b, i) is the average score of all the binding sites used to build the model. The last formula for IC(i), on the far right of equation (6), is the relative entropy, also known as Kullback-Leibler distance. It is a log-likelihood ratio (LLR) statistic between the observed frequencies, given by F(b, i), and those expected from a random sequence with 25% of each base. However, the genome sequence where the sites occur may not contain 25% of each base. In that case any selection of randomly chosen “sites” would have IC>0, violating our intuition that randomly chosen sequences should contain no information. This can be corrected by altering the relative entropy formula to use the actual background probabilities for each base, P(b), instead of 0.25, in the denominator. This is a log-odds (“LO”) weight matrix:

$${\mathit{W}}_{\mathit{LO}}:W_{LO}(b,i)=log\frac{F(b,i)}{P(b)}$$ (8)

from which one can define an alternative measure of information content:

$${IC}^{\ast }(i)={\sum }_{b}F(b,i){log}_2\frac{F(b,i)}{P(b)}={\sum }_{b}F(b,i)W_{LO}(b,i)$$ (9)

IC* is average score of all the sites used to build the model, where the score is logarithm of the ratio of their occurrence in the binding site collection compared to the expected background occurrence (assuming positional independence). Schneider et al. (25) suggested using the alternative definition of IC* for genomes with unequal base frequencies and W_LO is now probably the most commonly used method for determining the parameters of a PWM from a collection of known sites (hereafter we drop the “*” and references to IC will use the definition in equation (9)). It is also frequently the objective function that is maximized in motif discovery algorithms because larger IC values correspond to larger statistical significance (decrease in expected occurrence by chance, see below). Schneider and Stephens (26) invented the sequence logo method for visualizing a PWM (Fig. 2B). The height of the column at each position is the IC of that position and the individual base heights are in proportion to their frequencies, with the more frequent bases on top. This visualization technique is convenient for many purposes. The consensus sequence is just the top base at each position (nearly equal bases may be converted to degeneracies) and the total height at each position, the IC for that position, indicates how important that position is to the specificity. Positions with very high IC are critical to activity whereas those with low IC can tolerate variations with little effect.

Energy modeling

If the positions in a binding site contribute independently (additively) to the free energy of binding, the total binding energy of a TF to sequence S_j, E_j, can be defined with a PWM where the elements of W are the energetic contributions of each base at position:

$${\mathit{E}}_{\mathit{j}}=W\cdot S_j$$ (10)

Beginning in the late 1970s Peter von Hippel had considered the relationship between binding energy contributions of each base and the information required within binding sites for regulatory systems to work given the vast excess of non-functional sites in the genome (27,28). Initial models were based on the assumption that each non-consensus base contributed an equal amount, essentially a mismatch energy, but further theoretical analysis led to a quantitative relationship between the F(b, i) for a collection of binding sites and the energy contribution of each base at each position (29). This model assumes sites are selected by evolution if they have a binding energy that is “good enough” to be functional, while those with lower affinity will be lost. By considering all of the combinations of bases that can contribute to functional binding sites they show energy contributions are proportional to −logF(b, i), just as was obtained from the probabilistic model (but with the change in sign; lower energy bases are preferred):

$$W(b,i)=ln\frac{maxF(b,i)}{F(b,i)}\to E_j=E_{{\mathit{minS}}_j}-W_{LP}\cdot S_j$$ (11)

where maxF(b, i) it the maximum of F(b, i) at position i; this defines the most frequent base to have energy = 0. It is clear from probabilistic modeling that there are only three free parameters at each position, because the frequencies of all bases at each position sum to 1. In energy modeling one is free to assign an energy of 0 to a reference sequence, which they chose to be the consensus sequence. Using this convention the energy values in W are the difference in binding energy between the preferred base at each position and each other base, hence the relationship shown at the right of equation (11) that the W(b, i) matrix for binding energy is equivalent to W_LP but offset by the minimum energy sequence. That model was based on the background frequency for each base being 25% and for the positions contributing independently to the binding energy. In the appendix to the paper (29) they also showed that for non-equal background frequencies one gets the W_LO matrix described above (again offset by the minimum energy sequence) and that non-independence between adjacent positions could also be included in the model.

In later work it was shown that when sequences are selected based on their binding affinities, such as in an in vitro selection experiment, the W_LO matrix also corresponds to the sites being selected from a Boltzmann distribution (30,31), but now over the entire range of affinities, not just those that are “good enough” to survive evolutionary selection. This follows from F(S_j) being the probability of sequence S_j, with binding energy E_j, being in the bound fraction, and P(Sj) being its proportion in the collection of potential binding sites. If the sites are selected according to the Boltzmann distribution, then:

$$F(S_j)=\frac{P(S_j)e^{-E_j}}{Z}\to E_j=-ln\frac{F(S_j)}{P(S_j)}$$ (12)

where Z is the partition function, the sum of the numerator over all possible sequences S_j (and note that Z=1 for this definition of E_j). Note that this equation does not depend on independent contributions from the positions in the binding site, or on the background being random sequences. It is valid for any collection of sites when they are selected based on their binding energies via this Boltzmann relationship. If independence holds then the contributions can be factored into additive contributions at each position and one obtains the W_LO matrix obtained earlier from information theory considerations.

However, Djordjevic et al (11) pointed out that the Boltzmann distribution, eq. (12), is not appropriate in cases where binding sites approach saturation, which is common in both in vitro experimental conditions and in vivo for many regulatory systems. In such cases the Fermi-Dirac distribution describes the relationship between the binding energy of a sequence and its probability of being bound:

$$P(\mathit{bound}\mid S_j)=\frac{e^{-E_j}}{e^{-\mu }+e^{-E_j}}=\frac{1}{1+e^{E_j-\mu }}$$ (13)

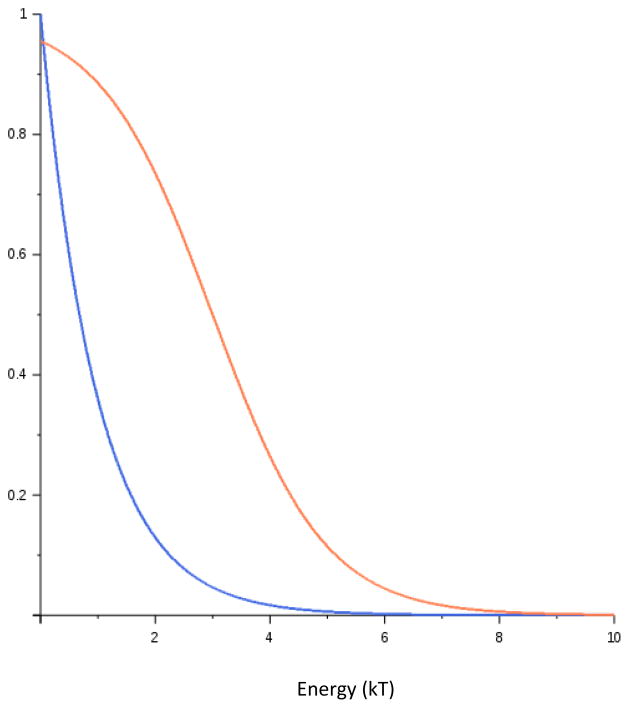
where μ is related to the TF concentration (μ = ln [TF]/K_D(S_ref), where K_D(S_ref) is the dissociation constant of the reference sequence, defined to have E_ref=0). When E_j − μ ≫ 0 ([TF] is very low or energy is very high) this reduces to the Boltzmann equation given above. But when [TF] is high, and E_j − μ ≪ 0, this approaches 1, the sites become nearly saturated. The difference between the two distributions can be quite large at high protein concentrations and low energies. Figure 3 graphs the differences in the probability distributions as a function of binding free energy (relative to the consensus sequence with E=0). For the Boltzmann distribution (blue line), the graph shows the decrease in relative binding probability compared to the consensus sequence, whereas for the Fermi-Dirac distribution (red line) it shows the absolute binding probability under conditions such that the consensus sequence is about 95% bound, near saturation. Under those conditions the probability falls off much more gradually for low energy sites than for higher energy sites. For example, a single variant that increased binding energy by 2 kT in the context of the consensus sequence would reduce binding from about 95% to about 80%. But in the context of a site that was originally bound at 50%, the same variant would reduce binding to about 10%. Only sites with high binding energy fit the Boltzmann assumption of exponential decrease in probability with increasing energy.

Figure 3.

Binding Probabilities as a function of binding energy. Blue line is the relative binding probability, compared to the consensus sequence (with E=0), for sequences with energy on the X-axis. Red line is the absolute binding probability under conditions where the consensus is about 95% bound (μ = 2).

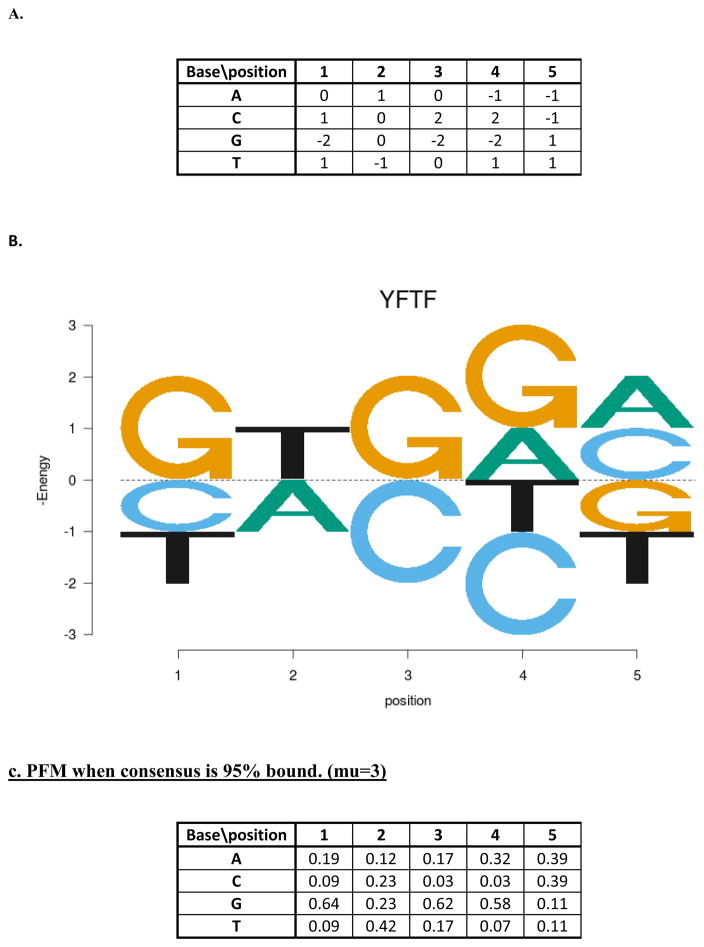
Modeling based on binding energy has some important advantages compared to the simple form of probabilistic modeling described above. The binding energy to a particular sequence is an intrinsic property of the protein (it will vary with different conditions, but we imagine that under “physiological conditions” it will be a constant), whereas binding probability also depends on the protein concentration. Figure 4A shows the energy matrix for the hypothetical YFTF. This energy matrix was used to generate the W_LO of Fig. 1A (assuming 0.25 background probabilities) and the PFM of Figure 2A (assuming a Boltzmann relationship between energy and probability for each base). Figure 4B is an energy logo (32,33) for YFTF. If binding sites for YFTF were collected at a high TF concentration, such that the consensus sequence is 95% bound, the PFM would be quite different (Fig. 4C), giving rise to a quite different W_LO (Fig. 4D) and IC logo (Fig. 4E). It can be readily seen that the logo is considerably reduced, making it appear the TF is much less specific, and also that different positions appear to have different relative contributions to the overall IC. That is also evident from the PFM and W_LO. Furthermore, as described above, at high TF concentrations the probabilities of specific bases at specific positions in the binding sites will depend on their context. This gives the appearance of non-independent contributions to binding from the simple probabilistic modeling framework, even though the energy contributions are entirely additive. For these reasons we have emphasized energy modeling in our recent work (described below).

Figure 4.

Energy modeling. A. The energy matrix for YFTF. The average energy at each position is defined as 0 in this matrix, and bases with negative values are preferred, and those with positive values are discriminated against, compared to the average. B. An energy logo showing the energies of each base at each position, with an average of 0 as in the matrix of part A. Note that the Y-axis is −E, so the preferred bases are on top. C. The PFM for binding sites under conditions where the preferred sequence is 95% bound. D. The log-odds matrix based on the PFM of part C (assuming an equal frequency background). F. The information content logo for the PFM of part C.

Modeling from qualitative binding segment data (motif finding)

It is much more common to identify segments of DNA that contain binding sites for a TF than to obtain the binding sites directly. In that case one can apply motif discovery algorithms to determine the motif from the segments. This problem is often thought of in a probabilistic manner as a problem with missing information. If one knew where the bindings sites were one could make a PWM to represent the motif from the aligned F(b, i). On the other hand, if one were given the PWM one could search across each of the sequences and find the highest scoring, or most likely, binding sites. But in this problem we are given neither type of information and wish to discover both the sites and the motif. A number of consensus based algorithms have been developed for this, including a very early one by Waterman and colleagues (34,35) and followed by many more in the ensuing decades. But since PWMs are better representations of binding site motifs, we concentrate on algorithms for identifying PWMs from unaligned sequences known to contain binding sites. The first method was a greedy approach that built up multiple alignments progressively, starting with pairs of sequences and adding new ones until the entire set of binding sites was included and the motif identified (36). The criterion used to identify the best alignments at each step to keep for further analysis was the IC of the W_LO matrix of the alignment. Later this was modified to a calculation of the E-value of the alignment which depends on both the W_LO and also the number of sequences containing sites (37). Soon after that an expectation maximization (EM) algorithm was developed for this problem (38,39). It maximizes the total probability of the data and the model which is similar to, but slightly different than, IC. A version of EM was even developed that could learn the variable spacing probabilities between the −10 and −35 regions of E. coli promoters (40). After that the Gibbs’ sampling algorithm was applied to the motif discovery problem (originally applied to motifs in protein sequences but more commonly used for DNA motifs) in which maximization of the IC of the W_LO matrix (including pseudocounts) was the objective function (41). A variety of related algorithms have been developed since then, many of them focused on finding motifs in very large datasets, such as those available from gene expression experiments where one seeks to find motifs from sets co-regulated genes and from chromatin immunoprecipitation (ChIP) experiments where one seeks motifs from the genomic DNA segments bound to particular TFs (42–46). In most cases these try to optimize a probabilistic model, usually maximizing IC or something related.

Modeling from quantitative binding site data

Quantitative binding data can be direct measurements of binding energies for many different sequences, but more commonly it is binding probabilities or functional activities. In either case the goal is to find a PWM that provides a good quantitative fit to the data. This approach was first described in 1986 where the data were nonsense codon suppression efficiencies that varied depending on the sequence context surrounding the stop codon (47). The elements of the PWM were obtained by multiple linear regression and the fit to the data, an adjusted R² of 0.86, showed that the assumption of additive contributions was reasonable. In fact just the two positions following the stop codon contributed additively and captured 76% of variance. A different example, on the context effects of mutation rates, was not well fit by an additive (PWM) model, but could be adequately explained using a simple extension of the PWM idea where the features are the di-nucleotides at each position rather than individual bases. That paper also emphasized that there are only three independent parameters at each position for a PWM, and 15 independent parameters for a di-nucleotide model, and increasing exponentially for higher-order models. Later work showed how to efficiently encode sequences, and their corresponding weight vectors, to capture each order of parameters independently so that the higher-order parameters are fit to the residuals from the lower order models (33).

An advantage of regression methods is that they provide the optimum fit to the data for any specified model, such as a PWM, and furthermore indicate how good the fit is so that one can decide if more complex models are necessary. Since a PWM will always be an approximation to the true specificity of a TF, the important question is how good an approximation it is and whether determining additional parameters for higher-order models will significantly improve binding site predictions. There are now several examples, with different TFs, where quantitative measures of binding affinity have shown non-independence of the positions in the binding sites, but in most cases a simple PWM still provides a good approximation to the binding data or if not then the addition of adjacent di-nucleotide parameters is sufficient for a good quantitative fit (48–58).

In each of those previous cases the binding sites were known so that the contributions of each position to the total activity could be assigned directly. It is also possible to search for PWMs that explain differences in activity when the exact binding sites are not known. This was first done using whole genome expression data with a search for consensus sequences that could predict differences in expression in different conditions (59). Later this was extended to a search for PWMs that were correlated with expression changes and with binding location experiments (32,60,61). They could easily find many PWMs that were highly significant and many of them correspond to known motifs for specific TFs. Those examples demonstrated that regression methods can be highly effective on large quantitative data sets without prior knowledge, or alignments, of the binding sites.

Modeling based on new high-throughput technologies

In recent years several high-throughput methods have been developed to determine binding affinities for many different binding sites in parallel. The rapidity with which large, quantitative data sets can be generated offers an unprecedented opportunity to determine the specificity of a large number of both natural and synthetic TFs. To take maximum advantage of the new, large datasets improved algorithms are needed that take into account the details of the experimental methods. We recently published a review of those experimental methods ((62)) but the details of the computational analyses were not included. In the following sections we describe computational approaches to model the specificity of TFs using several different types of high-throughput experimental data.

Mechanically induced trapping of molecular interactions (MITOMI)

The mechanically induced trapping of molecular interactions (MITOMI) method uses a microfluidic device with different DNA sequences localized to individual chambers and binding of TFs to each sequence can be monitored by fluorescent tags, allowing for the determination of binding affinities directly for each sequence variant (53). Because MITOMI can determine binding energies directly, one can apply simple linear regression to find the parameters for the energy PWM that best fits the data and also determine how good the fit is. One complication is that there is a lower bound wherethe affinity becomes non -specific (no longer depends on the sequence), but accounting for that allows one to determine if sequence-specific binding is additive across the binding site positions. Analysis of several TFs from the basic helix-loop-helix (bHLH) family demonstrated that the positions did not contribute independently to binding (53), but adding parameters to account for adjacent di-nucleotides fit the data within experimental error (54,55). In more recent work MITOMI has been made more high-throughput by including long oligos in the binding reaction instead of just variants of a known consensus site (63). This allowed them to identify the PWMs for each TF from a much larger collection of potential binding sites using a combination of regression method s(32,64).

SELEX-seq

SELEX was invented in 1990 as a means to identify binding sites for RNA binding proteins (65) but has been adapted and used many times to determine the binding specificity of TFs. It uses a random library of potential binding sites and those that bind to the protein are selected with probabilities that depend on their affinities. Traditionally the bound fraction would be amplified by PCR and after several cycles of binding and amplification a small number, typically 20–100, of individual binding sites would be sequenced. This was sufficient to gain knowledge about the specificity of the protein (eg. (66)) but due to the multiple rounds of selection it was not straightforward to determine relative binding affinities accurately. However, new sequencing technologies allow one to efficiently obtain binding site sequences for an enormous number of sites with large differences in binding affinities (55,67,68). Sequencing of the initial library gives us the prior distribution of all potential binding sites, P(S_j), and sequencing of the bound fraction after only a single round of selection gives us the posterior distribution, P(S_j|bound). Applying Bayes rule:

$$\frac{P(S_j\mid \mathit{bound})}{P(S_j)}=\frac{P(\mathit{bound}\mid S_j)}{{\sum }_{j}P(S_j)P(\mathit{bound}\mid S_j)}$$ (14)

shows how those measured quantities (on the left) are related to the energy parameters we want using the relationship of equation (13). A non-linear regression method called BEEML (Binding Energy Estimation by Maximum Likelihood) was applied to determine the optimal values of the energy PWM as well as the parameter and a non-specific binding energy (55). This approach provided a much better fit to the data than standard probabilistic motif discovery methods. While BEEML assumed that the position of each binding site was known, similar methods have been developed by others, and applied to large datasets of multiple TFs, that include the ability of inferring the binding sites along with modeling the specificity (69,70).

Protein binding microarrays (PBMs)

Protein binding microarrays (PBMs) were initially employed to measure binding in parallel of all 64 DNA triplets to several different individual zinc fingers as part of larger zinc finger proteins (49). Although it was shown that the positions do not contribute completely independently to binding, in this case a simple PWM model could be found that fit the data quite well for most proteins (48). In recent years PBMs have been expanded to include all possible 10-long binding sites (71,72)and have been used to de termine the specificities of many different TFs (see UniPROBE database (73)). Although the signal is analog, the fluorescence intensity due to protein binding at each location of the array, the data are similar to that from SELEX. We developed a modified version of BEEML, BEEML-PBM, that takes into account the specific characteristics of PBM data and finds the binding energy model that provides the best fit to the fluorescence data (56). In contrast to a previous report (74), we found that most TFs could be well modeled by a simple PWM of energy parameters. A further analysis of all available PBM datasets showed that the majority of TFs could be fit well, probably to within the experimental error, by an energy PWM, and for most of the others adding parameters for adjacent di-nucleotides captured the remaining variance (52). In a more recent comparison of many different algorithms for analyzing PBM data, including quite complex models with many more parameters, BEEML-PBM and similar algorithms were shown to perform as well as the more complex models except for a small number of TFs (75). In fact the models derived from PBM data fit the data from in vivo ChIP-seq experiments as well as the models obtained from those data, demonstrating the value of specificity models determined using in vitro experiments for understanding regulatory networks in cells. These results are consistent with the general paradigm that the specificity of most TFs can be well modeled by either a simple energy PWM or an extension that includes energy parameters for non-independence between adjacent bases. However, there were a few TFs that where the PBM data was only fit well using more complex models, indicating that some TFs can have multiple modes of binding, including variable spacing between half-sites for TFs that bind as dimers, and require more complex models of specificity.

Bacterial one-hybrid (B1H)

Bacterial one-hybrid (B1H) methods express TFs in E. coli and can identify high affinity binding sites by selecting for those that can strongly activate expression of a gene required for colony growth (76–78). Similar to SELEX methods, they typically use libraries of random sequences for the potential binding sites and they can be quite long; a 28bp randomized region is common. A primary advantage of B1H over in vitro methods, such as those described above, is that the TF does not need to be purified or synthesized in vitro, merely expressed in E. coli, making it quite reliable and efficient for most TFs. Early versions of B1H would select many fast growing colonies from which to sequence the binding sites, but current methods utilize high-throughput sequencing where cells from an entire plate (or even from liquid culture) are sequenced (79–83). This provides quantitative data, the number of times different binding sites are sequenced, for the whole range of binding affinities from the highest to those with only non-specific binding (cells without good binding sites do not grow but are still on the plate and are sequenced, similar to the non-specific background in SELEX experiments). There is one significant difference in the analysis between selection for cell growth, such as in B1H, and selection for binding affinity, as in SELEX or PBM. Cells containing good binding sites will continue dividing so the number of those sites will increase exponentially over time, depending on the growth rate afforded by the specific binding site. The growth rate, r_j, for cells with binding site S_j, is measured by sequencing the initial library to get the number of cells containing that site at time 0, N_j(0), and sequencing the library after time t of growth under selective conditions, N_j(t):

$$N_j(t)=N_j(0)2^{r_{j}t}$$ (15)

where, for example, r_j is doublings/hour and t is hours. Under the reasonable assumption that growth rate is proportional to the binding probability of the TF at the critical promoter (at least up to a point where expression of the selectable gene is no longer limiting for growth), which follows the Fermi-Dirac relationship with binding energy, we can determine the binding energy parameters from the relationship:

$$ln\frac{N_j(t)}{N_j(0)}=\frac{M}{1+e^{E_j-\mu }}$$ (16)

where M is the maximum growth rate. Although B1H is an indirect measure of binding affinity, using a version of B1H called constrained variation bacterial one-hybrid (CV-B1H), where the size of the library is small enough that comprehensive sequencing is possible and sites are coherently aligned, we showed that this approach could determine specificity models with accuracies comparable to in vitro assays (79). The more general use of B1H is more complicated. Long randomized regions preclude comprehensive sequencing and there are often effects on the strength of promoter activation in addition to TF binding affinity, such as the orientation and location of the binding site relative to the promoter. Currently the best methods for specificity modeling employ general motif discovery algorithms, such as MEME (44), and improved methods is an open problem.

Conclusions and Future Directions

Determining the specificity of TFs has been an important research area for over 30 years. For most of that time PWMs have been the primary method of representing specificity. New technologies greatly increase the rapidity with which new specificities can be determined and also facilitate significant increases in accuracy by providing large quantitative datasets. New computational approaches have also been developed to optimally extract the information from those datasets. There are likely to be still more advances to come, in both the experimental and computational aspects of the problem. The following sections briefly describe advances that are underway or likely to occur, and also describe a few of the important uses of TF specificity models in studies of regulatory networks within cells.

Experimental advances

As described above, the MITOMI approach has already been enhanced to work on long oligos so that a much larger collection of potential binding sites can be assayed (63). The PBM approach has been utilized to assay binding of longer segments of DNA, such as promoter and enhancer regions, which facilitates the study of interactions by combinations of TFs (84). A new method has recently been described called ‘high-throughput sequencing’-‘fluorescent ligand interaction profiling’ (HiTS-FLIP) that has some similarities to the PBM strategy but assays many more oligos in parallel (85). Instead of synthesizing oligos on an array, DNA segments are selected from a genome, arrayed and each one sequenced, as in a ChIP-Seq experiment. Once the sequence of each oligo is known they are converted to dsDNA and then the TF is added and detected by a fluorescent label, as in the PBM method, but now over millions of different oligos. Through analysis of the DNA sequence and the fluorescence intensity one can obtain specificity models for the binding sites, even for sites longer than can be assayed by current PBM methods. Although the data is much more extensive than using PBM, it is probably too expensive to be cost effective for the study of single TFs. But one can imagine arraying all of the regulatory regions of a cell, such as those obtained in a ChIP-seq experiment based on chromatin marks for regulatory regions, and then assaying the binding of many different TFs in succession. Such information could identify not only which TFs can bind to which regulatory regions but also the specificity model for each TF independently. Finally, we think that a modification to the SELEX-seq protocol can lead to more accurate models more efficiently. Recall that in the current method the initial library is sequenced along with the bound fraction to obtain the data needed to find the parameters of the energy PWM, equation (14). If instead we sequence both the bound and unbound fractions, we have a simpler relationship for estimating the energy parameters that doesn’t require determining the partition function because

$$\frac{P(\mathit{bound}\mid S_j)}{P(un\mathit{bound}\mid S_j)}=e^{\mu -E_j}$$ (17)

Furthermore, because we primarily care about relative binding affinities, we can determine the energy difference between any sequence, S_k, and a reference sequence, S_j, by simply taking the ratios of the measured quantities of equation (17):

$$ln\frac{P(S_j\mid \mathit{bound})}{P(S_k\mid \mathit{bound})}\frac{P(S_k\mid un\mathit{bound})}{P(S_j\mid un\mathit{bound})}=E_k-E_j$$ (18)

We utilized this approach several years ago in a method called Quantitative Multiple Fluorescence Relative Affinity (QuMFRA) assay (51), but it was limited to comparing a few sequences at a time because it used a different fluorescent dye for each sequence. Now, by using sequencing directly, we can essentially assay all possible binding sites in parallel from a single experiment and the computational component is much simpler, essentially multiple linear regression, and should be more accurate.

Computational advances

The PWM model of specificity was always known to be an approximation and it is somewhat surprising that it has worked as well as it has for as long as it has. Even with new technologies that have collected large datasets for many different TFs, the majority of them appear to be well modeled by energy PWMs (52,75). Of course all datasets contain noise, sometimes substantial noise, and it is likely that as more accurate datasets emerge more TFs will be found to be better described by more complex models. Some TFs are not well fit by PWMs, but in most cases simple extensions that include di-nucleotide parameters provide a good fit to the data (52). For the remaining ones, where neither PWMs nor simple extensions are adequate, more complex models are needed. Many different algorithms, with a variety of complexities, have been developed for PBM data and are described in a recent paper (75). The classes of TFs that require more complex models probably have alternative modes of binding to DNA. A common example is for dimeric TFs that can bind with variable spacings between the half sites. This is similar to the two-component motifs of E. coli promoters described earlier and HMM-based methods to deal with them have been developed previously (40). Another common example may be zinc finger proteins that contain many different fingers and may bind to different sites using different combinations. Regardless of the specific mechanism of alternative modes of binding, we advocate an energy-based biophysical modeling approach. Mathematically this is simple, equation (13) still applies but now the binding energy, E_j, to sequence S_j, can be composed of several distinct, and mutually exclusive, interactions that are combined by their Boltzmann weights. We already did this in a simplified case where the alternative modes are specific and non-specific binding (55):

$$e^{-E_j}=e^{-W\cdot S_j}+e^{-E_{ns}}$$

where W · S_j is the specific component that depends on the sequence via the energy matrix W and E_ns is the non-specific energy that is independent of the sequence. This is easily extended to having two (or more) energy matrices, W₁ and W₂, that correspond to sequence specific binding in alternative modes:

$$e^{-E_j}=e^{-W_1\cdot S_j}+e^{-W_2\cdot S_j}+e^{-E_{ns}}$$

Of course the challenge is estimating the parameters for such a complex model where the search space is likely to contain many local optima. It may be more effective to employ some other function of the sequence, F(S_j), such as a support vector machine (86). At this point we don’t know what fraction of TFs will require more complex models or how much improvement in accuracy will be obtained by using them.

Specificity modeling for in vivo regulatory networks

Predicting regulatory sites in vivo has always been one of the primary uses for PWMs. But the accuracy of the predictions is limited by at least two factors. One reason is that the accuracy of the PWMs, often built from a small number of sites, is often low and small changes can have large effects on the number of predicted sites (11). Another reason, especially relevant in eukaryotic cells, is that most of the genome is inaccessible to TF binding due to chromatin structure, but combining information about DNA accessibility with PWMs can lead to much higher accuracies of binding site predictions (87,88). In several areas of research models of TF specificity remain an important tool for elucidating in vivo regulatory networks. Recent experimental methods that identify the binding locations of TFs in vivo, such as ChIP-seq, provide very valuable information and can be used to infer regulatory networks. But even when TF binding sites are known the information provided by specificity models, such as PWMs, can be very useful. For example, genetic variants within TF binding sites may, or may not, cause changes in gene expression depending on whether the specific variants increase, decrease or have no effect on TF binding affinity, information provided by the PWM. By combining information from genome wide association studies with information about TF specificity one can often uncover causative genetic variants associated with specific diseases or other phenotypes (89–93). One important result from ChIP-seq experiments is the identification of the exact binding location of the TF which requires a specificity model, such as a PWM. Especially interesting are cases where there appear to be no high affinity binding sites within a ChIP-seq peak, which requires an accurate model of the TF specificity, because those are indicative of either indirect binding or cooperative binding, both of which indicate that the localization of the TF requires interaction with another factor (52). That knowledge leads to the search for the interacting factor(s) which helps to fill out the details of the regulatory network. While ChIP-seq experiments are very valuable, they must be done for each TF individually in each cell type of interest. An alternative to ChIP-seq experiments is to obtain DNaseI hypersensitive sites (DHS) which identify all of the regulatory regions within the cell type in a single experiment. The DHS data alone does not identify which TFs bind to each regulatory region, but by using catalogs of PWMs the TFs that bind can often be identified (94,95). By combining the general, genome wide accessibility information of DHS with TF-specific information in PWMs, one can efficiently map nodes in the regulatory networks. This approach will become more valuable as the number and quality of PWMs, and other specificity models, increases, as is happening rapidly. Furthermore, by including information regarding competition and cooperativity between different TFs, which can be inferred from combinations of experimental data and specificity models, much more comprehensive regulatory networks can be obtained. The coming years are likely to see significant increases in our knowledge not only of TF specificities but of their biological impact on gene regulation.