Dissipative self-assembly of particles interacting through time-oscillatory potentials

Significance

Dissipative self-assembly is the organization of a system requiring continuous input of energy to the system from its environment. Dissipative self-assembly is ubiquitous in biology, where it leads to structures unavailable in equilibrium conditions and to complex dynamical behavior. There are, however, only a few synthetic examples of this phenomenon. This work proposes a method for dissipative self-assembly through the oscillations of the interaction potentials. As an example, a mixture of pH-responsive particles subjected to fast pH oscillations self-assembles into different nonequilibrium structures that cannot be obtained in equilibrium at fixed pH. This result shows that nontrivial dissipative structures can be formed by periodic oscillation of the forces among particles and reveals a novel strategy to create far-from-equilibrium self-organized structures.

Abstract

Dissipative self-assembly is the emergence of order within a system due to the continuous input of energy. This form of nonequilibrium self-organization allows the creation of structures that are inaccessible in equilibrium self-assembly. However, design strategies for dissipative self-assembly are limited by a lack of fundamental understanding of the process. This work proposes a novel route for dissipative self-assembly via the oscillation of interparticle potentials. It is demonstrated that in the limit of fast potential oscillations the structure of the system is exactly described by an effective potential that is the time average of the oscillatory potential. This effective potential depends on the shape of the oscillations and can lead to effective interactions that are physically inaccessible in equilibrium. As a proof of concept, Brownian dynamics simulations were performed on a binary mixture of particles coated by weak acids and weak bases under externally controlled oscillations of pH. Dissipative steady-state structures were formed when the period of the pH oscillations was smaller than the diffusional timescale of the particles, whereas disordered oscillating structures were observed for longer oscillation periods. Some of the dissipative structures (dimers, fibers, and honeycombs) cannot be obtained in equilibrium (fixed pH) simulations for the same system of particles. The transition from dissipative self-assembled structures for fast oscillations to disordered oscillating structures for slow oscillations is characterized by a maximum in the energy dissipated per oscillation cycle. The generality of the concept is demonstrated in a second system with oscillating particle sizes.

Dissipative or dynamic self-assembly is the formation of order due to the continuous input of energy into the system and dissipation of energy by the system into the environment (1). If the input of energy is stopped, dissipative structures are destroyed as the system evolves toward equilibrium; therefore, these structures exist only far from equilibrium. Dissipative self-assembled structures are unique due to their ability to adapt to environmental changes. Consider, for example, a school of fish where each individual dynamically interacts with its neighbors and adjusts its position and velocity accordingly (2). Due to its dynamical nature, the school of fish responds as a whole when a predator threatens one of its individuals. This complex behavior is impossible for a static assembly. Nature excels in using dissipative structures to minimize wasted energy. For example, a swarm of bees can change its size and density to regulate its internal temperature, and a flock of Canada geese reduces energy dissipation due to aerodynamic drag by flying in a V-shaped formation (2).

Synthetic dissipative assemblies are restricted to a small number of examples, such as magnetic spinners at the air–water interface (1), magnetic droplets on surperhydrophobic surfaces (3), lanes of colloidal particles under the influence of external fields (4, 5), clusters of active colloids (6), and swarms of self-propelled particles (7). One reason for the scarcity of examples of synthetic dissipative self-assembly (in comparison with equilibrium self-assembly) is the lack of general design strategies. In equilibrium self-assembly, there is an optimal balance of the physical and chemical interactions in the system that dictates the formation of ordered structures from preexisting building blocks (8–10). The structure of these building blocks can be engineered to control their interactions and, thus, determine the outcome of equilibrium self-assembly. For example, the molecular architecture of block copolymers, which self-assemble according to the balance between enthalpic interactions and the conformational entropy of the chains, controls their equilibrium morphology (11). The structure of dissipative systems, on the other hand, depends not only on the relative strength of the physical and chemical interactions among building blocks, but also on dynamical variables, such as diffusion constants, chemical reaction rates, and time-dependent changes of external parameters, which make the effective particle interactions time dependent.

The goal of this work is to demonstrate and analyze a novel general strategy for dissipative self-assembly via the oscillation of interparticle forces controlled by an external variable. We derive the general result that for fast enough oscillations the dissipative self-assembly follows an equilibrium-like distribution with an effective interparticle potential. These interactions are the time average of the oscillating potentials. Namely (as shown in SI Text), the probability of a given configuration, $\left\{{\stackrel{\rightharpoonup }{r}}_i\right\}$, in nonequilibrium steady state for a fast oscillating potential is $P_{\text{neq}}\left(\left\{{\stackrel{\rightharpoonup }{r}}_i\right\}\right)\mathrm{\propto }\exp \left[\mathrm{-}\beta \langle U\left(\left\{{\stackrel{\rightharpoonup }{r}}_i\right\}\right)\rangle \right]$ with $\langle U\left(\left\{{\stackrel{\rightharpoonup }{r}}_i\right\}\right)\rangle =\left(1/\tau \right){\displaystyle {\int }_0^{\tau }U\left(\left\{{\stackrel{\rightharpoonup }{r}}_i\right\};t\right)dt}$ being the average interaction potential over the period of the oscillation τ. Whereas dissipative structures follow a Boltzmann distribution dictated by the time-averaged potentials, these interparticle potentials can be obtained only far from equilibrium. As a case study, we performed computer simulations on a model system of positively and negatively charged particles whose charges depend on the pH of the solution, which is externally oscillated. In previous work on light-switchable particles (12, 13) the time between light pulses was larger than the characteristic equilibration timescale; thus, the system relaxed to its equilibrium state between pulses. In contrast, we are interested in the regime where the switching time of the interparticle interactions and the characteristic timescale for equilibration are commensurate, such that the system is always out of equilibrium. We show that this condition is achieved in our system when the period of the oscillation is similar to or shorter than the diffusional timescale of the particles. In that case, the particles form dissipative structures that cannot be obtained in a simulation by equilibrium self-assembly at fixed pH. We characterized the transition between ordered dissipative structures at high oscillation frequencies and disordered oscillating structures at low oscillation frequencies and showed that this transition corresponds to a maximum of the energy dissipated per oscillation cycle. The generality of our results is also demonstrated for a different time-dependent potential where the sizes of the particles oscillate in time (details are shown in SI Text). Dissipative self-assembly via the oscillation of interparticle interactions has the potential to deliver self-assembled structures that are unavailable close to thermodynamic equilibrium and, therefore, to open previously unidentified routes in bottom–up nanofabrication.

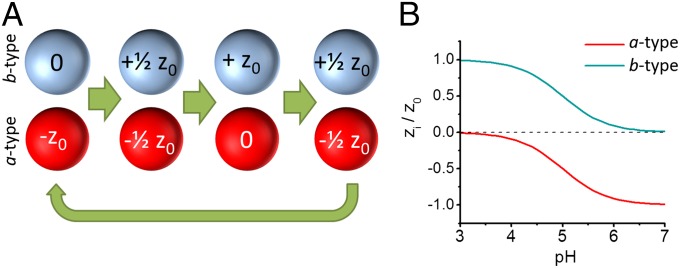
The simulated systems are composed of two types of particles, a and b, each of which represents a pH-responsive colloid (Fig. 1A). a-type and b-type particles have charges of opposite signs; the magnitudes of these charges depend on the pH of the system. We model the dependence of the charge of each particle type, z_i (with i = a or b) on the pH of the system with the well-known expression for acid–base equilibrium,

$$z_i=\mathrm{\pm }{z}_0\frac{1}{1+{10}^{\mathrm{\pm }\left(\text{pH}\mathrm{-}\text{p}{K}_a\right)}}.$$ [1]

Fig. 1.

Model system for dissipative self-assembly of pH-responsive particles. (A) The model system is composed of equal numbers of a-type and b-type particles: a-type particles model pH-responsive negatively charged colloids with pK_a = 5 (e.g., carboxylate-coated colloids), which have a −z₀ charge at pH 7 and zero charge at pH 3; b-type particles model pH-responsive positively charged colloids with pK_a = 5 (e.g., pyridine-coated colloids), which have a +z₀ charge at pH 3 and zero charge at pH 7. (B) Charge of the colloids as a function of pH (determined with Eq. 1).

For simplicity, we assume that a-type and b-type particles have the same maximum absolute charge (z₀) and the same pK_a (we used pK_a = 5 in all simulations). We also neglect the effects of the local environment on the acid–base equilibrium [i.e., charge regulation (14, 15)], hydrodynamic interactions, the effect of the substrate, and many-body interactions (16), because these effects do not influence our general conclusions on dissipative self-assembly and because implementing them in our simulations would result in a prohibitive computational cost. Fig. 1B shows the pH dependence of the charge of each particle. Particles of type a have a negative charge –z₀ at pH 7 and are uncharged at pH 3 (particle a models, for instance, a carboxylate-coated colloid). Particles of type b have a positive +z₀ charge at pH 3 and are uncharged at pH 7 (particle b models, for example, an amino- or pyridine-coated particle). The particles in our simulations interact via the combination of a short-range repulsive potential that models excluded volume interactions between the cores of the particles and a long-range screened electrostatic potential (Methods). The screened electrostatic potential is the Yukawa potential (4, 17) given by

$$u_{ij}^{\text{Yuk}}\left(r\right)=\frac{z_i}{z_0}\frac{z_j}{z_0}\frac{C}{r}{\text{e}}^{\mathrm{-}\left(r/{\lambda }_{\text{D}}\right)},$$ [2]

where λ_D is the solution Debye length and C is a constant that determines the strength of the electrostatic potential in the system (Methods). We simulated the systems of particles using Brownian dynamics (BD) in a 2D box with periodic boundary conditions either at constant pH (i.e., static interparticle potential) or by oscillating the pH between 3 and 7 with a period τ. We use dimensionless variables: The distances are measured in units of σ (diameter of the colloid), the energies in k_BT, and the time in units of the characteristic diffusion timescale, t_d = σ²/D (where D is the diffusion coefficient).

Results

Dissipative Self-Assembled Structures Are Different from Equilibrium Structures.

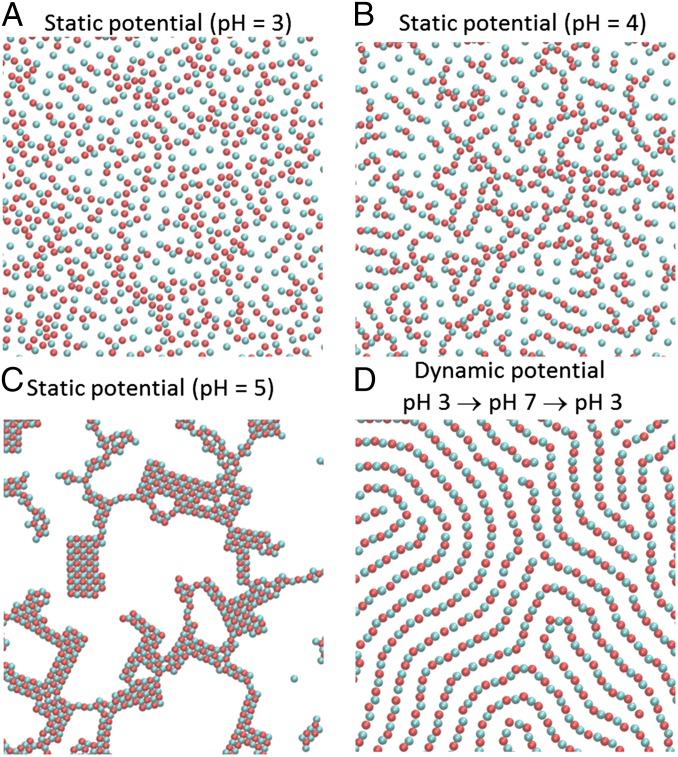
Fig. 2 A–C shows the simulated structures of the system after equilibration at fixed pH for pH 3, 4, and 5, respectively. For pH 3, particles of type a are neutral and particles of type b are positively charged. The b-type (cyan) particles attempt to form a 2D hexagonal crystal to reduce their electrostatic repulsions. On the other hand, neutral a-type (red) particles are distributed more randomly than b-type particles, as they interact through short-range repulsions only. For pH 4, particles of type a bear a charge of −0.25 ⋅ z₀ and particles of type b a charge of 0.75 ⋅ z₀. This system forms a low-order structure where b-type particles are distributed regularly (with some hexagonal order) to reduce electrostatic repulsions and are bridged by the negatively charged a-type particles. For pH 5, particles a and b have a charge of −0.5 and +0.5, respectively, and, as expected (17, 18), they form square lattice aggregates. The symmetry of the system ensures that the pH range 5 < pH < 7 produces the same structures described for the range 3 < pH < 5, but with the a-type and b-type particles interchanged.

Fig. 2.

Comparison of equilibrium (fixed pH) and dissipative (oscillating pH) simulations. (A–C) Snapshots of simulations for three different fixed pH scenarios. (D) Snapshot of a simulation for the oscillatory pH scenario for a linear pH–time program (Fig. 3 B, i). Simulation conditions: C = 1,000 k_BT ⋅ σ, ρ = 0.39 particles ⋅ σ⁻². a-type and b-type particles are shown in red and cyan, respectively. Only part of the simulation box is shown. The diameter of the colloids is σ.

Fig. 2D shows a snapshot of a simulation where the pH was oscillated linearly between 3 and 7 with an oscillation period τ = 0.08 t_d (program shown in Fig. 3 B, i) for the same density and interaction strength as in the static simulations shown in Fig. 2 A–C. Under these conditions, the pH oscillations lead to the formation of long fibers, that is, worm-like structures of alternating a and b particles. As shown in Fig. 2 A–C, these fiber-like structures cannot be obtained in equilibrium (fixed pH) simulations. Therefore, the oscillation of interparticle potentials is a novel strategy for dissipative self-organization, which can lead to nonequilibrium dissipative structures that are unavailable in self-assembly through equilibrium potentials. This strategy is not limited to 2D systems; in Fig. S1 we show that the pH-responsive particles also form fibers in a 3D simulation.

Fig. 3.

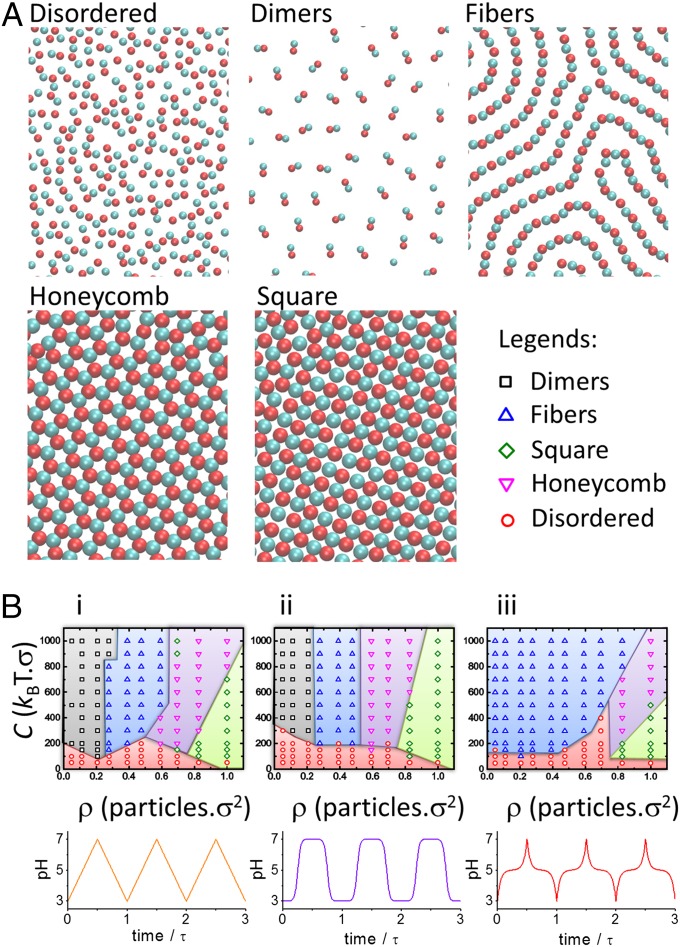
Morphologies and morphology diagrams of the dissipative self-assembled systems. (A) Snapshots of the morphologies of the system for various strengths of the Yukawa interaction, C, and the surface density of the system, ρ, for τ = 0.08t_d. These snapshots have been obtained for the following values of C (in k_BT ⋅ σ) and ρ (in particles ⋅ σ⁻²): C = 50, ρ = 0.39 (disordered); C = 1,000, ρ = 1.0 (honeycomb lattice); C = 200, ρ = 1.0 (square lattice); C = 1,000, ρ = 0.39 (fibers); and C = 1,000, ρ = 0.11 (dimers) and a linear pH–time program (B, i). Only part of the simulation box is shown. The diameter of the colloids is σ. (B) Morphology diagrams (Upper) showing the occurrence of the different morphologies in the C–ρ plane for different forms of the pH oscillation (Lower).

Morphology Diagram of Dissipative Structures.

Fig. 3A shows the different morphologies that the pH-oscillating system adopts, depending on the strength of the screened electrostatic interactions (parameter C in Eq. 2) and the surface density, ρ. These morphologies are disordered system, dimers, fibers (the same structure shown in Fig. 2D), honeycomb lattice, and square lattice. The particles in each of these structures have a different number of nearest neighbors: zero (disordered), one (dimers), two (fibers), three (honeycomb), and four (square lattice). The morphology diagrams in Fig. 3B show the stability regions in the C–ρ plane for the different morphologies and for three different forms of the pH oscillation and relatively fast oscillations. As expected, increasing the surface density favors the formation of the structures with higher number of nearest neighbors (honeycomb and square). Varying the strength of the electrostatic interactions, C, has a nonmonotonic effect on the morphology: Increasing C favors structures with high number of neighbors (i.e., dimers over disordered state) when the density is low, but increases the stability of structures with a low number of crystalline neighbors (i.e., honeycomb morphology over the square) when density is high. We attribute the dual role played by C to the competition between the attraction of oppositely charged particles and the repulsion of equally charged colloids in the Yukawa potential. Finally, the time dependence of the pH controls the region of the C–ρ plane where each morphology is stable; for example, the stability region for fibers is much larger for the functional form shown in Fig. 3 B, iii than for the linear pH–time program, Fig. 3 B, i. For fixed C and ρ, therefore, the morphology of the dissipative self-assembled structures can be tuned by simply changing the form of the pH perturbation.

An important question is whether any of the dissipative structures shown in Fig. 3 can be obtained in a fixed pH (i.e., a static-potential simulation). To address this question, we performed fixed pH simulations in the pH range 3–7 (every 0.25 pH units) for different values of ρ and C starting from a disordered state. The square lattice morphology was always obtained when the pH was close to 5, as is shown in Fig. 2C; however, we did not observe the formation of dimers, fibers, and honeycomb lattices. This result suggests that these dissipative structures cannot be produced via equilibrium self-assembly. This conclusion is supported by previously measured and predicted phase diagrams of systems of oppositely charged particles in the absence of external fields, which do not contain dimers, high-aspect ratio fibers, or honeycomb lattices (4, 19, 20). Note that simulations of oppositely charged particles interacting through static Yukawa potentials show the formation of fibers shorter than those in Fig. 2D at early times (17). The system shown in Fig. 2D, however, is a nonequilibrium steady state, not a transient structure on the path to an equilibrium structure, because it was obtained after stabilization of the morphological features under the continuously oscillating potential.

Ordered Dissipative Structures Require τ < t_d.

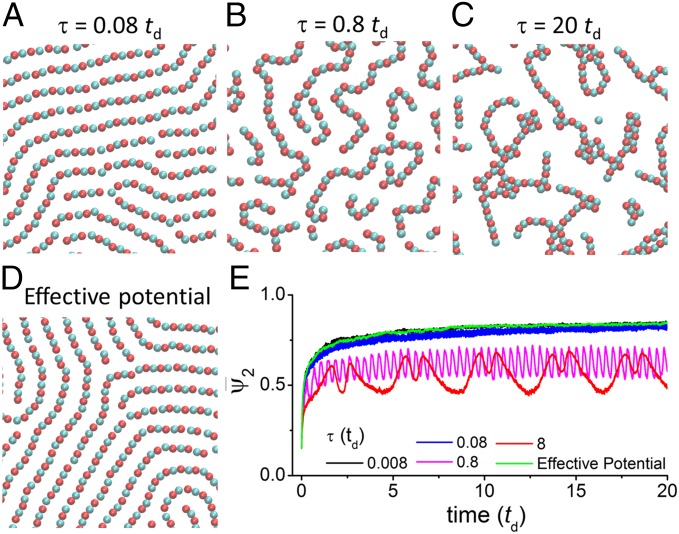
We turn our attention to the effect of the period of the oscillation, τ, on the degree of order of the dissipative structures. Fig. 4 A–C shows the structure of the fiber morphology for different values of τ. We observe that the order of the fibers decreases with increasing τ. To quantify the order of each of the different dissipative morphologies, we use the average bond-order parameter of order n (17, 21, 22), which we define as

$$\overline{{\psi }_n}\left(t\right)=\frac{1}{N}{\displaystyle \sum _{j=1}^N{\psi }_n\left(j,t\right)},$$ [3]

where N is the total number of particles in the system and ψ_n(j, t) is the 2D bond-order parameter of order n for the particle j at time t, which we calculate using

$$\begin{array}{cc}{\psi }_n\left(j,t\right)=\left|\frac{1}{NN\left(j\right)}{\displaystyle \sum _{k=1}^{NN\left(j\right)}\exp \left(n{\theta }_{jk}\left(t\right)i\right)}\right|& \mathrm{for}\mathrm{\hspace{0.5em}}NN\left(j\right)\mathrm{\ge }n\\ 0& \mathrm{for}\mathrm{\hspace{0.5em}}NN\left(j\right)\mathrm{<}n,\end{array}$$ [4]

where i is $\sqrt{\mathrm{-}1}$, NN(j) is the number of nearest neighbors of particle j determined with a cutoff distance of 1.5σ, and θ_jk is the angle of the vector formed by the positions of particles j and k and a fixed (arbitrary) axis. For each morphology, we choose the value of n according to the particle’s natural number of crystalline neighbors within that morphology (n = 1, 2, 3, and 4 for the dimers, fibers, honeycomb morphology, and square morphology, respectively). For a given n, the order parameter $\overline{{\psi }_n}$ has a maximum value of one for a completely ordered structure where each particle has n equivalent crystalline neighbors and a minimum value of zero for structures with a number of crystalline neighbors different from n (disordered systems produce small, but nonzero, $\overline{{\psi }_n}$). In Fig. S2 we show that the morphology diagram predicted using the average bond-order parameters $\overline{{\psi }_n}$ is in very good agreement with that obtained by visual structural characterization of simulation snapshots. Therefore, we use $\overline{{\psi }_n}$ to characterize the dissipative self-assembled structures in our system. In Fig. 4E, we show a plot of $\overline{{\psi }_2}\left(t\right)$ vs. t for the formation of fibers for different values of τ. We observe that $\overline{{\psi }_2}\left(t\right)$ decreases for increasing τ and that for τ ≥ 0.8 t_d, $\overline{{\psi }_2}\left(t\right)$ displays clear oscillations that are caused by the reorganization of the system during one oscillation period.

Fig. 4.

Effect of the frequency of the pH oscillations on the order of dissipative structures. (A–C) Snapshots of the fibers morphology for C = 1,000 k_BT ⋅ σ and ρ = 0.39 particles ⋅ σ⁻² and obtained at the middle of a half-oscillation period (i.e., an instantaneous pH 5) for different values of τ, the oscillation period. (D) Snapshot of the fibers morphology for a simulation with a static effective potential that is the time average of the oscillatory potential (Eq. 5) for the same C and ρ as in A–C. In A–D, only part of the simulation box is shown and the diameter of the colloids is σ. (E) Average bond-order parameter of order two as a function of simulation time for the formation of the fibers morphology for different values of τ (same conditions as in A–D). The initial state is a disordered system of particles interacting via a short-range repulsive potential only. A linear pH–time program (Fig. 3 B, i) has been used in these calculations.

Average Effective Potentials Describe Dissipative Structures in the Fast-Oscillation Limit.

In Fig. 4, we have shown that ordered dissipative structures form for τ < t_d. A perturbation analysis of the Fokker–Planck equation of the system (SI Text) shows that in the limit of very fast oscillations (τ << t_d) the states of the system follow a Boltzmann distribution with an effective interparticle potential that is exactly given by the time average of the oscillating potential over one cycle. Namely,

$${\langle u_{ij}\left(r\right)\rangle }_{\tau }=\frac{1}{\tau }{\displaystyle \underset{0}{\overset{\tau }{\int }}{u}_{ij}\left(r,t\right)dt}.$$ [5]

Fig. 4D shows that, as analytically predicted, the effective potential produces the same fiber morphologies observed for fast pH oscillations. Moreover, both simulations show overlapping radial distribution functions (Fig. S3). The green curve in Fig. 4E shows that the time evolution of $\overline{{\psi }_2}$ for a simulation using the effective potential curve is also very similar to that obtained for the pH-oscillating system with τ = 0.008 t_d. These results provide a numerical confirmation of our proven general result for the dissipative assemblies following a Boltzmann distribution of the time-average potential. This effective potential cannot be obtained as a combination of a short-range repulsion and a Yukawa potential; therefore it is not a possible equilibrium potential for our system.

Because the effective potential dictates the structure of the system in the limit of fast oscillations, we can analyze it to explain the structures of the dissipative assemblies. Replacing Eq. 2 into Eq. 5 provides an explicit expression for the effective interparticle potential due to screened electrostatic interactions, which is given by

$${\langle u_{ij}^{\text{Yuk}}\left(r\right)\rangle }_{\tau }={\langle \frac{z_i}{z_0}\frac{z_j}{z_0}\rangle }_{\tau }\frac{C}{r}{\text{e}}^{\mathrm{-}\left(r/{\lambda }_{\text{D}}\right)}.$$ [6]

This expression shows that the effective interparticle potential depends on ${\langle z_i/z_0\mathrm{\cdot }{z}_j/z_0\rangle }_{\tau }$ (the product of the fraction of charge of particles i and j averaged over one oscillation cycle). For a linear variation of the pH with time (Fig. 3 B, i), ${\langle z_i/z_0\mathrm{\cdot }{z}_j/z_0\rangle }_{\tau }$ is equal to 1/3 when i and j are particles of the same type or to −1/6 otherwise. The effective electrostatic repulsions between particles of the same kind are stronger than the effective electrostatic attractions between particles of different type. This property of the effective potential explains the formation of well-ordered dissipative structures with coordination numbers smaller than four (dimers, fibers, and honeycombs). Note, as a comparison, that the fixed-pH simulation with pH 5 (Fig. 2C) produces a square lattice and has $z_i/z_0\mathrm{\cdot }{z}_j/z_0$ equal to 1/4 when i and j are of the same type and to −1/4 when they are of different type. Moreover, the different forms of pH oscillations yield different values of ${\langle z_i/z_0\mathrm{\cdot }{z}_j/z_0\rangle }_{\tau }$, which explains why the form of the pH oscillation determines the relative stability of each morphology, as shown in the morphology diagrams of Fig. 3B.

Effect of the Oscillation Period on Self-Assembled Structure.

To understand the role of the oscillation period on the order of the self-assembling structures we define ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ as the time average of the bond-order parameter $\overline{{\psi }_n}\left(t\right)$ during one oscillation period,

$${\langle {\overline{\psi }}_n\rangle }_{\tau }=\frac{1}{\tau }{\displaystyle \underset{0}{\overset{\tau }{\int }}{\overline{\psi }}_n\left(t\right)dt}.$$ [7]

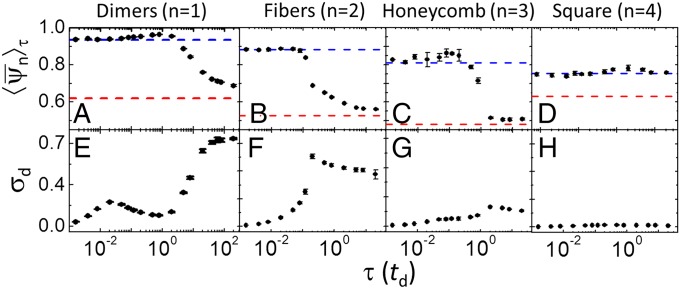
Fig. 5 A–D shows ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ vs. τ for the different dissipative morphologies studied. The blue and red dashed lines in Fig. 5 show the values of ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ expected in the limits of very fast and very slow oscillations, respectively. In the limit of very fast oscillations $\left(\mathrm{\tau \ll }{t}_{\text{d}}\right)$, we obtained ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ from simulations using the effective potential discussed in the previous section. In the limit of very slow oscillations, the structure of the system can adapt to the pH at any given time point and, thus, we obtained ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ as an average of the bond-order parameters of the equilibrium structures in the pH range 3–7, determined by fixed-pH simulations.

Fig. 5.

Characterization of the nonequilibrium order/disorder transition between dissipative structures for fast oscillations and oscillating structures for slow oscillations. (A–D) Period-averaged bond-order parameters, 〈ψ_n〉_τ, as a function of the period of the oscillation, τ, for dimers, fibers, honeycomb lattice, and square lattice. The blue dashed line shows the value 〈ψ_n〉_τ in the limit of very fast oscillations, obtained with the effective potential, Eq. 5. The red dashed line shows the value 〈ψ_n〉_τ in the limit of very slow oscillations obtained from an average of 〈ψ_n〉_τ determined for fixed-pH simulations in the pH range 3–7. (E–H) Energy dissipation per oscillation period (units of k_BT) as a function of the oscillation period for the different morphologies. The values of C and ρ for each morphology are the same used for the snapshots in Fig. 3. Error bars show 1 SD from the average result of four independent simulations. A linear pH–time program (Fig. 3 B, i) has been used in these calculations.

The results in Fig. 5 show that the dimers, fibers, and honeycomb structures display a transition from large ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ at small τ to small ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ at large τ. The inflection point in the transition indicates the critical period at which the dissipative structures disappear, τ^crit. Note that the square lattice does not show a transition in the range of τ under study. We ascribe this behavior to the combination of the following two factors: (i) The square lattices are high-density structures and therefore their relaxation times are very slow, and (ii) the square lattice is a natural equilibrium structure of the system (Fig. 2C). The value of the critical period depends on the morphology: τ^crit ∼ 10 t_d for the dimers, ∼0.5 t_d for the fibers, and ∼t_d for the honeycomb. The condition τ^crit < t_d (where the exact limit depends on the details of the system) is, therefore, a general requirement for the formation of steady-state dissipative structures in potential-oscillating systems. This rule is one of the main outcomes of the present paper as it imposes conditions on the physical/chemical stimuli that can be used in dissipative self-assembly via oscillatory interactions.

We estimated t_d as a function of colloid size (detailed calculations are presented in Table S1): t_d = 3 μs for σ = 10 nm, 3 ms for σ = 100 nm, 3 s for σ = 1 μm, and 3,000 s for σ = 10 μm. Experimental observation of dissipative self-assembly via oscillation of interparticle potential is limited by the experimentally achievable timescale of the potential perturbation (which is slower than ∼1 ms for chemical or electrical stimuli) and the timescale of image acquisition (also slower than ∼1 ms). On the other hand, the formation of order starting from a random system (which requires a few t_d in our simulations, Fig. 4E) should be completed in less than a few hours. Based on these considerations and the dependence of the diffusional timescale on the size of the colloid, we propose that our strategy for dissipative self-assembly can be used in the laboratory for particles of sizes between 100 nm and 10 μm.

The Energy Dissipation per Period Has a Maximum at the Period of the Order–Disorder Transition.

We analyze in this section the dependence of the rate of energy dissipation on the period of the pH oscillation. The rate of energy dissipation is determined from the work performed on the system, as detailed in SI Text. We proved mathematically that the energy dissipation per period should be zero in the asymptotic two limits of fast and slow oscillations (the slow limit is not achieved in the range of oscillation periods used in our simulations) (SI Text). The fact that the energy dissipated per period goes to zero for very fast oscillations can be understood by recalling that the structure of the system in this limit is equivalent to the equilibrium structure obtained with a time-averaged effective potential. In this case, the energy exchanged between the system and the bath during one half of the oscillation period (pH 3 → pH 7) cancels that exchanged on the second half (pH 7 → pH 3) because the structure of the system is independent of the instantaneous pH.

Fig. 5 shows that the energy dissipation per period, σ_d, for the fibers and honeycomb lattices (Fig. 5 F and G) displays a maximum at a period that is similar to (although not exactly the same as) the critical period observed for the order parameters ${\langle {\overline{\psi }}_n\rangle }_{\tau }$ in Fig. 5 B and C. This result suggests that the transition between the ordered dissipative self-assembled state and the disordered state is characterized by a peak in the energy dissipation per period. In the case of the dimers, σ_d shows a small peak at τ ∼ 0.02 t_d and a large peak is expected at τ > 100 t_d (note that σ_d should go to zero in the low-frequency limit). The large peak is attributed to the nonequilibrium order/disorder transition of the dimers as it occurs in a similar timescale to the inflection point of ${\langle {\overline{\psi }}_1\rangle }_{\tau }$ in Fig. 5A. We attribute the small peak at τ ∼ 0.02 t_d to the nonequilibrium order/disorder transition of a small population of trimers in the system (Fig. S4). Finally, in the range of τ under study, the square morphology has relatively small and constant energy dissipation per period (Fig. 5H; note that the plots in Fig. 5 E–H are all presented in the same energy scale), which is consistent with the observation that this morphology is always in its ordered state (Fig. 5D).

Discussion

This work addressed for the first time to our knowledge the dissipative self-assembly of particles via the oscillation of interparticle potentials. Our two main findings are as follows: (i) Dissipative self-assembly through the oscillation of interparticle potentials requires the period of oscillations to be faster than the diffusional timescale of the particles. This condition is an important design rule for any experimental implementation of our strategy for dissipative self-assembly. (ii) In the limit of fast oscillating potentials the dissipative self-assembly system is equivalent to an equilibrium system with an effective potential that corresponds to the time-averaged instantaneous potential. Therefore, these potentials, in general, have no equilibrium counterpart.

Oscillation of pH by acid–base titration takes seconds and, thus, it is restricted to colloids larger than 1 μm. Unfortunately, electrostatic self-assembly of colloids of this size requires very small ionic strengths and solvents with low dielectric constants (4, 18). This condition restricts the use of acid–base titration, which will increase continuously the salt concentration in the system. On the other hand, photochemical (23, 24) or electrochemical (25) control of pH allows much faster oscillations of pH than acid–base titration and avoids large changes in ionic strength. Therefore, an experimental realization of our model system should be based on one of these pH-control methods. Our strategy for dissipative self-assembly is general. For instance, in Figs. S5–S7, we show the existence of dissipative structures in a binary mixture of size-changing colloids. This example of dissipative self-assembly, based on interactions that are completely different from the screened electrostatic interactions discussed so far, demonstrates that the oscillation of interparticle potentials is a general strategy for dissipative self-assembly. In general, we believe that this strategy is feasible for binary mixtures of particles whose interactions can be controlled by an external variable.

An important open question in dissipative self-assembly is whether a variational principle exists that determines the state of the system under nonequilibrium steady-state conditions (26). For example, it has been proposed that nonequilibrium steady states occur with a probability that depends on their rate of energy dissipation (27). In the particular case of self-assembly through oscillation of interparticle potentials, we found that the structure of the system in the limit of fast oscillations is ruled by the following variational principles: (i) The dissipative structures in the high-frequency limit follow a Boltzmann distribution of states associated with a time-averaged (effective) potential, and (ii) the energy dissipated per period in the high-frequency limit is zero. The second principle is derived from the first one (SI Text) and, therefore, these two principles are probably equivalent. Further work should be devoted to search for similar variational principles in the whole range of oscillation frequencies.

We have theoretically proved that, in the limit of fast oscillations, the distribution of dissipative self-assembling states produced by oscillatory potentials is exactly equivalent to that created by time-averaged effective potentials that have no equilibrium counterparts. Therefore, our work shows, to our knowledge, the first example of a system where the outcome of dissipative self-assembly can be predicted and analyzed in terms of equilibrium self-assembly. Simulations showed that the effective potentials describe the structure of the system only when the oscillation period is smaller than the diffusional timescale of the particles, which makes our self-organization strategy well suited to experimentally assemble micrometer-size colloids. The effective potentials can be engineered by controlling the temporal evolution of the interparticle forces, which opens an avenue to dynamically tune the self-assembled structures and design tailor-made interactions. We believe that dissipative self-assembly through time-oscillating interactions will emerge as an important form of self-organization, which may outcompete equilibrium self-assembly in terms of morphology control and dynamical responsiveness.

Methods

We study a system of particles interacting through a combination of a purely repulsive Lennard-Jones potential (Eq. 8) and a screened electrostatic potential [specifically, the Yukawa potential (4, 17)] (Eq. 2), which are cut off and shifted according to Eq. 9:

$$u_{ij}^{\text{rep}}\left(r\right)={\left(\frac{\sigma }{r}\right)}^{12}$$ [8]

$$u_{ij}\left(r\right)=\begin{array}{cc}{u}_{ij}^{\text{rep}}\left(r\right)+u_{ij}^{\text{Yuk}}\left(r\right)\mathrm{-}\left[u_{ij}^{\text{rep}}\left(r_{\text{cutoff}}\right)+u_{ij}^{\text{Yuk}}\left(r_{\text{cutoff}}\right)\right]& \mathrm{for}\mathrm{\hspace{0.5em}}r\mathrm{<}{r}_{\text{cutoff}}\\ 0& \mathrm{for}\mathrm{\hspace{0.5em}}r\mathrm{\ge }{r}_{\text{cutoff}}.\end{array}$$ [9]

In the Yukawa potential, Eq. 2, the constant C determines the strength of the electrostatic potential in the system and is given by

$$C=\frac{4z_0^2{e}^{\sigma /{\lambda }_{\text{D}}}{\lambda }_{\text{B}}}{{\left(2+\sigma /{\lambda }_{\text{D}}\right)}^2},$$ [10]

where λ_B is the Bjerrum length of the solvent. We used a Debye length of λ_D⁻¹ = 1.5σ in all calculations, based on previous theoretical (17) and experimental (18) reports that show that crystalline order in a system of particles interacting through a Yukawa potential requires λ_D⁻¹ > 0.5σ and increases with increasing λ_D⁻¹. We used a cutoff radius of the interaction (r_cutoff) of 8σ, which ensures $u_{ij}^{\text{rep}}\left(r_{\text{cutoff}}\right)+u_{ij}^{\text{Yuk}}\left(r_{\text{cutoff}}\right)$ < 0.05 k_BT for all conditions studied.

We studied the system of pH-responsive particles, using BD simulations with a home-developed parallel code. In BD, the solvent is considered implicitly by adding a random force and a drag force to the equation of motion of the particles. These forces model the random collisions and the friction between the solvent molecules and the particles, respectively. In the equation of motion the inertial term is neglected with respect to the drag and random forces, as the characteristic inertial timescale is much smaller than the diffusional timescale (28). We simulated a 2D system of 1,250 a-type particles and 1,250 b-type particles with a total surface density of ρ in a square simulation box with periodic boundary conditions, using a simulation time step of 10⁻⁶ t_d.