Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jul 21;4:5764. doi: 10.1038/srep05764

The linear interplay of intrinsic and extrinsic noises ensures a high accuracy of cell fate selection in budding yeast

Yongkai Li 1,2, Ming Yi 3,4,a, Xiufen Zou 1,b
PMCID: PMC4104398  PMID: 25042292

Abstract

To gain insights into the mechanisms of cell fate decision in a noisy environment, the effects of intrinsic and extrinsic noises on cell fate are explored at the single cell level. Specifically, we theoretically define the impulse of Cln1/2 as an indication of cell fates. The strong dependence between the impulse of Cln1/2 and cell fates is exhibited. Based on the simulation results, we illustrate that increasing intrinsic fluctuations causes the parallel shift of the separation ratio of Whi5P but that increasing extrinsic fluctuations leads to the mixture of different cell fates. Our quantitative study also suggests that the strengths of intrinsic and extrinsic noises around an approximate linear model can ensure a high accuracy of cell fate selection. Furthermore, this study demonstrates that the selection of cell fates is an entropy-decreasing process. In addition, we reveal that cell fates are significantly correlated with the range of entropy decreases.

Cells from across biological kingdoms are continuously engaged in the process of decision-making. A growing number of cell types are being described as capable of decision-making under various circumstances. For example, unicellular organisms make vital decisions to enter various phases of the life cycle to adapt to environmental changes. In multicellular organisms, precursor cells mature into specialized cell types during development. Therefore, the selection of cell fate in response to both internal and external stimuli is essential in a cell's life1. As the simplest eukaryote, budding yeast is often used as a model organism to study the molecular mechanisms underlying life processes.

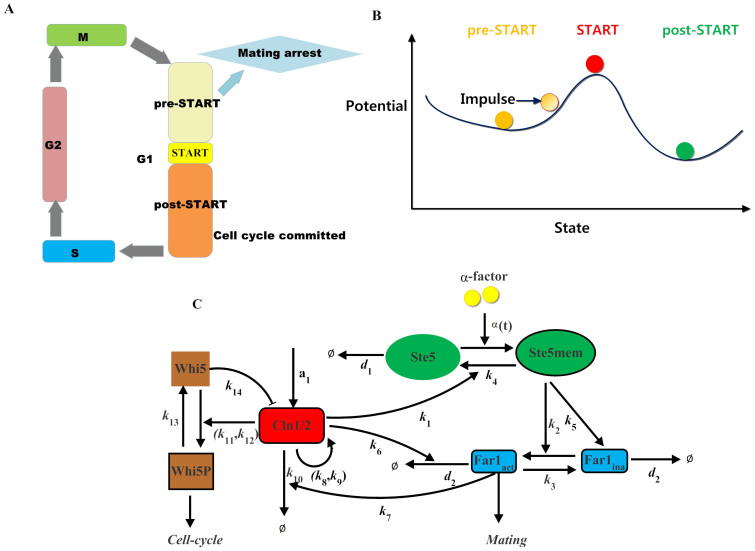
Recently, a quantitative single-cell analysis of commitment dynamics during the mating-mitosis switch in budding yeast has been provided2,3. The commitment points are frequently invoked in the explanation of differentiation processes. For the mating-mitosis switch process, the purpose of mating is to fuse two haploid cells, which must be restricted to the G1 phase prior to the initiation of DNA replication. The point where a cell loses mating competence and commits to the cell-cycle is called the Start point (Fig. 1 A). Depending on the progression level, the process can be divided into the following two stages: a pre-Start state and a post-Start state. As shown in Fig. 1 B, the dynamics can be roughly visualized as a “quasi-potential landscape” in which each potential well represents a state. In this pre-Start stage, the process is sometimes reversible to the post-Start state if appropriately treated, thus implying instability of the pre-Start state3. However, the post-Start state generally becomes irreversible if the system passes the critical Start point. As reported previously, the Start point is accurately predicted by the nuclear Whi5 concentration independent of cell size, type and G1 duration2. Our recent research has also confirmed that Start can be characterized by entropy4, as entropy defines the height in the landscape of cell fate decision-making.

Figure 1. Background of cell fate selection in budding yeast.

Figure 1

Open in a new tab

(A) Schematic of the cell-cycle. (B) Cell fate decision and potential landscape. The pre-Start state is situated immediately before the tipping point Start. At this stage, the system is sensitive to external stimuli. The post-Start state is the other stable state or a minimum of the potential function where the system is usually irreversible to the pre-Start state. (C) Schematic of the core interacting network between the G1 cell-cycle and the pheromone-induced MAPK pathway. All components and reactions considered in our mathematical model are included. All arrows for individual reactions are marked with the corresponding number of this reaction in the model.

Stochastic fluctuations are ubiquitous in many real dynamical systems as follows: physical, chemical, and biological systems. The information transduced in cellular signaling pathways is significantly limited by noise5,6,7. Noise is increasingly appreciated as a force shaping biology. Therefore, the importance of precisely understanding the mechanisms of cell fate decision in a noisy environment has already been recognized. Cells may exploit noise in different beneficial ways. For instance, phenotypic variability may be triggered by noise because fluctuations enable the exploration of the phase space through different types of dynamics8,9,10,11. This variability has been observed in several natural systems such as the galactose utilization network in budding yeast12, the process of DNA uptake from the environment in B. subtilis13,14, photoreceptor differentiation in the fruit fly retina15 and stem cell differentiation16,17,18. By combining mathematical modeling and gene expression studies in zebrafish, Zhang et al. demonstrated that noisy expression can actually facilitate boundary sharpening19. In addition, interactions among different types of noise have been studied theoretically20,21,22. For example, the advantage of noise in a regulatory network in a noisy environment has been demonstrated by Chou et al20,21. Interestingly, a general principle states that the capability of a feedback system to attenuate the input noise is dependent on the difference between the deactivation time and the activation time22.

However, due to complexity in highly interconnected biochemical networks, many related questions need to be further explored. For example, stochastic noise may interfere with the molecular regulations that cooperatively allow a single cell to choose between two different fates. However, the exact roles of stochastic noise on the cell fate decision process are not well established. The molecular basis for a yeast cell to use such a fundamentally stochastic process to generate extremely reliable outcomes also remains unclear. Thus, it is crucial to thoroughly characterize the features of stochastic cell fate decision. Furthermore, the combined influences of intrinsic and extrinsic noises on cell fate decision between cell-cycle commitment and mating arrest are poorly understood.

To select a mitotic fate, the upstream G1 cyclin (cell-cycle signal) activates the cyclin-dependent kinase (CDK) to phosphorylate the transcriptional inhibitor, Whi52,3. This initiates a positive feedback loop centered on the downstream G1 cyclins, Cln1 and Cln2, which drives entry into the cell-cycle23,24. Conversely, mating arrest is affected by Far1, most likely via stoichiometric inhibition of the G1 cyclin CDK complexes2,3. Upon pheromone stimulation, Far1 is regulated in a feedforward manner by the mitogen-activated protein kinase (MAPK), Fus3, which interacts physically with the scaffold protein, Ste524,25,26,27. In addition, the G1 cyclins inhibit the mating pathway by promoting the phosphorylation and degradation of both Far1 and the Ste5 scaffold2,25. Thus, in this study, we simplified the regulation network of the cell-cycle and pheromone-induced MAPK pathway as well as the mathematical model presented in the literatures2,4. Only the proteins mentioned above, tightly related to the crosstalk between the cell-cycle and MAPK pathway, were selected for our core interacting network. The schematic diagram used to build the mathematical model is shown in Fig. 1 C. We developed a simplified deterministic model (Ordinary-Differential-Equation (ODE) model) and a corresponding stochastic model (Chemical-Langevin-Equation (CLE) model28) responsible for selecting cell fates between cell-cycle commitment and mating arrest. Based on these two classes of models and quantitative measures of cell fate selections, we investigated the effects of both external and internal noises on the accuracy of cell fate decisions. These findings will provide new insights into the mechanisms of cell fate decision in a noisy environment.

Results

The consistency between the simulation results of the mathematical models and the experimental observations under wild type conditions

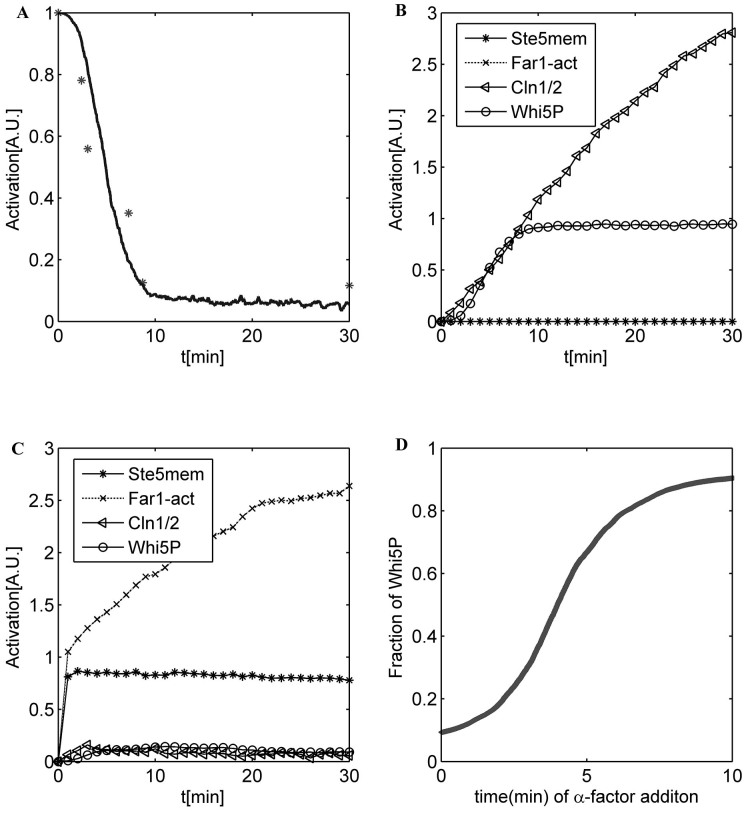
To validate our simplified ODE model, the signaling dynamics of the system, including the cell-cycle and the pheromone-induced MAPK pathways, were simulated. The initial values listed in Table 1 were suitable for the cells that had already finished at least one cell-cycle, and the cells were all at the beginning of G1 phase. Some biomarkers were chosen to indicate different cell fates as follows: cell-cycle commitment was represented by high levels of Cln1/2 and Whi5P, and mating arrest was predicted by high levels of Ste5mem and Far1. The detailed comparisons between the original model and the simplified model are shown in Supplementary text. The numerical results for the simplified ODE model are presented in Supplementary Fig. S1. Given the small size of a yeast cell (~30 fL) and the low concentration of regulatory proteins (~50 nM), the total number of molecules of each regulatory protein in a cell is limited (~1,000), and the intrinsic molecular fluctuations are not only inevitable but also large enough29. The system volume V was set to be 1000. Thus, the intrinsic molecular fluctuation was assigned to a Gaussian distribution with a mean of 0 and a standard deviation of 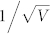Inline graphic ≈ 0.036. Fig. 2 A shows the simulation result of the CLE model compared to the experimental data. Fig. 2 B and C illustrate that the cell would commit without pheromone (Fig. 2 B) and arrest with the addition of pheromone (Fig. 2 C). The relationship between the activation of Whi5P (i.e., the mean proportion of Whi5 exported from the nucleus from 29.8 to 30 min) and the addition time of pheromone is shown in Fig. 2 D. According to our theoretical calculations, the critical ratio of Whi5P for WT simulated by our CLE model was approximately 50.43%. This result was close to the reported experimental results indicating that cell fate is determined when approximately half of the Whi5-GFP (52% ± 3%) has been exported2.

Table 1. Parameters and initial concentrations of all components in the simplified mathematical model.

Parameters Value Parameters Value
k1 0.6500 k9 10.0000
k2 8.0000 k10 0.1200
k3 0.1000 k11 2.6750
k4 0.0310 k12 1.0000
k5 0.2600 k13 0.1400
k6 0.5800 k14 0.1530
k7 0.6200 d1 0.3000
k8 0.3150 d2 0.0250
Signals Value Signals Value
α(t) 2.400(for t ≥ t-added) or 0 (otherwise) a1 0.2500
Components Concentrations (in the model) Components Concentrations (in the model)
Ste5 1.0000 Whi5 1.0000
Far1inact 1.0000    
Open in a new tab

The concentrations of other components that are not listed in the Table are 0.

Figure 2. Simulation results of the CLE model.

Figure 2

Open in a new tab

(A) Time course of Whi5P in our CLE model. The experimental data are marked with a star. (B) The time course of a WT yeast cell when no pheromone is added. (C) The time course of a WT yeast cell when pheromone is added at 0 min. (D) Relationship between the addition time of pheromone and the activation of Whi5P. Here we set R = 0, indicating that the intrinsic fluctuations in all the reaction channels are independent of each other.

Cell-cycle reentry as simulated by our models

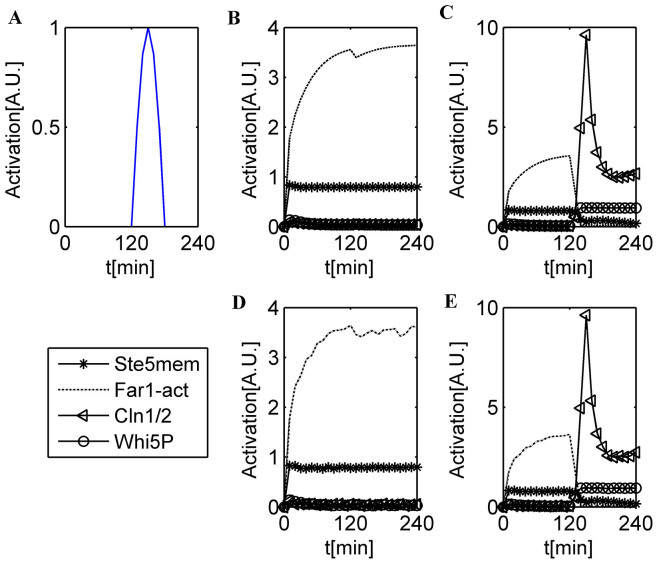
A recent experiment confirmed that for cell-cycle reentry from mating arrest, 64% ± 4% of nuclear Whi5 is required to be removed compared with 52% ± 3% for a cycling cell to progress through Start3. Here, we used a Cln1/2 signal pulse (sp) (Fig. 3 A) to simulate the exogenous Cln2 pulse used in biological experiments. In addition, the degradation rate of Far1act was set to 0 between 30 min and the end time of the exogenous Cln2 pulse to maintain a high Far1 expression level for the mating cells. Similar to Doncic's experimental design3, we varied the durations between 3 and 30 min to express variable amounts of exogenous Cln2 in our mathematical model. The simulation results are presented in Fig. 3 B–D. The pre-Start state cells can clearly commit reversibly to the post-Start state if appropriately treated. The relationship between the duration time of the Cln1/2 signal pulse and the maximum Whi5P value approximately 10 min after the end of the pulse (corresponding approximately to the time (5 min) it takes to inactivate the MET3 promoter30) is shown in Supplementary Fig. S2. The critical point that had the largest derivative in the dose-response curve had a critical Whi5P amount of 65.42%. This result agreed with the experimental result of 64% ± 4%.

Figure 3. Simulations of reentry and reversibility in cell fate selection.

Figure 3

Open in a new tab

(A) Time course of Cln1/2 signal pulse (sp). (B) The time course of a WT yeast cell when pheromone is added at 0 min in the ODE model. The duration is 3 min, and the cell fate remains in the mating program. (C) The time course of a WT yeast cell when pheromone is added at 0 min in the ODE model. The duration is 30 min, and the cell reenters the cell-cycle from the mating program. (D) The time course of a WT yeast cell when pheromone is added at 0 min in the CLE model. The duration is 3 min, and the cell remains in the mating program. (E) The time course of a WT yeast cell when pheromone is added at 0 min in the CLE model. The duration is 30 min, and the cell reenters the cell-cycle from the mating program.

Cell fates can be distinguished by the impulse of Cln1/2

Based on the experimental data, the histogram of WT yeast cells is shown in Supplementary Fig. S3. The histogram (the number of cells vs. the fraction of exported Whi5) indicates the number distribution of cells selecting different fates. The bin size of our histogram was set to 0.1. As mentioned in Ref. (2), the nuclear Whi5-GFP concentration was sufficient to predict cell fate in approximately 97% of WT G1 cells. Supplementary Fig. S3 shows that the number of cells possessing an arrest fate slightly increased as the fraction decreased from approximately 0.6 to 0.1 and that the number of cells committing increased as the fraction increased from approximately 0.6 to 1. It should be noted that this property was not captured by most of our numerical simulations. In the experiment, the cell fates of approximately 280 cells were observed, and the theoretical analysis was performed using the data of these 280 cells. Due to the lack of more experimental details, the concentrations of each protein in different cells were unclear. In addition, the study was focused on the coordination of intrinsic and extrinsic noises in cell fate decisions, and the initial concentration distribution would not change the roles that the noises play. Therefore, in our theoretical model, we considered the initial concentration of Whi5P from the different cells as a uniform distribution without loss of generality. However, this interesting property can also be reproduced by our simulation result if the initial concentrations of Whi5P for different cells are sampled from the probability distribution of concentrations in Fig. S3. The simulation result is shown in Supplementary Fig. S4.

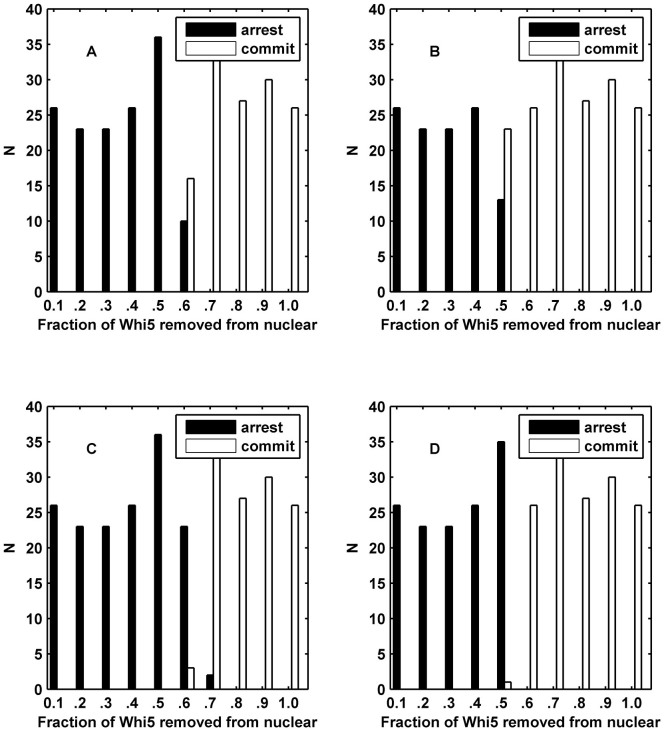
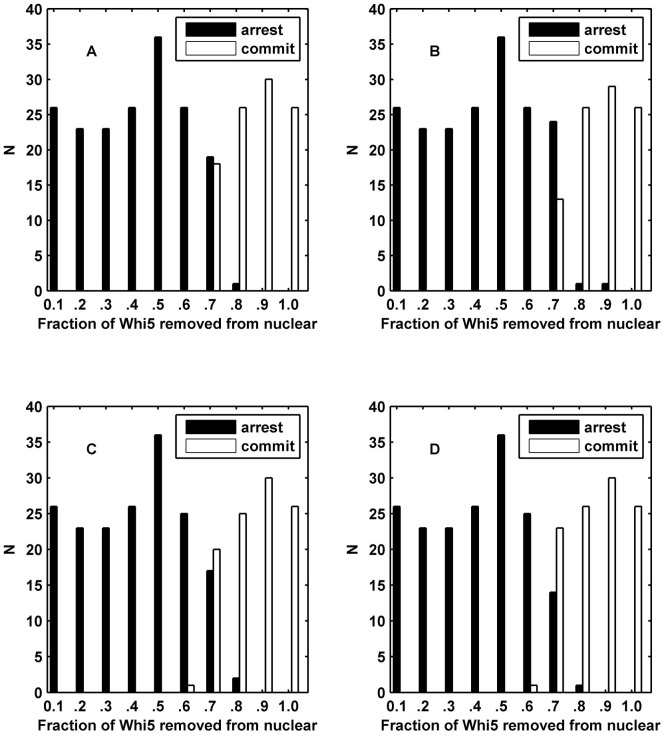
The histograms of the simulation results of the ODE model (Fig. 4 A and B) and CLE model (Fig. 4 C and D) are shown. Each cell is denoted by different random initial values in the pheromone environment. We utilized two numerical indexes to distinguish different cell fates in budding yeast. (i) In Fig. 4 A and C, we used the fraction of Whi5P after the G1 duration, i.e., the average fraction of Whi5P at 29.8–30 min, to identify different cell fates. If the amount of Whi5P from our model was larger than the critical amount of Whi5P at Start, the cell would commit; otherwise, the cell would arrest. (ii) In Fig. 4 B and D, the other numerical index was the impulse of Cln1/2 (See Methods) where the cell would commit if the impulse was larger than the critical impulse otherwise, the cell would arrest. The comparison between Fig. 4 A and Fig. 4 C (or Fig. 4 B and Fig. 4 D) revealed that the Whi5P index was inadequate to the intrinsic noise but that the impulse index benefitted from the fluctuations. Hence, under the perturbation of noise, the impulse of Cln1/2 can provide a reliable discrimination for cell fates due to the time integral of Cln1/2. In addition, the impulse of Cln1/2 enabled a more effective separation, with an accuracy of 99.17% (Fig. 4 D) compared with the fraction of Whi5P after the G1 duration. The accuracy of 99.17% was slightly better than the value of approximately 97% derived from the experimental data in Ref. (2). The histogram in Fig. 4 D conformed to the experiment results shown in Supplementary Fig. S3. The classification result validated our assumption that cell fates can be distinguished by the impulse of Cln1/2. This phenomenon suggests that the continuous operations of G1 cyclins, but not the instantaneous concentrations, determine the cell fates of yeast and clearly indicates that the impulse helps to decrease the uncertainty of cell fate at a molecular level. Therefore, the critical impulse of Cln1/2 was selected as the discrimination factor between mating and cell-cycle in the following sections. The results of R = 0.25 and R = 0.75 are shown in Supplementary Figs. S5 and S6. The result of R = 0.25 was similar to the uncorrelated result, but the higher correlation coefficient caused a competitive cell-cycle process. These results implied that the yeast cells adapted to the lower correlation between internal noises, which corroborated the logic of intrinsic noise generally being specific to any one gene. Therefore, the correlation coefficient of intrinsic noise R was set to 0 in the following sections.

Figure 4. Simulation histograms based on cell fate determined by the fraction of exported Whi5 at the time of pheromone addition.

Figure 4

Open in a new tab

N indicates the number of cells. (A) The cell fate is distinguished by Whi5P after G1 duration in the ODE model. (B) The cell fate is distinguished by the impulse of Cln1/2 in the ODE model. (C) The cell fate is distinguished by Whi5P after the G1 duration in the CLE model. (D) The cell fate is distinguished by the impulse of Cln1/2 in the CLE model showing a perfect threshold system. We set R = 0 for (C) and (D).

Large extrinsic noises and uncorrelated extrinsic noises disturb the separation of cell fates

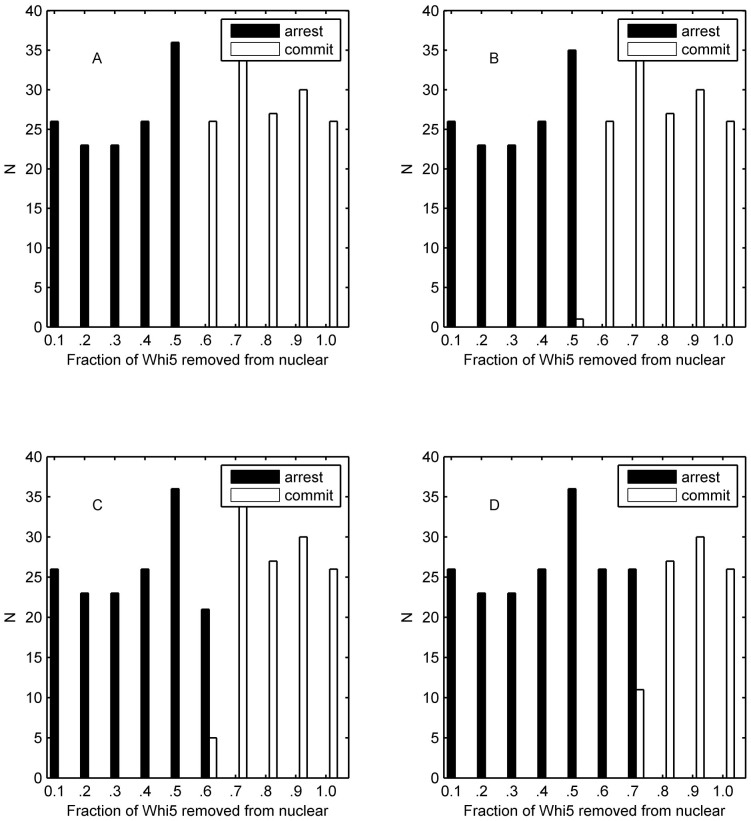
Extrinsic noise is common to genes of any one cell due to differences between cells, such as temperature and energy state31. When extrinsic noise is added, each parameter in the model is sampled from a Gaussian distribution with a mean equal to the listed value and a standard deviation equal to σ. The following three types of extrinsic noise were considered: (1) the extrinsic signal noise of the mating pathway, i.e., the extrinsic noise of pheromone introduced in the parameter of α(t) where the noise intensity of the signal in the mating pathway is denoted as σmating; (2) the extrinsic signal noise of the cell-cycle pathway considered in the parameter of a1, where the corresponding noise intensity is denoted with σcycle; and (3) the extrinsic noise of other biochemical reaction rates, where the noise intensity is marked with σbrc). And we would use ‘σ' to label the standard deviation of all types of extrinsic noise without causing ambiguity. We also considered the correlation between each extrinsic fluctuation. Here two cases were adopted to simplify the situation: correlation coefficient Rex is equal to 1 or 0. In Fig. 5, the correlation coefficient Rex was set to 1, and the noise intensity σ was set to 1 (the results of extrinsic the noise intensity of 0.1, 0.2 and 0.5 with Rex = 1 are shown in Supplementary Figs. S7–S9, respectively). When comparing Fig. 5 A, to Fig. 4 B, we found that the large extrinsic noise of the parameters would promote the competitiveness of mating pathway but fail in the separation of cell fates. If the large extrinsic signal noise of mating pathway was also taken into consideration, we found that the extrinsic noise of pheromone would promote the competitiveness of the mating program and disturb the separation of cell fates (Fig. 5 B). Fig. 5 C indicates that the large extrinsic noise of the cell-cycle pathway would enhance the competitiveness of the cell-cycle pathway but would not help the separation of cell fates. The result of all the extrinsic noises are shown in Fig. 5 D, it suggested that the large extrinsic signal noise of the cell-cycle pathway is more aggressive compared to the signal noise of the mating pathway with the same standard deviation.

Figure 5. Simulation histograms based on cell fate as determined by the fraction of exported Whi5 at the time of pheromone addition.

Figure 5

Open in a new tab

The cell fate is distinguished by the impulse of Cln1/2. (A) The result of the ODE model with extrinsic noise in the biochemical reaction parameters (σbrc = 1). (B) The result of the ODE model with extrinsic noise in the biochemical reaction parameters and the mating pathway signal (σbrc = 1 and σmating = 1). (C) The result of the ODE model with extrinsic noise in the biochemical reaction parameters and signal of the cell-cycle pathway (σbrc = 1 and σcycle = 1). (D) The result of the ODE model with extrinsic noise in the biochemical reaction parameters, the signal of the mating pathway and the signal of the cell-cycle pathway (σbrc = 1, σmating = 1 and σcycle = 1). Rex = 1 indicates that the correlation coefficient of the considered types of extrinsic noise equals 1.

The results of the correlation coefficient Rex = 0 and extrinsic noise intensity σ = 1 are illustrated in Supplementary Fig. S10 (the results of extrinsic noise intensity of 0.1, 0.2 and 0.5 with Rex = 0 are shown in Supplementary Figs. S11–S13). Supplementary Fig. S10 to Supplementary Fig. S13 suggested that uncorrelated extrinsic noises cause more misclassification and more cross-borders in different cell fates. These results suggested that cells can adapt to highly correlate extrinsic noises, and these results corroborated our general viewpoint that the origin of extrinsic noises, such as temperature, has a similar influence on each reaction channel. Therefore, the uncorrelated extrinsic noises will disrupt the cell fate decision due to the lack of adaptation to these noises. The correlation coefficient Rex was set to 1 in the following sections.

We then considered that the extrinsic signal noises in the cell-cycle and mating pathways have different strengths compared with noise in other biochemical reaction parameters. The results of the signal noise with intensities of 0.1 and 1 in addition to the noise in each reaction parameter with an intensity of 0.5 are shown in Supplementary Figs. S14 and S15. Figs. S9, S14 and S15 show that more cells became committed with greater strengths of extrinsic signal noise in the mating pathway and that the extrinsic signal noises played a more important role than the extrinsic noise of the reaction parameters. This property indicated that the extrinsic signal noises would greatly confuse the fate selection, and this confusion may result in the trigger role that the signals play.

In addition, we explored the role of the extrinsic signal noise without the extrinsic and intrinsic noises of the reaction parameters (detailed in Supplementary Figs. S16 and S17). Compared with each of the noises alone, we concluded that a small fluctuation in pheromone together with a relatively large fluctuation in the cell-cycle signal give rise to a higher performance in promoting the accuracy of fate selection.

Intrinsic noise and extrinsic noise play different roles in cell-fate selection

In this experiment, the intrinsic and extrinsic noises in yeast cell populations were integrated. At first, the system volume was set to 1000, and the effects of extrinsic signal noise were then examined. The results of the cell-cycle signal noise and the mating signal noise are shown in Supplementary Figs. S18 and S19. In contrast to the results shown in Fig. 4 D, the cell-fate selection depends almost entirely on intrinsic noise for a small extrinsic noise with a standard deviation of 0.1 and 0.2 (Supplementary Fig. S18 A and B; Supplementary Fig. S19 A and B). Supplementary Fig. S18 C and D as well as Supplementary Fig. S19 C and D illustrate that the selection of cell-fate was influenced by strong extrinsic noise. Furthermore, strong extrinsic noise in the mating signal caused a large decrease in the accuracy of fate decision (Supplementary Fig. S19 D). Previous studies have suggested that noise is dominated by intrinsic fluctuations at low expression levels. Thus, based on this conclusion, the results shown in Supplementary Figs. S18 and S19 confirmed that the extrinsic noise values were close to a well-delineated CVext less than 0.5, which was in agreement with previous studies31,32,33,34. In addition, the effects of intrinsic noise were studied for different system sizes (V = 10000, V = 1000, V = 100, and V = 10) with a fixed standard deviation of extrinsic noise. The corresponding histogram results with the fixed standard deviations of 0.1 and 1 for the extrinsic noise are plotted in Fig. 6 and Supplementary Fig. S20, respectively. Based on the observations above, increasing intrinsic fluctuations resulted in a parallel shift in the separation ratio of Whi5P, and the increasing extrinsic fluctuations led to the mixture of different cell fates. This result was consistent with the logic of extrinsic fluctuations being an unwelcome influencing factor while cells adopt the intrinsic fluctuations to decease the confusion in cell fates.

Figure 6. Simulation histograms based on cell fate as determined by the fraction of exported Whi5 at the time of pheromone addition.

Figure 6

Open in a new tab

The cell fate is distinguished by the impulse of Cln1/2, and extrinsic noise has a standard deviation σ = 0.1. The intrinsic noise has a standard deviation (A) 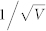Inline graphic ≈ 0.01 (V = 10000). (B) 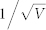Inline graphic ≈ 0.0316 (V = 1000). (C) 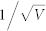Inline graphic ≈ 0.1 (V = 100). (D) Inline graphic ≈ 0.3162 (V = 10).

Extrinsic noise in Cln1/2-mediated phosphorylation of Whi5 plays an important role in the separation of cell fates

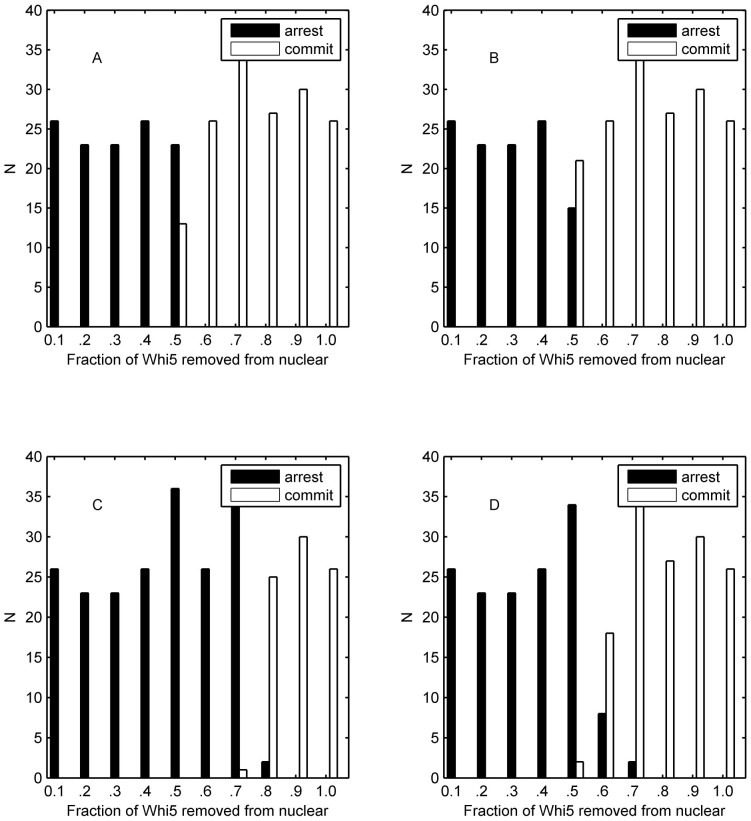
In this section, we focused our attention on the function of a single extrinsic or intrinsic noise. As mentioned above, extrinsic and intrinsic noises play different roles in the selection of cell fate, but it remains unknown which one (or ones) acts as the most important factor. As shown in Fig. 7, the extrinsic noise in k12 with both small and slightly large standard deviations benefitted the mating process (Fig. 7 A and B), but the noise with a larger standard deviation led to an orderless separation of cell fate (Fig. 7 C and D). However, extrinsic noises of other parameters (taking k10 as an example) will play a similar role even though the standard deviation was quite large as shown in Supplementary Fig. S21. Hence, our simulation results illustrated that only the extrinsic noise from k12 (a Michaelis constant) induced the mixture of different cell fates indicating that the extrinsic noise from the reaction of Cln1/2-mediated phosphorylation of Whi5 plays an important role in the separation of cell fates. This result suggested that a potential mechanism in decreasing the extrinsic noise of k12 is essential for budding yeast. In fact, this corresponding reaction of k12 (i.e., Cln1/2-mediated phosphorylation of Whi5) only occurs in the nucleus to reduce the extrinsic noise. The roles of single intrinsic noises in each reaction channel are presented in Supplementary Fig.S22. By numerical analysis, we classified all the reaction channels into two categories as follows: supporter of the mating pathway (resulting in more mating cells than Fig. 4 B) or cell-cycle program (resulting in more committed cells than Fig. 4 B). Interestingly, interaction between Cln1/2 and Far1act acted as the most important balance in the cell fate decision. It is clear that the intrinsic noise in the inhibition of Cln1/2 on Far1act belonged to the first three supporters of the mating program, and the inhibition of Far1act on Cln1/2 was the unique supporter of the cell-cycle program. It is well known that the interaction between Cln1/2 and Far1act is a crucial crosstalk between the cell-cycle and MAPK pathway. Our findings further verified that the noise from the crosstalk also contributes to the fate decision.

Figure 7. Simulation histograms based on cell fate as determined by the fraction of exported Whi5 at the time of pheromone addition.

Figure 7

Open in a new tab

The cell fate is distinguished by the impulse of Cln1/2, and only extrinsic noise in k12 is taken into consideration. (A) σ = 0.05. (B) σ = 0.1.(C) σ = 0.5. (D) σ = 1.

The linear interplay of intrinsic and extrinsic noises ensures a high accuracy of cell fate selection in budding yeast

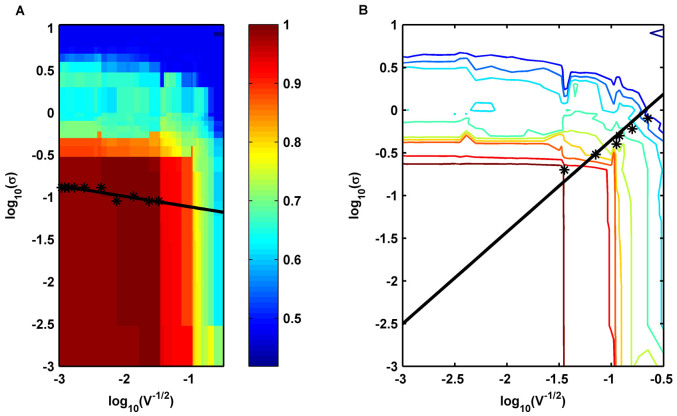
Furthermore, to quantitatively clarify the relationship between extrinsic and intrinsic noises, we proposed a formula to quantify the accuracy of cell fate selection (See Methods) and calculated Acc under different noises. The numerical results are shown in Fig. 8. Fig. 8 A shows that for small intrinsic noise, the accuracy of cell fate selections increased at first and then decreased with the increase of standard deviation of extrinsic noise. The result remained unchanged for small extrinsic noise when increasing the standard deviation of intrinsic noise. We also identified the point(s) with a maximum accuracy larger than 95% for each fixed intrinsic noise. The first three largest extrinsic noise strengths among these points for each fixed intrinsic noise were taken into consideration (only the largest one will be adopted if the total number of points is less than three). The average values of these three extrinsic noise strengths are marked with stars for each row in Fig. 8 A. Based on our analysis, these points were found to be approximated by the following straight line: y1 = −1.2391 − 0.1235x. The linear regression showed that it had the property of 0.8076 in the Pearson correlation coefficient suggesting that a proper strength of extrinsic and intrinsic noise near the straight line y1 helps to ensure a high accuracy in budding yeast cells. The contour lines of Fig. 8 A are shown in Fig. 8 B. The contour lines had the approximate right angle form. The stars in Fig. 8 B indicated the near edge points in each contour line, and these points can also be approximated by the following straight line: y2 = 0.7288 + 1.0769x. Therefore, the accuracy more likely depended on the intrinsic noise for the tuple 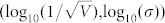Inline graphic under the line y2, and the accuracy was mainly determined by the extrinsic noise for the upper tuple 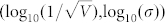Inline graphic. In addition, the cross point of these two straight lines was (−1.6394,−1.0366), which was close to the default noise strength of 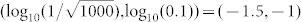Inline graphic obtained through the experiments. These results indicated that the noise strengths in wild type yeast cells contribute to ensure a high accuracy in fate selection as an inevitable consequence of intelligent evolution.

Figure 8. Selection accuracy in noisy environment.

Figure 8

Open in a new tab

(A) The accuracy as functions of the strength of extrinsic noise σ and intrinsic noise 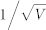Inline graphic. The average values of the three largest extrinsic noise strengths are marked with stars. The straight line y1 is obtained using linear regression. (B) The contour lines of the accuracy function shown in (A). The points with stars represent the near edge points in each contour line, and these data points are fitted well by a straight line y2.

Fluctuation range in entropy shows strong correlation with the cell fates

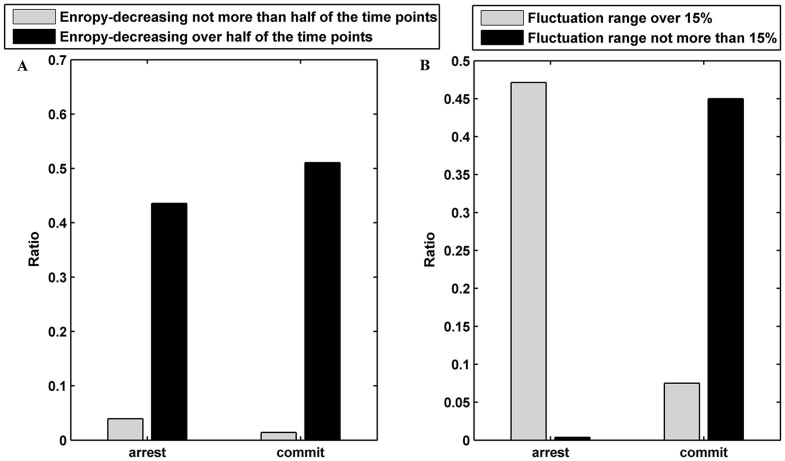
Network entropy exhibits dynamic changes in time course differentiation data, and it is in line with the cell fate stage35. We recorded the entropy of a yeast cell Y between 0 and 30 min every 0.01 min, and the entropy was represented by EY. The data were collected through the CLE model, and we set σ = 0.1 and V = 1000. For a yeast cell Y, we further computed the ratio of an entropy-decreasing time point, i.e., the time point where entropy is larger than the entropy of its following neighbor. The result is shown in Fig. 9, and it suggested that approximately 92.14% of the cells had more than 1500 entropy-decreasing time points. These results suggested that the cell fate selection program may be an entropy-decreasing process. Thus, we investigated if there were any differences in the fluctuation range between different cell fates. The fluctuation range for a yeast cell Y was defined as follows: 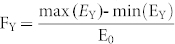Inline graphic, where E0 is the entropy of cell Y at 0 min. As observed in Fig. 9 B, the fluctuation range showed strong correlation with the cell fates (R = 0.8522 and p-value < 10−70). This result illustrated that the entropy of these cells selecting the mating fate was decreased significantly due to the input of pheromone information. However, these cells selecting cell-cycle fate shutdown the input of the mating signal and underwent a small fluctuation in entropy. This result was consistent with the theory of information entropy and negative entropy principle. In another way, the result suggests that the cell fate is determined by the impulse of Cln1/2 is somehow reasonable.

Figure 9. Cell fate and entropy.

Figure 9

Open in a new tab

(A) The fraction of entropy-decreasing cells for mating and cell-cycle fates. (B) The fraction of cells with an entropy fluctuation over or below 15% for mating and cell-cycle fates.

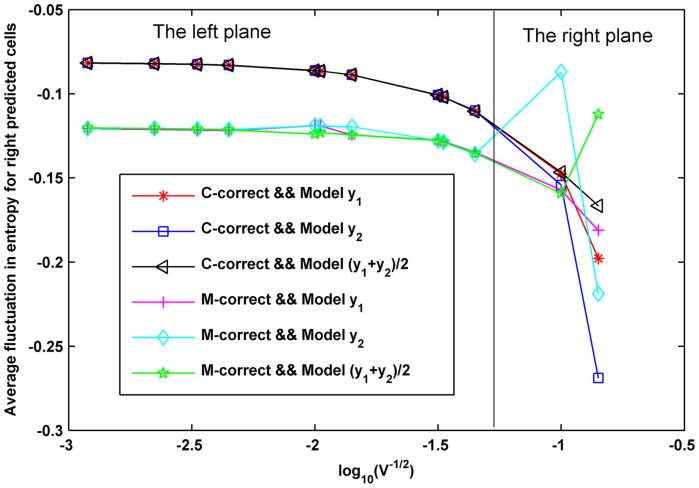
The correlations between entropy-decrease and cell fate for the CLE model with other tuples 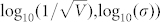Inline graphic characterized by the two linear relationships in Fig. 8 are shown in Supplementary Fig. S23. These results also suggested a great dependence between cell fate and the decrease of entropy, thereby indicating that a decrease in entropy can serve as a common rule for the selection of cell fate in budding yeast. In addition, the dependence of the average fluctuation in entropy for right predicted cells and the noise characterizing model was calculated and shown in Fig. 10. Fig. 10 shows that the accuracy decreased with an increase of 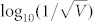Inline graphic according to the linear model y2. The high accuracy tuples 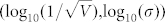Inline graphic characterized by model y1, model y2 as well as the combinatorial model of y1 and y2 (i.e., in the left plane) shared a sharp boundary in entropy fluctuation for different cell fates (the left plane) while low accuracy tuples suffered an unsharp boundary (the right plane). Thus, we conclude that cells in the high accuracy plane have smaller fluctuations and consistent differences in entropy decrease while the cells with low accuracy in the right plane have larger fluctuations and confused differences in entropy decrease, thereby suggesting that high accuracy results from both the sensitive decrease in entropy and the sharp boundary in entropy fluctuation.

Figure 10. The dependence of entropy decreasing and accuracy.

Figure 10

Open in a new tab

Here, C-correct indicates cells with more than 50% of the Whi5 removed from the nucleus, which are predicted to commit, and M-correct indicates cells with more than 50% of the Whi5 still in the nucleus, which are predicted to arrest.

Sensitivity analysis of the model parameters

In this section, the CLE model with σ = 0.1 and V = 1000 was used to perform the calculations. We perturbed each parameter with 10–30% variations. The results of the sensitivity analysis are presented in Table 2. The sensitivity analysis implied that a1 (the signal of the cell-cycle), k14 (Whi5–ICln1/2) and k11 (Whi5 + Cln1/2 → Whi5P) had relatively significant effects on Whi5P expression. The other parameters had a slight effect or almost no effect on Whi5P expression. These results demonstrated that the Start point was mainly dominated by the biochemical processes of Whi5. In addition, our model showed good dynamical robustness. Furthermore, we perturbed all of the parameters for 10%, 20% and 30%, and the simulated results indicated that the number of cells predicted to commit varied slightly with values of 12.24%, 12.59% and 7.14%, respectively.

Table 2. Sensitivity analysis of parameters in the CLE model.

Parameter (Pi) Reaction ΔPi = 10% ΔPi = 20% ΔPi = 30% Average
a1 The signal of Cell- Cycle 0.8231 0.8396 0.8790 0.8472
k14 Whi5 Inline graphic| Cln1/2 0.4450 0.4476 0.4512 0.4479
k11 Whi5 + Cln1/2 → Whi5P 0.2429 0.2440 0.2456 0.2442
k13 Whi5P → Whi5 0.0827 0.0827 0.0827 0.0827
k10 The degradation rate of Cln1/2 0.0746 0.0747 0.0747 0.0747
k8 Self-promoting rate of Cln1/2 0.0100 0.0100 0.0100 0.0100
others       <0.01  
Open in a new tab

Discussion

Despite considerable advances in the research of underlying mechanisms in cell fate decision, it has been largely unclear how individual cells make critical cell fate decisions in the presence of stochastic fluctuations in intracellular biochemical reactions and extracellular environments. The relative importance of intrinsic and extrinsic noises in cell fate decision also remains uncertain. We attempted to answer these questions with a simple theoretical model of the cell fate decision network responsible for cell-cycle commitment and mating arrest in budding yeast. Using ODE and CLE models, the combined effects of extrinsic and intrinsic noise on cell fate selection were clarified at a single cell level. As a driving factor of the Start point, the impulse of Cln1/2, which can effectively discriminate between different cell fates, was used to identify cell fates. In this study, we found that the uncorrelated extrinsic noises caused misclassification and cross-borders in different cell fates. Increasing intrinsic fluctuations gave rise to a parallel shift in the separation ratio of Whi5P, and increasing extrinsic fluctuations resulted in a mixture of different cell fates. Our investigation of the function of single extrinsic noise or intrinsic noise suggested that an effective method to decrease the extrinsic noise in the Michaelis constant of Cln1/2-mediated phosphorylation of Whi5 is required for budding yeast. Furthermore, our study indicated that the linear interplay of intrinsic and extrinsic noises contributes to a high accuracy of cell fate selection. It should be pointed out that the biochemical reaction network is highly nonlinear. Our key findings, i.e., that the approximate linear coordination between extrinsic and intrinsic noise may help cells transit more accurately from one fate to the other fate, were still a result of the nonlinear nature of biological processes. In addition, our study also suggested that the selection of cell fates is an entropy-decreasing process. We found that a large range of entropy-decreasing correlated with mating arrest and that a small range of entropy-decreasing was related to the fate of cell-cycle commitment.

The effects of noise on cell fate decision were quantitatively clarified by our theoretical model. Conventional scientific thinking has been that the random nature of such fluctuations within cells interferes with the reliable operation of biological systems. Our findings showed that the cells could still select the different cell fates due to the stochastic noise even if the cells had the same initial conditions. The coordination between extrinsic and intrinsic noise was beneficial by helping cells transform more accurately from one fate to another. Therefore, our work provides a new paradigm suggesting that cellular noise might have a constructive function in cell fate decision. In addition, by controlling the noise level within the yeast cells, we could prevent or prompt yeast cells to transition into a specific fate type by essentially tuning cellular behavior.

The budding yeast is a relatively well-studied example of a network with noisy environments. The cell-to-cell variability of the cell-fate decision system and the mating pheromone response pathway in yeast have been studied experimentally36. The quantitative output of the cell-fate decision system in response to the defined perturbations has been estimated. The mechanism that allows cells to respond more precisely to pheromones in the presence of a large variation has been provided. Furthermore, a combination of genetic elements, including pathway regulators, RNA-based transducers, constitutive promoters and pathway-responsive promoters, has been used to build modular network diverters37. Cell fate has been engineered through synthetic gene circuits, and cell fate determination has been measured through halo assays. Motivated by these experiments, it is expected that our theoretical results could be tested by natural and synthetic genetic circuits in individual cells in the future.

Our research presents a theoretical framework for cell fate decision in budding yeast and provides a clear investigation of the interaction between intrinsic and extrinsic noises. Understanding the mechanisms that increase the accuracy in cell-fate decision system might enable new therapeutic interventions. However, some problems should be discussed. First, the dynamics of a biological system can be modeled more accurately using a Markov jump process38,39,40. Exploring the Markov jump process of this decision-making system using the Gillespie algorithm41,42,43,44,45 may provide a molecular realization that is much closer to reality. Second, cellular transformations that involve a significant phenotypical change of the cell's state often use bistable biochemical switches as underlying decision systems10,44,45. Hence, the bistability and irreversibility of our simple model should be clarified. Third, the relationship between the accuracy of the cell fate and entropy-decreasing process is not studied. Our next task will be to analyze the change of entropy in the high accuracy region. Fourth, the regulatory mechanism to yield high accuracy of cell fate decision in large populations of cells is still poorly understood despite the underlying stochasticity36,46,47. The potential roles of positive feedback, feedforward, slow transcription and rapid phosphorylation in the reliable fate decision needs to be further analyzed3,48.

Methods

Mathematical models

To clarify the mechanism for selecting cell fates between cell-cycle commitment and mating arrest in a noisy environment, we presented two classes of mathematical models. First, based on mass action law and Michaelis–Menten kinetics, the dynamics of the regulation network of cell-cycle and pheromone-induced MAPK pathway presented in Fig. 1 C were characterized by a deterministic model, i.e., the ODE model. For simplification, the activities for total Ste5 and total Whi5 were assumed to be one unit. The parameters are listed in Table 1. We estimated these parameter values to reproduce the biological observations in budding yeast and the critical transition value for Start in the previous experiment simultaneously. To consider the effects of intrinsic noise, the corresponding CLE model based on the above ODE model was as follows:

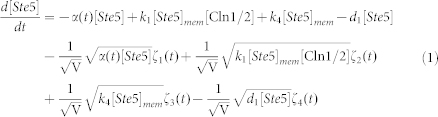graphic file with name srep05764-m1.jpg
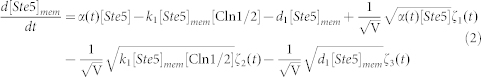graphic file with name srep05764-m2.jpg
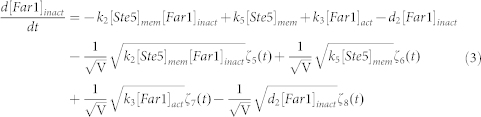graphic file with name srep05764-m3.jpg
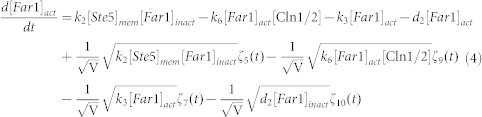graphic file with name srep05764-m4.jpg
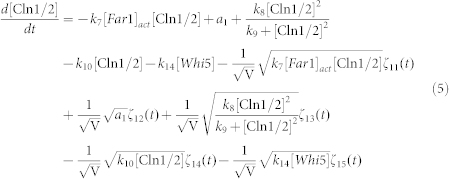graphic file with name srep05764-m5.jpg
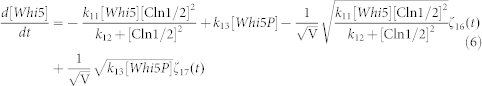graphic file with name srep05764-m6.jpg
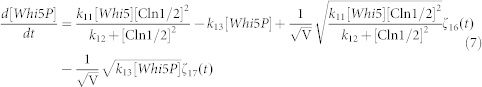graphic file with name srep05764-m7.jpg

where ζi(t) is Gaussian white noise, for i = 1, 2, 3,…,17, <ζi(t)> = 0, and for each i, j = 1, 2, 3,…,17,

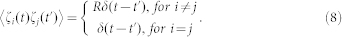graphic file with name srep05764-m8.jpg

here R is a constant number and V denotes the total number of molecules of each regulatory protein. Furthermore, when extrinsic noise was considered, each parameter pi in the model was sampled from a Gaussian distribution with a mean equal to the listed value and a standard deviation equal to σ, i.e., pi(1 + σεi(t)), here εi(t) is Gaussian white noise, <εi(t)> = 0, and for each i, j,

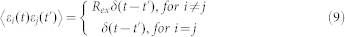graphic file with name srep05764-m9.jpg

where Rex = 1 indicates that the extrinsic noises we considered were correlated with each other; and Rex = 0 indicates that all these noises were independent.

The CLE model was solved with the Euler–Maruyama method49, and the temporal step size was set to 0.01 min. We simulated different yeast cells by stochastic initial values. Each cell had a set of random initial values. We obtained the initial concentration of Whi5P randomly at first, and the initial concentrations of the remained components are given according to the interactions in the simplified model. A. Doncic et al. compared the amount of Whi5-GFP exported to the largest value of nuclear Whi5-GFP within 30 min prior to pheromone exposure for each G1 cell. We recorded the amount of Whi5 exported, i.e., the stochastic initial value of Whi5P. Thus, we simulated the histograms based on cell fate through a theoretically defined cell fate.

Determination of the Start point

In yeast, the G1 checkpoint Start determines whether a cell enters the mitotic cycle or engages the mating program but never both because the aims of the two programs are diametrically opposed as follows: mating produces one cell from two; and mitosis produces two cells from one. Doncic et al. identified the main probe for the status of the Start trigger as the amount of Whi5 protein exported from the nucleus2. Our previous study showed the relationship between the activation of Whi5P (i.e., the proportion of Whi5 exported from the nucleus at 30 min calculated by our full ODE model) and the addition time of pheromone, and a critical point that had the largest derivative in the dose-response curve was defined to be the Start point. The Start point defined above was proven to be reasonable.

Impulse of cell fate

Because the cell fate can only be determined experimentally, the driving factor of Start must be defined if we want to trace back to the underlying mechanism. It is known that the G1 cyclins collaborate to drive yeast cells through the G1-S transition. According to classical mechanics, the impulse is the multiplication of the applied force and time interval equal to the change in momentum. Hence, the impulse will cause a change in mechanical motion of the particle. The impulse of Cln1/2, which was defined as the accumulation of Cln1/2 with time, was presented as follows:

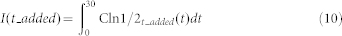graphic file with name srep05764-m10.jpg

The relationship between the Cln1/2 impulse and the addition time of pheromone was provided. The impulse of the point that had the largest derivative in addition time v.s. the proportion of exported Whi5 curve is further defined to be the critical impulse of cell fate. When a cell treated with the α-factor at 0 min was taken into consideration in our ODE or CLE model, the impulse of this cell was determined. We verified the assumption that the cell would commit if its impulse was larger than the critical impulse or otherwise arrest.

Entropy defined in our network

To further quantify the dynamics of the network, we provided a definition of the entropy E in this biochemical reaction network by extending the concept of entropy in statistical mechanics as follows:

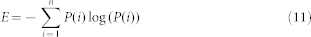graphic file with name srep05764-m11.jpg

where 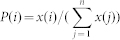Inline graphic is the distribution function of the proteins' concentration; x(i) denotes the concentration of the ith component, and n is the number of all components considered in the model (Here n = 7). From the viewpoint of evolutionary biology, the change of the entropy implies the evolution of the structure and function of a molecular network due to its adaptation ability.

Quantification of cell fate's accuracy

We observed that if the mating pheromone was applied to a cell when more than 50% of Whi5 was still in the nucleus, the cell almost always directly arrested, which is called pre-Start. If the mating pheromone was applied when more than 50% of nuclear Whi5 was removed, the cell almost always underwent one more mitotic cycle before arresting, which is called post-Start. Thus, the accuracy Acc can be defined as follows:

graphic file with name srep05764-m12.jpg

where NM-correct denotes the number of cells with more than 50% of the Whi5 still in the nucleus, which are predicted to arrest by our critical index; and NC-correct denotes the number of cells with more than 50% of the Whi5 removed from the nucleus, which are predicted to commit. The total number of cells in our model was set to 280, which was consistent with the average number of cells used by Doncic et al2.

Measure of sensitivity and robustness

Due to the lack of experimental data to determine all of the parameters, it was necessary to analyze the sensitivity of the system to changes of the parameters. Similar to the literature (4), each parameter was perturbed with 10–30% variations. The sensitivity function sj(t) of parameter Pj at time t was defined as follows:

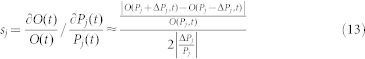graphic file with name srep05764-m13.jpg

where O(t) is the model output (Whi5P level) at time t; T is the total reaction time; ΔPj is a small perturbation; and 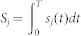Inline graphic is the sensitivity value of parameter Pj. In addition, we also perturbed all the parameters with 10–30% variations and measured the robustness as follows:

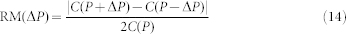graphic file with name srep05764-m14.jpg

where C(P) is the number of cells that are predicted to commit by our critical index for parameters P; and ΔP is a small perturbation of all the parameters.

Author Contributions

M.Y. and X.F.Z. designed the research; Y.K.L. performed computations; Y.K.L., M.Y. and X.F.Z. wrote the manuscript and all authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep05764-s1.pdf (910.7KB, pdf)

Acknowledgments

This work was supported by the Major Research Plan of the National Natural Science Foundation of China (No. 91230118 and No.91330113) and the National Natural Science Foundation of China (No.11275259 and No. 61173060).

References

  1. Furlong E. E. The Importance of Being Specified: Cell Fate Decisions and Their Role in Cell Biology. Mol. Biol. Cell 21, 3797–3798, DOI 10.1091/mbc.E10-05-0436 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Doncic A., Falleur-Fettig M. & Skotheim J. M. Distinct Interactions Select and Maintain a Specific Cell Fate. Mol. Cell 43, 528–539, DOI 10.1016/j.molcel.2011.06.025 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Doncic A. & Skotheim J. M. Feedforward Regulation Ensures Stability and Rapid Reversibility of a Cellular State. Mol. Cell 50, 856–868, DOI 0.1016/j.molcel.2013.04.014 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Li Y., Yi M. & Zou X. Identification of the Molecular Mechanisms for Cell-Fate Selection in Budding Yeast through Mathematical Modeling. Biophys. J. 104, 2282–2294 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cheong R., Rhee A., Wang C. J., Nemenman I. & Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science 334, 354–358 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Mugler A., Tostevin F. & ten Wolde P. R. Spatial partitioning improves the reliability of biochemical signaling. Proc. Natl. Acad. Sci. USA 110, 5927–5932 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Di Talia S., Skotheim J. M., Bean J. M., Siggia E. D. & Cross F. R. The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 448, 947–951 (2007). [DOI] [PubMed] [Google Scholar]
  8. Balazsi G., van Oudenaarden A. & Collins J. J. Cellular Decision Making and Biological Noise: From Microbes to Mammals. Cell 144, 910–925, DOI 10.1016/j.cell.2011.01.030 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Eldar A. & Elowitz M. B. Functional roles for noise in genetic circuits. Nature 467, 167–173, Doi 10.1038/Nature09326 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Losick R. & Desplan C. Stochasticity and cell fate. Science 320, 65–68, DOI 10.1126/science.1147888 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Raj A. & van Oudenaarden A. Nature, Nurture, or Chance: Stochastic Gene Expression and Its Consequences. Cell 135, 216–226, DOI 10.1016/j.cell.2008.09.050 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Acar M., Becskei A. & van Oudenaarden A. Enhancement of cellular memory by reducing stochastic transitions. Nature 435, 228–232, Doi 10.1038/Nature03524 (2005). [DOI] [PubMed] [Google Scholar]
  13. Maamar H., Raj A. & Dubnau D. Noise in gene expression determines cell fate in Bacillus subtilis. Science 317, 526–529, DOI 10.1126/science.1140818 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Suel G. M., Kulkarni R. P., Dworkin J., Garcia-Ojalvo J. & Elowitz M. B. Tunability and noise dependence in differentiation dynamics. Science 315, 1716–1719, DOI 10.1126/science.1137455 (2007). [DOI] [PubMed] [Google Scholar]
  15. Wernet M. F. et al. Stochastic spineless expression creates the retinal mosaic for colour vision. Nature 440, 174–180, Doi 10.1038/Nature04615 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Chambers I. et al. Nanog safeguards pluripotency and mediates germline development. Nature 450, 1230–1238, Doi 10.1038/Nature06403 (2007). [DOI] [PubMed] [Google Scholar]
  17. Li X. et al. Skin Stem Cell Hypotheses and Long Term Clone Survival - Explored Using Agent-based Modelling. Sci. Rep. 3, Doi 10.1038/Srep01904 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Zhang L., Lander A. D. & Nie Q. A reaction-diffusion mechanism influences cell lineage progression as a basis for formation, regeneration, and stability of intestinal crypts. BMC Syst. Biol. 6, Doi 10.1186/1752-0509-6-93 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zhang L. et al. Noise drives sharpening of gene expression boundaries in the zebrafish hindbrain. Mol. Sys. Biol. 8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Chou C.-S., Bardwell L., Nie Q. & Yi T.-M. Noise filtering tradeoffs in spatial gradient sensing and cell polarization response. BMC Syst. Biol. 5, 196 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zheng L., Chen M. & Nie Q. External noise control in inherently stochastic biological systems. J. Math. Phys. 53, 115616 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wang L., Xin J. & Nie Q. A critical quantity for noise attenuation in feedback systems. PLOS Comput. Biol. 6, e1000764 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. de Bruin R. A., McDonald W. H., Kalashnikova T. I., Yates III J. & Wittenberg C. Cln3 activates G1-specific transcription via phosphorylation of the SBF bound repressor Whi5. Cell 117, 887–898 (2004). [DOI] [PubMed] [Google Scholar]
  24. Skotheim J. M., Di Talia S., Siggia E. D. & Cross F. R. Positive feedback of G1 cyclins ensures coherent cell cycle entry. Nature 454, 291–296 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Gartner A. et al. Pheromone-dependent G1 cell cycle arrest requires Far1 phosphorylation, but may not involve inhibition of Cdc28-Cln2 kinase, in vivo. Mol. Cell. Biol. 18, 3681–3691 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Strickfaden S. C. et al. A mechanism for cell-cycle regulation of MAP kinase signaling in a yeast differentiation pathway. Cell 128, 519–531 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Garrenton L. S. et al. Nucleus-specific and cell cycle-regulated degradation of mitogen-activated protein kinase scaffold protein Ste5 contributes to the control of signaling competence. Mol. Cell. Biol. 29, 582–601 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Gillespie D. T. The chemical Langevin equation. J. Chem. Res. 113, 297 (2000). [Google Scholar]
  29. Kar S., Baumann W. T., Paul M. R. & Tyson J. J. Exploring the roles of noise in the eukaryotic cell cycle. Proc. Natl. Acad. Sci. USA 106, 6471–6476 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Charvin G., Cross F. R. & Siggia E. D. A microfluidic device for temporally controlled gene expression and long-term fluorescent imaging in unperturbed dividing yeast cells. PLOS one 3, e1468 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Stewart-Ornstein J., Weissman J. S. & El-Samad H. Cellular Noise Regulons Underlie Fluctuations in Saccharomyces cerevisiae. Mol. Cell. 45, 483–493 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Newman J. R. et al. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature 441, 840–846 (2006). [DOI] [PubMed] [Google Scholar]
  33. Raser J. M. & O'Shea E. K. Control of stochasticity in eukaryotic gene expression. Science 304, 1811–1814 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Taniguchi Y. et al. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 329, 533–538 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Banerji C. R. et al. Cellular network entropy as the energy potential in Waddington's differentiation landscape. Sci. Rep. 3, 3039 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Colman-Lerner A. et al. Regulated cell-to-cell variation in a cell-fate decision system. Nature 437, 699–706 (2005). [DOI] [PubMed] [Google Scholar]
  37. Galloway K. E., Franco E. & Smolke C. D. Dynamically Reshaping Signaling Networks to Program Cell Fate via Genetic Controllers. Science 341, 1235005 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Bettencourt L., Cintrón-Arias A., Kaiser D. I. & Castillo-Chavez C. The power of a good idea: Quantitative modeling of the spread of ideas from epidemiological models. Physica A, 364, 513–536 (2006). [Google Scholar]
  39. Higham D. J. Stochastic ordinary differential equations in applied and computational mathematics. IMA J. Appl. Math. 76(3), 449–474 (2011). [Google Scholar]
  40. Gillespie D. T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–55 (2007). [DOI] [PubMed] [Google Scholar]
  41. Gillespie D. T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 (1977). [Google Scholar]
  42. Wilkinson D. J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 10, 122–133 (2009). [DOI] [PubMed] [Google Scholar]
  43. Cardelli L. & Csikász-Nagy A. The cell cycle switch computes approximate majority. Sci. Rep. 2, 656 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Charvin G., Oikonomou C., Siggia E. D. & Cross F. R. Origin of irreversibility of cell cycle start in budding yeast. PLOS Biol. 8, e1000284 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Perkins T. J. & Swain P. S. Strategies for cellular decision-making. Mol. Sys. Biol. 5, 1 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Bassler B. L. Small talk: cell-to-cell communication in bacteria. Cell 109, 421–424 (2002). [DOI] [PubMed] [Google Scholar]
  47. Koyanagi M., Brandes R. P., Haendeler J., Zeiher A. M. & Dimmeler S. Cell-to-cell connection of endothelial progenitor cells with cardiac myocytes by nanotubes a novel mechanism for cell fate changes. Cir. res. 96, 1039–1041 (2005). [DOI] [PubMed] [Google Scholar]
  48. Kofahl B. & Klipp E. Modelling the dynamics of the yeast pheromone pathway. Yeast 21, 831–850 (2004). [DOI] [PubMed] [Google Scholar]
  49. Higham D. J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43, 525–546 (2001). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep05764-s1.pdf (910.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES