Sparse Additive Ordinary Differential Equations for Dynamic Gene Regulatory Network Modeling

Summary

The gene regulation network (GRN) is a high-dimensional complex system, which can be represented by various mathematical or statistical models. The ordinary differential equation (ODE) model is one of the popular dynamic GRN models. High-dimensional linear ODE models have been proposed to identify GRNs, but with a limitation of the linear regulation effect assumption. In this article, we propose a sparse additive ODE (SA-ODE) model, coupled with ODE estimation methods and adaptive group LASSO techniques, to model dynamic GRNs that could flexibly deal with nonlinear regulation effects. The asymptotic properties of the proposed method are established and simulation studies are performed to validate the proposed approach. An application example for identifying the nonlinear dynamic GRN of T-cell activation is used to illustrate the usefulness of the proposed method.

1. Introduction

The gene regulatory network (GRN) is a complex system associated with biological activities at the cellular level, such as cell growth, division, development, and response to environmental stimulus (Carthew and Sontheimer, 2009), which should be modeled in a dynamic way (Hecker et al., 2009). The new high-throughput technologies such as DNA microarray and next generation RNA-Seq enable us to observe the dynamic features of gene expression profiles in a genome scale. In particular, the time course gene expression data collected from these new technologies allow investigators to study gene regulatory networks from a dynamic point of view in more details. Currently, several models have been proposed for GRN construction, such as information theory models (Steuer et al., 2002;Stuart et al., 2003); Boolean networks (Kauffman, 1969; Thomas, 1973; Bornholdt, 2008); Bayesian Networks (Heckerman, 1996; Imoto et al., 2003; Needham et al., 2007; Werhli and Husmeier, 2007); latent variable models (Shojaie and Michailidis, 2009); and other regression models (Kim et al., 2009).

In particular, many popular models have been proposed for inferring gene regulatory networks using time course gene expression data. For examples, dynamic Boolean networks and probabilistic Boolean networks (Liang et al., 1998; Akutsu et al., 2000; Shmulevich et al., 2002; Martin et al., 2007), dynamic Bayesian networks (Murphy and Mian, 1999; Friedman et al., 2000; Hartemink et al., 2001; Zou and Conzen, 2005; Song et al., 2009), vector autoregressive and state space models (Hirose et al., 2008; Kojima et al., 2009; Shimamura et al., 2009); and differential equation models (Voit, 2000; Holter et al., 2001; DeJong, 2002; Yeung et al., 2002). Especially Xing and his associates have recently introduced temporal exponential random graph models and time-varying networks to capture dynamics of networks (Hanneke and Xing, 2006; Guo et al., 2007; Kolar et al., 2010). Most of these dynamic network models such as dynamic Bayesian networks and random graph models require extensive computations for posterior inference, which only allow us to deal with small networks. Song et al. (2009) also introduced a time-varying dynamic Bayesian network to model structurally varying directed graphs. Gupta et al. (2007) proposed a hierarchical hidden Markov regression model for determining gene regulatory networks from gene expression microarray data, which also allows for covariate effects varying between states and gene clusters varying over time. Furthermore, Gupta and Ibrahim (2007) introduced a hierarchical regression mixture model to combine gene clustering and motif discovery in an unified framework, in which a Monte Carlo method was used for simultaneous variable selection (for motifs) and clustering (for time course gene expression data). Shojaie et al. (2012) recently proposed an adaptive thresholding estimate under the framework of graphical Granger causality for reconstructing regulatory networks from time-course gene expression data.

In this paper we focus on ordinary differential equation (ODE) models for dynamic GRN construction. The ODE approach models the dynamic change of a gene expression (the derivative of the expression) as a function of expression levels of all related genes. So the dynamic feature of the GRN is automatically and naturally quantified. Both positive and negative as well as the feedback effects of gene regulations can be appropriately captured by the ODE model in a systematic way. A general ODE model for GRNs can be written as:

$$\mathit{X}\prime (t)=\mathit{F}(t,\mathit{X}(t),\mathit{\theta }),$$ (1.1)

where t ∈ [t₀, T] (0 ≤ t₀< T < ∞) is time, X(t) = (X₁(t), ⋯, X_p (t))^T is a vector representing the gene expression level of gene 1, ⋯, p at time t and X′(t) is the first order derivative of X(t). F serves as the link function that quantifies the regulatory effects of regulator genes on the expression change of a target gene which depends on a vector of parameters θ. In general F can take any linear or nonlinear functional forms. Many GRN models are based on linear ODEs due to its simplicity. Lu et al. (2011) proposed using the following linear ODEs for dynamic GRN identification and applied the SCAD approach for variable selection,

$$X_k^{\prime }(t)=\sum _{j=1}^p{\theta }_{kj}{X}_j(t),k=1,2,\cdots ,p,$$ (1.2)

where parameters θ = {θ_kj}_{k,j=1, ⋯, p} quantify the regulations and interactions among the genes in the network. In practice, however, there is little a priori justification for assuming that the effects of regulatory genes take a linear form. Thus, the linear ODE models may be very restrictive for practical applications. In fact, nonlinear parametric ODE models have been proposed for gene regulatory networks (Weaver et al., 1999; Sakamoto and Iba, 2001; Spieth et al., 2006), but the variable selection (network edge identification) problem for high-dimensional nonlinear ODEs has not been addressed. In this paper, we intend to extend the high-dimensional linear ODE models in Lu et al. (2011) to a more general additive nonparametric ODE model for modeling high-dimensional nonlinear GRNs:

$$X_k^{\prime }(t)={\mu }_k+\sum _{j=1}^p{f}_{kj}(X_j(t)),k=1,2,\cdots ,p,$$ (1.3)

where μ_k is an intercept term and f_kj (·) is a smooth function to quantify the nonlinear relationship among related genes in the GRN. Based on the sparseness principle of gene regulatory networks and other biological systems, we usually assume that the number of significant nonlinear effects, f_kj (·), is small for each of the p variables (genes), X_k, although the total number of variables (genes), p, in the network may be large. Thus, we refer to model (1.3) as the sparse additive ODE (SA-ODE) model. Also we assume that the measurements of gene expression for the kth gene are obtained at multiple time points, t_i, i = 1, ⋯, n, that is,

$$Y_k(t_i)=X_k(t_i)+{\epsilon }_k(t_i),k=1,2,\cdots ,p,$$ (1.4)

where the measurement errors ε_k(t_i) (i = 1, ⋯, n) are assumed to be i.i.d. with mean zero and variance ${\sigma }_k^2(0<{\sigma }_k^2<\infty )$. The challenging question is how to perform model selection for the nonparametric SA-ODE model (1.3) under the assumption of sparsity constraints on the index set {j : f_kj (·) ≠ 0} of functions f_kj (·) that are not identically zero.

There exist several classes of parameter estimation methods for ODE models, which include the nonlinear least squares method (NLS) (Hemker, 1972; Bard, 1974; Li et al., 2005; Xue et al., 2010), the two-stage smoothing-based estimation method (Varah, 1982; Brunel, 2008; Chen and Wu, 2008a,b; Liang and Wu, 2008; Wu et al., 2012), the principal differential analysis (PDA) and its extensions (Ramsay, 1996; Heckman and Ramsay, 2000; Ramsay and Silverman, 2005; Poyton et al., 2006; Ramsay et al., 2007; Varziri et al., 2008; Qi and Zhao, 2010) and the Bayesian approaches (Putter et al., 2002; Huang et al., 2006; Donnet and Samson, 2007). Among these methods, we are more interested in the two-stage smoothing-based estimation method, where in the first stage, a nonparametric smoothing approach is used to obtain the estimates of both the state variables and their derivatives from the observed data, and then in the second stage, these estimated functions are plugged into the ODEs to estimate the unknown parameters using a formulated pseudo-regression model. In particular, the two-stage smoothing-based estimation method avoids numerically solving the differential equations directly and does not need the initial or boundary conditions of the state variables. This method also decouples the high-dimensional ODEs to allow us to perform variable selection and parameter estimaion for one equation at a time (Voit and Almeida, 2004; Jia et al., 2011; Lu et al., 2011). These good features of the two-stage smoothing-based estimation method in addition to its computational efficiency greatly outweigh its disadvantage in a small loss of estimation accuracy in dealing with high-dimensional nonlinear ODE models (Lu et al., 2011).

In the past two decades, there has been much work on penalization methods for variable selection and parameter estimation for high-dimensional data, including the bridge estimator (Frank and Friedman, 1993); the least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996) and its extensions, such as the adaptive LASSO (Zou, 2006), the group LASSO (Yuan and Lin, 2006) and the adaptive group LASSO (Wang and Leng, 2008); the smoothly clipped absolute deviation (SCAD) penalty (Fan and Li, 2001); the elastic net (Zou and Hastie, 2006) among others. Recently, the LASSO approach has been applied to high-dimensional nonparametric sparse additive (regression) models to perform variable selection and parameter estimation simultaneously (Meier et al., 2009; Ravikumar et al., 2009; Huang et al., 2010; Cantoni et al., 2011). In this paper, we propose to couple the ideas of the two-stage smoothing-based estimation method and the high-dimensional variable selection techniques to perform variable selection and nonparametric function estimation for the proposed SA-ODE model (1.3). However, this is not just to trivially combine the two ideas, instead we have to tackle several critical challenges, which include: 1) the two-stage smoothing-based estimation method allows us to convert our nonparametric SA-ODE model into a pseudo-sparse additive regression model where the covariates and the response variables are derived from nonparametric smoothing estimates of the ODE state variables and their derivatives (instead of direct observed data); 2) the resulting errors in the pseudo-sparse additive regression model are not i.i.d., but dependent; and 3) the number of covariates, p, in the SA-ODE models is usually large (maybe greatly larger than the sample size). Thus, it is not trivial to establish the theoretical properties for the proposed method. To the best of our knowledge, this is the first attempt to propose a variable selection method for a high-dimensional nonparametric ODE model, and it is also the first time to establish the theoretical results for the penalized estimators for ODE models under the “large p, small n” setting.

The remainder of this paper is organized as follows. In Section 2, we propose a five-step variable selection procedure for the SA-ODE model (1.3). In Section 3, the theoretical properties of the proposed method are established in the “large p, small n” setting. In Section 4, we present some simulation results to validate the proposed method. To illustrate the usefulness of the proposed methods, we apply the proposed method to identify a dynamic gene regulatory network based on time course gene expression data from a T-cell activation study in Section 5. We conclude the paper with some remarks in Section 6. The detailed technical proofs are given in the Appendix.

2. Pseudo-Sparse Additive Model and Variable Selection

In this section, we propose a five-step variable selection procedure for the SA-ODE model (1.3). In Step I, we use one of the nonparametric smoothing approaches to estimate both the ODE state variables and their derivatives based on the measurement model (1.4). In Step II, we use spline functions to approximate each of the nonparametric additive components in the SA-ODE model (1.3), and then substitute the estimated state variables and their derivatives from Step I into the SA-ODE model (1.3) to form a ‘pseudo’ sparse additive model. In Step III, we apply the group LASSO approach to obtain an initial estimator and reduce the dimension of the problem. In Step IV, we apply the adaptive group LASSO approach (Wang and Leng, 2008; Huang et al., 2010) for component selection, which combines ideas from the adaptive LASSO (Zou, 2006) and the group LASSO (Yuan and Lin, 2006). In Step II, we usually use a larger number of basis functions to approximate the nonparametric functions and some of these basis functions may not be necessary. In Step V, we propose to use the regular LASSO again to the selected model from Step IV to further shrink some of the coefficients of B-spline basis to zero so that we can obtain a more parsimonious model at the end.

Step I. Nonparametric Smoothing

First we apply one of nonparametric smoothing approaches such as smoothing splines, regression splines, penalized splines or local polynomial to estimate the state variables and their derivatives, X_k (t) and $X_k^{\prime }(t)$ based on model (1.4). In this paper, we adopt the penalized splines (Ruppert et al., 2003; Li and Ruppert, 2008; Claeskens et al., 2009; Wu et al., 2012) to obtain the estimates, X̂_k (t) and ${\mathrm{X̂}}_k^{\prime }(t)$, k = 1, ⋯, p. That is, approximate X_k (t) one by one for 1 ≤ k ≤ p by $X_k(t)\approx {\sum }_{j=-\nu }^{K_k}{\delta }_{k,j}{N}_{k,j,\nu +1}(t)={\mathbf{N}}_{k,\nu +1}^T(t){\mathbf{\delta }}_k$, where δ_k = (δ_k,−ν, ⋯, δ_k,Kk)^T is the unknown coefficient vector to be estimated from the data, and N_k,ν+1(t) = {N_k,−ν,ν+1(t), ⋯, N_k,Kk,ν+1(t)}^T is the B-spline basis function vector of degree ν and dimension K_k + ν + 1 at a sequence of knots t₀ = τ_k,−ν = τ_k,−ν+1 = ⋯ = τ_k,−1 = τ_k,0 < τ_k,1 < ⋯ < τ_k,Kk < τ_k,Kk+1 = τ_k,Kk+2 = ⋯ = τ_k,Kk+ν+1 = T on [t₀, T] (Schumaker, 1981). Define n × (K_k + ν + 1) matrix N_k = {N_k,ν+1(t₁), ⋯, N_k,ν+1(t_n)}^T, Y_k = (Y_k (t₁), ⋯, Y_k (t_n))^T and let ${\mathbf{V}}_k={\int }_{t_0}^T[{\mathbf{N}}_{k,\nu +1}^{″}(t)]{[{\mathbf{N}}_{k,\nu +1}^{″}(t)]}^{T}dt$. The penalized spline (P-spline) objective function contains a penalized sum of squared differences with a penalized term by the integrated squared second order derivative of the spline function as

$$L_k({\mathit{\delta }}_k;{\lambda }_k)={({\mathbf{Y}}_k-{\mathbf{N}}_k{\mathit{\delta }}_k)}^T({\mathbf{Y}}_k-{\mathbf{N}}_k{\mathit{\delta }}_k)+{\lambda }_k{\mathit{\delta }}_k^T{\mathbf{V}}_k{\mathit{\delta }}_k.$$ (2.1)

The minimizer of (2.1) takes the form ${\mathbf{\delta ̂}}_k={({\mathbf{N}}_k^T{\mathbf{N}}_k+{\lambda }_k{\mathbf{V}}_k)}^{-1}{\mathbf{N}}_k^T{\mathbf{Y}}_k$. Then we have

$${\mathrm{X̂}}_k(t)={\mathbf{N}}_{k,\nu +1}^T(t){\mathit{\delta ̂}}_k,{\mathrm{X̂}}_k^{\prime }(t)={[{\mathbf{N}}_{k,\nu +1}^{\prime }(t)]}^T{\mathit{\delta ̂}}_k.$$ (2.2)

From de Boor (2001), the derivatives of spline functions can be simply expressed in terms of lower order spline functions, then we can obtain the explicit expressions of ${\mathbf{N}}_{k,\nu +1}^{\prime }(t)$ and ${\mathbf{N}}_{k,\nu +1}^{″}(t)$. To determine λ_k, we use the standard generalized cross validation (GCV) method (Craven and Wahba, 1979). Note that, if the longitudinally replicate data are available (see our application example in Section 5), the nonparametric mixed-effects smoothing methods can be used in this step in order to obtain better smoothing results (Wu and Zhang, 2006; Lu et al., 2011).

Step II. Pseudo-Sparse Additive Models

In this step, we propose a method to identify significant functions in model (1.3) using a high-dimensional variable selection technique, the group LASSO. First, following the idea similar to Varah (1982); Brunel (2008); Chen and Wu (2008a,b); Liang and Wu (2008);Wu et al. (2012), we substitute the estimated state variables X̂_k (t) and their derivatives ${\mathrm{X̂}}_k^{\prime }(t)$ into ODE model (1.3) to form the following pseudo-sparse additive (PSA) model:

$$H_{ki}={\mu }_k+\sum _{j=1}^p{f}_{kj}({\mathrm{X̂}}_{ji})+{\Upsilon }_{ki},k=1,2,\cdots ,p,i=1,2,\dots ,n,$$ (2.3)

where $H_{ki}={\mathrm{X̂}}_k^{\prime }(t_i)$ and X̂_ji = X̂_j (t_i), ϒ_ki is the sum of measurement errors and estimation errors of ${\mathrm{X̂}}_k^{\prime }(t)$ and X̂_k (t) from Step I. In model (2.3), the response variables and the covariates are derived from the nonparametric smoothing estimates of the state variables and their derivatives, respectively. Moreover, the resulting error terms ϒ_ki are not i.i.d., but dependent. Thus this is not a standard sparse additive regression model studied in the literature (Meier et al., 2009; Ravikumar et al., 2009; Huang et al., 2010; Cantoni et al., 2011). That is why we call it as a ‘pseudo’ sparse additive (PSA) model. Since X̂_k (t) and ${\mathrm{X̂}}_k^{\prime }(t)$ in the above model are estimated continuously at any time point t from Step I, we may augment more time points than the original observation times for the next step analysis. In fact, other investigators (D’Haeseleer et al., 1999; Wessels et al., 2001; Bansal et al., 2006) have used this data augmentation strategy for ODE parameter estimation. We adopt a similar idea here.

Remark 1. Decoupled property. Note that the substitution approach in model (2.3) allows us to decouple the p-dimensional ODE model into p one-dimensional ODEs independently (Voit and Almeida, 2004; Jia et al., 2011; Lu et al., 2011), so that we can deal with the variable selection problem for these ODEs one by one separately. This is a unique feature of the two-stage smoothing-based estimation method for ODEs (Varah, 1982; Brunel, 2008; Chen and Wu, 2008a,b; Liang and Wu, 2008; Wu et al., 2012).

We adopt a similar idea from Huang et al. (2010) and apply truncated series expansions with B-spline bases to approximate the additive components in model (2.3). Let t₀ = ξ₀ < ξ₁ < ⋯ < ξK_n < ξ_Kn+1 = T be a partition of the interval [t₀, T], where K_n = O(n^ϖ) (0 < ϖ < 0.5) is a positive integer such that max_0≤m≤Kn |ξ_m+1 − ξ_m| = O(n^−ϖ). Let 𝒮_n be the space of polynomial splines on [t₀, T] of degree l ≥ 1 consisting of functions s satisfying: (i) s is a polynomial of degree l on the subintervals I_m = [ξ_m, ξ_m+1), m = 0, ⋯, K_n − 1 and I_Kn = [ξ_Kn, ξ_Kn+1]; (ii) for l ≥ 2 and 0 ≥ l^′ ≤ l − 2, s is l^′ times continuously differentiable on [t₀, T]. Then there exists a normalized B-spline basis {ϕ_m, 1 ≤ m ≤ m_n} on [t₀, T] for 𝒮_n, where m_n ≡ K_n + l such that, for any $f_{kj}^{*}\in {𝒮}_n$, it can be expressed

$$f_{kj}^{*}(x)=\sum _{m=1}^{m_n}{\beta }_{kjm}{\varphi }_m(x),k,j=1,2,\cdots ,p,$$ (2.4)

where β_kjm are spline coefficients. Here we propose to conservatively choose the number of basis functions, m_n, as large as possible (more than enough or under-smoothing). Note that it is computationally prohibited to select different $m_n^{\prime }\mathrm{s}$ for different functions f_kj (·) when p is large. To deal with this problem, we will re-apply the LASSO approach to shrink unnecessary basis coefficients into zero in Step V. Replacing f_kj by its B-spline approximation in (2.4), model (2.3) can be expressed as

$$H_{ki}={\mu }_k+\sum _{j=1}^p\sum _{m=1}^{m_n}{\beta }_{kjm}{\varphi }_m({\mathrm{X̂}}_{ji})+{\Upsilon }_{ki}^{*},k=1,\cdots ,p,i=1,\cdots ,n,$$ (2.5)

where ${\Upsilon }_{ki}^{*}$ is the sum of ϒ_ki and the approximation errors of the additive regression functions by splines. Let β_kj = (β_kj1, ⋯, β_kjmn)^T (k, j = 1, ⋯, p) and ${\mathit{\beta }}_k={({\mathit{\beta }}_{k1}^T,\cdots ,{\mathit{\beta }}_{kp}^T)}^T$. Then we have p groups of parameters and our purpose is to select non-zero groups, i.e., nonzero β_kj, k, j = 1, ⋯, p.

Step III. Group LASSO

For model (1.3), we need a constraint to deal with unidentifiability problem, i.e., Ef_kj (X_j (t)) = 0 (j = 1, ⋯, p). Thus, for model (2.5), we impose the constraints ${\sum }_{i=1}^n{\sum }_{m=1}^{m_n}{\beta }_{kjm}{\varphi }_m({\mathrm{X̂}}_{ji})=0,1\le j\le p$. We may also use the centralization of the response and the basis functions to remove the restrictions. Let ${\mathrm{\varphi ̅}}_{jm}=\frac{1}{n}{\sum }_{i=1}^n{\varphi }_m({\mathrm{X̂}}_{ji})$ and ψ_m(x) ≡ ψ_jm(x) = ϕ_m(x) − ϕ̄_jm. Write Z_ij = {ψ₁(X̂_ji),⋯ ψ_mn(X̂_ji)}^T, Z_j = (Z_1j, ⋯, Z_nj)^T, and Z = (Z₁, ⋯,Z_p). Let ${\mathrm{H̄}}_k=\frac{1}{n}{\sum }_{i=1}^n{H}_{ki}$ and H_k = (H_k1 − H̄_k, ⋯, H_kn − H̄_k)^T. Similar to Brunel (2008) and Wu et al. (2012), a weight function with boundary restrictions should be imposed in order to achieve a better convergence rate for parameter estimation. Let D_k1 = diag{d_k1(t₁), ⋯, d_k1(t_n)}, D_k2 = diag{d_k2(t₁), ⋯, d_k2(t_n)} and D_k3 = diag{d_k3(t₁), ⋯, d_k3(t_n)}, where d_k1(t), d_k2(t) and d_k3(t) are prescribed non-negative weight functions on [t₀, T] with boundary conditions d_k1(t₀) = d_k1(T) = 0, d_k2(t₀) = d_k2(T) = 0 and d_k3(t₀) = d_k3(T) = 0. More discussions on how to select the weight function can be found in Brunel (2008) and Wu et al. (2012). With these notations, we can obtain the group LASSO estimator β̃_k by minimizing the following penalized weighted least squares criterion,

$$L_{k1}({\mathit{\beta }}_k;{\lambda }_{k1})={({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)+{\lambda }_{k1}\sum _{j=1}^p{\Vert {\mathit{\beta }}_{kj}\Vert }_2,$$ (2.6)

where λ_k1 is a penalty parameter, which can be determined by BIC or EBIC (Chen and Chen, 2008). Here we have dropped μ_k in the arguments of L_k1 with the centering μ̂_k = H̄_k. Based on the group LASSO estimator β̃_k, we can also obtain the estimates of the nonparametric functions, ${\mathrm{f̃}}_{kj}(x)={\sum }_{m=1}^{m_n}{\mathrm{\beta ̃}}_{kjm}{\psi }_m(x)$, 1 ≤ j ≤ p.

Step IV. Adaptive Group LASSO

The above group LASSO penalty treats coefficients from each group equally which is not optimal. In order to allow different amounts of shrinkage for different coefficients, an adaptive group LASSO is necessary. In this step, we perform the adaptive group LASSO based on the results from Step III by setting $w_{kj}={\Vert {\mathit{\beta ̃}}_{kj}\Vert }_2^{-1}$ if ‖β̃_kj‖₂ > 0, otherwise w_kj = ∞. Then we obtain the adaptive group LASSO estimator β̂_k by minimizing the penalized weighted least squares criterion,

$$L_{k2}({\mathit{\beta }}_k;{\lambda }_{k2})={({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)}^T{\mathbf{D}}_{k2}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)+{\lambda }_{k2}\sum _{j=1}^p{w}_{kj}{\Vert {\mathit{\beta }}_{kj}\Vert }_2$$ (2.7)

with a penalty parameter λ_k2, which can also be determined by BIC or EBIC (Chen and Chen, 2008). Then we obtain the adaptive group LASSO estimates of μ_k and f_kj, ${\mathrm{\mu ̂}}_k={\mathrm{H̄}}_k\equiv \frac{1}{n}{\sum }_{i=1}^n{H}_{ki}$ and ${\mathrm{f̂}}_{kj}(x)={\sum }_{m=1}^{m_n}{\mathrm{\beta ̂}}_{kjm}{\psi }_m(x)$, 1 ≤ j ≤ p.

Step V. Regular LASSO for Shrinking Basis Coefficients

In Step II, we approximate each of the nonparametric functions in the pseudo-sparse additive model intentionally using a larger number of basis functions (under-smoothing). Thus, some of these basis functions may not be necessary. In this step, we re-apply the regular LASSO or adaptive LASSO to the final model selected from the adaptive group LASSO in Step IV to shrink the coefficients of unnecessary basis functions into zero so that we can obtain a final parsimonious model. The minimization criterion for the adaptive LASSO is

$$L_{k3}({\mathit{\beta }}_k;{\lambda }_{k3})={({\mathbf{H}}_k^{(s)}-{\mathbf{Z}}^{(s)}{\mathit{\beta }}_k)}^T{\mathbf{D}}_{k3}({\mathbf{H}}_k^{(s)}-{\mathbf{Z}}^{(s)}{\mathit{\beta }}_k)+{\lambda }_{k3}\sum _{j=1}^s\sum _{m=1}^{m_n}{w}_{kjm}|{\beta }_{kjm}^{(s)}|$$ (2.8)

where the superscript “(s)” stands for the corresponding quantities for groups picked up from Step IV and s is the total number of groups. The weight w_kjm is set as ${|{\mathrm{\beta ̂}}_{kjm}^{(s)}|}^{-1}$ if $|{\mathrm{\beta ̂}}_{kjm}^{(s)}|>0$ and w_kjm = ∞, otherwise.

3. Theoretical Results

In this section, we establish the asymptotic properties of the proposed group LASSO estimator in Step III and the adaptive group LASSO estimator in Step IV for the pseudo-sparse additive model derived from a set of ODEs in the last section. This is challenging since we need to integrate the asymptotic results from the two-step smoothing-based estimation method for ODE models (Varah, 1982; Brunel, 2008; Chen and Wu, 2008a,b; Liang and Wu, 2008; Wu et al., 2012) and the sparse additive models (Meier et al., 2009; Ravikumar et al., 2009; Huang et al., 2010; Cantoni et al., 2011) together.

Let r be a nonnegative integer and ζ ∈ (0, 1] such that ϱ = r + ζ > 0.5. Let ℱ be the collection of functions f on [t₀, T] whose r-th derivative, f^(r) exists and satisfies the Lipschitz condition of order ζ: |f^(r)(s) − f^(r)(t)| ≤ C|s − t|^ζ for s, t ∈ [t₀, T] with a general positive constant C. In model (1.3), without loss of generality, suppose that the first q components are nonzero, that is, f_kj (x) ≠ 0, 1 ≤ j ≤ q, but f_kj (x) ≡ 0, q+1 ≤ j ≤ p. Let A₁ = {1, ⋯, q}, A₀ = {q+1, ⋯, p}, Ã₁ = {j :, ‖β̃_kj‖₂ ≠ 0, 1 ≤ j ≤ p}, and Ã₂ = A₁ ∪ Ã₁. Let |A| be the cardinality for any index set A. Define ${\Vert f\Vert }_2={[{\int }_a^b{f}^2(x)dx]}^{1/2}$ for any function f(x) at x ∈ [a, b], whenever the integral exists. For 1 ≤ k ≤ p, we make the following assumptions:

Assumption A:

• (A1)For $\kappa =\underset{0\le j\le K_k}{\text{max}}({\tau }_{k,j+1}-{\tau }_{k,j})$, there exists a constant M > 0 such that $\frac{\kappa }{\underset{0\le j\le K_k}{\text{min}}({\tau }_{k,j+1}-{\tau }_{k,j})}\le M$ and $\underset{0\le j\le K_k}{\text{max}}|\frac{{\tau }_{k,j+1}-{\tau }_{k,j}}{{\tau }_{k,j}-{\tau }_{k,j-1}}-1|=o(1)$.
• (A2)K_k ~ cn^ϑ with 1/(2ν + 3) ≤ ϑ < 1 and λ_k = O(n^π) with π ≤ ν /(2ν + 3).
• (A3)X_k(t) ∈ C^ν+1[t₀, T] with ν ≥ 2.
• (A4)K^* = (K_k + ν − 1)(λ_kc̃₁)^1/4n^−1/4 < 1 for some constant c̃₁.
• (A5)Random design points t₁, ⋯, t_n are i.i.d. with a cumulative distribution function Q(t) and a positive and continuous derivative density ρ(t). Moreover, ρ(t) is bounded away from 0 and +∞ and has a bounded and continuous first-order derivative.

Assumption B:

• (B1)l + 1 ≥ ϱ.
• (B2)The number of nonzero components q is fixed and there is a constant c_f > 0 such that min_1≤j≤q ‖f_kj‖₂ ≥ c_f for those nonzero f_kj ’s.
• (B3)The random variables ε_k(t_i) (i = 1, ⋯, n) are i.i.d. with E[ε_k(t_i)] = 0 and $\text{Var}[{\epsilon }_k(t_i)]={\sigma }_k^2(0<{\sigma }_k^2<\infty )$. Furthermore, their tail probabilities satisfy P{|ε_k(t_i)| > x} ≤ K exp(−Cx²), i = 1, ⋯, n, for all x ≥ 0 and for some constants C and K.
• (B4)E[f_kj (X_j (t))] = 0 and f_kj ∈ ℱ for k, j = 1, ⋯, p.
• (B5)ν ≥ 3ϱ.
• (B6)Both the weight functions d_k1(․) and d_k2(․) are bounded and nonnegative on [t₀, T] with d_k1(t₀) = d_k1(T) = 0 and d_k2(t₀) = d_k2(T) = 0. For simplicity, assume that ‖d_k1‖_∞ ≤ 1 and ‖d_k2‖_∞ ≤ 1. Moreover, both d_k1(t) and d_k2(t) have bounded and continuous first-order derivatives.

Note that Assumption A is required to derive the local properties for penalized splines estimates, which were also used by Claeskens et al. (2009) and Wu et al. (2012). Assumption B1 is required for the nonparametric smoothing approaches (Huang, 2003; Xue et al., 2010). Assumptions B2, B3 and B4 are standard conditions for nonparametric additive models (Huang et al., 2010). Assumption B5 means that the smoothness degrees for the state variables X_k (․) are higher than those for the additive functions f_kj(․), which is required to control the error of the first-step nonparametric smoothing in order to achieve the same order of the error rate in the pseudo-sparse additive model in Step II. Assumption B6 is for dealing with the boundary effect for the derivative estimation so that the proposed adaptive group LASSO estimator can achieve the optimal nonparametric convergence rate.

Theorem 1 Suppose that Assumptions A and B hold and ${\lambda }_{k1}\ge C\sqrt{n\text{log}(p{m}_n)}$ for a sufficiently large constant C. Then we have

1. With probability approaching to one, |Ã₁| ≤ M₁|A₁| = M₁q for a finite constant M₁ > 1.

2. If $m_n^2\text{log}(p{m}_n)/n\to 0$ and $({\lambda }_{k1}^2{m}_n^2)/n^2\to 0$ as n → ∞, then all the nonzero β_k,j, 1 ≤ j ≤ q, are selected with probability approaching to one.

3. ${\sum }_{j=1}^p{\Vert {\mathrm{\beta ̃}}_{kj}-{\beta }_{kj}\Vert }_2^2=O_p\left(\frac{m_n^2\text{log}(p{m}_n)}{n}\right)+O_p(\frac{m_n}{n})+O\left(\frac{1}{m_n^{2\varrho -1}}\right)+O(\frac{m_n^2{\lambda }_{k1}^2}{n^2})$.

Theorem 2 Suppose that Assumptions A and B hold and that ${\lambda }_{k1}\ge C\sqrt{n\text{log}(p{m}_n)}$ for a sufficiently large constant C. Then we have the following results:

1. Let Ã_f = {j : ‖f̃_k,j‖₂ > 0, 1 ≤ j ≤ p}. There is a constant M₁ > 1 such that, with probability approaching to 1, |Ã_f| ≤ M₁q.

2. If m_n log(pm_n))/n → 0 and $({\lambda }_{k1}^2{m}_n)/n^2\to 0$ as n → ∞, then all the nonzero additive components f_kj, 1 ≤ j ≤ q, are selected with probability approaching to one.

3. ${\Vert {\mathrm{f̃}}_{kj}-f_{kj}\Vert }_2^2=O_p\left(\frac{m_n\text{log}(p{m}_n)}{n}\right)+O_p(\frac{1}{n})+O\left(\frac{1}{m_n^{2\varrho }}\right)+O\left(\frac{m_n{\lambda }_{k1}^2}{n^2}\right)$, j ∈ Ã₂.

Corollary 1 Suppose that Assumptions A and B hold. If ${\lambda }_{k1}\asymp C\sqrt{n\text{log}(p{m}_n)}$ and m_n ≍ n^1/(2ϱ+1), we have

1. If n^{−2ϱ/(2ϱ+1)} log(p) → 0 as n → ∞, then with probability approaching to one, all the nonzero components f_kj, 1 ≤ j ≤ q, are selected and the number of selected components is no more than M₁q.

2. ${\Vert {\mathrm{f̃}}_{kj}-f_{kj}\Vert }_2^2=O_p(n^{-2\varrho /(2\varrho +1)}\text{log}(p{m}_n))$, j ∈ Ã₂.

Theorem 3 Suppose Assumptions A and B hold. If ${\lambda }_{k1}\asymp C\sqrt{n\text{log}(p{m}_n)}$, m_n ≍ n^1/(2ϱ+1), and λ_k2 ≤ O(n^1/2) and satisfies $\frac{{\lambda }_{k2}}{n^{(8\varrho +3)/(8\varrho +4)}}=o(1)$ and $\frac{n^{1/(4\varrho +2)}{\text{log}}^{1/2}(p{m}_n)}{{\lambda }_{k2}}=o(1)$, then P (‖f̂_kj − f_kj‖₂ > 0, j ∈ A₁ and ‖f̂_kj‖₂ = 0, j ∈ A₀) → 1, that is, the adaptive group LASSO consistently selects the nonzero components. In addition, ${\sum }_{j=1}^q{\Vert {\mathrm{f̂}}_{kj}-f_{kj}\Vert }_2^2=O_p\left(n^{-2\varrho /(2\varrho +1)}\right)$.

All detailed proofs of Theorems 1–3, Corollary 1 are given in the Appendix.

Remark 2. We note that, for the λ_k1, λ_k2 and m_n given in Theorem 3, the number of zero components can be as large as exp (o(n^2ϱ/(2ϱ+1))), which is much larger than n. Thus, under the conditions of the theorems, the proposed adaptive group LASSO estimator is selection consistent and achieves the optimal rate convergence even when p is much larger than n.

Remark 3. All of these theoretical results (Theorems 1–3 and Corollary 1) can be extended to the case of fixed design points t₁, ⋯, t_n, in which case we can assume that there exists a distribution function Q(t) with a positive and continuous derivative density ρ(t) such that for the empirical distribution Q_n(t), $Q_n(t),{\text{sup}}_{t\in [t_0,T]}|Q_n(t)-Q(t)|=o(K_k^{-1})$. This assumption was also adopted by Zhou et al. (1998) and Zhou and Wolfe (2000).

For the pseudo-sparse additive models derived from a set of nonlinear/nonparametric ODEs, we have achieved similar theoretical results (Theorems 1–3 and Corollary 1) to those obtained by Huang et al. (2010) for nonparametric additive regression models. To prove these results, we develop an important lemma (Lemma A.1 in the Appendix) on the convergence rate of the projection involving the weighted residuals of the derivative estimate of the state variables in the ODEs. In addition, we used the weight functions, D_k1 and D_k2, in the group LASSO objective function (2.6) and the adaptive group LASSO objective function (2.7), respectively. Under a parametric ODE model setting, Wu et al. (2012) used the weighted function with similar boundary conditions for estimation of constant coefficients in ODE models. They found that the parametric estimator has different convergence rates for different boundary conditions of the weight function, that is, if the weight function is zero at both boundaries, the standard root n rate for the constant ODE parameter estimates can be achieved; otherwise, only an optimal nonparametric convergence rate can be reached. In the situation of the pseudo-sparse additive models, we have achieved the optimal nonparametric convergence rate for the adaptive group LASSO estimator (Theorem 3) of the nonparametric functions in the SA-ODE model under the zero boundary assumption for the weight function. If the zero boundary assumption of the weight function does not hold, a lower than the optimal nonparametric convergence rate is expected although we did not provide a detailed proof for this claim. Here we adopt similar ideas in the proofs of Theorems 1–3 and Corollary 1 to those in Huang et al. (2010), but we have to tackle some challenges in the detailed proofs due to the difference between the pseudo-sparse additive model and the sparse additive regression model in Huang et al. (2010).

4. Simulation Studies

In this section, we design simulation experiments to validate the proposed variable selection method for the SA-ODE model. We consider a true SA-ODE model with 8 coupled ODEs as a dynamic network (a higher dimensional SA-ODE model is prohibited for simulation studies due to the limitation of current computational power):

$$X_1^{\prime }=f_{1,1}(X_1)+f_{1,2}(X_2),X_2^{\prime }=f_{2,1}(X_1)+f_{2,2}(X_3),X_3^{\prime }=f_{3,1}(X_2)+f_{3,2}(X_5),$$ (4.1)

$$X_4^{\prime }=f_{4,1}(X_8),X_5^{\prime }=f_{5,1}(X_4)+f_{5,2}(X_6)+f_{5,3}(X_8),X_6^{\prime }=f_{6,1}(X_5),$$ (4.2)

$$X_7^{\prime }=f_{7,1}(X_6)+f_{7,2}(X_8),X_8^{\prime }=f_{8,1}(X_4)+f_{8,2}(X_6)$$ (4.3)

and we set

$$f_{1,1}(x)=-\text{sin}(2x),f_{1,2}(x)=0.1x^2-1,f_{2,1}(x)=x,f_{2,2}(x)=e^{-x},$$ (4.4)

$$f_{3,1}(x)=x^{1.5}-2,f_{3,2}(x)=10\text{sin}(2x)/(10-\text{cos}(2x)),f_{4,1}(x)=0.1x^2-0.5,$$ (4.5)

$$f_{5,1}(x)=10\text{cos}(2x),f_{5,2}(x)=10\text{cos}(2x)+10x\times \text{sin}(2x),f_{5,3}(x)=x^{1/3}+x^{1/5},$$ (4.6)

$$f_{6,1}(x)=-x\times \text{cos}(2x),f_{7,1}(x)=0.1x+x^2,f_{7,2}(x)=-0.01x^3,$$ (4.7)

$$f_{8,1}(x)=\sqrt{|x|}\times \text{cos}(2x),f_{8,2}(x)=0.01x^3+0.01x^2.$$ (4.8)

We assume the measurement model as

$$Y_k(t_{ij})=X_k(t_{ij})+{\epsilon }_k(t_{ij}),i=1,2,\cdots ,n,j=1,2,\cdots ,n_k,k=1,2,\cdots ,8$$ (4.9)

Note that, to mimic the real data example in the next section, we also allow to have replicates of measurements, j = 1, 2, ⋯, n_k at each time point for the kth equation, and the number of replicates may be different for different equations. In our simulation studies, we assume the numbers of replicates for the 8 equations as (n₁, n₂, n₃, n₄, n₅, n₆, n₇, n₈) = (50, 60, 70, 40, 50, 30, 45, 35), respectively; and the number of measurement time points is taken as n = 15 and 150 (equally-spaced), respectively. If the replicates are repeated measures or longitudinal data as in our real data example in next section, we can use the nonparametric mixed-effects smoothing approach (Wu and Zhang, 2006) for the first step nonparametric smoothing, which is more efficient (Lu et al., 2011). In our simulation studies, we also consider the case of longitudinal replicates. We first generated the mean trajectory of the observational data, X̄_k (t), by numerically solving the ODE models (4.1)–(4.3) using the initial values of the state variables (in log-scale), X_k (0) = X_k0, sampled from a normal distribution with a mean 8 and a standard deviation 5. Then, assuming the real observational data to have a random departure from the mean trajectory at time t_i, b_ki, which is assumed to follow a standard normal distribution. In addition, the measurement error ε_k(t_ij) is assumed to follow a normal distribution with mean zero and variance σ², and we took σ² = 0.01 and 0.1, respectively in our simulation studies. In summary, the observational data were generated as y_k (t_ij) = X̄_k (t_ij) + b_ki + ε_k(t_ij). The number of simulation runs is taken as 100.

We evaluate the performance of the proposed adaptive group LASSO for the pseudo-sparse additive models derived from a set of ODEs based on the simulated data that are described above. In Step II, the number of basis functions for approximating the non-parametric components was taken as 12 and the data augmentation strategy (D’Haeseleer et al., 1999; Wessels et al., 2001; Bansal et al., 2006; Lu et al., 2011) was used (2000 data points were taken from the smoothed estimates in Step I). The simulation results are reported in Table 1. From Table 1, we can see that, when the sample size is smaller (n = 15) and the measurement error is larger (σ² = 0.1), the true positive rate (TP) of the variable selection by the proposed adaptive group LASSO method ranges from 51% to 84%, and the false positive rate(FP) ranges from 33% to 45% for the eight ODEs respectively. However, when the sample size is increased (n = 150), the minimum TP for the eight ODEs is increased to 74% and the FP is decreased to 17–30%. When the measurement error is reduced from σ² = 0.1 to σ² = 0.01 for the sample size n = 15, the minimum TP for the eight ODEs is 68% and the FP is decreased to 25–36%. When both the sample size is increased (n = 150) and the measurement error is reduced (σ² = 0.01), the TP ranges 88–100% and the FP is further decreased to 7–16%. These simulation results show that the proposed adaptive LASSO method is reasonably good and tends to perform perfectly when the measurement error is small and the sample size is large.

Table 1.

Simulation results for the adaptive group LASSO in Step IV. The numbers are the averages of true positive rate (TP%) and false positive rate(FP%) from 100 simulation replicates for different scenarios of sample sizes and measurement errors. Standard deviations are given in parenthesis.

δ2	n	Eqn#	TP%	FP%	n	Eqn#	TP%	FP%
0.1	15				150
		(1)	51(0.57)	45(0.64)		(1)	74(0.39)	30(0.27)
		(2)	55(0.48)	44(0.37)		(2)	78(0.27)	27(0.34)
		(3)	61(0.56)	39(0.42)		(3)	80(0.37)	22(0.4)
		(4)	84(0.39)	45(0.53)		(4)	100(0.0)	17(0.33)
		(5)	61(0.72)	38(0.61)		(5)	78(0.31)	26(0.33)
		(6)	70(0.42)	33(0.39)		(6)	94(0.12)	25(0.27)
		(7)	72(0.37)	39(0.48)		(7)	93(0.22)	21(0.33)
		(8)	75(0.62)	37(0.69)		(8)	96(0.11)	19(0.17)
0.01	15				150
		(1)	71(0.83)	29(0.21)		(1)	88(0.22)	7(0.09)
		(2)	74(0.51)	33(0.31)		(2)	95(0.13)	12(0.16)
		(3)	68(0.44)	25(0.25)		(3)	94(0.17)	8(0.20)
		(4)	89(0.26)	28(0.63)		(4)	100(0.0)	10(0.34)
		(5)	68(0.29)	29(0.79)		(5)	91(0.12)	16(0.14)
		(6)	79(0.47)	36(0.58)		(6)	100(0.0)	9(0.18)
		(7)	80(0.48)	31(0.44)		(7)	97(0.11)	13(0.12)
		(8)	88(0.33)	28(0.83)		(8)	100(0.0)	11(0.23)

To illustrate the effect of Step V (the regular LASSO for shrinking basis coefficients) in the proposed variable selection procedure in Section 2, we plot the estimated nonparametric functions from Step IV (adaptive group LASSO) and Step V as well as the true function from one simulation run in Figure 1. From this figure, we can see that, the two estimated nonparametric functions have similar trends and can capture the complex non-linear functions, but the adaptive group LASSO estimates from Step IV are too wiggly (dotted lines), which is presumably due to too many basis functions included (under-smoothing). That is why Step V is necessary to shrink some of the unnecessary basis coefficients to zero using the regular LASSO, which produces better (smoother) estimates (dashed lines in Figure 1). We can also see that Step V estimates perform better at boundaries and inection points of the curves compared to Step IV estimates, although this observation is only based on one simulation case. But in general, Step V estimates should be better for more smooth functions compared to those of Step IV, since Step V is designed to correct the under-smoothing problem for Step IV. To quantify the gains from Step V, a comparison of residual sum of squares (RSS) between Step IV and V for each of 15 nonlinear functions are listed in Table 2. The RSS for each function f_ij is defined as $RSS={\sum }_{n_{ij}=1}^{n_{ss}}{\left[f_{ij}\right(x_{n_{ij}})-\widehat{f_{ij}\left(x_{n_{ij}}\right)}]}^2$, where $\widehat{f_{ij}(x_{n_{ij}})}$ is estimated from Step IV or V and f_ij(x_nij) is the true function value. n_ss is the sample size (here we use 2,000). Table 2 shows that the RSS is reduced by Step V from Step IV in most cases. However, for two functions, f₂₂ and f₅₁, out of 15 functions, the RSS from Step V is larger than that from Step IV.

Figure 1.

Simulation example: A comparison of the true functions (solid lines) and estimated functions from the adaptive group LASSO in Step IV (dotted lines) and from Step V after further basis coefficient shrinking (dashed lines) from one simulation run.

Table 2.

Comparisons of residual sum of squares (RSS) from Step IV and V.

	f11	f12	f21	f22	f31	f32	f41	f51
			(×103)		(×10)	(×103)	(×103)	(×103)
Step IV	7.0	53.1	8.2	1.5	34.3	7.0	9.0	1.1
Step V	6.8	9.9	8.0	2.7	8.6	5.8	1.2	2.8
	f52	f53	f61	f71	f72	f81	f82
	(×106)	(×10−2)	(×105)	(×106)	(×10)	(×102)	(×103)
Step IV	8.6	35.3	1.5	1.2	19.2	8.0	4.0
Step V	8.1	9.0	1.4	1.1	8.4	5.1	3.9

5. Application: Identification of Nonlinear Dynamic Gene Regulatory Networks

In this section, we apply the proposed method to identify a nonlinear dynamic gene regulatory network based on time course microarray data for T-cell activation. The central event in generation of an immune response is the activation of T-lymphocytes (T-cells). Activated T-cells proliferate and produce cytokines involved in the regulation of effector cells such as B cells and macrophages, which are the primary mediators of the immune response. T-cell activation is initiated by the interaction between the T-cell receptor (TCR) complex and the antigenic peptide presented on the surface of an antigen-presenting cell. This event triggers a network of signaling molecules, including kinases, phosphatases and adaptor proteins that couple the stimulatory signal received from the TCR to gene transcription events in the nucleus (Iwashima et al., 1994; Ley et al., 1991).

In order to better understand the gene regulation network during T-cell activation, Rangel et al. (2004) performed two experiments to characterize the response of a human T cell line (Jurkat) to PMA and ionomicin treatment. In the first experiment, they monitored the expression of 88 genes using cDNA array technology across 10 unequally spaced time points (0, 2, 4, 6, 8, 18, 24, 32, 48, 72h) and each gene was replicated 34 times. In the second experiment, an identical experimental protocol was used, but additional genes were added to the arrays and each gene was replicated 10 times. Genes that displayed very poor reproducibility between the two experiments were removed and the expression data for 58 genes were considered for final analysis by Rangel et al. (2004). Details of data collection and preprocessing can be found in Rangel et al. (2004). Rangel et al. (2004) applied a linear state space model (SSM) to identify the transcriptional network based on this highly replicated expression profiling data. Beal et al. (2005) proposed a variational Bayesian treatment for identifying suitable dimension of hidden state space in SSM. In this paper, we intend to apply the proposed SA-ODE model and the proposed variable selection method in the previous sections to establish a nonlinear dynamic regulatory network among 58 genes for the T-cell activation process. Through this application example, we will demonstrate that some of the gene regulation effects are essentially nonlinear and the linear network model may not be sufficient to capture the nonlinear features of the dynamic network.

We consider the 58 T-cell activation genes that were identified as reproducible from the two experiments by Rangel et al. (2004). For consistency, we only use the expression data from the first experiment with each gene replicated 34 times at 10 time points. The 34 replicates for each gene showed a similar expression pattern during the T-cell activation experiments. It is legitimate to smooth the data for each of the genes using the nonparametric mixed-effects smoothing splines technique (Wu and Zhang, 2006; Lu et al., 2011) to obtain the estimates of the mean expression curves and their derivative curves for each gene, respectively. At the second step, these estimates were plugged in ODE model (1.3) to form the pseudo-sparse additive (PSA) model (2.3). The penalized pseudo-least squares methods, the group LASSO and adaptive group LASSO approaches were used to identify significant regulations (connections) among the 58 genes with potential nonlinear regulation effects. We obtained the fitted curves for all genes by integrating 58 genes concurrently with parameters estimated from the adaptive grouped LASSO approach in Step IV and after shrinking the basis coefficients using regular LASSO in Step V, respectively.

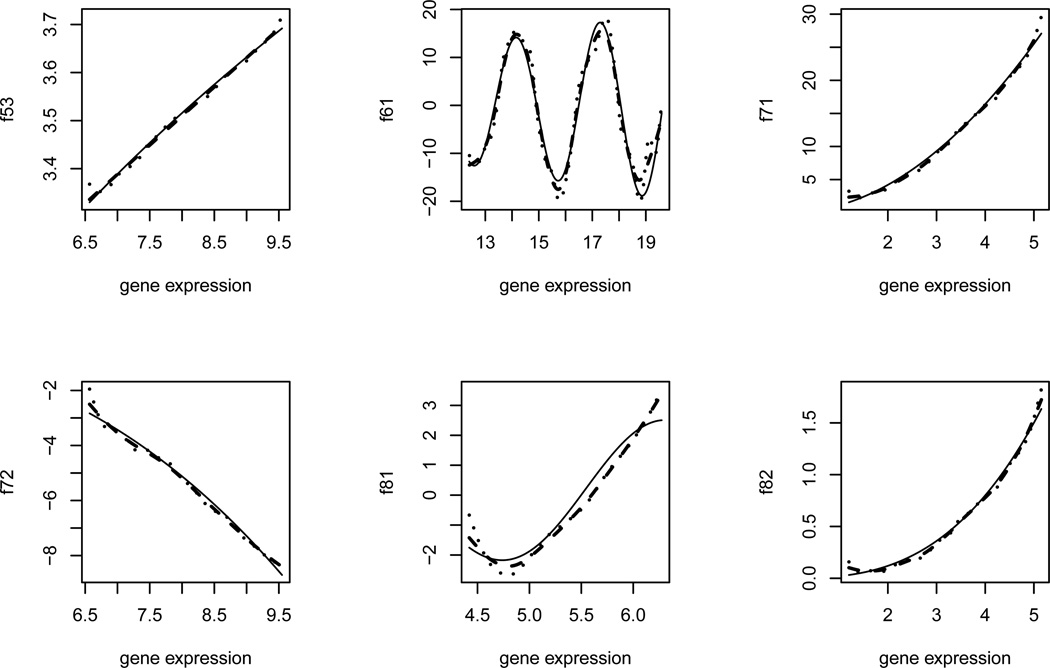
We plot the fitted expression curves (dashed lines) for 9 genes from Step V of the proposed procedure, overlaid with the raw data (dots) and the smoothed mean curves (solid lines) from Step I in Figure 2. For comparison purpose, the estimation results from the linear ODE model (Lu et al., 2011) were also obtained and plotted (dotted lines). From this figure, we can see that the proposed nonparametric additive ODE models fit the data better (also closer to the smoothed mean curves), compared to the linear ODE model fit. We also notice that the proposed SA-ODE models not only can fit the simple monotonic curves well, but also can exibly fit complex nonlinear curves reasonably good. For each of 58 genes, we list the regulatory genes, identified by the proposed method in Table 3. One important feature of the identified GRN is that each of these 58 genes is regulated by only a few other genes (ranging from 1 to 8 genes), which reects the fact of sparseness of the network connections.

Figure 2.

Real data analysis for T cell activation experimental data (dots): the estimation results for gene FYB (gene 45) and 9 genes regulated by gene FYB which include nonparametric smoothing estimates of mean expression curves from Step I (solid lines), the estimated curves (dashed lines) based on the proposed SA-ODE model from Step V of the proposed procedure, and the estimated curves (dotted lines) using the linear ODE model fit from Lu et al. (2011).

Table 3.

T-cell activation gene regulatory network: variable selection results from the adaptive group LASSO. For a particular gene listed in Columns 1 and 4, Columns 2 and 5 provide the list of genes that have a significant regulation effects (inward inuence) on this gene, and Columns 3 and 6 provide the list of genes that this particular gene has a significant regulation effect on (outward inuence).

Gene	Inward Inuence Genes	Outward Inuence Genes	Gen	Inward Inuence Genes	Outward Inuence Genes
1	29, 32, 43		30	6, 46, 52
2	32, 41, 45		31	25	6, 10, 23, 27, 35, 46, 48
3	29, 35, 41		32	48	1, 2, 5, 21, 24, 26, 56, 57
4	25		33	27, 28, 41	11, 23
5	32, 35		34	6, 27
6	6, 25, 31	6, 9, 16, 26, 30, 34, 42, 52	35	20, 31	3, 5, 9, 14, 18, 20, 21, 38
7	45, 52, 57	11, 23	36	37	23
8	25		37	25	12, 13, 16, 22, 27, 36, 40, 56
9	6, 17, 27, 28, 35, 45		38	11, 28, 29, 35
10	31, 51, 52		39	25	53
11	7, 13, 33, 46, 57	14, 18, 21, 38	40	37, 46
12	29, 37		41	20, 55	2, 3, 15, 17, 25, 33, 42, 50, 58
13	37	11, 14, 15, 23, 50	42	6, 41, 46
14	11, 13, 20, 28, 29, 35		43	27	1
15	13, 41, 45		44	28, 29, 45, 57
16	6, 27, 37		45	52	2, 7, 9, 15, 18, 44, 46, 49, 55
17	41, 48	9, 54	46	31, 45	11, 23, 24, 30, 40, 42, 58
18	11, 35, 45, 54		47	27
19	25	58	48	31, 48	17, 28, 32, 48
20	29, 35, 55	14, 25, 35, 41, 57	49	35, 45, 52
21	11, 28, 32, 35		50	13, 41, 57
22	27, 37, 52		51	25	10
23	7, 13, 31, 33, 36, 46, 57		52	6	7, 10, 22, 29, 30, 45, 49, 53, 55
24	32, 46, 57		53	39, 52
25	20, 28, 41	4, 6, 8, 19, 26, 31, 37, 39, 51	54	17
26	6, 25, 32		55	27, 45, 52	20, 41
27	31, 37	9, 16, 22, 33, 34, 43, 47, 55, 58	56	32, 37
28	48, 57	9, 14, 21, 25, 33, 38, 44	57	20, 32	7, 11, 23, 24, 28, 44, 50
29	52	1, 3, 12, 14, 20, 38, 44	58	19, 27, 41, 46

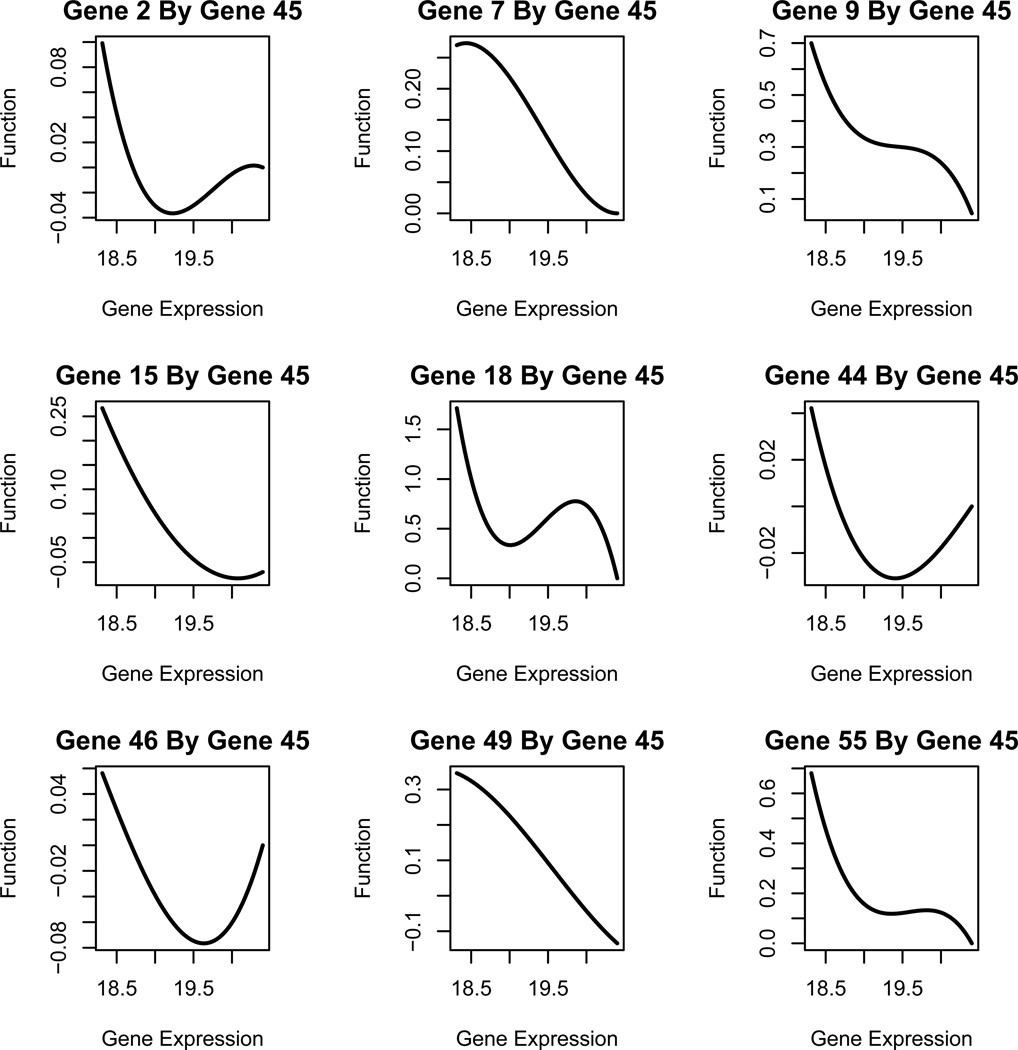
In agreement with the findings from Rangel et al. (2004), our model identified the important adaptor molecule in T-cell receptor signaling pathway, FYB (gene 45 in Table 3) as one of the genes having the highest number of outward connections. In addition to the 6 genes, found by Rangel et al. (2004), that are regulated by FYB, we identified three more FYB-regulated genes which carry functions in proliferation (gene 2), interference (gene 44) and apoptosis (gene 49). This is presumably due to that the proposed nonparametric additive ODE model and the variable selection method allow us to identify significant nonlinear regulation effects compared to the linear state space model (SSM) used by Rangel et al. (2004). As another interesting finding based on the proposed model, we identified the direct regulation of integrin (gene 15) by FYB, which has already been corroborated by the experimental study (Peterson et al., 2001). On the contrary, the linear SSM used by Rangel et al. (2004) only found the indirect regulation mediated by IL3Rθ (gene 55) and TRAF5 (gene 3). The estimated regulation functions of FYB (gene 45 in Table 3) to other genes are shown in Figure 3. Our results show that the gene FYB always has a positive regulation on genes 9, 18, 46 and 55, but a negative effect on gene 7, which agree with the findings from Rangel et al. (2004). For gene 15 which was found to be indirectly regulated by FYB in Rangel et al. (2004), we discover that the direct regulation effect is positive when the FYB expression level is low and turns to be negative when the FYB expression level is high. Similarly, for the three newly discovered FYB-regulated genes, genes 2, 44 and 49, by our method, we found that the regulation effect changes from positive to negative when the FYB expression is high. This demonstrates that the proposed nonparametric additive ODE model may help us to discover not only nonlinear regulation effects, but also varying effects due to the expression level of the regulator genes.

Figure 3.

Estimated regulation functions of genes inuenced by gene 45 (FYB)

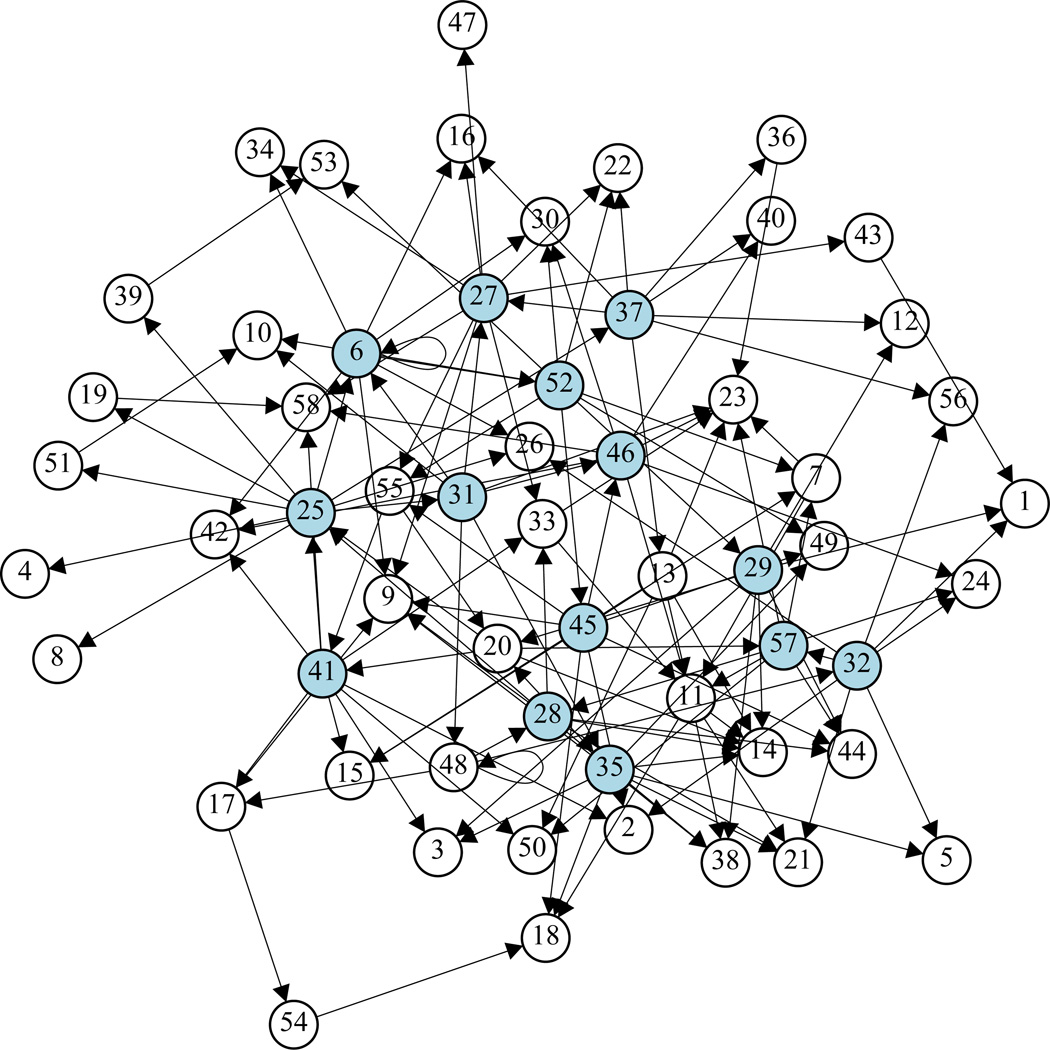
We use R function ‘igraph’ to plot the obtained GRN in Figure 4 in order to visualize the complete network. From this figure, we can clearly see that there are 14 ‘big’ regulator genes that regulate more than 5 other genes for each of them (see also Table 3). Due to space limitation, we will report more detailed annotations and biological implications of this established dynamic GRN for T-cell activation somewhere else. Notice that any statistical methods and modeling approaches can only identify potential regulation effects in actual GRNs. Usually some of these findings can be confirmed by existing literature and some others may need new experiments to validate. We expect that the proposed SA-ODE model and the variable selection methods provide a exible tool to explore and identify additive nonlinear regulation effects in the GRNs.

Figure 4.

Graph of T cell activation GRN formed by 58 genes. Each gene is represented as a node. Arrow stands for the direction of inuence. The 14 “big” regulators are in blue.

6. Concluding Remarks

In this paper, we have proposed a sparse additive ordinary differential equation (SA-ODE) model for dynamic gene regulatory networks (GRN) in order to capture the nonlinear regulation effects. A five-step variable selection and estimation procedure by coupling the two-step smoothing-based ODE estimation method and LASSO techniques is developed. The asymptotic properties of the proposed methods are established. Simulation studies are conducted to demonstrate the good performance of the proposed variable selection method. We have successfully applied the proposed method to construct a nonlinear dynamic GRN for T cell activation. We discovered additional new regulation effects in the complicated nonlinear network consisting of 58 genes, compared to the existing linear network modeling approach. The real data analysis results also show that the proposed SA-ODE model not only can capture complex nonlinear regulation effects, but also it can identify the varying-effects due to the expression levels of regulator genes.

In the theoretical development in Section 3, we have shown that the adaptive group LASSO selects the correct model with probability approaching 1 and achieves the optimal nonparametric convergence rate for the proposed SA-ODE model, which are similar to those obtained by Huang et al. (2010) for a nonparametric additive regression model. Notice that we convert the proposed SA-ODE model into a ‘pseudo’ sparse additive (PSA) model, which is different from the additive regression model in Huang et al. (2010) in the sense that both response variables and covariates in the PSA model are derived from the first step nonparametric smoothing of state variables and their derivatives, instead of observed data, and the error terms in the PSA model are not i.i.d. but dependent. To tackle the challenges in this complex model, we used a weight function with boundary restrictions in the penalized least squares (LASSO) criteria and established a critical lemma in order to achieve the optimal convergence rate.

Alternative models for dynamic GRNs include boolean network, Bayesian network, hidden Markov models among others (Liang et al., 1998; Akutsu et al., 2000; Shmulevich et al., 2002; Martin et al., 2007; Murphy and Mian, 1999; Friedman et al., 2000; Hartemink et al., 2001; Zou and Conzen, 2005; Song et al., 2009; Hirose et al., 2008; Kojima et al., 2009; Shimamura et al., 2009; Gupta et al., 2007). It is interesting to compare these modeling approaches with the proposed ODE modeling method from the perspectives of computational cost and likelihood to recover the true network. But the computational cost for this comparison is beyond the limit of our current computational power. We employed the two-stage smoothing-based ODE estimation method for the SA-ODE model in order to reduce the computational cost and simplify the implementation of LASSO-based variable selection methods. One limitation of the two-stage smoothing-based ODE estimation method is its requirement of direct observations of all state variables in the system. It is still a challenging problem to perform variable selection for high-dimensional ODE models with partially observed state variables. Some other more efficient estimation approaches for ODE models such as the numerical discretization-based estimation method (Wu et al., 2012) and generalized profiling approach (Ramsay et al., 2007) may also be considered for high-dimensional ODE variable selection. We believe that it is worth future exploration along a similar line, although the computational cost and implementation details need to be carefully considered. In the proposed SA-ODE model (1.3), we only consider the nonparametric additive structure of related variables. It could be extended to a nonparametric structure involving interactions (Radchenko and James, 2010) since co-regulations are very often in gene regulatory networks. We are currently working on this problem and will report the results elsewhere.

APPENDIX

Proofs

We can prove the theoretical results in Theorems 1–3 and Corollary 1 similarly to Huang et al. (2010). But there are more technical challenges that we need to deal with. The major differences between the ‘pseudo’ sparse additive (PSA) model (2.3) and the additive regression model in Huang et al. (2010) include: 1) both response variables and covariates in the PSA model are derived from the first step nonparametric smoothing of state variables and their derivatives, instead of observed data, and ii) the error terms, ϒ_ki in the PSA model, are not i.i.d. but dependent. To tackle these problems, we establish the following lemma. For 1 ≤ k ≤ p, let $T_{jm}=n^{-1/2}{m}_n^{1/2}{\sum }_{i=1}^n{\psi }_m(X_j(t_i))d_{k1}^{1/2}(t_i)({\mathrm{X̂}}_k^{\prime }(t)-E[{\mathrm{X̂}}_k^{\prime }(t)])$ for 1 ≤ j ≤ p, 1 ≤ m ≤ m_n (for notational simplicity, we suppress the dependence of k), and T_n = max_{1≤j≤p,1≤m≤mn} |T_jm|.

Lemma A.1 Under Assumptions A, B2–B4 and B6 in Section 3, we have $E(T_n)=O(1)\sqrt{\text{log}(p{m}_n)}$.

Proof: From (2.2), we know that T_jm can be expressed as follows.

$$T_{jm}=n^{-1/2}{m}_n^{1/2}\sum _{i=1}^n{\psi }_m(X_j(t_i))d_{k1}^{1/2}(t_i){[{\mathbf{N}}_{k,\nu +1}^{\prime }(t_i)]}^T{({\mathbf{N}}_k^T{\mathbf{N}}_k+{\lambda }_k{\mathbf{V}}_k)}^{-1}{\mathbf{N}}_k^T{\mathbf{\epsilon }}_k=n^{-1/2}{m}_n^{1/2}\sum _{\omega =1}^n[\sum _{i=1}^n{\psi }_m(X_j(t_i))d_{k1}^{1/2}(t_i)g_{\omega }(t_i)]{\epsilon }_k(t_{\omega }),$$

with ε_k = (ε_k(t₁), ⋯, ε_k(t_n))^T and g_ω(t_i) being the ω-th component of the n-dimensional vector ${[{\mathbf{N}}_{k,\nu +1}^{\prime }(t_i)]}^T{({\mathbf{N}}_k^T{\mathbf{N}}_k+{\lambda }_k{\mathbf{V}}_k)}^{-1}{\mathbf{N}}_k^T$. Under Assumption B3, ε_k(t_i)’s are i.i.d. and sub-Gaussian. Moreover, for given t_i’s, the coefficient ${\sum }_{i=1}^n{\psi }_m(X_j(t_i))d_{k1}^{1/2}(t_i)g_{\omega }(t_i)$ of ε_k(t_ω) is given. Therefore conditional on t_i’s, T_jm’s are sub-Gaussian.

Let $s_{jm}^2=\text{Var}(T_{jm}|t_1,\cdots ,t_n)$ and $s_n^2={\text{max}}_{1\le j\le p,1\le m\le m_n}{s}_{jm}^2$. Then by the maximal inequality for sub-Gaussian random variables (Lemmas 2.2.1 and 2.2.2, van der Vaart and Wellner, 1996), we have $\mathrm{E}({\text{max}}_{1\le j\le p,1\le m\le m_n}|T_{jm}||t_1,\cdots ,t_n)\le C_1{s}_n\sqrt{\text{log}(p{m}_n)}$, where C₁ > 0 is a constant. Therefore,

$$\mathrm{E}(\underset{1\le j\le p,1\le m\le m_n}{\text{max}}|T_{jm}|)\le C_1\sqrt{\text{log}(p{m}_n)}\mathrm{E}(s_n).$$ (A.1)

Now we discuss the order of E(s_n). Similar to Wu et al. (2012), we consider the integral approximation of T_jm because of the boundary effects. By the strong law of large number, we have

$$\frac{1}{n}\sum _{i=1}^n{\psi }_m(X_j(t_i))d_{k1}^{1/2}(t_i)({\mathrm{X̂}}_k^{\prime }(t_i)-\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t_i)])={\int }_{t_0}^T{\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)({\mathrm{X̂}}_k^{\prime }(t)-\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t)])dt+o(1).$$ (A.2)

From the integration by parts, it follows that

$${\int }_{t_0}^T{\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)({\mathrm{X̂}}_k^{\prime }(t)-\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t)])dt={\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)({\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)]){|}_{t_0}^T-{\int }_{t_0}^T({\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)])\frac{d}{dt}[{\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)]dt=-{\int }_{t_0}^T({\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)])\frac{d}{dt}[{\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)]dt,$$

where $\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t)]=(\mathrm{E}[{\mathrm{X̂}}_k(t)])\prime$ and the second equality holds because of the boundary condition d_k1(t₀) = d_k1(T) = 0. Denote $A(t)={\psi }_m(X_j(t))d_{k1}^{1/2}(t)\rho (t)$ and

$${\mathrm{\Sigma }}_X={\int }_{t_0}^T{\int }_{t_0}^{T}A\prime (s)\text{Cov}\{{\mathrm{X̂}}_k(s)-\mathrm{E}[{\mathrm{X̂}}_k(s)],{\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)]|t_1,\cdots ,t_n\}A\prime (t)dsdt.$$

By the Hölder’s inequality, we have

$${\mathrm{\Sigma }}_X\le {\Vert A\prime (s)A\prime (t)\Vert }_{\infty }{\int }_{t_0}^T{\int }_{t_0}^T\text{Cov}\{{\mathrm{X̂}}_k(s)-\mathrm{E}[{\mathrm{X̂}}_k(s)],{\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)]|t_1,\cdots ,t_n\}dsdt.$$ (A.3)

From the proof of Lemma 6 in Wu et al. (2012), we know that

$${\int }_{t_0}^T{\int }_{t_0}^T\text{Cov}\{{\mathrm{X̂}}_k(s)-\mathrm{E}[{\mathrm{X̂}}_k(s)],{\mathrm{X̂}}_k(t)-\mathrm{E}[{\mathrm{X̂}}_k(t)]|t_1,\cdots ,t_n\}dsdt\le C_2{n}^{-1}$$ (A.4)

for some positive constant C₂. By the extremal equality, it follows that ${\Vert A\prime (s)A\prime (t)\Vert }_{\infty }=\text{sup}\{|{\int }_{t_0}^T{\int }_{t_0}^{T}A\prime (s)A\prime (t)g(s,t)dsdt|:g\in L^1(\mu ,\mu ),{\Vert g\Vert }_1\le 1\}$, where L¹(μ, μ) is the bi-variate Lebesgue function space with L¹-norm. Continuing to apply integration by parts and the boundary condition d_k1(t₀) = d_k1(T) = 0, we have

$${\int }_{t_0}^T{\int }_{t_0}^{T}A\prime (s)A\prime (t)g(s,t)dsdt={\int }_{t_0}^T\{A\prime (s)[g(t,s)A(t)]{|}_{t=t_0}^{t=T}-{\int }_{t_0}^{T}A(t)\frac{\partial g(t,s)}{\partial t}dt\}ds=-{\int }_{t_0}^T{\int }_{t_0}^{T}A\prime (s)A(t)\frac{\partial g(t,s)}{\partial t}dsdt=-{\int }_{t_0}^{T}A(t)dt{\int }_{t_0}^T\frac{\partial g(t,s)}{\partial t}dA(s)={\int }_{t_0}^T{\int }_{t_0}^{T}A(s)A(t)\frac{{\partial }^{2}g(t,s)}{\partial t\partial s}dsdt.$$

Then $|{\int }_{t_0}^T{\int }_{t_0}^{T}A\prime (s)A\prime (t)g(s,t)dsdt|\le C_3\text{Cov}[{\psi }_m(X_j(s)),{\psi }_m(X_j(t))]$ for some positive constant C₃. By the properties of B-splines, we have

$$\text{Cov}[{\psi }_m(X_j(s)),{\psi }_m(X_j(t))]\le C_4{m}_n^{-1}$$ (A.5)

for some positive constant C₄. Combining (A.3)–(A.5) together, it follows that ${\mathrm{\Sigma }}_X\le C{n}^{-1}{m}_n^{-1}$ for some positive constant C. Then from (A.2), we have that $s_{jm}^2=\text{Var}(T_{jm}|t_1,\cdots ,t_n)\le C$. Therefore $\mathrm{E}{s}_n\le {(\mathrm{E}{s}_n^2)}^{1/2}\le C$ for some positive constant C. Thus from (A.1), we have

$$\mathrm{E}(\underset{1\le j\le p,1\le m\le m_n}{\text{max}}|T_{jm}|)\le C\sqrt{\text{log}(p{m}_n)}$$

for some positive constant C.

Proof of Theorem 1. The proof of part (i) is similar in spirit to the proof of Theorem 1 in Huang et al. (2010). But some technical challenges have to be tackled since here we need to consider the estimation errors of ${\mathrm{X̂}}_k^{\prime }(t)$ and X̂_k(t) (involving the measurement error) and the approximation error of the additive regression functions by splines. Specifically, from (2.3) and Taylor expansion, we have

$${\Upsilon }_{ki}^{*}={\mathrm{X̂}}_k^{\prime }(t_i)-X_k^{\prime }(t_i)+\sum _{j=1}^q{f}_{kj}(X_j(t_i))-\sum _{j=1}^q{f}_{kj}^{*}({\mathrm{X̂}}_j(t_i))={\mathrm{X̂}}_k^{\prime }(t_i)-X_k^{\prime }(t_i)+\sum _{j=1}^q{f}_{kj}(X_j(t_i))-\sum _{j=1}^q{f}_{kj}({\mathrm{X̂}}_j(t_i))+\sum _{j=1}^q{f}_{kj}({\mathrm{X̂}}_j(t_i))-\sum _{j=1}^q{f}_{kj}^{*}({\mathrm{X̂}}_j(t_i))={\mathrm{X̂}}_k^{\prime }(t_i)-X_k^{\prime }(t_i)+\sum _{j=1}^q{f}_{kj}^{\prime }(X_{ji})(X_j(t_i)-{\mathrm{X̂}}_j(t_i))+\sum _{j=1}^q[f_{kj}({\mathrm{X̂}}_j(t_i))-f_{kj}^{*}({\mathrm{X̂}}_j(t_i))]={\mathrm{X̂}}_k^{\prime }(t_i)-\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t_i)]-\sum _{j=1}^q{f}_{kj}^{\prime }(X_{ji})\{{\mathrm{X̂}}_j(t_i)-\mathrm{E}[{\mathrm{X̂}}_j(t_i)]\}+\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t_i)]-X_k^{\prime }(t_i)-\sum _{j=1}^q{f}_{kj}^{\prime }(X_{ji})\mathrm{E}[{\mathrm{X̂}}_j(t_i)]-X_j(t_i)\}+\sum _{j=1}^q[f_{kj}({\mathrm{X̂}}_j(t_i))-f_{kj}^{*}({\mathrm{X̂}}_j(t_i))],$$

where X_ji locates between X̂_j(t_i) and X_j(t_i).

For D_k1 = diag{d_k1(_t1), ⋯, d_k1(t_n)}, we have ${\mathbf{D}}_{k1}^{1/2}=\text{diag}\{d_{k1}^{1/2}(t_1),\cdots ,d_{k1}^{1/2}(t_n)\}$. Let ${\mathit{\xi }}_k={\mathbf{D}}_{k1}^{1/2}({\mathbf{\Xi }}_k+{\mathbf{\Pi }}_k+{\mathit{\delta }}_k)$, where Ξ_k = (Ξ_k(t₁), ⋯, Ξ_k(t_n))^T, Π_k = (Π_k1, ⋯, Π_kn)^T and δ_k = (δ_k1, ⋯, δ_kn)^T with ${\mathrm{\Xi }}_k(t_i)=d_{k1}^{1/2}(t_i)({\mathrm{X̂}}_k^{\prime }(t_i)-\mathrm{E}[X_k^{\prime }(t_i)]-\sum _{j=1}^q{f}_{kj}^{\prime }(X_{ji})\{{\mathrm{X̂}}_j(t_i)-\mathrm{E}[{\mathrm{X̂}}_j(t_i)]\},{\mathrm{\Pi }}_{ki}=d_{k1}^{1/2}(t_i)(\mathrm{E}[X_k^{\prime }(t_i)]-X_k^{\prime }(t_i)-\sum _{j=1}^q{f}_{kj}^{\prime }(X_{ji})\mathrm{E}[{\mathrm{X̂}}_j(t_i)]-X_j(t_i)\}),{\delta }_{ki}=d_{k1}^{1/2}(t_i)\sum _{j=1}^q[f_{kj}({\mathrm{X̂}}_j(t_i))-f_{kj}^{*}({\mathrm{X̂}}_j(t_i))]$. For any integer m, let

$${\chi }_m=\underset{|A|=m}{\text{max}}\underset{{\Vert U_{A_k}\Vert }_2=1,1\le k\le m}{\text{max}}\frac{|{\mathit{\xi }}_k^T{V}_A({\mathbf{S}}_A)|}{{\Vert V_A({\mathbf{S}}_A)\Vert }_2},\text{and}{\chi }_m^{*}=\underset{|A|=m}{\text{max}}\underset{{\Vert U_{A_k}\Vert }_2=1,1\le k\le m}{\text{max}}\frac{|{\mathbf{\Xi }}_k^T{V}_A({\mathbf{S}}_A)|}{{\Vert V_A({\mathbf{S}}_A)\Vert }_2},$$

where $V_A({\mathbf{S}}_A)={\mathit{\xi }}_k^T{[{\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_A({\mathbf{Z}}_A{\mathbf{D}}_{k1}){\mathbf{Z}}_A)}^{-1}{\mathbf{S}}_A-(\mathrm{I}-{\mathrm{P}}_A)\mathbf{Z}\mathit{\beta }]$ for |A| = q₁ = m ≥ 0 (here the inverse matrix can also be replaced by the generalized inverse), ${\mathbf{S}}_A={(S_{A_1}^T,\cdots ,S_{A_m}^T)}^T$, S_Ak = λ_k1U_Ak and ‖U_Ak‖₂ = 1. Then from the expression of ${\mathrm{X̂}}_k^{\prime }(t)$ and X̂_k(t), we have ${\mathbf{\Pi }}_k={\mathbf{N}}_k^{\prime }{({\mathbf{N}}_k^T{\mathbf{N}}_k+{\lambda }_k{\mathbf{V}}_k)}^{-1}{\mathbf{N}}_k^T{\epsilon }_k+{\sum }_{j=1}^q\text{diag}\{f_{kj}^{\prime }(X_{j1}),\cdots ,f_{kj}^{\prime }(X_{jn})\}{\mathbf{N}}_j{({\mathbf{N}}_j^T{\mathbf{N}}_j+{\lambda }_j{\mathbf{V}}_j)}^{-1}{\mathbf{N}}_j^T{\epsilon }_j$ with ${\mathbf{N}}_k^{\prime }={\{{\mathbf{N}}_{k,\nu +1}^{\prime }(t_1),\cdots ,{\mathbf{N}}_{k,\nu +1}^{\prime }(t_n)\}}^T$.

For a sufficiently large constant C₁ > 0, Define

$${\mathrm{\Omega }}_{m_0}=\{(\mathbf{Z},{\mathbf{\Xi }}_k):{\chi }_m\le {\sigma }_k{C}_1\sqrt{(m\vee 1)m_n\text{log}(p{m}_n),}\forall m\ge m_0\}$$

and

$${\mathrm{\Omega }}_{m_0}^{*}=\{(\mathbf{Z},{\mathbf{\Xi }}_k):{\chi }_m^{*}\le {\sigma }_k{C}_1\sqrt{(m\vee 1)m_n\text{log}(p{m}_n),}\forall m\ge m_0\},$$

where m₀ ≥ 0. Similar to the proof of Theorem 2.1 of Wei and Huang (2010), it can follow that (Z, Ξ_k) ∈ Ω_q ⇒ |Ã₁| ≤ M₁q for a constant M₁ > 1 and

$$\mathrm{P}({\mathrm{\Omega }}_q^{*})\to 1.$$ (A.6)

By the triangle and Cauchy-Schwarz inequalities,

$$\frac{|{\mathit{\xi }}_k^T{V}_A({\mathbf{S}}_A)|}{{\Vert V_A({\mathbf{S}}_A)\Vert }_2}=\frac{|{({\mathbf{\Xi }}_k+{\mathbf{\Pi }}_k+{\mathit{\delta }}_k)}^T{V}_A({\mathbf{S}}_A)|}{{\Vert V_A({\mathbf{S}}_A)\Vert }_2}\le \frac{|{\mathbf{\Xi }}_k^T{V}_A({\mathbf{S}}_A)|}{{\Vert V_A({\mathbf{S}}_A)\Vert }_2}+{\Vert {\mathbf{\Pi }}_k\Vert }_2+{\Vert {\mathit{\delta }}_k\Vert }_2.$$ (A.7)

Since ${\Vert f_{kj}-f_{kj}^{*}\Vert }_2=O(m_n^{-\varrho })=O(n^{-\varrho /(2\varrho +1)})$ for m_n = n^1/(2ϱ+1), we have that, for all m ≥ q and n sufficiently large,

$${\Vert {\mathit{\delta }}_k\Vert }_2\le C_2\sqrt{{nqm}_n^{-2\varrho }}=C_2{q}^{1/2}{n}^{1/(4\varrho +2)}\le {\sigma }_k{C}_1\sqrt{(m\vee 1)m_n\text{log}(p{m}_n)},$$ (A.8)

for some constant C₂ > 0. From Lemma 1(i) of Wu et al. (2012) and Theorem 2(a) of Claeskens et al. (2009), we have $\mathrm{E}[{\mathrm{X̂}}_k^{\prime }(t)]-X_k^{\prime }(t)=O({\kappa }^{\nu })+O({\lambda }_k{n}^{-1}{\kappa }^{-3})=O(n^{-\nu /(2\nu +3)})$ and E[X̂_k(t)]−X_k(t) = O(κ^ν+1)+O(λ_kn⁻¹κ⁻²) = O(n^{−(ν+1)/(2ν+3)}) for κ = n^−1/(2ν+3) and λ_k = O(n^ν/(2ν+3)). Then Π_ki = O(qn^{−ν/(2ν+3)}). Under Assumption B5, it follows that 3/(4ν + 6) ≤ 1/(4ϱ + 2). Then for all m ≥ q and n sufficiently large, we have

$${\Vert {\mathbf{\Pi }}_k\Vert }_2\le C_3\sqrt{{nqn}^{-2\nu /(2\nu +3)}}=C_3{q}^{1/2}{n}^{3/(4\nu +6)}\le {\sigma }_k{C}_1\sqrt{(m\vee 1)m_n\text{log}(p{m}_n)},$$ (A.9)

for some constant C₃ > 0. Finally, it follows from (A.6)–(A.9) that P(Ω_q) → 1. This completes the proof of part (i) of Theorem 1.

Before proving part (ii), we first prove part (iii) of Theorem 1. By the definition of ${\mathit{\beta ̃}}_k={({\mathrm{\beta ̃}}_{k1}^T,\cdots ,{\mathrm{\beta ̃}}_{kp}^T)}^T$,

$${({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta ̃}}_k)}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta ̃}}_k)+{\lambda }_{k1}\sum _{j=1}^p\Vert {\mathit{\beta ̃}}_{kj}{\Vert }_2\le {({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)+{\lambda }_{k1}\sum _{j=1}^p{\Vert {\mathit{\beta }}_{kj}\Vert }_2.$$ (A.10)

Let A₂ = {j : ‖β_kj‖₂ ≠ 0 or ‖β̃_kj‖₂ ≠ 0} and d_k2 = |A₂|. By part (i), d_k2 = O_p (q). By (A.10) and the definition of A₂,

$${({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta ̃}}_{k{A}_2})}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta ̃}}_{k{A}_2})+{\lambda }_{k1}\sum _{j\in A_2}{\Vert {\mathit{\beta ̃}}_{kj}\Vert }_2\le {({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta }}_{k{A}_2})}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta }}_{k{A}_2})+{\lambda }_{k1}\sum _{j\in A_2}{\Vert {\mathit{\beta }}_{kj}\Vert }_2.$$ (A.11)

Let ${\mathit{\eta }}_k={\mathbf{D}}_{k1}^{1/2}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)$ and ${\mathit{\nu }}_k={\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_{A_2}({\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2})$. Write ${\mathbf{D}}_{k1}^{1/2}({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta ̃}}_{k{A}_2})={\mathbf{D}}_{k1}^{1/2}({\mathbf{H}}_k-\mathbf{Z}{\mathit{\beta }}_k)-{\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_{A_2}({\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2})={\mathit{\eta }}_k-{\mathit{\nu }}_k$. We have ${({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta ̃}}_{k{A}_2})}^T{\mathbf{D}}_{k1}({\mathbf{H}}_k-{\mathbf{Z}}_{A_2}{\mathit{\beta ̃}}_{k{A}_2})={\mathit{\eta }}_k^T\mathit{\eta }k-2{\mathit{\eta }}_k^T{\mathit{\nu }}_k+{\mathit{\nu }}_k^T{\mathit{\nu }}_k$. (A.11) can therefore be expressed as ${\mathit{\nu }}_k^T{\mathit{\nu }}_k-2{\mathit{\eta }}_k^T{\mathit{\nu }}_k\le {\lambda }_{k1}{\sum }_{j\in A_1}({\Vert {\mathit{\beta }}_{kj}\Vert }_2-{\Vert {\mathit{\beta ̃}}_{kj}\Vert }_2)$. Note that $|{\sum }_{j\in A_1}({\Vert {\mathit{\beta }}_{kj}\Vert }_2-{\Vert {\mathit{\beta ̃}}_{kj}\Vert }_2)|\le \sqrt{|A_1|}{\Vert {\mathit{\beta ̃}}_{k{A}_1}-{\mathit{\beta }}_{k{A}_1}\Vert }_2\le \sqrt{|A_1|}{\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2$. These two expressions indicate that

$${\mathit{\nu }}_k^T{\mathit{\nu }}_k-2{\mathit{\eta }}_k^T{\mathit{\nu }}_k\le {\lambda }_{k1}\sqrt{|A_1|}{\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2.$$ (A.12)

Let ${\mathit{\eta }}_k^{*}$ be the projection of η_k on the span of ${\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_{A_2}$; i.e., ${\mathit{\eta }}_k^{*}={\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_{A_2}{({\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}{\mathbf{Z}}_{A_2})}^{-1}{\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}^{1/2}{\mathit{\eta }}_k$. By Cauchy-Schwarz inequality and ab ≤ a² + b²/4, we have that

$$2|{\mathit{\eta }}_k^T{\mathit{\nu }}_k|\le 2{\Vert {\mathit{\eta }}_k^{*}\Vert }_2·{\Vert {\mathit{\nu }}_k\Vert }_2\le 2{\Vert {\mathit{\eta }}_k^{*}\Vert }_2^2+\frac{1}{2}{\Vert {\mathit{\nu }}_k\Vert }_2^2.$$ (A.13)

From (A.12) and (A.13), we have

$${\mathit{\nu }}_k^T{\mathit{\nu }}_k\le 4{\Vert {\mathit{\eta }}_k^{*}\Vert }_2^2+2{\lambda }_{k1}\sqrt{|A_1|}{\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2.$$ (A.14)

By the definition of D_k1, we know that ${\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}{\mathbf{Z}}_{A_2}/n$ is a nonnegative definite matrix and its smallest positive eigenvalue c_n* exists. Under Assumptions A5 and B3, by Lemma 3 in Huang et al. (2010) and part (i), we have $c_{n*}\asymp m_n^{-1}$ with probability converging to one. Since ${\Vert {\mathit{\nu }}_k\Vert }_2^2\ge n{c}_{n*}{\Vert {\mathrm{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2$ and 2ab ≤ a² + b², from (A.14), we have

$$n{c}_{n*}{\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2\le 4{\Vert {\mathit{\eta }}_k^{*}\Vert }_2^2+\frac{{(2{\lambda }_{k1}\sqrt{|A_1|})}^2}{2n{c}_{n*}}+\frac{1}{2}n{c}_{n*}{\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2.$$

It follows that

$${\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2\le \frac{8{\Vert {\mathit{\eta }}_k^{*}\Vert }_2^2}{n{c}_{n*}}+\frac{4{\lambda }_{k1}^2|A_1|}{n^2{c}_{n*}^2}.$$ (A.15)

Let $f_k(\mathrm{X̂}(t_i))={\sum }_{j=1}^p{f}_{kj}({\mathrm{X̂}}_j(t_i)),f_{kA}(\mathrm{X̂}(t_i))={\sum }_{j\in A}{f}_{kj}({\mathrm{X̂}}_j(t_i)),f_k^{*}(\mathrm{X̂}(t_i))={\sum }_{j=1}^p{f}_{kj}^{*}({\mathrm{X̂}}_j(t_i))$ and $f_{kA}^{*}(\mathrm{X̂}(t_i))={\sum }_{j\in A}{f}_{kj}^{*}({\mathrm{X̂}}_j(t_i))$ with f^* (․) Defined by (2.4). For each component η_i of η_k, we have

$${\eta }_i=d_{k1}^{1/2}(t_i)[H_k(t_i)-{\mathrm{H̄}}_k-\sum _{j\in A_2}{\mathbf{Z}}_{ij}^T{\mathit{\beta }}_{kj}]=d_{k1}^{1/2}(t_i)\{[{\mathrm{X̂}}_k^{\prime }(t_i)-X_k^{\prime }(t_i)]+[X_k^{\prime }(t_i)-{\mu }_k-f_k(X(t_i))]+({\mu }_k-{\mathrm{H̄}}_k)+[f_{k{A}_2}(X(t_i))-f_{k,A_2}(\mathrm{X̂}(t_i))]+[f_{k{A}_2}(\mathrm{X̂}(t_i))-f_{k{A}_2}^{*}(\mathrm{X̂}(t_i))]\}=d_{k1}^{1/2}(t_i)\{[{\mathrm{\Gamma }}_k(t_i)+({\mu }_k-{\mathrm{H̄}}_k)+[f_{k{A}_2}(X(t_i))-f_{k{A}_2}(\mathrm{X̂}(t_i))]+[f_{k{A}_2}(\mathrm{X̂}(t_i))-f_{k{A}_2}^{*}(\mathrm{X̂}(t_i))]\}.$$

Since |μ_k − H̄_k|² = O_p(n⁻¹) and ${\Vert f_{kj}-f_{kj}^{*}\Vert }_{\infty }=O(m_n^{-\varrho })$, we have

$${\Vert {\mathit{\eta }}_k^{*}\Vert }_2^2\le 2{\Vert {\mathbf{\Gamma }}_k^{*}\Vert }_2^2+2{\Vert {\mathbf{\Lambda }}_k^{*}\Vert }_2^2+O_p(1)+O(n{d}_{n2}{m}_n^{-2\varrho }),$$ (A.16)

where ${\mathbf{\Gamma }}_k^{*}$ and ${\mathbf{\Lambda }}_k^{*}$ are projections of Г_k = {Г_k(t₁), ⋯, Г_k(t_n)}^T and Λ_k = {f_kA2(X̂ (t₁)), ⋯, f_kA2 (X̂ (t_n))}^T on the span of ${\mathbf{D}}_{k1}^{1/2}{\mathbf{Z}}_{A_2}$, respectively. We have ${\Vert {\mathbf{\Gamma }}_k^{*}\Vert }_2^2={\Vert {({\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}{\mathbf{Z}}_{A_2})}^{-1/2}{\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k\Vert }_2^2\le 1/n{c}_{n*}{\Vert {\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k\Vert }_2^2$. Now

$$\underset{A:|A|\le d_{n2}}{\text{max}}{\Vert {\mathbf{Z}}_{A_2}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k\Vert }_2^2=\underset{A:|A|\le d_{n2}}{\text{max}}\sum _{j\in A}{\Vert {\mathbf{Z}}_j^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k\Vert }_2^2\le d_{n2}{m}_n\underset{1\le j\le p,1\le m\le m_n}{\text{max}}{|{𝒵}_{jm}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k|}^2,$$

where 𝒵_jm = {ψ_m(X̂_j (t₁)), ⋯, ψ_m(X̂_j(t_i))}^T. By Lemma A.1, we have

$$\underset{1\le j\le p,1\le m\le m_n}{\text{max}}{|{𝒵}_{jm}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k|}^2=n{m}_n^{-1}\underset{1\le j\le p,1\le m\le m_n}{\text{max}}{|{(m_n/n)}^{1/2}{𝒵}_{jm}^T{\mathbf{D}}_{k1}^{1/2}{\mathbf{\Gamma }}_k|}^2=O_p(1)n{m}_n^{-1}\text{log}(p{m}_n).$$

It follows that,

$${\Vert {\mathbf{\Gamma }}_k^{*}\Vert }_2^2=O_p(1)\frac{d_{n2}\text{log}(p{m}_n)}{c_{n*}}\text{and similarly}{\Vert {\mathbf{\Lambda }}_k^{*}\Vert }_2^2=O_p(1)\frac{d_{n2}\text{log}(p{m}_n)}{c_{n*}}.$$ (A.17)

Combining (A.15)–(A.17), we get

$${\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2=O_p\left(\frac{d_{n2}\text{log}(p{m}_n)}{n{c}_{n*}^2}\right)+O_p\left(\frac{1}{n{c}_{n*}}\right)+O\left(\frac{d_{n2}{m}_n^{-2\varrho }}{c_{n*}}\right)+\frac{4{\lambda }_{k1}^2|A_1|}{n^2{c}_{n*}^2}.$$

Since d_n2 = O_p(q), $c_{n*}\asymp m_n^{-1}$ with probability converging to one, we have

$${\Vert {\mathit{\beta ̃}}_{k{A}_2}-{\mathit{\beta }}_{k{A}_2}\Vert }_2^2=O_p\left(\frac{m_n^2\text{log}(p{m}_n)}{n}\right)+O_p\left(\frac{m_n}{n}\right)+O\left(\frac{1}{m_n^{2\varrho -1}}\right)+O\left(\frac{m_n^2{\lambda }_{k1}^2}{n^2}\right).$$ (A.18)

This completes the proof of part (iii).

We now prove part (ii). Under Assumption B2, ‖f_kj‖₂ ≥ c_f, 1 ≤ j ≤ q,${\Vert f_{kj}-f_{kj}^{*}\Vert }_2=O(m_n^{-\varrho })$ and ${\Vert f_{kj}^{*}\Vert }_2\ge {\Vert f_{kj}\Vert }_2-{\Vert f_{kj}-f_{kj}^{*}\Vert }_2$, we have ${\Vert f_{kj}^{*}\Vert }_2\ge 0.5c_f$ for n sufficiently large. By a result of de Boor (2001), see also (12) of Stone (1986), there are positive constants c₁ and c₂ such that $c_1{m}_n^{-1}{\Vert {\mathit{\beta }}_{kj}\Vert }_2^2\le {\Vert f_{kj}^{*}\Vert }_2^2\le c_2{m}_n^{-1}{\Vert {\mathit{\beta }}_{kj}\Vert }_2^2$. It follows that ${\Vert {\mathit{\beta }}_{kj}\Vert }_2^2\ge c_2^{-1}{m}_n{\Vert f_{kj}^{*}\Vert }_2^2\ge 0.25c_2^{-1}{c}_f^2{m}_n$. Therefore, if ‖β_kj‖₂ ≠ 0 but ‖β̃_kj‖₂ = 0, then ${\Vert {\mathit{\beta ̃}}_{kj}-{\mathit{\beta }}_{kj}\Vert }_2^2\ge 0.25c_2^{-1}{c}_f^2{m}_n$, which contradicts part (iii) since $m_n^2\text{log}(p{m}_n)/n\to 0$ and $({\lambda }_{k1}^2{m}_n^2)/n^2\to 0$ as n → ∞.

Proof of Theorem 2. By the definition of _kj, 1 ≤ j ≤ p, parts (i) and (ii) follow from parts (i) and (ii) of Theorem 1 directly. Now, consider part (iii). By the properties of spline (de Boor, 2001), there exist positive constants c₁ and c₂ such that $c_1{m}_n^{-1}{\Vert {\mathit{\beta ̃}}_{kj}-{\mathit{\beta }}_{kj}\Vert }_2^2\le {\Vert {\mathrm{f̃}}_{kj}-f_{kj}^{*}\Vert }_2^2\le c_2{m}_n^{-1}{\Vert {\mathit{\beta ̃}}_{kj}-{\mathit{\beta }}_{kj}\Vert }_2^2$ Thus

$${\Vert {\mathrm{f̃}}_{kj}-f_{kj}^{*}\Vert }_2^2=O_p\left(\frac{m_n\text{log}(p{m}_n)}{n}\right)+O_p(\frac{1}{n})+O\left(\frac{1}{m_n^{2\varrho }}\right)+O\left(\frac{4m_n{\lambda }_{k1}^2}{n^2}\right).$$ (A.19)

By Assumption B3, ${\Vert f_{kj}-f_{kj}^{*}\Vert }_2^2=O(m_n^{-2\varrho })$. Part (iii) follows.

Corollary 1 follows from Theorem 2 directly. The proof of Theorem 3 essentially follows the proof of Corollary 2 in Huang et al. (2010) by similar changes to those given in the proof of part (iii) of Theorem 1, and we omit it here.