Simple network motifs can capture key characteristics of the floral transition in Arabidopsis

Abstract

The floral transition is a key decision during plant development. While different species have evolved diverse pathways to respond to different environmental cues to flower in the correct season, key properties such as irreversibility and robustness to fluctuating signals appear to be conserved. We have used mathematical modeling to demonstrate how minimal regulatory networks of core components are sufficient to capture these behaviors. Simplified models inevitably miss finer details of the biological system, yet they provide a tractable route to understanding the overall system behavior. We combined models with experimental data to qualitatively reproduce characteristics of the floral transition and to quantitatively scale the network to fit with available leaf numbers. Our study highlights the value of pursuing an iterative approach combining modeling with experimental work to capture key features of complex systems.

Global approaches to understand the regulatory transcriptional network involved in controlling the floral transition have revealed that hundreds of transcripts are specifically affected in their expression in the apex upon floral induction.^1-4 Modeling such large genetic regulatory networks is a challenging task as the determination of all relevant parameters is rarely experimentally feasible. The limited knowledge of component concentrations and kinetic interactions can result in a mathematically highly underdetermined problem. This means that the available data are not sufficient to uniquely determine the underlying parameters in the model, something that with typical biological data and models is rarely achieved.⁵ Methods have been developed, such as Boolean networks or systems identification, which simplify the description, thereby reducing the numbers of parameters. Boolean networks aim to capture the underlying biology in that the gene network structure is maintained but the complexity of the interactions is reduced, whereas systems identification (“black box”) focuses on capturing the overall behavior, typically employing small systems of linear equations that do not map well onto the underlying biological mechanisms.^6,7 Another approach is to reduce the gene network while preserving its core structure. Following this strategy,⁸ we sought to simplify the large regulatory network that controls flowering down to a core set of regulatory activities.⁹ As shown in Jaeger et al. (2013), a fairly simple network of core flowering time hubs¹⁰ is able to capture important characteristics of the floral transition.⁸ We approximated the effect of the various regulatory pathways that govern the floral transition by assuming they converge on the key regulator of flowering in higher plants, FT.^11-15 FT expression increases under inductive conditions, and together with the FD transcription factor,^16,17 FT activates key floral meristem identity genes such as AP1. For a number of species, homologs of the Arabidopsis master regulator FT are a core element of the photoperiod pathway.^18,19 We use AP1 hub levels as a proxy for the flowering state. Rosette leaves, cauline leaves, or flowers are produced based on the levels of AP1 in the model. Increasing FT signals promote flowering time, noisy input signals are filtered out, and once initiated, the transition is irreversible. Although the degree to which this behavior manifests itself is very much parameter dependent, at a qualitative level the model is consistent with the experimental observations. Furthermore, the model could be scaled to available leaf number data for a number of mutant genotypes. The modeling suggested how TFL1 signals contribute to the molecular basis for a non-flowering phenotype that has not been understood until now. For an extended network we found that, for some parameter values, initial levels of LFY and TFL1 seem to control the final determinacy of the cell. Cells with higher initial TFL1 levels are able to repress LFY, and thus also AP1, to remain in a vegetative state, or high initial LFY levels can cause a floral fate as specified by AP1 levels.

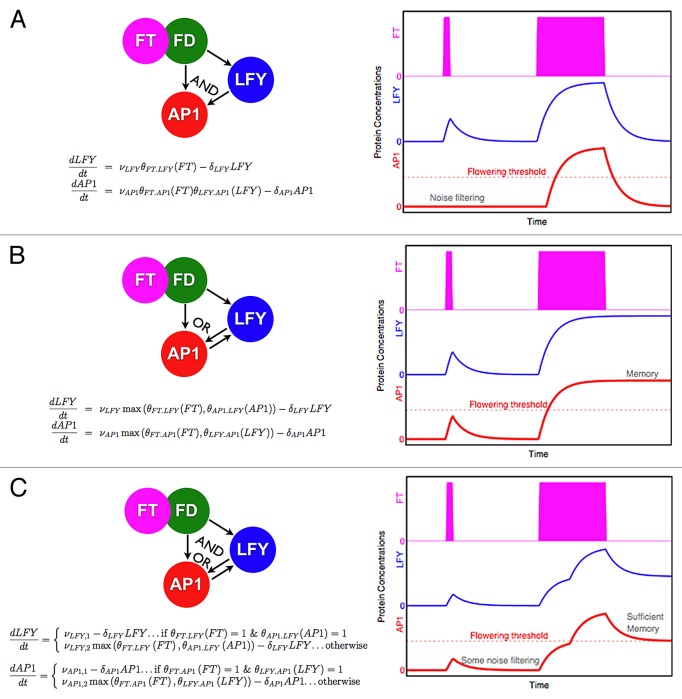
Here we demonstrate how 2 important properties of the floral transition, namely noise-filtering and irreversibility, can be implemented by 3-node networks in feed-forward loops. The coherent feed-forward loop is a network motif that is commonly found in signaling networks.²⁰ As a major floral pathway integrator, we have placed the active FT/FD complex^16,17 at the start of the transcriptional feed-forward loop, upregulating another integrator, the LFY hub (which includes the functional effect of SOC1), which both activate the floral initiator hub AP1,^21,22 (Fig. 1A). If the joint regulation is with AND logic, this simple network has persistence detection and thus is able to be used as a noise filter that removes small blips in a signal.²⁰ The equations are shown in Figure 1 and explained in the supplemental information along with the parameters and an IPython notebook.²⁷ As the correct timing of the floral transition is crucial, it is important that the system is not incorrectly activated by noise. Another similar network, called regulated feedback, that uses an OR gating can exhibit irreversibility. With the same 3-node set up, an extra activating connection between the 2 targets, LFY and AP1, of the first transcription factor, FT/FD, will result in the targets being stably on once activated, (Fig. 1B). AP1 mutually activates LFY in a positive feedback loop, thus creating the important memory element that is responsible for irreversibility of a plant committed to flowering. So while these simple network motifs capture separate characteristics of the floral transition, they are a crude approximation to the larger system.^23,24 Both some level of noise filtering and irreversibility as well as the qualitative fit to ft-10 and lfy-12 mutants can be achieved by introducing 2 transcription rates,¹⁰ a low rate that can be activated by either FT or LFY and a higher rate that requires the presence of both FT and LFY, (Fig. 1C).

Figure 1. Simple network motifs can capture characteristics of the floral transition. On the left hand side of the figure, 3 simple networks are shown. The nodes consist of the complex FT with FD, and the floral proteins LFY and AP1. On the right hand side, we show the responses of LFY (blue) and AP1 (red) to a short and a long incoming FT signal (magenta). The model uses a set of ordinary differential equations to describe the dynamic behavior of the system. We used step functions for the transcriptional activation of genes and AND, OR, and AND/OR gating, depending on the network. In (A) a coherent feed-forward loop²⁰ using an AND gate at AP1 is shown. This network motif has been described previously^20,26 and has been shown to exhibit noise filtering properties for short bursts of the incoming signal that are below the delay time through the different routes in the pathway. In (B) we show a regulated feed-forward loop with an OR gate at AP1. Once LFY reaches a concentration level that can activate AP1, this interaction is sufficient to maintain AP1 production even in the absence of the incoming signal FT. The network therefore shows a memory effect and irreversibility.²⁶ In (C) we combine the key features of both networks. The logic gating uses OR for transcriptional activation at a reduced level but requires AND for maximal activation. This gives rise to compromised characteristics for the individual properties but through the introduction of a flowering threshold for AP1 it is possible to capture a level of robustness to noise and partial memory that, depending on the threshold choice and parameters of the model, can give rise to irreversibility. These networks are reductions of the simple network presented in Jaeger et al. (2013) that included additional nodes with connections and Hill type gene activation.¹⁰ The ordinary differential equations governing the behavior of LFY and AP1 are given below the network motifs. All initial conditions are 0. The FT signal is modeled as a step function active at time points given in the supplement. An IPython notebook²⁷ to enable full reproducibility of this work can be found as supplemental material and is also available from Nick Pullen (nick.pullen@jic.ac.uk).

In summary, we have sought to show how simple regulatory networks can capture important properties of the floral transition. Genes with similar effects can be grouped into distinct hubs (denoted by underlining) or functional modules.²⁵ Such a reduced network that represents the core structure underlying the floral transition can be mapped to the simple feed-forward loops discussed above. Such a simple 3-node system, as presented here, can give intuitive understanding to a complex biological system. We point out that even for these simple networks, the available data was not sufficient to provide good estimates of the parameters. However, predictions¹⁰ can be made without precise knowledge of all the parameters.⁵ Adding further hubs to this network, for example including the floral repressor TFL1, is relatively straightforward.¹⁰ To begin modeling a new pathway, looking for the basic properties of simple networks that exhibit the desired behavior may be a good first step. As with all simplifications, this approach inevitably cannot account for the full spectrum of interacting pathways and variables seen in nature, but it may be a useful entry point for an iterative modeling-experimental cycle.

Glossary

Abbreviations:

FT

Flowering Locus T

FD

Flowering Locus D

TFL1

Terminal Flower 1

AP1

Apetala 1

LFY

Leafy

ODE

Ordinary differential equation

Jaeger KE, Pullen N, Lamzin S, Morris RJ, Wigge PA. Interlocking feedback loops govern the dynamic behavior of the floral transition in Arabidopsis. Plant Cell. 2013;25:820–33. doi: 10.1105/tpc.113.109355.

10.4161/psb.26149

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Supplemental Materials

Supplemental materials may be found here: http://www.landesbioscience.com/journals/psb/article/26149/