The role of covariate heterogeneity in meta-analysis of gene-environment interactions with quantitative traits

Abstract

With challenges in data harmonization and covariate heterogeneity across various data sources, meta-analysis of gene-environment interaction studies can often involve subtle statistical issues. In this paper, we study the effect of environmental covariate heterogeneity (within and between cohorts) on two approaches for fixed-effect meta-analysis: the standard inverse-variance weighted meta-analysis and a meta-regression approach. Akin to the results in Simmonds and Higgins (2007), we obtain analytic efficiency results for both methods under the assumption of gene-environment independence. The relative efficiency of the two methods depends on the ratio of within- versus between- cohort variability of the environmental covariate. We propose to use an adaptively weighted estimator (AWE), between meta-analysis and meta-regression, for the interaction parameter. The AWE retains full efficiency of the joint analysis using individual level data under certain natural assumptions. Lin and Zeng (2010a, b) showed that a multivariate inverse-variance weighted estimator also had asymptotically full efficiency as joint analysis using individual level data, if the estimates with full covariance matrices for all the common parameters are pooled across all studies. We show consistency of our work with Lin and Zeng (2010a, b). Without sacrificing much efficiency, the AWE uses only univariate summary statistics from each study, and bypasses issues with sharing individual level data or full covariance matrices across studies. We compare the performance of the methods both analytically and numerically. The methods are illustrated through meta-analysis of interaction between Single Nucleotide Polymorphisms in FTO gene and body mass index on high-density lipoprotein cholesterol data from a set of eight studies of type 2 diabetes.

1 Introduction

Genome-wide association studies (GWAS) provide tremendous opportunities for large-scale exploration of associations between genetic variants and complex traits. Searching genetic associations based on GWAS has been successfully identifying marginal effects of variants at multiple susceptibility loci for a wide spectrum of complex traits, e.g. type 2 diabetes (T2D) (Scott et al. (2007), Zeggini et al. (2008), Morris et al. (2012), Saxena et al. (2013)), cardiovascular outcomes (Psaty et al. (2009), Sarwar et al. (2012)) and cancer (Song et al., 2013). The agnostic discovery strategy of GWAS can be used to detect gene-environment interactions (GEI) that can further characterize the genetic architecture of complex traits through sub-group or joint effects (Khoury and Wacholder (2009); Mukherjee et al. (2012)). In general, the definition of ‘environment’ can be broad, including demographic factors (age, gender etc.), behavioral factors (smoking, alcohol consumption, diet, medication use etc.), and external factors (exposure to air pollution, radio-active substances etc.). Complex traits are influenced by both genetic and environmental factors and possibly their interaction, e.g., physical activity appeared to attenuate the effect of fat mass associated FTO gene variants on obesity risk (Kilpeläinen et al., 2011). With limited number of findings on GEIs so far, it is likely that the GEI effects are small to modest, warranting the need for larger sample sizes and collaboration across different study sites for joint or meta-analysis. Many collaborative networks have been formed to share individual or summary level data from multiple GWAS of related traits, e.g. the DIAGRAM (T2D) (Zeggini et al. (2008), Voight et al. (2010), Morris et al. (2012)), MAGIC (glucose and insulin related traits) (Dupuis et al. (2010), Scott et al. (2012)), CHARGE (heart and aging research) (Psaty et al., 2009), GIANT (anthropometrics) (Speliotes et al., 2010), and Global Lipids (Teslovich et al., 2010) GWAS consortia. There are also computationally efficient tools (e.g. METAL (Willer et al., 2010)) to implement GWA meta-analysis (GWAMA). However, there are relatively few papers that explore analytical issues for meta-analysis of GEI (e.g. Manning et al. (2011), Aschard et al. (2011) to name a couple) compared to meta-analysis of marginal genetic associations.

Several meta-analytic techniques used for randomized clinical trials can be adapted in genetic epidemiology, e.g., the fixed-effects model (FEM) (Whitehead and Whitehead, 1991) and random-effects model (REM) (DerSimonian and Laird, 1986). The term ‘fixed effect model’ in the classical literature (Whitehead and Whitehead (1991), Fleiss (1993), Borenstein et al. (2010), Lin and Zeng (2010b)) most often refers to a model with fixed and common effect. But in general, ‘fixed effects model’ (in plural) only requires that there are fixed and unrelated effects in each study, regardless of the homogeneity assumption. Effect homogeneity can be tested by the Cochran’s Q-test (Cochran, 1954). In this paper, we consider the fixed and common effect framework as in Lin and Zeng (2010b) to derive our analytical results. We comment on this choice as opposed to a general fixed effects model where the interaction parameter can be different across studies later in the paper.

The joint analysis of individual patient data (IPD) from all studies is typically regarded as the ‘gold standard’ for evidence synthesis. However, considerable time and resources are required to share individual level data even in an existing consortium. We refer to the joint analysis of raw data from all studies as IPD analysis (also called mega-analysis in some papers, e.g. Lin and Zeng (2010a)), and classify the methods that combine summary statistics derived from analysis of different studies as meta-analysis. A natural question to ask is how much efficiency gain, if any, can be achieved by analyzing IPD over meta-analysis. Recently, Lin and Zeng (2010b) considered a multivariate IVW (MIVW) estimator under the common effect model. In constructing the MIVW, if the estimates with full covariance matrix for all the common parameters are pooled across studies, then the MIVW is asymptotically equivalent to the IPD estimator. However, in meta-analysis of published results, it is often difficult to obtain the full covariance matrix, while univariate summary statistics (e.g. estimate and standard error) for the effects of interest are more likely to be available. Lin and Zeng also quantified the efficiency loss of using an univariate IVW (UIVW) versus a MIVW estimator. The results from Lin and Zeng are derived in a very general setting. In this paper, we specifically focus on the estimation and testing of GEI parameter. Our goal is to construct estimator for GEI parameter using only univariate summary statistics, bypassing issues with sharing individual level data or multivariate covariance matrices across studies, without sacrificing much efficiency or incurring increased bias.

Another pragmatic question to ask is whether we can detect GEI from summary statistics obtained from previously conducted genome-wide meta-analysis of marginal genetic effects, without the knowledge of IPD. Meta-regression (MR) is a regression-based technique to investigate whether some particular study-level covariates explain heterogeneity among effect estimates from multiple studies. Many studies (e.g., Simmonds and Higgins (2007); Kovalchik (2013)) have compared aggregate data analysis (e.g. MR) with IPD analysis to detect treatment-biomarker interactions for randomized clinical trials (analogous to gene-environment interactions in our case). Simmonds and Higgins considered three methods IPD, UIVW and MR and showed that under certain natural assumptions, analytical power formulae to detect interactions can be expressed in terms of total, within and between study sum of squares (TSS, WSS and BSS respectively) corresponding to the environmental covariate. In absence of IPD, they recommended using UIVW rather than MR if the WSS exceeds BSS and vice versa. We borrow from their work to derive similar analytical expressions for testing GEI under certain assumptions.

Instead of making a discrete choice between UIVW versus MR, we propose a novel adaptively weighted estimator (AWE) combining UIVW and MR, and archiving the same asymptotic efficiency as the IPD estimator under certain conditions. The AWE has two major advantages over the MIVW estimator shown in the following main text: (1) AWE requires only univariate summary statistics from each study (study-specific estimate and standard error for the marginal association of G and GEI parameter, and study-level mean of E); (2) AWE has less efficiency loss compared to MIVW under model misspecification, for example, when the main effects of G or E are heterogeneous across studies or when a continuous covariate E is centered within each study at the study level mean. Our simulation studies indicate that AWE is very robust across multiple model violation scenarios we considered, including presence of non-linearity in interaction term.

The rest of the paper is organized as follows. In the methods section we describe different strategies for meta-analysis of GEI, followed by analytical results on bias, variance and power properties of the newly proposed method. A comprehensive simulation study was performed to assess the performance of the meta-analysis methods under a variety of scenarios. We primarily focus on the issue of covariate heterogeneity, but also explore several other important factors that could potentially affect the relative performance of these methods: (1) departures from gene-environment independence; (2) heterogeneity in minor allele frequencies (MAFs) across cohorts; (3) lack of a common set of covariates to adjust for across studies; (4) misspecification of the genetic susceptibility model (dominant/co-dominant/additive); and finally (5) the presence of a non-linear form of interaction. In the results section, we report simulation findings followed by an illustrative example, where we examine whether variants in FTO gene modify the effect of environmental factors (age and BMI) on high-density lipoprotein cholesterol (HDL-C) levels, a T2D related quantitative trait. This paper is expected to provide useful insights and guidelines for practitioners conducting meta-analyses of GEI.

2 Methods

2.1 Meta-analysis of GEI under a common effect model

Consider a quantitative trait Y , a continuous environmental exposure E, a bi-allelic genetic locus G with genotypes of AA, Aa and aa (where A is the minor allele), and other covariates Z. Suppose that there are K independent studies and a total of N participants, with n_k participants in the k-th study, $k=1,\dots ,K,{\sum }_{k=1}^K{n}_k=N$. Let Y_ki, E_ki, G_ki and Z_ki be the corresponding observations for participant i in study k, for i = 1, ..., n_k and k = 1, ..., K. The assumed model for individual responses follows

$$Y_{ki}={\beta }_{0k}+{\beta }_G{G}_{ki}+{\beta }_E{E}_{ki}+\delta G_{ki}{E}_{ki}+{\beta }_Z^T{\mathit{Z}}_{ki}+{∊}_{ki},$$ (1)

where β_0k is the study specific intercept, β_G, β_E and β_Z are the main effects corresponding to G, E and Z, and δ is the GEI effect of primary interest. The vector β = (β_G, β_E, δ, β_Z) is assumed to be fixed and common across studies. The random errors ε_ki's are assumed as ${∊}_{ki}\stackrel{iid}{\sim }N(0,{\sigma }_k^2)$. Our interest lies in estimating the common interaction parameter δ and in testing H₀ : δ = 0.

There are multiple reasons for assuming a common effect model (1). First, this model is used quite frequently in the literature (Lin and Zeng (2010a),Lin and Zeng (2010b), Hartung et al. (2011)). Second, the analytical derivation of the relative efficiency and power are facilitated; Third, meta-regression can only be meaningfully conceptualized if the interaction parameter is assumed to be same across studies; Fourth, with unrelated but distinct fixed effects across studies, it is often hard to find a scientific interpretation/relevance of the limiting/expected value of the population parameter to which the standard inverse-variance weighted estimator converges to; thus quantities like bias and mean-squared error become less interpretable. Finally, there was no evidence of effect heterogeneity for the interaction parameters in our T2D data analysis example of 8 European studies. However, as we will discuss subsequently, the ‘common effect’ assumption can be relaxed for testing purposes and most of the methods we discuss are valid to test the stronger null hypothesis H₀ : δ₁ = ... = δ_K = 0, if we allowed study specific parameters δ_k in (1).

Various susceptibility models including the dominant model (G = 1 if AA and Aa; G = 0 if aa), recessive model (G = 1 if AA; G = 0 if Aa and aa), additive model (G = 2 if AA; G = 1 if Aa; G = 0 if aa) and co-dominant model (G = AA, Aa or aa with aa as the reference level) are considered. For co-dominant model, ${\beta }_G=({\beta }_G^{Aa},{\beta }_G^{AA})$ and δ = (δ^Aa, δ^AA) for genotypes Aa and AA can be modified accordingly in model (1).

In the following, we first describe in section 2.1.1 three traditional approaches to detect GEI under model (1). The approaches are IPD analysis, standard meta-analysis (UIVW or MIVW) and MR. For the sake of completeness, we also describe a two-step estimator previously suggested by Simmonds and Higgins (2007). We then propose the new AWE in section 2.1.2. Throughout the paper, we use the generic notation $\mathbf{v}\left(\widehat{\delta }\right)$ for the asymptotic variance (covariance matrix for multivariate $\widehat{\delta }$) of any given estimator $\widehat{\delta }$, and $\widehat{\mathbf{v}}\left(\widehat{\delta }\right)$ for the corresponding estimated variance.

2.1.1 Existing methods

(i) Individual patient data analysis (IPD)

The IPD analysis fits model (1) using individual level data. Methods such as weighted least square (WLS) can be used to handle the heterogeneous ${\sigma }_k^2$ across studies, if ${\sigma }_k^2$ can be estimated with sufficient accuracy. However, for simplicity, we consider a simple linear regression model that assumes common residual variance ${\sigma }_k^2={\sigma }^2$ for k = 1, ..., K in (1), as the standard implementation of the IPD analysis. Denote the maximum likelihood estimate (MLE) of δ as ${\widehat{\delta }}^{\mathrm{IPD}}$, and its estimated variance as $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)$.

(ii) Meta-analysis using inverse-variance weighted estimator: Since the data required for IPD analysis are seldom available in published results, meta-analysis combining summary statistics across individual studies is often used. We consider some variants of IVW estimator under model (1). (ii.A) UIVW: A UIVW estimator needs the collection of the MLEs ${\widehat{\delta }}_k$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}_k\right)$ estimated from model (1) using data from only study k. Under the above model, ${\widehat{\delta }}_k\stackrel{iid}{\sim }N(\delta ,\mathbf{v}\left({\widehat{\delta }}_k\right))$. The UIVW estimator is given by,

$$\begin{array}{cc}\hfill & {\widehat{\delta }}^{\mathrm{UIVW}}={\left\{\sum _k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}\right\}}^{-1}\sum _k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}{\widehat{\delta }}_k\hfill \\ \hfill & \widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)={\left\{\sum _k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}\right\}}^{-1}.\hfill \end{array}$$

The validity of the method requires that ${\widehat{\delta }}_k$ is asymptotically normal ${\widehat{\delta }}_k\stackrel{iid}{\sim }N(\delta ,\mathbf{v}\left({\widehat{\delta }}_k\right))$ for a large n_k and the asymptotic variance $\mathbf{v}\left({\widehat{\delta }}_k\right)$ can be estimated by $\widehat{\mathbf{v}}\left({\widehat{\delta }}_k\right)$ with negligible error (Whitehead and Whitehead, 1991). We refer to these conditions as ‘standard conditions’ throughout, and we note that it is often implicitly assumed to hold in classic meta-analysis literature (e.g., DerSimonian and Laird (1986), Whitehead and Whitehead (1991), Lin and Zeng (2010b) ).

(ii.B) MIVW: Let ${\widehat{\beta }}_k=({\widehat{\beta }}_{Gk},{\widehat{\beta }}_{Ek},{\widehat{\delta }}_k,{\widehat{\beta }}_{Zk})$ be the MLE of β from study k, with estimated variance-covariance matrix $\widehat{\mathbf{v}}\left({\widehat{\beta }}_k\right)$. When both ${\widehat{\beta }}_k$ and $(\widehat{\mathbf{v}}\left({\widehat{\beta }}_k\right)$ are available from each study, we consider the MIVW estimator following Lin and Zeng (2010b),

$$\begin{array}{cc}\hfill & {\widehat{\beta }}^{\mathrm{MIVW}}={\left\{\sum _k\widehat{\mathbf{v}}{\left({\widehat{\beta }}_k\right)}^{-1}\right\}}^{-1}\sum _k\widehat{\mathbf{v}}{\left({\widehat{\beta }}_k\right)}^{-1}{\widehat{\beta }}_k\hfill \\ \hfill & \widehat{\mathbf{v}}\left({\widehat{\beta }}^{\mathrm{MIVW}}\right)={\left\{\sum _k\widehat{\mathbf{v}}{\left({\widehat{\beta }}_k\right)}^{-1}\right\}}^{-1}.\hfill \end{array}$$

Then ${\widehat{\delta }}^{\mathrm{MIVW}}$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{MIVW}}\right)$ corresponding to the interaction parameter δ can be obtained from the corresponding element in ${\widehat{\beta }}^{\mathrm{MIVW}}$ and $\widehat{\mathbf{v}}\left({\widehat{\beta }}^{\mathrm{MIVW}}\right)$ respectively. Following Lin and Zeng (2010b), ${\widehat{\delta }}^{\mathrm{MIVW}}$ has full asymptotic efficiency as ${\widehat{\delta }}^{\mathrm{IPD}}$ under the common effect model (1). However the full covariance matrix $\widehat{\mathbf{v}}\left({\widehat{\beta }}_k\right)$ is not likely to appear in meta-analysis of published results and different studies may adjust for different covariates Z. So ${\widehat{\delta }}^{\mathrm{UIVW}}$ remains the most commonly used meta-analytic method in spite of potential efficiency loss as compared to ${\widehat{\delta }}^{\mathrm{MIVW}}$ and ${\widehat{\delta }}^{\mathrm{IPD}}$.

(iii) Meta-regression: The true model (1) implies that the Y − G association depends linearly on E. So we consider a linear MR model to reveal the underlying dependence between the marginal genetic effects and the aggregated study mean values of E (say m_k = δ_i E_ki/n_k). Screening for the marginal effect of G is routinely performed as the first step in GWA analysis. For each study k, we first consider the association model

$$Y_{ki}={\lambda }_{0k}+{\lambda }_{Gk}{G}_{ki}+{\lambda }_{Zk}^{\mathsf{T}}{\mathit{Z}}_{ki}+{\eta }_{ki},i=1,\dots ,n_k.$$ (2)

where the errors ${\eta }_{ki}\stackrel{iid}{\sim }N(0,{\sigma }_{{\eta }_k}^2)$. At the second step, the MLE ${\widehat{\lambda }}_{Gk}$ is regressed on m_k through the MR model

$${\widehat{\lambda }}_{Gk}={\gamma }_0=\gamma m_k+{\nu }_k,k=1,\dots ,K.$$ (3)

To account for the potential heterogeneity in $\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}\right)$ across studies, we consider the WLS estimator of γ, with weight $w_k=\widehat{\mathbf{v}}{\left({\widehat{\lambda }}_{Gk}\right)}^{-1}$ assumed as known, i.e., ${\nu }_k\sim N(0,\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}\right))$. Denote the WLS estimator of γ in model (3) by ${\widehat{\delta }}^{\mathrm{MR}}$. Then ${\widehat{\delta }}^{\mathrm{MR}}$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$ can be expressed as

$$\begin{array}{cc}\hfill {\widehat{\delta }}^{\mathrm{MR}}=& \frac{\left({\sum }_k{w}_k\right)\left({\sum }_k{w}_k{m}_k{\widehat{\lambda }}_{Gk}\right)-\left({\sum }_k{w}_k{m}_k\right)\left({\sum }_k{w}_k{\widehat{\lambda }}_{Gk}\right)}{\left({\sum }_k{w}_k\right)\left({\sum }_k{w}_k{m}_k^2\right)-{\left({\sum }_k{w}_k{m}_k\right)}^2},\hfill \\ \hfill \widehat{\mathbf{v}}\left({\delta }^{\mathrm{MR}}\right)=& \frac{{\sum }_k{w}_k}{\left({\sum }_k{w}_k\right)\left({\sum }_k{w}_k{m}_k^2\right)-{\left({\sum }_k{w}_k{m}_k\right)}^2}{\widehat{\sigma }}^2.\hfill \end{array}$$

The advantage of MR approach is that one can identify GEI with only limited summary data on E (only the mean m_k's) and published results of marginal genetic effects (${\widehat{\lambda }}_{Gk}$ and $\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}\right)$).

(iv) Two-stage estimator

Let $m={\sum }_{k,i}{E}_{ki}∕N$ denote the overall sample mean of E, $s_E^2=N^{-1}{\sum }_{k,i}{(E_{ki}-m)}^2$ be the total sample variance of E, $s_{Ek}^2=n_k^{-1}{\sum }_{k=1}^{n_k}{(E_{ki}-m_k)}^2$ be the sample variance of E within the k-th study. Denote the corresponding population parameters for m, m_k, $s_E^2$, $s_{Ek}^2$ as μ, μ_k, ${\sigma }_E^2$, ${\sigma }_{Ek}^2$ respectively. We make the usual partition of the total sum of squares (T SS) of E as the sum of the within-study sum of squares (W SS) and between-study sum of squares (BSS), i.e., T SS = W SS +BSS, where $TSS={\sum }_{k,i}{(E_{ki}-m)}^2=N{s}_E^2$, $WSS={\sum }_k{\sum }_i{(E_{ki}-m_k)}^2={\sum }_k{n}_k{s}_{Ek}^2$ and $BSS={\sum }_k{n}_k{(m_k-m)}^2$. Throughout this paper, we assume n_k/N → k ∈ (0,1) as N → ∞ Consider the limiting true population quantities as $tss={\sigma }_E^2$, $wss={\sum }_k{\varrho }_k{\sigma }_{Ek}^2$ and $bss={\sum }_k{\varrho }_k{({\mu }_k-\mu )}^2$. We have $TSS∕N\stackrel{p}{\to }tss$, $WSS∕N\stackrel{p}{\to }wss$, $BSS∕N\stackrel{p}{\to }bss$, as N → ∞.

Motivated by the fact that asymptotic relative efficiency (ARE) of ${\widehat{\delta }}^{\mathrm{MR}}$ compared to ${\widehat{\delta }}^{\mathrm{UIVW}}$ is driven by bss/wss, we consider a two-stage approach analogous to Simmonds and Higgins (2007) as

$${\widehat{\delta }}^{\mathrm{TS}}=\{\begin{array}{cc}{\widehat{\delta }}^{\mathrm{UIVW}},\hfill & \text{if}BSS∕WSS\le 1;\hfill \\ {\widehat{\sigma }}^{\mathrm{MR}},\hfill & \text{if}BSS∕WSS>1,\hfill \end{array}\phantom{\}}$$

i.e., using ${\widehat{\delta }}^{\mathrm{UIVW}}$ instead of ${\widehat{\delta }}^{\mathrm{MR}}$ if W SS ≥ BSS and vice versa. Note that ${\widehat{\delta }}^{\mathrm{TS}}$ is an ad-hoc procedure of discretely determining which method to use, based on the statistic BSS/W SS that measures heterogeneity in E between studies relative to within study variation in E.

2.1.2 Adaptively weighted estimator

We note that, using only summary statistics, both ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$ can potentially lack precision. Moreover, ${\widehat{\delta }}^{\mathrm{MR}}$ can have significant ecological bias (Morgenstern (1982), Greenland (1987), Schwartz (1994), Berlin et al. (2002)) if the aggregate data relationship differs from the one observed in individual level data. Thus, we propose an adaptive estimator that combines ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$ to trade-off between bias and efficiency in a data adaptive way. We first prove the following lemma which is also used in Kooperberg and LeBlanc (2008) and Dai et al. (2012).

Lemma 1. Let Y_i be independent random variables with equal variance, for i = 1, ..., n, and let $X_j={(X_{1j},\dots ,X_{nj})}^{\mathsf{T}}$ be the j-th predictor, j = 1, ..., p + q. Let ${\widehat{\lambda }}_j(j=1,\dots ,p)$ and ${\widehat{\beta }}_j$ be the MLEs of the parameters under the two nested linear regression models

$$Y_i={\lambda }_0+\sum _{j=1}^p{\lambda }_j{X}_{ij}+{\eta }_{i}and{Y}_i={\beta }_0+\sum _{j=1}^{p+q}{\beta }_j{X}_{ij}+{∊}_i,$$

then $({\widehat{\lambda }}_1,\dots ,{\widehat{\lambda }}_p)$ and $({\widehat{\beta }}_{p+1},\dots ,{\widehat{\beta }}_{p+q})$ are asymptotically independent.

Proof of Lemma 1 is presented in Appendix B.1.

Applying Lemma 1 to models (1) and (2), the marginal genetic association ${\widehat{\lambda }}_{Gk}$ and GEI ${\widehat{\delta }}_k$ are asymptotically independent within each study k, as they are coming from two nested linear regression models using data within study k. Note that ${\widehat{\delta }}^{\mathrm{UIVW}}$ is a linear combination of ${\widehat{\delta }}_k$, and that ${\widehat{\delta }}^{\mathrm{MR}}$ is a linear combination of ${\widehat{\lambda }}_{Gk}$, then the following corollary holds.

Corollary 1. ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$ are asymptotically independent.

The independence of the two estimators are critical as we can now borrow the classical idea of constructing an IVW estimator using these two independent ingredients. Assuming the standard conditions, we propose an AWE of the form

$${\widehat{\delta }}^{\mathrm{AWE}}={\{\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}\}}^{-1}\{\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}{\widehat{\delta }}^{\mathrm{UIVW}}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}{\widehat{\delta }}^{\mathrm{MR}}\},$$

which combines ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$ using their inverse-variances as weights. In order to calculate ${\widehat{\delta }}^{\mathrm{AWE}}$, summary statistics of study-specific effect estimates (${\widehat{\delta }}_k$, $\widehat{\mathbf{v}}\left({\widehat{\delta }}_k\right)$, ${\widehat{\lambda }}_{Gk}$ and $\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}\right)$) and study-level covariate means m_k are needed from each study k. The intuitive rationale behind the AWE is that, when $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)$ is relatively smaller than $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$, ${\widehat{\delta }}^{\mathrm{AWE}}$ puts more weight on ${\widehat{\delta }}^{\mathrm{UIVW}}$ and vice versa.

Theorem 1. For the class of weighted estimators ${\widehat{\delta }}^{\mathrm{AWE}}\left(w\right)=w{\widehat{\delta }}^{\mathrm{UIVW}}+(1-w){\widehat{\delta }}^{\mathrm{MR}}$, 0 ≤ w ≤ 1, $\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{AWE}}\left(w\right)\right)}^{-1}$ attains its maximum at $\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}$ if and only if the weight $w=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)∕\{\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)+\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)\}$.

Theorem 1 proved in Appendix B.1 establishes the optimality of the inverse variance weights for AWE. A consequence of Theorem 1 is that the precision of ${\widehat{\delta }}^{\mathrm{AWE}}$ is the sum of the precisions of ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$. Under the standard conditions, the estimated variance of the AWE estimator is given by $\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{AWE}}\right)}^{-1}=\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}$. We will further show that ${\widehat{\delta }}^{\mathrm{AWE}}$ is fully efficient as ${\widehat{\delta }}^{\mathrm{IPD}}$ under certain plausible assumptions in section 2.2.

Remark 1: Co-dominant model. For the co-dominant model with $\delta =({\delta }^{Aa},{\delta }^{AA})$, it is straightforward to translate the proposed methods to their bivariate counterparts. In particular, ${\widehat{\delta }}^{\mathrm{IPD}}$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)$ can be directly obtained from (1); ${\widehat{\delta }}^{\mathrm{UIVW}}$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)$ can be obtained as ${\left\{{\sum }_k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}\right\}}^{-1}{\sum }_k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}{\widehat{\delta }}_k$ and ${\left\{{\sum }_k\widehat{\mathbf{v}}{\left({\widehat{\delta }}_k\right)}^{-1}\right\}}^{-1};{\widehat{\delta }}^{\mathrm{MIVW}}$ and $\widehat{\mathbf{v}}\left({\widehat{\delta }}^{\mathrm{MIVW}}\right)$ can be obtained from ${\widehat{\beta }}^{\mathrm{MIVW}}$ and $\widehat{\mathbf{v}}\left({\widehat{\beta }}^{\mathrm{MIVW}}\right)$; MR model can be modified as a multiple response regression ${\widehat{\lambda }}_k={\gamma }_0+\gamma m_k+{\nu }_k$, where ${\widehat{\lambda }}_k={({\widehat{\lambda }}_{Gk}^{Aa},{\widehat{\lambda }}_{Gk}^{AA})}^{\mathsf{T}}$ and ${\nu }_k\stackrel{iid}{\sim }N(0,\widehat{\mathbf{v}}\left({\widehat{\lambda }}_k\right))$. Corollary 1 and Theorem 1 also hold following Lemma 1 for bivariate δ. A bivariate form of AWE can be considered as ${\widehat{\delta }}^{\mathrm{AWE}}={\{\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}\}}^{-1}\{\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}{\widehat{\delta }}^{\mathrm{UIVW}}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}{\widehat{\delta }}^{\mathrm{MR}}\}$.

2.2 Analytical results

This section presents some analytical results regarding bias, variance and power properties for the adaptive estimator described in section 2.1.2. We consider models without covariate Z to simplify the presentation.

2.2.1 Bias

Following classic linear regression and meta-analysis results, ${\widehat{\delta }}^{\mathrm{IPD}}$, ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MIVW}}$ are all asymptotically unbiased estimators of δ. However, ${\widehat{\delta }}^{\mathrm{MR}}$ is not necessarily unbiased for δ in general. The relationship between the marginal effect of G and the study-specific means m_k may differ from the underlying relationship between the marginal effect of G and individual level data for E. This phenomenon is known as ‘ecological bias’ or ‘ecological fallacy’, and is well characterized in the literature (Morgenstern (1982), Greenland (1987), Schwartz (1994)). However, we note that ${\widehat{\delta }}^{\mathrm{MR}}$ is an unbiased estimator of δ under the following G-E independence assumption, which is a plausible assumption well-discussed in the literature. We use the generic notation P (·) to denote the distribution of a random variable.

Assumption 1. P(G, E| study = k) = P(G| study = k)P (E| study = k), for k = 1, ..., K, i.e., G and E are independent within each study.

Proposition 1. Under Assumption 1, ${\widehat{\delta }}^{\mathrm{MR}}$ of model (3) is asymptotically unbiased for δ.

Proof of Proposition 1 is presented in Appendix B.2. In the following Remark 2, we further discuss the issue of potential bias of ${\widehat{\delta }}^{\mathrm{MR}}$ and thus in ${\widehat{\delta }}^{\mathrm{AWE}}$ (which assigns a positive weight on the MR estimator) if Assumption 1 is violated.

Remark 2: Bias of ${\widehat{\delta }}^{\mathrm{MR}}$ and ${\widehat{\delta }}^{\mathrm{AWE}}$. Without Assumption 1, we showed (in Appendix B.2) that the limiting value of the bias of ${\widehat{\delta }}^{\mathrm{MR}}$ is proportional to the ratio tss/bss and the correlation between G and E. If the G-E correlations within each study are 0, then $E\left({\widehat{\delta }}^{\mathrm{MR}}\right)-\delta \stackrel{p}{\to }0$. If Assumption 1 holds, ${\widehat{\delta }}^{\mathrm{AWE}}$ is an asymptotically unbiased estimator of σ as both its components are unbiased. Moreover, we show later in section 2.2.2 that the limiting value of the weight corresponding to ${\widehat{\delta }}^{\mathrm{MR}}$ in ${\widehat{\delta }}^{\mathrm{AWE}}$ is bss/tss. So ${\widehat{\delta }}^{\mathrm{AWE}}$ adaptively puts less weight on ${\widehat{\delta }}^{\mathrm{MR}}$ when the bias of ${\widehat{\delta }}^{\mathrm{MR}}$ increases. We find through our numerical investigation that ${\widehat{\delta }}^{\mathrm{AWE}}$ is robust to potential ecological bias in ${\widehat{\delta }}^{\mathrm{MR}}$ even when the ecological bias is substantial (please see Appendix Figure 9 and Table 6 for the simulation results, and main text Table 4 corresponding to the T2D example).

Table 4.

IPD/Meta-analysis results of GEI for the T2D study, where log transformed HDL-C level was regressed on SNP, age, BMI, sex, T2D status, cohorts, and SNPxE interaction (E as BMI and age in two separate analysis) in the IPD model. Estimates, SEs and CIs have been multiplied by 1000.

Methodsa	rs1121980 (additive) x BMI			P-value*
	Estimate	SEb	95% CIb	Additive	Co-dominant
IPD	1.474	0.687	(0.128,2.821)	0.03**	0.03*
UIVW	1.731	0.675	(0.407 , 3.054)	0.01*	0.02*
MIVW	1.518	0.663	(0.219 , 2.816)	0.02*	0.01*
MR	−0.719	3.136	(−6.866, 5.429)	0.81	0.69
AWE	1.622	0.660	(0.328, 2.916)	0.01*	0.02*
	rs1121980 (additive) x age			Additive Co-dominant
IPD	0.011	0.304	(−0.585 , 0.606)	0.97	0.68*
UIVW	0.046	0.337	(−0.613 , 0.706)	0.89	0.74
MIVW	−0.008	0.307	(−0.610, 0.594)	0.97	0.69
MR	0.180	0.522	(−0.843 , 1.203)	0.73	0.77
AWE	0.086	0.283	(−0.469 , 0.640)	0.76	0.69

^aIPD: individual patient data; UIVW: univariate inverse-variance weighted estimator; MIVW: multivariate inverse-variance weighted estimator; MR: Meta-regression; AWE: adaptively weighted estimator combining UIVW and MR.

^bSE: standard error; CI: confidence interval.

^*indicating significance at α = 0.05 level.

^*indicating whether additive or co-dominant model has smaller AIC under the IPD model.

2.2.2 Variance and Relative Efficiency

Explicit variance formulae $\widehat{\mathbf{v}}\left(\widehat{\delta }\right)$ and $\mathbf{v}\left(\widehat{\delta }\right)$ for each estimator of δ are derived under Assumption 1 in Appendix B.3. Because the linear regression likelihood ${\prod }_{k,i}P(Y_{ki}\mid G_{ki},E_{ki})$ corresponding to model (1) does not use any assumptions about the joint distribution of G and E, the role of the G-E independence assumption in this paper is only to provide simpler expressions for the variances. This is different from case-control studies where assuming G-E independence and using the retrospective likelihood can lead to large gains in efficiency (Piegorsch et al. (1994), Umbach and Weinberg (1997), Chatterjee and Carroll (2005)).

In this section 2.2.2, for simplicity of presentation we assume ${\sigma }_k^2={\sigma }^2$ for k = 1, ..., K, and consider a dominant susceptibility model for stating Theorems 2 and 3. Let G = 1 (G = 0) indicate whether an individual is a carrier (non-carrier) of the minor allele A, and let p_k denote P(G = 1| study = k) the carrier frequencies in study k, k = 1, ... , K.

Theorem 2. Under Assumption 1, $\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{IPD}}\right)}^{-1}\ge \mathbf{v}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)=\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{AWE}}\right)}^{-1}$. The equality holds if and only if p_k = p, for k = 1, 2, ..., K, where p is the common carrier frequency across all studies.

Proof of Theorem 2 is given in Appendix B.4. Under Assumption 1, the precision of ${\widehat{\delta }}^{\mathrm{IPD}}$ is in general greater than that of ${\widehat{\delta }}^{\mathrm{AWE}}$. However, under the additional assumption of homogeneity of the MAFs (Assumption 2 stated below), we have equality $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{AWE}}\right)$.

Assumption 2. The MAFs corresponding to the susceptible SNP are constant across all studies, i.e. p_k = p, for k = 1, 2, ..., K.

Theorem 3. Under Assumptions 1 and 2, $\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{IPD}}\right)}^{-1}=\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{AWE}}\right)}^{-1}=\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\mathbf{v}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}$, where $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)={\left\{Np(1-p)wss\right\}}^{-1}{\sigma }^2$, $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)={\left\{Np(1-p)bss\right\}}^{-1}{\sigma }^2$ and $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{AWE}}\right)={\left\{Np(1-p)tss\right\}}^{-1}{\sigma }^2$.

Proof of Theorem 3 is given in Appendix B.5. Following Theorem 3, the asymptotic variances $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)$, $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)$, $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$ and $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{AWE}}\right)$ are all expressed in terms of covariate heterogeneity of E. The ARE between ${\widehat{\delta }}^{\mathrm{UIVW}}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$ and ${\widehat{\delta }}^{\mathrm{IPD}}$ is wss/tss (bss/tss). So $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)\le \mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$, if wss bss, and vice versa. For the extreme case, when there is no between-study heterogeneity in the study means of E (i.e. μ_k = μ), $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)$), and ${\widehat{\delta }}^{\mathrm{AWE}}$ reduces to ${\widehat{\delta }}^{\mathrm{UIVW}}$; in contrast, if all ${\sigma }_{Ek}^2=0$ (i.e. E is constant within each study), $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)$, and ${\widehat{\delta }}^{\mathrm{AWE}}$ reduces to ${\widehat{\delta }}^{\mathrm{MR}}$.

The limiting weights in ${\widehat{\delta }}^{\mathrm{AWE}}$ can be simplified as $w=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)∕\{\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVR}}\right)+\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MR}}\right)\}=bs{s}^1∕\{ws{s}^{-1}+bs{s}^{-1}\}=wss∕tss$. Since $WSS∕TSS\stackrel{p}{\to }wss∕tss$ and $BSS∕TSS\stackrel{p}{\to }bss∕tss$, as N → ∞ we can use the estimated weights W SS/T SS and BSS/T SS in ${\widehat{\delta }}^{\mathrm{AWE}}$, which leads to

$${\widehat{\delta }}^{\mathrm{AWE}}=\frac{WSS}{TSS}{\widehat{\delta }}^{\mathrm{UIVW}}+\frac{BSS}{TSS}{\widehat{\delta }}^{\mathrm{MR}}.$$

${\widehat{\delta }}^{\mathrm{AWE}}$ adaptively captures the precision trade-off between the two estimators: ${\widehat{\delta }}^{\mathrm{AWE}}$ puts more weight on ${\widehat{\delta }}^{\mathrm{UIVW}}$ if W SS is relatively larger than BSS, and vice versa. In summary, under Assumptions 1 and 2, ${\widehat{\delta }}^{\mathrm{AWE}}$ is a consistent, unbiased, and asymptotically fully efficient estimator, which uses only univariate summary statistics without the knowledge of the original IPD. The operating characteristics for the proposed meta-analytic methods are summarized in Table 1. The results in Theorems 2 and 3 are numerically evaluated through a simulation study to examine the effect of relaxing Assumption 1 or 2, and relaxing the homogeneity assumption of ${\sigma }_k^2$.

Table 1.

Glossary of the meta-analysis methods for GEI with summary properties. [IPD: individual patient data analysis; UIVW: univariate inverse-variance weighted estimator; MIVW: multivariate inverse-variance weighted estimator; MR: Meta-regression; AWE: adaptively weighted estimator combining UIVW and MR. ${\widehat{\lambda }}_k$ stands for estimates of marginal genetic association and ${\widehat{\delta }}_k$ stands for gene-environment interaction respectively.]

Methods	Data shared	Bias	AREa
IPD	individual level data	unbiased	1
UIVW	${\widehat{\delta }}_k,\widehat{v}\left({\widehat{\delta }}_k\right)$	unbiased	wss/tss under Assumptions 1 and 2
MIVW	${\widehat{\beta }}_k,\widehat{v}\left({\widehat{\beta }}_k\right)$	unbiased	1 under assumptions in LZ
MR	${\widehat{\lambda }}_{Gk},\widehat{v}\left({\widehat{\lambda }}_{Gk}\right)$ and mk	unbiased under Assumption 1	bss/tss under Assumptions 1 and 2
AWE	${\widehat{\lambda }}_k,\widehat{v}\left({\widehat{\lambda }}_k\right);{\widehat{\lambda }}_{Gk},\widehat{v}\left({\widehat{\lambda }}_{Gk}\right)$ and m k	unbiased under Assumption 1b	1 under Assumptions 1 and 2

^aARE: asymptotic relative efficiency as compared to ${\widehat{\delta }}^{\mathrm{IPD}}$

^bbias adaptively controlled in AWE.

Remark 3: Additive and co-dominant models. In general, it is difficult to provide analytical results related to ${\widehat{\delta }}^{\mathrm{AWE}}$ in Theorems 2 and 3 for an additive model, but we can directly translate Theorems 2 and 3 for δ^Aa and δ^AA respectively under a co-dominant model if we assume $diag(\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}^{Aa}\right),\widehat{\mathbf{v}}\left({\widehat{\lambda }}_{Gk}^{AA}\right))$ for $\widehat{\mathbf{v}}\left({\widehat{\lambda }}_k\right)$ in the MR model, i.e., two separate MRs. The statements in Theorems 2 and 3 are numerically evaluated for additive and co-dominant models through a simulation study relaxing Assumptions 1 or 2, and relaxing the homogeneity assumption of ${\sigma }_k^2$.

Remark 4: Centering of covariate E. Continuous E is often centered to facilitate the interpretation of β_G as the main effect of G at the mean value of E. Under a meta-analysis set-up, it is natural to consider each study k fits model (1) with E centered at their respective study specific means m_k. For the IPD analysis, it is natural to consider that E is centered at the overall mean m. With these centering strategy, ${\widehat{\delta }}^{\mathrm{IPD}}$, ${\widehat{\delta }}^{\mathrm{UIVW}}$, ${\widehat{\delta }}^{\mathrm{MR}}$ and ${\widehat{\delta }}^{\mathrm{AWE}}$ remain invariant, and results in Theorems 1-3 still hold for the centered models. The details are shown in Appendix B.4. However, properties of ${\widehat{\delta }}^{\mathrm{MIVW}}$ do not hold under the above centering strategy. It is not fully efficient, because m_k-centered model creates artificial heterogeneous main effects of G (depending on m_k) across studies. The m_k-centered model only has two common fixed-effects compared to the true model having three common fixed-effects (Appendix B.4), and this leads to efficiency loss of ${\widehat{\delta }}^{\mathrm{MIVW}}$ according to Lin and Zeng (2010b). In terms of efficiency, ${\widehat{\delta }}^{\mathrm{AWE}}$ is preferable to ${\widehat{\delta }}^{\mathrm{MIVW}}$ when covariate E is m_k-centered using the study level means.

Remark 5: Relaxing the common effect assumption. First, we consider heterogeneous main effects of G and E, namely (δ_Gk, δ_Ek) with a common GEI δ across studies in model (1). To handle effect heterogeneity, we could replace (β_G, β_E) by (β_Gk, β_Ek) in model (1) for the IPD analysis; replace MR model (3) by ${\widehat{\lambda }}_{Gk}={\gamma }_{0k}+\gamma m_k+{\nu }_k$ for the MR analysis; and still use ${\widehat{\delta }}^{\mathrm{UIVW}}$ as it does not require homogeneity of (β_Gk, β_Ek). According to Lin and Zeng (2010b), the modified estimator has the property that $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{IPD}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{MIVW}}\right)=\mathbf{v}\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)$ because δ is the only common parameter across studies. Theorem 1 still holds since it makes no homogeneity assumption on (β_Gk, β_Ek). Then we have $\mathbf{v}\left({\widehat{\delta }}^{\mathrm{AWE}}\right)<\left({\widehat{\delta }}^{\mathrm{MIVW}}\right)$. In terms of precision, ${\widehat{\delta }}^{\mathrm{AWE}}$ is better than ${\widehat{\delta }}^{\mathrm{MIVW}}$ when (β_Gk, β_Ek) are heterogeneous. Next, we consider heterogeneous GEI δ₁, ..., δ_K across studies in model (1), regardless of (β_Gk, β_Ek) are homogeneous or not. In this case, it is hard to interpret the expected value of ${\widehat{\delta }}^{\mathrm{UIVW}}$, ${\widehat{\delta }}^{\mathrm{MIVW}}$, ${\widehat{\delta }}^{\mathrm{MR}}$ or ${\widehat{\delta }}^{\mathrm{AWE}}$ as a scientifically relevant population parameter. Thus, estimation properties such as bias and mean squared error (MSE) become less meaningful. In this case we are simply getting an weighted average of within study interaction estimates. Although the analytical results corresponding to ${\widehat{\delta }}^{\mathrm{AWE}}$ are derived under a common effect model, the test based on ${\widehat{\delta }}^{\mathrm{AWE}}$ is still valid for the stronger null hypothesis H₀ : δ₁ = ... = δ_K = 0. We will numerically evaluate the power and Type-I error under violation of the common effect assumption through simulation studies.

2.2.3 Power

For dominant and additive models, we consider the Wald-type test statistic $T=\widehat{\mathbf{v}}{\left(\widehat{\delta }\right)}^{-\frac{1}{2}}\widehat{\delta }$ for testing the null hypothesis H₀: δ = 0 against H₁: δ≠ = 0. The power to detect an effect size δ* at level α is approximately $P_w({\delta }^{\ast },\alpha )=\Phi (-z_{\frac{\alpha }{2}}+\widehat{\mathbf{v}}\left(\widehat{\delta }\right){}^{-\frac{1}{2}}{\delta }^{\ast })+\Phi (-z_{\frac{\alpha }{2}}-\widehat{\mathbf{v}}{\left(\widehat{\delta }\right)}^{-\frac{1}{2}}{\delta }^{\ast })$, where Φ is the cumulative distribution function (CDF) of a standard normal variable Z and $z_{\frac{\alpha }{2}}$ is the corresponding $\frac{\alpha }{2}$ th upper percentile. For co-dominant models, we consider a joint Wald test statistic $T={\widehat{\delta }}^{\mathsf{T}}\widehat{\mathbf{v}}{\left(\widehat{\delta }\right)}^{-1}\widehat{\delta }\stackrel{H_0}{\sim }{\chi }_2^2$ for testing H₀: δ = 0 against H₁: δ ≠ 0, where ${\chi }_2^2$ is a Chi-square distribution with two degrees of freedom. The power is approximately $P_w({\delta }^{\ast },\alpha )=1-{\Phi }_{{\chi }_2^2}({\chi }_{2,\alpha }^2-{\delta }^{\ast \mathsf{T}}\widehat{\mathbf{v}}{\left(\widehat{\delta }\right)}^{-1}{\delta }^{\ast })$, where ${\Phi }_{{\chi }_2^2}$ is the CDF for a ${\chi }_2^2$ distributed random variable and ${\chi }_{2,\alpha }^2$ is the corresponding th upper percentile. The power functionP_w(δ*, α) or simply P_w, is strictly decreasing in the variance $\widehat{\mathbf{v}}\left(\widehat{\delta }\right)$ Thus, the results regarding variances in Theorems 1-3 also determine relative power properties.

Table 1 provides a glossary table for all the methods we have discussed, along with their properties, and the summary statistics required to carry out these procedures.

2.3 Simulation study

In order to study the role of G-E independence (Assumption 1) and homogeneity in MAFs across cohorts (Assumption 2), we consider P (G, E) under four different settings: when Assumptions 1 and 2 hold and do not hold. To study the role of covariate heterogeneity in E, we consider cases where wss is greater or smaller than bss, for a fixed value of tss. The details of generating data pair (G_ki, E_ki) jointly are described in Appendix B.6.

Given (G_ki, E_ki), we then generate the continuous trait Y_ki under the IPD model (1), where the study specific intercepts are sampled from ${\beta }_{0k}\stackrel{iid}{\sim }U(1.3,1.5)$, and the true effect sizes (${\beta }_E^{\ast }$, ${\beta }_G^{\ast }$, β*) are determined such that G, E and GEI explain 1%, 10% and 0.5 − 1% of the total variation in Y respectively, in terms of partial R². The residuals follow a $N(0,{\sigma }_k^2)$ distribution, i.e. no requirement for homogeneity of ${\sigma }_k^2$ is made. In particular, we generate ${\sigma }_k^2\stackrel{iid}{\sim }U(0.3,0.45)$ that leads to a marginal distribution of Y ~ N(1.4, 0.4²). The choice of N(1., 0.4²) is motivated by the distribution of log HDL-C level (mmol/l) in our T2D data set. We generate K = 20 studies with different sample sizes involving a total of N = 10, 000 participants (n_k = 200, for k = 1, ..., 6; n_k = 400, for k = 7, ..., 11; n_k = 500, for k = 12, ..., 17; n₁₈ = 800; n₁₉ = 1000; n₂₀ = 2000).

We calculate $\widehat{\delta }$ and $\widehat{\mathbf{v}}\left(\widehat{\delta }\right)$ corresponding to each proposed estimator, including ${\widehat{\delta }}^{\mathrm{IPD}}$, ${\widehat{\delta }}^{\mathrm{UIVW}}$, ${\widehat{\delta }}^{\mathrm{MIVW}}$, ${\widehat{\delta }}^{\mathrm{MR}}$, ${\widehat{\delta }}^{\mathrm{TS}}$ and ${\widehat{\delta }}^{\mathrm{AWE}}$. We carry out R = 1, 000 replications under each setting, and summarize the results in terms of relative bias $(\frac{1}{R}{\sum }_{r=1}^R{\widehat{\delta }}_{\left(r\right)}-{\delta }^{\ast })∕{\delta }^{\ast }\times 100\%$, average model based variance $\frac{1}{R}{\sum }_{r=1}^R\widehat{\mathbf{v}}\left({\widehat{\delta }}_{\left(r\right)}\right)$, empirical variance $\frac{1}{R-1}{\sum }_{r=1}^R{({\widehat{\delta }}_{\left(r\right)}-{\overline{\widehat{\delta }}}_{\left(r\right)})}^2$, $\mathrm{MSE}\left(\frac{1}{R}{\sum }_{r=1}^R{({\widehat{\delta }}_{\left(r\right)}-{\delta }^{\ast })}^2\right)$, power (proportion of simulations rejecting the null hypothesis using the Wald test) and Type-I error (proportion of simulations rejecting the null hypothesis when the data are generated under the null).

Lack of common set of covariates across studies: We then consider covariate Z = (Z¹, Z², Z³) that stand for typical covariates (age, sex, race) in the IPD model (1). In particular, age (Z¹) is continuous and associated with E, gender (Z²) is binary and independent of both (G, E), race (Z³) is a 3-level categorical variable and associated with both (G, E), with ${\beta }_Z^{\ast }$ is determined such that the Type-III partial R² corresponding to (Z¹, Z², Z³) is (2%, 1%, 1%) respectively. Let Z_k be the set of covariates for the k-th study. We consider an analysis where Z_k is only partially available from individual studies, and refer to this situation as ‘lack of common set of covariates across studies’. In particular, we consider ${\mathit{Z}}_k=(Z_k^1,Z_k^2,Z_k^3)$ for k = 1, 2, 3; ${\mathit{Z}}_k=(Z_k^1,Z_k^2)$ for k = 4, 5, 6; ${\mathit{Z}}_k=(Z_k^1,Z_k^3)$ for k = 7, 8, 9; ${\mathit{Z}}_k=(Z_k^2,Z_k^3)$ for k = 10, 11, 12; ${\mathit{Z}}_k=Z_k^1$ for k = 13, 14; ${\mathit{Z}}_k=Z_k^2$ for k = 15, 16; ${\mathit{Z}}_k=Z_k^3$ for k = 17, 18; No Z_k available for k = 19, 20. For IPD analysis without any imputation of covariates, one can only obtain an IPD estimator based on the common subset of variables available across all studies, which reduces to an unadjusted model in the above setting. We refer it as a naive IPD estimator $\left({\widehat{\delta }}^{\mathrm{NIPD}}\right)$. For the meta-analysis, we obtain ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MIVW}}$ from the k-th study model adjusted for available Z_k, for k = 1, ..., K. For MR, we adjust for Z_k at the first stage in the marginal genetic association model, and regress the MLEs of adjusted effects of G on m_k. These methods are compared with an ideal IPD estimator ${\widehat{\delta }}^{\mathrm{IPD}}$ that adjusted for all Z.

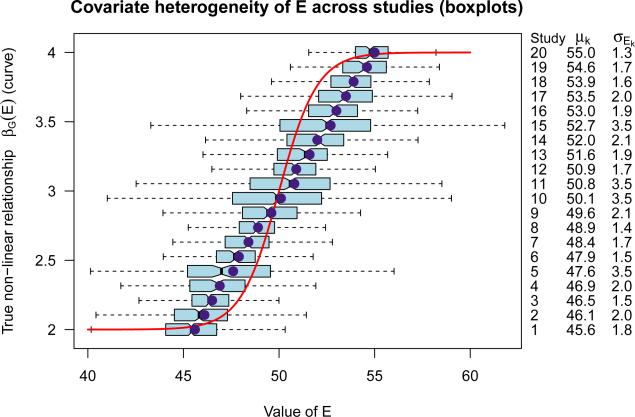
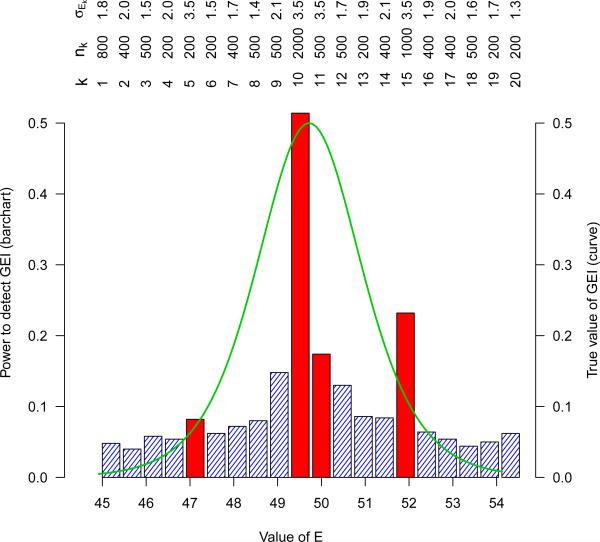
Non-linear GEI model: We consider a non-linear GEI model where the phenotype-genotype association parameter β_G(E) varies with E through a sigmoid function β_G(E) = 2 exp(E − 50) /{1 + exp(E − 50)} + 2, instead of the assumed linear interaction (shown in Figure 1). In this case, β_G(E) changes at different rates for different values of E (sharper around the mean value of E, flatter at more extreme values of E), which leads to non-linear interaction. In Figure 1, most studies only contribute to a restricted range of E, leading to heterogeneity of individual interaction estimates across studies. In this case, meta-analysis with a misspecified linear interaction model might fail to detect the true non-linear interaction. In the simulation study, we generate K = 20 studies, where 4 studies have relatively larger within study variability (studies 5, 10, 11, 15 in Figures 1 and 2) as compared to the other 16 studies. The complete description of n_k, m_k and σ_Ek for the 20 studies are given in Figures 1 and 2. We generate Y through the non-linear interaction model Y_ki = β_0k + β_G(E_ki)G_ki + ε_ki, where ${\epsilon }_{ki}\stackrel{iid}{\sim }N(0,{\sigma }_k^2)$. The within study relationships of the marginal effects of G as a function of E, namely, β_G(E) are substantially different across studies. The effect heterogeneity and non-linearity might influence the validity and relative performance of the proposed methods where a linear form of interaction is assumed. Therefore, we evaluate the robustness of the proposed meta-analysis estimators under this non-linear GEI model.

Figure 1.

Non-linear GEI model: the (red) sigmoid curve shows the true relationship between Y -G association and E, namely, β_G(E) = 2 exp(E − 50)/{1 + exp(E − 50)} +2; the boxplots show the covariate heterogeneity of E across studies where the dots show the corresponding covariate means of E.

Figure 2.

Non-linear GEI model: the height of the bars represent the power to detect GEI across individual studies; the (green) curve shows the value of the true non-linear GEI parameter; the top panel shows the sample sizes n_k and the within study standard deviations σ_Ek of E, the four studies with relatively greater σ_Ek are highlighted (in red).

3 Results

3.1 Simulation results

The simulation results are summarized in terms of bias, variance, MSE and power (Appendix Tables 1-4). The relative performances of the methods are very similar across all three susceptibility models and all four settings, so we only present in the main text the most general setting where the data are generated without either Assumption 1 or 2. The detailed simulation results are given in the Appendix, and we only summarize the key features in the following.

Gene-environment independence and ecological bias:

For bias, comparing settings with and without G-E independence, we observe no substantial difference the proposed estimators, including the potentially biased estimators ${\widehat{\delta }}^{\mathrm{MR}}$ and ${\widehat{\delta }}^{\mathrm{AWE}}$ (Appendix Tables 1-4). When Assumption 1 is relaxed (Appendix Tables 3 and 4), the magnitude of relative bias of ${\widehat{\delta }}^{\mathrm{MR}}$ may be up to ±7% but bias of ${\widehat{\delta }}^{\mathrm{AWE}}$ is still well controlled (up to ±4%). Comparing to the Monte Carlo error (up to ±3% even for the unbiased estimators), the bias of ${\widehat{\delta }}^{\mathrm{AWE}}$ is not to a level of practical concern even when there is some bias in ${\widehat{\delta }}^{\mathrm{MR}}$. In additional simulation settings where ${\widehat{\delta }}^{\mathrm{MR}}$ is susceptible to substantial ecological bias (up to 35%) and when G-E correlation is extremely strong, our results (Appendix Figure 9 and Table 6) indicate the adaptive feature of ${\widehat{\delta }}^{\mathrm{AWE}}$ in controlling the bias from ${\widehat{\delta }}^{\mathrm{MR}}$ by assigning decreased weight. The relative bias of ${\widehat{\delta }}^{\mathrm{AWE}}$ is still < 5%. Thus the issue of ecological bias for aggregate analysis in ${\widehat{\delta }}^{\mathrm{MR}}$ is less of a concern for ${\widehat{\delta }}^{\mathrm{AWE}}$. For variance, we did not observe precision gain by making the G-E independence assumption as expected. Results stated in Theorem 2 appear to hold numerically for all three genetic susceptibility models, even when Assumption 1 is relaxed (Appendix Tables 3 and 4).

Homogeneity in allele frequencies across cohorts

Comparing settings with and without homogeneous allele frequencies across studies, we did not observe any appreciable differences in results. Results in Theorem 3 hold numerically for all three genetic susceptibility models, even when Assumption 2 is relaxed.

Covariate heterogeneity in E

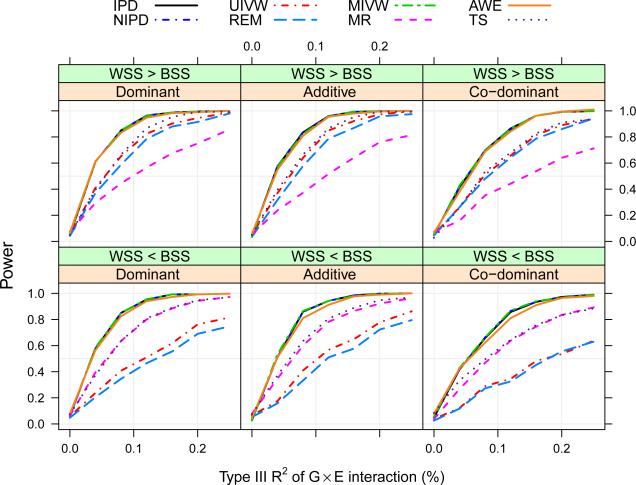
We observe that the ARE between ${\widehat{\delta }}^{\mathrm{UIVW}}\left({\widehat{\delta }}^{\mathrm{MR}}\right)$ and ${\widehat{\delta }}^{\mathrm{IPD}}$ can be well characterized in terms of wss/tss (bss/tss) respectively. We found that ${\widehat{\delta }}^{\mathrm{UIVW}}$ is more efficient than ${\widehat{\delta }}^{\mathrm{MR}}$ if wss > bss, and vice versa. The precision trade-off is captured well by the adaptively determined weights in ${\widehat{\delta }}^{\mathrm{AWE}}$. We observe that ${\widehat{\delta }}^{\mathrm{AWE}}$ is more efficient than the usual meta-analytic estimators ${\widehat{\delta }}^{\mathrm{UIVW}}$, ${\widehat{\delta }}^{\mathrm{MR}}$ or ${\widehat{\delta }}^{\mathrm{TS}}$, and had almost the same efficiency as ${\widehat{\delta }}^{\mathrm{IPD}}$ and ${\widehat{\delta }}^{\mathrm{MIVW}}$ under all simulation scenarios. The findings with finite samples are consistent with our analytical results in Theorems 2 and 3 and Lin and Zeng (2010b).

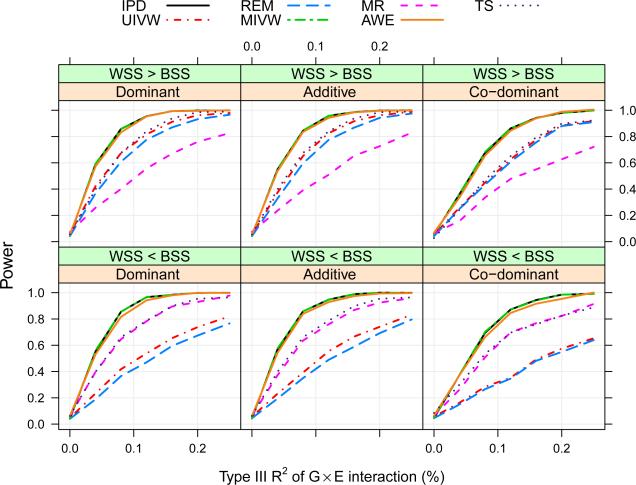
In terms of power, we find the proposed methods (IPD, UIVW, MIVW, MR, TS and AWE) are divided into three groups in Figure 3, as expected. Group 1: IPD, MIVW and AWE; group 2: UIVW; group 3: MR. Group 1 has the most powerful tests, which is consistent with our analytical results and Lin and Zeng (2010b); group 2 is more powerful than group 3 if bss < wss, and vice versa. TS performs similarly as the better group between groups 2 and 3. The empirical estimates of Type-I error are close to the true 0.05 level for all tests.

Figure 3.

Comparison of the proposed meta-analytical methods (in terms of power) under different scenarios of susceptibility models and covariate heterogeneity through a simulation study, where data are simulated without any assumption on gene-environment independence or homogeneity in allele frequencies across studies.

Heterogeneous GEI effects across studies

We examine the power and Type-I error corresponding to the proposed methods, where δ₁, ..., δ_K are heterogeneous across studies in model (1). In particular, for each true effect size δ* determined by a given R² as in section 2.3, we generate ${\sigma }_k^{\ast }\stackrel{iid}{\sim }U(0,2{\delta }^{\ast })$ that vary across studies but has the same mean δ*. Appendix Table 5 shows the power and Type-I error under data generated from the heterogeneous GEI model, where we do not observe any substantial difference with the testing results under homogeneous GEI model.

Misspecification of the genetic susceptibility model

We examine the power under misspecified susceptibility models (dominant/additive), where the true generating model is co-dominant. When δ^AA = 1.5 δ^Aa (we accordingly choose ${\beta }_G^{AA}=1.5{\beta }_G^{Aa}$), i.e., the second copy of A has an effect size between the two assumed in dominant (δ^AA = δ^Aa) and additive (δ^AA = 1.5 δ^Aa) models, there is no substantial difference of power between the misspecified dominant/additive model and the co-dominant model (shown in Appendix Figures 7), because the misspecification is not strong and the fitted dominant or additive models use one less parameter. When δ^AA = − δ^Aa (we accordingly choose ${\beta }_G^{AA}=-{\beta }_G^{Aa}$, i.e., the second copy of A has a reverse effect, the fitted dominant or additive models had much less power than the co-dominant model (shown in Figure 5). Thus, it could happen that the co-dominant model has more power compared to other simpler models, though it uses two additional parameters for capturing GEI.

Figure 5.

Power curves under misspecified susceptibility models (dominant/additive), where the gen erating co-dominant model has δ^AA = −δ^Aa, where data are simulated without any assumption on gene-environment independence or homogeneity in allele frequencies.

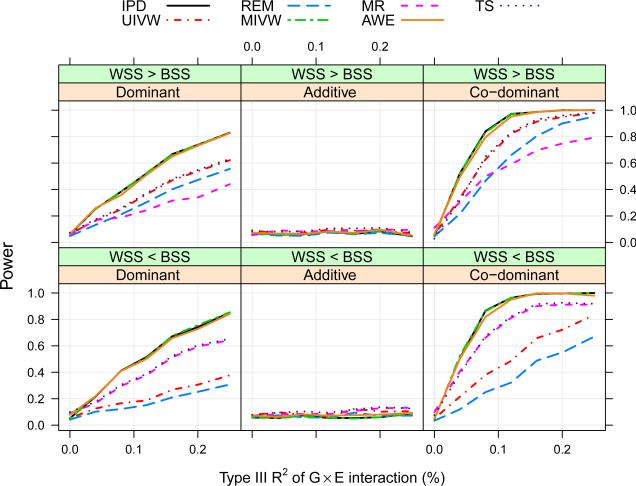
Lack of common set of covariates across studies

Figure 4 shows the power curves under this situation without either Assumption 1 or 2. Compared to the basic setting without covariate adjustment (Figure 3), there is no substantial difference in the relative performances of these methods. We observe that the GEI estimate $\widehat{\delta }$ and variance $\widehat{\mathbf{v}}\left(\widehat{\delta }\right)$ is fairly stable, though the main effects of ${\widehat{\beta }}_G$ and ${\widehat{\beta }}_E$ are substantially influenced under this situation. VanderWeele et al. (2012) also show similar results that, under G-E independence, there is no effect of unmeasured environmental confounding on the GEI parameter; and that if G and E are dependent, the environmental confounding needs to be very strong to incur substantial bias in GEI. Power curves under various other settings with similar results are given in Appendix Figures 4-6.

Figure 4.

Comparison of the proposed meta-analytical methods (in terms of power) under different scenarios of susceptibility models and covariate heterogeneity through a simulation study (representing the situation of lack of common set of covariates across studies), where data are simulated without any assumption on gene-environment independence or homogeneity in allele frequencies.

Non-linear GEI model

When the IPD are generated under the non-linear GEI model, the power to detect GEI from individual studies is very low (< 0.25), except study 10 where the sample size n₁₀, effect size (depends on E) and variance ${\sigma }_{E_{10}}^2$ are all relatively larger than the other studies (Figure 2). In Table 2, IPD, MIVW and AWE show the highest powers. $P_w^{\mathrm{MIVW}}$ is close to $P_w^{\mathrm{IPD}}$ because the model based standard errors of ${\widehat{\delta }}^{\mathrm{IPD}}$ and ${\widehat{\delta }}^{\mathrm{MIVW}}$ are asymptotically the same. Because most of the 20 studies are unable to capture the true non-linear GEI, especially those with restricted range of E at the two extremes of the E distribution, the non-linearity of GEI leads to the low power of ${\widehat{\delta }}^{\mathrm{UIVW}}$. In this particular example, we observe that $P_w^{\mathrm{MR}}$ is greater than $P_w^{\mathrm{UIVW}}$. Instead of choosing alternatively between ${\widehat{\delta }}^{\mathrm{UIVW}}$ and ${\widehat{\delta }}^{\mathrm{MR}}$, we can use ${\widehat{\delta }}^{\mathrm{AWE}}$ as the default meta-analytic estimator. The relative performance of ${\widehat{\delta }}^{\mathrm{AWE}}$ is close to ${\widehat{\delta }}^{\mathrm{IPD}}$. This is a practically noteworthy finding as a linear interaction model is typically the initial screening tool, and the AWE is able to pick up signals under model misspecification that univariate meta-analysis methods can not.

Table 2.

Comparison of methods in terms of estimate, standard error of the estimate and power for GEI, under a simulation study of non-linear GEI. [IPD: individual patient data; UIVW: univariate inverse- variance weighted estimator; MIVW: multivariate inverse-variance weighted estimator; MR: Meta-regression; AWE: adaptively weighted estimator combining UIVW and MR; TS: two-stage approach.]

Methods	Estimate	SEa	Power
IPD	0.21	0.045	0.98
UIVW	0.18	0.070	0.69
MIVW	0.21	0.045	0.98
MR	0.23	0.060	0.82
AWE	0.21	0.045	0.98
TS			0.85

^aSE: standard error.

3.2 Data analysis for a set of studies investigating T2D

The proposed methods are applied to a set of studies investigating T2D, including 8 European cohorts: FIN-D2D 2007 study (D2D2007), DIAbetes GENetic study (DIAGEN), Finnish Diabetes Prevention Study (DPS), Finland-United States Investigation of NIDDM Genetics study (FUSION, FUSION S2), Nord-Trϕndelag Health Study 2 (HUNT), METabolic Syndrome in Men study (METSIM) and Tromsϕ study (TROMSO). A number of SNPs in the FTO gene region (16q12.2) have previously been identified to be associated with T2D and BMI in the DIAGRAM consortium (Zeggini et al. (2008), Voight et al. (2010)), where the variants at FTO gene are known to influence T2D predisposition through an effect on BMI. Age, BMI and sex are all known risk factors for T2D and the T2D related quantitative trait HDL-C (Scott et al. (2012), Morris et al. (2012)). In this paper, we investigated whether SNPs in FTO gene modifies the effect of environmental factors (e.g. age and BMI) on HDL-C. The effect modification characterized by interaction on HDL-C has not been reported so far, though marginal association between SNPs in FTO and HDL-C have been noted previously (Kring et al. (2008), Doney et al. (2009)).

Among the 8 cohorts, we have a total of N = 11, 150 genotyped participants who have HDL-C levels, age, sex and BMI available, with sample sizes ranging between 172 and 2,729. Participants known to be on lipid medication are excluded from this analysis. The descriptive summary statistics for the 8 cohorts are shown in Table 3. Since the SNPs we initially examined (namely, 10 SNPs in FTO strongly associated with T2D/obesity/BMI that are listed on the National Human Genome Research Institute GWAS catalog) are in high linkage disequilibrium and show very similar results, we only present our results for one representative SNP, rs1121980. The SNP's genotype follows Hardy-Weinberg equilibrium, and we did not need any imputation given the missing genotype proportion < 0.1%. The MAF of rs1121980 ranges from 0.40-0.49 across cohorts, as a suggestive evidence for no violation of Assumption 2. As in Table 3, the mean age ranges from 55-67 years except FUSION (mean age=39). This cohort is younger because it is actually a sub-cohort of the original FUSION study, with either spouse or offspring of T2D selected. The mean BMI ranges from 26-28 kg/m² except the DPS cohort (mean BMI=31). DPS cohort has an inclusion criterion of having BMI> 25 at baseline. The covariate heterogeneity of E between cohorts is relatively small, where BSS_age/T SS_age = 15% and BSS_BMI/T SS_BMI = 2% respectively. The two ‘outlier’ cohorts, FUSION and DPS, both have only very small sample sizes compared to the other studies, so their influence on UIVW and MIVW is expected to be small. However, their influence on MR could be substantial due to a small number of studies.

Table 3.

Summary statistics for the 8 European cohorts.

		T2D	HDL-C (mmol/l)	rs1121980	Age (year)	BMI (kg/m2)	Gender	SNP*Age	SNP*BMI
Cohortsa	N		Mean (SD)	MAFb	Mean (SDb)	Mean (SD)	Female (%)	Corr (P)c	Corr (P)
D2D2007	2116	14	1.46 (0.35)	0.41	58.8 (8.3)	27.2 (4.8)	54	−0.03 (0.19)	0.03 ( 0.24)
DIAGEN	1510	29	1.45 (0.47)	0.46	63.3 (14.3)	27.9 (5.2)	55	−0.01 (0.76)	0.03 ( 0.24)
DPS	433	0.0	1.22 (0.29)	0.44	55.1 (7.1)	31.3 (4.6)	68	−0.02 (0.69)	0.16 (<.01)
FUSION	172	0.0	1.29 (0.32)	0.43	38.6 (10.9)	26.2 (4.9)	55	0.04 (0.56)	0.23 (<.01)
FUSION-S2	2729	31	1.45 (0.41)	0.40	57.3 (8.4)	27.9 (5.1)	44	−0.02 (0.22)	0.06 (<.01)
HUNT	1324	43	1.26 (0.38)	0.47	67.2 (13.1)	28.0 (4.4)	48	<.01 (0.94)	0.06 ( 0.03)
METSIM	1456	43	1.42 (0.40)	0.44	56.3 (6.6)	27.9 (4.7)	0	−0.05 (0.08)	0.03 ( 0.32)
TROMSO	1410	50	1.43 (0.42)	0.49	59.9(12.5)	27.6 (4.7)	50	<.01 (0.91)	0.04(0.15)
Entire study	11150	31	1.41 (0.40)	0.44	59.4(11.3)	27.8 (4.9)	44	<.01 (0.85)	0.05 (<.01)

^aData reflect patients who were genotyped from the 8 European cohorts;

^bSD: standard deviation; BMI: body mass index; MAF: minor allele frequency;

^cCorr(P): Spearman correlation between SNP rs1121980 and environmental factor with corresponding P-value.

Analysis Model: The IPD model we fitted is given by log(HDL-C_ki) = β_0k + β_GG_ki + δG_ki×E_ki + β_aage_ki + β_b BMI_ki + β_ssex_ki + β_tT2D_ki + ε_ki(4) for k = 1, ..., 8; i = 1, ..., n_k. In model (4), SNP rs1121980 is used for G with both additive and co-dominant coding; BMI and age is used as E in two separate analyses; T2D status is adjusted to account for biased sampling of the genotyped subjects (more T2D cases are genotyped than non-cases). HDL-C is log-transformed in order to reduce the skewness of its distribution. The proposed methods, including IPD, UIVW, MIVW, MR and AWE, are implemented and compared. G-E independence appears to be violated for rs1121980×BMI analysis (Spearman correlations across studies are reported in Table 3). This is expected as FTO is an obesity related gene. G-E independence does not appear to be violated for rs1121980×age (Table 3).

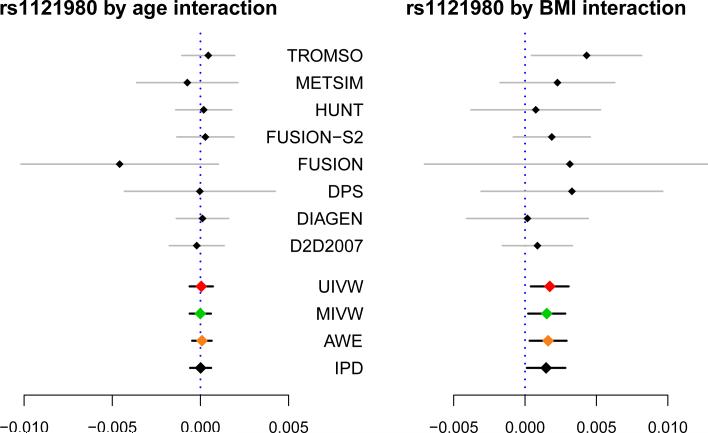
Results: Figure 6 shows the forest plots of estimated GEI from individual cohorts and the combined estimates using joint analysis and meta-analysis. The corresponding numerical results are summarized in Table 4. There is no evidence of effect heterogeneity for both rs1121980×BMI (P = 0.87) and rs1121980×age (P = 0.90) interactions based on Cochran's Q test, so we proceed with a common effect model. In Figure 6 and Table 4, all these meta-analytical methods UIVW, MIVW and AWE showed very similar results as IPD, except MR. For example, rs1121980×BMI, the marginal SNP effects of rs1121980 with mean BMI values across cohorts are shown in Appendix Figure 8, where MR is very sensitive to the outliers as the number of cohorts is small (K=8). MR also appears to lack efficiency due to small K and small ratio BSS/W SS. Here, ${\widehat{\delta }}^{\mathrm{AWE}}$ is robust to the bias from ${\widehat{\delta }}^{\mathrm{MR}}$ since it only assigned a weight of 0.05 on ${\widehat{\delta }}^{\mathrm{MR}}(\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}∕\{\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{UIVW}}\right)}^{-1}+\widehat{\mathbf{v}}{\left({\widehat{\delta }}^{\mathrm{MR}}\right)}^{-1}\})$. This is further evidence that ${\widehat{\delta }}^{\mathrm{AWE}}$ can data adaptively shrink to the ‘better’ estimator.

Figure 6.

Forest plots showing the estimated gene-environment interactions (under additive model of rs1121980) across the 8 European cohorts, as well as the combined estimates through meta-analysis. [IPD: individual patient data; UIVW: univariate inverse-variance weighted estimator; MIVW: multi variate inverse-variance weighted estimator; AWE: adaptively weighted estimator combining UIVW and Meta-regression.]

In the interaction model (4), positive rs1121980×BMI interactions are found under all proposed methods (except MR) in Table 4, with P-values ranging from 0.01 to 0.03 for the additive model. In particular, the estimates obtained from model (4), when converted in terms of percentage change in actual HDL-C levels, indicated that: with 1 kg/m² increase in BMI, (1) under additive model, HDL-C level on average decreased by 1.53% (95% CI: (1.37, 1.70)) given rs1121980=GG, by 1.39% (95% CI: (1.28, 1.49)) given rs1121980=AG or GA; and by 1.24% (95% CI: (1.06, 1.42)) given rs1121980=AA; (2) under co-dominant model, HDL-C level decreased by 1.51% (95% CI: (1.33, 1.69)) given rs1121980=GG, by 1.41% (95% CI: (1.27, 1.56)) given rs1121980=AG or GA; and by 1.21% (95% CI: (0.99, 1.42)) given rs1121980=AA. The results under additive and co-dominant models are very close. The trend of the effects of BMI among the three groups defined by rs1121980 indicated that the presence of minor allele A in rs1121980 attenuated the negative association between BMI and HDL-C. We did not find similar rs1121980×BMI interaction effect on low-density lipoprotein cholesterol (LDL-C), total cholesterol or LDL-C/HDL-C ratio. The suggestive effect modification of BMI by the SNPs on FTO that we have found for HDL-C needs to be replicated in independent studies and validated in larger meta-analysis.

4 Discussion

In this paper, we proposed and compared a set of meta-analysis approaches for analyzing GEI. We showed the proposed AWE, as a combination of meta-analysis and meta-regression estimators, performed better than discretely choosing between the two estimators in terms of precision and power. We showed that the precision trade-off between the two components in AWE depends on the covariate heterogeneity through the ratio of the between and within study variances of the covariate E, and that the AWE adaptively weights its component estimators to minimize the variance of the resulting hybrid estimator. The resulting AWE retains full efficiency of the joint analysis using IPD under certain assumptions. The AWE is very simple to calculate based on summary statistics for marginal genetic association and gene-environment interaction parameters (estimate and standard error) along with the covariate mean of E (see Table 1). The computation is simple and scalable to genomewide analysis. We suggest possible use of AWE as a default choice for the meta-analysis of GEI based on summary data. We studied several key features that could potentially influence the efficiency and power for meta-analysis of GEI. The features included: (1) departures from G-E independence; (2) heterogeneity in MAFs across cohorts; (3) lack of a common set of covariates across studies; (4) misspecification of the genetic susceptibility model (dominant/co-dominant/additive); and (5) the presence of a nonlinear form of interaction. Under all the above situations, we found the performance of AWE is close to IPD estimator. In particular, under the non-linear interaction model setting, where standard meta-analytical technique failed and the AWE is able to capture the lost efficiency based on the summary data. We also reported some suggestive evidence for GEI between rs1121980 on the FTO gene and BMI on HDL-C levels.

As a reviewer has pointed out, we are risking some bias for gaining precision in AWE by including MR as a component, and MR is susceptible to ecological bias. However, as we note in the analysis of the T2D example in Table 4, where the MR estimate is quite different from the rest, the AWE aligns itself with the more sensible UIVW estimator. Our simulation results also indicate this adaptive feature of AWE in controlling the bias from the MR component by assigning decreased weight to it (Appendix Figure 9 and Table 6). Moreover, regardless of ecological fallacy, under the additional assumption of G-E independence, AWE remains unbiased. Thus the issue of ecological bias for aggregate analysis in MR is less of a concern for AWE. We also noted that AWE performs well across the whole spectrum of BSS/T SS ratio, not just intermediate values of this quantity (Appendix Figure 9 and Table 6).

We have mainly focused on quantitative traits with an underlying common fixed effect model. The potential limitation of this approach is that the results might not translate directly to dichotomous traits under a case-control design, where assuming G-E independence can lead to huge gain in efficiency (Piegorsch et al. (1994), Umbach and Weinberg (1997), Chatterjee and Carroll (2005)). We plan to extend our methods using a retrospective likelihood framework under a case-control design. Investigating the results under a truly random effects meta-analysis model is another possible extension to our work. Sample code for all methods is available at http://www-personal.umich.edu/~bhramar/software/.