Abstract
We develop a general numerical/analytic theory of non-faradaic impedance of an evaporating droplet, and validate the model by experiments involving droplets of various analyte concentrations deposited on a surface defined by coplanar electrodes. The impedance of the droplet Z(n0, t, f) is analyzed as a function of concentration (n0) of the ions in the solution, the measurement frequency (f) and the evaporation time (t). We illustrate the versatility of the model by determining the sensitivity enhancement α(t) of the droplet-based impedimetric nano-biosensor under different regimes of operation. The model should have broad applications in characterization/optimization of droplet-based systems, especially lab-on-chip components involving digital microfluidics.
Keywords: Evaporation, Biosensing, Droplet Characterization, Impedance spectroscopy, Non-Faradaic
Introduction
Droplets occur in broad range of natural and engineered systems. In natural systems, for example, a drop of water on a lotus leaf forms a spherical shape to minimize the surface energy1. When a drop of liquid with suspended particles dries on a substrate, it leaves a ring-shaped stain on the surface generally known as the “coffee-ring effect2–4”. On the other hand, in the engineered systems, micro/nano-liter sized droplets have been used in broad range of applications including drop-on-demand inkjet printing5, molecule transport6, single-cell analysis and sorting7 through microfluidic channels, electrically-addressable biochemical reactions in sub-nanoliter droplets8, etc. Evaporating droplets have also found a number of interesting applications. Jing et al. have used tiny evaporating droplets to elongate and fix DNA molecules on derivatized surfaces9; De Angelis et al. have reported attomolar-detection of DNA concentration by concentrating few copies of DNA to a localized SPR sensor by evaporation of droplet10; and most recently Ebrahimi et al. have reported a label-free on-chip non-faradaic impedance based detection of attomolar (aM) concentration of DNA11. The concentration of biomolecules was enhanced through evaporation of the droplet and an enhanced signal was obtained for even a few copies of DNA in micro-liter sized droplets.
Optical techniques such as high-speed imaging12, confocal microscopy13 and laser light scattering14,15 have been used to characterize the geometry and composition of droplets. For probing the dynamics of droplet on a surface, an electrical characterization technique such as impedance spectroscopy can provide complementary information. In this regard, it is desirable to have a theoretical model which can map the system parameters like the droplet composition, shape and size to an electrical signal (i.e. impedance) as the droplet evaporates. Faradaic impedimetric sensors16 have long been used for highly selective detection of biomolecules. If the analyte is known and only its concentration is desired, non-Faradaic Impedance spectroscopy (NFIS) provides a simpler non-intrusive way to provide wealth of information regarding the composition of the droplet and the kinetics of evaporation. Important initial work on NFIS has already been reported. For example, Sadeghi et al. performed on-chip impedance based droplet characterization for a parallel plate electrode system17. For a broader range of applications, however, all droplet models must be generalized to include accumulation of ionic charges (double layer) near the electrode surface, arbitrary geometry of electrodes, the time dynamics and droplet shape dependence of impedance components, and all the parasitic components.”
In this paper, we formulate a comprehensive theory for droplet impedance with focus on nano-biosensing9–11. We solve for the time dynamics of droplet evaporation and relate the composition, size and shape of the droplet to the time-varying impedance. We demonstrate that the approach can be used in optimization of the sensor design and operate the sensor in optimal frequency range. Indeed, the model is general and can be used in a broad range of microfluidic systems.
The paper is arranged as follows. In section 1, we describe the device structure and operation principle of the droplet based sensor. In section 2.1, we describe the impedance/admittance response of the system for a fixed droplet geometry. In section 2.2, we describe the time dynamics of droplet evaporation and describe the geometry variation as a function of time. In section 2.3, we provide the time dependence of circuit components/impedance for the system. In section 3.1 and 3.2, we explain the sensitivity enhancement of the droplet based sensor in various operation regimes and discuss the implications of parasitic impedance respectively. Finally, the model is validated with the experiments on droplets containing DNA molecules in section 3.3.
1. Device structure and Principle of operation
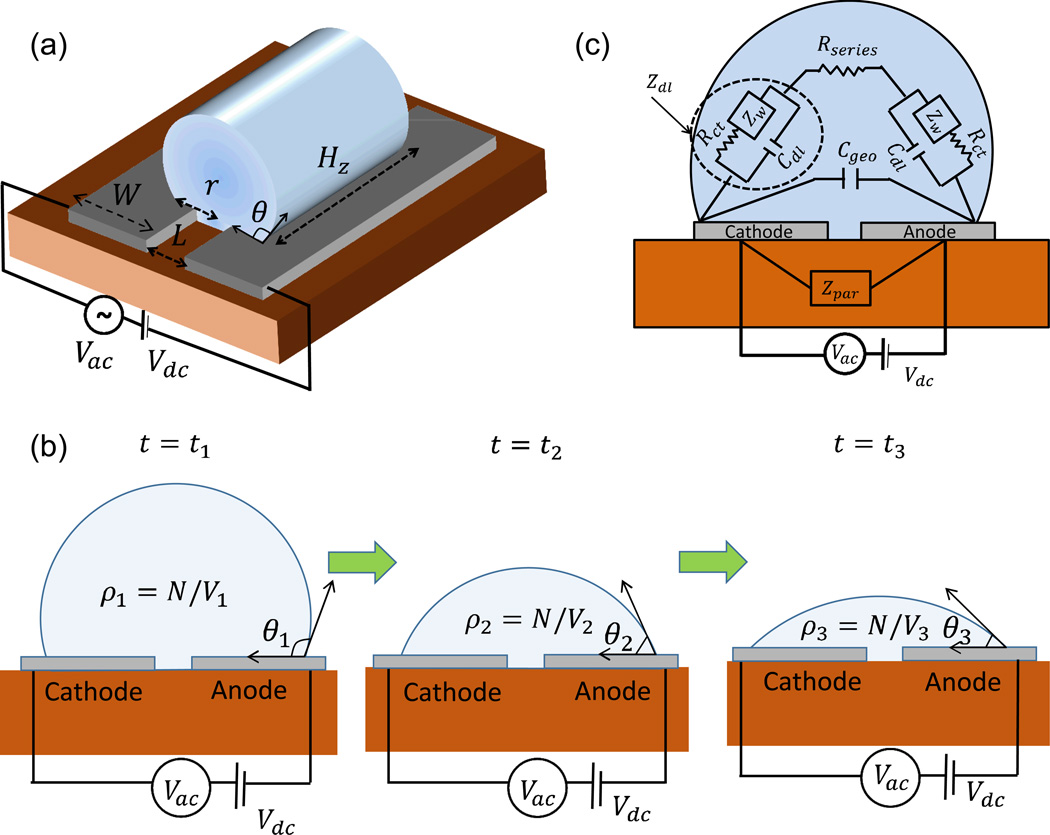
As a model system for the theoretical framework, we consider an evaporating droplet containing chemical/biomolecules resting on a substrate with co-planar electrodes, as shown in Fig. 1(a) and (b). We assume that the surface is designed in such a way that the droplet is pinned and maintains constant contact line as it evaporates11. The contact width (r) and the contact angle (θ) that the droplet makes with the surface depends on the surface wettability and the droplet volume. The electrical impedance of the droplet is measured by applying a small ac signal (with a dc bias) between the electrodes. The impedance of the droplet, Zdrop(n0, f, t), depends on the time-dependent (t) shape of the droplet, the initial concentration of ions (n0), and the characterization frequency (f). As the droplet evaporates, Zdrop changes due to two distinct but correlated effects: the increase in ionic concentration associated with decrease in the droplet volume, and the change of the droplet geometry due to evaporation. The changes in Zdrop can be used as a characterization tool for many droplet-based problems and applications discussed earlier. For droplet-based nanobiosensors, the positive implications are obvious (see Fig. 1(b)): the shrinking droplet brings the analyte biomolecules close to the sensor surface faster than the diffusion limit18. As a result, the concentration of the biomolecules increases inversely with the volume of the droplet and this increased concentration is reflected in enhanced sensitivity19, S(t) defined as change in conductance (ΔY(t)) with respect to known reference solution (DI water).
Fig. 1.
(a) Model system for numerical/analytic modeling (b) Evaporation dynamics of droplet: As the droplet evaporates, the contact angle (θ) decreases while the contact line remains pinned. The concentration of the chemical/biomolecules (ρ) increases as the volume (V) decreases with time (t) with number of chemical/biomolecules (N) remaining constant (c) Equivalent circuit representation of the system.
For simplicity, we assume that the droplet is self-aligned to coplanar electrodes, as shown in Fig. 1(b). The conclusions of the paper, however, are general and would apply to any electrode geometry. The electrodes are multi-functional: they define the superhydrophobic surface that pins the droplet and can also be used as an addressable heater. If the electrodes are simultaneously used as heater and prober, a complex interaction is likely. Therefore, for simplicity of model development, we use the electrodes exclusively for impedance measurement, and the heating effects are not considered. The applied voltage is presumed small to suppress the Faradaic current20. However, if a higher applied voltage is necessary for application under consideration, electrodes maybe coated with a thin dielectric layer to block any charge transfer between the electrode and the solution (refer to Supplementary Information 3 for implications). Finally, the substrate offers a parasitic path for signal to travel between the electrodes (see, Fig. 1(b)) and thereby defines the upper limit for the frequency of operation. At high enough frequencies, the impedance of the overall system, Znet is dictated by the parasitic impedance, Zpar and becomes insensitive to the properties of the droplet itself. Depending on the substrate (e.g. glass vs. silicon-on-insulator, SOI), the parasitic impedance may change by orders of magnitude; therefore, the choice of the substrate is important in defining the sensitivity of the sensor.
2. Numerical/Compact modeling of droplet impedance
2.1. Frequency response of the droplet impedance
Let us first consider the frequency dependence of impedance of a droplet (see Fig. 1(a)) with constant contact angle θ resting on a substrate with two planar electrodes. For an arbitrary electrode (faradaic/non-faradaic), the different components which can affect the impedance are shown in Fig. 1(c). Here, Rct denotes the charge transfer resistance20, Zw the Warburg impedance21, Cdl double layer capacitance, Rseries denotes resistance of the solution and Cgeo the dielectric (geometric) capacitance of the droplet. The net impedance of the system is therefore given by
| (1) |
where represents the double layer impedance and Zpar the parasitic impedance. For a non-faradaic electrode, there is no charge transfer at the surface, so that Rct → ∞ and hence the net impedance of the system simplifies to
| (2) |
The rest of the paper will focus on this reduced ‘non-faradaic’ model with the understanding that it can be easily generalized to include Faradaic contributions as well.
Physically, Rseries originates from the finite conductivity of the solution, σ as Rseries = g/(σ Hz) where g = g(θ, r, W, L), which we call geometry factor. This factor depends on the width (W), separation (L) between the electrodes and droplet contact angle θ and contact width r. Hz represents the length of cylindrical segment as shown in Fig. 1(a). The conductivity σ can be related to the ionic concentration (ni) as σ = qni(μp + μn) where μp and μn are respectively the ionic mobilities of the positive and negative ions in the solution.
Similarly, the geometry capacitance which depends on the permittivity of the solution (ε) and the same geometry factor, g as in Rseries (refer to Supplementary Section 1) can be written as Cgeo = Hzε/g. Henceforth, unless explicitly specified, we assume that the analyte concentration is small so that ε ≈ εfluid and is unaffected by the salt/analyte concentration.
Finally, Cdl originates from the adsorbed charge layer and diffuse layer charge22 and can be written where CS is the Stern capacitance23 and Cdiff is called the differential capacitance. For electrode separation/droplet dimensions much larger than the debye length (λd ~ 1 µm for pure water), the diffuse layer capacitance can be described by analytic formula where A = rHz is the area of the electrode in contact with the solution and Ve is the applied bias on the electrode, q the electronic charge, k the boltzman constant, and T temperature of the solution. While applicability of this analytic formula is well established for bulk solutions22, we show through detailed numerical simulations (refer to Supplementary Section 1 (b)) that this can also be applied to micro-liter sized droplets. For medium to low ionic concentrations (< 100 mM), Debye length is much larger than the thickness of the Stern layer (~0.4 nm)24 so that Cdiff ≪ CS and hence, Cdl ≈ Cdiff. Once the droplet/electrode geometry are specified, the fluid properties are given (e.g. εfluid), and the salt (n0)/analyte concentrations (ρ) is known, Zdrop is fully determined, and can be plotted, among other variables, as a function of frequency f.
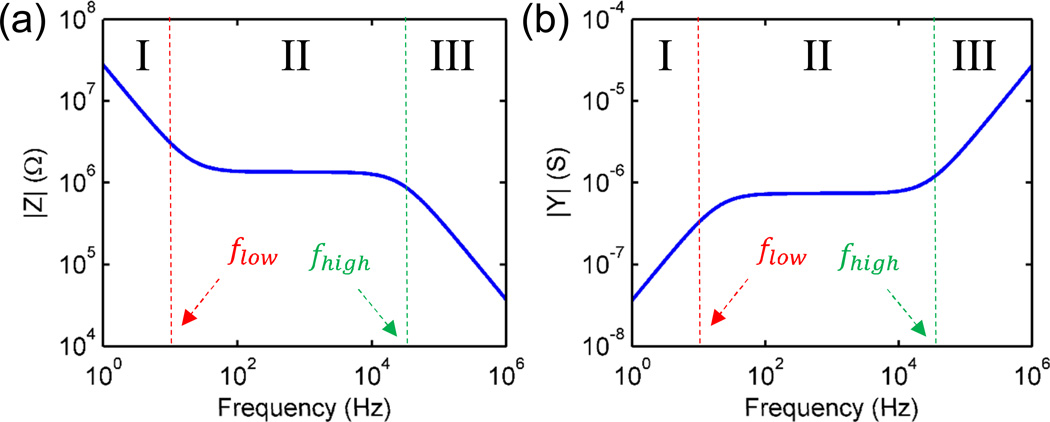
Frequency response of an ideal system with no parasitic losses can be divided into three distinct regions (see, Fig. 2(a)), such that impedance components Rseries, Cdl and Cgeo are dominant in each of these three regions. For , Cdl dominates the net impedance, for , Rseries is the dominant component, and finally for f > fhigh, Cgeo dominates. The numerical/analytic estimation of different circuit components and cut-off frequencies is described in Supplementary Section 1 and 2, respectively. For a conductivity based sensor, we should be operating in either regime I or II, while detection can be done in the regime III if the change in permittivity of the solution upon addition of biomolecules is considerable.
Fig. 2.
(a) Impedance of the droplet as a function of frequency. Cdl dominates at f < flow, Rseries dominates for flow < f < fhigh and Cgeo dominates the impedance at very high frequency (f > fhigh). Similar trend (2(b)) is visible in the admittance vs. frequency response.
The admittance of the droplet (see Fig. 2(b)) is defined as Ydrop = 1/Zdrop. We can define the limit of detection as the minimum measurable change in conductance ΔYdrop of the droplet upon introduction of salt/biomolecule.
In order to improve the limit of detection several design parameters can be considered, i.e. electrode separation (L), electrode width (W), electrode length (Hz) in contact with droplet. These factors have considered by Hong et al. albeit with a bulk solution. The higher the electrode length and the smaller the electrode spacing, the better is the sensitivity25. However, for ultra-small concentration of biomolecules, the diffusion of the ions limits the detection time. Therefore, in order to improve the sensitivity and response time of the system, we need to explore droplet volume (V) (or contact angle (θ)) as an additional design parameter. This can be achieved by evaporation of the droplet which is considered next.
2.2. Dynamics of droplet evaporation
Droplet forms as a result of balance of surface tensions at the triple contact line between air, liquid and surrounding medium. Equivalently, the shape of the droplet can be determined by energy minimization26. Our earlier work11 showed that the droplet placed on nanotextured-superhydrophobic electrodes assumes a nearly ellipsoidal shape with pinned contact lines at the edges of the droplet. Contact line pinning of droplet is critical for highly stable impedance characterization. A constant contact width for evaporating droplet is also obtainable using chemically heterogeneous striped surface27.
In order to determine the time evolution of impedance of such a pinned droplet, we must first determine the evolution of droplet shape with time. Numerical calculations show and high-speed images confirm that as the droplet evaporates, it maintains the shape of an elongated ellipsoid, defined by a constant contact width r and decreasing perpendicular (θ⊥) and parallel (θ‖) contact angles11. For analytic simplicity, we will approximate the elongated ellipsoid as a truncated cylinder with contact width r and contact angle θ, while keeping all other constraints (e.g. initial volume) unaltered, see Fig. 1(b). Our model is directly applicable in scenarios where the elongation of the droplet parallel to the coplanar electrodes is large as compared to that in direction perpendicular to the electrodes. However, the ‘cylindrical’ approximation is not restrictive – the formulation is general and can be applied to any system where the evolution of droplet shape (i.e. the geometry factor, g(t)) and droplet volume (V(t)) is known through numerical simulation28 or high-speed imaging12.
Similar to Rowan et al.29 and Birdi et al.30, we consider droplet evaporation as a gas diffusion process and assume that the rate of mass loss from droplet is given by Φm = ∫ J⃗. dS⃗ where J⃗ is the diffusion flux of liquid molecules away from the surface and integral of the flux is taken over the surface of the droplet. The diffusion flux can be written in terms of the concentration of liquid vapors (c(r, θ, z)) as J⃗ = −D∇⃗c where D is the diffusion coefficient of liquid vapors in the ambient surroundings. Therefore, the rate of mass loss would be, Φm = −∫ΩD∇⃗c. dS⃗. In order to evaluate this integral, we use the equivalence between the electric potential (ψ) and vapor concentration (c) as discussed in Supplementary Section 4. For an electrical system, we can write charge Q = −∫ ε∇ψ. dS⃗ = Ce (ψs − ψ∞) where Ce is the electrical capacitance. Similarly, the diffusion flux of molecules can be written as31 Φm = CD (cs − c∞) where cs is the saturation vapor density of liquid and c∞ is the vapor density of liquid far away from surface. CD is the diffusion equivalent capacitance of a truncated cylinder with finite length32 which is given by,
| (3) |
where where Rs is the radius of curvature of the droplet. Note, that the diffusion equivalent capacitance of the cylinder with finite length has been appropriately scaled for reduced surface area of the truncated cylinder. If we assume that the density of liquid is constant as the droplet evaporates, the rate of mass loss can be expressed as,
| (4) |
where P is the density of liquid, m is the mass of droplet, V is the volume of liquid for a given contact angle and t is time. Therefore,
| (5) |
For simplicity, we assume that the evaporation occurs at a constant temperature so that cs is independent of time. Also, the equation assumes that the evaporation from the front and back surfaces of the cylinder is negligible, which is justified as long as Hz ≫ r. Once we relate V and Rs to the contact angle θ (see, Supplementary Table 4), the rate of change of contact angle as a function of θ is given by,
| (6) |
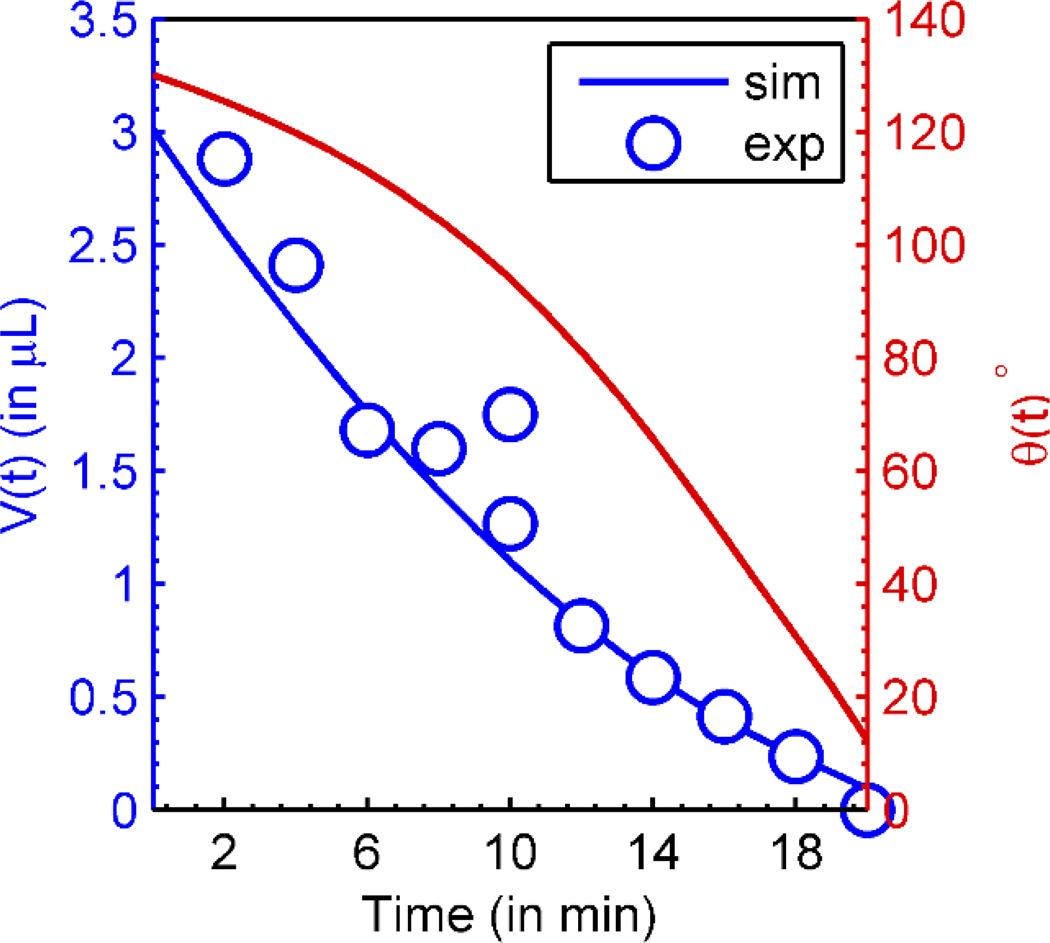
where captures the material parameters of the droplet. This equation can be numerically integrated to obtain θ(t) and V(t). Fig. 3 shows the evolution of droplet contact angle (θ) and volume (V) as a function of time (t). Simulation parameters are listed in Supplementary Table 2 and 3. Interestingly, despite the complexity of the equation, one finds that the volume evolution of the droplet can often be described by a power-low33
| (7) |
where τ and n are empirical parameters defined by the shape of the droplet and the mode of the evaporation. For the experimental data obtained from Ebrahimi et al.11, we find that the parameter n = 3/2 and τ = 20 min.
Fig. 3.
Evolution of droplet contact angle (θ) (right) and droplet volume (V) (left) as a function of time. Symbols are the experimental data obtained from Ebrahimi et al11. The variation of droplet volume as a function of time can analytically be approximated as with n = 3/2 where V0 is the initial volume of the droplet and τ the total evaporation time. Simulation Parameter: (cs − c∞)/cs = 0.88
2.3. Time evolution of impedance/conductance
The net impedance of the droplet is given by
| (8) |
Given the geometry dependence of the circuit components and time dependence of geometry, we can determine the time dependence of different circuit components as follows:
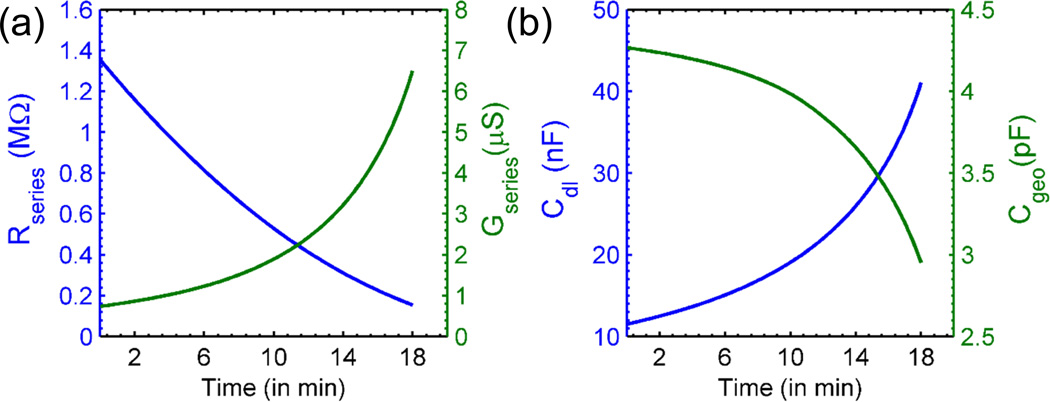
- Series Resistance/Conductance: Variation in series resistance due to evaporation comes from two distinct effects. First, the geometry factor g(r, θ) evolves with θ(t), so that g(t) = g(θ(t)), see Fig. 3 and SFig. 1(b). Second, the concentration of the ions in the solution increases inversely with the volume of the evaporating droplet, V(t). If the electrolyte composing the droplet solution is fully ionized, we can assume that conductivity is directly proportional to the ionic concentration. Therefore, the conductivity σ(t) = σ0 V0/V(t) increases as a function of time. At any time, series resistance is given by,
where R0 represents the resistance of the solution at time t = 0 and g0 = g(t = 0). Here, V0 and σ0 are the initial volume and conductivity of the droplet, respectively. Fig. 4(a) shows the evolution of Rseries and as a function of time.(9) - Double Layer Capacitance: The increased concentration of the evaporating droplet is also reflected in CDL, as follows: Since, the concentration at any time t is given by ni(t) = n0V0/V(t), the double layer capacitance would be,
where CDL,o is the double layer capacitance at t = 0. Fig. 4(b) shows the evolution of the double layer capacitance as a function of time.(10) Geometry Capacitance: The geometry (dielectric) capacitance is independent of the ion concentration (any dependence can come through only permittivity of the solution, ε), but depends on the geometry of the droplet through g(t). The variation of Cgeo as a function of time is shown in Fig. 4(b). Our numerical simulations show that both g(θ) and θ(t) are monotonically decreasing functions of θ (SFig. 1 (b)) and t (Fig. 3) respectively; therefore g(t) is monotonically increasing function of time t. Therefore, the geometry capacitance decreases with time unlike Gseries and CDL.
Fig. 4.
(a) Time dependence of series resistance (left) and series conductance (right) (b) Time evolution of double layer capacitance (left) and Geometry capacitance (right) for n0 = 10 µM and V0 = 3 µL.
To summarize, the impedance evolution is specified by two parameters, g(r, θ(t)) and V(t)/V0. Once these two parameters are known either from experiments, or detailed numerical models such as surface evolver28; or by approximate analytical/numerical model discussed above, one can compute any electrical characteristics associated with evaporating droplets. In the next section, we will illustrate the concept by analyzing a droplet-based sensor.
3. Application of model to a droplet based sensor
3.1 Frequency-dependent time response of Biosensors
Our earlier work showed that a droplet based sensor has improved sensitivity over sensors based on bulk liquid11. In order to determine the relative improvement in sensitivity, we define sensitivity of the droplet-based sensor as normalized change in admittance of droplet containing analyte (Yρ) with respect to a reference solution i.e. DI water (YDI). Therefore,
| (11) |
a) Low frequency operation
In this range of frequency f ≪ flow(t) for all 0 < t < T, the double layer capacitance is the dominant component i.e. Y(t) ~ jωCdl (t). As the droplet shrinks and the concentration increases, the reduction in the double layer thickness is reflected in increasing Cdl. The sensitivity of this mode of operation can be defined as the change in the double layer capacitance upon addition of chemical/biomolecule (Cdl,ρ) with respect to a reference solution (DI water) (Cdl,DI). Using Eq. 11 with Y(t) = jωCdl(t), sensitivity is given by
| (12) |
The amplification in sensitivity relative to time t = 0 is obtained by inserting Eq. 10 in Eq. 12 i.e.
| (13) |
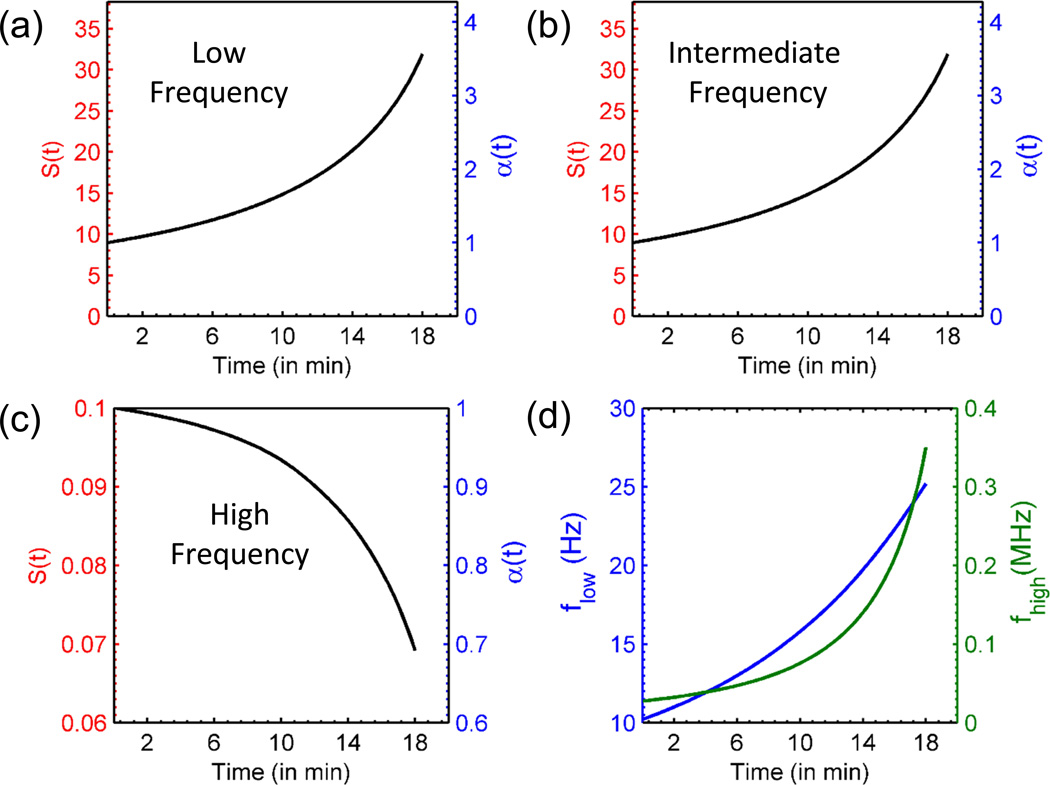
where we have used the empirical approximation of V(t)/V0 from Eq. 7. Note that the amplification factor is independent of the contact angle of the droplet at any time. Fig. 5(a) shows the sensitivity and amplification factor for very low frequency mode of operation of a sensor with initial ion concentration n0 = 10 µM.
Fig. 5.
Sensitivity as a function of evaporation time for (a) low frequency operation (b) intermediate frequency operation (c) high frequency operation (d) Evolution of cut-off frequencies as a function of time for n0 = 10 µM and V0 = 3 µL.
b) Intermediate frequency operation
This regime of operation occurs when flow (t) ≪ f ≪ fhigh (t), and therefore Y(t) ~ Gseries(t). In this regime, the capacitive response of the ions is no longer relevant and the in-phase response of the ions with respect to the applied signal dictates the net impedance.
The sensitivity S(t) in this regime of operation can be defined in terms of the conductance change upon addition of chemical/biomolecule (Gρ) with reference to DI water (GDI), i.e
| (14) |
where ΔG0 = Gρ(t = 0) − GDI(t = 0) and the amplification factor,
| (15) |
relates the sensitivity enhancement obtained as a function of time. Note that even though, g(t) is monotonically increasing as a function of time, the net amplification factor (α(t)) still increases due to considerable reduction in droplet volume V(t). This equation suggests that a very high sensitivity can be achieved if we operate the sensor in a frequency regime where Gseries is dominant. Fig. 5(b) shows the sensitivity and amplification factor for intermediate frequency mode of operation of a sensor with initial ion concentration n0 = 10 µM.
c) High frequency operation
This regime occurs when f ≫ fhigh (t), so that Y(t) ~ jωCgeo (t). Again the sensitivity of the system can be defined as
| (16) |
where Cgeo,ρ and Cgeo,DI are respectively the geometry capacitances for the droplet with chemical/biomolecules and the reference solution (DI water). The amplification in sensitivity relative to time t = 0, is given by
| (17) |
Since g(t) is a monotonically increasing function of time, the sensitivity in this regime of operation degrades with time i.e. α(t) ≤ 1. Fig. 5(c) shows the evolution of sensitivity (S(t)) and amplification factor (α(t)) as a function of time. It is assumed that the permittivity change of the solution upon addition of chemical/biomolecules is 10%.
Further, for a conductance based sensor (with negligible change in solution permittivity), ΔCgeo,ρ = 0 and hence this regime is unsuitable for biomolecule detection. However, if one is interested in characterizing the time-dependent evolution of the geometry of the droplet (e.g. shape or volume), this frequency regime is ideally suited, since the impedance is independent of salt/analyte concentration and depends exclusively on droplet geometry.
In general, as the droplet evaporates, the relative importance of a particular circuit component changes as well. This is because the cut-off frequencies, and , themselves evolve with time; as the boundaries of the frequency band shift, the circuit may become more resistive/capacitive at a given frequency of operation. Fig. 5(d) shows the evolution of lower and upper cutoff frequencies for a droplet containing salt solution with initial concentration n0 = 10 µM. Given the time and frequency dependence as discussed in section 2.3, one can determine the frequency of operation for which ΔY(t) is maximum for a given set of parameters, such as mobility of ions (μ) and applied bias (Ve). For example, in case μ of ions is large, it would be preferable to operate the sensor in resistive regime for optimal sensitivity. For such an operation, a frequency choice, foptimal such that
would be appropriate, since this will ensure that the resistive component at any time is atleast 10 times larger than the capacitive component. When the applied bias is large, so that double layer capacitance is significant, a frequency of operation foptimal ≤ 1/10 min (flow) would ascertain the operation in capacitive regime. However, a very large applied bias may not be desirable because it would yield unreasonably low frequencies for capacitive operation and lead to faradaic currents20 that can contaminate results of impedance spectroscopy. For a more realistic case, when substrate parasitic capacitance must be accounted for (discussed in next section), the upper cut-off frequency is given by . This implies that, the upper cut-off frequency can be substantially lower if the parasitic capacitance (Cpar) is large. If 10 max(flow) ≥ min (fhigh/10), it is impossible to operate the sensor in dominantly resistive regime and the parasitic capacitance must be suppressed to increase fhigh.
3.2 Implications of parasitic impedance of the substrate, Zpar
So far, we have focused exclusively on Zdrop, assuming that the parasitic capacitance/resistance of the substrate is negligible. However, in real systems the parasitic capacitance can be a major limitation to the sensitivity of the device and must be accounted for. Parasitic capacitance dominates at intermediate to high frequencies and can limit frequency range of operation of the sensor. It can either be obtained from experiments with droplet-free measurements11 or through detailed numerical simulation/analytic modeling. Here, we consider numerical/analytic evaluation of parasitic capacitance for two different substrates which are commonly used for impedance-based sensors:
-
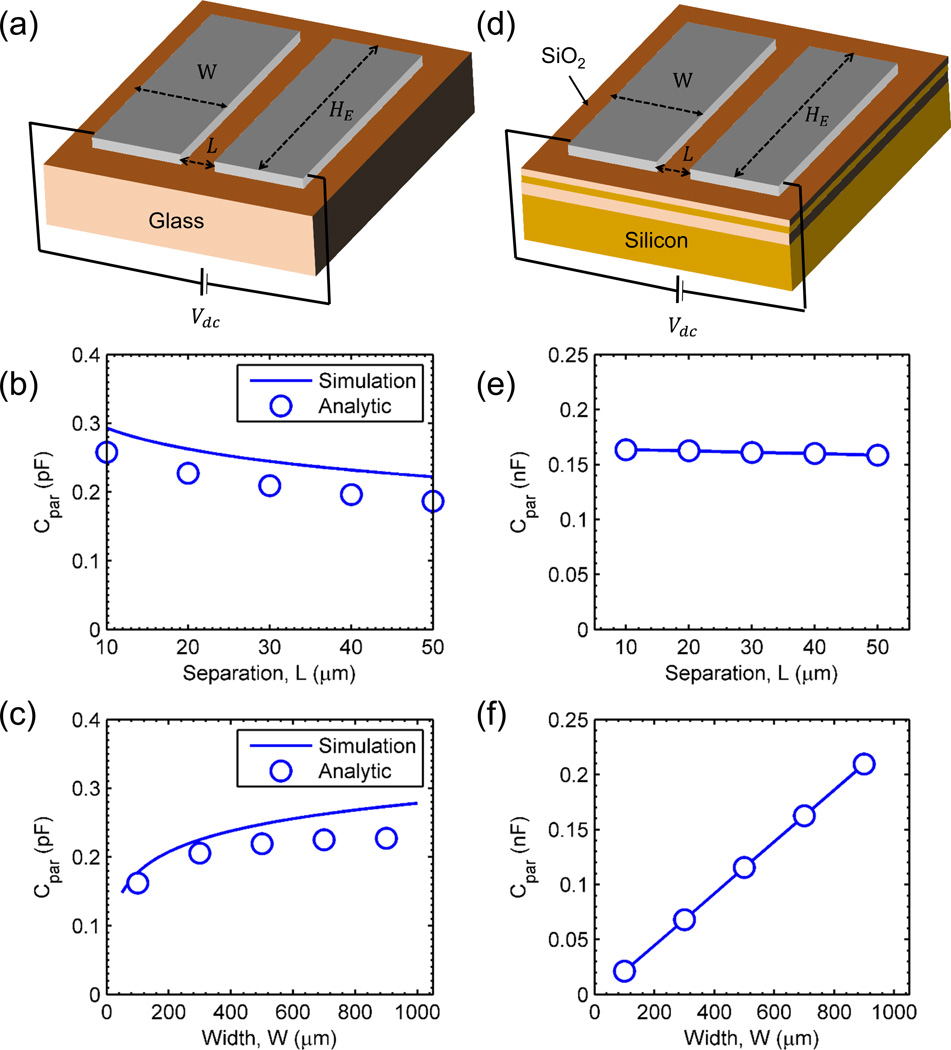
Glass as the sensor substrate: Due to its low dielectric constant, glass is an ideal candidate for use as a substrate for the sensor. The parasitic capacitance is estimated by numerical simulation of the structure shown in Fig. 6(a) using Sentaurus, an advanced multidimensional device simulator34. A bias Vdc is applied between the electrodes and Laplace equation (∇․ (εglass ∇(ϕ)) = 0 is solved to determine the potential, ϕ and electric field, E inside the substrate. Charge Qdc is estimated on the positive electrode by Gauss Law i.e. Qdc = ∫Ω D⃗․ d S⃗ = ∫Ω εglassE⃗․ dS⃗. The capacitance of the substrate is then given by Cpar = Qdc/Vdc. An analytic expression for capacitance of coplanar electrodes was derived by Wei35, i.e.
where K(k) is the complete elliptical integral of first kind with k = L/(L + W), εglass denotes the permittivity of glass substrate and HE is the electrode length.(18) Fig. 6(b) and 6(c) show the simulation (numerical/analytic) of the parasitic capacitance for different electrode separations (width = 900 µM) and for different electrode width (separation = 20 µM). The capacitance is very weakly dependent on the electrode separation and width. Numerical simulation is in good agreement with the analytic expression. The marginal difference in simulation and analytic estimate comes from the fact that Eq. 18 was derived by Wei neglecting the fringing fields in the transformed coordinate system.
SOI as the sensor substrate: The silicon-on-insulator (SOI) is a popular substrate in the semiconductor industry because it minimizes the leakage currents, radiation-induced photocurrents, latch-up effects, etc.36 in comparison to conventional bulk substrates. However, the same leads to huge parasitic losses for impedance sensors, as the electrodes can couple to the doped silicon below the top oxide layer which leads to a large parasitic capacitance. Fig. 6(e) and 6(f) shows the numerical simulation results for parasitic capacitance of an SOI substrate (Fig. 6(d)) for different electrode separations (with width W = 700 µM) and different widths (with separation, L = 20 µM) respectively. The parasitic capacitance of SOI structure (~0.1 nF) is nearly 3 orders of magnitude larger than that of the glass substrate (~0.1 pF). Also, the parasitic capacitance for the SOI substrate increases linearly with increase in the width of the electrodes.
Fig. 6.
Simulation of parasitic capacitance for two different substrates. Geometry used for the simulation for glass substrate (a) and SOI substrate (d). Variation of parasitic capacitance as a function of (b), (e) electrode separation and (c), (f) electrode width for glass and SOI substrate respectively.
A first order estimate of parasitic capacitance can be obtained by assuming the top silicon layer to be metal, so that net capacitance . However, since the top silicon layer has finite conductivity, the actual capacitance is smaller than the estimate which is observed in the simulation. Regardless, such a large parasitic coupling decreases and confines the optimum sensor operation close to the low/intermediate frequency regimes11.
If one must perform droplet characterization on SOI substrate at very high frequencies, a parallel plate detection system as described in Sadeghi et al.17 may be used. This will ensures that most of the electric field from the electrode is confined within the droplet resulting in lesser sensitivity to the substrate.
3.3 Experimental verification
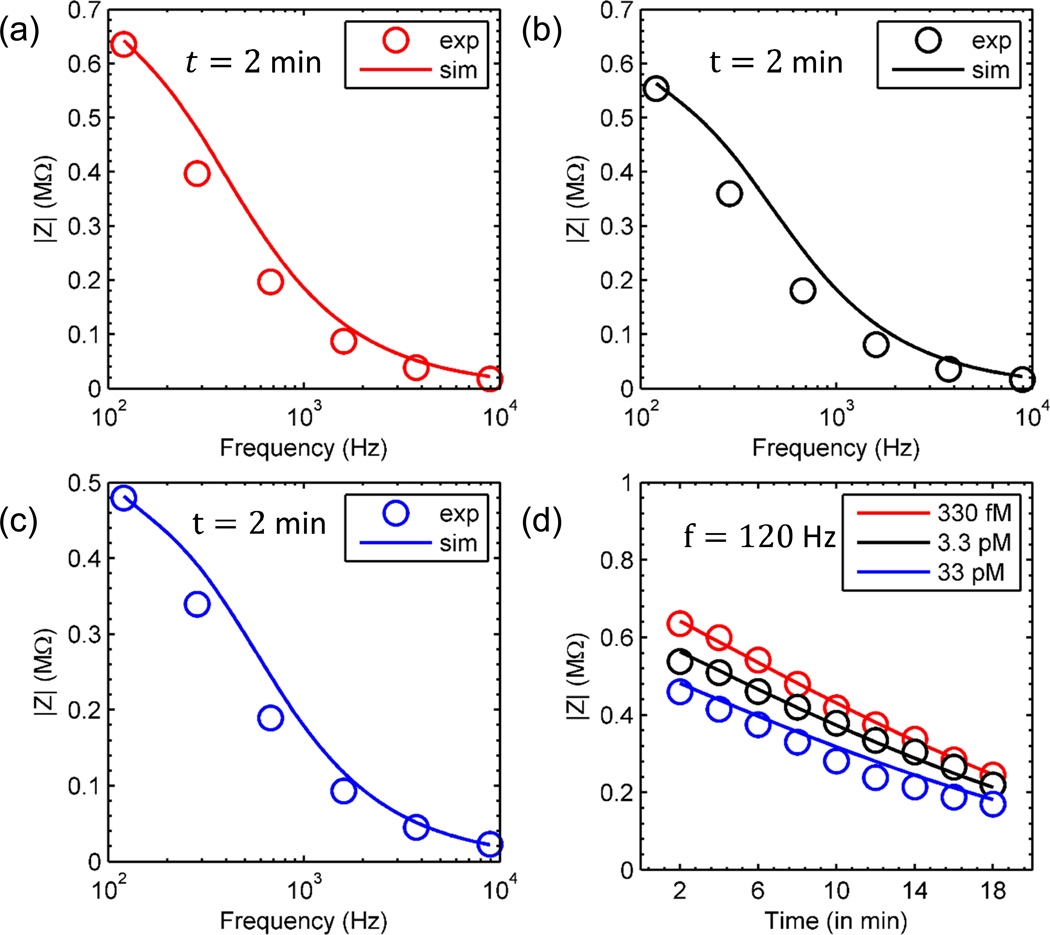
In order to validate the model described in the numerical section, both time and frequency response of droplets containing different DNA concentrations were analyzed. The data was obtained from Ebrahimi et al.11. Frequency response of the system at t = 2 min was calibrated with the numerical model (see, Eq. 2) to determine the ionic conductivity (σ) for different DNA concentrations (see, Fig. 7(a), (b), (c))37. Using this ionic conductivity (σ), the time response of the system was determined using Z = Zdroplet (t)‖Zpar (see, Eq. 8, Fig. 7 (d)). Zpar was obtained from the droplet free measurement on the substrate11. The ionic conduction was assumed to take place due to H+ and OH− ions as the experiments were performed using DI water containing DNA molecules. The DNA solution (purchased from Fermentas, Inc.) had 850 bp long synthetic molecules in 1×TAE buffer solution. The DNA molecules were precipitated using an isopropanol precipitation method and resuspended in nuclease-free DI water. Additional experimental details are provided in Ebrahimi et al.11.
Fig. 7.
Impedance vs. Frequency (calibration curves) at t = 2 min for different DNA concentration (a) 330 fM, (b) 3.3 pM and (c) 33 pM. (d) Impedance vs. Time for different DNA concentration: 330 fM (red), 3.3 pM (black) and 33 pM (blue). Lines and circles represent simulation and experiment respectively. Experimental data was taken from Ebrahimi et al.11
Despite of the various simplifying assumptions made in section 1, the model (solid lines) predictions agree with the experimental results (circles) remarkably well. Indeed, apart from fitting the t = 2 min conductivity at various analyte concentration, the model describes the time-evolution and frequency dependence of the droplet impedance consistently without any other fitting parameters. The key features of the experiments are reproduced: First, the model correctly estimates the frequency response of the system. At low frequency, the impedance is dependent on the composition of droplet (DNA) (compare, Fig. 7(a), (b) and (c)). At high frequency, the impedance of the parasitic substrate dominates and yields essentially same impedance for different DNA concentrations, making high frequency regime unsuitable for detection. Second, Fig. 7(d) shows that the time-evolution of the impedance predicted by the theoretical model correctly reproduces the features observed in the experiment. The impedance of the droplets with different DNA concentrations converge at higher times, due to decrease in droplet volume (ΔZ(t) ∝ V(t)η, where η ≈ ½ or 1 depending on whether Cdl or Rseries is dominant (refer Eq. 8, 9 and 10). Due to large parasitic capacitance, fhigh varies in range 350 HZ − 960 HZ from t= 0 to t = 18 min respectively. This limits the operation of the device to sub-KHz range for sensing operation even at larger times. Additional results with phase plots that validates the robustness and accuracy of the model are presented in the Supplementary Section 4.
CONCLUSIONS
We have developed a comprehensive numerical and compact modeling framework for the impedance of an evaporating droplet. The model is simple, and yet the theoretical framework correctly predicts the complex, time-dependent electrical response of an evaporating droplet containing analyte molecules. Indeed, once the geometry factor g(t) and the volume evolution V(t) are determined, either through experiments or through numerical/analytic modeling, the response of the system is completely specified. As a result, this physics-based model can be used to optimize variety of droplet-related systems (e.g. the operation of a droplet-based sensor) once the system parameters, such as mobility of ions and applied bias, are specified. The model also highlights the critical importance of the substrate for highly sensitive impedance-based chem-bio sensing. Specifically, for example, the model suggests that, compared to typical SOI substrate, the reduced parasitic impedance of a glass substrate would improve the overall sensitivity as well as provide a broader bandwidth of operation. Furthermore, higher frequencies can be used to characterize the droplet shape and size, since the impedance in that regime is independent of the droplet composition. If one must use SOI substrate for integration purposes, a comparable level of sensitivity is obtained only if the operating frequency is reduced to an extent that completely eliminates the effects of parasitic impedance on the overall impedance of the system.
Supplementary Material
ACKNOWLEDGMENT
This work was supported by the National Science Foundation through the NCN-NEEDS program (1227020-EEC) and the National Institute of Health (R01-CA20003). The authors also thank Prof. Rashid Bashir, Prof. Suresh Garimella and Prof. Pradeep Nair for useful discussions.
Footnotes
The code for droplet impedance model can be downloaded from https://engineering.purdue.edu/~alamgrp/dak_files/droplet_impedance.zip
REFERENCES
- 1.Marmur A. Langmuir. 2004;20:3517–3519. doi: 10.1021/la036369u. [DOI] [PubMed] [Google Scholar]
- 2.Deegan RD, Bakajin O, Dupont TF, Huber G, Nagel SR, Witten TA. Nature. 1997;389:827–829. doi: 10.1103/physreve.62.756. [DOI] [PubMed] [Google Scholar]
- 3.Deegan R. Phys. Rev. E. 2000;61:475–485. doi: 10.1103/physreve.61.475. [DOI] [PubMed] [Google Scholar]
- 4.Yunker PJ, Still T, Lohr MA, Yodh AG. Nature. 2011;476:308–311. doi: 10.1038/nature10344. [DOI] [PubMed] [Google Scholar]
- 5.Chen AU, Basaran OA. Phys. Fluids. 2002;14:L1. [Google Scholar]
- 6.Berná J, Leigh DA, Lubomska M, Mendoza SM, Pérez EM, Rudolf P, Teobaldi G, Zerbetto F. Nat. Mater. 2005;4:704–710. doi: 10.1038/nmat1455. [DOI] [PubMed] [Google Scholar]
- 7.Mazutis L, Gilbert J, Ung WL, Weitz DA, Griffiths AD, Heyman JA. Nat. Protoc. 2013;8:870–891. doi: 10.1038/nprot.2013.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Salm E, Guevara CD, Dak P, Dorvel BR, Reddy B, Alam MA, Bashir R. Proc. Natl. Acad. Sci. U. S. A. 2013;110:3310–3315. doi: 10.1073/pnas.1219639110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jing J, Reed J, Huang J, Hu X, Clarke V, Edington J, Housman D, Anantharaman TS, Huff EJ, Mishra B, Porter B, Shenker A, Wolfson E, Hiort C, Kantor R, Aston C, Schwartz DC. Proc. Natl. Acad. Sci. U. S. A. 1998;95:8046–8051. doi: 10.1073/pnas.95.14.8046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.De Angelis F, Gentile F, Mecarini F, Das G, Moretti M, Candeloro P, Coluccio ML, Cojoc G, Accardo A, Liberale C, Zaccaria RP, Perozziello G, Tirinato L, Toma A, Cuda G, Cingolani R, Di Fabrizio E. Nat. Photonics. 2011;5:682–687. [Google Scholar]
- 11.Ebrahimi A, Dak P, Salm E, Dash S, Garimella SV, Bashir R, Alam MA. Lab Chip. 2013;13:4248–4256. doi: 10.1039/c3lc50517k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thoroddsen ST, Etoh TG, Takehara K. Annu. Rev. Fluid Mech. 2008;40:257–285. [Google Scholar]
- 13.Ghosh S, Chattoraj S, Mondal T, Bhattacharyya K. Langmuir. 2013;29:7975–7982. doi: 10.1021/la400840n. [DOI] [PubMed] [Google Scholar]
- 14.Chen G, Mohiuddin Mazumder M, Chang RK, Christian Swindal J, Acker WP. Prog. Energy Combust. Sci. 1996;22:163–188. [Google Scholar]
- 15.Glover AR, Skippon SM, Boyle RD. Appl. Opt. 1995;34:8409–8421. doi: 10.1364/AO.34.008409. [DOI] [PubMed] [Google Scholar]
- 16.Guan J-G, Miao Y-Q, Zhang Q-J. J. Biosci. Bioeng. 2004;97:219–226. doi: 10.1016/S1389-1723(04)70195-4. [DOI] [PubMed] [Google Scholar]
- 17.Sadeghi S, Ding H, Shah GJ, Chen S, Keng PY, Kim C-J, van Dam RM. Anal. Chem. 2012;84:1915–1923. doi: 10.1021/ac202715f. [DOI] [PubMed] [Google Scholar]
- 18.Nair PR, Alam MA. Appl. Phys. Lett. 2006;88:233120. [Google Scholar]
- 19.Nair PR, Alam MA. Nano Lett. 2008;8:1281–1285. doi: 10.1021/nl072593i. [DOI] [PubMed] [Google Scholar]
- 20.Bard AJ, Faulkner LR. Electrochemical Methods: Fundamentals and Applications. 2001 [Google Scholar]
- 21.Randles JEB. Discuss. Faraday Soc. 1947;1:11. [Google Scholar]
- 22.Grahame DC. Chem. Rev. 1947;41:441–501. doi: 10.1021/cr60130a002. [DOI] [PubMed] [Google Scholar]
- 23.van Hal REG, Eijkel JCT, Bergveld P. Adv. Colloid Interface Sci. 1996;69:31–62. [Google Scholar]
- 24.Hiemstra T, Van Riemsdijk WH. Colloids and Surfaces. 1991;59:7–25. [Google Scholar]
- 25.Hong J, Yoon DS, Kim SK, Kim TS, Kim S, Pak EY, No K. Lab Chip. 2005;5:270–279. doi: 10.1039/b410325d. [DOI] [PubMed] [Google Scholar]
- 26.Chen Y, He B, Lee J, Patankar Na. J. Colloid Interface Sci. 2005;281:458–464. doi: 10.1016/j.jcis.2004.07.038. [DOI] [PubMed] [Google Scholar]
- 27.Lin LJ, Chuang SY, Yang YC, Chen YJ. AIChE 2013 Annu. Meet [Google Scholar]
- 28.Brakke KA. Surface Evolver, version 2.70. Selinsgrove, PA: Susquehanna University; 2013. [Google Scholar]
- 29.Rowan SM, Newton MI, McHale G. J. Phys. Chem. 1995;99:13268–13271. [Google Scholar]
- 30.Birdi KS, Vu DT, Winter A. J. Phys. Chem. 1989;93:3702–3703. [Google Scholar]
- 31.Picknett R, Bexon R. J. Colloid Interface Sci. 1977;61:336–350. [Google Scholar]
- 32.Jackson JD. Am. J. Phys. 2000;68:789. [Google Scholar]
- 33.Dash S, Garimella SV. Langmuir. 2013;29:10785–10795. doi: 10.1021/la402784c. [DOI] [PubMed] [Google Scholar]
- 34.Sentaurus. version H–2013.03. United States; 2013. [Google Scholar]
- 35.Wei J. IEEE J. Quantum Electron. 1977;13:152–158. [Google Scholar]
- 36.Celler GK, Cristoloveanu S. J. Appl. Phys. 2003;93:4955. [Google Scholar]
- 37.Liu Y-S, Banada PP, Bhattacharya S, Bhunia AK, Bashir R. Appl. Phys. Lett. 2008;92:143902. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.