What Do Differences Between Multi-voxel and Univariate Analysis Mean? How Subject-, Voxel-, and Trial-level Variance Impact fMRI Analysis

Abstract

Multi-voxel pattern analysis (MVPA) has led to major changes in how fMRI data are analyzed and interpreted. Many studies now report both MVPA results and results from standard univariate voxel-wise analysis, often with the goal of drawing different conclusions from each. Because MVPA results can be sensitive to latent multidimensional representations and processes whereas univariate voxel-wise analysis cannot, one conclusion that is often drawn when MVPA and univariate results differ is that the activation patterns underlying MVPA results contain a multidimensional code. In the current study, we conducted simulations to formally test this assumption. Our findings reveal that MVPA tests are sensitive to the magnitude of voxel-level variability in the effect of a condition within subjects, even when the same linear relationship is coded in all voxels. We also find that MVPA is insensitive to subject-level variability in mean activation across an ROI, which is the primary variance component of interest in many standard univariate tests. Together, these results illustrate that differences between MVPA and univariate tests do not afford conclusions about the nature or dimensionality of the neural code. Instead, targeted tests of the informational content and/or dimensionality of activation patterns are critical for drawing strong conclusions about the representational codes that are indicated by significant MVPA results.

1. Introduction

The advent of multivoxel pattern analysis (MVPA) has led to dramatic changes in how fMRI data are analyzed and interpreted. The majority of past and current fMRI analyses have employed voxel-wise analysis to identify how experimental variables affect the overall engagement of individual voxels or mean engagement across a region of interest (ROI; Friston et al. 1994; Poldrack et al. 2011). Contrastingly, MVPA allows researchers to test how distributed patterns of BOLD activation across multiple voxels relate to experimental variables (Cox and Savoy, 2003; Haxby et al. 2001; Haynes and Rees, 2006; Kamitani and Tong, 2005; Norman et al. 2006). Because MVPA makes use of patterns of activation across voxels, MVPA is able to detect a broader class of task-related effects than voxel-wise analysis. Oftentimes, however, researchers are not only interested in harnessing MVPA’s enhanced ability to detect task-related effects – they are also interested in using differences between univariate and MVPA results to draw conclusions about how task-related effects are coded in the brain (Coutanche, 2013; Jimura and Poldrack, 2012).

It is well known that voxel-wise analysis and MVPA can differ in their sensitivity to psychological or physical dimensions underlying task processing (Coutanche, 2013; Davis and Poldrack, 2013a; Drucker and Aguirre, 2009; Jimura and Poldrack, 2012). Univariate voxel-wise analysis relates psychological or physical dimensions to the activation of single voxels (see Figure 1A), and thus can fail to map the neural basis of experimental variables and conditions when these variables have a distributed multidimensional effect on activation. Here we use the term distributed multidimensional effect to refer to contexts in which different voxels within a region carry non-identical information about psychological variables or experimental conditions (e.g., Diedrichsen et al. 2013; Naselaris et al. 2011). Multidimensional effects contrast with unidimensional effects in which each voxel within a region codes for a single psychological variable or condition, albeit to potentially differing degrees. In the context of a multidimensional effect, MVPA measures that take into account information from multiple voxels (Figure 1B) may be necessary to answer whether a region codes for a particular psychological dimension or experimental condition.

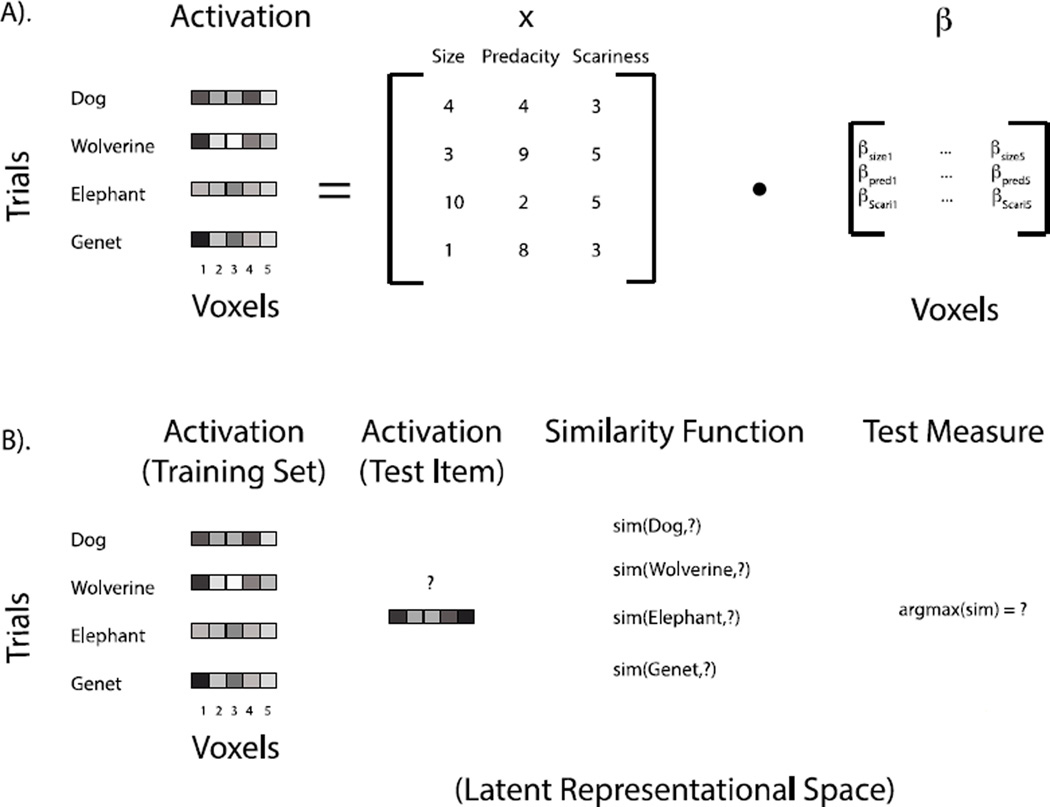
Figure 1.

(A). A graphical depiction of how the neural response to different stimulus dimensions is measured via univariate voxel-wise analysis. The most common practice for testing whether the dimensions Size, Predacity, and Scariness are coded in the brain using voxel-wise analysis is to test whether the beta weights for the three dimensions are significantly different from zero in individual voxels or across an ROI. (B). A graphical depiction of one way in which MVPA may be used to examine whether a region of the brain codes for differences between the mammals. Activation patterns for test items are compared to those for a number of items using a similarity function. Here, the new pattern is classified as the mammal with highest similarity and the accuracy of this prediction is assessed. Accurate classification indicates that the activation patterns contain information about the differences between these mammals in some latent neural representational space. The question we address in the present paper is whether any conclusions can be reached about the content or dimensionality of this latent space using prediction accuracy or other basic similarity tests alone

Consider, for example, a hypothetical experiment seeking to map the neural basis of the psychological dimension ‘scariness’ for a set of mammals (Figures 1&2; see also Weber et al. 2009; Davis and Poldrack, 2013a). This experiment would be condition-rich (Kriegeskorte et al., 2008), with exemplars (i.e., individual mammals) differing on a number of underlying dimensions in addition to scariness, such as size and predacity. If scariness were related directly to activation in individual voxels within an ROI (Figure 2A), then univariate voxel-wise analysis would be successful at mapping the neural basis of scariness in this experiment. However, in some ROIs, scariness may only be decodable by taking into account activation across multiple voxels, such as if an ROI contains voxels that separately represent size and predacity, with which scariness is presumably related (Figure 2B; for further examples, see Haynes and Rees, 2006). In this case, taking into account only a single voxel that codes either size or predacity will not decode scariness as accurately as MVPA methods that combine information from both size and predacity voxels. Such multidimensional effects can also arise in contexts for which the information that is distributed across voxels relates to latent subfeatures of the representation of scariness that do not directly admit a psychological interpretation.

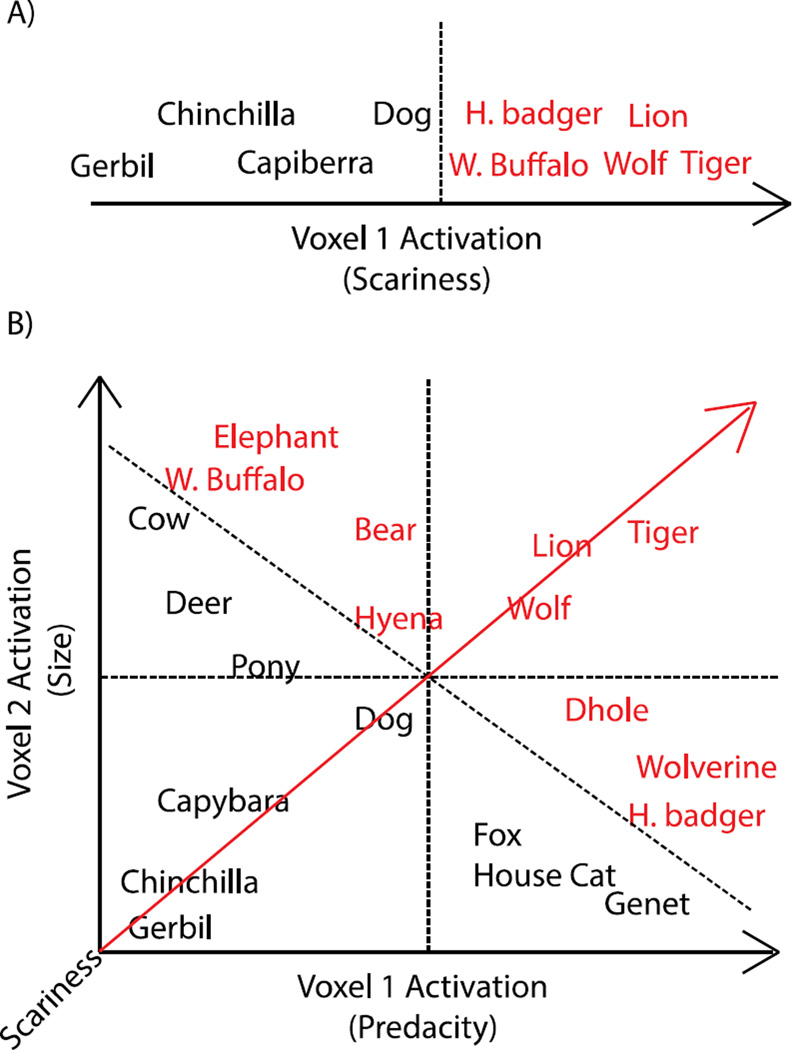
Figure 2.

An example of (A) unidimensional (B) multidimensional effects with respect to the scariness dimension. Mammals differ with respect to three dimensions: size, predacity, and scariness. Scary animals are depicted in red. In the case of a unidimensional effect, there is a direct mapping of scariness onto voxels within a region. Here Voxel 1 increases as a function of scariness, and scary and non-scary animals can be differentiated (i.e., the dotted-line marks a ‘scariness boundary’) based on the activation in this voxel. In the case of a multidimensional effect, no voxel activates for scariness per se; instead, voxels activate for either size or predacity, which are correlated with scariness. Decoding of mammals’ scariness (the latent dimension represented by the red line) is improved by taking into account both the voxels that code for size and the voxels that code for predacity. Scariness boundaries that take into account only a single dimension (i.e., the dotted lines that are orthogonal to the size and predacity dimensions) may be able to achieve some decoding of scariness, but will not achieve classification as accurate as scariness boundaries that take into account both dimensions (i.e., the dotted line orthogonal to the latent scariness dimension). Note that in the present example, a linear classifier could achieve high accuracy by assigning equal weight to both voxels, and thus in this context, it would also be possible to achieve high decoding accuracy by comparing the mean of the two voxels to an appropriate criterion.

Because univariate voxel-wise tests and MVPA differ in their ability to detect multidimensional effects, it is tempting to conclude that MVPA tests have identified a multidimensional code for a variable when MVPA results are significant but voxel-wise tests are not (for review, see Coutanche, 2013; Davis and Poldrack, 2013a). For example, if univariate voxel-wise tests were unable to isolate voxels or regions that activated for scariness, but MVPA tests were, one might be tempted to conclude that the coding of scariness is distributed across multiple voxels within these identified regions.

One potential problem with using differences between univariate voxel-wise analysis and MVPA results to infer the dimensionality of the underlying neural code is that the inductive validity of this inference depends upon how likely differences between univariate voxel-wise analysis and MVPA are to arise when only a single dimension underlies activation patterns (see e.g., Poldrack, 2006). Here, we use simulations to demonstrate the challenge of drawing conclusions regarding the dimensionality of the underlying neural code based upon differences between univariate voxel-wise analysis and MVPA. We highlight one key difficulty, which is that the two analysis techniques differ in their sensitivities to the sources of variability that are assumed to underlie activation patterns in fMRI data; critically, these sources of variability do not, in and of themselves, indicate anything about the dimensionality of the underlying activation patterns.

Specifically, our simulation results indicate that MVPA is sensitive to voxelby-voxel (i.e., voxel-level) variability in the parameters (beta weights) relating activation within voxels to experimental variables, even when these voxel-wise parameters are draws from the same unidimensional distribution (i.e., activation in all voxels directly maps to the same psychological dimension). Contrastingly, univariate voxel-wise methods are sensitive to the variability in the parameters relating activation to experimental variables between subjects (i.e., subject-level variability), whereas MVPA is insensitive to such subject-level variability. In cases in which an underlying neural space is unidimensional but high subject-level variability renders voxel-wise tests nonsignificant, many common MVPA tests neutralize this subject-level variability and will be significant as long as there is reliable voxel-level variability within subjects.

Our simulations, together with other possible differences in sensitivity to trial-level variability within subjects (see Section 4.0, Discussion), suggest that, on their own, differences between MVPA and univariate voxel-wise analysis techniques do not afford any conclusions about the dimensionality (or any other representational status) of the neural response to a stimulus or experimental condition. Instead, we argue that conclusions about whether multi-voxel patterns constitute a distributed representation or some other multidimensional feature space require explicit modeling of the hypothesized feature space or other targeted tests of the dimensionality of the underlying activation patterns, which we discuss in detail below (Section 4.2).

2. Methods

2.1 Analytic Framework: Sources of Variability in fMRI data

To establish the characteristics of fMRI data that univariate voxel-wise analysis and MVPA are sensitive to, it is useful to consider what the different sources of variability are in fMRI data. Common practice in voxel-wise fMRI analysis suggests that there are three primary sources of variability: trial-, voxel-, and subject-level variability (Friston et al. 1994; Poldrack et al. 2011). Thus, the activation (A) observed on any given trial t, in voxel v, for subject s is a combination of the fixed effects (γ) of experimental variables (X) across all subjects and random trial, voxel, and subject-level deviations from these fixed effects (Figures 3 & 4). These fixed and random effects can be simulated as a three-level mixed-effects model (e.g., Pinheiro and Bates, 2000; Raudenbush and Bryk, 2002; see Diedrichsen et al. 2011 for a related random-effects model). This simulation model captures the intuition that experimental variables are repeated measures over both voxels and subjects in standard univariate voxel-wise analysis.

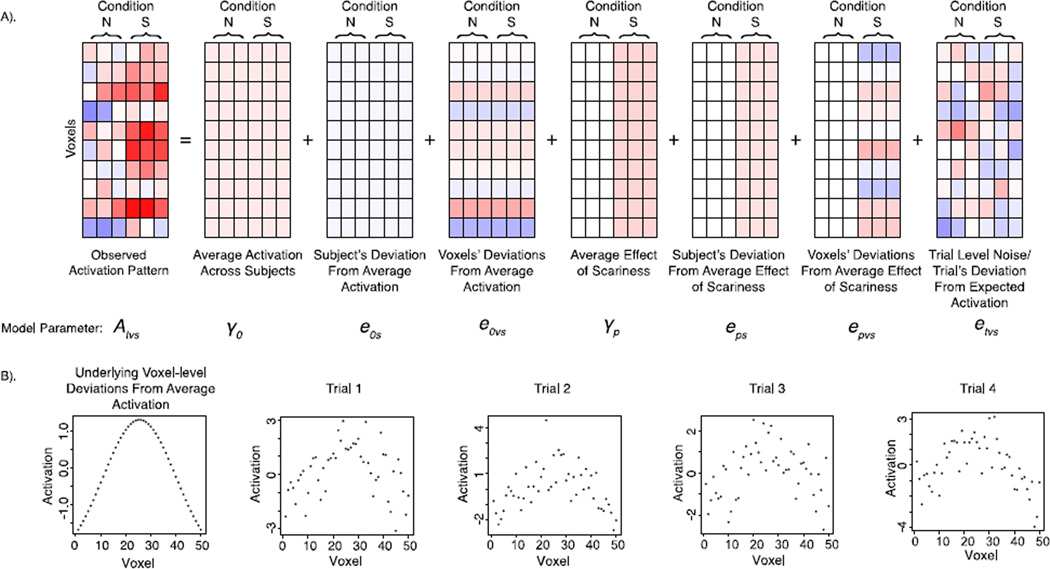
Figure 3.

A formal description of the 3-level mixed model for simulating fMRI data. At the trial level, the model simulates the activation on trial t, in voxel v, for subject s, as a linear combination of the voxel-wise regression coefficients α and trial-level error e_tvs, observed on trial t, in voxel v, for subject s. The voxel-wise regression coefficients included are an intercept term α_0vs, which corresponds to the mean or baseline activation in voxel v, for subject s, that is shared across trials, and α_pvs, which are the regression coefficients relating the p trial-level experimental X variables to activation in voxel v, for subject s. The trial-level errors, e_tvs represent the deviation on trial t, in voxel v, for subject s from the activation predicted by the αs, and are assumed to be normally distributed with mean of 0 and variance equal to σ². The voxel-wise regression coefficients in the trial-level model can be expanded into voxel-level models that take into account the repeated measurement of the baseline and X variables across voxels. The voxel-level models contain subject-wise β parameters that give the average baseline or effect of experimental variable p across all voxels for subject s (for, β_0s and β_ps, respectively), and voxel-level errors that give each voxel v’s deviation from the βs for subject s. These voxel-level error terms are assumed to be normally distributed with a mean of 0 and standard deviations equal to τ. In the present simulations, the voxel-level distributions for the baseline (e_0vs) and effect of experimental X variable (e_pvs) errors each have their own variance term (τ₀ and τ_p, respectively) and are uncorrelated. The subject-wise coefficients can likewise be expanded to subject-level models that take into account the repeated measurement of the baseline and X variables across subjects. The subject-level models have γ parameters, which correspond to the fixed effects of baseline and X variables across all subjects. Like the other levels, this subject-level has error terms, which correspond to the deviation from the fixed effect parameters observed for subject s. These error terms are also assumed to be normally distributed and uncorrelated in the present simulations, which is consistent with their estimation in standard univariate analysis. Substituting the parameters from the voxel- and subject-level models into the trial-level model gives the combined equation for activation A on trial t, in voxel v, for subject s, and illustrates how it is a function of the fixed effects parameters as well as the trial-,voxel-, and subject-level deviations from these fixed effects.

Figure 4.

(A) A graphical depiction of the 3-level mixed model for simulating fMRI data (Figure 2). Each level of the mixed model (subject, voxel, and trial) contributes variability to the observed trial-wise activation patterns. This example depicts a case in which a dummy coded scariness variable (Not Scary (N) = 0; Scary (S) = 1) is included, and thus trials for scary stimuli receive an added fixed effect of S in addition to added subject-level and voxel-level random deviations from the fixed effect of S. (B) A graphical depiction of how spatial variability in mean/baseline activation persists over repeated trials and is not influenced by centering with respect to the mean activation across voxels (e.g., Baseline Variability Simulation). In this example, mean activation in individual voxels tends to decrease as a function of distance from the peak voxel in the region-of-interest (ROI), such that across trials the central voxels tend to have the highest signal, whereas the outside voxels have a lower signal. Such an effect may arise as a function of distance-to-capillary or any other anatomical differences that create reliable variability in signal across voxels. The pattern caused by voxel-level variability persists across trials and is not eliminated by centering with respect to the mean activation across voxels because the ROI mean does not include information about the voxel-wise deviations.

The first level of the simulation model is the trial level. The trial-level model implements what are often referred to as ‘first level’ or within-subjects fMRI analyses. The variance component of interest in the trial-level model corresponds to the trial-by-trial variability in a voxel’s activation from its expected value for a given subject and condition. Activation in voxels often tends to vary from trial-to-trial even for the same conditions. For example, viewing a scary mammal may elicit activation that varies randomly across trials such that, even for the same level of scariness, there are random trial-level deviations around a voxel’s mean activation. In most contexts in fMRI analysis, these trial-level deviations from a voxel’s expected activation are assumed to be normally distributed with a mean of zero and standard deviation equal to σ.

The second level of the simulation model is the voxel level. The voxel-level model describes how activation varies across voxels. The variance components of interest in the voxel-level model correspond to the voxel-by-voxel variability in average activation and the effects of experimental variables (Figures 3 & 4). In almost any ROI, there are voxels that reliably (across trials) have a higher degree of average response relative to other voxels. Likewise, the effects of experimental variables often vary across voxels. For example, in our hypothetical mammal experiment, even amongst voxels that exhibit a scariness effect, there will be voxel-level variability within most ROIs in terms of how strongly each voxel reflects this effect. Common examples of how variability may manifest include contexts in which there is a mixture of relevant and irrelevant voxels (e.g., some voxels track scariness and some do not), and contexts in which there are spatially isolated peaks of activation and the effect of scariness decreases as a function of distance-from-peak (e.g., Figure 4B). Although voxel-level variability is assumed to exist in fMRI data, it is rarely explicitly modeled, and in univariate voxel-wise analysis, it often only comes into play in cluster-based correction for multiple comparison (see Discussion). Here we explicitly simulate voxel-level variability, which is expressed by the matrix, T, in our formalism. This T matrix is related to the G matrix in Diedrichsen et al.’s (2011) random effects model.

The final, third level of the simulation model is the subject level. The subject-level model implements what are often referred to as ‘group level’ or between-subjects fMRI analyses. The variance components of interest in the subject-level model correspond to the subject-by-subject variability in mean activation and the effects of experimental variables. All fMRI analyses assume that the effects of experimental variables, such as scariness, on activation will differ from person to person. Group-level statistical maps reported from voxel-wise analysis examine whether the value of the fixed effects corresponding to experimental variables are large relative to subject-level variability. In the present simulation model, the subject-level deviations from the fixed effects are assumed to be normally distributed with a zero mean across subjects and variability described by the matrix, Σ.

Altogether, this mixed model assumes that the activation on any given trial is some linear combination of trial-, voxel-, and subject-level effects, which is shown in the combined model in Figure 3. These components make up the activation patterns that underlie fMRI analysis regardless of whether one takes a univariate voxel-wise or MVPA approach.

2.2 Simulation Methods

In our simulations, we varied parameters of the three-level mixed model and examined how they impact univariate voxel-wise analysis and MVPA. Each of our simulations can be thought of as implementing the hypothetical mammal experiment discussed in the Introduction. The simulations all include 60 trials or presentations of mammal stimuli. The neural response for each trial is modeled as a multi-voxel activation pattern over 50 voxels. All simulated measures are calculated over independent draws of the model.

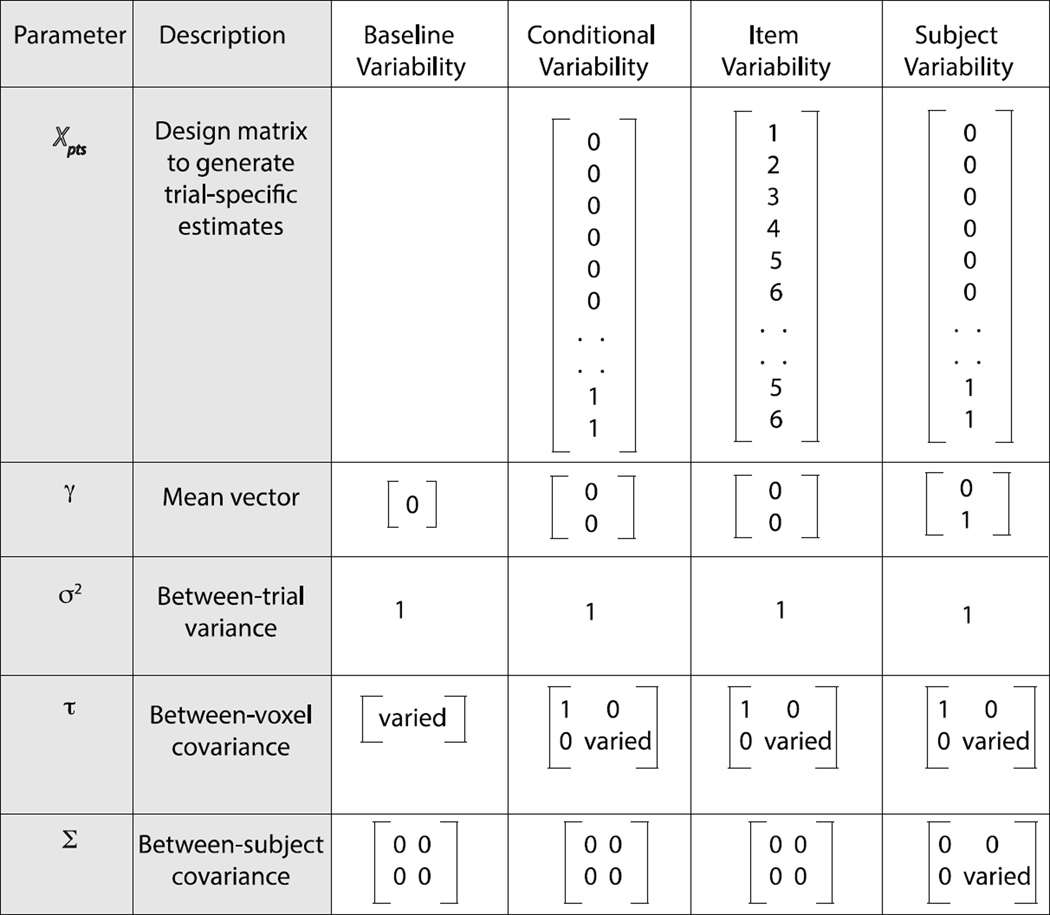
The Baseline Variability simulation (Section 3.1.1; 3^rd column in Figure 5) was designed to examine how voxel-level variability in baseline activation affects the clustering of activation patterns and how its effects are modulated by its relationship to trial-level variability. To this end, there were no effects of condition (scary or not-scary); all stimuli only shared a baseline activation pattern consisting of voxel-wise deviations between the voxel means and the expected mean across all voxels (i.e., 0). These voxel-wise deviations were draws from a single Gaussian distribution with mean of 0 and standard deviation equal to τ₀. The main parameter of interest for this simulation was τ₀, which was varied across simulations from zero to two in units of 0.25. The trial-by-trial variability (σ) was set to one. All other parameters were set to 0. Only one subject was simulated because between-subject variability (Σ) terms were set to 0.

Figure 5.

Parameter settings for different simulation models. The first column shows the parameters from Figure 3 and the second column has a short description of the parameter. The following 4 columns illustrate the settings for the 4 simulations.

The Condition Variability Simulation (Section 3.1.2; 4^th Column in Figure 5) was designed to examine how differences in voxel-level variability between conditions affected within-condition clustering and thus the ability for MVPA tests to discriminate between conditions. To this end, the Condition Variability Simulation was the same as the Baseline Variability Simulation except half of the 60 trials were assigned to the “scary” condition and half were assigned to the “not-scary” condition. A dummy-coded conditioning variable X was included such that trials in the not-scary condition were indicated with a 0 and trials in the scary condition were indicated with a 1. This type of parameterization is common in univariate mixed-model approaches to repeated measures designs (Pinheiro and Bates, 2000). A dummy-coded parameterization assumes that the effect of not-scary stimuli is equivalent to the baseline activation in each voxel, and an additional unidimensional effect is added to each voxel for stimuli that are perceived as scary. These voxel-wise deviations for the effect of scariness are draws from a single unidimensional Gaussian distribution with mean of 0 and variance of τ_p. The voxel-wise standard deviation for the baseline between-voxel variability (τ₀) was set to 1, while the standard deviation corresponding to between-voxel variability in the effect of scariness (τ_p) was varied across simulations from zero to two in units of 0.25. All other parameters were set to 0.

The Item Variability Simulation (Section 3.1.3; 5^th column in Figure 5) was designed to extend the results of the Condition Variability Simulation to a continuous scariness variable X with six values (1 to 6). This creates a unidimensional space in which each of the six values is represented. Ten trials were assigned to each of the six levels of X. The standard deviation corresponding to the between-voxel variability in the effect of the continuous scariness variable X (τ_p) was varied across simulations from zero to five in units of 0.25. The voxel-wise standard-deviation for the baseline between-voxel variability (τ₀) was set to 1.

The Subject Variability Simulation (Section 3.2; 6^th Column in Figure 5) was designed to examine how univariate voxel-wise and MVPA tests’ abilities to differentiate scary and not-scary stimuli were impacted by between-subject variability in the effect of scariness on activation, and how or whether between subject variability interacts with voxel-level variability. The Subject Variability Simulation therefore returned to a dummy coded scariness variable X. In the context of the subject-level model, a dummy coded parameterization assumes that not-scary stimuli have the same effect as baseline for all subjects, and an additional univariate effect is added to each activation pattern for stimuli that are perceived as scary. These subject-level deviations for the effect of scariness are assumed to be draws from a single univariate Gaussian distribution with mean of 0 and variance of Σ_p. This parameterization is equivalent to common univariate ROI-based repeated measures procedures for testing whether an ROI exhibits a mean effect of scariness across subjects. The standard deviation corresponding to between-subject variability in the mean effect of the scary condition, Σ_p, was varied from zero to four in units of one for each of four levels of voxel-level variability in the effect of scariness (τ_p ; 0.01, 0.1, 0.2, 0.3). The voxel-wise standard-deviation for the baseline between-voxel variability (τ₀) was set to 1. Because the Subject Variability Simulation varied between-subject variability, we included multiple subjects (s = 20) and report all outcome variables in terms of the distributions of parameter values between subjects for consistency with how between-subject effects are tested and reported in empirical studies.

The statistical measures employed in our simulations include two multivariate measures, correlation and classification accuracy using support vector machines (SVMs), as well as standard univariate measures such as mean activation across voxels. Correlation is a useful measure in this context because it is insensitive to the mean value of activation patterns for each stimulus (but see, section 3.2 “Why is MVPA Often More Powerful than Univariate Analysis?”). Thus relationships between stimuli cannot be due to effects of mean activation (which voxel-wise analysis is most concerned with), and the expected between-trial correlations remain the same regardless of whether parameters of the three-level model that affect mean activation for a stimulus are explicitly manipulated. To extend the same properties to SVMs, we normalized (z-scored) each stimulus’s activation pattern across voxels prior to classification in all simulations. A linear-ν SVM, with ν fixed at 0.01, was used for all simulations (V was not varied because our goal was not to optimize the SVMs, but rather to simply illustrate their sensitivity to spatial variability). Code for all of the simulations reported here is available at http://www.poldracklab.org/software/.

3. Results

3.1 Do Significant MVPA Effects Indicate Multidimensional Patterns?

Our first set of simulations examined the impact of voxel-level variability on MVPA results. Voxel-level variability is assumed to exist in standard applications of voxel-wise analysis. For example, nearly all efforts to localize cognitive function assume that the effects of experimental variables differ across voxels that belong to different anatomical regions (Cohen et al. 1994), or even within regions as a function of distance from focal peaks of activation. However, in and of itself, voxel-level variability does not indicate that the included voxels code different dimensions or that there is a multidimensional effect present. Indeed, in all of the present simulations, the deviations between a voxel’s activation and the mean activation across voxels are draws from a single univariate Gaussian distribution, meaning that all voxels code for the same, single dimension, but just to different degrees.

3.1.1 Baseline Variability Simulation: Voxel-level Variability Makes Activation Patterns More Similar

To examine how and why MVPA is sensitive to voxel-level variability, we calculated the correlation between activation patterns for trials over changes in voxel-level variability in baseline activation (τ₀) while holding trial-level variability (σ) constant. In this first simulation, there are no effects of condition (e.g., scary or not-scary).

The simulation revealed that as voxel-level variability in baseline activation (τ₀) increases relative to the trial-level error, the correlations between trial-wise activation patterns increase despite the fact that there are no multidimensional effects or mean activation differences between trials (Figure 6A).

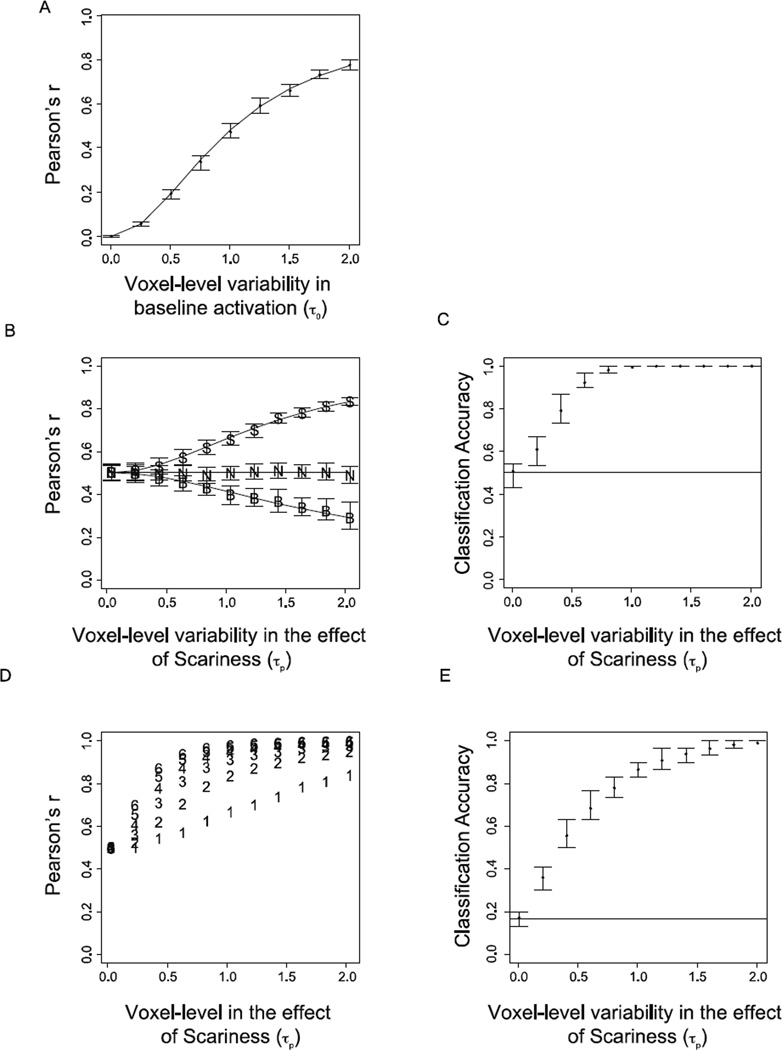
Figure 6.

Results from the Baseline, Condition, and Item Variability simulations. (A). Results from Baseline Variability Simulation. Points indicate the observed mean of the between-trial correlations for each level of voxel-level variance in baseline activation (τ₀) averaged over simulations. Error bars depict the 1st and 3rd quartiles of the distribution of the simulation means. The line depicts the analytical prediction for between-trial correlations generated using Equation A2. (B). Correlation results from Condition Variability Simulation. Points indicate observed mean correlations across simulations between trials within the scary (S) and not-scary (N) conditions, as well as between conditions (B). The lines depict analytical predictions for each correlation generated using Equations A2–A4. (C). Support vector machine classification results for Condition Variability Simulation (chance = 0.5). (D). Correlation results for Item Variability Simulation. Points indicate within-item correlation for 6 items that differ continuously with respect to a continuous scariness variable. (E). Support vector machine classification results for Item Variability Simulation. The support vector machine was trained to classify each of the 6 different items that varied continuously with respect to a single conditioning variable (chance = 0.167).

To better understand why the correlations between trials are non-zero when voxel-level variability in baseline activation is greater than zero, we can examine what information is contained in the activation patterns (Equation A1). Subtracting the sample mean, which occurs automatically in correlations (and all trial-normalized MVPA measures), removes subject- and group-level information about the overall mean activation within an ROI. However, it leaves in the voxel-level variability or how voxels tend to deviate from this mean across trials (e.g., Figure 4B). Because these voxel-level deviations are repeated across trials, the expected correlations between two trials will always be greater than zero when there is reliable voxel-level variability; because correlations are sensitive to shared variability, correlations rise as this shared voxel-level variability increases. In the present case, the properties of the distribution of voxel-level effects are known; the distribution is a univariate Gaussian distribution with mean of 0 and standard deviation of τ₀. Therefore it is possible to predict the average correlation between trials analytically by examining the proportion of total variability in the voxel-wise coefficients (voxel- and trial-level; Figure 6A) that is related to voxel-level variability (Equation A2).

Generalizing to more real-world contexts, this simulation suggests that the average expected correlation or ‘similarity’ between any two trials in a task will nearly always be non-zero. Voxel-level variability in baseline activation, which is the focus of this simulation, is ubiquitous. Signal differences stemming from partial voluming of white and grey matter, proximity to venous outflow, and a number of other anatomical considerations (e.g., susceptibility artifacts), all create variability in the mean BOLD response of voxels that will tend to be reliable across trials. Subtracting the mean activation (across voxels) from the trial-wise activation patterns does not eliminate these voxel-level patterns because mean activation and voxel-wise variability are independent parameters of the activation patterns.

3.1.2 Condition Variability Simulation: Voxel-level Variability in the Effect of a Condition Can Create Within-Condition Similarity and Facilitates Accurate Classification

The results from the Baseline Variability Simulation (Section 3.1.1) can be directly extended to more common applications of MVPA, such as when the goal is to examine whether activation patterns differ between levels of an experimental variable. In the Condition Variability Simulation, we set voxel-level variability in baseline activation (τ₀) to a fixed value of 1, but now included an experimental “scariness” variable X with two levels, “scary” and “not-scary”. X was dummy coded such that when a trial is categorized as not-scary, X = 0, and when a trial is categorized as scary, X = 1. Analogous to the Baseline Variability Simulation (Section 3.1.1), we varied the magnitude of the voxel-level variability in the effect of X (τ_p) relative to the trial-level errors. Because the Condition Variability Simulation involved a conditioning variable, we investigated how changes in voxel-level variability affect the observed mean correlations between trials within the scary and not-scary conditions (within-condition correlations) as well as the mean correlation between trials from different conditions (between-condition correlations).

The Condition Variability Simulation revealed that within-condition similarity increases in the scary condition as voxel-level variability in the effect of scariness (τ_p) increases relative to the trial-level errors (Figure 6B). This is for the same reason that general between-trial correlation increased in the Baseline Variability Simulation (Section 3.1.1); the voxel-wise deviations from the mean effect of scariness are repeated across trials, and thus they increase similarity within the scary condition. The mean correlations within the not-scary condition do not change with increases in τ_p, because the not-scary condition is coded with a 0 for the scariness variable X and thus the voxel-wise deviations from the mean effect of scariness only affect similarity within the scary condition. Likewise, voxel-level variability in the effect of the scariness variable adds variability to activation patterns for stimuli in the scary condition that is not added to activation patterns for stimuli in the not-scary condition. Thus pairwise correlations between activation patterns for scary and not-scary stimuli decrease as a function of τ_p. As with the Baseline Variability Simulation, the precise values of these correlations can be predicted analytically by evaluating how large the voxel-level variance components (τ₀ & τ_p) are relative to the trial-level variability, σ (Equations A3–4; Figure 6B).

To examine whether voxel-level variability in the effect of a variable impacts other types of MVPA beyond correlation, we performed the same simulation using a linear ν-support vector machine (SVM) classifier. Consistent with the findings that within-condition similarity increases and between-condition similarity decreases as a function of increasing τ_p, classification accuracy increased as voxel-level variability in the effect of scariness (τ_p) increased (Figure 6C).

Consistent with the Baseline Variability Simulation, we found that voxel-level variability in the effect of an experimental “scariness” variable leads to higher within-condition similarity for activation patterns that share this variance component. Further, this voxel-level variability leads to accurate decoding of condition (scary or not-scary) using SVMs. The voxel-level deviations in the effect of scariness that drive the effect are independent draws from the same univariate Gaussian distributions, and thus carry the same information about the experimental variable (i.e., that a trial was categorized as scary).

These results suggest that reliable classification and within-condition similarity arise when there is reliable voxel-level variability in the effects of experimental variables, and thus do not necessarily reflect distributed multidimensional effects or any conclusions that are not warranted by standard univariate voxel-wise analysis. Indeed, in all cases, the activation patterns for stimuli were generated by, and thus consistent with, a simple linear voxel-wise mapping of a single experimental condition onto activation in individual voxels.

3.1.3 Item Variability Simulation: Voxel-level Variability in the Effect of a Continuous Variable Can Increase Similarity Within Items and Cause Accurate Single Item Classification in Multiple Item Designs

The results of the Baseline and Condition Variability Simulations (Sections 3.1.1 and 3.1.2) extend directly to cases in which stimuli vary continuously with respect to an experimental variable, which is assumed to occur in almost all cognitive domains from basic visual and auditory perception (Jäncke et al. 1998; Tootell et al. 1998) to language and memory research (Clark, 1973; Rouder and Lu, 2005). For example, in our hypothetical mammal experiment, different stimuli are assumed to be associated with different levels of scariness (Figure 2). In the Item Variability Simulation, we examined how, by sharing the same level of a continuous scariness variable, activation patterns for repetitions of stimuli or “items” may become more similar to each other or classifiable. These measures have been used in previous studies to support claims that activation patterns reflect multidimensional representations of individual stimuli.

The Item Variability Simulation extended the Condition Variability Simulation (Section 3.1.2) such that six ‘items’ were presented ten times each. Critically, each item was associated with a unique value with respect to the scariness variable (1 to 6; as opposed to two conditions represented by 0 or 1 values), thus creating a single dimension in which the six different items are represented. Again, we find that this manipulation increased shared variability between within-item pairs, resulting in increased within-item correlations as voxel-level variability in the effect of scariness (τ_p) increased (Figure 6D). As with the above dummy coded case, the introduction of voxel-level variability in the effect of a continuous conditioning variable leads to better than chance classification performance with SVMs trained to discriminate between the six individual items (Figure 6E).

These results reveal that findings of high within-item similarity or successful individual item classification do not necessarily imply that an activation pattern contains a multidimensional representation. Discrimination of individual items based on multi-voxel patterns can arise simply from the tendency for items to be associated with similar values of an experimental variable across repeated presentations.

3.1.4 Interim Conclusions

Together, the results of the first three simulations illustrate that significant MVPA results do not definitively indicate that the processing or representation of a stimulus is multidimensional or differs in any other meaningful way from what is assumed by the univariate voxel-wise analysis. Instead, MVPA may only indicate what is already assumed in most contexts in which the voxel-wise analysis is employed -- that the effect of an experimental variable varies across voxels. Knowing how large voxel-level variability is relative to the trial-level error variability is potentially useful information that is often not directly computed in the voxel-wise analysis; however, it does not, in and of itself, indicate anything beyond there being some reliability in the effect of an experimental variable across trials within a subject.

3.2 Why is MVPA Often More Powerful than Univariate Analysis?

The foregoing results raise the question of why MVPA is often more powerful than univariate voxel-wise analysis, if it is not picking up on distinct non-redundant information in the multi-voxel activation patterns (e.g., Jimura and Poldrack, 2012). Although there may be numerous reasons for MVPA’s heightened power, a primary reason may be that voxel-wise analysis depends on how strongly an experimental variable activates voxels or an ROI relative to the variability in activation between subjects, whereas the above simulations hint that MVPA may largely depend on the relationship between voxel-level variability in the effect of experimental variables and trial-level error.

3.2.1 Subject Variability Simulation: Sensitivity to Subject-Level Variability Leads to Differences Between MVPA and Univariate Results

To examine the sensitivity of voxel-wise analysis and the imperviousness of MVPA to subject-level variability in mean activation, we ran a simulation in which we varied the value of subject-level variability in the mean effect of scariness (Σ_p). We simultaneously varied voxel-level variability in the effect of scariness (τ_p) to test how and whether subject-level variability interacted with voxel-level variability and as a general test of how sensitive group-level MVPA results are to small levels of voxel-level variability. To this end, we simulated τ_p at values of 0.01, 0.1, 0.2 and 0.3, which correspond to contexts in which voxel-level variability in the effect of scariness makes up 0.005%, 0.5%, 1.96%, and 4.3% of the total within-subject variability for scary trials, respectively.

As predicted, we found that increasing subject-level variability in the effect of scariness (Σ_p) increases the observed variability in the univariate voxel-wise effect magnitude, resulting in decreased statistical significance for the univariate effect of scariness as between-subject variability increases (Figure 7; Column 1). This same basic pattern was found regardless of the level of voxel-level variability in the effect of scariness (τ_p): at values of Σ_p of approximately 2, about half of the group-level univariate significance tests were non-significant regardless of the value of τ_p.

Figure 7.

Results from Subject-level Variability Simulation. Column 1 depicts group-level t-tests for the mean effect of scariness. Column 2 depicts group-level t-tests for the difference in within-condition correlations between scary and not-scary stimuli. Column 3 indicates classification accuracy for linear SVMs trained to classify activation patterns of scary and not-scary stimuli. The dotted lines in the t-test figures reflect the minimum t needed for statistical significance. The black lines in the SVM analysis depict chance classification (50%). Rows correspond to different levels of voxel-level variability in the effect of memory (A = 0.01; B = 0.1; C = 0.2; D = 0.3).

Group-level statistical tests for the MVPA measures showed the opposite results (Figure 7; Columns 2–3). At low levels of τ_p (0.01; Figure 7A), neither the correlation-based nor SVM tests revealed significant group-level results regardless of the level of Σ_p. Correlation-based and SVM group-level statistical tests became more significant as τ_p increased but remained independent of Σ_p. SVMs were considerably more powerful than the correlation-based measure, with better than chance accuracy (across subjects) occurring at values of τ_p as low as 0.1 (Figure 7B). However, both measures were significant and impervious to subject-level variability at values of voxel-level variability that are realistic given known signal-to-noise properties of BOLD fMRI (e.g., Ogawa et al., 1998).

Given that subject-level variability in mean activation is the primary variance component that goes into group-level univariate statistical tests, it is of little surprise that when it is high, there is less power to detect a significant univariate effect. However, it is somewhat more surprising that this variance component has no impact on our MVPA measures¹. This is because increasing the variability of mean activation (Σ) across subjects has no impact on the voxel-level variability (the τ matrix) for cases in which a single mean is sufficient for describing the effect of an experimental variable across voxels and there are no interactions between voxels and the effect of an experimental variable (see also, Davis and Poldrack, 2013a). For contexts in which there are voxel-level interactions with experimental variables (e.g., some voxels in an ROI do not activate), as would likely occur in many ROIs, increasing the between-subject variability in mean activation may also increase voxel-level variability and the between-subject variability of the voxel-level variances (the τ matrix). Thus, in cases of voxel-by-condition interactions, group-level MVPA may be affected by between-subject variability in activation (see e.g., LaRocque et al. 2013; Smith et al. 2011; Tong et al. 2012). Because of the infinite ways that voxel-by-condition interactions can manifest, it is not possible to give precise a priori predictions for how they impact MVPA in all contexts. However, we have found no cases in which subject-level variability in activation eliminates MVPA effects in the presence of reliable voxel-level variability within subjects.

Altogether, these results suggest a plausible context in which MVPA and univariate results will differ. High subject-level variability in mean activation is ubiquitous in neuroimaging studies. Being able to neutralize the effects of this subject-level variability thus results in MVPA having greater sensitivity to detect effects relative to voxel-wise analysis. Importantly, however, this does not indicate that there is anything beyond a simple linear mapping of the same experimental variable to individual voxels driving the results.

4. Discussion

In our simulations and supporting formalism (see Appendix), we illustrate how an omnipresent signal in univariate voxel-wise analysis, the variability of an experimental effect across voxels, can lead to significant similarity relationships between items, as well as significant within-condition clustering of multi-voxel activation patterns that is detectable using common MVPA methods. Moreover, because this clustering only depends on the magnitude of voxel-level variability in the effect of a condition relative to that of within-subject trial-level error, it is insensitive to subject-level variability in mean activation, the primary variance component that impacts group-level univariate voxel-wise tests. Thus MVPA methods may be more powerful than univariate voxel-wise tests, not because they are inherently better at tapping into multidimensional neural representations and processes than voxel-wise analysis, but because they are able to (a) exploit voxel-level variability within subjects that is discarded in univariate voxel-wise analysis, and (b) discard subject-level variability in mean activation that can reduce sensitivity in univariate voxel-wise analysis.

In our simulations of a hypothetical fMRI experiment, it was possible to decode a ‘scariness’ variable with MVPA that was not detectable using univariate tests. However, as each voxel coded only for the single neural dimension of scariness, it would be problematic to use these divergent results to conclude that coding of scariness across voxels is multidimensional in the sense that non-overlapping information about scariness is coded in different voxels. Although we frame much of our discussion in terms of such differences between multidimensional and unidimensional effects, these results directly extend to other occasions when substantive conclusions are drawn about the nature of the underlying data based solely on differences in the sensitivity of MVPA and univariate voxel-wise analysis. Because MVPA and voxel-wise analysis are sensitive to different aspects of activation patterns, differences in the distribution of significant MVPA and univariate tests across the brain do not (in and of themselves) allow for definitive conclusions about the nature of processing in those regions.

Our simulations focus on how differences between univariate voxel-wise analysis and MVPA can arise because of differences in their sensitivity to the variance components that are assumed to exist in activation patterns by application of standard voxel-wise analysis. However, it is important to note that there may be a number of additional reasons why the results of MVPA tests will differ from voxel-wise tests in any given context. For example, even within a single subject (a case in which subject-level variance is no longer relevant), MVPA effects may be more powerful than voxel-wise tests simply because MVPA is able to reduce the noise inherent in single-voxel observations by integrating information from multiple noisy sources.

Our simulations of univariate analysis focus on the influence of subject-level variability, which is the primary variance component of interest in the majority of studies examining univariate activation. However it is possible to develop decoding tests based on mean activation that, like MVPA, are insensitive to subject-level variability. One of these is to use the mean of an ROI to decode conditions within subjects instead of using the multi-voxel activation patterns (e.g., Coutanche, 2013). Such a test effectively neutralizes between-subject variability in the magnitude of the effect of condition: conditions will be decodable as long as the effects of condition within individual subjects are large relative to the trial-level error. Importantly, while this technique can make MVPA and univariate analysis more comparable in their sensitivity to subject-level variability, divergence in results across the two techniques does not necessarily provide additional information about the dimensionality of a neural representation. Indeed, in our within-subject simulations (Simulations 2–3; 3.12 & 3.13), there was no mean effect of condition (which renders decoding based on mean activation in an ROI ineffective), but we still achieved reliable MVPA results.

The extent to which MVPA and classification based on mean activation within an ROI will yield different results within a given subject depends simply on the relationship between mean activation across an ROI and the voxel-level variability. If the mean effect of condition on activation is high relative to the trial-level error, conditions will be decodable based on means; if voxel-level variability is high relative to trial-level error, conditions will be decodable with MVPA. If either of these effects is small relative to trial-level error, only one effect may be observed. For example, in cases in which there is no voxel-level variability and all voxels simply activate to the same level for scariness within a subject, classification of scariness by mean activation will be successful, but mean centered MVPA measures would not. Likewise, if an ROI contains equal numbers of voxels that are positively and negatively responsive to scariness (thus canceling each other out in terms of the mean), classification will only be possible with MVPA.

4.1 Voxel-level Variability in fMRI Analysis

The present results raise the question: How does voxel-level variability relate to information processing in the brain? At a large scale, voxel-level variability in the neural response to an experimental manipulation is usually taken as evidence for anatomical selectivity in function related to that manipulation (Cohen and Bookheimer, 1994). Of course, voxel-level variability due to anatomical selectivity is only one situation in which variability arises. Variability may also arise from spatially distributed effects within clusters or anatomical regions, as a function of distance from peak of activation (Figure 4B), as a function of distance from venous flow, or as a result of an ROI containing a mixture of active and non-active voxels. Thus voxel-level variability is an omnipresent component of fMRI data that, on its own, cannot be automatically assumed to reflect the brain’s underlying coding of experimental variables.

As these examples highlight, in most real-world contexts, aside from well-circumscribed ROIs with high spatial homogeneity, the distribution of voxel-level deviations from the mean of an ROI will not conform to the idealized Gaussian distributions that we use to simulate voxel-level variability here. For example, in the cases of mixtures where an ROI contains some voxels that activate for an experimental variable and some that do not, the distribution of voxel-level deviations will likely manifest as a bimodal distribution. Depending on the extent to which the voxel-level distributions deviate from Gaussian, our formal quantitative predictions for how voxel-level variability relates to MVPA measures (see Appendix) may no longer hold precisely. However, the general qualitative conclusions will hold regardless of the form of the distribution for the voxel-level deviations. As voxel-level variability in activation increases relative to trial-level error, MVPA effects will be increasingly detectable regardless of the form of this variability. Likewise, systematic voxel-level variability due to mixtures of active and non-active voxels will have no effect on univariate voxel-wise analysis. The significance of univariate voxel-wise activation within any individual voxel or subset of voxels will still depend upon the subject-level variability in activation; high between-subject variability in the effect of a condition will lead to non-significant voxel-wise results regardless of how the voxels are spatially organized.

Although the basic conclusions of our results are not restricted to Gaussian distributed data, it is important to note that Gaussian distributions are critical for allowing us to systematically manipulate the different mean and variance parameters in our simulations. In many real-world distributions, such as cases of mixtures of active and non-active voxels, increasing the mean activation of active voxels simultaneously increases the voxel-level variability because it increases the difference between the active voxels and the non-active voxels that do not exhibit the experimental effect. Thus even though the conclusions we reach are not unique to a particular type of distribution, Gaussian distributions are useful in that they allow us to easily and independently manipulate the signals that impact voxel-wise analysis and MVPA.

A final interesting question is how systematic, non-Gaussian, voxel-level variability between subjects would be accounted for within our simulation framework. As discussed above, on many occasions, researchers predict that there is systematic voxel-level variability across subjects because this indicates anatomical specificity in the effect of an experimental variable of interest. A conceptually straightforward way of including anatomical specificity within our three-level mixed model would be to include anatomical regions as fixed effects; in this analysis, additional voxel-level indicator variables would be included that add an effect of condition only if a voxel is a member of an anatomical region. It is important to note, however, that the significance tests for these fixed effect coefficients relating experimental variables to activation within a specified ROI will still depend upon the variability of the subject-level deviations from these parameters, as demonstrated in our simulations.

It would also be possible to account for anatomical specificity using cluster-correction methods, which are the most common way of taking systematic voxel-level variability into account in univariate voxel-wise analysis. In cluster-correction, voxels are assigned to groups or clusters at the very end of data analysis based on a statistical criterion, such as whether the average parameter estimate across subjects is large relative to its variability between subjects. As subject-level variability is incorporated directly in this cluster-forming threshold, increased subject-level variability will also necessarily reduce the ability of cluster-correction methods to detect significant clusters, by reducing the extent to which individual voxels reach the inclusion threshold.

4.2 When Does Evidence Support the Presence of a Multidimensional Effect?

Our results suggest that differences between voxel-wise and MVPA results do not warrant conclusions about the dimensionality of the underlying activation space, raising the question of when it is possible to draw such conclusions. The most straightforward way to conclude that multiple dimensions underlie an effect is to employ a voxel-wise encoding model to test how a hypothesized set of dimensions map onto activation patterns (Mitchell et al. 2008; Naselaris et al. 2011). Encoding models work by mapping a basis set of features that underlie processing of a group of stimuli in a task onto their neural response, often times using standard univariate voxel-wise models. For example, in the mammal space we introduced above, an encoding model would start with the known size and predacity of a set of mammals and regress these dimensions on the voxel-wise activation patterns elicited by the mammals during the task. Instead of examining whether these dimensions significantly activate voxels or clusters, as is commonly done in univariate voxel-wise tests, the test of significance for encoding models is often based on the reconstruction accuracy of the multi-voxel response for left out items (e.g., how well these items are classified). If reconstruction is improved by including a dimension in the basis set, then the hypothesis that this dimension (or multiple dimensions) underlies processing in the space is supported. Relating this to the mammal space, if including both size and predacity of mammals in the encoding model improves reconstruction of the multi-voxel activation patterns for other mammals not included in the original model, then the hypothesis that multiple dimensions shape the brain’s processing of mammals is supported.

The challenge for encoding models, in the present context, is that they require at least some of the dimensions hypothesized to underlie processing of conditions or stimuli to be included in the model. Contrastingly, MVPA decoding methods do not require that the precise dimensions underlying a stimulus space or the feature values of each stimulus along these dimensions to be known. Instead, decoding is accomplished from a latent feature space, but as we saw in the above simulations, MVPA decoding results themselves do not give any information about the content or dimensionality of this space.

The desire to draw multidimensional conclusions from neuroimaging data has inspired recent efforts to develop methods for measuring the dimensionality of neural activation patterns underlying MVPA results. Diedrichsen et al. (2013) proposed a method for revealing the dimensionality of multi-voxel activation patterns that involves decomposing fMRI images into a linear combination of independent components, and then adding those components one-by-one into the classifier analysis. If classifier performance does not increase by adding additional pattern components, then it is concluded that only a single, unidimensional pattern component is driving MVPA results, whereas if adding components leads to increased performance, the dimensionality is concluded to be greater than one.

Importantly, knowing the dimensionality of a space is only one part of what researchers are often interested in. Often times it is important to also know the content of these dimensions or what representational or process-level information they contain. Multidimensional scaling (MDS) techniques can be used either in isolation (Davis and Poldrack, 2013b; Diedrichsen et al. 2011; Kriegeskorte et al., 2008; Liang, Wagner, & Preston, 2013) or in tandem with Diedrichsen et al.’s (2013) analytic dimensionality solution to uncover the content of the dimensions underlying classifier performance or similarity analysis. MDS techniques project the similarities or classification confusion matrices between stimuli/conditions onto a lower dimensional space that can be more easily visualized. Two criteria are often considered important in multidimensional scaling: how interpretable the recovered dimensions are, and how much variability in the original similarity/confusion matrices is accounted for by the scaling solution. However, as variability accounted for will never decrease as dimensions are added in MDS, it will often be useful to pair MDS with a cross-validation technique like Diedrichsen et al.’s (2013) method or another method that will penalize for complex models that overfit the data, such as the BIC (Lee, 2001).

One important point to keep in mind when drawing conclusions about the dimensionality of a space is to avoid conflating the dimensionality of the measurement or decoding technique with the true dimensionality of the activation patterns underlying the analysis. The dimensionality extracted by a decoding technique will often be constrained by mathematical assumptions and it is important to be cognizant of how these assumptions constrain the extracted dimensionality in any given analysis context. For example, linear classifiers, as used in Diedrichsen et al.’s (2013) model and in our linear-kernel SVMs will reveal a maximum of C – 1 independent dimensions (or margins) that separate stimuli (where C is the number of classes the classifier is trained to discriminate between). Thus, given only two categories, ‘scary’ and ‘not scary’, linear classifiers will always separate the mammals in the mammal-space based on a single pattern dimension. However, if a linear classifier is trained to classify individual exemplars (e.g., the individual mammals; see Weber et al. 2009) or techniques like MDS are used on the pairwise similarities between exemplars, the dimensionality can be as high as K-1 (where K is the number of unique exemplars). Each of these techniques could lead to a different solution for the dimensionality of the mammal space in our example (Figure 2B), depending on how the data are analyzed. This point further highlights how the assumptions underlying various analysis techniques can constrain results and the importance of considering multiple techniques when making strong conclusions about dimensionality.

Likewise, it is important to avoid conflating the psychological or neural dimensions contained in the activation patterns with the dimensions extracted by decoding models. In some cases, a single dimension in a model (e.g., a single linear discriminant) may correspond to multiple dimensions in the activation patterns. For example, in our hypothetical mammal experiment, a single linear discriminant could lead to accurate decoding of the mammal space and scariness, but this would not mean that the neural representation of the mammal space was unidimensional with respect to the properties coded by the two voxels (Figure 2B). In other cases, a measured dimension in a model, such as a linear discriminant, may be a true single-dimensional measure with respect to the contents of activation patterns, such as in our simulations where each voxel simply differentiates between whether or not a mammal is perceived as scary, albeit to different degrees (see also, Haynes and Rees, 2006). Building encoding models of information processing within a region therefore remains the only definitive way to make strong conclusions about the region’s dimensionality and representational content (for related arguments, see Naselaris et al. 2011).

4.3 Between-Subject Variability in MVPA

In another recent study that did not consider multidimensional effects per se, but touched on principles related to our between-subject variability findings, Todd et al. (2013) found that because MVPA discards directional information, it can allow confound variables that are typically controlled for in group-level univariate analysis to impact MVPA results. In the present study, we examined a more general situation where there is simply high between-subject variability in the impact of an experimental variable on activation. As our mixed-model formulation of the voxel-wise analysis illustrates, MVPA remains sensitive to differences between conditions even under high between-subject variability not because it discards directional information per se, but because MVPA tests are primarily dependent on the relative magnitudes of voxel-level variability and trial-level error. If there is reliable variability across voxels within subjects, an effect will be significant regardless of the characteristics of the distribution of subject-level activation effects (e.g., high variance; subjects having opposite effect directions as in Todd et al., 2013). This suggests that, although differences between MVPA and univariate voxel-wise results may be due to susceptibility to confounds, as suggested by Todd et al. (2013), they could also arise from something as simple as variability in activation between subjects. Because high subject-level variability in activation is ubiquitous in fMRI studies, our results hint that many dissociations between univariate voxel-wise and MVPA results may be due to MVPA’s ability to neutralize subject-level variability in mean activation and not because of more theoretically relevant signals that MVPA decoding methods are sensitive to, such as multidimensional effects.

4.3 Conclusions

Although multi-voxel methods are promising techniques for fMRI data analysis, they do not necessarily allow for any special conclusions about how information in the underlying activation patterns is encoded, whether an effect is multidimensional or unidimensional, or that an effect differs in any other substantive way from a simple linear mapping of a single experimental variable onto voxels within a region. In many cases, MVPA tests may be providing information that is largely assumed by the group-level statistical maps already reported in most papers (e.g., Rissman, Greely, & Wagner, 2010): experimental effects vary across voxels. As formal tests of this variability, MVPA results may have use as more sensitive indicators of heterogeneity of response across regions or voxels within a region. However, knowledge of this variability does not confer any special theoretical status to the results in and of itself. Instead, to make conclusions about the dimensionality or content of the activation patterns that stimuli elicit, it is important to incorporate additional methods that explicitly measure these aspects of the activation patterns, such as encoding models, classifier-based tests of dimensionality, and multidimensional scaling.

Highlights.

• Significant multi-voxel pattern analysis results may reflect multidimensional coding

• MVPA is sensitive to magnitude of spatial variability in activation

• MVPA is insensitive to subject-level variability in mean activation

• Voxel-wise analyses are sensitive to subject-level variability in mean activation

• Differences between MVPA and voxel-wise results do not indicate multidimensionality

Appendix

How Voxel-level Variability Impacts MVPA

Our simulations show that manipulations affecting a single underlying cognitive dimension can be sensitively detected by MVPA measures that are, by definition, insensitive to the mean level of activation across voxels. For example, pattern correlation subtracts out the mean level of activation across voxels; how does pattern correlation achieve the levels of sensitivity shown in our simulations, despite its insensitivity to the mean? This occurs because the sample mean across voxels on trial t for subject s (μ_ts) only contains information about the model parameters that do not differ between voxels (i.e., that do not contain a voxel index). For example, the sample mean for trial t within subject s contains information about the mean coefficients across subjects (the γ vector) as well as subject-level deviations from these mean coefficients (βs). However, because the trial-level errors (e_tvs) and voxel-level deviations from subjects’ mean coefficient values (e_vs) are independent of (i.e., not correlated with) the sample mean for a given trial, subtracting out the sample mean leaves these coefficients in the trial-wise activation patterns. In contexts for which there is only baseline/mean activation across voxels (Baseline Variability Simulation; Section 3.1.1), subtracting the sample mean for the trial (μ_ts) leaves in the voxel-wise deviations from subjects’ baseline evoked response:

$${\mathit{A}}_{tvs}-{\mathit{\mu }}_{ts}={\mathit{e}}_{0vs}+{\mathit{e}}_{tvs}$$ (A1)

Because e_0vs is repeated across trials, it will appear in the expected mean centered activation pattern for every t trial within subject s. This voxel-level variability that is repeated across trials induces positive average correlations between trials within a subject. Due to this repeated pattern from the voxel-level deviations, the expected correlation (E(r_in)) between any two trials i and n can be estimated formally by:

$$\mathit{E}({\mathit{r}}_{in})=\frac{{\mathit{\tau }}_0^2}{{\mathit{\tau }}_0^2+{\mathit{\sigma }}^2},$$ (A2)

for cases with normally distributed and uncorrelated voxel-level (e_0vs) and trial-level (e_tvs) deviations. In mixed-modeling, Equation A2 is often used as an estimate of the intra-class correlation coefficient (Raudenbush and Bryk, 2002).

The principles behind the derivation of A1 and A2 can be extended straightforwardly to any number of conditioning variables when the values of the voxel- and trial-level variances (i.e., the τ matrix) are known. This leads to greater than zero within-condition correlations whenever the values of τ for a condition p are non-zero, and greater than zero between-condition correlations whenever the conditions share a common effect repeated across voxels (e.g., baseline evoked response) that has non-zero variability (e.g., τ₀) For example, the inclusion of a single dummy coded “scariness” variable (x = 0 if trial t = not-scary; x = 1 if trial t = scary; Condition Variability Simulation), leads to expected correlation of A2 between two not-scary stimuli (r_withinF) and expected correlations of:

$${\mathit{r}}_{\mathit{\text{within}}S}=\frac{{\mathit{\tau }}_0^2+{\mathit{\tau }}_p^2}{{\mathit{\tau }}_0^2+{\mathit{\tau }}_p^2+{\mathit{\sigma }}^2}$$ (A3)

$${\mathit{r}}_{\mathit{\text{between}}SN}=\frac{{\mathit{\tau }}_0^2}{\sqrt{{\mathit{\tau }}_0^2+{\mathit{\tau }}_p^2+{\mathit{\sigma }}^2}\sqrt{{\mathit{\tau }}_0^2+{\mathit{\sigma }}^2}}$$ (A4)

between scary stimuli and between scary and not-scary stimuli, respectively.

Thus, in practice, as long as there is non-zero voxel-level variability in baseline evoked response, there will tend to be non-zero correlations between trials. Moreover, these correlations will be further increased for a given condition if there is non-zero voxel-level variability in the effect this conditioning variable. In both cases, these non-zero correlations will remain even when controlling for the effect of mean activation across voxels.