Giant vacuum forces via transmission lines

Significance

Quantum theory states that at zero temperature and in the absence of any radiation, there still exist fluctuations of the electromagnetic field, the so-called vacuum fluctuations. These fluctuations give rise to the well-known van der Waals (vdW) or Casimir forces between neutral objects, which underlie diverse phenomena in physics and chemistry. We find that these forces can be drastically enhanced for neutral particles near a transmission line (TL), the standard workhorse of electronic signal transmission. The vacuum fluctuations are then confined to propagate along the TL axis, resulting in a giant long-range vdW force. This dramatic effect would have profound implications on vdW and Casimir phenomena and may find novel applications in emerging quantum technologies.

Abstract

Quantum electromagnetic fluctuations induce forces between neutral particles, known as the van der Waals and Casimir interactions. These fundamental forces, mediated by virtual photons from the vacuum, play an important role in basic physics and chemistry and in emerging technologies involving, e.g., microelectromechanical systems or quantum information processing. Here we show that these interactions can be enhanced by many orders of magnitude upon changing the character of the mediating vacuum modes. By considering two polarizable particles in the vicinity of any standard electric transmission line, along which photons can propagate in one dimension, we find a much stronger and longer-range interaction than in free space. This enhancement may have profound implications on many-particle and bulk systems and impact the quantum technologies mentioned above. The predicted giant vacuum force is estimated to be measurable in a coplanar waveguide line.

The seminal works of London (1), Casimir and Polder (2), and Casimir (3) identified quantum electromagnetic fluctuations to be the source of both short-range [van der Waals (vdW)] and retarded, long-range (Casimir) interactions between polarizable objects, which may be viewed as an exchange of virtual photons from the vacuum. Subsequent studies of these interactions (4–14) revealed their modifications, such as retardation and nonadditivity (15), brought about by the geometry of the polarizable objects. The ability to design these interactions is important for their possible use and exploration in emerging quantum technologies such as microelectromechanical systems (16), quantum information processing (17, 18), and circuit quantum electrodynamics, where the dynamical Casimir effect has been recently demonstrated (19, 20). Here we show that effectively one-dimensional (1D) transmission-line environments can induce strongly enhanced and longer-range van der Waals and Casimir interactions compared with free space. Such enhanced interactions may have profound implications on the quantum technologies mentioned above and give rise to a variety of new many-body phenomena involving polarizable particles in effectively 1D environments.

A key point in determining how these interactions depend on distance is the spatial propagation and scattering of the virtual photon modes that mediate them. Like any other waves, photons are scattered differently off objects with different geometries. For example, light is much more effectively scattered off a mirror than off a point-like atom. This explains the stronger and longer-range vacuum interaction between mirrors (3), compared with that between atoms (2). This idea also underlies the dependence of Casimir forces on the geometrical shape of the interacting objects. Here, we take a somewhat different approach toward the geometry dependence of vdW- and Casimir-related phenomena. Instead of considering the interaction energy of extended objects with different geometries, we revisit the original Casimir and Polder (2) configuration of a pair of point-like dipoles while changing the geometry of their surrounding environment such that it confines the propagation of virtual photons to a certain direction. More specifically, we consider the energy of the interaction between two dipoles, mediated by vacuum photon modes along a 1D transmission line (TL). The resulting attractive interaction is found to be much stronger and longer range than its free-space counterpart. Surprisingly, this interaction scales with the interdipolar distance r as const. + (r/λ) ln(r/λ) or as 1/r³ for shorter or longer r than the typical dipolar wavelength λ, respectively, as opposed to the corresponding 1/r⁶ or 1/r⁷ scalings in free space (2, 4). This enhancement implies a drastic modification of Casimir-related effects for many-body and bulk polarizable systems in such an effectively 1D geometry.

This article is organized as follows: Analysis Principles presents the analytical approaches used to obtain the van der Waals and Casimir interactions in a TL environment, Eqs. 6 and 7. Predictions reveals the giant enhancement of these interactions by comparing them to the case of free space (see Fig. 3 C and D), considering possible experimental realizations and imperfections. The consequences of this giant interaction to generalized Casimir effects in 1D is addressed in Prospects: Casimir Physics in 1D, followed by Conclusions.

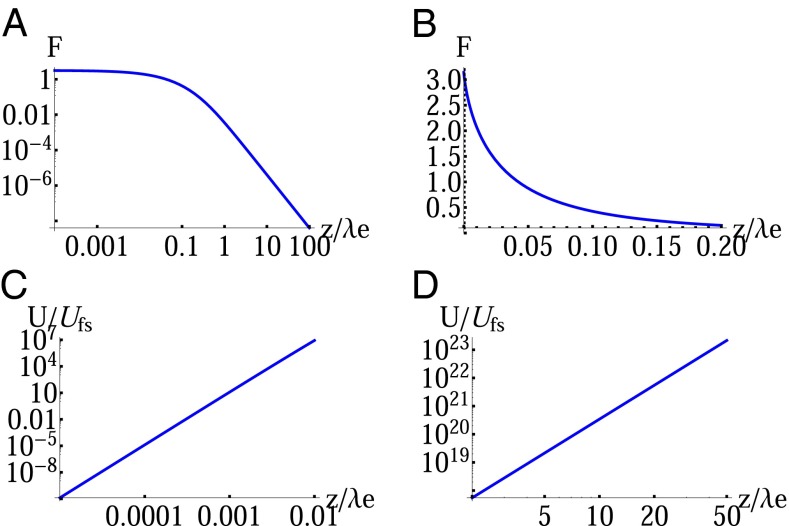
Fig. 3.

The TEM-mode–mediated interaction potential as a function of interdipolar distance z. (A) Log–log plot of F(z), Eq. 6. For long distances, z ≫ λ_e, the linear dependence implies a power-law behavior as in Eq. 7. (B) F(z) at short distances. (C) Log–log plot of the ratio between the TEM-mediated energy U(z), Eq. 6, and the free-space vdW energy at short distances z ≪ λ_e, $U_{fs}\left(z\right)=-\left({\left|{\mathbf{d}}_e\right|}^4/48{\pi }^2{\mathit{ϵ}}^2{E}_e\right)\left(1/z^6\right)$ (26), with ${\left|{\mathbf{d}}_e^{\perp }\right|}^2=\left(2/3\right){\left|{\mathbf{d}}_e\right|}^2$ and $\sqrt{A_{\mathrm{1,2}}}=a$ (main text). Here a = 10⁻⁴λ_e, consistent with typical cases considered in the main text (Predictions), where a equals approximately a few micrometers and E_e/(2πℏ) equals approximately a few gigahertz. Beyond z ∼ 10⁻³λ_e, the huge enhancement of the interaction with respect to its free-space counterpart is apparent. (D) Same as C, but for long distances z ≫ λ_e, where the free-space energy takes the Casimir–Polder form, $U_{fs}\left(z\right)=-\left(23/64{\pi }^3\right)\left(\hslash c/{\mathit{ϵ}}^2\right)\left(4/9\right)\left({\left|{\mathbf{d}}_e\right|}^4/E_e^2\right)\left(1/z^7\right)$ (26).

Analysis Principles

One-Dimensional Photons in Transmission Lines.

The ability to change the geometry of photon vacuum modes is widely used in quantum optics, e.g., for the enhancement of spontaneous emission (21, 22) and resonant dipole–dipole interactions (23). Here, effectively 1D propagation of the virtual photons is attained in waveguide structures that support transverse-electromagnetic (TEM) modes, namely, modes whose propagation axis, the electric and the magnetic fields, are perpendicular to each other. These are typically the fundamental transverse modes of electric TLs, i.e., waveguides composed of two conductors as shown in Fig. 1, which constitute the standard workhorse of electronic signal transmission. They possess a dispersion relation ω_k = |k|c and an electric field-mode function (24)

$${\mathbf{u}}_{kj}\left(\mathbf{r}\right)=\frac{1}{\sqrt{A\left(x,y\right)L}}{e}^{ikz}{\mathbf{e}}_j,$$ [1]

where z is the propagation axis, L is its corresponding quantization length, A(x, y) is the effective area in the transverse xy plane, e_j=x,y is the polarization unit vector, k and ω_k are the wavenumber in the z direction and the angular frequency, respectively, and $c=1/\sqrt{\mu \mathit{ϵ}}$ is the phase velocity, with μ and ε being the effective permeability and permittivity of the TEM mode, set by the geometry and materials of the TL.

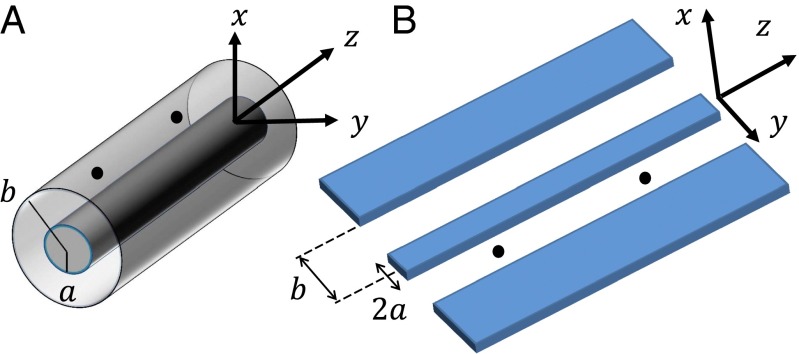
Fig. 1.

Geometries of transmission-line–mediated vdW and Casimir interactions. (A) Coaxial line: two concentric metallic cylinders, the inner one with radius a and the outer (hollow) one with radius b. Two dipoles represented by black circles are placed in between the cylinders, along the wave propagation direction z. They interact via modes of the coaxial line that are in the vacuum state, giving rise to a vdW-like interaction energy. (B) Coplanar waveguide: similar to A. Here the central conductor of width 2a is separated from a pair of ground plane conductors that are 2b apart.

Unlike modes of other waveguides, such as optical fibers or hollow metallic waveguides, here the effective area A(x, y) is independent of frequency. Hence, considering its dispersion relation, the unique feature of the TEM mode is that it forms an effective plane wave in 1D. This special property enables the TEM mode to guide or confine virtual photons over much longer distances than all other higher-order transverse modes supported by the TL, such as the transverse electric (TE) and transverse magnetic (TM) modes in a coaxial TL (24). As recently shown by us for metallic waveguides (25), such modes do not contribute to the long-range interaction (Materials and Methods).

Having identified the key role of the TEM mode in mediating vacuum interactions in a TL, we proceed to analytically calculate the vdW/Casimir interaction between a pair of dipoles mediated by the TEM mode, using two different methods (Quantum Electrodynamics Perturbation Theory and Scattering of Vacuum Fluctuations), and present the results (Analytical Results).

Quantum Electrodynamics Perturbation Theory.

We first adopt the quantum electrodynamics (QED) perturbative approach of ref. 26 to two identical atomic or molecular dipoles with a ladder of excited levels {|n〉}, both in their ground state |g〉, which are coupled to the vacuum of photon modes given by Eq. 1, via the interaction Hamiltonian

$$H_I=-\hslash {\displaystyle \sum _{\nu =1}^2{\displaystyle \sum _{n_{\nu }}{\displaystyle \sum _{k,j}\left(|n_{\nu }\rangle \langle g|+\mathrm{h}.\text{c}.\right)\left(i{g}_{kj\nu n}{\widehat{a}}_{kj}+\mathrm{h}.\text{c}.\right)}}}.$$ [2]

Here $g_{kj\nu n}=\sqrt{\left({\omega }_k/2\mathit{ϵ}\hslash \right)}{\mathbf{d}}_{n_{\nu }}\cdot {\mathbf{u}}_{kj}\left({\mathbf{r}}_{\nu }\right)$ is the dipolar coupling between the dipole ν = 1, 2 and the kj field mode, for the |g〉 to |n_ν〉 transition with dipole matrix element ${\mathbf{d}}_{n_{\nu }}$, ${\widehat{a}}_{kj}$ being the lowering operator for the kj mode. The vdW energy is then obtained by perturbation theory as the fourth-order correction to the energy of the ground state |G〉 = |g₁, g₂, 0〉, where |0〉 is the vacuum of the photon modes (26),

$$U=-{\displaystyle \sum _{I_1,I_2,I_3}\frac{\langle G|H_I|I_3\rangle \langle I_3|H_I|I_2\rangle \langle I_2|H_I|I_1\rangle \langle I_1|H_I|G\rangle }{\left(E_{I_1}-E_G\right)\left(E_{I_2}-E_G\right)\left(E_{I_3}-E_G\right)}}.$$ [3]

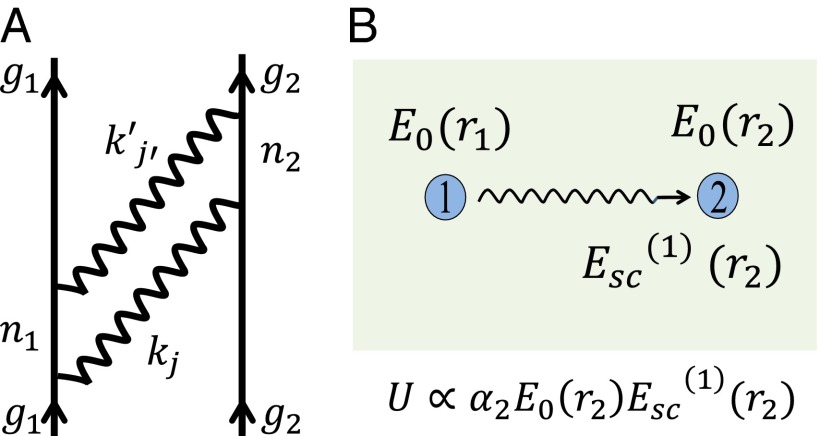
Here |I_j〉 are intermediate (virtual) states (of the free Hamiltonian) and E_m is the energy of the state |m〉. The sum in Eq. 3 includes 12 different terms, each corresponding to a different set of virtual processes and represented by a diagram, e.g., that of Fig. 2A (26). Each of the 12 terms contains a summation over all of the dipolar states |n₁〉 and |n₂〉, and the photonic polarizations j, j′, and integrations over the wavevectors k and k′. The energy is then obtained by summing all 12 terms and performing the integrations (Materials and Methods).

Fig. 2.

Calculation methods of the interaction energy. (A) QED perturbation theory: one of 12 possible processes (diagrams) that contribute to the energy correction of the state |G〉 = |g₁, g₂, 0〉, Eq. 3. Here the intermediate states are $|I_1\rangle =|n_1,g_2,1_{kj}\rangle ,\hspace{0.5em}\hspace{0.17em}|I_2\rangle =|g_1,g_2,1_{kj}{1}_{k^{\prime }{j}^{\prime }}\rangle$, and $|I_3\rangle =|g_1,n_2,1_{k^{\prime }{j}^{\prime }}\rangle$, where $|1_{kj}\rangle ={\widehat{a}}_{kj}^{†}|0\rangle$. (B) Scattering of vacuum fluctuations: the vacuum field ${\widehat{\mathbf{E}}}_0\left(\mathbf{r}\right)$ exists in all space and interacts with both dipoles at their positions r₁ and r₂; hence it is also scattered by the dipoles. The scattered field from dipole 1, ${\widehat{\mathbf{E}}}_{sc}^{\left(1\right)}\left(\mathbf{r}\right)$, arrives at dipole 2, resulting in an interaction interpreted as the vdW/Casimir interaction U.

Scattering of Vacuum Fluctuations.

A more transparent approach is based on the solution of the 1D electromagnetic wave equation “driven” by the vacuum field (4). Accordingly, we consider two point dipoles with polarizabilities α_1,2(ω), subject to a fluctuating (vacuum) field ${\widehat{\mathbf{E}}}_0$ (Fig. 2B). The electromagnetic energy of, say, dipole 2, is given by a sum over all k of $-\left(1/2\right){\alpha }_2\left({\omega }_k\right)\left[{\widehat{\mathbf{E}}}_k\left({\mathbf{r}}_2\right){\widehat{\mathbf{E}}}_k^{†}\left({\mathbf{r}}_2\right)+{\widehat{\mathbf{E}}}_k^{†}\left({\mathbf{r}}_2\right){\widehat{\mathbf{E}}}_k\left({\mathbf{r}}_2\right)\right]$, where ${\widehat{\mathbf{E}}}_k\left({\mathbf{r}}_2\right)$ is the k mode component of the electromagnetic field at the location of this dipole. The field at r₂ includes two components: ${\widehat{\mathbf{E}}}_{0,k}\left({\mathbf{r}}_2\right)$, the external fluctuating (vacuum) field, and ${\widehat{\mathbf{E}}}_{sc,k}^{\left(1\right)}\left({\mathbf{r}}_2\right)$, the scattered field, which to lowest order is that scattered from dipole 1, where it is driven by the vacuum fluctuations ${\widehat{\mathbf{E}}}_{0,k}\left({\mathbf{r}}_1\right)$ at r₁. Because the TEM field exhibits diffractionless propagation in 1D, this scattered field is found by essentially solving

$$\left({\partial }_z^2+k^2\right){\widehat{\mathbf{E}}}_{sc,k}^{\left(1\right)}\left(z\right)=-\mu {\omega }_k^2{\alpha }_1^{\left(1D\right)}\left({\omega }_k\right){\widehat{\mathbf{E}}}_{0,k}\left(z_1\right)\delta \left(z-z_1\right),$$ [4]

where the quantum (vacuum) field in 1D is ${\widehat{\mathbf{E}}}_{0,k}\left(z\right)=i\sqrt{\left(\hslash {\omega }_k/2\mathit{ϵ}\right)}\left(1/\sqrt{L}\right)e^{ikz}{\mathbf{e}}_j{\widehat{a}}_{kj}$ and ${\alpha }_{\nu }^{\left(1\text{D}\right)}={\alpha }_{\nu }/A\left(x_{\nu },y_{\nu }\right)$. The vdW/Casimir energy is then obtained as the interaction energy between the dipoles, which to lowest order becomes

$$\begin{array}{l}U=-2{\displaystyle \sum _k{\alpha }_2^{\left(1\text{D}\right)}\left({\omega }_k\right)}\\ \times \langle 0|\left[{\widehat{\mathbf{E}}}_{sc,k}^{\left(1\right)}\left(z_2\right){\widehat{\mathbf{E}}}_{0,k}^{†}\left(z_2\right)+{\widehat{\mathbf{E}}}_{0,k}\left(z_2\right){\widehat{\mathbf{E}}}_{sc,k}^{\left(1\right)†}\left(z_2\right)\right]|0\rangle .\end{array}$$ [5]

Here we average over the quantized fields in the vacuum state |0〉 and multiply by 4 to account for both field polarizations j and the energy at the locations of both dipoles.

Analytical Results.

Both calculation methods yield the same result for the TEM-mediated interaction energy between dipoles with excited levels {|n〉} (Materials and Methods). In the main text, we present the resulting energy only for the case where one excited level |e〉 with energy E_e and corresponding wavelength λ_e = 2πℏc/E_e has a dominant dipole transition, such that all other excited levels |n ≠ e〉 can be neglected. This yields

$$\begin{array}{c}U\left(z\right)=-\frac{\pi {\left|{\mathbf{d}}_e^{\perp }\right|}^4}{2{\mathit{ϵ}}^2{E}_e}\frac{1}{A_1{A}_2{\lambda }_e^2}F\left(z\right),\\ F\left(z\right)=\left(4\pi \frac{z}{{\lambda }_e}+i\right)e^{-i4\pi \left(z/{\lambda }_e\right)}\text{Ei}\left(i4\pi \frac{z}{{\lambda }_e}\right)\\ +\hspace{0.17em}\pi \left(1+i4\pi \frac{z}{{\lambda }_e}\right)e^{i4\pi \left(z/{\lambda }_e\right)}+\text{c}.\text{c}.,\end{array}$$ [6]

where z = |z₂ − z₁| is the interdipolar distance in the TL propagation direction, A_ν = A(x_ν, y_ν), ${\mathbf{d}}_e^{\perp }$ is the projection of the dipole matrix element d_e on the transverse xy plane, c.c. stands for complex-conjugate, and $\text{Ei}\left(x\right)=-\text{P}{\displaystyle {\int }_{-x}^{\infty }dt{e}^{-t}/t}$ is the exponential integral function. This interaction is attractive and its dependence on distance z is described by the monotonously decreasing function F(z), plotted in Fig. 3 A and B. From F(z) we obtain the energy dependence for small and large z/λ_e, respectively,

$$\begin{array}{l}F\left(z\ll {\lambda }_e\right)\approx \pi +16\pi \frac{z}{{\lambda }_e}\text{ln}\frac{z}{{\lambda }_e}+8\pi \left[2\gamma -1+2\ln \left(4\pi \right)\right]\frac{z}{{\lambda }_e},\\ F\left(z\gg {\lambda }_e\right)\approx \frac{1}{8{\pi }^3}\frac{{\lambda }_e^3}{z^3},\end{array}$$ [7]

where γ ≅ 0.577 is Euler’s constant. These expressions for F(z) in the vdW, z ≪ λ_e, and Casimir (retarded), z ≫ λ_e, regimes reveal a universal scaling with distance z; namely, it does not depend on λ_e or any other length scale, but rather on z ln z and 1/z³, respectively. This scaling is thus independent of the type of dipole involved in the interaction and is expected to hold for multilevel dipoles as verified by Eqs. 11 and 13 in Materials and Methods: The level structure merely affects the prefactor, i.e., the coefficient of the interaction.

Predictions

The expressions given above for the interaction energy in the vdW and Casimir regimes suggest the possibility of a much stronger interaction than its free-space counterpart. In the nonretarded vdW regime, it decreases very slowly with z compared with the familiar 1/z⁶ scaling, whereas in the retarded Casimir regime, it falls off with a power law that is four powers weaker than its 1/z⁷ Casimir–Polder counterpart.

Quantitative Comparison with Free-Space Vacuum Forces.

Let us make this comparison more quantitative by considering a general TL with separation a between its two guiding conductors (Fig. 1). The effective TEM mode area A(x, y) then scales as a² (Materials and Methods). Moreover, assuming the polarizability is isotropic on average, we can estimate ${\left|{\mathbf{d}}_e^{\perp }\right|}^2=\left(2/3\right){\left|{\mathbf{d}}_e\right|}^2$. Then, for $\sqrt{A_{\mathrm{1,2}}}=a$ and $a/{\lambda }_e\sim {10}^{-4}$, typical of the circuit QED realizations considered below, where a is approximately a few micrometers and λ_e is approximately a few centimeters, the ratio between the TEM-mediated energy and its free-space counterpart is plotted in Fig. 3 C and D for short and long distances, respectively (26). At distances longer than z = 10⁻³λ_e, the TEM-mediated interaction is enhanced by orders of magnitude compared with free space, and the enhancement factor increases drastically with z.

At very short distances, however, the free-space vdW interaction 1/z⁶ is stronger. This occurs at z < a, where the dipoles are close enough so that they do not “sense” the TL structure. The transition to free-space behavior in this regime can be described by including higher-order transverse modes. These modes become significant at such short distances, where their contributions sum up to give the free-space result (Materials and Methods).

Possible Experimental Realizations.

It is important to consider the possibilities of measuring the predicted effects. Here we focus on the coplanar waveguide (CPW) TL (Fig. 1B) that is extensively used in the emerging field of circuit QED (27–29). We consider the dominant dipole transition between the ground and first excited states of a pair of superconducting transmons, where other dipolar transitions from the ground state are indeed negligible (27) such that the two-level approximation is valid. The transmons, at distance z, are both capacitively coupled to the CPW. Then, the TEM-mediated interaction should induce a z-dependent energy shift on the dipole-transition levels, U(z) as per Eq. 6. We estimate this energy shift using the parameters of a recent experiment (28): The dipole frequency is E_e/(2πℏ) ∼ 5 GHz and the dipole coupling to a closed CPW cavity of length λ_e can reach g ∼ π × 720 MHz. From the relations $g=\sqrt{\left(\left(E_e/\hslash \right)/2\mathit{ϵ}\hslash \right)}\left(\left|{\mathbf{d}}_e\right|/\sqrt{AL}\right)$ and L = λ_e (28, 29), we can extract the factor $\left|{\mathbf{d}}_e^{\perp }\right|/\sqrt{A}$ for each dipole, obtaining [U(z)/F(z)]/h ∼ 0.84 MHz, where h is Planck’s constant; e.g., for distances z = 0.001λ_e or 0.01λ_e (both much larger than a of approximately a few micrometers), the energy shift becomes U(z)/h ∼ 1.8 or 2.47 MHz, respectively, about twice the dephasing rate of the dipole, 1 MHz (28), that limits the resolution of the shift. This resolution can be considerably improved, as in ref. 29, where a dephasing time of about 20 μs is reported. Then, upon taking E_e/h ∼ 2 GHz with the parameters of ref. 28, one can obtain U(z)/h ∼ 28 MHz for z = 0.01λ = 1.5 mm, which is much larger than the dephasing rate.

Probing the interaction in the retarded regime, where z > λ_e, is currently more challenging: For the latter case, with z = 2λ_e = 30 cm, we obtain U(z)/h ∼ 6.62 kHz, which is currently too small to be observed. Nevertheless, these results imply the remarkable possibility to directly observe the vdW and Casimir interaction of a single pair of point-like dipoles (here the size of the dipoles is ∼1–100 μm ≪ λ_e) over a wide range of distances where the interaction scales nontrivially according to Eq. 6.

We note that the ratio of the TL-length scale a to λ_e does not affect the scaling of the ratio U/U_fs between the TEM-mediated energy and its free-space counterpart with z (Fig. 3 C and D), but only its prefactor (Eq. 6). Hence, the same scaling of U/U_fs is expected for atoms, although their dipolar λ_e can become much smaller than that of the superconducting transmon. For instance, considering the D1 line of Rb87 atoms, where λ_e ∼ 780 nm, and keeping the same TL with a ∼ 1 μm, we obtain a/λ_e > 1 (instead of a/λ_e ∼ 10⁻⁴ in Fig. 3 C and D). The plots of Fig. 3 C and D then retain the same slope but are shifted down. Namely, an enhancement, U/U_fs > 1, still exists, but at larger distances z, where the enhanced interaction may be too weak to be observed for a single pair of atoms. Nevertheless, this enhancement can be very important for many-atom systems where it would increase the nonadditivity of their dispersion interactions (Prospects: Casimir Physics in 1D below).

Imperfections.

Let us consider the consequences of possible imperfections in the dipoles or the conductors of the TL.

Dipoles.

The description of sharp energy levels may fit the case of atoms but not that of artificial dipolar systems such as transmons or quantum dots, for which nonradiative dephasing may result in level widths. This dephasing may give a lower bound for measurable vdW/Casimir interaction-induced shifts, as discussed above for the circuit QED realization. Another imperfection for artificial dipoles is their inhomogeneity, e.g., that the dipole matrix element d_e and the energy E_e of the dipolar transition in two different transmons are not identical. This does not change the scaling of the vdW interaction U(z); however, it requires one to first measure the transmons’ parameters if one wishes to obtain an exact result for U(z) (Eqs. 11–13 and SI Text).

TLs.

The existence of TEM modes as in Eq. 1 is exactly correct for TLs made from perfect conductors. However, it is also an excellent approximation to the propagation of fields in finite-conductivity, low-loss TLs that are currently used (24), particularly in the microwave to gigahertz domain that is relevant in our case. This supports the validity of our results for TEM-mediated interaction in Eqs. 6 and 7 in realistic circuit QED systems. The conductors of the TL can also induce a modified Lamb shift on dipole levels due to the photon modes near a metal surface, the so-called Casimir–Polder atom–surface interaction (2, 30). This single-dipole (rather than interaction-related) energy shift is of no interest here, yet it may change E_e. Whereas for artificial dipoles E_e is not precisely known anyway due to inhomogeneity, so that this effect is unimportant, the evaluation of this shift for atoms is described in SI Text. Surface roughness along the TL conductors may slightly change the transverse profile of the TEM mode $1/\sqrt{A\left(x,y\right)}$; however, the 1D-like TEM mode, and hence the 1D vdW/Casimir interaction discussed above, still exists. Impurities and sharp edges in the conductors can be treated as scatterers characterized by a reflectivity or polarizability, whose interaction with the dipoles contributes to the dipoles’ energy shift.

Prospects: Casimir Physics in 1D

The vacuum force between two point dipoles underlies other vdW- or Casimir-related phenomena. Hence, the giant enhancement and nontrivial scaling of these forces with distance found here may open the door to unexplored Casimir-related effects in 1D, upon extending the present results to either multiple point-like dipoles or extended (bulk) objects, as detailed in what follows.

Many-Particle Systems.

Because the open geometry of the CPW allows for the coupling of the TEM mode to clouds of trapped atoms above its surface (31), the predicted long-range interaction may be explored in a many-body setting. This may entail a modification of the nonadditivity of the vdW and Casimir interactions, which currently attracts considerable interest (15). In free space, the vdW energy of a gas is approximately additive; namely, it can be obtained by pairwise summation of the vdW energies of all pairs, as long as α/r³ is small, r being a typical interdipolar separation (4). This scaling is, however, a direct consequence of dipole–dipole interactions in free space and is expected to change when atomic dipoles interact via the TEM mode of the CPW, for the same reasons that the 1/r⁶ scaling was shown here to change. Such atomic clouds are anticipated to exhibit nonadditive effects at smaller densities than usual, which in turn may influence their dielectric properties, which may deviate from those obtained by the Clausius–Mossotti equation (32). Furthermore, it would be interesting to consider how the enhanced interaction we predict is modified at finite temperatures or out of equilibrium (33–35).

From a more applied point of view, the van der Waals energy shift between (out-of-equilibrium) Rydberg atoms, which underlies the blockade mechanism used to design quantum gates (17), may be enhanced when the atoms are coupled to a TL. For Rydberg atoms (λ_e ∼ 1 cm) in free space, blockade distances of ∼10 μm have already been observed (18), and the long-range scaling expected for their TL-mediated interaction may lead to the extension of the blockade distance even further.

Extended (Bulk) Objects.

Another direction to explore is the modification of the Casimir interaction involving bulk objects in a TL environment and its possible relevance for actuation of microelectromechanical systems (16). For example, one could consider the interaction energy between a dipole and a mirror (2, 4), where the role of the mirror may be played by a short circuit at one of the ends of the TL. A mirror, whose reflection is not necessarily perfect, could be realized by an impedance characterized by capacitance and inductance.

In fact, in 1D there is no difference between a point dipole and an imperfect mirror. As shown above, for distances z > a between the interacting objects, the TEM mode is dominant and a TL environment is effectively 1D. Hence, the theory of the Casimir interaction between mirrors in 1D (36) finds a realistic context in TL environments. It is therefore interesting to compare its results to ours. The Casimir force between two mirrors in 1D, with frequency-dependent reflection coefficients r_1,2(k) (ω = kc), is (36)

$$f\left(z\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{dk}{2\pi }\hslash ck\frac{-r_1\left(k\right)r_2\left(k\right)e^{i2kz}}{1-r_1\left(k\right)r_2\left(k\right)e^{i2kz}}}+\text{c}.\text{c}.$$ [8]

For the case of dipoles, which we assume to be weak scatterers, we take r₁r₂ ≪ 1. The integral for the energy $U=-{\displaystyle \int dz\hspace{0.17em}f\left(z\right)}$ over imaginary frequencies k = iu (Wick rotation) (Materials and Methods) then becomes

$$U\left(z\right)\approx \frac{\hslash c}{2\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}du{r}_1\left(iu\right)r_2\left(iu\right)e^{-2uz}}.$$ [9]

In the Casimir–Polder limit of large separations z, upon taking ω → 0 (4, 26) and hence replacing r_1,2(iu) with r_1,2(0), we obtain U ∝ −r₁(0)r₁(0)/z. The 1/z dependence is shown in ref. 36 to be universal and holds for any magnitude of the reflectivity r_1,2. This is in contrast to our U ∝ −1/z³ scaling (Eq. 7). The latter can be recovered from [9] upon taking the limit ω → 0 more carefully: From the Helmholtz Eq. 4 we obtain that the reflection coefficient of the dipole, defined by ${\widehat{\mathbf{E}}}_{sc,k}^{\left(1\right)}=r_1\left({\omega }_k\right){\widehat{\mathbf{E}}}_{0k}$, becomes r_1,2(ω) ∝ ωα₁(ω). Our results are then retrieved from the integral in [9] (Eq. 15). In particular, taking the Casimir–Polder limit r_1,2(ω → 0) ∝ ωα_1,2(0) in [9], we obtain U ∝ −1/z³ as in Eq. 7. This shows that the scaling of the energy U with distance z strongly depends on the frequency dependence of the reflectivities near ω → 0; e.g., for r_1,2(ω → 0) ∝ ω^p, we obtain in the retarded Casimir–Polder limit U ∝ −1/z^2p+1.

Conclusions

We have studied how TL structures, typically used to transmit electromagnetic signals in electronic devices, can effectively transmit vacuum fluctuations between dipoles and drastically enhance their dispersion forces. This comes about because of the unique nondiffractive 1D character of virtual-photon propagation via the TEM mode in TLs. We have shown how the resulting vdW and Casimir–Polder interactions can become longer range and larger by orders of magnitude than their free-space counterparts. To this end, we have analytically found, by two independent methods, an expression (Eq. 6) for the dominant TEM-mediated interaction at all interdipolar distances and described how the free-space result is restored at very short distances, by including higher-order modes in the calculations. Although our approach assumes that the TL is composed of perfect conductors at zero temperature, it remains accurate for a realistic superconducting coplanar waverguide, for which we have estimated that the enhanced interaction may be directly measured for a single pair of superconducting transmons.

We stress the uniqueness of the vdW/Casimir force mediated by a TL compared with that of other waveguides. The fact that any waveguide allows waves to propagate only in one direction does not guarantee its support of 1D long-range vacuum forces; such modified 1D-like forces are mediated only by the TEM mode that has no cutoff and exists only in TLs. For example, in a hollow metal waveguide, where all transverse modes possess a cutoff, the vdW energy between a pair of dipoles can become extremely short ranged (25). In a fiber, the fundamental HE₁₁ mode might give rise to a more extended vacuum interaction, but because its effective area, unlike that of the 1D-like TEM mode, depends on frequency (37), it is diffractive and does not give rise to the 1D interaction found here.

Our result may pave the way toward the exploration of more complex Casimir phenomena than the simple dipole–dipole nonretarded vdW interaction due to two major effects: retardation and nonadditivity (15). As discussed above, both of these may be drastically modified in a 1D geometry, namely, by the presence of a transmission line. Finally, the predicted modification of the basic interaction between dipoles may prove relevant to diverse areas of applied and basic research: circuit QED, where it can provide a fundamental demonstration of the 1D vacuum effect enabled by such systems; quantum information, where Rydberg-blockade–based quantum gates may be enhanced; and classical electromagnetism, where the macroscopic dielectric properties of a gas have to be revisited.

Materials and Methods

QED Perturbation Theory.

The sum in Eq. 3 includes 12 different terms, each corresponding to a different set of intermediate states and represented by a diagram (26); e.g., the term corresponding to the diagram in Fig. 2A is given by

$$\begin{array}{l}-\frac{{\hslash }^2{c}^2}{16{\pi }^2{\mathit{ϵ}}^2{A}_1{A}_2}{\displaystyle \sum _{n_1,n_2}{\left({\mathbf{d}}_{n_1}^{\perp }\cdot {\mathbf{d}}_{n_2}^{\perp }\right)}^2}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}dk}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{k}^{\prime }}\\ \times \frac{\left|k\right|\left|k^{\prime }\right|e^{ikz}{e}^{ik\prime z}}{\left(E_{n_1}+\hslash c\left|k\right|\right)\left(\hslash c\left|k\right|+\hslash c\left|k^{\prime }\right|\right)\left(E_{n_1}+\hslash c\left|k^{\prime }\right|\right)}.\end{array}$$ [10]

Summing all 12 terms and then performing the integration over k′, we arrive at

$$\begin{array}{c}U=-\frac{\pi }{2{\mathit{ϵ}}^2{A}_1{A}_2}{\displaystyle \sum _{n_1,n_2}\frac{{\left({\mathbf{d}}_{n_1}^{\perp }\cdot {\mathbf{d}}_{n_2}^{\perp }\right)}^2}{{\lambda }_{n_1}^2{E}_{n_1}}{F}_{n_1{n}_2}\left(z\right)},\\ F_{n_1{n}_2}={\displaystyle \underset{0}{\overset{\infty }{\int }}dk\sin \left(2kz\right)\frac{-2{\lambda }_{n_1}{k}^2\left(k+k_{n_1}+k_{n_2}\right)}{\pi \left(k_{n_1}+k_{n_2}\right)\left(k+k_{n_1}\right)\left(k+k_{n_2}\right)}},\end{array}$$ [11]

where k_n = E_n/(ℏc) = 2π/λ_n. The integration over k is performed by regularization, yielding

$$\begin{array}{l}{F}_{n_1{n}_2}\left(\xi ,b\right)=\frac{2b}{b^2-1}\{-2\text{Ci}\left(4\pi \xi \right)\sin \left(4\pi \xi \right)+2b\text{Ci}\left(4b\pi \xi \right)\sin \left(4b\pi \xi \right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}-\hspace{0.17em}\text{cos}\left(4\pi \xi \right)\left[\pi -2\text{Si}\left(4\pi \xi \right)\right]+b\cos \left(4b\pi \xi \right)\left[\pi -2\text{Si}\left(4b\pi \xi \right)\right]\},\end{array}$$ [12]

where Ci(x) and Si(x) are the cosine and sine integral functions, respectively. Here $F_{n_1{n}_2}\left(\xi ,b\right)$ is the dimensionless vdW/Casimir energy contributed by the interaction between the dipolar transition |g〉 → |n₁〉 of the first dipole and the |g〉 → |n₂〉 transition of the second dipole, where $\xi =z/{\lambda }_{n_1}$, and $b=E_{n_2}/E_{n_1}$ represents the asymmetry between the two transitions. Eq. 11 then reveals that the total vdW/Casimir energy is given by a sum over all such possible interactions between dipolar transitions of the two dipoles. In the vdW and Casimir limits, ξ ≪ 1 and ξ ≫ 1, respectively, we obtain

$$\begin{array}{l}{F}_{n_1{n}_2}\left(\xi \ll 1,b\right)\approx \frac{2b\pi }{1+b}+\frac{16b\pi }{1-b^2}\xi \left[\ln \left(4\pi \xi \right)-b^2\ln \left(4b\pi \xi \right)\right],\\ F_{n_1{n}_2}\left(\xi \gg 1,b\right)\approx \frac{1}{8b{\pi }^3}\frac{1}{{\xi }^3}.\end{array}$$ [13]

Expressions [13] yield the same universal scalings as those of Eq. 7 for the two-level dipole case, which is recovered by appropriately taking the limit b → 1. Alternatively, by directly performing the integration over k in Eq. 11 for a single excited level |e〉 in each dipole, we obtain Eq. 6 in the main text.

Scattering of Vacuum Fluctuations.

The scattered field is proportional to the Green’s function of the Helmholtz equation in 1D, Eq. 4, which is found to be $\left(i/2\left|k\right|\right)e^{i\left|k\right|\left|z-z_1\right|}$. Then, inserting this field into the energy Eq. 5, we arrive at

$$U=\frac{\hslash c}{2\pi {\mathit{ϵ}}^2{A}_1{A}_2}{\displaystyle \underset{0}{\overset{\infty }{\int }}dk{\alpha }_1\left(k\right){\alpha }_2\left(k\right)k^2\sin \left(2kz\right)}.$$ [14]

Taking the integration on the imaginary axis k = iu in a complex k plane [Wick rotation, assuming the poles of α_1,2(k) have some width, i.e., pushing them slightly below the real axis], we obtain

$$U=\frac{-\hslash c}{2\pi {\mathit{ϵ}}^2{A}_1{A}_2}{\displaystyle \underset{0}{\overset{\infty }{\int }}du{\alpha }_1\left(iu\right){\alpha }_2\left(iu\right)u^2{e}^{-2uz}}.$$ [15]

Upon taking the polarizabilities α_1,2 of a system with a discrete set of transitions as in an atom, $\alpha \left(k\right)=\left(2/3\right){\displaystyle {\sum }_n\left(E_n{\left|{\mathbf{d}}_n\right|}^2/\left(E_n^2-{\hslash }^2{c}^2{k}^2\right)\right)}$ (26), the integration can be performed. The resulting energy U, described by special functions, is equivalent to that of Eq. 11 when ${\left|{\mathbf{d}}_e^{\perp }\right|}^2=\left(2/3\right){\left|{\mathbf{d}}_e\right|}^2$ is assumed. Specifically, for the vdW and Casimir limits, we obtain exactly the same analytical expressions of Eqs. 13 and 7.

Contribution of Higher-Order Transverse Modes.

In SI Text we calculate, for a coaxial TL, the interaction energy due to the TE and TM modes. We find that the energy contribution of the TE_lm and TM_lm modes with cutoff frequency ck_lm scales like K₀(k_lmz) and $e^{-k_{lm}z}$, respectively, where K₀(x) is the modified Bessel function. Because k_lm > π/a, at long distances z > a both decay exponentially and are negligible with respect to the TEM mode energy. However, at short distances z ≪ a, we numerically verify that the dominant TM modes sum up to give exactly the free-space interaction. This was also recently shown for the dispersion interaction in a metallic waveguide (25), and we expect it to hold for all TLs. Namely, for distances z ≫ a we can indeed consider only the TEM mode, whereas the free-space result is recovered for z ≪ a, owing to the role of other transverse modes.

Scaling of A(x, y) with a.

Considering a coaxial line for example (Fig. 1A), upon normalizing the electric field of the TEM mode, we find $\sqrt{A}=\sqrt{2\pi \ln \left(b/a\right)}\rho$, with $\rho =\sqrt{x^2+y^2}$ (24). Because a < ρ < b, taking, e.g., b = 2a and ρ = a we obtain $\sqrt{A}\approx 2.1a$, such that A ∼ a².