Algorithms, games, and evolution

Significance

Theoretical biology was founded on the mathematical tools of statistics and physics. We believe there are productive connections to be made with the younger field of theoretical computer science, which shares with it an interest in complexity and functionality. In this paper, we find that the mathematical description of evolution in the presence of sexual recombination and weak selection is equivalent to a repeated game between genes played according to the multiplicative weight updates algorithm, an algorithm that has surprised computer scientists time and again in its usefulness. This equivalence is informative for the pursuit of two key problems in evolution: the role of sex and the maintenance of variation.

Abstract

Even the most seasoned students of evolution, starting with Darwin himself, have occasionally expressed amazement that the mechanism of natural selection has produced the whole of Life as we see it around us. There is a computational way to articulate the same amazement: “What algorithm could possibly achieve all this in a mere three and a half billion years?” In this paper we propose an answer: We demonstrate that in the regime of weak selection, the standard equations of population genetics describing natural selection in the presence of sex become identical to those of a repeated game between genes played according to multiplicative weight updates (MWUA), an algorithm known in computer science to be surprisingly powerful and versatile. MWUA maximizes a tradeoff between cumulative performance and entropy, which suggests a new view on the maintenance of diversity in evolution.

Precisely how does selection change the composition of the gene pool from generation to generation? The field of population genetics has developed a comprehensive mathematical framework for answering this and related questions (1). Our analysis in this paper focuses particularly on the regime of weak selection, now a widely used assumption (2, 3). Weak selection assumes that the differences in fitness between genotypes are small relative to the recombination rate, and consequently, through a result due to Nagylaki et al. (4) (see also ref. 1, section II.6.2), evolution proceeds near linkage equilibrium, a regime where the probability of occurrence of a certain genotype involving various alleles is simply the product of the probabilities of each of its alleles. Based on this result, we show that evolution in the regime of weak selection can be formulated as a repeated game, where the recombining loci are the players, the alleles in those loci are the possible actions or strategies available to each player, and the expected payoff at each generation is the expected fitness of an organism across the genotypes that are present in the population. Moreover, and perhaps most importantly, we show that the equations of population genetic dynamics are mathematically equivalent to positing that each locus selects a probability distribution on alleles according to a particular rule which, in the context of the theory of algorithms, game theory, and machine learning, is known as the multiplicative weight updates algorithm (MWUA). MWUA is known in computer science as a simple but surprisingly powerful algorithm (see ref. 5 for a survey). Moreover, there is a dual view of this algorithm: each locus may be seen as selecting its new allele distribution at each generation so as to maximize a certain convex combination of (i) cumulative expected fitness and (ii) the entropy of its distribution on alleles. This connection between evolution, game theory, and algorithms seems to us rife with productive insights; for example, the dual view just mentioned sheds new light on the maintenance of diversity in evolution.

Game theory has been applied to evolutionary theory before, to study the evolution of strategic individual behavior (see, e.g., refs. 6, 7). The connection between game theory and evolution that we point out here is at a different level, and arises not in the analysis of strategic individual behavior, but rather in the analysis of the basic population genetic dynamics in the presence of sexual reproduction. The main ingredients of evolutionary game theory, namely strategic individual behavior and conflict between individuals, are extraneous to our analysis.

We now state our assumptions and results. We consider an infinite panmictic population of haplotypes involving several unlinked (i.e., fully recombining) loci, where each locus has several alleles. These assumptions are rather standard in the literature. They are made here to simplify exposition and algebra, and there is no a priori reason to believe that they are essential for the results, beyond making them easily accessible. For example, Nagylaki’s theorem (4), which is the main analytical ingredient of our results, holds even in the presence of diploidy and partial recombination.

Nagylaki’s theorem states that weak selection in the presence of sex proceeds near the Wright manifold, where the population genetic dynamics becomes (SI Text)

$$x_i^{t+1}\left(j\right)=\frac{1}{X^t}{x}_i^t\left(j\right)\left(F_i^t\left(j\right)\right),$$

where $x_i^t\left(j\right)$ is the frequency of allele j of locus i in the population at generation t, X is a normalizing constant to keep the frequencies summing to 1, and $F_i^t\left(j\right)$ is the mean fitness at time t among genotypes that contain allele j at locus i (see ref. 4 and SI Text). Under the assumption of weak selection, the fitnesses of all genotypes are close to one another, say within the interval [1 − ε, 1 + ε], and so the fitness of genotype g can be written as F_g = 1 + εΔ_g, where ε is the selection strength, assumed here to be small, and Δ_g ∈ [−1, 1] can be called the differential fitness of the genotype. With this in mind, the equation above can be written

$$x_i^{t+1}\left(j\right)=\frac{1}{X^t}{x}_i^t\left(j\right)\left(1+\mathit{ϵ}{\mathrm{\Delta }}_i^t\left(j\right)\right),$$ [1]

where ${\mathrm{\Delta }}_i^t\left(j\right)$ is the expected differential fitness among genotypes that contain allele j at locus i (see Fig. 1 for an illustration of population genetics at linkage equilibrium).

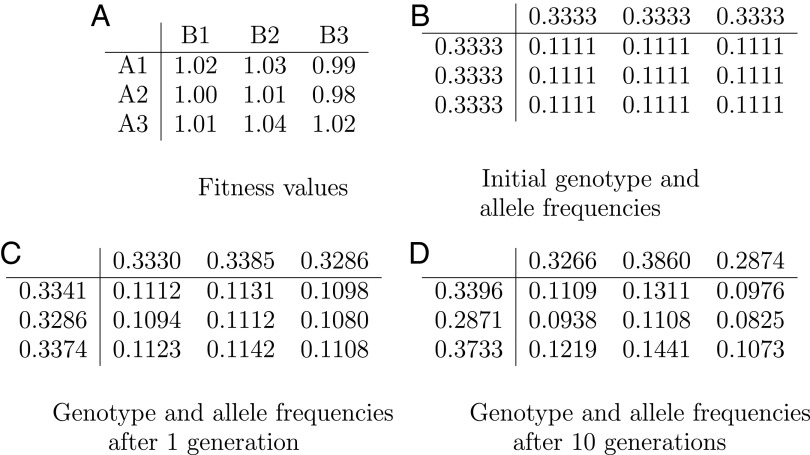
Fig. 1.

Equations of population genetics formulated in the 1930s constitute the standard mathematical way of understanding evolution of a species by tracking the frequencies of various genotypes in a large population. In the simple example shown here, a haploid organism with two genetic loci A and B has three alleles in each of its two loci named A1, A2, A3 and B1, B2, B3 for a total of nine genotypes. In A we show the fitness of each genotype, that is, its expected number of offspring. The fitness numbers shown in A are all close to each other, reflecting weak selection, where the individual alleles’ contributions to fitness are typically minuscule. Initially, each genotype occurs in the population with some frequency; in this particular example these numbers are initially equal (B); naturally, their sum over all nine genotypes is 1 (frequencies are truncated to the fourth decimal digit). C shows how the genotype frequencies evolve in the next generation: each individual of a given genotype produces a number of offspring that is proportional to its fitness shown in A, and the resulting offspring inherits the alleles of its parents with equal probability (because we are assuming, crucially, sexual reproduction). The genotype frequencies in the next generation are shown in C, calculated through the standard recurrence equations of population genetics. We also show in the margins of the table the allele frequencies, obtained by adding the genotype frequencies along the corresponding row or column. Ten generations later, the frequencies are as shown in D.

We now introduce the framework of game theory (see Fig. 2 for an illustration) and the MWUA (SI Text), studied in computer science and machine learning, and rediscovered many times over the past half-century; as a result of these multiple rediscoveries, the algorithm is known with various names across subfields: “the experts algorithm” in the theory of algorithms, “Hannan consistency” in economics, “regret minimization” in game theory, “boosting” and “winnow” in artificial intelligence, etc. Here we state it in connection to games, which is only a small part of its applicability (see SI Text for an introduction to the MWUA in connection to the so-called “experts problem” in computer science).

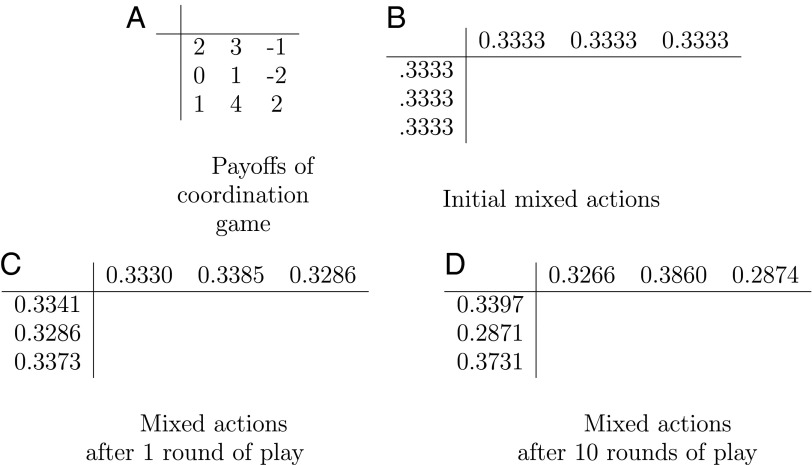
Fig. 2.

A simple coordination game is played by two players: the row player, who chooses a row, and the column player, who chooses a column. After the two players make a choice, they both receive (or both pay, in case of a negative entry) the same amount of money, equal to the number at the chosen row and column (A). Coordination games are the simplest possible kind of a game, one in which the strategic interests of all players are completely aligned—that is to say, there is no conflict at all. They are of interest when it is difficult for the players to know these numbers, or to communicate and agree on a mutually beneficial combination (in this example, third row and second column). Notice that this particular coordination game is closely related to the fitness landscape shown in Fig. 1A: If P is a payoff in this game, the corresponding entry of Fig. 1A is equal to 1 + ε ⋅ P, where ε is a small parameter here taken to be 0.01. Suppose that each of the two players chooses each of the three options with some probability, initially $1/3$ for all (B); in game theory such probabilistic play is called a mixed action. How do we expect these probabilities to change over repeated play? One famous recipe is the MWUA, in which a player “boosts” the probability of each option by multiplying it by 1 + εG, where G is the expected amount of money this option is going to win the player in the current round of play, and ε is the same small parameter as above. For example, the second action of the row player has G equal to 2 (the average of 3, −1, and 4), and so the probability of playing the second row will be multiplied by 1.02. Then these weights are “renormalized” so they add up to 1, yielding the marginal probabilities shown in C. The probabilities after 10 such rounds of play are shown in D. Comparing now the numbers in the margins of Figs. 1D and 2D, we notice that they are essentially the same. This is what we establish mathematically in this paper: the two processes—repeated coordination games played through multiplicative updates, and evolution under weak selection—are essentially identical. This conclusion is of interest because the MWUA is known in computer science to be surprisingly powerful.

A game has several players, and each player i has a set A_i of possible actions. Each player also has a utility, capturing the way whereby her actions and the actions of the other players affect this player’s well-being. Formally the utility of a player is a function that maps each combination of actions by the players to a real number (intuitively denoting the player’s gain, in some monetary unit, if all players choose these particular actions). In general, rather than choosing a single action, a player may instead choose a mixed or randomized action, that is, a probabilistic distribution over her action set. Here we only need to consider coordination games, in which all players have the same utility function—that is, the interests of the players are perfectly aligned, and their only challenge is to coordinate their choices effectively. Coordination games are among the simplest games; the only challenge in such a game is for the players to “agree” on a mutually beneficial action.

How do the players choose and adjust their choice of randomized (mixed) actions over repeated play? Assume that at time t, player i has mixed action $x_i^t$, assigning to each action j ∈ A_i the probability $x_i^t\left(j\right)$. The MWUA algorithm (5) adjusts the mixed strategy for player i in the next round of the game according to the following rule:

$$x_i^{t+1}\left(j\right)=\frac{1}{Z^t}{x}_i^t\left(j\right)\left(1+\mathit{ϵ}{u}_i^t\left(j\right)\right),$$ [2]

where Z^t is a normalizing constant designed to ensure that ${\displaystyle {\sum }_j{x}_i^t\left(j\right)}=1$, so $x_i^{t+1}$ is a probability distribution; ε is a crucial small positive parameter, and $u_i^t\left(j\right)$ denotes the expected utility gained by player i choosing action j in the regime of the mixed actions by the other players effective at time t. This algorithm (i) is known to converge to the min–max actions if the game is two-player zero-sum; (ii) is also shown here to converge to equilibrium for the coordination games of interest in the present paper (SI Text, Corollary 5); (iii) is a general “learning algorithm” that has been shown to be very successful in both theory and practice; and (iv) if, instead of games, it is applied to a large variety of optimization problems, including linear programming, convex programming, and network congestion, it provably converges to the optimum quite fast.

It can be now checked that the two processes expressed in Eqs. 1 and 2, evolution under natural selection in the presence of sex and multiplicative weight updates in a coordination game, are mathematically identical (SI Text, Theorem 3). That is, the interaction of weak selection and sex is equivalent to the MWUA in a coordination game between loci in which the common utility is the differential fitness of the organism. The parameter ε in the algorithm, which, when small signifies that the algorithm is taking a “longer-term view” of the process to be solved (SI Text), corresponds to the selection strength in evolution, i.e., the magnitude of the differences between the fitness of various genotypes.

The MWUA is known in computer science as an extremely simple and yet unexpectedly successful algorithm, which has surprised us time and again by its prowess in solving sophisticated computational problems such as congestion minimization in networks and convex programming in optimization. The observation that multiplicative weight updates in a coordination game are equivalent to evolution under sex and weak selection makes an informative triple connection between three theoretical fields: evolutionary theory, game theory, and the theory of algorithms–machine learning.

So far we have presented the MWUA by “how it works” (informally, it boosts alleles proportionally to how well they do in the current mix). There is an alternative way of understanding the MWUA in terms of “what it is optimizing.” That is, we imagine that the allele frequencies of each locus in each generation are the result of a deliberate optimization by the locus of some quantity, and we wish to determine that quantity.

Returning to the game formulation, define $U_i^t\left(j\right)={\displaystyle {\sum }_{\tau =0}^t{u}_i^{\tau }\left(j\right)}$ to be the cumulative utility obtained by player i by playing strategy j over all t first repetitions of the game, and consider the quantity

$${\displaystyle \sum _j{x}_i^t\left(j\right)U_i^t\left(j\right)}-\frac{1}{\mathit{ϵ}}{\displaystyle \sum _j{x}_i^t\left(j\right)\ln x_i^t\left(j\right)}.$$ [3]

The first term is the current (at time t) expected cumulative utility. The second term of 3 is the entropy (expected negative logarithm) of the probability distribution {x_i(j), j = 1, … $\left|A_i\right|$}, multiplied by a large constant $1/\mathit{ϵ}$. Suppose now that player i wished to choose the probabilities of actions $x_i^t\left(j\right)$s with the sole goal of maximizing the quantity 3. This is a relatively easy optimization problem, because the quantity 3 to be maximized is strictly concave, and therefore it has a unique maximum, obtained through the Karush–Kuhn–Tucker conditions of optimality (8) (SI Text, section 4):

$$U_i^t\left(j\right)-\frac{1}{\mathit{ϵ}}\left(1+\ln x_i^t\left(j\right)\right)+{\mu }^t=0.$$

[Here μ^t is the Lagrange multiplier associated with the constraint ${\displaystyle {\sum }_j{x}_i^t\left(j\right)}=1$ seeking to keep the $x_i^t\left(j\right)$s a probability distribution; see SI Text.] Subtracting this equation from its homolog with t replaced by t + 1, and applying the approximation $\exp \left(\mathit{ϵ}{u}_i^t\left(j\right)\right)\approx \left(1+\mathit{ϵ}{u}_i^t\left(j\right)\right)$, we obtain the precise Eq. 2 (the normalization Z^t is obtained from μ^t and μ^t+1; see SI Text for the more detailed derivation).

Thus, because Eqs. 1 and 2 are identical, we conclude that, in the weak selection regime, natural selection is tantamount to each locus choosing at each generation its allele frequencies in the population so as to maximize the sum of the expected cumulative differential fitness over the alleles, plus the distribution’s entropy. Note that quantity 3 is maximized by genes, not by individuals, and that, interestingly, it is maximized with respect to current frequencies while being dependent (through U^t) on all past frequencies, and although there is some precedent to the use of “historical fitness” (9), its importance in this context is unexpected.

This alternative view of selection provides a new insight into an important question in evolutionary biology, namely: How is genetic diversity maintained in the presence of natural selection (10)? That the MWUA process enhances the entropy of the alleles’ distribution (while at the same time optimizes expected cumulative utility) hints at such a mechanism. In fact, entropy is enhanced inversely proportional to s (the quantity corresponding in the population genetics domain to the parameter ε), the selection strength: The weaker the selection, the more it favors high entropy. Naturally, entropy will eventually vanish when the process quiesces at equilibrium: One allele per locus will eventually be fixed, and in fact this equilibrium may be a local, as opposed to global, fitness maximum. However, we believe that it is interesting and significant that the entropy of the allele distribution is favored by selection in the transient; in any event, mutations, environmental changes, and finite population effects are likely to change the process before equilibrium is reached. This new way of understanding the maintenance of variation in evolution (selection as a tradeoff between fitness and entropy maximization) is quite different from previous hypotheses for the maintenance of variation (e.g., refs. 11, 12). Another rather surprising consequence of this characterization is that, under weak selection, all past generations, no matter how distant, have equal influence on the change in the allele mix of the current generation.

Our discussion has focused on the evolution of a fixed set of alleles; that is, we have not discussed mutations. Mutations are, of course, paramount in evolution, as they are the source of genetic diversity, and we believe that introducing mutations to the present analysis is an important research direction. Here we focus on the selection process, which is rigorously shown to be tantamount to a tradeoff, for each locus, between maximizing diversity and maximizing expected cumulative fitness.

We can now note a simple yet important point. Because multiplicative weight updates by the loci operate in the presence of sex, the triple connection uncovered in this paper is informative for the “queen of problems in evolutionary biology,” namely the role of sex in evolution (13, 14). The notion that the role of sex is the maintenance of diversity has been critiqued (15), because sex does not always increase diversity, and diversity is not always favorable. The MWUA connection sheds new light on the debate, because sex is shown to lead to a tradeoff between increasing entropy and increasing (cumulative) fitness.

The connection between the three fields, evolution, game theory, and learning algorithms, described here was not accessible to the founders of the modern synthesis, and we hope that it expands the mathematical tracks that can be traveled in evolution theory.