Abstract
Purpose:
Nonstationarity is an important aspect of imaging performance in CT and cone-beam CT (CBCT), especially for systems employing iterative reconstruction. This work presents a theoretical framework for both filtered-backprojection (FBP) and penalized-likelihood (PL) reconstruction that includes explicit descriptions of nonstationary noise, spatial resolution, and task-based detectability index. Potential utility of the model was demonstrated in the optimal selection of regularization parameters in PL reconstruction.
Methods:
Analytical models for local modulation transfer function (MTF) and noise-power spectrum (NPS) were investigated for both FBP and PL reconstruction, including explicit dependence on the object and spatial location. For FBP, a cascaded systems analysis framework was adapted to account for nonstationarity by separately calculating fluence and system gains for each ray passing through any given voxel. For PL, the point-spread function and covariance were derived using the implicit function theorem and first-order Taylor expansion according toFessler [“Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): Applications to tomography,” IEEE Trans. Image Process. 41(8), 493–506 (1996)]. Detectability index was calculated for a variety of simple tasks. The model for PL was used in selecting the regularization strength parameter to optimize task-based performance, with both a constant and a spatially varying regularization map.
Results:
Theoretical models of FBP and PL were validated in 2D simulated fan-beam data and found to yield accurate predictions of local MTF and NPS as a function of the object and the spatial location. The NPS for both FBP and PL exhibit similar anisotropic nature depending on the pathlength (and therefore, the object and spatial location within the object) traversed by each ray, with the PL NPS experiencing greater smoothing along directions with higher noise. The MTF of FBP is isotropic and independent of location to a first order approximation, whereas the MTF of PL is anisotropic in a manner complementary to the NPS. Task-based detectability demonstrates dependence on the task, object, spatial location, and smoothing parameters. A spatially varying regularization “map” designed from locally optimal regularization can improve overall detectability beyond that achievable with the commonly used constant regularization parameter.
Conclusions:
Analytical models for task-based FBP and PL reconstruction are predictive of nonstationary noise and resolution characteristics, providing a valuable framework for understanding and optimizing system performance in CT and CBCT.
Keywords: image quality, noise-power spectrum, modulation transfer function, imaging task, detectability index, nonstationary noise, cone-beam CT, cascaded systems analysis, statistical reconstruction, penalized-likelihood reconstruction
I. INTRODUCTION
Accurate description of image quality is integral to system design, optimization, and assessment. A wealth of literature has been devoted to studying the noise characteristics of x-ray computed tomography (CT) in terms of the pixel variance, spatial domain covariance matrix, or Fourier domain noise-power spectrum (NPS).1–6 Moreover, it is generally accepted that image quality should be defined with respect to the imaging task,7,8 where detectability is calculated to account for noise, spatial resolution as well as the task function and observer model. Such task-based frameworks are increasingly employed in system design, performance assessment, and optimization.9–11
An aspect of image quality that is somewhat less frequently reported is the spatially varying, i.e., nonstationary—characteristics of noise, spatial resolution, and detectability. In x-ray CT and cone-beam CT (CBCT), nonstationarity may arise from the discrete nature of reconstructed images, detector defects and nonlinearity, angular sampling, the divergent beam, variable fluence transmitted to the detector at different view angles, and the reconstruction algorithm. Several researchers have examined nonstationarity in filtered-backprojection reconstruction (FBP). For example, Pineda et al.12 calculated the local NPS throughout FBP reconstructions, showing the variation in NPS associated with variable fluence transmitted to the detector (and the effect of a bowtie filter). They furthermore quantified the difference between the diagonal and off-diagonal elements of the Fourier transform of the covariance matrix as a metric of stationarity. Baek and Pelc13,14 studied nonstationary noise in fan-beam and cone-beam FBP reconstructions as a result of varying magnification, projection weighting, and cosine weighting, and quantified the NPS at different spatial locations within reconstructions of air and a water cylinder. Bartolac et al.15 investigated the nonstationary signal and noise characteristics in CBCT arising specifically from sampling along a circular source-detector trajectory (i.e., the spatially varying null cone associated with violation of Tuy's condition). Nonstationarity in relation to task-based performance was investigated by Brunner et al.,5 who evaluated the location-dependent NPS and covariance matrix in FBP reconstructions and calculated Hotelling observer performance for simple tasks. Wunderlich and Noo16 estimated the covariance in FBP reconstruction of fan-beam CT data and examined the location-dependent noise and lesion detectability using a channelized Hotelling observer. Such work demonstrates the spatially varying noise characteristics intrinsic to CT and CBCT and motivated investigation of the corresponding effect on detectability.
The need for a framework that can describe nonstationary imaging performance is pronounced in light of growing interest in statistical reconstruction methods. Compared to conventional FBP, statistical reconstruction has demonstrated potential for dose reduction, artifact reduction, and the incorporation of prior information.17 Such methods also carry distinct noise and resolution characteristics, as well as the means to explicitly enforce stationarity, e.g., the ability to enforce uniformity in the point-spread function (PSF) throughout the image.18–20 In the past several years, commercial CT systems with the capability for statistical reconstruction have emerged in clinical settings, raising the need to understand the imaging performance associated with such algorithms for assessment, optimization, and possible dose reduction. Compared to FBP, image quality assessment in statistical reconstruction faces the additional challenge that the nonlinear algorithm itself imparts nonuniform noise and resolution with explicit dependence on the contrast of the signal of interest. Image quality in statistical reconstruction has been evaluated empirically in terms of the variance, kurtosis, contrast-dependent edge-spread function, and associated modulation transfer function (MTF).21–24 Efforts toward task-based assessment and optimization of statistical reconstruction have mostly been concentrated in emission tomography.25–37
The work reported below investigates the nonstationary noise, resolution, and task-based performance in CBCT reconstructed with both FBP and statistical algorithms. For the latter, the current analysis pertains to penalized likelihood (PL) estimation with a quadratic penalty. The FBP model builds on the cascaded systems model established in previous work38–40 to account for noise nonstationarity as a result of variable fluence transmitted to the detector at different views. Noise and resolution estimation for PL is adapted from work by Fessler for implicitly defined function estimators.18,41 Imaging performance is reported in terms of the local MTF, NPS, and detectability index (d′), analogous to the approach adopted by Wilson42 in SPECT, where the local MTF and NPS were used to calculate a local NEQ. Although imaging performance in both FBP and PL is examined below, the purpose of this work is not to rate the performance of the two algorithms. In fact, as apparent in the results below, the performance of the two algorithms is highly dependent on the imaging task, object, spatial location, and imaging conditions, and it is difficult to reach a fair, general conclusion of the algorithms. Finally, we present a simple task-based method for optimal selection of the PL regularization strength parameter (β), including spatially varying regularization to improve detectability.
II. METHODS
II.A. Nonuniform noise and resolution due to variable fluence to the detector
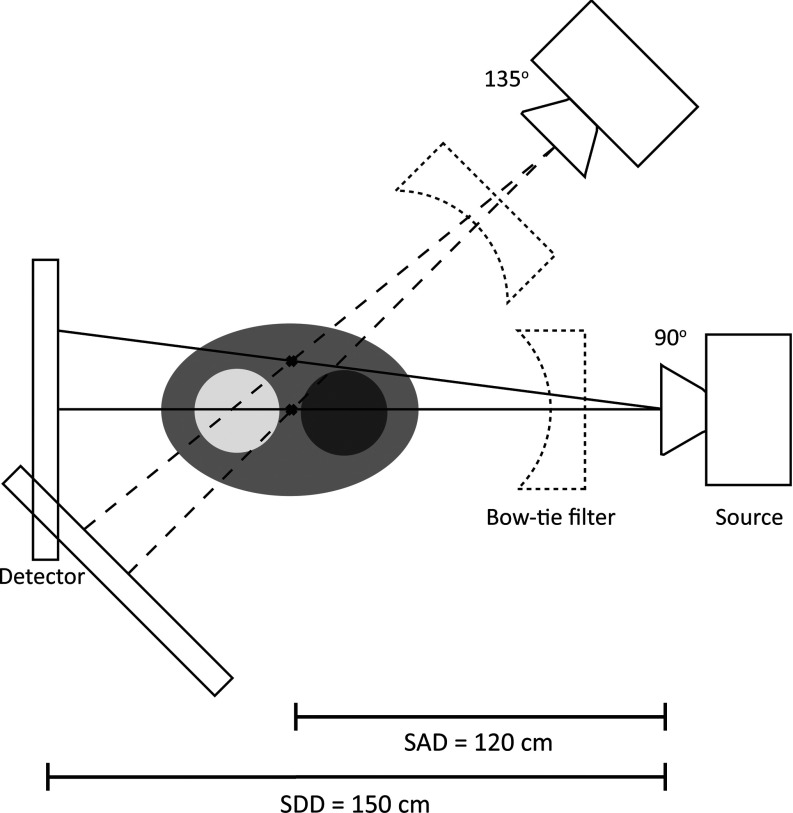
The main source of nonuniform noise and resolution investigated in this work is variable fluence transmitted to the detector at different view angles (and, to a lesser extent, azimuthal angles) as illustrated in Fig. 1. For the general case of a heterogeneous, noncircular object, the line integral of the ith projection ray passing through a given voxel is dependent on the object and in most cases different for each view angle. It is also evident that the line integrals are dependent on the location of the voxel within the object. Such view- and location-dependent fluence (and therefore, noise) is propagated through the reconstruction process and reflected in the noise correlation according to the central slice theorem. It is important to note that such a property is intrinsic to CT and is evident in both linear and nonlinear reconstruction algorithms.
FIG. 1.
Illustration of line integrals at different view angles transmitting variable fluence to the detector, thereby imparting nonuniformities in detector signal and noise which are then propagated to image reconstruction.
The line integrals, l, can be calculated through a forward projection matrix, A, according to
| (1) |
where μ is the vectorized representation of attenuation coefficients in the object and would carry energy dependence [μ(E), giving rise to l(E)] for a polyenergetic beam model. Let nvox denote the number of voxels in the voxelized representation of the object and ndet the number of detector measurements over all projection views, the dimension of A is ndet × nvox, that of μ is nvox × 1 and l ndet × 1. The forward projection operator was implemented following a separable footprint algorithm43 elaborated in Sec. II C. The detector element (and, therefore, the line integral) associated with a given voxel was identified through a view-specific 3 × 4 projection matrix that relates the voxel location in the object to the location of its projection on the detector. The line integrals (and, therefore the local signal and noise characteristics) can then be calculated for any voxel location.
As illustrated in Fig. 1, the presence of a bowtie filter (or equivalently, other fluence modulation device, e.g., a dynamic bow-tie44 or multileaf collimators45) can be readily incorporated into the model by accounting for attenuation through the device as part of the object model, μ. A bowtie filter was excluded in the work below to be consistent with many CBCT systems (including many breast, C-arm, and image-guided radiotherapy imaging systems) and to better demonstrate the basic nonstationary noise characteristics.
Additional sources of nonuniform noise and resolution exist and were not directly investigated in this work. A point x-ray source was assumed, thereby neglecting spatially-varying focal spot blur in the system MTF. We also excluded the heel effect, which would result in decreased fluence at the anode side of the projection. The spatially varying “null cone” associated with the cone-beam geometry in a circular source-detector orbit was ignored. The response of each detector element was assumed to be the same, thereby assuming a perfect correction of gain and offset variations in the detector. Such effects could potentially be incorporated in the description of image quality in future work.
II.B. The spatially-varying NPS and MTF for FBP
Previous work has established a cascaded systems analysis model for signal and noise propagation through discrete stages corresponding to the physical processes of projection formation and the mathematical processes of FBP reconstruction.38–40,46 Each stage may result in one of the following effects: (1) the amplification (or loss) of signal through a gain factor , (2) spatial spreading (deterministic or stochastic) of signal according to a transfer function Ti, and (3) sampling characterized by a comb function III. Using notation consistent with previous work and briefly summarized in Table I, the system MTF and NPS of a 3D CBCT/CT reconstruction is given by
| (2) |
| (3) |
where Sproj denotes the 2D projection NPS,
| (4) |
Such work has primarily reported results and validation pertaining to the center of a uniform cylinder (or averaged along circular paths concentric with the cylinder), although calculation of nonstationary noise as a function of spatial location can be accommodated within the same framework.
TABLE I.
Notations used in the cascaded systems analysis consistent with Ref. 40.
| Term | Definition |
|---|---|
| Mean fluence incident on the detector per projection | |
| Quantum detection efficiency | |
| Conversion gain from x-rays to secondary quanta (e.g., optical photons) | |
| Pk | Gain and spreading factors associated with K-fluorescence |
| T3 | Transfer function due to stochastic spread of secondary quanta |
| Coupling efficiency of photodiode | |
| apd | Width of (square) photodiode |
| T5 | Transfer function due to photodiode aperture |
| III6 | Detector pixel sampling (2D comb function) |
| σadd | Additive electronics noise |
| III8 | Postreadout projection resampling (optional) |
| T8 | Transfer function due to 2D binning aperture (optional) |
| T10 | Ramp filter |
| T11 | Apodization filter |
| T12 | Interpolation filter |
| T13 | Transfer function associated with backprojection of signal |
| Θ13 | Transfer function associated with backprojection of noise |
| III14 | 3D voxel sampling (3D comb function) |
| III15 | Postreconstruction sampling (optional) |
| T15 | Transfer function due to 3D binning aperture (optional) |
| m | Number of projections acquired across a circular orbit |
| θtot | Total angular extent of acquisition |
| M | Magnification factor, source-detector distance (SDD)/source-axis distance (SAD) |
| FOV | Size of the reconstruction field of view |
| fProj | 2D projection frequency domain, (fu, fv) |
| f3D | 3D reconstruction frequency domain, (fx, fy, fz) |
To model the effect of variable fluence to the detector, of the ith projection, denoted as (x-ray quanta/mm2), was calculated according to Beer's law using line integrals calculated from Eq. (1). Consequently, any parameters in the model that are dependent on the spectrum also need to be calculated separately for each view, including the effective (energy-averaged) gain factors , , and Pk. For simplicity, the spatial spreading of optical quanta (T3) and K x-rays (Tk, absorbed in the Pk term) in the scintillator are assumed to have negligible dependence on the incident energy. This assumption could be removed in refinement of the model in future work. Aperture integration (T5), the ramp filter (T10), apodization (T11), and interpolation (T12) of the projections are independent of the incident spectrum.
The NPS of the ith projection is therefore as follows, with view-dependent terms indicated by the superscript i and notation otherwise consistent with Eq. (4),
| (5) |
The term then needs to be individually propagated through the FBP reconstruction process. The transfer function associated with the backprojection of each view is given by
| (6) |
where θi is the view angle and FOV is the reconstruction field of view. Summing over all projections, the NPS of the 3D image reconstruction is given by
| (7) |
If the noise contribution from each view is equal, e.g., at the center of a uniform cylinder, , , , and can be moved out of the summation, and in the limit of a large number of projections, the transfer function for Stage 13 can be simplified to the view-independent form
yielding the familiar form of NPS shown in Eq. (3).
Similarly for the MTF,
| (8) |
Since is the only term dependent on view angle, the MTF reduces to
| (9) |
The summation of over a large number of projections cancels out the ramp filter (T10) and reduces to the same form as Eq. (2), which is independent of the incident spectrum and view angle. The system MTF is therefore the same for all voxel locations.
Various simplifying assumptions are invoked in the cascaded systems model. Apart from local linearity and shift-invariance, the backprojection stage was modeled according to a parallel beam geometry although line integrals were calculated using a divergent beam geometry. This is reasonable within a small neighborhood where divergent beam geometry can be approximated as parallel. Incorporating divergent beam geometry and associated weighting in the FDK algorithm is within the capacity of the cascaded systems model and could be an area of future work.
From the resulting NPS and MTF, the noise-equivalent quanta (NEQ) can also be defined locally
| (10) |
Together, Eqs. (7), (9), and (10) demonstrate the capacity of the cascaded systems framework to describe the spatially varying signal and noise characteristics in FBP in terms of local descriptors of MTF, NPS, and NEQ.
It is generally acknowledged that image quality should be assessed with regard to the imaging task. Imaging tasks investigated in this work involve the detection of known signal stimuli. The mathematical description of task, denoted, WTask, is given by the difference in the Fourier transform of the “signal-present” and “signal-absent” hypotheses. Task-based imaging performance was quantified in terms of detectability index, d′, which relates metrics of MTF, NPS, and NEQ to the imaging task and the observer model. An observer is the entity performing the imaging task and governs the decision-making paradigm. A variety of observer models can be employed in the calculation of d′, including the basic prewhitening (PW) form:
| (11) |
and various “anthropomorphic” observer models intending to better approximate the performance of human observers, such as the nonprewhitening matched filter observer model with eye filter and internal noise (NPWEi),
| (12) |
The subscript of the frequency domain symbol, f, is dropped to indicate generic descriptions in both 2D and 3D forms. The NPWEi model has demonstrated good correspondence with human observer performance in previous work and is therefore the nominal form of observer model employed below. The eye filter was47
| (13) |
where c equals 2.2 mm−1 for a typical viewing distance of 50 cm, yielding peak response at 4 cycles/deg. The internal noise was modeled as uncorrelated white noise according to
| (14) |
where D is the viewing distance (50 cm), and Seq is the white NPS equivalent in total power to the image noise. The scale factor 0.001 was consistent with previous work to yield reasonable agreement with experimental measurements.48 In the current work, only reconstructions at the central slice were considered, therefore f in Eqs. (11)–(13) represents (fx, fy). The effect of out-of-plane (z-direction) beam divergence and associated cone-beam artifacts were not included. Just as Eqs. (7), (9), and (10) allow calculation of the NPS, MTF, and NEQ at any location within the image, Eqs. (11) and (12) allow calculation the spatially varying detectability index, d′(x,y).
II.C. The spatially varying NPS and MTF for iterative statistical image reconstruction
Iterative statistical reconstruction algorithms seek a reconstruction estimate, , that maximizes an objective function, Φ(μ; p) relating the measured projections, p, to the object, μ. This work focuses on the PL family of algorithms where the objective function includes the likelihood term L(μ; p) and a penalty function R(μ) scaled by the regularization strength parameter, β,
| (15) |
The measured projections, p, are assumed for simplicity to follow a Poisson distribution, with the mean, , related to μ by the forward model
| (16) |
where I0 is the bare-beam fluence (x-ray quanta/pixel), and l is the line integral following Eq. (1). Consistent with notation from Sec. II A, vectorized representations of p and have dimension ndet × 1. For simplicity, the energy dependence in μ was dropped. Moreover, the assumption of Poisson noise is an obvious simplification in light of known complexities of the image noise distribution, for example, Poisson excess, blur, and additive noise as described by the cascaded systems model in Sec. II B. Incorporation of such complexities into model-based statistical reconstruction is an area of ongoing and future work.49
We consider a quadratic penalty, R(μ), of the form
| (17) |
where R is a nvox × nvox constant matrix that defines how voxels are combined and penalized quadratically. It is also the Hessian of R(μ). In the work below, we used a particular class of quadratic penalty that penalizes voxel differences in a first order neighborhood about a voxel location, j, i.e., , where wjk = 1 for the nearest neighbors (4–8 in a 2D axial slice reconstruction, or 6–26 in a 3D reconstruction) and 0 otherwise. The strength of the penalty is governed by the regularization strength parameter, β. While normally treated as a constant in most cases, β can also be implemented as a regularization “map” to impart a spatially-varying penalty in the reconstruction.18–20
Fessler41 derived the covariance estimate of PL reconstructions for transmission tomography using the first-order Taylor expansion and the Implicit Function Theorem. The nvox × 1 column vector, , describing the covariance of voxel j with every other voxel in the reconstruction is given by
| (18) |
where the transpose of the forward projection operator, AT, is the backprojection operator and D{} represents a square diagonal matrix with the vector argument corresponding to the diagonal entries. The nvox × 1 unit vector δj effectively extracts a column from the full covariance matrix and allows the calculation of covariance at any arbitrary voxel location (x, y). The term is the forward projection of the reconstruction from noiseless data, i.e., . When μtrue and are not available to compute (e.g., when performing variance estimation for real data), the measured projection data, p, can be used as a substitution, because both forward- and backprojection are smoothing operations that reduce the effect of noise on the resulting estimate. Equation (18) reveals a dependence of noise on the spatial location and on the object itself, but only through the projections (i.e., and p). Therefore, knowledge of the true object is not required to estimate the covariance for PL reconstruction with a quadratic penalty. Equation (18) can be solved iteratively using the conjugate gradient algorithm.41
Assuming the image noise to be slowly varying, a local stationarity assumption can be invoked, i.e., within a small neighborhood, , the covariance of voxel j with every other voxel in the neighborhood, , is the same for all voxels
| (19) |
If there are voxels in the neighborhood, the dimensions of and are both × 1. Assuming further that the two voxels at opposite ends of the ROI have the same covariance as two adjacent voxels at the center (e.g., digital wrap-around), which is reasonable if only short-range correlations exist, the local covariance matrix can be approximated as circulant. For such matrices, the magnitude of the DFT of a row/column is equal to the diagonal of the DFT of the full covariance matrix, which is in turn equal to the NPS of the neighborhood by definition. We can therefore write the local NPS in the neighborhood for quadratic PL image reconstruction as
| (20) |
Here, diag{} denotes the extraction of the diagonal from the square matrix [not to be confused with D{}].
The point spread function (PSF) for PL reconstruction was derived using similar principles as the covariance18
| (21) |
The equation reveals a dependence of spatial resolution on the spatial location and on the object itself (again, through the projection data). This finding is in contrast to FBP reconstruction which carries uniform spatial resolution to the extent described by Eq. (9), recognizing the potential for nonuniform spatial resolution associated with sampling13,14 and modified FDK algorithms with shift-variant filters.50
The PSF at each voxel in a neighborhood is assumed to be the same, or equivalently, the system is locally shift-invariant. The first-order Taylor expansion used in the derivation of Eqs. (18) and (21) amounts to a local linearity approximation.18 Therefore, the system is locally linear and shift-invariant, and the MTF can be calculated as the magnitude of the DFT of the PSF normalized at zero frequency
| (22) |
The above relation can also be derived in a manner similar to the covariance case, where the system matrix is circulant with shifted copies of the PSF as its column entries.5 The local NPS and MTF can then be related to task-based imaging performance via Eqs. (11) and (12).
II.D. Digital phantoms and image simulation
To validate theoretical predictions of noise and spatial resolution in FBP and PL, model calculations of NPS and MTF were compared with measurements in simulated data. Three digital phantoms of increasing complexity were investigated in this study as illustrated in Fig. 2: (1) a uniform Circular disk phantom of radius 9 cm with attenuation coefficient 0.02 mm−1; (2) an Elliptical phantom with major axis of 24 cm and minor axis of 16 cm. The background of the ellipse was uniform with attenuation coefficient 0.0164 mm−1 (corresponding to water in a 90 kV beam filtered with 2 mm Al and 0.4 mm Cu), with two circular inserts of 7.75 cm diameter and attenuation coefficients 0.0211 and 0.0144 mm−1 corresponding to acetal and polypropylene, respectively; (3) an anthropomorphic Thorax constructed from a slice through a phantom imaged on a clinical CT scanner. For simplicity, the soft tissue (skin, muscle, fat, and heart) was assigned a uniform attenuation coefficient 0.0203 mm−1, and bones (ribs and spine) 0.0432 mm−1. Attenuation values for the lung tissue were preserved from the CT reconstruction, with an approximate mean value of 0.0074 mm−1. For the monoenergetic (57 keV) simulations considered in this work, the attenuation coefficient of each component was a scalar. The phantoms can be adapted to polyenergetic simulations in future studies by using an energy-dependent attenuation coefficient [μ(E)] for each tissue component.
FIG. 2.
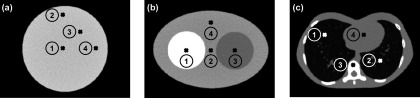
Three digital phantoms investigated in this work. (a) A uniform circular disk phantom. (b) An elliptical object composed of three materials approximating water, bone, and fat. (c) A thorax approximating a realistic distribution of tissue heterogeneities. The numeric symbols (1–4) mark four locations at which the local MTF, NPS, NEQ, and detectability index were analyzed.
The monoenergetic x-ray source was simulated with bare-beam fluence, I0, equal to 2.1 × 105 x-ray quanta/pixel, corresponding to a 90 kV beam at 1 mAs with an exposure of 0.70 mR to the detector. Using a monoenergetic beam implies that the energy dependence in the cascaded systems analysis model was dropped, and the only view dependent term was . System geometry was simulated at SAD = 120 cm and SDD = 150 cm. For simplicity and to focus on the intrinsic nonstationarities associated with FBP and PL reconstruction methods, an ideal detector model was considered, i.e., there was no detector blur beyond that of the pixel aperture, and Poisson-distributed quantum noise constituted the only noise source. Detector pixel pitch was simulated at 0.834 mm, and reconstructions were performed at a voxel size of 0.667 mm. Poisson noise was added independently to the projection data according to Ref. 51. Note that although simulations were performed for a single-row detector, and only the central axial slice was reconstructed in order to save computation time associated with the large number of PL reconstructions required to validate covariance and NPS estimation, the theoretical methods are applicable to 3D CBCT and multidetector CT (MDCT) data. The notation associated with the simulated data is therefore presented in a 2D form.
Both FBP and PL reconstruction algorithms were implemented in MATLAB with external calls to a custom C++ library to perform forward- and backprojection operations on GPU. Projection data were generated with a separable footprint projector.43 For FBP, the FDK algorithm for cone-beam reconstruction was used,52 recognizing that for a single-row detector at the central plane (as in the simulation studies), the FDK algorithm amounts to fan-beam reconstruction.53 For PL, image updates were performed using a paraboloidal surrogate approach.54 Ordered-subset subiterations55 were adopted to speed convergence, where the number of subsets decreased from an initial value of 60 in increments of −5 at every 50 iterations. An additional 200 iterations were performed after the number of subsets decreased to 1 in order for the algorithm to converge, giving a total of 800 iterations for each PL reconstruction. A sufficiently converged solution was confirmed by examining the image difference between reconstructions at 800 iterations from those at 2000 iterations, with a maximum image difference on the order of 10−4 mm−1. Reconstructions were performed for different values of smoothing parameters for each algorithm. For PL, the regularization parameter, β, spanned 4 orders of magnitude from 104.7 to 108.5. For FBP, variable smoothing was achieved through the apodization filter, T11,
| (23) |
where the apodization window, hwin, was varied from 0.5 to 1.0, and the ratio of the cutoff frequency to the Nyquist frequency, f0/fNqy, was varied from 0.1 to 1.0.
For the purpose of initial qualitative validation of the model, two low-contrast line-pair detection tasks were implemented. Figure 3(a) shows a “vertical” line-pair detection task consisting of 5 lines of 1 × 10 voxels, each separated from its neighbor by 2 voxels. The contrast of the lines from the background was +0.0010 mm−1, and the voxels between the lines were assigned a contrast of −0.0005 mm−1 from the background (note the positive and negative contrast). The contrast was simulated such that the average contrast of the lines is equal to the attenuation of the background. The imaging task therefore represents a simple binary hypothesis of: (i) detection of the oscillations associated with the line pair pattern; versus (ii) a uniform background. The task function is shown in Fig. 3(b), exhibiting signal power concentrated in two regions along the fx axis (corresponding to “vertical” striations in the spatial domain). The second task was a “horizontal” line-pair detection task, constructed from the same line-pair rotated 90°, with the majority of signal power concentrated along the fy axis.
FIG. 3.

Vertical and horizontal line-pair patterns and associated task functions.
Two additional imaging tasks were defined directly in the Fourier domain to investigate the more general dependence of d′ on contrast and frequency content: (1) a radially symmetric midfrequency task defined as the difference between 2 Gaussians of different widths,
| (24) |
where C = 0.04, σ1 = 0.05, and σ2 = 0.02 mm−1; and (2) an all-frequency task (constant in the Fourier domain) corresponding to a delta function detection task of contrast 0.02 mm−1.
II.E. Analysis of noise and spatial resolution
Conventional NPS measurements frequently involve computing the NPS over multiple regions-of-interest (ROIs) [or volumes-of-interest (VOIs)] within an image and averaging the outcome (the Bartlett method for nonoverlapping ROIs or the Welch method for overlapping ROIs). This method invokes stationarity assumptions both locally within the ROI (intrinsic to the Fourier transform) and globally over the ensemble of ROIs contributing to the NPS estimate (by way of the averaging operation). In CBCT, for example, ROIs are often selected at a fixed distance from the center of the reconstruction of a uniform cylinder under the assumption that the NPS is invariant within such an annulus.
An alternative method to compute noise that does not invoke the stationarity assumption involves calculating the full covariance matrix. For an n × n ROI, the covariance matrix is n2 × n2, with the entry on the jth row and kth column, , calculated as
| (25) |
The diagonal of the DFT of the covariance matrix corresponds to the NPS, i.e., the NPS describes the variance of the Fourier components of the noise. As mentioned in Sec. II C, if noise is stationary and correlations are short-ranged, the covariance is a circulant matrix diagonalizable by the DFT. In this case, the NPS captures the full noise characteristics. If noise is not stationary, the NPS ignores the off-diagonal elements in the DFT of the covariance matrix, the magnitude of which has been shown to the small (∼2 orders of magnitude smaller) compared to the main diagonal at different locations within a 16 cm uniform water cylinder.12 Empirical determination of the full covariance matrix requires a large number of noisy realizations to achieve reasonable accuracy. As a rule of thumb,5,6 the number of reconstructions required is at least 10 times the number of samples, i.e., 10 × n2. This is challenging even in simulated data, although efforts have been made to improve estimation accuracy using fewer data sets with assumptions on the correlation length in linear reconstruction algorithms (e.g., FBP).56
In this work, noise measurements were performed under the assumption of local stationarity (i.e., within the ROI itself, but not necessarily throughout the image) just as in the theoretical methods detailed in Secs. II B and II C. Noise was characterized by the local NPS within a ROI at a fixed location, i.e., instead of marching the ROI through the image, NPS was measured at the same location in a large ensemble of reconstructions and then averaged. The method for NPS measurement is otherwise consistent with previous work.57 For each phantom (the Circular disk, the Elliptical phantom, and the Thorax), reconstruction algorithm (FBP and PL), and choice of smoothing parameter (hwin, f0/fNqy, and β), 1000 reconstructions were simulated. Each image was subtracted from the next to form 999 difference images. The subtraction process eliminated anatomical structures, leaving only quantum noise in the difference image (scaling the NPS by a factor of 2 from image subtraction). In physical (nonsimulated) data, subtraction of two images also helps to minimize deterministic image artifacts, e.g., shading. The NPS was measured as the sample average of the square of the Fourier transform of a fixed ROI in all difference images according to
| (26) |
where n is the number of voxels along each direction of the ROI (n = 49 in this case) and a is the voxel size. Note that the NPS considered here is a simple 2D form (with units [(mm−1)2mm2]) appropriate to simulation of a 2D slice.
Spatial resolution at a given location in the image can be measured as the local impulse response,18,58 calculated by injecting a small impulse of magnitude ∂ into at voxel j of the true object μtrue. No noise was added to the simulated projection following the forward model. The resulting noiseless reconstruction subtracted from the noiseless unperturbed image was divided by the magnitude of the impulse to yield the local impulse response. At voxel j, the PSF is therefore given by
| (27) |
The MTF was computed as the modulus of the Fourier transform of the PSF within a 49 × 49 voxel neighborhood following Eq. (22) with the same assumption of linearity and shift-invariance within the local extent of the ROI.
To reduce the MTF to a simple scalar metric of spatial resolution, the value denoted f50 was analyzed as the frequency at which the MTF drops to a value of 0.5. Since the MTF in PL reconstruction is often anisotropic, we analyzed the radial average f50 from 49 evenly distributed spokes through the origin of the MTF, recognizing that this is still a fairly coarse representation of spatial resolution.
II.F. Optimization of reconstruction parameters in PL
Just as cascaded systems analysis has been applied in previous work11,59,60 to optimize various aspects of the CBCT imaging chain using FBP reconstruction, the image quality analysis described above for quadratic PL estimation can be used to optimize aspects of the iterative image reconstruction process. In particular, optimizing the PL reconstruction algorithm holds enormous promise due to the freedom in designing custom, spatially-varying smoothing in the image domain (by way of the β map, the penalty function, or both). Sections II F 1–II F 3 show how the task-based framework can be applied in selecting the regularization parameter in three scenarios.
II.F.1. Choosing a constant β to maximize local d ′
Optimizing detectability in a local ROI amounts simply to computing the local d′ for a range of constant β values and picking the β that gives the maximum d′. A preliminary study (not shown) demonstrated that β values at locations far from the ROI have negligible effects on the noise and resolution characteristics within the ROI if the reconstruction is fully sampled without long-range correlations. Example applications can be found in image-guided interventions where the location of interest in the patient is known.
II.F.2. Choosing a constant β to maximize global d ′
When the location of the signal is unknown, we may aim to optimize d′ over the entire image. A simple model involves the global average detectability, denoted ⟨d′⟩, defined as the average d′ over the entire object, or over multiple ROIs (e.g., in the left and right lungs in a thorax image). More generally, ⟨d′⟩ can be calculated as a weighted average of local d′, where the weights could be assigned to areas of the image based on their importance or disease prevalence (e.g., d′ in the air region assigned a weight of 0). Note that although this model of d′ optimizes performance over the entire image, it does not describe the process associated with search.
The local detectability index was calculated throughout the image in 49 × 49 voxel ROIs across a rectangular grid with neighboring ROIs separated by 25 voxels. The calculation was performed for PL reconstructions using a range of constant β values, and the value that maximized ⟨d′⟩ was identified as the optimum.
II.F.3. Choosing a spatially varying β to improve global d′ beyond scenario 2
The value of β that maximizes local d′ varies throughout the image due to the nonuniform noise and resolution characteristics in PL reconstruction. A simple extension of the previous method is to identify the optimal local β value at each grid point and interpolate the results across the image, yielding a spatially varying β map that could potentially improve performance beyond that achievable with a constant β. The interpolation assumes the local optimal β to be smoothly varying, which is reasonable given that noise and resolution in the image are also smoothly varying. Interpolation was performed using radial basis functions61 to produce a smooth β map, β(x, y). The performance achieved with the spatially varying β map (scenario 3) was compared to that achieved with a constant β (scenario 2) in terms of the global average ⟨d′⟩.
III. RESULTS
III.A. Spatially varying NPS and MTF
Figure 4 illustrates the variance at each voxel (i.e., “variance map”) computed from 1000 FBP and PL reconstructions for each of the three phantoms. In each case, reconstruction parameters (indicated on the respective variance maps) were chosen to match the radial average f50 at the center of the phantom, yielding a reasonably fair comparison of noise at “matched” resolution, recognizing the previously mentioned challenges in this respect. The variance maps for FBP show a greater degree of spatial variation than PL in all phantoms. The highest variance is observed at regions through which rays traverse with the longest path lengths–namely, the center of the Circular disk phantom, the high density insert of the Elliptical phantom, and the spine and heart of the Thorax. The variance map for PL reconstructions is considerably more uniform in each case, demonstrating lower noise than FBP in highly attenuating regions (e.g., the dense insert of the Elliptical phantom and the spine of the Thorax) and higher noise in less attenuating regions. The PL variance map also shows a sharp drop at the boundary of the object due to the non-negativity constraint.
FIG. 4.

Variance maps, σ2(x,y), calculated from multiple realizations of FBP (top) and PL (bottom) reconstructions of the three phantoms shown in Fig. 2.
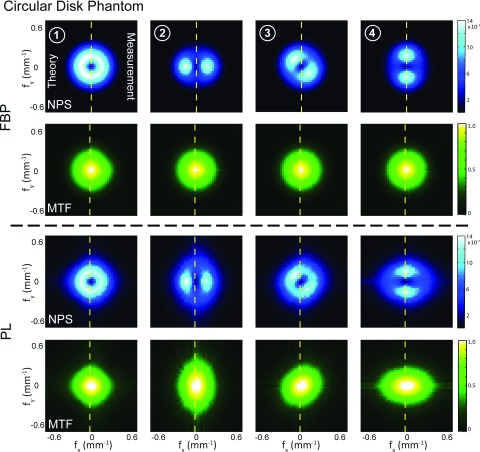
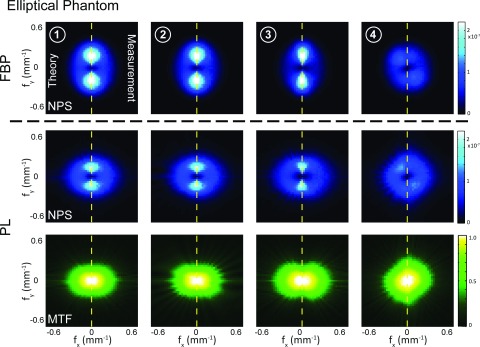
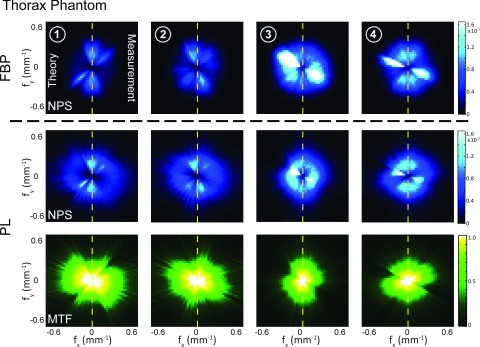
Figures 5–7 illustrate the NPS and MTF evaluated at four locations in the three phantoms of Fig. 2 reconstructed with FBP and PL. Reconstruction parameters were the same as in Fig. 4. In each plot, the left half shows theoretical prediction [Eqs. (7), (9), (20), and (22)], and the right half shows the measurement from 999 simulated difference images, separated by a vertical dotted line. Such presentation results in no loss of information due to the radial symmetry of the Fourier transform.
FIG. 5.
Measured and theoretical NPS and MTF at four locations within the uniform Circular disk phantom, illustrating the nonstationary, anisotropic characteristics of each for FBP and PL. Reconstruction parameters were chosen to “match” spatial resolution (in terms of the radial average f50) in FBP and PL at the center of the image. In each plot, the left half shows theoretical prediction, and the right half shows measurement from simulated images, with excellent agreement between the two. The anisotropic nature of the NPS is similar in both FBP and PL and is consistent with attenuation of rays traversing different pathlengths through the phantom. The MTF of FBP is isotropic and independent of locations, whereas that of PL is anisotropic and roughly “complementary” to the shape of the NPS at the corresponding location.
FIG. 6.
The same as Fig. 5 but for the Elliptical phantom. Regions of higher noise in the NPS correspond to rays traversing the major axis of the ellipse (locations 1, 2, and 3) and the high-density insert (location 4). The MTF for FBP is the same as in Fig. 5 and is not shown for brevity.
FIG. 7.
The same as Fig. 5 but for the Thorax phantom. Slight discrepancies between theory and measurement is likely associated with violation of the local stationarity assumption in regions of strongly heterogeneous structures. The MTF for FBP is the same as in Fig. 5 and is not shown for brevity.
The NPS for both FBP and PL is anisotropic and dependent on both the object and the location within the object. As illustrated in Fig. 1, such characteristics are due to variable fluence transmitted to the detector at different view angles, a property intrinsic to x-ray tomography and is independent of the reconstruction algorithm; therefore, the NPS at corresponding locations in FBP and PL reconstructions exhibit similar anisotropic nature. For example, at the center of the Elliptical phantom, rays traversing the major axis (sampling along the fy axis) are attenuated more strongly and therefore carry higher noise than rays traversing the minor axis (the fx axis). Due to the presence of the higher density insert (resulting in longer line integrals), the NPS at location 1 has a broader extent compared to that at location 3 (the low density insert). By comparison, all rays through the center of the Circular disk phantom have the same pathlength and therefore carry the same noise, giving the familiar “doughnut” shaped NPS reported in previous work. In the Thorax, the NPS is highly anisotropic with noisy rays associated with attenuation through the ribs, spine (location 3), and heart (location 4).
The MTF in FBP is isotropic and shift-invariant within first-order approximation as shown for the Circular disk phantom in Fig. 5. Similar results were found for the Elliptical and Thorax phantom but are not shown for brevity. The MTF in PL reconstructions, however, is anisotropic and exhibits dependence on both the object and spatial location. As evident from Eq. (21), spatial resolution in PL is affected by the amount of noise in the projection data—even when β is held constant. When the projection data are noisy, the algorithm places higher weights on the penalty term which results in greater smoothing.18 Therefore, the radial frequencies sampled by noisier projections will be smoother compared to the less noisy views. This is evident in that the shape of the MTF is roughly complementary to that of the NPS, e.g., lower MTF along ∼−45° at locations 3 and 4 in the Thorax, corresponding to noisy rays through the heart and spine. Note that even though greater smoothing is applied to the noisier rays, the noise carried by those rays is still higher than the less noisy rays.
Excellent agreement is observed between the measured and theoretical NPS and MTF for all three phantoms for both the FBP and PL reconstructions. The NPS for the Thorax shows a slight discrepancy likely due to the violation of the local stationarity assumption for an object containing highly heterogeneous structure (e.g., ribs, spine, lung parenchyma, and muscle). This discrepancy highlights the subtle difference in the interpretation of theoretical and measured NPS. The theoretical method computes the noise characteristics associated with one particular voxel, i.e., one row from the full covariance matrix which is then assumed to be circulant and consist of shifted versions of that row. The NPS calculated as such should be interpreted as the NPS of a hypothetical ROI within which all other voxels have the same first and second order statistics as the given voxel. The measured NPS, on the other hand, amounts to calculating the DFT of the full covariance matrix of the ROI and extracting the diagonal. The difference between theory and measurement is indicative of the degree of local stationarity and shift-invariance within the ROI. Furthermore, a rigorous assessment of the spatial locality assumption is presented in the Appendix.
III.B. Optimization of reconstruction parameters
Detectability index for the vertical line pair (top) and horizontal line pair (bottom) detection tasks in PL reconstructions is plotted in Fig. 8 as a function of β at three locations in the Ellipse. Corresponding images (37 × 37 voxels about the line-pair pattern) are shown at example values of β. For the vertical line pairs, detectability exhibits an optimum at β ∼105.4 in coarse qualitative agreement with the example images. Furthermore, although the line-pair task is fairly conspicuous in each case, detectability is the highest at location 3 since the noise power (see NPS in Fig. 6) associated with the vertical line-pair task (along the fx axis as in Fig. 3) is the lowest.
FIG. 8.
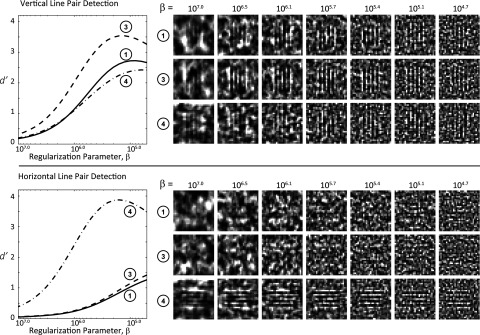
Detectability index at locations 1, 3, and 4 in the Elliptical phantom (Fig. 2) as a function of regularization parameter β for the vertical line pair detection (top) and horizontal line pair detection tasks (bottom). Example ROIs in reconstructions at select values of β are shown on the right. Both the trends and magnitude in d′ agree qualitatively with visual assessment of the images.
Detectability for the horizontal line-pair detection task is much lower than for the vertical line pair detection task at locations 1 and 3. This presents a clear example of noise “masquerading” as signal, where the middle and high frequency components of the NPS at locations 1 and 3 coincide closely with the spatial frequencies of the task function along the fy axis. Detectability is the highest at location 4, in qualitative agreement with the example image. Results for FBP reconstruction (not included for reasons of brevity) showed similar trends as in Fig. 8 with regard to location and smoothing parameters with approximately the same level of detectability.
Figure 9 plots the detectability index for the midfrequency and all-frequency task defined in Sec. II D as a function of smoothing parameters in FBP and PL reconstructions of the Elliptical phantom. The plots show calculations at locations 1, 3, and 4 as well as the global average ⟨d′⟩ within the phantom. The magnitude of the optimal global average ⟨d′⟩ in FBP is comparable to that in PL for all tasks considered, demonstrating that PL with a quadratic penalty achieves approximately the same performance as FBP, consistent with experimental observations in other work.62
FIG. 9.
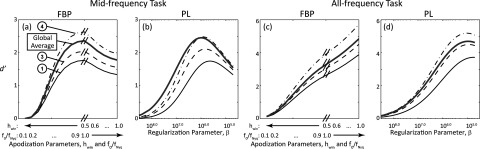
Detectability index computed as a function of smoothing parameters for FBP [(a) and (c)] and PL [(b) and (d)] reconstructions for the midfrequency task [(a) and (b)] and the all-frequency task [(c) and (d)] defined in Sec. II D. The optimal smoothing required for PL is dependent on the location within the reconstruction, while the difference is considerably smaller in FBP.
For the midfrequency task in Fig. 9, an optimal choice of smoothing parameter is observed for both FBP and PL, illustrating the familiar noise-resolution tradeoff: toward the left of the curves, the images are over-smoothed, and task performance is impeded by a lack of spatial resolution; toward the right of the curves, the images are sharper, but task performance is impeded by image noise. For the all-frequency task, maximum detectability occurs at parameter settings associated with higher spatial resolution, shifting the optimum to sharper kernels for FBP (a pure ramp filter or even sharper) and weaker regularization for PL.
The detectability map, d′(x,y), for the midfrequency task is shown in Fig. 10 for both FBP and PL reconstructions of the Circular disk, Elliptical, and Thorax phantoms. The object boundaries (black dotted line) demark the region for computing the global average ⟨d′⟩. Smoothing parameters were chosen to give the best global average ⟨d′⟩ within the object and are indicated on each plot. Overall, the magnitude of d′ is comparable in FBP and PL, though the latter exhibits a somewhat greater range of spatial variability. In the Circular disk phantom, for example, PL exhibits a slightly greater reduction in d′ at the center. Similarly for the Elliptical phantom—a slightly greater reduction in the vicinity of the high-density insert. The greater degree of spatial variability in d′ for PL presents an interesting counterpoint to the variance maps shown in Fig. 4 (where the noise for PL was shown to be more spatially uniform than the FBP case): specifically, whereas the MTF of FBP is shift-invariant to a first-order approximation, the MTF of PL reconstruction not only varies spatially, but does so in a way that may be disadvantageous to the task. For example, comparing the high- and low-density regions in the Elliptical phantom, the difference in d′ in FBP results solely from the difference in noise; however, in PL, not only is the NPS higher in the high density region, but the MTF is reduced, resulting in a stronger decrease in detectability. This effect is more pronounced for tasks involving mid- to high-frequencies due to a greater sensitivity to spatial resolution.
FIG. 10.
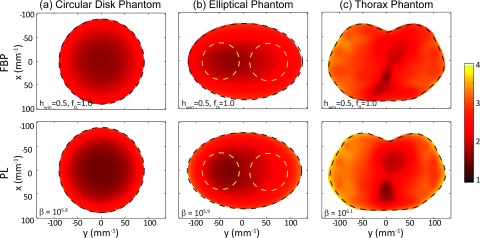
Detectability maps, d′(x, y), computed for FBP and PL reconstructions in each phantom for the midfrequency task. Reconstruction parameters were chosen to maximize the global average ⟨d′⟩.
III.C. Design of an “optimal” regularization map
Looking closely Fig. 9, one notes that the optimal smoothing parameter for PL reconstruction is different among the various locations, suggesting location-dependent noise-resolution tradeoffs. The effect is less pronounced for FBP, since the spatial resolution for FBP is less spatially variant as discussed above. The location-dependent optimal β motivates the design of a spatially varying β map that could potentially improve performance overall. As described in Sec. II E, the spatially varying β map [denoted β*(x,y)] constructed from local optimal β values is shown in Fig. 11: (a) the Elliptical phantom and the vertical line-pair task; (b) the Elliptical phantom and the midfrequency task; and (c) the Thorax phantom and the midfrequency task. The resulting detectability map is shown in Figs. 11(d)–11(f). The global average ⟨d′⟩ resulting from the spatially varying β map is compared to that for a constant β in Figs. 11(g)–11(i). Figures 11(j)–11(l) show the ratio of d′(x,y) from using the spatially varying β map [Fig. 11(d)–11(f)] to the corresponding d′ map from the optimal constant β that gives the maximum ⟨d′⟩ in Fig. 11(g)–11(i). A fairly modest improvement up to ∼10% in detectability is achieved with the spatially varying β map.
FIG. 11.
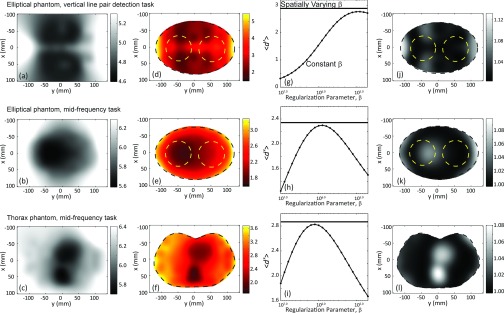
Spatially varying regularization. (a)–(c) Spatially varying β maps designed to maximize d′ at each point in the image. (d)–(f) The resulting detectability maps. (g)–(i) Comparison of the global average ⟨d′⟩ resulting from the spatially varying β map (straight horizontal line) plotted in comparison to ⟨d′⟩ achieved with a constant value of β (plotted as a function of β). A slight improvement in detectability is achieved with the spatially varying β map. (j)–(l) Ratio of detectability index achieved with the spatially varying and the optimal constant β, showing improvement up to ∼10%, particularly in more heavily attenuating regions of the phantom.
IV. DISCUSSION AND CONCLUSIONS
This work investigated the nonuniform noise and resolution characteristics of FBP and PL reconstruction and related the findings to task-based imaging performance. The work yielded at least three advances: explicit extension of cascaded systems to describe the spatially varying (i.e., nonstationary) NPS and detectability index in FBP; extension of task-based imaging performance analysis to penalized likelihood image reconstruction; and a method for designing spatially varying regularization maps in iterative image reconstruction to improve task-based performance.
As illustrated in Fig. 1, the presence of a bowtie filter or other more complex fluence modulation device could be incorporated in the modeling for both FBP and PL. Such devices have been shown to produce more stationary noise and detectability in a water cylinder.16 However, some level of nonstationarity will persist even for well matched bowties or other fluence modulation devices in the presence of objects with complex shapes and heterogeneous structure. The current work did not include a bowtie—consistent with many CBCT imaging systems and to better illustrate the fundamental nonuniform noise and resolution characteristics for purposes of initial investigation.
The cascaded systems analysis model for FBP has been validated extensively in terms of NPS, MTF, and d′ in previous studies.40,59,63 For PL, the work presented above validated theoretical predictions of NPS and MTF in comparison to measurements in simulated data in a variety of phantoms of increasing complexity. Future work will validate such theoretical predictions in comparison to real data, requiring a more realistic forward model accounting for nonidealities in detector response (e.g., blur and additive noise) and a polyenergetic x-ray beam.64 An additional challenge with experimental validation is anticipated to be the large number of acquisitions required for accurate noise estimation. Validation with simulated data was sufficient for initial investigation and offered the advantage of isolating image quality dependence on the object and the reconstruction algorithms apart from other complications that could also cause nonuniform noise and resolution as mentioned in Sec. II A.
Although image quality was examined in both FBP and PL, this work did not intend a strict comparison between the two algorithms. As evident in Figs. 5–7, a fair “matching” of spatial resolution and/or noise in FBP and PL is challenging due to their highly anisotropic nature. Comparison of task-based performance in FBP versus PL should therefore be considered carefully. In volumetric reconstructions especially, the mismatch between the typical axial plane filtering in FDK and the fully 3D regularization in PL should be resolved for fair comparison at matched 3D spatial resolution (e.g., by applying an additional Hann window the z direction in FDK). For the imaging conditions, imaging tasks, and observer models considered in this work, the results suggest comparable task performance between FBP and quadratic PL, which is consistent with experimental observations in other work.62 The advantages of penalized likelihood reconstruction were found to be more apparent in nonquadratic penalties.62 Noise and resolution descriptions for nonquadratic penalties are more challenging due to their image dependence (in contrast to the quadratic case where R is independent of the image). Extension of the theoretical model to such algorithms has been proposed for emission tomography.65 Adaptation of such models to transmission tomography and evaluation in relation to task-based performance is the subject of future work. Other iterative algorithms (e.g., those present on commercial scanners) may also offer superior image quality compared to FBP. The evaluation of such algorithms is a subject of active research.
The assumption of “locality” encompasses a multitude of implications. First, the use of Fourier metrics assumes “spatial locality” within a small neighborhood where the noise is wide-sense stationary, and the system can be assumed to be linear and shift-invariant. The extent over which the locality assumption holds is expected to depend on various factors including the size of the ROI, heterogeneity within the ROI, the object, and the smoothing parameter. An assessment of the degree of spatial locality and its impact on task-based detectability is provided in the Appendix. Second, with respect to detectability index, the locality assumption further implies that the perturbation associated with the signal (stimulus) is small and does not change the local noise and resolution characteristics—analogous to the classic “small signal difference” common to image quality and perception analysis. Third, in the derivation of PSF and covariance in PL reconstruction, the system is locally linearizable.
Optimizing the regularization parameter in statistical reconstruction has been investigated in emission tomography. Fessler proposed a spatially varying β map to enforce more uniform spatial resolution throughout the image.18 Qi et al.36 proposed a method for selecting regularization to optimize the contrast-to-noise ratio. Yendiki and Fessler66,67 further examined the effect of β on detectability in both location-known and location-unknown tasks. The work shown above proposed a simple method for selecting both a constant β and a spatially-varying β map to improve task-based performance. Optimization of PL reconstruction holds particular promise. First, compared to hardware-based fluence modulation, only one set of projections needs to be acquired, and the regularization parameters can then be changed to produce different reconstructions suitable for different tasks. Second, regularization in PL is applied in the reconstruction domain, which imparts greater freedom in differential smoothing within different parts of the image that is not achievable with conventional FBP. One can extend this further to a scenario in which different parts of the image could be optimized to accommodate different tasks. For example, in imaging the thorax, one could design a regularization map that optimizes for low-frequency, low-contrast soft-tissue tumor detection in the mediastinum, and optimizes for high-frequency, high-contrast detection in the lung parenchyma. By further example, in imaging the head, one could design a regularization map that optimizes for low-frequency, low-contrast detection of blood in the brain, while optimizing for high-frequency, high-contrast detection of fracture in the surrounding cranium. Finally, within the general context of “ROI imaging,” one can design a regularization map that optimizes task-based detectability within a specific ROI without regard for the consequences in surrounding regions. For efficient implementation of β map design in practical situations, noise and resolution of PL reconstructions can be estimated using Fourier approximations instead of iterative solutions.68
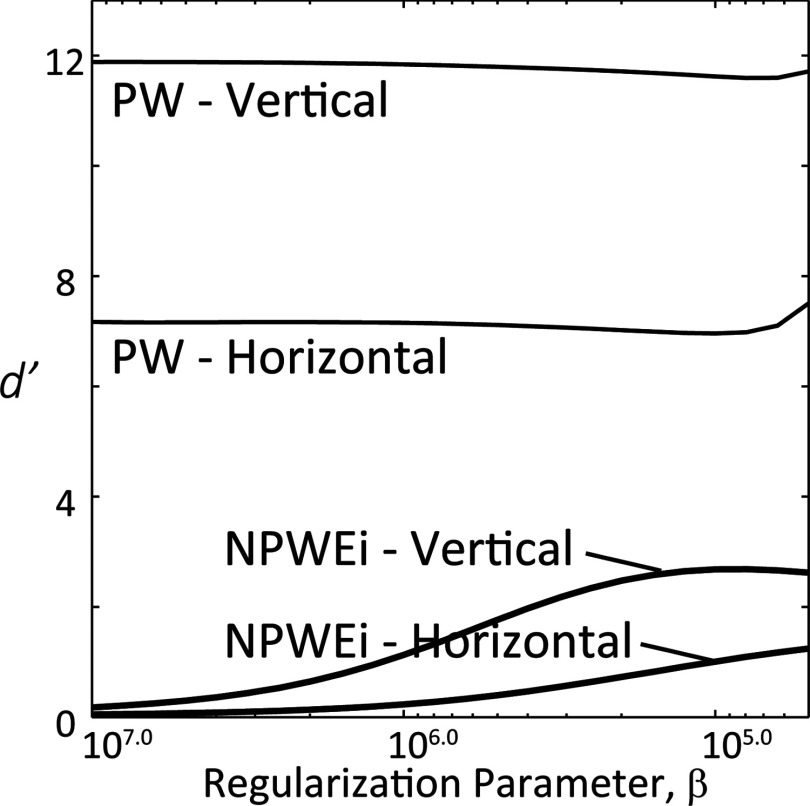
Calculation of task-based detectability in this work used the anthropomorphic NPWEi model, though many observer models could be considered within the analytical framework. Figure 12, for example, illustrates the dependence of d′ on β for the vertical and horizontal line pair detection tasks at location 1 of the Elliptical phantom using the PW observer model [Eq. (11)] in comparison to the NPWEi model. The PW model suggests significantly higher d′ than the NPWEi model, and shows minimal dependence on β, consistent with findings by Yendiki.66,67 The PW model represents the ideal observer for a signal-known exactly, background-known-exactly task, therefore yielding d′ considerably higher than what one might expect from visual inspection of the images in Fig. 9. Such observer models may be useful for optimization when the images are to be analyzed by a computer program which can potentially make use of image information not appreciable by humans. Another popular observer model, the channelized Hotelling observer, has also been shown to exhibit optima dependent on different implementations of channels in emission tomography.66,67,69 The question of which observer model to use for optimization is the subject of ongoing research. In the current work, the NPWEi model demonstrated qualitative agreement with observations in terms of the optimal β, recognizing that more rigorous observer studies are required in future work to validate the model with human performance.
FIG. 12.
Detectability index for the vertical and horizontal line-pair tasks computed as a function of β for the PW and NPWEi observer models. Each case corresponds to Location 1 in the Elliptical phantom. The PW model suggests a much higher level of performance and a lack of optimum, whereas the NPWEi model suggests a stronger dependence of detectability on β, in qualitative agreement with Fig. 8.
ACKNOWLEDGMENTS
The authors extend thanks to Dr. Yoshito Otake, Dr. Adam Wang, and Mr. Ali Uneri (Department of Biomedical Engineering and Department of Computer Science, Johns Hopkins University) for assistance with computational tools for iterative image reconstruction employed in this work. Stimulating discussions with Dr. Angel Pineda regarding task-based assessment of image quality are gratefully acknowledged. Thanks also to Dr. Jerry Prince (Department of Electrical and Computer Engineering, Johns Hopkins University) and Dr. Katsuyuki “Ken” Taguchi (Department of Radiology, Johns Hopkins University) for valuable inputs. This work was supported by NIH Grant No. 2R01-CA-112163.
APPENDIX: ASSESSMENT OF SPATIAL LOCALITY
The use of Fourier metrics assumes that within the local region of analysis, the noise is wide-sense stationary (WSS), and the system is linear and shift-invariant (LSI). The extent to which the locality assumption holds is expected to depend on various factors including the acquisition technique (e.g., mA modulation), the nature of the object (e.g., size, shape, heterogeneity), reconstruction method, and, of course, the size of the ROI. A simple check on the validity of such assumption is to assess the uniformity of noise and resolution at various locations within the ROI. To directly evaluate the effect of the locality assumption on task-based performance, detectability index calculated using the Fourier domain metrics can be compared with that computed using their spatial domain counterparts (viz., system matrix and covariance matrix instead of MTF and NPS) which do not necessarily invoke the LSI or WSS assumptions. The spatial domain d′ for a prewhitening observer model can be calculated according to70,71
| (A1) |
where H is the nvox × nvox system matrix mapping a voxelized representation of an object to its reconstruction, is the spatial domain task function defined as the mean difference between the two hypotheses, and K−1 is the inverse of the covariance matrix. Note that the resolution of the voxelized object may be higher than that of the reconstruction, which is important in avoiding nonlinear partial volume effects for small objects. The mean signal, , was estimated as the difference of the noiseless reconstructions of the object with and without the imaging task inserted at the locations of interest. For FBP reconstruction, the covariance matrix was estimated according to Eq. (22) from a total of 30 000 simulated images. For PL reconstruction, the covariance matrix was calculated according to Eq. (18). The term was solved iteratively70,71 using the conjugate gradient method.
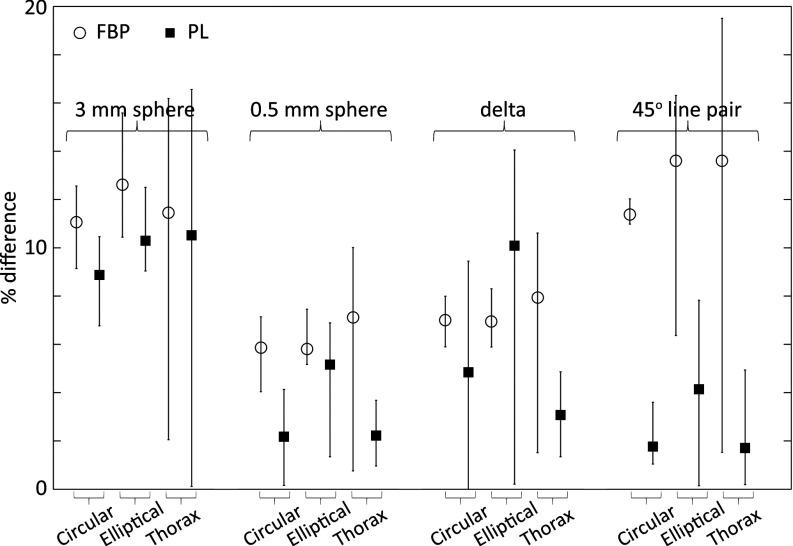
The detectability index calculated using the Fourier and spatial domain methods was compared for four imaging tasks emphasizing different frequency content: (1) a low frequency 3 mm sphere detection task; (2) a low-mid frequency 0.5 mm sphere detection task; (3) an all-frequency delta function detection task; and (4) a high frequency 45° line pair detection task. Imaging tasks were inserted at four locations in the three digital phantoms of Fig. 2, and detectability index was calculated for the prewhitening observer model. For each phantom, the mean [as well as range bars spanning the best-case (min) and worst-case (max)] percent difference in d′ between the two methods over all four locations is summarized in Fig. 13. The smoothing parameters for FBP reconstruction is set to hwin = 0.5 and f0/fNqy = 0.8; the regularization parameter, β, for PL reconstruction is 106. The difference shows a dependence on the imaging task, and the level of agreement between the two methods is typically better in PL reconstructions (mean discrepancy of 5.6%) compared to FBP reconstruction (mean discrepancy of 9.5%). Perhaps surprisingly, the dependence on the shape and heterogeneity of the object was fairly weak, showing a similar level of agreement between spatial and Fourier domain estimates for the Circular, Elliptical, and Thorax phantoms. For all cases considered, the spatial and Fourier domain calculations of d′ agreed to ∼5%–10%. The largest difference observed was 19.5%, and the smallest difference was 0.1%. The advantages and limitations of each approach have been investigated in previous studies.5,70,72 Both can provide meaningful metrics for system performance if applied with recognition of underlying assumptions. Ongoing developments in the spatial domain methods include means of reducing the bias in estimates of d′ when the sample size is small.73–75 In various previous studies aimed at system development and optimization (including this work),76–79 the Fourier approach has been employed for reasons of practicality, computational speed, and the ability to estimate the MTF, NPS, and d′ with a small sample of realizations. The performance of the Fourier approach was found to be reasonable when only a small sample size is available, for example, d′ calculated from 10 samples (in a 49 × 49 ROI) was within 12.0% of that calculated using 30 000 samples (0.5 cm sphere detection task in location 1 of the Thorax phantom). Increasing the sample size to 50 and 100 samples reduced the difference to 2.0% and 0.1%, respectively. Evaluation for other tasks and locations in each phantom yielded similar results.
FIG. 13.
Percentage difference between the Fourier and spatial domain calculations of detectability index using the prewhitening observer model (each computed from 30 000 realizations). Each plot shows the mean and range in percent difference calculated over the four locations in each of the phantoms in Fig. 2. Four imaging tasks were selected to exercise different regions of frequency response. The level of agreement between Fourier and spatial domain detectability calculations depend somewhat on the imaging task, and a higher level of disagreement was observed in FBP than PL, consistent with the higher degree of stationarity in the latter.
REFERENCES
- 1.Barrett H., Gordon S., and Hershel R., “Statistical limitations in transaxial tomography,” Comput. Biol. Med. 6(4), 307–323 (1976). 10.1016/0010-4825(76)90068-8 [DOI] [PubMed] [Google Scholar]
- 2.Faulkner K. and Moores B., “Analysis of x-ray computed tomography images using the noise power spectrum and autocorrelation function,” Phys. Med. Biol. 29(11), 1343–1352 (1984). 10.1088/0031-9155/29/11/003 [DOI] [PubMed] [Google Scholar]
- 3.Kijewski M. F. and Judy P. F., “The noise power spectrum of CT images,” Phys. Med. Biol. 32(5), 565–575 (1987). 10.1088/0031-9155/32/5/003 [DOI] [PubMed] [Google Scholar]
- 4.Hanson K. M., “Detectability in computed tomographic images,” Med. Phys. 6, 441–451 (1979). 10.1118/1.594534 [DOI] [PubMed] [Google Scholar]
- 5.Brunner C. C., Abboud S. F., Hoeschen C., and Kyprianou I. S., “Signal detection and location-dependent noise in cone-beam computed tomography using the spatial definition of the Hotelling SNR,” Med. Phys. 39, 3214–3228 (2012). 10.1118/1.4718572 [DOI] [PubMed] [Google Scholar]
- 6.Zeng R., Petrick N., Gavrielides M. A., and Myers K. J., “Approximations of noise covariance in multi-slice helical CT scans: Impact on lung nodule size estimation,” Phys. Med. Biol. 56(19), 6223–6242 (2011). 10.1088/0031-9155/56/19/005 [DOI] [PubMed] [Google Scholar]
- 7.Wagner R. F. and Weaver K. E., “An assortment of image quality indexes for radiographic film-screen combinations—Can they be resolved?” Proc. SPIE 83–94 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Barrett H. H., “NEQ: Its progenitors and progeny,” Proc. SPIE 72630F–1 72630F–7 (2009). 10.1117/12.817795 [DOI] [Google Scholar]
- 9.Glick S. J., Vedantham S., and Karellas A., “Investigation of optimal kVp settings for CT mammography using a flat-panel imager,” Proc. SPIE 392–402 (2002). 10.1117/12.465581 [DOI] [Google Scholar]
- 10.Reiser I. and Nishikawa R., “Task-based assessment of breast tomosynthesis: Effect of acquisition parameters and quantum noise,” Med. Phys. 37, 1591–1600 (2010). 10.1118/1.3357288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Prakash P., Zbijewski W., Gang G., Ding Y., Stayman J., Yorkston J., Carrino J., and Siewerdsen J., “Task-based modeling and optimization of a cone-beam CT scanner for musculoskeletal imaging,” Med. Phys. 38, 5612–5629 (2011). 10.1118/1.3633937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pineda A. R., Tward D. J., Gonzalez A., and Siewerdsen J. H., “Beyond noise power in 3D computed tomography: The local NPS and off-diagonal elements of the Fourier domain covariance matrix,” Med. Phys. 39, 3240–3252 (2012). 10.1118/1.4705354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baek J. and Pelc N. J., “Local and global 3D noise power spectrum in cone-beam CT system with FDK reconstruction,” Med. Phys. 38, 2122–2131 (2011). 10.1118/1.3556590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baek J. and Pelc N. J., “The noise power spectrum in CT with direct fan beam reconstruction,” Med. Phys. 37, 2074–2081 (2010). 10.1118/1.3378673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bartolac S., Clackdoyle R., Noo F., Siewerdsen J., Moseley D., and Jaffray D., “A local shift-variant Fourier model and experimental validation of circular cone-beam computed tomography artifacts,” Med. Phys. 36, 500–512 (2009). 10.1118/1.3062875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wunderlich A. and Noo F., “Image covariance and lesion detectability in direct fan-beam x-ray computed tomography,” Phys. Med. Biol. 53(10), 2471–2493 (2008). 10.1088/0031-9155/53/10/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fessler J. A., “Statistical image reconstruction methods for transmission tomography,” Handb. Med. Imaging 2, 1–70 (2000). [Google Scholar]
- 18.Fessler J. A. and Rogers W. L., “Spatial resolution properties of penalized-likelihood image reconstruction: Space-invariant tomographs,” IEEE Trans. Image Process. 5(9), 1346–1358 (1996). 10.1109/83.535846 [DOI] [PubMed] [Google Scholar]
- 19.Stayman J. W. and Fessler J. A., “Regularization for uniform spatial resolution properties in penalized-likelihood image reconstruction,” IEEE Trans. Med. Imaging 19(6), 601–615 (2000). 10.1109/42.870666 [DOI] [PubMed] [Google Scholar]
- 20.Stayman J. W. and Fessler J. A., “Compensation for nonuniform resolution using penalized-likelihood reconstruction in space-variant imaging systems,” IEEE Trans. Med. Imaging 23(3), 269–284 (2004). 10.1109/TMI.2003.823063 [DOI] [PubMed] [Google Scholar]
- 21.Evans J. D., Politte D. G., Whiting B. R., O’Sullivan J. A., and Williamson J. F., “Noise-resolution tradeoffs in x-ray CT imaging: A comparison of penalized alternating minimization and filtered backprojection algorithms,” Med. Phys. 38(3), 1444–1458 (2011). 10.1118/1.3549757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wilson J. M., Christianson O. I., Richard S., and Samei E., “A methodology for image quality evaluation of advanced CT systems,” Med. Phys. 40, 031908 (9pp.) (2013). 10.1118/1.4791645 [DOI] [PubMed] [Google Scholar]
- 23.Richard S., Husarik D. B., Yadava G., Murphy S. N., and Samei E., “Towards task-based assessment of CT performance: System and object MTF across different reconstruction algorithms,” Med. Phys. 39, 4115–4122 (2012). 10.1118/1.4725171 [DOI] [PubMed] [Google Scholar]
- 24.Pachon J. H., Yadava G., Pal D., and Hsieh J., “Image quality evaluation of iterative CT reconstruction algorithms: A perspective from spatial domain noise texture measures,” Proc. SPIE 83132K–1 83132K–9 (2012). 10.1117/12.912424 [DOI] [Google Scholar]
- 25.Barrett H. H., Yao J., Rolland J. P., and Myers K. J., “Model observers for assessment of image quality,” Proc. Natl. Acad. Sci. U.S.A. 90(21), 9758–9765 (1993). 10.1073/pnas.90.21.9758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bonetto P., Qi J., and Leahy R. M., “Covariance approximation for fast and accurate computation of channelized Hotelling observer statistics,” IEEE Trans. Nucl. Sci. 47(4), 1567–1572 (2000). 10.1109/23.873017 [DOI] [Google Scholar]
- 27.Dutta J., Ahn S., and Li Q., “Quantitative statistical methods for image quality assessment,” Theranostics 3(10), 741–756 (2013). 10.7150/thno.6815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Frey E. C., Gilland K. L., and Tsui B. M. W., “Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT,” IEEE Trans. Med. Imaging 21(9), 1040–1050 (2002). 10.1109/TMI.2002.804437 [DOI] [PubMed] [Google Scholar]
- 29.Gilland D. R., Tsui B., Metz C. E., Jaszczak R. J., and Perry J. R., “An evaluation of maximum likelihood-expectation maximization reconstruction for SPECT by ROC analysis,” J. Nucl. Med. 33(3), 451–457 (1992). [PubMed] [Google Scholar]
- 30.Karakatsanis N. A., Lodge M. A., Zhou Y., Wahl R. L., and Rahmim A., “Dynamic whole-body PET parametric imaging: II. Task-oriented statistical estimation,” Phys. Med. Biol. 58(20), 7419–7445 (2013). 10.1088/0031-9155/58/20/7419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Llacer J., Veklerov E., Baxter L., Grafton S., Griffeth L., Hawkins R., Hoh C., Mazziotta J., Hoffman E., and Metz C., “Results of a clinical receiver operating characteristic study comparing filtered backprojection and maximum likelihood estimator images in FDG PET studies,” J. Nucl. Med. 34(7), 1198–1203 (1993). [PubMed] [Google Scholar]
- 32.Myers K., Barrett H., Borgstrom M., Patton D., and Seeley G., “Effect of noise correlation on detectability of disk signals in medical imaging,” J. Opt. Soc. Am. A 2(10), 1752–1759 (1985). 10.1364/JOSAA.2.001752 [DOI] [PubMed] [Google Scholar]
- 33.Qi J., “Optimization of PET system design for lesion detection,” IEEE Trans. Nucl. Sci. 48(4), 1470–1476 (2001). 10.1109/23.958382 [DOI] [Google Scholar]
- 34.Qi J. and Huesman R. H., “Theoretical study of lesion detectability of MAP reconstruction using computer observers,” IEEE Trans. Med. Imaging 20(8), 815–822 (2001). 10.1109/42.938249 [DOI] [PubMed] [Google Scholar]
- 35.Qi J. and Huesman R. H., “Penalized maximum-likelihood image reconstruction for lesion detection,” Phys. Med. Biol. 51(16), 4017–4029 (2006). 10.1088/0031-9155/51/16/009 [DOI] [PubMed] [Google Scholar]
- 36.Qi J. and Leahy R. M., “A theoretical study of the contrast recovery and variance of map reconstructions with applications to the selection of smoothing parameters,” Nuclear Science Symposium Conference Record (IEEE, 1998), Vol. 3, pp. 2078–2085 [Google Scholar]
- 37.Yang L., Zhou J., and Qi J., “Regularization design for breast lesion detection in penalized maximum likelihood image reconstruction,” in Proceedings of the 9th IEEE International Symposium on Biomedical Imaging (ISBI) (IEEE, 2012), pp. 626–629 [Google Scholar]
- 38.Siewerdsen J., Antonuk L., El-Mohri Y., Yorkston J., Huang W., and Cunningham I., “Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology,” Med. Phys. 25, 614–628 (1998). 10.1118/1.598243 [DOI] [PubMed] [Google Scholar]
- 39.Siewerdsen J. H., Antonuk L. E., El Mohri Y., Yorkston J., Huang W., Boudry J. M., and Cunningham I. A., “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 24(1), 71–89 (1997). 10.1118/1.597919 [DOI] [PubMed] [Google Scholar]
- 40.Tward D. J. and Siewerdsen J. H., “Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT,” Med. Phys. 35(12), 5510–5529 (2008). 10.1118/1.3002414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fessler J. A., “Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): Applications to tomography,” IEEE Trans. Image Process. 5(3), 493–506 (1996). 10.1109/83.491322 [DOI] [PubMed] [Google Scholar]
- 42.Wilson D. W., “Noise and resolution properties of FB and Ml-Em reconstructed spect images” Ph.D. thesis (The University of North Carolina at Chapel Hill, 1994). [Google Scholar]
- 43.Wu M. and Fessler J. A., “GPU acceleration of 3D forward and backward projection using separable footprints for x-ray CT image reconstruction,” in Proceedings of the International Meeting on Fully 3D Image Reconstruction in Radiology and Nuclear Medicine (Potsdam, Germany, 2011). [Google Scholar]
- 44.Bartolac S., Graham S., Siewerdsen J., and Jaffray D., “Fluence field optimization for noise and dose objectives in CT,” Med. Phys. 38, S2–S17 (2011). 10.1118/1.3574885 [DOI] [PubMed] [Google Scholar]
- 45.Galvin J. M., Chen X.-G., and Smith R. M., “Combining multileaf fields to modulate fluence distributions,” Int. J. Radiat. Oncol., Biol., Phys. 27(3), 697–705 (1993). 10.1016/0360-3016(93)90399-G [DOI] [PubMed] [Google Scholar]
- 46.Richard S., Siewerdsen J., Jaffray D., Moseley D., and Bakhtiar B., “Generalized DQE analysis of radiographic and dual-energy imaging using flat-panel detectors,” Med. Phys. 32, 1397–1413 (2005). 10.1118/1.1901203 [DOI] [PubMed] [Google Scholar]
- 47.Burgess A. E., Li X., and Abbey C. K., “Visual signal detectability with two noise components: Anomalous masking effects,” J. Opt. Soc. Am. A Opt. Image Sci. Vis. 14(9), 2420–2442 (1997). 10.1364/JOSAA.14.002420 [DOI] [PubMed] [Google Scholar]
- 48.Gang G. J., Lee J., Stayman J. W., Tward D. J., Zbijewski W., Prince J. L., and Siewerdsen J. H., “Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance,” Med. Phys. 38, 1754–1768 (2011). 10.1118/1.3560428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Stayman J. W., Zbijewski W., Tilley S., and Siewerdsen J. H., “Generalized least-squares CT reconstruction with detector blur and correlated noise models,” Proc. SPIE 903335–1 903335–6 (2013). 10.1117/12.2043067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pan X. and Yu L., “Image reconstruction with shift-variant filtration and its implication for noise and resolution properties in fan-beam computed tomography,” Med. Phys. 30, 590–600 (2003). 10.1118/1.1556608 [DOI] [PubMed] [Google Scholar]
- 51.Press W., Teukolsky S., Vetterling W., and Flannery B., Numerical Recipes in C++ (Cambridge University Press, Cambridge, England, 2002). [Google Scholar]
- 52.Feldkamp L., Davis L., and Kress J., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1(6), 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- 53.Kak A. C. and Slaney M., Principles of Computerized Tomographic Imaging (Society for Industrial and Applied Mathematics, Philadelphia, PA, 2001). [Google Scholar]
- 54.Fessler J. A. and Erdogan H., “A paraboloidal surrogates algorithm for convergent penalized-likelihood emission image reconstruction,” Nuclear Science Symposium, 1998. Conference Record (IEEE, 1998), pp. 1132–1135 [Google Scholar]
- 55.Erdogan H. and Fessler J. A., “Ordered subsets algorithms for transmission tomography,” Phys. Med. Biol. 44(11), 2835–2851 (1999). 10.1088/0031-9155/44/11/311 [DOI] [PubMed] [Google Scholar]
- 56.Wunderlich A. and Noo F., “Band-restricted estimation of noise variance in filtered backprojection reconstructions using repeated scans,” IEEE Trans. Med. Imaging 29(5), 1097–1113 (2010). 10.1109/TMI.2009.2034961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Siewerdsen J., Cunningham I., and Jaffray D., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 29, 2655–2671 (2002). 10.1118/1.1513158 [DOI] [PubMed] [Google Scholar]
- 58.Wilson D. and Tsui B., “Spacial resolution properties of FB and ML-EM reconstruction methods,” Nuclear Science Symposium and Medical Imaging Conference, Conference Record (IEEE, 1993), pp. 1189–1193 [Google Scholar]
- 59.Gang G. J., Zbijewski W., Stayman J. W., and Siewerdsen J. H., “Cascaded systems analysis of noise and detectability in dual-energy cone-beam CT,” Med. Phys. 39, 5145–5156 (2012). 10.1118/1.4736420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Siewerdsen J. H. and Jaffray D. A., “Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography),” Med. Phys. 27, 1903–1914 (2000). 10.1118/1.1286590 [DOI] [PubMed] [Google Scholar]
- 61.Powell M. J., “Radial basis functions for multivariable interpolation: A review,” Algorithms for Approximation (Clarendon, Oxford, 1987). [Google Scholar]
- 62.Wang A. S., Schafer S., Stayman J. W., Otake Y., Sussman M. S., Khanna A. J., Gallia G. L., and Siewerdsen J. H., “Soft-tissue imaging in low-dose, C-arm cone-beam CT using statistical image reconstruction,” Proc. SPIE 86681F–1 86681F–7 (2013). 10.1117/12.2008421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Richard S. and Siewerdsen J. H., “Comparison of model and human observer performance for detection and discrimination tasks using dual-energy x-ray images,” Med. Phys. 35(11), 5043–5053 (2008). 10.1118/1.2988161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Nuyts J., De Man B., Fessler J. A., Zbijewski W., and Beekman F. J., “Modelling the physics in the iterative reconstruction for transmission computed tomography,” Phys. Med. Biol. 58(12), R63–R96 (2013). 10.1088/0031-9155/58/12/R63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ahn S. and Leahy R. M., “Spatial resolution properties of nonquadratically regularized image reconstruction for PET,” in Proceedings of the 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006 (IEEE, 2006), pp. 287–290 [Google Scholar]
- 66.Yendiki A. and Fessler J. A., “Analysis of observer performance in known-location tasks for tomographic image reconstruction,” IEEE Trans. Med. Imaging 25(1), 28–41 (2006). 10.1109/TMI.2005.859714 [DOI] [PubMed] [Google Scholar]
- 67.Yendiki A. and Fessler J. A., “Analysis of observer performance in unknown-location tasks for tomographic image reconstruction,” J. Opt. Soc. Am. A 24(12), B99–B109 (2007). 10.1364/JOSAA.24.000B99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Stayman J. W. and Fessler J. A., “Efficient calculation of resolution and covariance for penalized-likelihood reconstruction in fully 3-D SPECT,” IEEE Trans. Med. Imaging 23(12), 1543–1556 (2004). 10.1109/TMI.2004.837790 [DOI] [PubMed] [Google Scholar]
- 69.Fessler J. A. and Yendiki A., “Channelized Hotelling observer performance for penalized-likelihood image reconstruction,” Nuclear Science Symposium Conference Record (IEEE, 2002), pp. 1040–1044 [Google Scholar]
- 70.Barrett H. H. M. and Myers K. J., Foundations of Image Science (Wiley-Interscience, Hoboken, NJ, 2004). [Google Scholar]
- 71.Barrett H. H., Myers K. J., Gallas B. D., Clarkson E., and Zhang H., “Megalopinakophobia: Its symptoms and cures,” Proc. SPIE 299–307 (2001). 10.1117/12.430869 [DOI] [Google Scholar]
- 72.Pineda A. R., Schweiger M., Arridge S. R., and Barrett H. H., “Information content of data types in time-domain optical tomography,” J. Opt. Soc. Am. A 23(12), 2989–2996 (2006). 10.1364/JOSAA.23.002989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Sanchez A. A., Sidky E. Y., Reiser I., and Pan X., “Comparison of human and Hotelling observer performance for a fan-beam CT signal detection task,” Med. Phys. 40(3), 031104 (9pp.) (2013). 10.1118/1.4789590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Witten J. M., Park S., and Myers K. J., “Partial least squares: A method to estimate efficient channels for the ideal observers,” IEEE Trans. Med. Imaging 29(4), 1050–1058 (2010). 10.1109/TMI.2010.2041514 [DOI] [PubMed] [Google Scholar]
- 75.Wunderlich A. and Noo F., “New theoretical results on channelized Hotelling observer performance estimation with known difference of class means,” IEEE Trans. Nucl. Sci. 60(1), 182–193 (2013). 10.1109/TNS.2012.2227340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Cunningham I. A. and Shaw R., “Signal-to-noise optimization of medical imaging systems,” J. Opt. Soc. Am. A 16(3), 621–632 (1999). 10.1364/JOSAA.16.000621 [DOI] [Google Scholar]
- 77.Maidment A. D., Ullberg C., Lindman K., Adelöw L., Egerström J., Eklund M., Francke T., Jordung U., Kristoffersson T., and Lindqvist L., “Evaluation of a photon-counting breast tomosynthesis imaging system,” Proc. SPIE 61420B–1 61420B–11 (2006). 10.1117/12.654651 [DOI] [Google Scholar]
- 78.Zhao W., Zhao B., Fisher P. R., Warmoes P., Mertelmeier T., and Orman J., “Optimization of detector operation and imaging geometry for breast tomosynthesis,” Proc. SPIE 65101M–1 65101M–12 (2007). 10.1117/12.713718 [DOI] [Google Scholar]
- 79.Acciavatti R. J. and Maidment A. D., “Optimization of phosphor-based detector design for oblique x-ray incidence in digital breast tomosynthesis,” Med. Phys. 38(11), 6188–6202 (2011). 10.1118/1.3639999 [DOI] [PMC free article] [PubMed] [Google Scholar]