Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1995 Aug 29;92(18):8438–8442. doi: 10.1073/pnas.92.18.8438

Conformation, energy, and folding ability of selected amino acid sequences.

M Sasai 1
PMCID: PMC41172  PMID: 7667308

Abstract

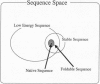
Evolutionary selection of sequences is studied with a knowledge-based Hamiltonian to find the design principle for folding to a model protein structure. With sequences selected by naive energy minimization, the model structure tends to be unstable and the folding ability is low. Sequences with high folding ability have only the low-lying energy minimum but also an energy landscape which is similar to that found for the native sequence over a wide region of the conformation space. Though there is a large fluctuation in foldable sequences, the hydrophobicity pattern and the glycine locations are preserved among them. Implications of the design principle for the molecular mechanism of folding are discussed.

Full text

PDF

Images in this article

8442Fig. 6
on p.8442

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bowie J. U., Lüthy R., Eisenberg D. A method to identify protein sequences that fold into a known three-dimensional structure. Science. 1991 Jul 12;253(5016):164–170. doi: 10.1126/science.1853201. [DOI] [PubMed] [Google Scholar]
  2. Bryngelson J. D., Wolynes P. G. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci U S A. 1987 Nov;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Camacho C. J., Thirumalai D. Kinetics and thermodynamics of folding in model proteins. Proc Natl Acad Sci U S A. 1993 Jul 1;90(13):6369–6372. doi: 10.1073/pnas.90.13.6369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Dill K. A., Fiebig K. M., Chan H. S. Cooperativity in protein-folding kinetics. Proc Natl Acad Sci U S A. 1993 Mar 1;90(5):1942–1946. doi: 10.1073/pnas.90.5.1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Friedrichs M. S., Goldstein R. A., Wolynes P. G. Generalized protein tertiary structure recognition using associative memory Hamiltonians. J Mol Biol. 1991 Dec 20;222(4):1013–1034. doi: 10.1016/0022-2836(91)90591-s. [DOI] [PubMed] [Google Scholar]
  6. Go N. Theoretical studies of protein folding. Annu Rev Biophys Bioeng. 1983;12:183–210. doi: 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
  7. Goldstein R. A., Luthey-Schulten Z. A., Wolynes P. G. Optimal protein-folding codes from spin-glass theory. Proc Natl Acad Sci U S A. 1992 Jun 1;89(11):4918–4922. doi: 10.1073/pnas.89.11.4918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hendlich M., Lackner P., Weitckus S., Floeckner H., Froschauer R., Gottsbacher K., Casari G., Sippl M. J. Identification of native protein folds amongst a large number of incorrect models. The calculation of low energy conformations from potentials of mean force. J Mol Biol. 1990 Nov 5;216(1):167–180. doi: 10.1016/S0022-2836(05)80068-3. [DOI] [PubMed] [Google Scholar]
  9. Jones D. T., Taylor W. R., Thornton J. M. A new approach to protein fold recognition. Nature. 1992 Jul 2;358(6381):86–89. doi: 10.1038/358086a0. [DOI] [PubMed] [Google Scholar]
  10. Lau K. F., Dill K. A. Theory for protein mutability and biogenesis. Proc Natl Acad Sci U S A. 1990 Jan;87(2):638–642. doi: 10.1073/pnas.87.2.638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Leopold P. E., Montal M., Onuchic J. N. Protein folding funnels: a kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci U S A. 1992 Sep 15;89(18):8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lüthy R., Bowie J. U., Eisenberg D. Assessment of protein models with three-dimensional profiles. Nature. 1992 Mar 5;356(6364):83–85. doi: 10.1038/356083a0. [DOI] [PubMed] [Google Scholar]
  13. Sali A., Shakhnovich E., Karplus M. How does a protein fold? Nature. 1994 May 19;369(6477):248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
  14. Sander C., Schneider R. Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins. 1991;9(1):56–68. doi: 10.1002/prot.340090107. [DOI] [PubMed] [Google Scholar]
  15. Sasai M, Wolynes PG. Molecular theory of associative memory Hamiltonian models of protein folding. Phys Rev Lett. 1990 Nov 19;65(21):2740–2743. doi: 10.1103/PhysRevLett.65.2740. [DOI] [PubMed] [Google Scholar]
  16. Sasai M, Wolynes PG. Unified theory of collapse, folding, and glass transitions in associative-memory Hamiltonian models of proteins. Phys Rev A. 1992 Dec 15;46(12):7979–7997. doi: 10.1103/physreva.46.7979. [DOI] [PubMed] [Google Scholar]
  17. Shakhnovich E. I., Gutin A. M. Engineering of stable and fast-folding sequences of model proteins. Proc Natl Acad Sci U S A. 1993 Aug 1;90(15):7195–7199. doi: 10.1073/pnas.90.15.7195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Shakhnovich E. I., Gutin A. M. Influence of point mutations on protein structure: probability of a neutral mutation. J Theor Biol. 1991 Apr 21;149(4):537–546. doi: 10.1016/s0022-5193(05)80097-9. [DOI] [PubMed] [Google Scholar]
  19. Shakhnovich EI. Proteins with selected sequences fold into unique native conformation. Phys Rev Lett. 1994 Jun 13;72(24):3907–3910. doi: 10.1103/PhysRevLett.72.3907. [DOI] [PubMed] [Google Scholar]
  20. Sippl M. J. Calculation of conformational ensembles from potentials of mean force. An approach to the knowledge-based prediction of local structures in globular proteins. J Mol Biol. 1990 Jun 20;213(4):859–883. doi: 10.1016/s0022-2836(05)80269-4. [DOI] [PubMed] [Google Scholar]
  21. Wilmanns M., Eisenberg D. Three-dimensional profiles from residue-pair preferences: identification of sequences with beta/alpha-barrel fold. Proc Natl Acad Sci U S A. 1993 Feb 15;90(4):1379–1383. doi: 10.1073/pnas.90.4.1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Yue K., Dill K. A. Inverse protein folding problem: designing polymer sequences. Proc Natl Acad Sci U S A. 1992 May 1;89(9):4163–4167. doi: 10.1073/pnas.89.9.4163. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES