Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Aug 1;4:5918. doi: 10.1038/srep05918

A new method for constructing networks from binary data

Claudia D van Borkulo 1,2,a, Denny Borsboom 2, Sacha Epskamp 2, Tessa F Blanken 2, Lynn Boschloo 1, Robert A Schoevers 1, Lourens J Waldorp 2
PMCID: PMC4118196  PMID: 25082149

Abstract

Network analysis is entering fields where network structures are unknown, such as psychology and the educational sciences. A crucial step in the application of network models lies in the assessment of network structure. Current methods either have serious drawbacks or are only suitable for Gaussian data. In the present paper, we present a method for assessing network structures from binary data. Although models for binary data are infamous for their computational intractability, we present a computationally efficient model for estimating network structures. The approach, which is based on Ising models as used in physics, combines logistic regression with model selection based on a Goodness-of-Fit measure to identify relevant relationships between variables that define connections in a network. A validation study shows that this method succeeds in revealing the most relevant features of a network for realistic sample sizes. We apply our proposed method to estimate the network of depression and anxiety symptoms from symptom scores of 1108 subjects. Possible extensions of the model are discussed.

Research on complex networks is growing and statistical possibilities to analyse network structures have been developed to great success in the past decade1,2,3,4,5. Networks are studied in many different scientific disciplines: from physics and mathematics to the social sciences and biology. Examples of topics that have recently been subjected to network approaches include intelligence, psychopathology, and attitudes6,7,8,9,10. Taking psychopathology as an example, nodes (elements) in a depression network may involve symptoms, whereas edges (connections) indicate to what extent symptoms influence each other. The structure of such a network, however, is unknown due to the absence of a sufficiently formalised theory of depression. Consequently, the network structure has to be extracted from information in data. The challenging question is how to extract it.

Methods that are currently used to discover network structures in the field of psychology are based on correlations, partial correlations, and patterns of conditional independencies7,11,12,13. Although such techniques are useful to get a first impression of the data, they suffer from a number of drawbacks. Correlations and partial correlations, for example, require assumptions of linearity and normality, which are rarely satisfied in psychology, and necessarily false for binary data. Algorithms like the PC-algorithm14,15, which can be used to search for causal structure, often assume that networks are directed and acyclic, which is unlikely in many psychological cases. Finally, in any of these methods, researchers rely on arbitrary cutoffs to determine whether a network connection is present or not. A common way to determine such cutoff-values is through null-hypothesis testing, which often depends on the arbitrary level of significance of α = .05. In the case of network analysis, however, one often has to execute a considerable number of significance tests. One can either ignore this, which will lead to a multiple testing problem, or deal with it through Bonferonni corrections, (local) false discovery rate, or other methods16,17,18, which will lead to a loss of power.

For continuous data with multivariate Gaussian distributed observations, the inverse covariance matrix is a representation of an undirected network (also called a Markov Random Field19,20). A zero entry in the inverse covariance matrix then corresponds to the presence of conditional independence between the relevant variables, given the other variables21. To find the simplest model that explains the data as adequately as possible according to the principle of parsimony, different strategies are investigated to find a sparse approximation of the inverse covariance matrix. Such a sparse approximation can be obtained by imposing an ℓ1-penalty (lasso) on the estimation of the inverse covariance matrix13,22,23. The lasso ensures shrinkage of partial correlations and puts others exactly to zero24. A different take involves estimating the neighborhood of each variable individually, as in standard regression with an ℓ 1-penalty25, instead of using the inverse covariance matrix. This is an approximation to the ℓ1-penalised inverse covariance matrix. This Gaussian approximation method is an interesting alternative: it is computationally efficient and asymptotically consistent25.

In psychology and educational sciences, variables are often not Gaussian but discrete. Although discrete Markov Random Fields are infamous for their computational intractability, we propose a binary equivalent of the Gaussian approximation method that involves regressions and is computationally efficient26. This method for binary data, which we describe in more detail in the Methods section, is based on the Ising model19,27. In this model, variables can be in either of two states, and interactions are at most pairwise. The model contains two node-specific parameters: the interaction parameter βjk, which represents the strength of the interaction between variable j and k, and the node parameter τj, which represents the autonomous disposition of the variable to take the value one, regardless of neighbouring variables. Put simply, the proposed procedure in our model estimates these parameters with logistic regressions: iteratively, one variable is regressed on all others. However, to obtain sparsity, an ℓ1-penalty is imposed on the regression coefficients. The level of shrinkage depends on the penalty parameter of the lasso. The penalty parameter has to be selected carefully, otherwise the lasso will not lead to the true underlying network – the data generating network25. The extended Bayesian Information Criterion28 (EBIC) has been shown to lead to the true network when sample size grows and results in a moderately good positive selection rate, but performs distinctly better than other measures in having a low false positive rate29.

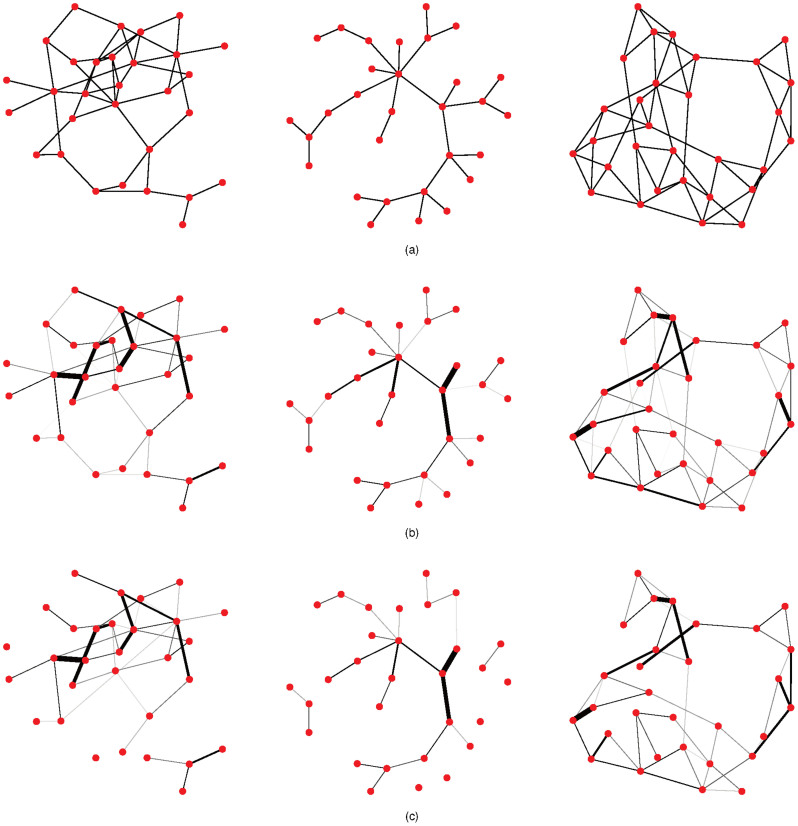
Using this approach, we have developed a coherent methodology that we call eLasso. The methodology is implemented in the freely available R package IsingFit (http://cran.r-project.org/web/packages/IsingFit/IsingFit.pdf). Using simulated weighted networks, the present paper studies the performance of this procedure by investigating to what extent the methodology succeeds in estimating networks from binary data. We simulate data from different network architectures (i.e., true networks; see Figures 1a and 1b), and then use the resulting data as input for eLasso. The network architectures used in this study involve random, scale-free, and small word networks30,31,32. In addition, we varied the size of the networks by including conditions with 10, 20, 30, and 100 nodes, and involve three levels of connectivity (low, medium, and high). Finally, we varied the sample size between 100, 500, 1000, and 2000 observations. After applying eLasso, we compare the estimated networks (Figure 1c) to the true networks. We show that eLasso reliably estimates network structures, and demonstrate the utility of our method by applying it to psychopathology data.

Figure 1. Examples of networks with 30 nodes in the simulation study.

Figure 1

Open in a new tab

(a) Generated networks. From left to right: random network (probability of an extra connection is 0.1), scale-free network (power of preferential attachment is 1) and small world network (rewiring probability is 0.1). (b) Weighted versions of (a) that are used to generate data (true networks). (c) Estimated networks.

Results

Validation study

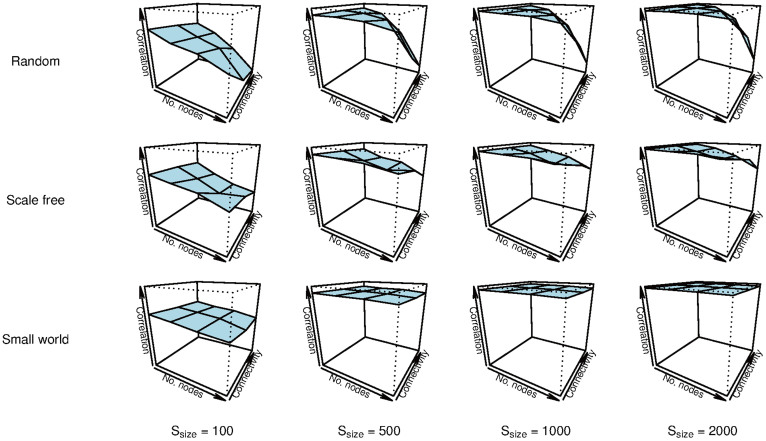
The estimated networks show high concordance with the true networks used to generate the data (Figure 2). Average correlations between true and estimated coefficients are high in all conditions with 500 observations or more (M = .883, sd = .158, see Table 1). In the smallest sample size condition involving only 100 observations, the estimated networks seems to deviate somewhat more from the true networks, but even in this case the most important connections are recovered and the average correlation between generating and estimated networks remains substantial (M = .556, sd = .155). Thus, the overall performance of eLasso is adequate.

Figure 2. Mean correlations (vertical axes) of the upper triangles of the weighted adjacency matrices of true and estimated networks of 100 simulations with random, scale-free, and small world networks for sample sizes ssize = 100, 500, 1000, and 2000, with number of nodes nnodes = 10, 20, 30, and 100.

Figure 2

Open in a new tab

We used three levels of connectivity (random networks: probability of an extra connection Pconn = .1, .2, and .3; scale-free networks: power of preferential attachment Pattach = 1, 2, and 3; small world networks: rewiring probability of Prewire = .1, .5, and 1). For the condition with 100 nodes, we used different levels of connectivity for random and scale-free networks in order to obtain more realistic networks (random networks: Pconn = .05, .1, and .15; scale-free networks: Pattach = 1, 1.25, and 1.5).

Table 1. Correlations as a measure of performance of eLasso. Correlations are computed between upper triangle of weighted adjacency matrix of data generating network and estimated network. Data is simulated under various conditions (ssize, nnodes, connectedness (p (probability of a connection), pa (preferential attachment), pr (probability of rewiring)) when the AND-rule and γ = .25 is applied. For networks with 100 nodes, deviating levels of connectedness are displayed between brackets. Results of applying eLasso with the OR-rule and γ = 0 are displayed between brackets.

    Random Scale-free Small world
ssize nnodes p = .1(.05) p = .2(.10) p = .3(.15) pa = 1 pa = 2(1.25) pa = 3(1.5) pr = .1 pr = .5 pr = 1
100 10 0.769 (0.693) 0.730 (0.750) 0.676 (0.736) 0.696 (0.735) 0.693 (0.701) 0.671 (0.734) 0.688 (0.730) 0.673 (0.711) 0.671 (0.723)
  20 0.659 (0.700) 0.604 (0.689) 0.550 (0.573) 0.649 (0.697) 0.568 (0.603) 0.516 (0.538) 0.654 (0.702) 0.642 (0.696) 0.623 (0.673)
  30 0.613 (0.700) 0.506 (0.583) 0.337 (0.330) 0.610 (0.666) 0.423 (0.457) 0.393 (0.356) 0.612 (0.732) 0.608 (0.672) 0.596 (0.671)
  100 0.487 (0.575) 0.144 (0.170) 0.045 (0.050) 0.504 (0.613) 0.453 (0.523) 0.326 (0.392) 0.583 (0.663) 0.520 (0.631) 0.534 (0.623)
500 10 0.928 (0.935) 0.936 (0.943) 0.930 (0.943) 0.925 (0.944) 0.916 (0.946) 0.900 (0.953) 0.930 (0.940) 0.926 (0.932) 0.929 (0.940)
  20 0.932 (0.939) 0.917 (0.927) 0.859 (0.883) 0.913 (0.923) 0.810 (0.878) 0.786 (0.831) 0.925 (0.942) 0.917 (0.926) 0.912 (0.931)
  30 0.919 (0.934) 0.860 (0.881) 0.594 (0.641) 0.894 (0.916) 0.728 (0.743) 0.742 (0.696) 0.923 (0.935) 0.908 (0.925) 0.911 (0.922)
  100 0.863 (0.883) 0.442 (0.451) 0.114 (0.111) 0.843 (0.873) 0.761 (0.805) 0.579 (0.658) 0.908 (0.925) 0.888 (0.911) 0.884 (0.902)
1000 10 0.972 (0.961) 0.965 (0.973) 0.968 (0.971) 0.959 (0.971) 0.960 (0.975) 0.957 (0.969) 0.964 (0.971) 0.965 (0.969) 0.966 (0.968)
  20 0.966 (0.970) 0.958 (0.965) 0.921 (0.940) 0.948 (0.969) 0.904 (0.937) 0.893 (0.920) 0.964 (0.968) 0.958 (0.965) 0.961 (0.965)
  30 0.963 (0.966) 0.915 (0.925) 0.702 (0.752) 0.940 (0.954) 0.798 (0.843) 0.821 (0.800) 0.964 (0.966) 0.957 (0.962) 0.958 (0.963)
  100 0.927 (0.942) 0.588 (0.586) 0.161 (0.164) 0.913 (0.921) 0.819 (0.86) 0.676 (0.682) 0.957 (0.963) 0.946 (0.954) 0.944 (0.952)
2000 10 0.975 (0.978) 0.985 (0.985) 0.985 (0.986) 0.982 (0.988) 0.983 (0.986) 0.976 (0.986) 0.983 (0.985) 0.982 (0.983) 0.984 (0.984)
  20 0.984 (0.985) 0.980 (0.983) 0.961 (0.967) 0.978 (0.975) 0.926 (0.928) 0.930 (0.936) 0.985 (0.985) 0.981 (0.983) 0.98 (0.982)
  30 0.983 (0.983) 0.961 (0.959) 0.804 (0.818) 0.974 (0.984) 0.855 (0.892) 0.836 (0.851) 0.983 (0.984) 0.979 (0.982) 0.977 (0.982)
  100 0.963 (0.969) 0.693 (0.711) 0.222 (0.227) 0.958 (0.962) 0.881 (0.868) 0.681 (0.700) 0.979 (0.981) 0.975 (0.977) 0.973 (0.976)
Open in a new tab

More detailed information about eLasso's performance is given by sensitivity and specificity. Sensitivity expresses the proportion of true connections which are correctly estimated as present, and is also known as the true positive rate. Specificity corresponds to the proportion of absent connections which are correctly estimated as zero, and is also known as the true negative rate. It has been shown that sensitivity and specificity tend to 1 when sample sizes are large enough29,33; the question is for which sample sizes we come close. Overall, specificity is very close to one across all conditions (M = .990, sd = .014) with somewhat lower specificity scores for the largest and most dense random networks (see Table 2). Overall, sensitivity is lower (M = .463, sd = .238) but becomes moderate for conditions involving more than 100 observations (M = .568, sd = .171). The reason that sensitivity is lower than specificity lies in the use of the penalty function (lasso); to manage the size of the computational problem, eLasso tends to suppress small but nonzero connections towards zero. Thus, lower sensitivity values mainly reflect the fact that very weak connections are set to zero; however, the important connections are almost aways correctly identified. In addition, the specificity results indicate that there are very few false positives in the estimated networks; thus, eLasso handles the multiple testing problem very well. Figure 1 nicely illustrates these results: almost all estimated connections in Figure 1c are also present in the generating network depicted in Figure 1b (high specificity), but weaker connections in the original network are underestimated (low sensitivity).

Table 2. Sensitivity and specificity, as a measure of performance of eLasso. Data is simulated under various conditions (ssize, nnodes, connectedness (p (probability of a connection), pa (preferential attachment), pr (probability of rewiring)) when the AND-rule and γ = .25 is applied. For networks with 100 nodes, deviating levels of connectedness are displayed between brackets. Results of applying eLasso with the OR-rule and γ = 0 are displayed between brackets.

      Random Scale-free Small world
ssize nnodes   p = .1(.05) p = .2(.10) p = .3(.15) pa = 1 pa = 2(1.25) pa = 3(1.5) pr = .1 pr = .5 pr = 1
100 10 SEN 0.256 (0.348) 0.241 (0.395) 0.229 (0.409) 0.221 (0.363) 0.184 (0.380) 0.172 (0.397) 0.253 (0.458) 0.257 (0.412) 0.260 (0.434)
    SPE 0.997 (0.968) 0.996 (0.950) 0.991 (0.929) 0.997 (0.953) 0.994 (0.958) 0.997 (0.969) 0.989 (0.893) 0.988 (0.912) 0.987 (0.907)
  20 SEN 0.183 (0.324) 0.166 (0.339) 0.173 (0.339) 0.168 (0.315) 0.104 (0.288) 0.074 (0.305) 0.188 (0.359) 0.189 (0.349) 0.168 (0.342)
    SPE 0.998 (0.976) 0.997 (0.961) 0.991 (0.933) 0.998 (0.978) 0.998 (0.986) 0.999 (0.987) 0.997 (0.960) 0.995 (0.962) 0.997 (0.958)
  30 SEN 0.146 (0.295) 0.128 (0.307) 0.118 (0.242) 0.146 (0.269) 0.064 (0.186) 0.044 (0.126) 0.160 (0.328) 0.147 (0.287) 0.144 (0.305)
    SPE 0.999 (0.982) 0.996 (0.956) 0.982 (0.922) 0.999 (0.986) 0.999 (0.99) 0.999 (0.991) 0.999 (0.976) 0.999 (0.978) 0.999 (0.976)
  100 SEN 0.080 (0.186) 0.056 (0.132) 0.031 (0.134) 0.081 (0.185) 0.067 (0.139) 0.040 (0.085) 0.121 (0.238) 0.087 (0.205) 0.092 (0.195)
    SPE 1.000 (0.995) 0.990 (0.962) 0.983 (0.904) 1.000 (0.997) 1.0000 (0.997) 1.000 (0.998) 1.000 (0.995) 1.000 (0.995) 1.000 (0.995)
500 10 SEN 0.550 (0.649) 0.551 (0.672) 0.617 (0.704) 0.561 (0.687) 0.501 (0.713) 0.499 (0.734) 0.650 (0.726) 0.628 (0.765) 0.623 (0.757)
    SPE 0.998 (0.975) 0.993 (0.945) 0.982 (0.922) 0.996 (0.957) 0.997 (0.958) 0.995 (0.966) 0.953 (0.879) 0.964 (0.869) 0.964 (0.862)
  20 SEN 0.539 (0.633) 0.537 (0.678) 0.527 (0.643) 0.492 (0.613) 0.364 (0.619) 0.302 (0.557) 0.569 (0.691) 0.538 (0.665) 0.538 (0.676)
    SPE 0.998 (0.976) 0.989 (0.944) 0.971 (0.904) 0.998 (0.980) 0.999 (0.985) 0.999 (0.990) 0.992 (0.945) 0.989 (0.945) 0.990 (0.945)
  30 SEN 0.508 (0.637) 0.498 (0.620) 0.298 (0.470) 0.461 (0.598) 0.260 (0.465) 0.247 (0.391) 0.536 (0.662) 0.505 (0.639) 0.504 (0.628)
    SPE 0.997 (0.977) 0.984 (0.939) 0.964 (0.879) 0.999 (0.985) 0.999 (0.992) 0.999 (0.994) 0.996 (0.969) 0.996 (0.965) 0.995 (0.965)
  100 SEN 0.416 (0.537) 0.189 (0.336) 0.091 (0.164) 0.372 (0.498) 0.311 (0.420) 0.174 (0.289) 0.481 (0.600) 0.433 (0.554) 0.428 (0.558)
    SPE 0.999 (0.989) 0.982 (0.932) 0.964 (0.913) 1.000 (0.996) 1.000 (0.997) 1.000 (0.998) 0.999 (0.992) 0.999 (0.992) 0.999 (0.992)
1000 10 SEN 0.726 (0.794) 0.671 (0.752) 0.710 (0.783) 0.662 (0.756) 0.620 (0.781) 0.622 (0.818) 0.738 (0.814) 0.751 (0.814) 0.758 (0.820)
    SPE 0.998 (0.974) 0.993 (0.950) 0.979 (0.921) 0.994 (0.952) 0.992 (0.966) 0.995 (0.974) 0.954 (0.862) 0.957 (0.867) 0.956 (0.869)
  20 SEN 0.666 (0.752) 0.665 (0.784) 0.630 (0.770) 0.599 (0.736) 0.533 (0.699) 0.431 (0.709) 0.680 (0.776) 0.664 (0.764) 0.681 (0.772)
    SPE 0.998 (0.976) 0.987 (0.936) 0.968 (0.886) 0.998 (0.977) 0.999 (0.984) 0.999 (0.987) 0.991 (0.946) 0.990 (0.938) 0.988 (0.938)
  30 SEN 0.658 (0.736) 0.603 (0.710) 0.420 (0.583) 0.578 (0.699) 0.389 (0.566) 0.340 (0.545) 0.669 (0.752) 0.663 (0.738) 0.661 (0.740)
    SPE 0.996 (0.974) 0.982 (0.931) 0.956 (0.870) 0.999 (0.985) 0.999 (0.991) 0.999 (0.993) 0.995 (0.966) 0.993 (0.963) 0.994 (0.961)
  100 SEN 0.572 (0.671) 0.286 (0.427) 0.125 (0.199) 0.519 (0.624) 0.409 (0.544) 0.284 (0.351) 0.636 (0.713) 0.579 (0.679) 0.593 (0.680)
    SPE 0.999 (0.987) 0.979 (0.919) 0.957 (0.908) 1.000 (0.996) 1.000 (0.997) 1.000 (0.998) 0.999 (0.991) 0.999 (0.991) 0.999 (0.991)
2000 10 SEN 0.711 (0.808) 0.775 (0.830) 0.810 (0.842) 0.746 (0.842) 0.728 (0.870) 0.712 (0.891) 0.821 (0.880) 0.829 (0.864) 0.822 (0.866)
    SPE 0.996 (0.986) 0.994 (0.951) 0.983 (0.921) 0.996 (0.955) 0.995 (0.967) 0.993 (0.968) 0.956 (0.871) 0.960 (0.873) 0.946 (0.846)
  20 SEN 0.741 (0.804) 0.770 (0.838) 0.754 (0.840) 0.691 (0.805) 0.624 (0.769) 0.566 (0.754) 0.793 (0.837) 0.769 (0.836) 0.762 (0.844)
    SPE 0.997 (0.977) 0.987 (0.942) 0.962 (0.876) 0.998 (0.977) 0.998 (0.984) 0.999 (0.988) 0.988 (0.942) 0.987 (0.936) 0.986 (0.932)
  30 SEN 0.756 (0.808) 0.740 (0.808) 0.529 (0.656) 0.698 (0.807) 0.483 (0.712) 0.430 (0.612) 0.772 (0.837) 0.762 (0.818) 0.754 (0.825)
    SPE 0.996 (0.974) 0.974 (0.917) 0.944 (0.851) 0.999 (0.984) 0.999 (0.990) 0.999 (0.993) 0.994 (0.963) 0.992 (0.961) 0.993 (0.959)
  100 SEN 0.688 (0.767) 0.385 (0.539) 0.160 (0.250) 0.648 (0.736) 0.548 (0.607) 0.349 (0.398) 0.738 (0.793) 0.708 (0.776) 0.703 (0.777)
    SPE 0.998 (0.986) 0.973 (0.906) 0.954 (0.895) 1.000 (0.996) 1.000 (0.997) 1.000 (0.998) 0.999 (0.991) 0.999 (0.990) 0.999 (0.990)
Open in a new tab

The above pattern of results, involving adequate network recovery with high specificity and moderately high sensitivity, is representative for almost all simulated conditions. The only exception to this rule results when the largest random and scale-free networks (100 nodes) are coupled with the highest level of connectivity. In these cases, the estimated coefficients show poor correlations with the coefficients of the generating networks, even for conditions involving 2000 observations (.222 and .681, respectively). For random networks, the reason for this is that the number of connections increases as the level of connectivity increases. For scale-free networks, the number of connections does not increase with increasing level of connectivity, but it does result in a peculiar arrangement of network connections, in which one node comes to have disproportionately many connections. Because eLasso penalises variables for having more connections, larger sample sizes are needed to overcome this penalty for these types of networks.

Although the lower level of sensitivity is partly inherent in the chosen method to handle the computational size of the problem and the solution to multiple testing through penalisation, it might be desirable in some cases to have a higher sensitivity at the expense of specificity. In eLasso, sensitivity can generally be increased in two ways. First, eLasso identifies the set of neighbours for each node by computing the EBIC28 (extended BIC). EBIC penalises solutions that involve more variables and more neighbours. This means that if the number of variables is high, EBIC tends to favour solutions that assign fewer neighbours to any given node. In this procedure, a hyperparameter called γ determines the strength of the extra penalty on the number of neighbours29,33. In our main simulation study, we used γ = .25. When γ = 0, no extra penalty is given for the number of neighbours, which results in a greater number of estimated connections. Second, we applied the so-called AND-rule to determine the final edge set. The AND-rule requires both regression coefficients βjk and βkj (from the ℓ1-regularised logistic regression of Xj on Xk and of Xk on Xj) to be nonzero. Alternatively, the OR-rule can be applied. The OR-rule requires only one of βjk and βkj to be nonzero, which also results in more estimated connections.

By applying the OR-rule and γ = 0, correlations between true and estimated coefficients are even higher in all conditions with 500 observations and more (M = .895, sd = .156; Table 1). Sensitivity also improved across all conditions (M = .584, sd = .221; Table 2). With more than 100 observations, average sensitivity is higher (M = .682, sd = .153). Applying the OR-rule and setting γ = 0 thus indeed increases the sensitivity of eLasso. As expected, this gain in sensitivity results in a loss of specificity; however, this loss is slight, as specificity remains high across all conditions (M = .956, sd = .039; Table 2).

Finally, it should be noted that with sparse networks, specificity partly takes on high values due to the low base rate of connections, since it is based on the number of true negatives. Therefore, we also investigated another measure, the so-called F1 score, that is not based on true negatives but on true positives, false positives and false negatives34; as such, it is independent of the base rate. For most conditions, the trends in the results are comparable. However, for larger and/or more dense random networks, the proportion of estimated connections that are not present in the true network is larger. More details about these results are provided in the online Supplementary Information.

To conclude, eLasso proves to be an adequate method to estimate networks from binary data. The validation study indicates that, with sample sizes of 500, 1000, and 2000, the estimated network strongly resembles the true network (high correlations). Specificity is uniformly high across conditions, which means there is a near absence of false positives among estimated network connections. Sensitivity is moderately high, and increases with sample size. For the most part, sensitivity is lowered because of weak connections that are incorrectly set to zero; in these cases, however, eLasso still adequately picks up the most important connectivity structures. For larger networks with either higher connectivity or a higher level of preferential attachment, sensitivity becomes lower; in these cases, more observations are needed.

Application to real data

To demonstrate the utility of eLasso, we apply it to a large data set (N = 1108) containing measurements of depression of healthy controls and patients with a current or history of depressive disorder. We used 27 items of the Inventory of Depressive Symptomatology35, which was administered in the Netherlands Study of Depression and Anxiety36 (NESDA). Using eLasso, we investigate how individual depression symptoms are related, as this may reveal which symptoms are important in the depression network; in turn, this information may be used to identify targets for intervention in clinical practice.

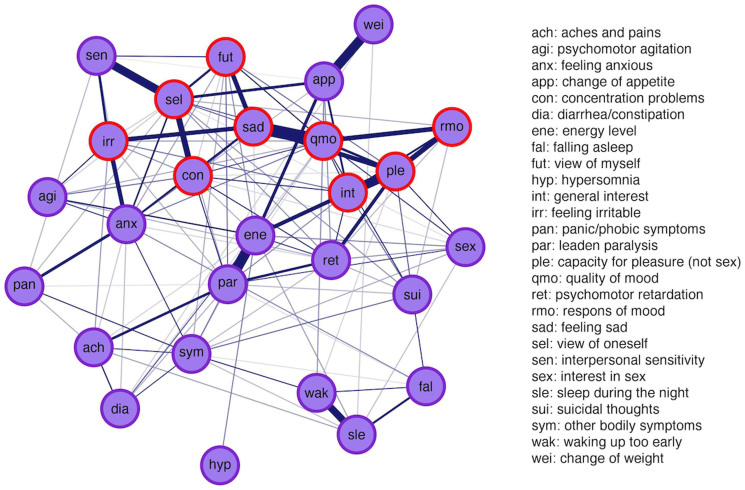
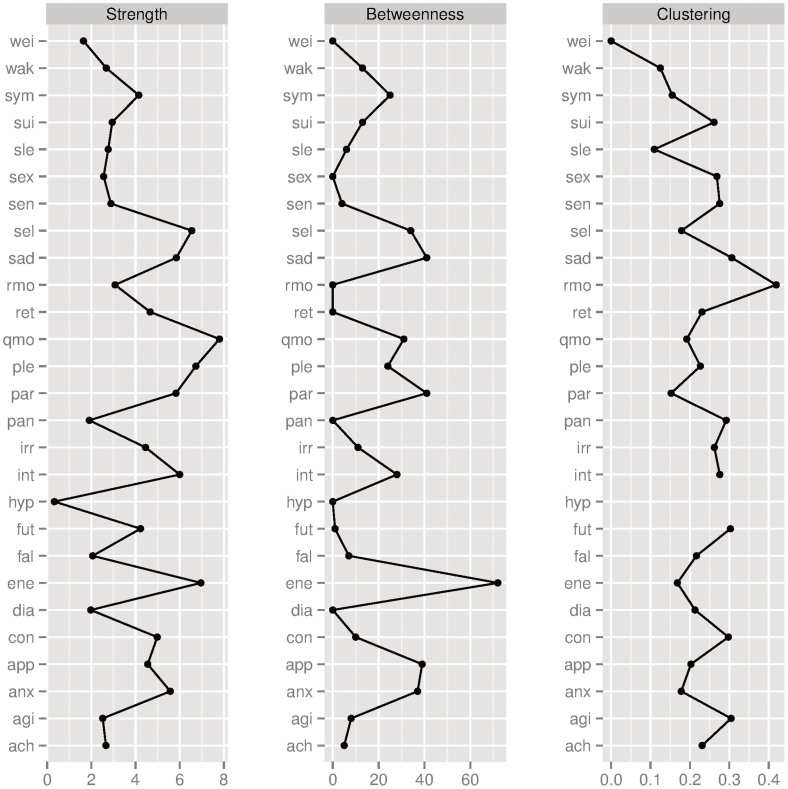
The eLasso network for these data is given in Figure 3. To analyse the depression network, we focus on the most prominent properties of nodes in a network: node strength, betweenness, and clustering coefficient (Figure 4). Node strength is a measure of the number of connections a node has, weighted by the eLasso coefficients37. Betweenness measures how often a node lies on the shortest path between every combination of two other nodes, indicating how important the node is in the flow of information through the network38,39. The local clustering coefficient is a measure of the degree to which nodes tend to cluster together. It is defined as how often a node forms a triangle with its direct neighbours, proportional to the number of potential triangles the relevant node can form with its direct neighbours38. These measures are indicative of the potential spreading of activity through the network. As activated symptoms can activate other symptoms, a more densely connected network facilitates symptom activation. Moreover, we inspect the community structure of the networks derived from the empirical data, to identify clusters of symptoms that are especially highly connected.

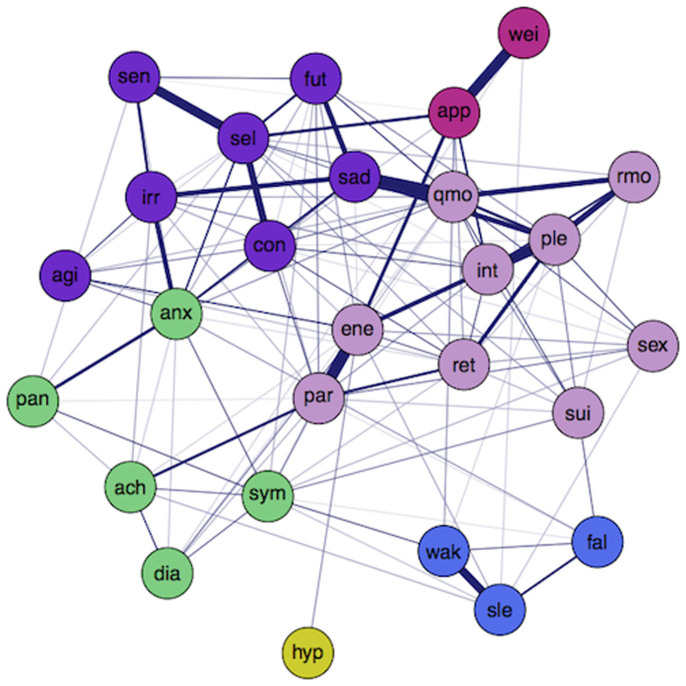
Figure 3. Application of eLasso to real data.

Figure 3

Open in a new tab

The resulting network structure of a group of healthy controls and people with a current or history of depressive disorder (N = 1108). Cognitive symptoms are displayed as ○ and thicker edges (connections) represent stronger associations.

Figure 4. Three centrality measures of the nodes in the network based on real data.

Figure 4

Open in a new tab

From left to right: node strength, betweenness, and clustering coefficient. “Hypersomnia” (hyp) has no clustering coefficient, since it has only one neighbour.

Figure 3 reveals that most cognitive depressive symptoms (e.g., “feeling sad” (sad), “feeling irritable” (irr), “quality of mood” (qmo), “response of your mood to good or desired events” (rmo), “concentration problems” (con), and “self criticism and blame” (sel)) seem to be clustered together. These symptoms also seem to score moderate to high on at least two out of three centrality measures (Figure 4). For example, “rmo” has a moderate strength and a very high clustering coefficient, whereas it has a low betweenness. This indicates that activation in the network does not easily affect response of mood to positive events (low betweenness), but that, if the symptom is activated, the cluster will tend to stay infected because of the high interconnectivity (high clustering coefficient). Another interesting example is “energy level” (ene), which has a high node strength and betweenness, but a moderate clustering coefficient. Apparently, energy level has many and/or strong connections (high strength) and lies on many paths between symptoms (high betweenness), whereas it is not part of a strongly clustered group of symptoms (moderate clustering coefficient). This symptom is probably more important in passing information through the network, or between other clusters, and might, therefore, be an interesting target for intervention.

As opposed to cognitive depressive symptoms, most anxiety and somatic symptoms (e.g., “panic/phobic symptoms” (pan), “aches and pains” (ach), “psychomotor agitation” (agi)) feature low scores on at least two centrality measures. Apparently, most anxiety and somatic symptoms either are less easily affected by other activated symptoms, do not tend to stay infected because of low interconnectivity (low clustering coefficient), or are less important for transferring information through the network (low betweenness). This is to be expected, since participants with a current or history of anxiety disorder are excluded from our sample. The item “feeling anxious” (anx), however, seems to be an important exception; feeling anxious does have a high node strength, a relatively high betweenness, and a moderate clustering coefficient. Apparently, feeling anxious does play an important role in our sample of depressive and healthy persons: it can be activated very easily, since a lot of information flows through it (high betweenness), and, in turn, it can activate many other symptoms because it has many neighbours (high node strength, moderate clustering). The role of feeling anxious in our network is in line with high comorbidity levels of anxiety and depressive disorders found in the literature40,41,42. Still, feeling anxious is not a symptom of depression according to current classifications, even though recent adaptations in DSM-5 propose an anxiety specifier for patients with mood disorders43. In line with this, our data suggest that people with a depressive disorder experience depressive symptoms often also feel anxious, although they may not have an anxiety disorder. This supports criticisms of the boundaries between MDD and generalised anxiety, which have been argued to be artificial8.

Another interesting feature of networks lies in their organization in community structures: clusters of nodes that are relatively highly connected. In the present data, the Walktrap algorithm44,45 reveals a structure involving six communities (see Figure 5). The purple cluster contains mostly negative mood symptoms, such as “feeling sad” (sad) and “feeling irritable” (irr); the pink cluster contains predominantly positive mood symptoms, such as “capacity of pleasure” (ple) and “general interest” (int); the green cluster is related to anxiety and somatic symptoms, such as “anxiety” (anx) and “aches and pains” (ach); the blue and yellow clusters represent sleeping problems.

Figure 5. Community structure of the network based on real data, detected by the Walktrap algorithm44,45.

Figure 5

Open in a new tab

Discussion

eLasso is a computationally efficient method to estimate weighted, undirected networks from binary data. The present research indicates that the methodology performs well in situations that are representative for psychology and psychiatry, with respect to the number of available observations and variables. Network architectures were adequately recovered across simulation conditions and, insofar as errors were made, they concerned the suppression of very weak edges to zero. Thus, eLasso is a viable methodology to estimate network structure in typical research settings in psychology and psychiatry and fills the gap in estimating network structures from non-Gaussian data.

Simulations indicated that the edges in the estimated network are nearly always trustworthy: the probability of including an edge, that is not present in the generating network, is very small even for small sample sizes. Due to the use of the lasso, more regression coefficients are set to zero in small sample sizes, which results in a more conservative estimation of network structure. For larger networks that are densely connected or that feature one node with a disproportionate number of connections, more observations are needed to yield a good estimate of the network. As the sample size grows, more and more true edges are estimated, in line with the asymptotic consistency of the method.

The model we presented may be extended from its current dichotomous nature to accommodate ordinal data, which are also prevalent in psychiatric research. For multinomial data, for example, the Potts model could be used46. This model is a generalisation of the Ising model with two states to a model with more than two states. Another straightforward extension of the model involves generalisation to binary time series data (by conditioning on the previous time point to render observations independent).

Methods

In this section we briefly explain the newly implemented method eLasso, provide the algorithm, describe the validation study and the real data we used to show the utility of eLasso.

eLasso

Let x = (x1, x2, …, xn) be a configuration where xi = 0 or 1. The conditional probability of Xj given all other nodes X\j according to the Ising model26,47 is given by

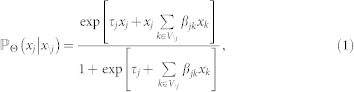graphic file with name srep05918-m1.jpg

where τj and βjk are the node parameter (or threshold) and the pairwise interaction parameter respectively.

In practice, the graph structure of psychological constructs is unknown. Therefore, the estimation of the unknown graph structure and the corresponding parameters is of central importance. By viewing Xj as the response variable and all other variables X\j as the predictors, we may fit a logistic regression function to investigate which nodes are part of the neighbourhood of the response variable. The intercept τj of the regression equation is the threshold of the variable, while the slope βjk of the regression equation is the connection strength between the relevant nodes. In order to perform the logistic regression, we need multiple independent observations of the variables.

To establish which of the variables in the data are neighbours of a given variable, and which are not, we used ℓ1–regularised logistic regression25,26. This technique is commonly called the lasso (least absolute shrinkage and selection operator) and optimises neighbourhood selection in a computationally efficient way, by optimising the convex function

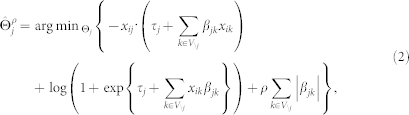graphic file with name srep05918-m2.jpg

in which i represents the independent observations {1, 2, .., n}, 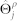Inline graphic contains all βjk and τj parameters, and ρ is the penalty parameter. The final term with ρ ensures shrinkage of the regression coefficients24,26. Parameter τj can be interpreted as the tendency of the variable to take the value 1, regardless of its neighbours. Parameter βjk represents the interaction strength between j and k.

The optimisation procedure is applied to each variable in turn with all other variables as predictors. To this end, the R package glmnet can be used48. The glmnet package uses a range of maximal 100 penalty parameter values. The result is a list of 100 possible neighbourhood sets, some of which may be the same. To choose the best set of neighbours, we used the EBIC28 (extended Bayesian Information Criterion). The EBIC is represented as

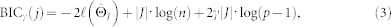graphic file with name srep05918-m3.jpg

in which 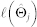Inline graphic is the log likelihood (see below), |J| is the number of neighbours selected by logistic regression at a certain penalty parameter ρ, n is the number of observations, p − 1 is the number of covariates (predictors), and γ is a hyperparameter, determining the strength of prior information on the size of the model space33. The EBIC has been shown to be consistent for model selection and to performs best with hyperparameter γ = 0.25 for the Ising model29. The model with the set of neighbours J that has the lowest EBIC is selected. From equation (1), it follows that the log likelihood of the conditional probability of Xj given its neighbours Xne(j) over all observations is

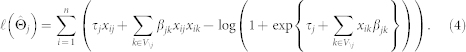graphic file with name srep05918-m4.jpg

At this stage, we have the regression coefficients of the best set of neighbours for every variable; i.e., we have both βjk and βkj and have to decide whether there is an edge between nodes j and k or not. Two rules can be applied to make the decision: the AND rule, where an edge is present if both estimates are nonzero, and the OR rule, where an edge is present if at least one of the estimates is nonzero25,26.

Although we do have the final edge set by applying one of the rules, note that for any two variables j and k, we get two results: the result of the regression of j on k (βjk), and the result of the regression of k on j (βkj). To obtain an undirected graph, the weight of the edge between nodes j and k, ωjk, is defined as the mean of both regression coefficients βjk and βkj. All steps of the described method are summarised in the algorithm below and is incorporated in R package IsingFit (http://cran.r-project.org/web/packages/IsingFit/IsingFit.pdf).

Input data set X for p variables and n subjects

Output (weighted) edge set for all pairs Xj and Xk

  1. Initialise: Select (randomly) one variable from the set of variables. This is the dependent variable.
    1. Perform ℓ1-regularised logistic regression on all other variables (glmnet uses 100 values of penalty parameter ρ).
    2. Compute the EBIC for ρ (i.e., each set of neighbours).
    3. Identify the set of neighbours that yield the lowest EBIC.
    4. Collect the resulting regression parameters in matrix Θ with τ on the diagonal and β on the off-diagonal.
    5. Repeat steps a through d for all p variables.

  2. Determine the final edge set by applying the AND rule: if both regression coefficients βjk and βkj in Θ are nonzero, then there is an edge between nodes j and k.

  3. Average the weights of the regression coefficients βjk and βkj. Define Θ* as the averaged weighted adjacency matrix with thresholds τ on the diagonal. This is now a symmetric matrix.

  4. Create a graph corresponding to the off-diagonal elements of the averaged weighted adjacency matrix Θ*. This can be done with qgraph in R49.

Validation study

We generated data from the three most popular types of network architectures: random networks, scale-free networks, and small world (clustered) networks30,31,32. Figure 1a shows illustrative examples of each type of networks. Network sizes were chosen to be comparable to the most common number of items in symptom checklists (10, 20, and 30 nodes), but also large networks were included (100 nodes). The level of connectivity of the networks was chosen to generate sparse networks. For this reason, in case of random networks, the probability of a connection (Pconn) between two nodes was set to 0.1, 0.2, and 0.3. For small world networks, the neighbourhood was set to 2, and for scale-free networks only one edge is added per node at each iteration in the graph generating process. To obtain a wide variety of well known graph structures, the rewiring probability (Prewire) in small world networks was set to 0.1, 0.5 and 1, and the power of preferential attachment (Pattach) in scale-free networks was set to 1, 2 and 3. For the condition with 100 nodes, we used different levels of connectivity for random and scale-free networks (random networks: Pconn = .05, .1, and .15; scale-free networks: Pattach = 1, 1.25, and 1.5). Otherwise, nodes will have too many connections.

The generated networks are binary: all connections have weight 1 or 0. To create weighted networks, positive weights were assigned from squaring values from a normal distribution with a mean of 0 and a standard deviation of 1 to obtain weights in a realistic range. Examples of resulting weighted networks are displayed in Figure 1b. Besides weights, thresholds of the nodes are added. To prevent nodes with many connections to be continuously activated and consequently having no variance, thresholds were generated from the normal distribution between zero and minus the degree of a node.

From the weighted networks with thresholds, data was generated according to the Ising model by drawing samples using the Metropolis-Hastings algorithm, implemented in R using the IsingSampler package50,51,52. Four sample size conditions were chosen that are realistic in psychology and psychiatry: 100, 500, 1000, and 2000. The generated data were used to estimate networks with eLasso. Examples of the resulting estimated networks are displayed in Figure 1c.

This setup led to a 3 × 4 × 3 × 4 quasi-factorial design, with the factors network type (random, small world, scale-free), level of connectedness, network size (10, 20, 30, 100), and sample size (100, 500, 1000, 2000). Thus, the total simulation study involved 144 conditions. Each of these conditions was replicated 100 times. For each condition, the mean correlation between data generating and estimated parameters, the mean sensitivity, and the mean specificity is computed. These served as outcome measures, indicating the quality of network recovery. Sensitivity, or the true positive rate, is defined as SEN = TP/(TP + FN), in which TP is the number of true positives and FN is the number of false negatives. Specificity, or the true negative rate, is defined as SPE = TN/(TN + FP), in which TN is the number of true negatives and FP is the number of false positives. Note that, in order to compute sensitivity and specificity, the off-diagonal elements of the weighted adjacency matrix Θ* (βjk), have to be dichotomised.

Since specificity naturally takes on high values for sparse networks, also the F1 score is computed. For more details about the F1 score and the results, see Supplementary Information online.

Data description

We used data from the Netherlands Study of Depression and Anxiety36 (NESDA). This is an ongoing cohort study, designed to examine the long-term course and consequences of major depression and generalised anxiety disorder in the adult population (aged 18–65 years). At the baseline assessment in 2004, 2981 persons were included. Participants consist of a healthy control group, people with a history of depressive or anxiety disorder and people with current depressive and/or anxiety disorder.

To demonstrate eLasso, we selected individuals from NESDA with a current or history of depressive disorder and healthy controls. To this end, we excluded everyone with a current or history of anxiety disorder. The resulting data set contains 1108 participants. To construct a network we used 27 items of the self-report Inventory of Depressive Symptomatology35 that relates to symptoms in the week prior to assessment (IDS).

Data were dichotomised in order to allow the application of the Ising model. Therefore, the four response categories of the IDS items were recoded into 0 and 1. The first response category of each item indicates the absence of the symptom. In the case of “feeling sad”, the first answering category is “I do not feel sad”. This option is recoded to 0, since it indicates the absence of the symptom. The other three options (“I feel sad less than half the time”, “I feel sad more than half the time”, and “I feel sad nearly all of the time”) are recoded to 1, indicating the presence of the symptom to some extent. Other items are recoded similarly.

Analysing the dichotomised data with our method and visualising the results with the qgraph package for R49, results in the network in Figure 3. The layout of the graph is based on the Fruchterman-Reingold algorithm, which iteratively computes the optimal layout so that nodes with stronger and/or more connections are placed closer to each other53. This network conceptualisation of depressive symptomatology might give new insights in issues that are still unexplained in psychology.

Author Contributions

C.v.B., D.B. and L.J.W. wrote the main manuscript. C.v.B., S.E. and T.F.B. carried out the validation study, C.v.B. and S.E. prepared Figures 1 and 3, C.v.B. and L.J.W. prepared Figure 2, C.v.B. prepared Tables 1–2. C.v.B., L.B. and R.A.S. wrote the Application to real data section. All authors contributed to manuscript revisions.

Supplementary Material

Supplementary Information

Supplementary Information

srep05918-s1.pdf (891.6KB, pdf)

References

  1. Barabási A. L. The network takeover. Nat. Phys. 8, 14–16 (2012). [Google Scholar]
  2. Barzel B. & Barabási A. L. Universality in network dynamics. Nat. Phys. 9, 673–681 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kitsak M. et al. Identification of influential spreaders in complex networks. Nat. Phys. 6, 888–893 (2010). [Google Scholar]
  4. Liu Y. Y., Slotine J. J. & Barabási A.-L. Controllability of complex networks. Nature 473, 167–173 (2011). [DOI] [PubMed] [Google Scholar]
  5. Vespignani A. Modelling dynamical processes in complex socio-technical systems. Nat. Phys. 8, 32–39 (2012). [Google Scholar]
  6. Borsboom D. Psychometric perspectives on diagnostic systems. J. Clin. Psychol. 64, 1089–1108 (2008). [DOI] [PubMed] [Google Scholar]
  7. Borsboom D. & Cramer A. O. J. Network analysis: An integrative approach to the structure of psychopathology. Annu. Rev. Clin. Psychol. 9, 91–121 (2013). [DOI] [PubMed] [Google Scholar]
  8. Cramer A. O. J., Waldorp L. J., Van Der Maas H. L. J. & Borsboom D. Comorbidity: A network perspective. Behav. Brain Sci. 33, 137–150 (2010). [DOI] [PubMed] [Google Scholar]
  9. Schmittmann V. D. et al. Deconstructing the construct: A network perspective on psychological phenomena. New Ideas Psychol. 31, 43–53 (2011). [Google Scholar]
  10. Van Der Maas H. L. J. et al. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychol. Rev. 113, 842 (2006). [DOI] [PubMed] [Google Scholar]
  11. Schäfer J. & Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Molec. Biol. 4, 32 (2005). [DOI] [PubMed] [Google Scholar]
  12. Bickel P. J. & Levina E. Covariance regularization by thresholding. Ann. Stat. 36, 2577–2604 (2008). [Google Scholar]
  13. Friedman J., Hastie T. & Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kalisch M., Mächler M., Colombo D., Maathuis M. H. & Bühlmann P. Causal inference using graphical models with the r package pcalg. J. Stat. Softw. 47, 1–26 (2012). [Google Scholar]
  15. Spirtes P., Glymour C. & Scheines R. Causation, Prediction, and Search (MIT press, Cambrigde, Massachusetts, 2001). [Google Scholar]
  16. Drton M. & Perlman M. Multiple testing and error control in gaussian graphical model selection. Statist. Sci. 22, 430–449 (2007). [Google Scholar]
  17. Efron B. Large-scale simultaneous hypothesis testing: The choice of a null hypothesis. J. Am. Statist. Assoc. 99, 96–104 (2004). [Google Scholar]
  18. Strimmer K. fdrtool: a versatile r package for estimating local and tail area-based false discovery rates. Bioinformatics 24, 1461–1462 (2008). [DOI] [PubMed] [Google Scholar]
  19. Kindermann R. & Snell J. L. Markov Random Fields and their Applications, vol. 1 (American Mathematical Society Providence, RI, 1980). [Google Scholar]
  20. Lauritzen S. Graphical Models (Oxford University Press, USA, 1996). [Google Scholar]
  21. Speed T. & Kiiveri H. Gaussian markov distributions over finite graphs. Ann. Stat. 14, 138–150 (1986). [Google Scholar]
  22. Foygel R. & Drton M. Extended bayesian information criteria for gaussian graphical models. Adv. Neural Inf. Process. Syst. 23, 2020–2028 (2010). [Google Scholar]
  23. Ravikumar P., Wainwright M. J., Raskutti G. & Yu B. et al. High-dimensional covariance estimation by minimizing l1-penalized log-determinant divergence. Electron. J. Statist. 5, 935–980 (2011). [Google Scholar]
  24. Tibshirani R. Regression shrinkage and selection via the lasso. J. Roy. Statist. Soc. Ser. B 58, 267–288 (1996). [Google Scholar]
  25. Meinshausen N. & Bühlmann P. High-dimensional graphs and variable selection with the lasso. Ann. Stat. 34, 1436–1462 (2006). [Google Scholar]
  26. Ravikumar P., Wainwright M. J. & Lafferty J. D. High-dimensional ising model selection using l1-regularized logistic regression. Ann. Stat. 38, 1287–1319 (2010). [Google Scholar]
  27. Ising E. Beitrag zur theorie des ferromagnetismus. Z. Phys. A-Hadrons. Nucl. 31, 253–258 (1925). [Google Scholar]
  28. Chen J. & Chen Z. Extended bayesian information criteria for model selection with large model spaces. Biometrika 95, 759–771 (2008). [Google Scholar]
  29. Foygel R. & Drton M. High-dimensional ising model selection with bayesian information criteria. arXiv preprint arXiv:1403.3374 (2014).
  30. Barabási A. L. & Albert R. Emergence of scaling in random networks. Science 286, 509–512 (1999). [DOI] [PubMed] [Google Scholar]
  31. Erdös P. & Rényi A. On random graphs. Publ. Math. Debrecen 6, 290–297 (1959). [Google Scholar]
  32. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  33. Foygel R. & Drton M. Bayesian model choice and information criteria in sparse generalized linear models. arXiv preprint arXiv:1112.5635 (2011).
  34. Jardine N. & van Rijsbergen C. J. The use of hierarchic clustering in information retrieval. Inform. Storage Ret. 7, 217–240 (1971). [Google Scholar]
  35. Rush A. et al. The inventory of depressive symptomatology (IDS): Psychometric properties. Psychol. Med. 26, 477–486 (1996). [DOI] [PubMed] [Google Scholar]
  36. Penninx B. W. et al. The netherlands study of depression and anxiety (NESDA): Rationale, objectives and methods. Int. J. Method. Psych. 17, 121–140 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Barrat A., Barthelemy M., Pastor-Satorras R. & Vespignani A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. U.S.A. 101, 3747–3752 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Boccaletti S., Latora V., Moreno Y., Chavez M. & Hwang D. Complex networks: Structure and dynamics. Phys. Rep. 424, 175–308 (2006). [Google Scholar]
  39. Opsahl T., Agneessens F. & Skvoretz J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Networks 32, 245–251 (2010). [Google Scholar]
  40. Goldberg D. & Fawcett J. The importance of anxiety in both major depression and bipolar disorder. Depress. Anxiety 29, 471–478 (2012). [DOI] [PubMed] [Google Scholar]
  41. Kessler R. C., Nelson C. B., McGonagle K. A. & Liu J. et al. Comorbidity of DSM-III—R major depressive disorder in the general population: Results from the US National Comorbidity Survey. Br. J. Psychiatry 30, 17–30 (1996). [PubMed] [Google Scholar]
  42. Schoevers R. A., Beekman A. T. F., Deeg D. J. H., Jonker C. & Van Tilburg W. Comorbidity and risk-patterns of depression, generalised anxiety disorder and mixed anxiety-depression in later life: results from the amstel study. Int. J. Geriatr. 18, 994–1001 (2003). [DOI] [PubMed] [Google Scholar]
  43. American Psychiatric Association. . The Diagnostic and Statistical Manual of Mental Disorders (5th ed.) (Arlington, VA: American Psychiatric Publishing, 2013). [Google Scholar]
  44. Orman G. K. & Labatut V. A Comparison of Community Detection Algorithms on Artificial Networks (Springer, Berlin Heidelberg, 2009). [Google Scholar]
  45. Pons P. & Latapy M. Computing communities in large networks using random walks. J. Graph Algorithms Appl. 10, 191–218 (2006). [Google Scholar]
  46. Wu F.-Y. The potts model. Rev. Mod. Phys. 54, 235 (1982). [Google Scholar]
  47. Loh P. L. & Wainwright M. J. Structure estimation for discrete graphical models: Generalized covariance matrices and their inverses. Ann. Stat. 41, 3022–3049 (2013). [Google Scholar]
  48. Friedman J., Hastie T. & Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1 (2010). [PMC free article] [PubMed] [Google Scholar]
  49. Epskamp S., Cramer A. O. J., Waldorp L. J., Schmittmann V. D. & Borsboom D. qgraph: Network visualizations of relationships in psychometric data. J. Stat. Softw. 48, 1–18 (2012). [Google Scholar]
  50. Hastings W. K. Monte carlo sampling methods using markov chains and their applications. Biometrika 57, 97–109 (1970). [Google Scholar]
  51. Epskamp S. IsingSampler: Sampling methods and distribution functions for the Ising model (2013). URL github.com/SachaEpskamp/IsingSampler. R package version 0.1. [Google Scholar]
  52. Murray I. Advances in Markov chain Monte Carlo methods. PhD thesis, Gatsby Computational Neuroscience Unit, University College London (2007). [Google Scholar]
  53. Fruchterman T. M. & Reingold E. M. Graph drawing by force-directed placement. Software Pract. Exper. 21, 1129–1164 (1991). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep05918-s1.pdf (891.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES