Postmortem validation of breast density using dual-energy mammography

Abstract

Purpose:

Mammographic density has been shown to be an indicator of breast cancer risk and also reduces the sensitivity of screening mammography. Currently, there is no accepted standard for measuring breast density. Dual energy mammography has been proposed as a technique for accurate measurement of breast density. The purpose of this study is to validate its accuracy in postmortem breasts and compare it with other existing techniques.

Methods:

Forty postmortem breasts were imaged using a dual energy mammography system. Glandular and adipose equivalent phantoms of uniform thickness were used to calibrate a dual energy basis decomposition algorithm. Dual energy decomposition was applied after scatter correction to calculate breast density. Breast density was also estimated using radiologist reader assessment, standard histogram thresholding and a fuzzy C-mean algorithm. Chemical analysis was used as the reference standard to assess the accuracy of different techniques to measure breast composition.

Results:

Breast density measurements using radiologist reader assessment, standard histogram thresholding, fuzzy C-mean algorithm, and dual energy were in good agreement with the measured fibroglandular volume fraction using chemical analysis. The standard error estimates using radiologist reader assessment, standard histogram thresholding, fuzzy C-mean, and dual energy were 9.9%, 8.6%, 7.2%, and 4.7%, respectively.

Conclusions:

The results indicate that dual energy mammography can be used to accurately measure breast density. The variability in breast density estimation using dual energy mammography was lower than reader assessment rankings, standard histogram thresholding, and fuzzy C-mean algorithm. Improved quantification of breast density is expected to further enhance its utility as a risk factor for breast cancer.

I. INTRODUCTION

Among American women breast cancer is the most common cancer and the second leading cause of death from cancer.¹ Mammographic density, which is defined as the ratio of fibroglandular tissue to the total fibroglandular and adipose tissue, is an important risk factor in the development of breast cancer.^2–8 Additionally, it has been shown that the sensitivity of screening mammography is lower among women with dense breasts.^9–17 Previous reports have shown that women with the highest mammographic density (75%–100% fibroglandular volume) have four- to fivefold increased risk of developing breast cancer compared with the lowest density (0%–25% fibroglandular volume).^9,18,19 The current standard of care for breast density (BD) evaluation involves visual assessment of mammograms.¹³ This subjective classification scheme is limited by its considerable intra- and interreader variability.^20–22 Several groups have reported more quantitative approaches^23–25 for measuring breast density. Area-based techniques have included qualitative and semiquantitative classification schemes,^18,25 and also quantitative estimations from manual or semimanual segmentation of a digital image histogram.^24,26 Although these segmentation techniques provide a more quantitative measure of breast density, one of the limitations is the binary classification of a pixel into either 100% fibroglandular or 100% adipose tissue. Additionally, an important limitation is that an area measurement ignores the physical 3D character of a real breast. Breasts of different thicknesses can potentially all yield the same measurement of area breast density yet correspond to widely varying volumetric breast density values.^6,27

Volume-based techniques, which overcome some of the limitations of area-based techniques, have included efforts to standardize^28,29 and calibrate^30,31 mammographic image data. However, these techniques require assumptions related to a breast shape model in order to measure breast density and thickness from a single image. The assumptions required in the breast shape model and the errors associated with the paddle thickness measurement are the fundamental limitations of these techniques.

There have also been previous reports using digital breast tomosynthesis,³² cone-beam CT,³³ dual energy cone-beam CT,³⁴ and MRI (Ref. 33) for breast density measurement. However, these modalities are not currently available for breast screening.

Dual energy mammography can exploit differences between the effective atomic numbers (Z) of fibroglandular and adipose tissues to provide separate quantitative thickness measurements for each tissue. It does not require any assumption for breast density measurement since glandular and adipose thickness measurements are based on two separate physical measurements using low and high energy images. There have been previous studies using dual energy x-ray absorptiometry (DXA) for the measurement of breast density.^35–39 The energies of DXA were primarily designed for whole body bone mineral measurement, which might be suboptimal for breast density measurement. A dual energy mammography technique for breast density measurement has previously been validated in phantoms.^40,41

The purpose of the current study was to validate the dual energy breast density technique using chemical analysis as the reference gold standard. A comparison was also made between breast density estimation using radiologist reader assessment, histogram threshold segmentation, and fuzzy C-mean segmentation.

II. MATERIALS AND METHODS

II.A. Image acquisition

Twenty pairs (left and right) of postmortem breasts (N = 40, 136–2330 g) were acquired from the Willed Body Program in our School of Medicine. The postmortem breasts were surgically removed to the pectoralis major muscle and placed in plastic bags. The postmortem breasts were kept in the sealed plastic bags during the entire imaging process.³³ Dual energy images were acquired using a full field digital mammography system (Selenia, Hologic Inc., Bedford, MA). This system uses an amorphous selenium direct conversion detector with a pixel pitch of 70 μm. The raw images were binned by a factor of 4 in each dimension and an image pixel size of 280 × 280 μm² was used for breast density analysis. The system uses a Tungsten (W) anode x-ray tube with a maximum beam energy of 49 kVp. Low energy images were acquired at 28 kVp with a 50 μm rhodium filter at 60 mAs. High energy images were acquired at 49 kVp with a 300 μm copper filter at 30 mAs. The mean energies of the low and high energy beams were calculated to be 18.8 and 38.0 keV, respectively. The radiation dose was estimated to be 0.85 mGy.⁴⁰ Each breast was imaged at two different projections. Half of the breasts were rotated about their horizontal axis and the rest of the breast samples were manually reconfigured to simulate cranial caudal (CC) and mediolateral-oblique (MLO) views. Imaging at these different orientations provided both a measure of technique repeatability and the ability to test the sensitivity of the technique to changes in spatial configuration.

All images were acquired with the use of a grid [cellular(cross-hatch) 4:1 grid ratio, 15 lines/cm], and then further corrected for x-ray scatter using a convolution-based technique modified for dual energy imaging.⁴⁰ The time between each exposure was set to 4 min to minimize the effect of detector ghosting.⁴² All image processing was performed using ImageJ.⁴³

II.B. Breast density measurement

II.B.1. Radiologist reader assessment

All the low energy images of the postmortem breasts were read by three board certified radiologists dedicated to breast imaging. They were asked to rank the breasts into four density categories of fatty (1), scattered densities (2), heterogeneously dense (3), and extremely dense (4). The averaged categorical ranking for the three readers was also converted into percentage values by using linear interpolations, which assumed ranking 1 and 4 as 12% and 87%, respectively. The appearance of the postmortem breast images is different from the standard mammograms. Therefore, five postmortem mammograms and their known ranking assignments from chemical analysis results were used for a training session. The entire 40 images were then read in a random order blinded from the chemical analysis results.

II.B.2. Histogram thresholding method

In this method, a visual inspection of the image and the corresponding histogram is used to choose a single threshold to segment glandular and adipose tissues in the low energy images. Two medical physicists performed this measurement independently after a training session which included five pairs of images with estimated breast densities in the range of approximately 10%–70%. The 40 images were then arranged in a random order for a blind study.

II.B.3. Fuzzy C-mean method

The Fuzzy C-mean algorithm classifies pixels with similar gray values into distinct clusters allowing for the separation of different tissues by their attenuation properties.²⁶ A total of five clusters were used for segmentation of the images. After the clusters for glandular and adipose tissues were chosen, the algorithm was used in a semiautomated format for all the images.

II.B.4. Dual energy method

Dual energy decomposition of the low and high energy images yielded individual pixel measurements of glandular and adipose equivalent material thickness. This is due to the physical differences in the mass attenuation coefficients of glandular and adipose tissues as a function of beam energy. The decomposition was based on a previous calibration⁴⁰ with glandular and adipose equivalent phantoms. The calibration accounted for beam hardening and image magnification differences due to a diverging beam. Histogram thresholding was used to automatically segment the whole breast from the background. Dual energy material decomposition was used to calculate the mean glandular and adipose thicknesses.⁴⁰ The glandular (V_G) and adipose volumes (V_A) were then calculated using the mean glandular and adipose thicknesses along with the area of the region of interest (ROI) that included the whole breast. These values were used to calculate BD according to:

$$\mathrm{BD}=100\times \left(\frac{V_G}{V_G+V_A}\right).$$

The total breast volume was calculated by summing the product of the area per pixel by the combined thickness of glandular and adipose tissues for all points in the breast.

II.B.5. Chemical analysis

After image acquisition, all postmortem breasts, including skin, were chemically decomposed into their water, lipid, protein, and mineral contents using chemical analysis as the reference standard for the tissue compositional analysis. The chemical analysis method was based on a standardized procedure devised by the United States Department of Agriculture.⁴⁴

Each postmortem breast was weighed before and after image acquisition. The change in breast tissue mass was assigned to water loss during image acquisition so it was added back into the final water fraction. The breast tissue was then cut into pieces of approximately 5 × 5 × 5 mm³ and placed into a vacuum oven at 95 °C for 48 h in order to evaporate all the remaining water. The reduction in tissue mass was assumed to be the water content. The dried tissue was then mixed with petroleum ether, ground into slurry and agitated at 30 °C for approximately 1 h to dissolve the lipid content. The mixture was kept at room temperature for 24 h before vacuum filtering the ether solution through a Buchner funnel. One additional liter of pure petroleum ether was poured over the material remaining in the filter to wash away any residual lipid contents. At this point, it was assumed that the petroleum ether solution contained the entire lipid in the breast tissue. The lipid material was then isolated from the solution by evaporating the petroleum ether under vacuum distillation and weighed.

The remaining material in the filter contained primarily protein with a very small amount of minerals, such as Ca. The residual fat and membrane bound lipids were determined using a previously reported method.⁴⁵ Pure protein mass was determined by using an ashing procedure.⁴⁶ In this procedure, the residual material was placed in a furnace with excess air at 550 °C for 18 h, which oxidizes all the carbon-based compounds. The difference in weight before and after the ashing procedure was assigned to be pure protein mass. Further analysis was performed on the remaining ash to determine the amount of Ca in the tissue by removing the water soluble components. The mass of the remaining ash was very small so the volume of the minerals was negligible as compared with the other components. Therefore, the mineral contents were excluded from further calculations. Finally, the measured masses of water, lipid, and protein were converted into volumes using densities of 1, 0.924, and 1.35 g/cm³, respectively.

The error in volumetric fraction of water, lipid, and protein has been shown to be less than 1%.⁴⁶ A detailed description of the chemical analysis technique has been reported in Ref. 33.

The next step was to compare breast density from imaging, which is a two compartment model of glandular and adipose tissues, to chemical analysis results, which is a three compartment model of water, lipid, and protein.³³ However, water, lipid, and protein are common to both glandular and adipose tissues with different concentrations. A previous report has used fibroglandular volume as a metric for breast tissue composition.⁴⁷ Percent fibroglandular volume (%FGV) can be defined as the volumetric ratio of water and protein to the total volume of water, lipid, and protein in breast tissue.^33,48 Therefore, %FGV can be written as

$$\%\mathrm{FGV}=100\times \left(\frac{V_W+V_P}{V_W+V_L+V_P}\right),$$

where V_W, V_L, and V_P represent the volumes of water, lipid, and protein, respectively. This model assumes that there are no additional components other than water, lipid, and protein in breast tissue and it does not distinguish between different types of lipid. In other words, the summation of volume fractions of water, lipid, and protein is assumed to be one.

II.B.6. Statistical analysis

Two sets of statistical analysis were performed in this study. First, the precision of each technique was evaluated by linear regression of the breast densities measured from the left and the right breasts of the same pair. Then, the accuracy of different methods was determined using the linear correlation between the measured breast density and the %FGV from chemical analysis. In order to compare radiologist reader assessment results to the quantitative measurement of breast density from the other techniques, the averaged radiologist categorical ranking for the three readers was converted into percentage values by using linear interpolations, which assumed ranking 1 and 4 as 12% and 87%, respectively. Pearson's r and standard error estimate obtained from the linear regression was used to assess the precision and accuracy of different techniques for breast density measurement.

III. RESULTS

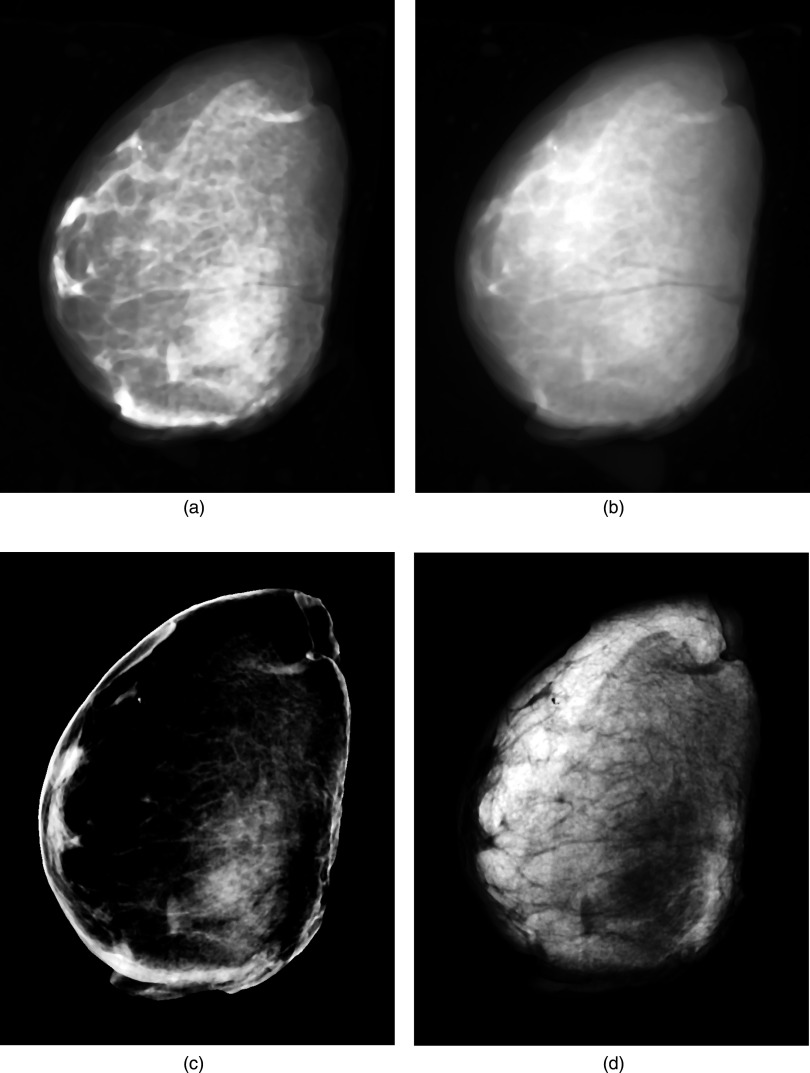
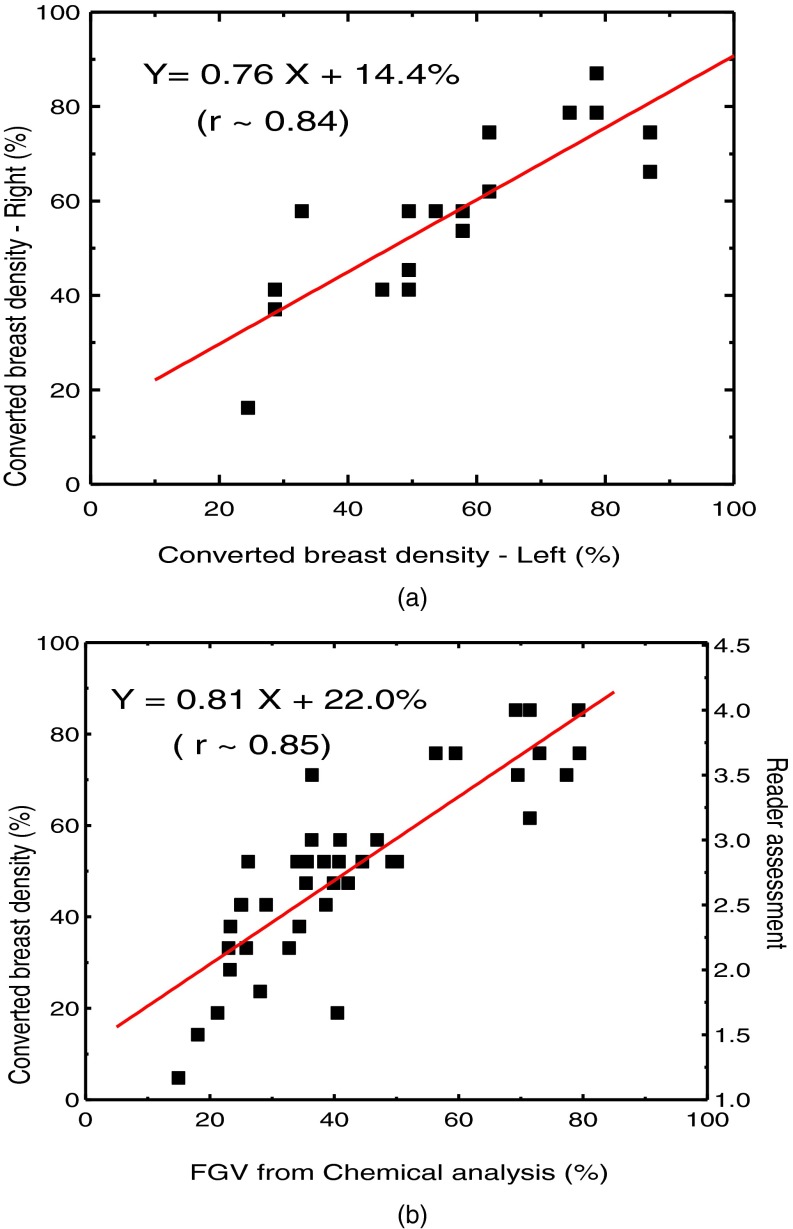
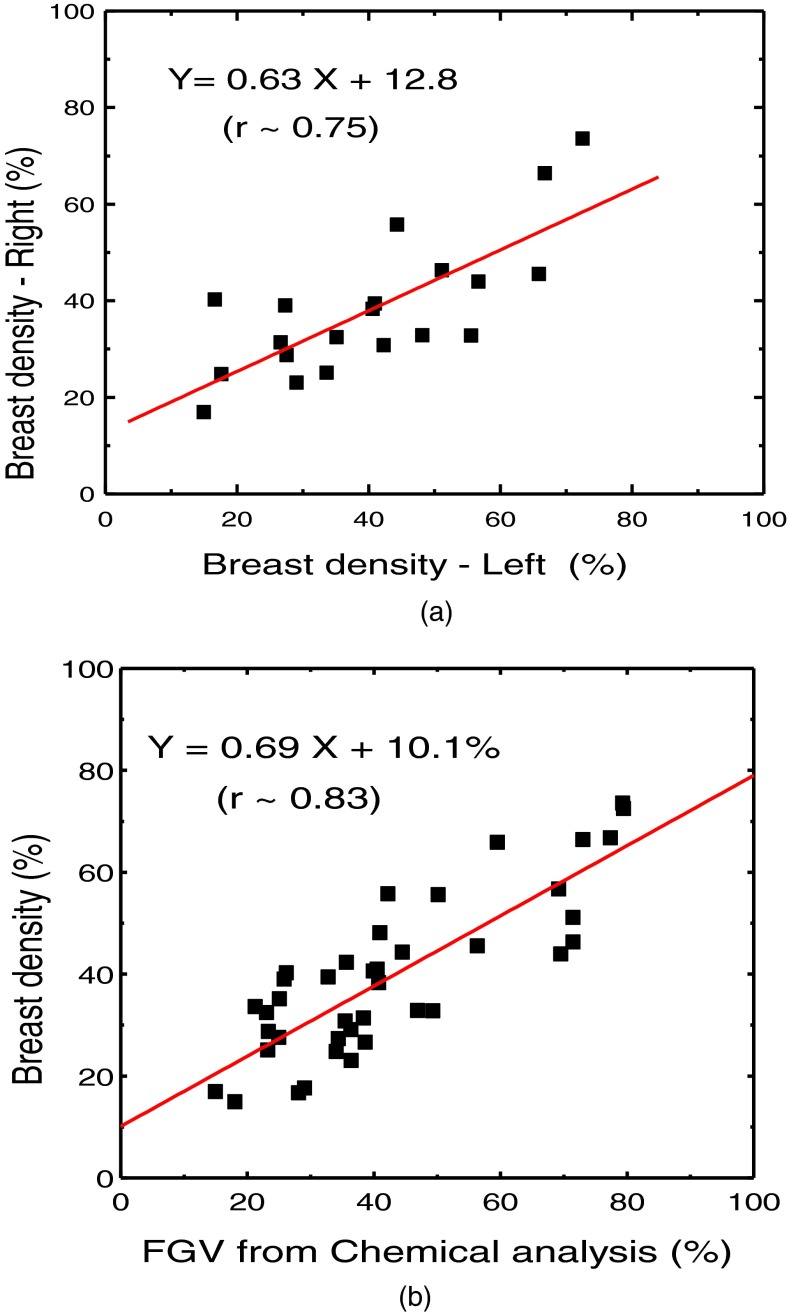
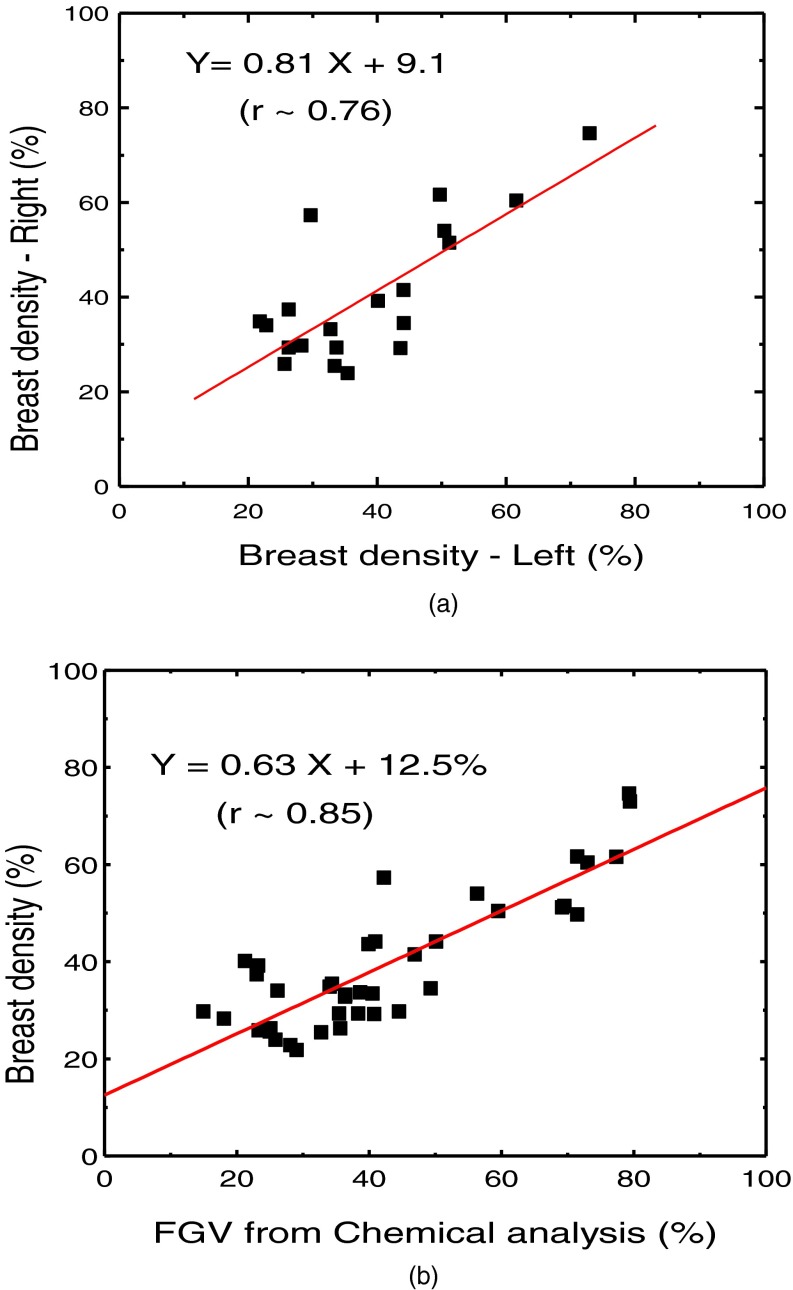
Figure 1 shows examples of low energy (a) and high energy (b) images along with the decomposed images of glandular (c) and adipose (d) tissues. The comparison of breast density from radiologist reader assessments for the left and right breasts is shown in Fig. 2(a). The relation between breast density from radiologist reader assessments for all the breasts and the %FGV from chemical analysis is shown in Fig. 2(b). They both show positive correlation with large variability. Breast density measurement for the left and right breasts from standard image thresholding is shown in Fig. 3(a). The relation of breast density from standard image thresholding and the %FGV from chemical analysis is shown in Fig. 3(b). There is a slight improvement in correlation using standard image thresholding as compared with radiologist reader assessments. However, the variability is still quite high. Similar results using automated Fuzzy C-mean algorithm is shown in Fig. 4.

FIG. 1.

Examples of low energy (a) and high energy (b) images along with the decomposed images of glandular (c) and adipose (d) tissues.

FIG. 2.

(a) Right-left correlation of breast density from the converted radiologist reader assessment for the breast pairs. (b) Breast density from converted radiologist reader assessment as a function of %FGV from chemical analysis.

FIG. 3.

(a) Right-left correlation of the breast densities obtained by using standard histogram thresholding method. (b) Correlation between breast density from standard histogram thresholding and %FGV from chemical analysis.

FIG. 4.

(a) Right-left correlation of the breast densities obtained by using Fuzzy C-means clustering. (b) Correlation between breast density from Fuzzy C-means clustering and %FGV from chemical analysis.

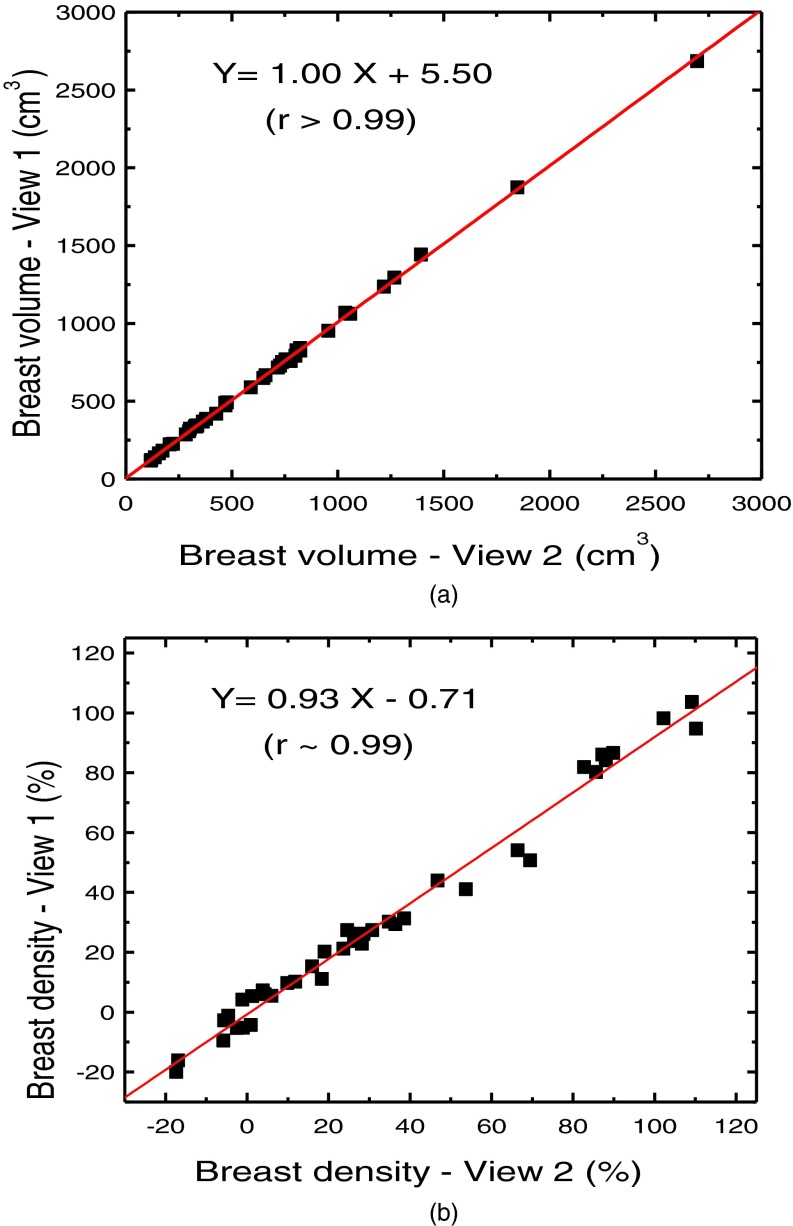
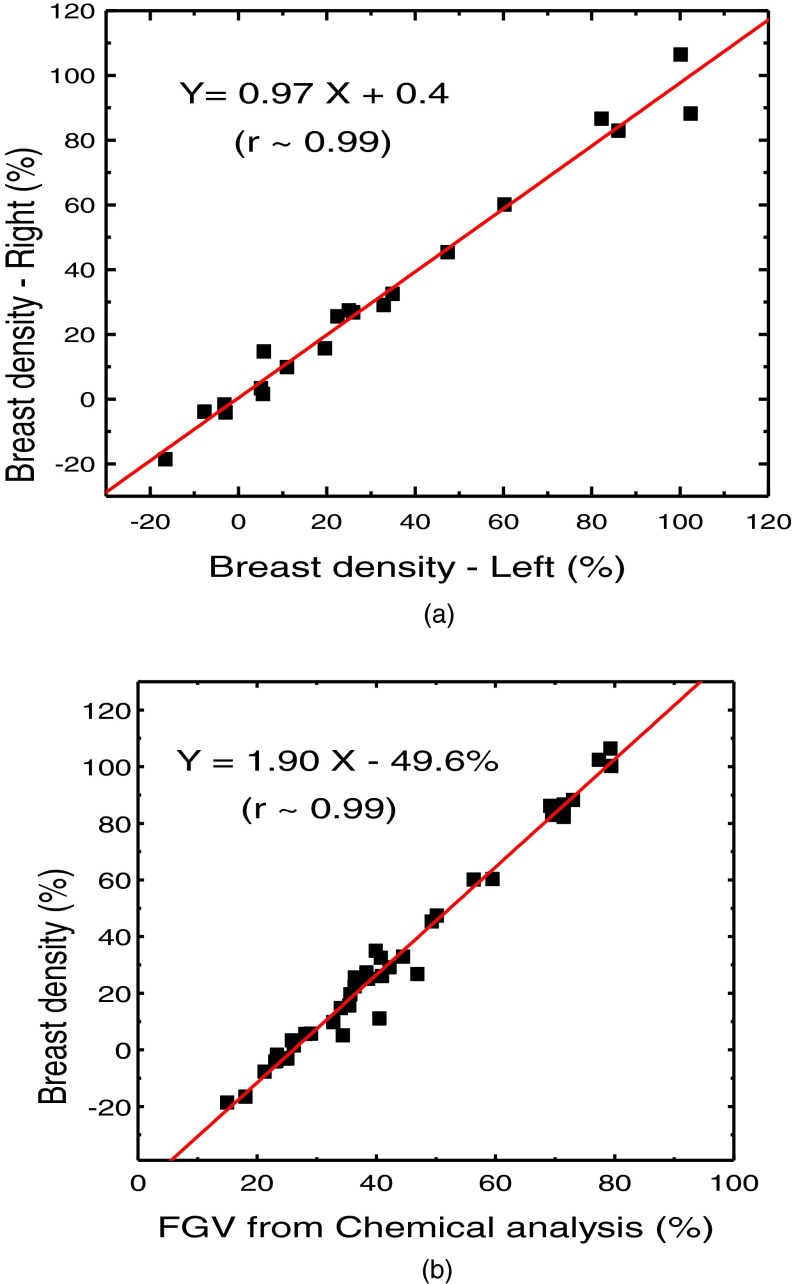
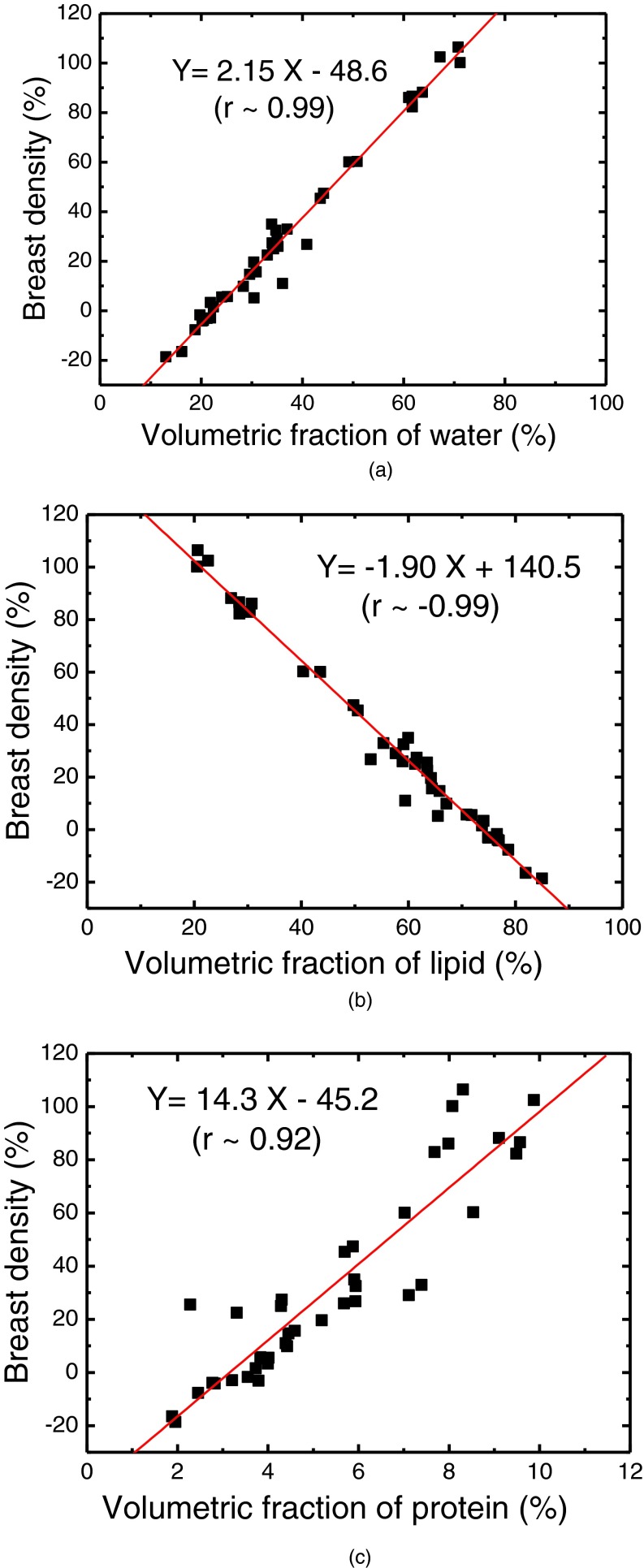
The relationship of breast volume measurement using dual energy mammography for the first (V₁) and second (V₂) orientations is shown in Fig. 5(a). The measurements were related by V₂ = 1.00, V₁ + 5.5 (r² > 0.99). The relative RMS difference between the two sets was 2.66% (The absolute RMS difference is 14.8 cm³). The relationship of breast density measurement for the first (D1) and second (D2) orientations is shown in Fig. 5(b). The measurements were related by D2 = 0.93 D1 – 0.71 (r² = 0.99). The RMS difference between the two sets was 5.97%. Breast density measurement for the left and right breasts is shown in Fig. 6(a). The relation of breast density and the %FGV from chemical analysis is shown in Fig. 6(b). The negative values in breast density results are due to the previously investigated mismatch between the glandular and adipose calibration phantoms and the actual glandular and adipose tissues.⁴⁸ The relationships between breast density and the percentage fractions of water, lipid, and protein contents are shown in Fig. 7. Table I shows a summary of the linear regression analysis between left and right breast density measurements for all the different techniques used to measure breast density. Table II shows a summary of the linear regression parameters for the relation of breast density from images and the %FGV from chemical analysis for various techniques. The results from dual energy mammography show substantial improvement in correlation as compared with the other techniques.

FIG. 5.

Correlations of breast volume (a) and breast density (b) between two different views of the same breast obtained from dual energy decomposition technique.

FIG. 6.

(a) Right-left correlation of the volumetric breast densities obtained by using dual energy decomposition. (b) Correlation between volumetric breast density from dual energy decomposition and %FGV from chemical analysis.

FIG. 7.

Correlations between breast densities obtained from dual energy decomposition and the volumetric percentages of water (a), lipid (b), and protein (c) contents from chemical analysis.

TABLE I.

Summary of the linear regression analysis between left and right breast density measurements for various methods. The relative SEE is shown in the parentheses.

	Reader assessment	Thresholding	FCMa	Dual energy
Slope	0.76	0.63	0.81	0.97
Intercept	14.4%	12.8%	9.1%	0.4%
Pearson's r	0.84	0.75	0.76	0.99
SEE	9.1% (2.0)	9.1% (2.0)	9.2% (2.0)	4.6% (1.0)

^aFuzzy C-mean.

TABLE II.

Summary of the linear regression analysis between breast density and %FGV for various methods. The relative SEE is shown in the parentheses.

	Reader assessment	Thresholding	FCMa	Dual energy
Slope	0.81	0.69	0.63	1.90
Intercept	22.0%	10.1%	12.5%	–49.6%
Pearson's r	0.85	0.83	0.85	0.99
SEE	9.9% (2.1)	8.6% (1.8)	7.2% (1.5)	4.7% (1.0)

^aFuzzy C-mean.

IV. DISCUSSION

There is currently no reference gold standard to evaluate the accuracy of breast density measurement techniques in patients. Breast density measurement algorithms such as Cumulus,²³ Quantra (Hologic Inc., Bedford, MA) and Volpara (Volpara Solutions, Wellington, New Zealand) have been clinically implemented. However, to the best of our knowledge, there are no studies validating these techniques against a reference gold standard, such as chemical analysis. Therefore, the accuracy of these techniques is not known. In this study, precision and accuracy of different breast density techniques were assessed using a postmortem study. Precision was determined using a right and left breast density comparison.^33,41 Chemical analysis was used as a reference gold standard to determine the accuracy.³³ Breast density estimation from radiologist reader assessment showed considerable reader variability, which is in agreement with previous reports.^22,49 Two area-based techniques using standard histogram thresholding and fuzzy C-mean were also evaluated. These two techniques were chosen because they could be used to assess breast density using images from excised postmortem breast samples. Standard histogram thresholding, which is fundamentally similar to the previously reported Cumulus algorithm,²³ requires the operator to manually determine the glandular tissue gray level threshold. On the other hand, the fuzzy C-mean technique is semiautomated. However, both of these techniques also showed highly variable breast density estimation. This indicates that the fundamental limitation of these techniques is the segmentation of fibroglandular tissue from adipose tissue, which requires visual or automated estimation technique.

There are a number of other breast density techniques such as Quantra and Volpara that require a shape model to estimate breast thickness in the periphery of the breast where the compression paddle is not in contact with the breast.^50,51 These techniques could not be used to estimate breast density in this study since the shape models are not appropriate for estimation of breast thickness in an excised postmortem breast sample. Therefore, the evaluation of these techniques was not possible using this postmortem study. Future postmortem validation studies will need to account for the inherent assumptions of the shape models in the design of the study.

Dual energy mammography, on the other hand, can exploit physical differences between fibroglandular and adipose tissues. It provides separate quantitative thickness measurements for each tissue using low and high energy images. The results from dual energy measurements of breast volume and density, using different projections, show that the technique is highly reproducible (Fig. 5). Breast density measurements from right and left breasts and comparison to %FGV from chemical analysis were highly correlated. The SEE from dual energy measurements is improved by approximately factor of 2 as compared with the other techniques. The linear regression fitting parameters (slope = 1.90 and intercept = −49.6%) between breast density measurements and %FGV from chemical analysis is similar to fitting parameters (slope = 2.00 and intercept = −35.6%) in a previous report using bovine tissue.⁴⁸ This close similarity in linear fitting parameters suggests a similarity in tissue composition. Furthermore, the high correlations between measured breast density and %FGV from chemical analysis serve to validate the use dual energy mammography as a breast density measurement technique.

The water, lipid, and protein contents of the breasts can be measured with an error of approximately 1% using chemical analysis.³³ The highly linear relationships between breast density and the water, lipid, and protein contents indicate that knowing breast density is akin to knowing the average water, lipid, and protein content of the whole breast. As expected, the relationship between breast density and water and protein contents were positively correlated, while it was negatively correlated with its lipid content. The measured volumetric fraction of protein was approximately 2%–10%. Therefore, breast density can be expected to be similar to volumetric fraction of water in the breast tissue. Furthermore, %FGV from chemical analysis can be used as an analogous metric for breast density.³³ The only difference between the two metrics is that the adipose tissue also contains some water and a small amount of protein.

Dual energy mammography includes the skin in breast density measurements. This is due to the projection nature of the technique. The skin was also included in chemical analysis, which simplified the validation procedure. However, it is potentially possible to estimate the skin volume and subtract it from the measured fibroglandular volume. This step will be necessary before the clinical implementation of this technique.

Dual energy mammography was previously validated in phantoms as an accurate technique for breast density measurement.⁴⁰ However, the current breast density measurements in postmortem breasts produced data beyond 0% and 100% breast density. These results are in agreement with a previous report using dual energy for density measurement in bovine tissue.⁴⁸ This is due to the limitations of the existing glandular and adipose phantom material used for dual energy calibration, which is caused by the discrepancy in chemical composition of the phantoms and the actual glandular and adipose tissues.⁴⁸ Glandular and adipose equivalent calibration phantoms were manufactured based on chemical compositions reported from a relatively few number of samples. Development of new phantom materials for dual energy mammography calibration is the matter of current research.

Radiation dose associated with dual energy mammography is an important factor that needs careful consideration before its clinical implementation. The current dual energy technique requires approximately 40% additional radiation exposure for the high energy image, which is not practical for clinical implementation. Therefore, future clinical implementation of this technique will require methods to minimize the radiation dose in addition to minimizing the time between low and high energy image acquisition and the potential motion misregistration artifacts. Another solution is the recent clinical implementation of a spectral mammography system based on energy resolved photon counting detector, which addresses both the radiation dose limitation and the potential misregistration artifacts.⁵² The energy information is recorded during a single low dose image.^53–56 The dual energy decomposition process can be easily automated for future clinical implementation of breast density quantification.

Establishment of dual energy mammography as an accurate measurement of breast density would allow better integration of breast density into breast cancer risk models. Additionally, this objective measure of breast density could potentially allow for improved prediction of mammographic sensitivity in a given breast than possible with radiologist reader assessment of breast density which entails moderate intra- and interobserver variability.

The term “personalized screening” implies that because breast cancer risk and screening sensitivity differ among different women, the recommended ages to begin and end screening, frequency of screening, use of digital tomosynthesis instead of 2D mammography, and addition of supplementary modalities, such as screening ultrasound and MRI, should depend on a patient's age, risk group, and breast density.

Addition of supplementary screening with ultrasound to mammography was shown to increase cancer detection rates among high risk women in ACRIN Trial 6666.^57,58 However, the biopsy positive predictive value for lesions detected by ultrasound alone in this and other studies has been 5%–10% so that increased cancer detection was achieved at the cost of a substantial increase in false positive biopsies.⁵⁹ Screening with digital tomosynthesis has been shown to increase detection of invasive cancers at initial screening along with a decrease in both recall rates and false positive rates but the radiation dose with their protocol was double that for digital mammography alone.^60,61 MRI screening of very high risk women has been shown to increase cancer detection rates above those for mammography across nine overlapping studies.^62,63 However, MRI is costly ^64–66 and requires use of intravenous contrast injection. Because breast cancer screening guidelines should be based on achieving a reasonable trade-off of benefits, risks, and costs, use of a more objective measurement of breast density should have substantial clinical value. At present, the American Cancer Society (ACS) as well as the American College of Radiology (ACR) and the Society of Breast Imaging (SBI) recommend annual screening mammography beginning at age 40 for average risk women with no upper age limit to stop screening for those in generally good health and at least 5 years of life expectancy.^67,68 However, “personalized screening” is already practiced to some degree. Both ACS and ACR/SBI guidelines recommend that very high risk women start screening mammography at an earlier age and that those having a 20% or higher lifetime risk receive supplementary screening with MRI. With regard to women with dense breasts, neither of these organizations has yet recommended screening ultrasound due to concern for false positive biopsy rates. At the other end of the guideline spectrum, one group of investigators has recommended that women aged 50–79 years with fatty breasts (BI RADS I) and no family history of breast cancer be screened with mammography only every 3–4 years.⁶⁹ Clearly, a more objective method of density assignment, such as dual energy mammography would be useful for consideration of any supplementary imaging recommendation and for prediction of breast cancer risk.

In summary, the results indicate that dual energy mammography can be used to accurately measure breast density. The variability in breast density estimation using dual energy mammography was lower than radiologist reader assessments, standard histogram thresholding, and the fuzzy C-mean algorithm. Improved quantification of breast density with dual energy mammography is expected to further enhance its utility as a risk factor for breast cancer as well as a predictive marker for the relative sensitivity of mammography in that breast.