Tensional Homeostasis in Single Fibroblasts

Abstract

Adherent cells generate forces through acto-myosin contraction to move, change shape, and sense the mechanical properties of their environment. They are thought to maintain defined levels of tension with their surroundings despite mechanical perturbations that could change tension, a concept known as tensional homeostasis. Misregulation of tensional homeostasis has been proposed to drive disorganization of tissues and promote progression of diseases such as cancer. However, whether tensional homeostasis operates at the single cell level is unclear. Here, we directly test the ability of single fibroblast cells to regulate tension when subjected to mechanical displacements in the absence of changes to spread area or substrate elasticity. We use a feedback-controlled atomic force microscope to measure and modulate forces and displacements of individual contracting cells as they spread on a fibronectin-patterned atomic-force microscope cantilever and coverslip. We find that the cells reach a steady-state contraction force and height that is insensitive to stiffness changes as they fill the micropatterned areas. Rather than maintaining a constant tension, the fibroblasts altered their contraction force in response to mechanical displacement in a strain-rate-dependent manner, leading to a new and stable steady-state force and height. This response is influenced by overexpression of the actin crosslinker α-actinin, and rheology measurements reveal that changes in cell elasticity are also strain- rate-dependent. Our finding of tensional buffering, rather than homeostasis, allows cells to transition between different tensional states depending on how they are displaced, permitting distinct responses to slow deformations during tissue growth and rapid deformations associated with injury.

Introduction

The interplay between microenvironmental forces and cell-generated forces is an increasingly important subject of study, as researchers seek to elucidate the myriad of ways in which physical signals affect biological processes, from differentiation (1) to metastasis (2). Adherent cells not only transduce applied forces into biochemical signals, but they also adjust their own mechanical state in response (3). This can be manifested through organizational changes within the cell that alter cytoskeletal architecture, modulate cellular elasticity, or generate a concomitant contractile response to applied forces.

The concept of tensional homeostasis has received significant attention as a way of defining the interplay between the external and internal mechanical state of cells. First described as a basal equilibrium stress state (4), the term “tensional homeostasis” was later coined by Brown et al. (5) to explain the tendency of millions of fibroblast cells embedded in a three-dimensional collagen gel to counteract external force application and move toward a previous force setpoint that had been established before external force application. The disruption of tensional homeostasis has been implicated in numerous disease states, from cardiovascular disease and developmental disorders to cancer (6). In particular, a 2010 study, looking at the disease known as floppy-eyelid syndrome, reported a significantly larger tensile setpoint for diseased fibroblast cells than for healthy fibroblasts (7). Additionally, metastatic cancer is thought to be associated with a disruption of tensional homeostasis (2).

Although tensional homeostasis is a pervasive concept within cellular mechanobiology, there have been no studies, to our knowledge, that have shown direct evidence of a cell’s ability to respond to external loading by maintaining a homeostatic level of tension. The only evidence consists of indirect measures of this behavior, either by extrapolating the direction of force response to a step load (5,7) or using cell stiffness as a proxy for contractile tension (8). Furthermore, the nature of tensional homeostasis at the single cell level is obscured by observations that cells stiffen and spread more when cultured in a stiffer microenvironment (9). Several studies have provided insights into the complex relationships among the substrate stiffness, spread area, and homeostatic tension (10–12), but the ability of the cell to regulate one of those properties independent of the others has yet to be shown.

We set out to look for direct evidence of tensional homeostasis in fibroblast cells using a single-cell contraction-force microscopy system (13–15). Like previous experiments investigating tensional homeostasis, we worked with fibroblasts as a model cell system because of the importance of tension in their native connective tissue environment and their previous use in tensional homeostasis experiments. We used micropatterning to constrain the spread area of a cell and to identify the role of the spreading process in establishing a steady-state force. Then, we tested for the presence of tensional homeostasis by displacing one of the surfaces or by changing the apparent stiffness experienced by the cell in the direction of contraction and observing its contractile response. Our findings indicate that fibroblasts are unable to maintain a fixed tensional setpoint but can modulate their tension in response to external strains, a process we call “tensional buffering”. The regulation of tension through buffering instead of feedback on a single tension setpoint allows for a tunable response to external perturbations of different rates, depending on the cell’s previous mechanical state.

Materials and Methods

Cell culture and sample preparation

NIH 3T3 fibroblasts were cultured in DMEM (Mediatech, Manassas, VA) supplemented with 10% fetal bovine serum (Lonza, Walkersville, MD), and 1% Penicillin/Streptomycin (Sigma, St. Louis, MO). Cells were collected by incubating in 0.25% trypsin for 3 min, followed by resuspension in trypsin-neutralizing solution, centrifugation (300g for 5 min), and resuspension in preheated CO₂-independent media (Invitrogen, Carlsbad, CA) supplemented with 10% FBS and 1% Pen/Strep. Cells were then given at least 15 min to recover from trypsinization before experiments began.

Cells were transiently transfected with the GFP-vinculin (kind gift of C. Waterman, National Institutes of Health, Bethesda, MD), mCherry-LifeAct (kind gift of C. Stefani and E. Lemichez, the University of Nice Sophia Antipolis, Nice, France), or GFP-α-actinin 1 (from Addgene, Cambridge, MA) plasmids by electroporation (Life Technologies, Carlsbad, CA). This was performed according to manufacturer’s protocol. Cells were harvested for experiments after 18–48 h of transfection. Nonfluorescent cells were incubated with CellMask Orange (Invitrogen) for 3 min, washed with phosphate-buffered saline, and added to the imaging chamber to monitor cell spreading.

Micropatterning of adhesion

To prevent the cells from spreading unevenly between the substrate and cantilever surfaces, we patterned both surfaces with 220–320 μm² of fibronectin, blocking the remaining surface with 10% bovine serum albumin solution to prevent adhesion. Substrate patterning was done through microcontact printing as described in von Philipsborn et al. (16). On the cantilever, a constrained pattern of extracellular matrix (ECM) ligand was achieved using the dipping method, as previously described in Parekh et al. (17). Briefly, a micromanipulator was used to dip only the end of a cantilever in a 50 μg/mL fibronectin solution (Sigma). After a 20-min incubation period, the cantilever was rinsed in ultra-pure water and was incubated in a 10% bovine serum albumin solution at 37°C for 1 h to passivate the uncoated surface. The cantilever was then rinsed in ultra-pure water again and mounted directly onto the atomic force microscope (AFM). By adding 1% fluorescently labeled fibronectin, we were then able to visualize the patterned areas and measure the size of available ligand on both surfaces.

Contraction-force microscopy

Experiments were conducted using a BioScope Catalyst Atomic Force Microscope (Bruker AXS, Santa Barbara, CA) with a temperature-controlled stage mounted atop an inverted optical microscope (Zeiss Axio Observer Z1; Carl Zeiss, Thornwood, NY). Data acquisition and AFM control was done using a signal access module and custom-designed software (LabVIEW; National Instruments, Austin, TX). Tipless, uncoated All-in-One silicon cantilevers from BudgetSensors (Sofia, Bulgaria) were used in all experiments with an average spring constant of 200 nN/μm, as determined by fitting thermal fluctuations of each cantilever in air.

Cell contraction was measured with the AFM as previously described in Webster et al. (14). Briefly, we established simultaneous contact between a cell and the top and bottom patterned substrates. Then, we measured the deflection of the cantilever as the cell spread onto both surfaces. A cell usually undergoes a fast contraction phase, followed by a force plateau phase, which marks the beginning of steady state. We evaluated whether or not the cell has achieved a tensile steady state based on a significant drop in contraction force rate compared to during initial spreading and over 10 min of force fluctuations that are <10% of the average value.

Once the cell has reached a steady-state force, we tested whether this force was a regulated value (tensional homeostasis) using a closed-loop piezoelectric scanner to control the separation of the base of the cantilever (or the cantilever chip) from the substrate. We applied a 0.1 μm/min, 1 μm/min, or step change in cantilever position. By measuring how the cell force changes with these different perturbations, we can evaluate whether the force is unregulated (leaves the steady-state condition) or is regulated (remains within the steady-state condition).

Stiffness-clamp technique

The apparent stiffness of the AFM cantilever was modulated using the stiffness-clamp feedback algorithm, as described in Webster et al. (14). The apparent stiffness of the cantilever, k_apparent, which is the stiffness experienced by the cell in the direction of contraction, is related to the force generated by the cell (ΔF) by Hooke’s Law,

$$k_{\text{apparent}}=\frac{\Delta F}{\Delta x_{\text{cell}}},$$ (1)

where Δx_cell is the change in cell height as it contracts and deforms the AFM cantilever (Δx_cantilever, k_cantilever). Without a stiffness clamp, Δx_cell = Δx_cantilever and k_apparent = k_cantilever. However, by adjusting the displacement of the cantilever with the piezo actuator (Δx_piezo) through a feedback algorithm written in the software LabVIEW running at 100 Hz, we can modulate the displacement of the cell (Δx_cell = Δx_cantilever − Δx_piezo) to attain a desired apparent stiffness, k_apparent.

Microscopy and image analysis

Images of focal adhesions and the micropatterned surface were acquired by total internal reflection fluorescence (TIRF) microscopy on an inverted microscope (Axio Observer.Z1, Zeiss), equipped with a 100×/1.46 NA oil immersion objective (Plan-Apochromat, Zeiss) and an electron-multiplying charge-coupled device Ixon camera (Andor, South Windsor, CT). Z-stack images of cells were collected on a spinning disk confocal microscope (Axio Observer.Z1, Zeiss) with a 63×/1.4 NA oil immersion objective (Plan-Apochromat, Zeiss). Time-lapse images were taken at 30-s intervals to monitor cell spreading and adhesion dynamics during loading perturbations. Analyses of cell spreading and focal adhesion dynamics were performed using the softwares ImageJ (National Institutes of Health) and MATLAB (The MathWorks, Natick, MA). Cell area was computed from thresholded images of either GFP-vinculin or CellMask Orange (Invitrogen). For the analysis of adhesion dynamics, a mask for adhesions was obtained by thresholding the maximum projection of a time-lapse movie 1 min before and after the loading perturbation. The average pixel intensity within the segmented adhesions was then computed. Normalized intensity change was computed as

$$\Delta I/I=\left(I_{\text{after}}-I_{\text{before}}\right)\text{/}{I}_{\text{before}},$$ (2)

where I_after and I_before correspond to average intensities before and after a ramp or step displacement, respectively.

Single cell microrheology

Microrheology experiments were conducted on single cells using a custom code written in the software LabVIEW (National Instruments) to apply a 20-nm amplitude, 2-Hz sinusoidal input to the cantilever holder piezo for a 30-s period. A DSP lock-in amplifier (Ametek, Oak Ridge, TN) was used to read the magnitude and phase delay of the cantilever deflection, after correcting for magnitude and delay offsets by first running the measurement directly on the hard substrate. The following equations were used to calculate the dynamic moduli of cells, namely the storage (E′) and loss (E″) moduli at 2 Hz,

$$E^{\prime }=\frac{FH}{Ad}\cos \theta ,$$ (3)

$$E^{″}=\frac{FH}{Ad}\sin \theta ,$$ (4)

where F is the amplitude of the force of the cantilever deflection, H is the cell height, A is the cross-sectional area of cell between the surfaces, d is the amplitude of cell deformation, and θ is the phase lag of the cantilever deflection from the piezo displacement. The units of the storage and loss moduli are in Pascals and they describe the elasticity (or stiffness) and the viscosity of the cell, respectively.

Statistical analysis

Tests for significance in force, storage modulus, and focal adhesion intensity change after strain were conducted using the Student’s t-test, with a two-tailed, p ≤ 0.05 or p ≤ 0.1 threshold for significance. The significance of force and storage modulus change compared to steady state was tested using the paired Student’s t-test, with a two-tailed, p ≤ 0.05 threshold for significance. Average values were presented ± SE unless otherwise noted.

Results

Steady-state tension is achieved upon completion of cell spreading

To observe whether cells will actively maintain a constant level of tension, we first considered the conditions necessary to allow an NIH 3T3 fibroblast to reach a steady-state force. We used contraction-force microscopy, which is a technique based on AFM, to measure cell-generated forces with nanoNewton resolution, as previously demonstrated in our group (13–15). We presented cells with two parallel surfaces coated with the ECM protein fibronectin. The two surfaces consisted of a tipless AFM cantilever on one side and a glass coverslip on the other (Fig. 1 A). To limit cell spreading, we micropatterned both surfaces to provide an attachment area of 220–320 μm² on each surface, equivalent to the total spread area occupied by fibroblasts on a single flat surface, and we observed that cells pull the two surfaces together as they filled the patterns (Fig. 1 B). Contracting cells form an extended columnar shape, spanning both the substrate and the cantilever, as seen by confocal microscopy (Fig. 1 C).

Figure 1.

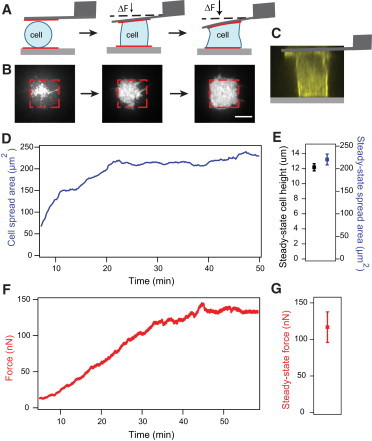
Single cells spread between two surfaces reach a steady-state height, spread area, and tension. (A) Schematic diagram of the contraction-force microscopy setup. Cartoon depicts a cell undergoing morphological changes as it spreads between an AFM cantilever and a glass substrate. The two surfaces are patterned with fibronectin to constrain cell adhesion and spreading. The cell spreads and contracts against the cantilever, which enables nanoNewton-level measurements of traction force in the vertical direction. The cell eventually fills up the micropatterned substrates to form an hourglass shape. Note that the deflection of the cantilever is exaggerated to illustrate changes in force measurements. (B) TIRF images of the spreading process on the bottom surface. The cell was visualized using a membrane dye (scale bar: 10 μm). (C) A side projection of an NIH3T3 fibroblast expressing mCherry-LifeAct at steady state taken with confocal microscopy showing a columnar shape and cortical actin underneath the membrane. (D) Example trace of cell spread area increasing over time and eventually reaching a steady state when the cell has filled up the patterned area. (E) Average height (N = 39) and spread area (N = 19) during steady state. Error bars indicate standard error. (F) Example trace of cell tension also increasing during spreading and reaching a plateau when spreading ceased. Note: Area and force traces from panels E and F are taken from different cells. (G) Average steady-state force (N = 42). Error bars indicate standard error. To see this figure in color, go online.

In the confocal image, we observed a cortical actin mesh surrounding the columnar region of the cell, although no distinct stress fibers. Constraining cell spread area on both surfaces was necessary to limit cell motility and increase the likelihood of cells staying attached to both surfaces during our experiments, because cells tended to commit to the uniformly-coated ECM surface if only one surface was patterned (percentage of cells adhered to both surfaces with ECM pattern on both sides: 94%; with ECM pattern on one surface: 10%; with neither surface patterned: 4%). Using patterned surfaces that were too large (>600 μm²) also lowered the reliability of cell adhesion to both surfaces. In our assay, the cell can contract against the two ECM-coated surfaces to generate out-of-plane (vertical) forces, as well as across each surface to generate in-plane (horizontal) forces. This geometry adds an additional dimension beyond conventional two-dimensional assays, and it partially mimics the three-dimensional forces that exist for fibroblast cells embedded in a matrix (18). With our AFM-based technique, we are able to directly measure the out-of-plane contractile forces, but not the in-plane forces typically measured using two-dimensional traction force microscopy.

We quantified cell spreading during force generation by imaging cells stained with membrane dye using TIRF microscopy (Fig. 1 B). As the cell’s lamellipodia reached the edges of the pattern, the spread area stopped increasing and the cell maintained this spread area throughout the experiment (Fig. 1 D). Similarly, contraction force increased over time and leveled off to a steady-state value within 15 min after spreading ceased (Fig. 1 F). The average steady-state force for fibroblasts, when they contracted against an AFM cantilever with average stiffness of 200 nN/μm, was 117 nN (±21 nN) and the average cell height was 12.2 μm (±0.5 μm), reflecting the physical diversity of the population (Fig. 1, E and G). The average cell spread area was 220 μm² (±12 μm²), consistent with the size of the patterned area (Fig. 1 E). This steady-state force remained unchanged over long times (>30 min) after spreading was complete, in the absence of any perturbations. Thus, force generation and spreading appear to be closely correlated in our experimental setup, as expected from previous studies of spreading on elastic substrates (9,10,12).

Steady-state tension is not maintained in response to mechanical perturbations

Fibroblasts in connective tissues experience strains of varying magnitudes and rates due to body motion or muscle contraction (19). Having demonstrated that single cells reach a steady-state force, we set out to test whether the cell is capable of maintaining this tension when it is strained. We first ensured that a spread cell has reached steady state by waiting until the cell has remained at a constant contraction force (<10% deviation) for at least 10 min. With the cell in steady state, we strained the cell by linearly increasing its height by 1 μm at different rates and then quantified cell tension at the new cell height (Fig. 2 A). For a 12-μm-tall cell, the height change corresponds to a 8% strain, which is comparable to a ∼7% strain that occurs when a sarcomere unit contracts (19).

Figure 2.

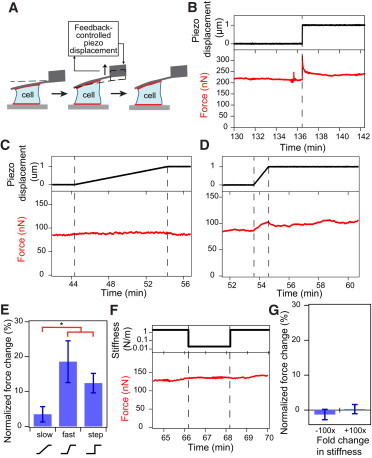
Steady-state tension of single cells is altered by cell displacement in a rate-dependent manner, but not by changes in extracellular stiffness. (A) Cartoon depicting the loading perturbation applied by displacing the cantilever by 1 μm either toward the bottom substrate or away from the substrate at rates of 0.1 μm/min, 1 μm/min, or with a step motion, after a cell has reached steady state. (B) Application of a 1-μm step displacement induced a jump in contractile force, followed by a partial viscous dissipation to a smaller but still significantly higher value compared to before loading. (C) Contractile force increased slightly when a cell was slowly strained at 0.1 μm/min by 1 μm. (D) Force was increased when a cell was quickly strained at 1 μm/min by 1 μm and the cell remained at higher tension even after the ramp displacement ended. (E) Force changes for each loading condition were calculated as the difference between average force before and after ramp or step displacement and were normalized to initial steady-state force. Normalized force change after a fast ramp or step displacement was significantly larger than force change after a slow ramp. Error bars represent standard error. Paired t-tests indicate that changes in steady-state force before and after mechanical perturbations were statistically significant for all three strain rates (N = 16, 13, and 9, for the slow ramp, fast ramp, and step conditions, respectively; ^∗p < 0.05). (F) After a cell has reached steady-state force, the apparent cantilever stiffness was cycled from 2000 nN/μm to 20 nN/μm, and back to 2000 nN/μm at 2-min intervals. (G) Normalized force change after a 100× decrease in stiffness and a 100× increase in stiffness. There was no significant change in steady-state force during step changes in the apparent cantilever stiffness. Error bars represent standard error. (Number of step changes, N_step = 9, 11 for decreasing and increasing stiffnesses, respectively.) To see this figure in color, go online.

When we applied a step displacement of 1 μm on a cell to increase its height, we measured an immediate increase in force, followed by a viscoelastic relaxation to a new steady-state force that was on average 14% higher than the cell’s initial contractile force (Fig. 2, B and E). Interestingly, when we increased the cell height at a slower rate of 0.1 μm/min, we not only avoided observing the viscoelastic relaxation effects on the force trace, but we also observed a much smaller increase in steady-state force of 3% after the ramp perturbation (Fig. 2, C and E). To further elucidate the role of strain rate in tensional homeostasis, we displaced a cell by 1 μm at a rate that is an order-of-magnitude faster (1 μm/min) and we observed a 19% change in steady-state force and no viscoelastic relaxation (Fig. 2, D and E).

In all experiments, whether ramp or step perturbations, cellular tension did not return to the original steady-state value, in contrast to what was expected from tensional homeostasis. Instead, the cell maintained its tension at a new steady-state value, or setpoint force, for >20 min. We found that the cell’s steady-state tension was increased after a positive strain and reduced after a negative strain. Because the change in force was similar in magnitude for both positive and negative strains, the normalized contractile responses to displacements in both directions were averaged together (Fig. 2 E). We included data from positive and negative strains for all subsequent analyses of cellular response to strain. We did not observe a further increase in the magnitude of normalized force change after a step displacement compared to a fast ramp displacement. This could potentially be attributed to an upper limit in force change before plastic deformation of the cytoskeletal network, or partial fluidization, occurs (20).

These results show that steady-state force generated by single fibroblasts, an average of 117 nN, can be altered by mechanical strain in a rate-dependent manner, with a maximal change of 19% when cells were strained at 1 μm/min. This is a speed comparable to the migration rate of some cells, and thus, the strain rate they exert on neighboring cells in a tissue that are displaced by the movement (21). This behavior is in contrast to the strict definition of tensional homeostasis that predicts a fixed contractile force setpoint, which is actively maintained despite mechanical perturbations. The increasing change in new steady-state force with increasing strain indicates that tension is not directly proportional to cell height, and that fibroblasts can buffer changes in tension, albeit incompletely. We refer to this varying compensation of tension, which could be an active or passive process, as tensional buffering.

Steady-state tension is insensitive to stiffness change

Next, we investigated the stiffness-sensing behavior of the fibroblast after it reaches a steady state. Substrate stiffness has been shown to influence cell contractility, which can drive differentiation and tumorigenesis (1,2,22). Fibroblasts in particular have been found to have higher contractility and spread area when cultured on stiffer substrates (2,9). We have previously found that the fibroblast spreading and contraction rate is dependent on stiffness in the direction of contraction using an AFM-based contraction-force microscopy technique known as a “stiffness clamp”. This is a technique by which the effective cantilever stiffness can be dynamically altered through feedback (14,15). The same stiffness response was observed in skeletal muscle cells using a parallel microplate system (23). We applied the stiffness-clamp approach to evaluating the response of fibroblasts in steady state. After a cell has spread and contracted to a steady-state force under the AFM cantilever’s native stiffness of ∼200 nN/μm, we cycled the apparent stiffness of the cantilever between 2000 and 20 nN/μm at 2-min intervals (Fig. 2 F). Interestingly, we did not observe a significant change in cellular tension in response to step changes in stiffness, implying that cells not actively spreading do not respond to changes in resistance to contraction (i.e., microenvironmental stiffness) after initial spreading is completed and the cytoskeleton is organized for contraction (Fig. 2 G).

Strain-rate-dependent change in steady-state tension is accompanied by a change in cellular stiffness

Because the contractile state of a cell is driven by the acto-myosin machinery, we postulated that mechanical properties of the cell would also be altered after a change in steady-state force. Therefore, we set out to observe whether the cell’s mechanical properties changed with mechanical displacement in a strain-rate-dependent manner. To that end, we used AFM microrheology to track the storage and loss moduli as the cell spread, contracted, and reached steady state. In brief, a very small sinusoidal oscillation of 20-nm amplitude at 2 Hz was applied on a cell with an AFM cantilever, and the corresponding magnitude and phase lag of cell deformation as a result of the applied oscillations was measured to determine the viscoelastic properties of the cell. A more elastic, or stiffer, cell will have a larger storage modulus whereas a more viscous, or fluidlike cell, will have a larger loss modulus. We observed that cellular elasticity (storage modulus) increased as the cytoskeleton organized during spreading into a contractile structure, peaking when the cell reached steady state (p < 0.003, n = 18, Fig. 3, A–C). The loss modulus of the cell, proportional to its dynamic viscosity, also increased during spreading and plateaued when spreading ceased (p < 0.002, n = 18). Notably, in the absence of an external perturbation, the cell remained at a steady-state force, spread area, and elasticity.

Figure 3.

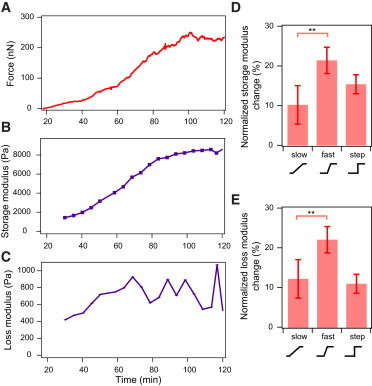
Mechanical properties of single cells reach a steady state after spreading but are altered after cell displacement. (A) Contractile force increased during spreading and reached a plateau when spreading ceased. (B) The storage modulus and (C) loss modulus of a cell increased during spreading. Both moduli reached a plateau when the cell was no longer increasing its tension. (D) Normalized change in storage modulus after ramp and step displacements of the cell. (E) Normalized change in loss modulus after ramp and step displacements of the cell. (N = 9, 10, and 9, for the slow ramp, fast ramp, and step conditions, respectively; ^∗∗p < 0.1). Error bars represent standard error. To see this figure in color, go online.

To test whether changes in setpoint force due to strain affected elasticity, we conducted the same ramp and step perturbations described above after a cell reached steady state, while measuring cell rheology before and after each perturbation. We observed the largest normalized change in storage modulus after a rapid strain at 1 μm/min (21%), followed by a step strain (15%), and slow strain at 0.1 μm/min (10%) (Fig. 3 D). The positive correlation between force change and elasticity change could be due to stress stiffening of the acto-myosin network (24). Interestingly, the normalized change in loss modulus also exhibited the same trend, indicating that the cell became more elastic and viscous both during spreading and after fast ramp displacements (Fig. 3 E). These results suggest a compensatory mechanism to buffer force change by which minimal cytoskeleton rearrangement occurs for slow strains, whereas significant reorganization of the cytoskeleton is induced upon rapid strains. The reorganization of the cytoskeleton could be an effect of realignment of the actin filaments, which are bound in a meshwork by actin crosslinking proteins, leading to the observed change in elasticity of the cell after a rapid strain.

Strain-rate-dependent change in steady-state tension does not affect focal adhesions

Many studies have elucidated the diversity of signaling pathways that regulate cellular tension. These pathways converge on regulation of the proteins that constitute the acto-myosin network and can influence force generation as well as the cytoskeletal and adhesion architecture through multiple feedback loops (2,3,6,25). Because we observed that cytoskeletal mechanics of single fibroblasts are altered by strain, we hypothesized that the strain-rate dependence of tensional buffering is a function of the structural properties of the cell, namely its adhesions and cytoskeletal architecture.

Focal adhesion proteins play an important role in force transmission and activation of signaling cascades that alter contractility by mechanically linking the acto-myosin cortex with the extracellular matrix. The localization of several focal adhesion proteins, including vinculin, to adhesion sites has been shown to be force-sensitive at short timescales (25–27). Therefore, we expected to see a change in vinculin assembly at focal adhesions when a cell is strained rapidly.

We tracked the growth of GFP-vinculin clusters in a cell by measuring average vinculin intensity with TIRF microscopy while simultaneously measuring contraction force. We found vinculin to form clusters that localized primarily near the edges of the patterned substrate (Fig. 4 A). After the cell reached a steady-state force, we applied fast (1 μm/min) and slow (0.1 μm/min) displacements to the cell. Surprisingly, there was no significant change in vinculin intensity during either loading condition. We observed vinculin reinforcement in TIRF only when cellular tension was increased by >10-fold beyond the steady-state tension, which was generated by multiple displacement steps of 2–6 μm (Fig. 4, B and C). These results suggest that tensional buffering during intermediate strains (∼10%) does not require significant reinforcement or disassembly of focal adhesions, irrespective of strain rate.

Figure 4.

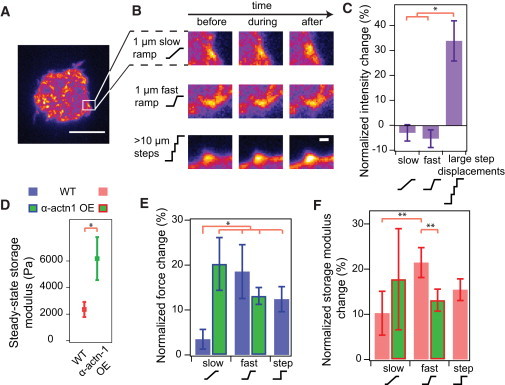
Rate-dependent changes in steady-state tension are dependent on cytoskeletal crosslinking but do not involve changes in adhesions. (A) A pseudo-colored image of vinculin after a cell has reached steady-state spread area (scale bar: 10 μm). (Open square) Size of the subset region. (B) Vinculin intensity was tracked before, during, and after ramp displacements in height. Images show the intensity of a subset region of different cells over time subjected to a slow ramp, fast ramp, or a large step strain (see panel A for subset area depiction). Vinculin intensity change was observed only after a large strain (consisting of multiple step displacements) was applied (scale bar: 1 μm). (C) The average intensity of adhesions remained unchanged after slow and fast ramp displacements. However, significant reinforcement was observed when a very large strain was applied to the cell. Error bars represent standard error (N_slow = 2, N_fast = 4, N_step = 3; ^∗p < 0.05). (D) Cells overexpressing α-actinin-1 were significantly stiffer than normal cells (N_wt = 18, N_actn = 9; ^∗p < 0.05). (E) Cells overexpressing α-actinin 1 showed a large normalized force change when they were displaced by 1 μm at a slow (0.1 μm/min) and fast (1 μm/min) rate. The contractile responses of wild-type cells after slow, fast, and step strains were presented again for easier comparison. Error bars represent standard error (N_slow = 6, N_fast = 6; ^∗p < 0.05). (F) Normalized changes in storage modulus of cells overexpressing α-actinin-1 after slow and fast ramp displacements. The normalized changes in storage modulus of wild-type cells after slow, fast, and step strains were presented again for easier comparison. No significant difference in storage modulus change was observed for the two loading rate conditions. Error bars represent standard error (N_slow = 6, N_fast = 6; ^∗∗p < 0.1). To see this figure in color, go online.

Strain-rate-dependent change in steady-state tension is altered by actin crosslinking changes

The architecture of the acto-myosin network can be regulated by the degree of actin filament crosslinking (28,29). The actin binding protein α-actinin is a dynamic crosslinker that localizes to the actin cortex and stress fibers and modulates actin network reorganization via its own binding rates and abundance in the cytoplasm (29,30). Multiple studies have demonstrated the importance of α-actinin in regulating stress fiber assembly, cortical stiffness, cytokinesis, and stiffness adaptation (29,31,32). Given the role of cytoskeletal reorganization in strain-rate-dependent force change, we set out to determine whether altering the initial cytoskeletal architecture by increased crosslinking could affect tension buffering during a slow mechanical displacement of the cell.

We transiently transfected fibroblasts with GFP-α-actinin-1 and selected cells with high GFP expression, corresponding to high protein expression, for mechanical analysis. As before, we applied fast (1 μm/min) and slow (0.1 μm/min) ramp displacements to single cells overexpressing α-actinin-1 after they reached steady-state tension and then measured the contractile response of these cells. We found that cells overexpressing α-actinin-1 were stiffer than normal cells, consistent with previous studies (Fig. 4 D) (32,33). When the cell was slowly strained by 1 μm at 0.1 μm/min, the steady-state force increased by 20%, much more than a wild-type cell (3%) at the same rate and comparable to the change in steady-state force for a wild-type cell strained at the fast rate (Fig. 4 E). Surprisingly, the normalized change in steady-state force did not further increase when the cell was strained more rapidly at 1 μm/min. The plateau in normalized force change as a function of strain rate was also reflected in the change in storage modulus of the α-actinin-1 overexpressed cells after slow and fast displacements (Fig. 4 F). These results suggest that tensional buffering no longer occurs within the 0.1–1 μm/min strain-rate range in cells with overexpression of α-actinin. This may be due to increased connectivity of the actin cytoskeleton, as reflected by the higher stiffness that limits reorganization under load.

Discussion

Adherent cells maintain a steady-state tension for a fixed spread area and height

In this study, we established an AFM-based contraction force microscopy assay to quantify tensional homeostasis in single cells. Our experimental setup provides high temporal resolution measurements of force generation during and after spreading. Our results quantify and correlate the dynamics of force generation and elasticity change when a cell spreads onto a defined area and shape, further supporting the notion that spreading is necessary to initiate force buildup in a cell (34).

We observed that a steady-state force was established by fibroblasts during cell spreading as they filled up available adhesive area. Our results extend previous studies showing the correlated nature of cell spreading and traction forces (12,34,35) to the generation of out-of-adhesive-plane traction forces, a geometry that is closer to the three-dimensional microenvironment of cells embedded in a matrix (18). During initial spreading, area increases without generating much force, consistent with previous observations of the initial P₀/P₁ phases of cell spreading (35,36). As area increases further, tension then starts to increase. However, as the available ECM area of 220–320 μm² on each side becomes completely filled, spreading ceases and cellular traction force levels off to a steady-state value at ∼117 nN for a microenvironmental stiffness of ∼200 nN/μm in the direction of contraction. This steady-state value is within the same order of magnitude as the ∼90 nN total force measured for smooth muscle cells spread to 400 μm² on a plane using PDMS micropillars, which is approximately the combined spread area of the cell on the top and bottom surfaces (34). The higher setpoint force could be due to different cell types and difference in total ECM-coated areas. Although not directly measured, we expect traction forces to be nonzero across the top and bottom planes where the cell attaches to the stiff substrate. Although the effects of different patterned fibronectin areas on steady-state force were not directly evaluated, we expect a positive correlation between constrained spread area and setpoint force based on evidence from the literature (12,34).

Adherent cells maintain a steady-state stiffness for a fixed spread area and height

By measuring cell stiffness during cell spreading, we observed that stiffening is correlated with increases in cell tension and spread area, reaching a storage modulus, on average, of 2.4 (±0.5) kPa, consistent with previous observations of fibroblast elasticity (37). The stiffening of the cell could be the result of organization and crosslinking of the actin cytoskeleton, along with myosin engagement and associated filament sliding, as the cell spreads and contracts against the top and bottom substrates (38). The correlation between cell tension or prestress and its storage modulus is consistent with the predictions of the tensegrity model (39). Material characterization studies of in vitro actin networks show a similar trend in network stiffening after addition of myosin and crosslinking proteins (28,40).

Most studies that relate steady-state traction forces to substrate stiffness involve exposure of cells to a fixed substrate stiffness, which cells encounter, spread on, and pull on. Our contraction-force microscopy system enables us to present the same cell with changes in stiffness in the vertical direction after the cell has reached a steady-state spread area and tension. We observed no change in tension once a cell reached steady state even though we changed stiffness by two orders of magnitude, implying that a cell is insensitive to stiffness change when the cell is no longer spreading and actively building or undergoing large-scale remodeling of its cytoskeleton.

Steady-state tension is tunable by strain rate rather than homeostatic or independent of strain

The fact that cells established a contractile steady state in our system presented us with the opportunity to test the widely asserted notion that cells maintain tensional homeostasis with their environment against opposing influences of external displacements (4,5). Several studies have alluded to this strict definition of tensional homeostasis in single cells but have not directly quantified cellular responses (5,7,8,24,41). To that end, our study is the first direct test of tensional homeostasis in single cells. Surprisingly, fibroblasts do not exhibit tensional homeostasis in the strictest sense, that is, they do not have an inherent basal setpoint tension. However, cells do minimize changes in force due to strain in a rate-dependent manner, likely by passive relaxation of the cytoskeleton.

Additionally, cells exhibit an altered setpoint tension after a rapid strain that does not relax back to the original steady-state force over at least 20 min. We term this strain-rate-dependent process “tensional buffering”. The normalized change in steady-state force is larger when a cell is subjected to more rapid strain, where passive relaxation is not rapid enough to accommodate cell strain. The nonlinear relationship between normalized force change and strain rate indicates an upper limit to strain rate before the acto-myosin network fails or undergoes partial fluidization, and this trend was reflected in the normalized change in storage modulus. In the earlier tensional homeostasis work measuring bulk tension in a matrix embedded with fibroblast cells, the change in tension was found to dissipate over a long timescale (5,7). The longer relaxation timescale could be a result of extracellular matrix remodeling and migration of cells within the matrix, in addition to the response of individual cells.

Our results are consistent with a recent discrete network model that predicts rate-dependent elasticity in fibrous actin networks consisting of only actin, motors, and crosslinkers (42). As a bulk material, the observed change in elasticity that accompanies change in force could reflect stress stiffening, which has been seen in many actin network studies, or alignment of the cytoskeleton in the direction of strain (40,43). However, the mechanism by which the acto-myosin cytoskeleton and other cellular components interact to give rise to tensional buffering remains unclear, as does how the new setpoint force could be maintained. Recent evidence suggests a potential role of actin as a tension sensor (43,44) whereby actin binding protein affinity is affected by structural changes (45) or bending (46) of the actin filament. These changes can either drive increased crosslinking with load (47,48) or inhibition of depolymerization when the filament is under tension (49).

A model presented by Kaunas et al. (50) focuses on the role of stress fibers and myosin in tensional homeostasis. Starting by simplifying a stress fiber with a sarcomeric model, Kaunas et al. (50) relate the tension and deformation of the stress fiber to the myosin cross-bridge cycling rate and the substrate loading rate. Using model parameters derived from experiments, they found a frequency dependence of the tension on stress fibers when undergoing sinusoidal loading. This model has been extended to irregular loading schemes (51) where, notably, it was found that the loading rate, and not the frequency, was the determinant of cellular tension, consistent with our findings. One result of this model is that for high strain rates, stress fibers behave elastically, with changes in length corresponding to a proportional change in tension. However, for low strain rates, myosin activity counteracts substrate deformation and stress fiber tension does not change. Instead, acto-myosin filaments simply slide past each other. This predicts that cells should exhibit tensional buffering as we observe, and that cellular elasticity would not change during slow loading. However, the model does not yet predict a new setpoint force after strain, nor does it predict a decrease in the normalized change in force after a very rapid strain, such as a step displacement, that might involve significant changes in the structure or breakage of the stress fiber. Hence, additional features may need to be incorporated into the model to characterize both how the cell responds during loading and how it behaves after loading.

Changes in cytoskeletal architecture alter tensional buffering

Based on our observation of tensional buffering, we hypothesized that a change in cytoskeletal architecture generated by mechanical displacement of the cell would lead to modifications in adhesions as well. Surprisingly, we did not observe any change in cell adhesions, marked by vinculin, during slow or fast loading. The cell’s adhesions are still sensitive to strain, but only at very high levels, demonstrating that mature adhesions can bear significant changes in cell displacement and load without reinforcement (52).

Instead, we found that perturbing the mechanics of the cytoskeleton by increasing actin crosslinking density affects the relationship between setpoint force and strain rate. We modified the mechanical state of cells by overexpression of the crosslinking protein, α-actinin-1. Previous reports have shown that changes in the binding and unbinding rate of crosslinking proteins to actin can tune the timescale of the viscoelastic response of F-actin networks (28). We postulated that higher expression of α-actinin-1 will increase the overall timescale at which filaments stay connected to each other, altering the cell’s ability to buffer changes in strain. Indeed, we found that cells with high expression of α-actinin-1 had a higher elasticity, and they showed a significant increase in setpoint force after both slow and fast displacements. The larger abundance of α-actinin in the cell may also increase the bundling of actin filaments as the crosslinked network becomes realigned during mechanical displacement, which increases the likelihood of myosin binding and exerting force on the filaments (43). Interestingly, the normalized force change for slow and fast displacements in cells with overexpression of α-actinin-1 followed the trend for fast and step displacements, respectively, in wild-type cells. Networks that are more crosslinked have been shown, via computational simulations, to soften due to crosslink rupture at smaller strains (53). The smaller force and elasticity change observed after a fast ramp displacement could be due to strain softening of the highly crosslinked acto-myosin network. Hence, we expect the tensional buffering regime of cells overexpressing α-actinin-1 to be shifted to strain rates below 0.1–1 μm/min.

Conclusions

By constraining the spread area for fibroblast cells spreading between a substrate and an AFM cantilever, we were able to isolate the response of contractile cells to mechanical displacement and test the tensional homeostasis hypothesis. We observed that once cells stopped spreading, they reached a steady-state force, thus highlighting the necessity of spreading to generate out-of-plane forces. We then found, by loading the cell at different rates, that single cells do not maintain a single tensional state but instead alter tension through a buffering response, wherein cells accommodate deformation and minimize tension increase more efficiently at low strain rates. Once the perturbation ceases, the cell buffers change in force around the new steady-state value, giving rise to a tunable force setpoint, a process we call tensional buffering.

The differences between tensional homeostasis and tensional buffering are analogous to the differences in regulation of blood glucose level around a constant setpoint and buffering of pressure change in blood vessels by aortic compliance. Measuring cellular elasticity throughout the contraction and loading conditions, we observed that the stiffness of the cell also changed in a strain-rate-dependent manner. Perturbation of crosslinking density by α-actinin-1 disrupted the buffering capacity of cells even at slow strain rates, where change in steady-state force was minimal for wild-type cells. Rather than maintain a constant mechanical state, cells may make use of tensional buffering to permit different responses to i), slowly changing strains in tissue during development, which they need to accommodate, and ii), rapidly changing strains during wounding, which they may need to actively resist.