Anomalous Surface Diffusion of Protons on Lipid Membranes

Abstract

The cellular energy machinery depends on the presence and properties of protons at or in the vicinity of lipid membranes. To asses the energetics and mobility of a proton near a membrane, we simulated an excess proton near a solvated DMPC bilayer at 323 K, using a recently developed method to include the Grotthuss proton shuttling mechanism in classical molecular dynamics simulations. We obtained a proton surface affinity of −13.0 ± 0.5 kJ mol⁻¹. The proton interacted strongly with both lipid headgroup and linker carbonyl oxygens. Furthermore, the surface diffusion of the proton was anomalous, with a subdiffusive regime over the first few nanoseconds, followed by a superdiffusive regime. The time- and distance dependence of the proton surface diffusion coefficient within these regimes may also resolve discrepancies between previously reported diffusion coefficients. Our simulations show that the proton anomalous surface diffusion originates from restricted diffusion in two different surface-bound states, interrupted by the occasional bulk-mediated long-range surface diffusion. Although only a DMPC membrane was considered in this work, we speculate that the restrictive character of the on-surface diffusion is highly sensitive to the specific membrane conditions, which can alter the relative contributions of the surface and bulk pathways to the overall diffusion process. Finally, we discuss the implications of our findings for the energy machinery.

Introduction

The proton concentration gradient between two cellular compartments is an essential part of the cellular energy machinery. In combination with the transmembrane electrical potential difference (Δϕ), it generates a protonmotive force that is utilized to synthesize ATP (1). Because measurements of the bulk-to-bulk protonmotive force correlate poorly with measured ATP yields (2–4), a simple chemiosmotic theory is inadequate. Hence, a steady-state model has been proposed (4,5), in which protons are continuously pumped across the membrane. These protons are then retained at the surface by a barrier that separates the surface volume from the bulk, so that a sufficiently high protonmotive force arises between the two faces of the membrane.

Recent equilibrium experiments (6,7) and calculations (8,9) have revealed that the proton concentration is indeed markedly higher on the membrane surface than in the bulk. In addition, a delay in surface-to-bulk as well as bulk-to-surface equilibration has been observed in kinetic experiments (10–12). These data suggest the presence of a barrier, which separates the surface from the bulk, and thus support the steady-state model.

A wide range of diffusion coefficients have been reported for the proton on a lipid membrane. In experiments, in which protons were instantaneously released on the membrane, very fast diffusion of the proton over the surface has been measured (3–12 × 10⁻⁵ cm² s⁻¹) (11,13–15), yet much lower surface diffusion has been observed in similar experiments (0.034 × 10⁻⁵ cm² s⁻¹) (10,16) as well as NMR measurements (0.44 × 10⁻⁵ cm² s⁻¹) (17), equilibrium experiments (0.02 × 10⁻⁵ cm² s⁻¹) (6), and simulations (0.15–0.23 × 10⁻⁵ cm² s⁻¹) (8,9). The reported diffusion coefficients thus cover two orders of magnitude. To obtain more insight into the surface diffusion of the proton and to understand why such a wide range in diffusion coefficients has been observed, we have performed extensive simulations of a proton near a hydrated DMPC membrane.

In aqueous environments, proton diffusion takes place via the Grotthuss mechanism; in principle, this requires a quantum mechanical description. However, the timescales and system size required for simulating this process in a realistic model system preclude the use of quantum mechanical methods. Instead, we used the HYDYN simulation protocol (18), a method that includes explicit proton transfer in classical force-field molecular-dynamics simulations.

Although proton transfer to lipid headgroups could be included in HYDYN as well, we have excluded this possibility in our simulations for the following two reasons:

• 1.Efficient proton diffusion over the membrane surface seems to be independent of the availability of proton carriers in the form of buffer molecules (13) or lipid-ionizable groups (14); and
• 2.Yamashita and Voth (9), who used a protonatable multi-state empirical valence bond (MS-EVB) model of dimethyl phosphate, have not observed any protonation of DOPC, DOPE, or DOPG lipids in their MD simulations of excess proton.

We obtained extensive sampling (∼5 μs) by extended trajectories (50 ns), which yielded a converged proton density profile and allowed an in-depth investigation of the dynamic properties of an excess proton near a DMPC lipid bilayer.

We found a proton surface affinity of −13.0 ± 0.5 kJ mol⁻¹, which is in agreement with previous results from both experiments (6,7,10,11) and computations (8,9), and supports the steady-state model. Furthermore, we found that proton diffusion over a lipid membrane surface is highly anomalous, with a subdiffusive regime over the first 1 ns, followed by a superdiffusive regime. The origin of the initial subdiffusive regime is the restricted diffusion of the proton on the surface by either strong binding to the lipids or entrapment inside small water clusters within the lipid headgroup region. The superdiffusive regime results from occasional excursions into the bulk solvent that lead to long-range surface diffusion. Due to the existence of a sub- and a superdiffusive regime, the proton surface diffusion coefficient is time- and length-scale dependent, which could provide an explanation for the wide range of diffusion coefficients reported in the literature.

Methods

Proton transfer

To describe the excess proton, we used the HYDYN protocol, a method that includes the Grotthuss proton shuttling mechanism in MD simulations (18). In HYDYN, a proton acceptor is selected at regular intervals from among all possible acceptors around the current donor, using a Monte Carlo criterion. In between selection steps, the excess proton evolves on the free-energy surface associated with proton transfer between the donor and the selected acceptor using λ-dynamics (19,20). A proton transfer step is considered successful if, at the end of this period, the proton resides on the acceptor. After this period, the evolution is terminated and a new acceptor is selected from among the molecules nearest to the molecule that now carries the excess proton. In this way, the excess proton can visit every protonatable site in the system, mimicking the Grotthuss mechanism.

The potential on which λ evolves is a linear interpolation between the potential energy functions of the reactant state (proton on donor) and product state (proton on acceptor). Therefore, during λ-dynamics, the system samples configurations in which the excess proton is either localized on a single water, forming a hydronium or Eigen complex, or delocalized over two waters, forming a Zundel complex.

To keep the hydronium model compatible with the MM force field, the hydronium parameters are based on the water model used in our simulations (TIP3P (21)). These parameters were optimized to reproduce the main characteristics of an excess proton in small water clusters and in bulk water (see the Supporting Material) (22).

Simulation setup

We simulated 100 copies of a DMPC membrane, modeled with the Berger force field (23) in TIP3P-water (21) with one excess proton for 50 ns each using HYDYN (18) (Fig. 1 a). In addition, we simulated 10 copies of the same membrane including a hydroxide (see the Supporting Material for parameters) for 50 ns each with the software GROMACS 4.5.4 (24). The system consisted of 64 lipids, 3658 water molecules, and one hydronium or hydroxide in a 4.6 × 4.6 × 8.8 nm box. The excess proton or hydroxide was initially positioned at the center of the water phase. Because the proton typically migrated to the membrane surface within 2 ns, we used the last 48 ns of each trajectory for analysis.

Figure 1.

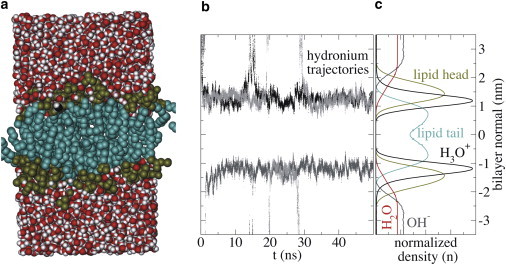
Excess proton near a membrane surface. (a) Simulation box, (b) examples of the time evolution of the excess proton along the bilayer normal, and (c) ensemble-average normalized number densities along the bilayer normal for the various components of the simulated system. The bilayer center is positioned at 0 nm and periodic boundary conditions connect the top and bottom of the graphs. To see this figure in color, go online.

Bond distances were constrained using the algorithms SHAKE (25) and SETTLE (26) for hydronium/ lipids and water molecules, respectively, enabling a 2-fs time step. Simulations were performed at 323 K, above the gel-to-liquid phase transition of DMPC (T_m = 296 K), using the Berendsen thermostat (τ_t = 0.5 ps). The λ-particle was coupled to an Andersen heat bath (27) of 323 K with a coupling constant of 0.1 ps. The pressure was maintained constant at 1 atm using semiisotropic coupling via the Berendsen barostat (28) with τ_p set to 2.5 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹. Lennard-Jones interactions were cut-off at 0.9 nm and the electrostatic interactions were treated using PME (29) with a real-space cutoff of 0.9 nm and a reciprocal spacing of 0.12 nm. Neighbor searching was performed every step.

Analysis

To determine the number of lipid-hydronium hydrogen bonds, we considered all lipid oxygens as acceptors and the three hydronium hydrogens as donors. A hydrogen bond was considered present when the O_lipid-O_hydronium distance was <0.35 nm and the O_lipid-O_hydronium-H_hydronium angle was <30°.

The hydrogen-bond existence function (either 0 when absent or 1 when present) was used to calculate the autocorrelation for each lipid-hydronium hydrogen bond. The hydrogen-bond autocorrelation functions shown in this work are averages over all these individual autocorrelations.

The lateral mean-square displacement (MSD) of the hydronium was calculated for all trajectories except those that include a transition of the proton to the periodic image membrane. Furthermore, we removed the center of mass motion corresponding to the membrane leaflet, upon which the hydronium resided. For the MSD of the lipid atoms, the values were calculated separately for the upper and lower leaflet, while removing the center of mass motion of the leaflet in question. Subsequently, the lipid MSD values of the lower and upper leaflet were combined.

For most observables, including MSD, proton transfer rates, and hydrogen-bond autocorrelation function, we calculated the corresponding value x for each separate trajectory, and displayed the average

$$\overline{x}=\frac{1}{n}\sum x$$

and standard error

$${\sigma }_{\overline{x}}=\frac{1}{n(n-1)}\sqrt{\sum {\left(x-\overline{x}\right)}^2}.$$

In cases where sampling was insufficient to determine a specific observable from one simulation, we combined 10 trajectories before calculating that observable. This was done for the hydronium free-energy profiles and density plots.

Results

Proton diffusion in water can proceed either as an excess proton (H⁺) via the Grotthuss mechanism, or by reunion with a proton hole (OH⁻) created by water autoionization. We modeled the excess proton and proton hole as a hydronium and a hydroxide, respectively. The density profile in Fig. 1 c and the free-energy profile in Fig. 2 show that the affinities for the membrane of these two species are very different. Hydronium has an increased affinity for the membrane surface, whereas hydroxide prefers the bulk. In this respect, the membrane surface is similar to the air/water interface, for which hydroniums also have affinity, but hydroxides do not (22,30). Because hydroxide does not bind to the surface, we focus on hydronium from now on.

Figure 2.

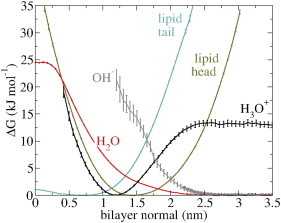
Free energy profiles along the bilayer normal demonstrate the strong proton surface affinity. The error bars denote the standard error. To see this figure in color, go online.

The excess proton moved to the membrane surface within 2 ns (Fig. 1 b). In more than half of the simulations the proton remained at the surface for the rest of the 50-ns simulation time, whereas in the other simulations the proton made one or multiple brief excursions into the water phase before reattaching onto the surface. We considered our simulations converged after 4.8 μs, when the proton density profiles on the lower and upper membrane leaflet were identical.

As shown in Fig. 1 b, proton bulk excursions lead to occasional migration of the excess proton to the periodic image of the bilayer, which occurred in ∼20% of our trajectories. For ensemble properties, these trajectories were simply added to the ensemble. For dynamic properties, however, these trajectories were excluded, because the influence of the periodic image bilayer on the time-dependent observables could introduce systematic errors.

Equilibrium distributions

As shown in Fig. 1 c, the hydronium has the largest normalized density at the interface, between the lipid headgroup region and the lipid tail region. The water density at the hydronium’s maximum density is already significantly reduced to 13% of the bulk density. Nevertheless, despite the decreased number of excess proton carriers in the lipid headgroup region (lower water density), the excess proton density in this region was 200 times higher than in bulk.

Free energy profiles were obtained via ΔG(z) = −RTlnp(z), with z as the bilayer normal, R as the gas constant, T as the temperature (323 K), and p(z) as the normalized number density at z (Fig. 1 c, and also shown in Fig. 2). The excess proton gains −13.0 ± 0.5 kJ mol⁻¹ upon moving from the water phase to the membrane surface.

On the surface, the proton resides mostly in close proximity to the lipid’s phosphate and carbonyl oxygens. The probability distribution of the minimum distance between the hydronium and the lipid oxygens (d_H-LipidO) shows that the formation of such pairs is very favorable (first peak in Fig. 3). The hydronium interacted with both the phosphate oxygen of the lipid headgroup and the carbonyl oxygen of the lipid linker. The free-energy profile extracted from the probability distribution (inset in Fig. 3) revealed that a hydronium approaching a lipid oxygen gains 5.8 ± 0.5 kJ mol⁻¹ in the second solvation shell around a lipid oxygen. A small barrier of 2.0 ± 0.6 kJ mol⁻¹ separates this first minimum from the much deeper second free-energy minimum of −22 ± 0.5 kJ mol⁻¹, which arises from direct hydronium-lipid oxygen interactions. Similar binding modes have also been observed by Smondyrev and Voth (8) and Yamashita and Voth (9).

Figure 3.

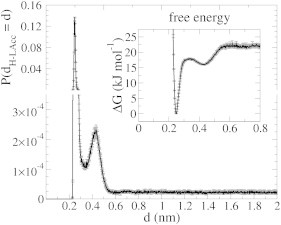
Probability distribution of the minimum distance between the hydronium and lipid oxygens. (Inset) Associated free-energy profile. The very favorable interaction of a hydronium in direct contact with a lipid oxygen (low free energy at 0.25-nm separation) explains the strong proton surface affinity. The second peak shows that a hydronium in a second solvation shell around a lipid oxygen is already favored over a bulk hydronium.

Dynamics

The preference of the proton for the headgroup region of the membrane restricts its motion and the diffusion over the surface is significantly lower than in water, in line with the results of Smondyrev and Voth (8) and Yamashita and Voth (9). Furthermore, because the correlation between the mean-square surface displacement and time deviates significantly from the linear relation characteristic for Fickian diffusion (Fig. 4), the diffusion of the excess proton is highly anomalous. The power-law exponent α of the relation

$$\langle {\left[r\left(t\right)-r\left(0\right)\right]}^2\rangle \sim t^{\alpha }$$

changes from 0.5 to 1.2 within the timeframe of our simulations (inset in Fig. 4 a). A plot of the self-part of the van Hove correlation function (G_s(r,t)) in the Supporting Material shows that the probability distribution of the surface displacement is non-Gaussian with a long tail, which also confirms that the diffusion is anomalous. A consequence of the anomalous proton surface diffusion is that the associated diffusion coefficient is not constant. Therefore, we calculated a time-dependent diffusion coefficient D(t) instead via

$$D\left(t\right)=\frac{\langle {\left[r\left(t\right)-r\left(0\right)\right]}^2\rangle }{2dt},$$ (1)

with d as the number of diffusion dimensions. Fig. 4 b shows that the time-dependent diffusion coefficient has a minimum at 1 ns of 0.069 ± 0.005 × 10⁻⁵ cm² s⁻¹. After a short increase, the diffusion coefficient appears to level off after 10 ns at 0.084 ± 0.13 × 10⁻⁵ cm² s⁻¹. For comparison, HYDYN yields a proton diffusion coefficient in bulk water at 300 K of 4.4 × 10⁻⁵ cm² s⁻¹ (18).

Figure 4.

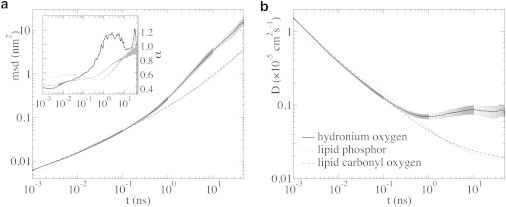
Surface diffusion of the hydronium oxygen (solid), lipid phosphor (dotted), and lipid carbonyl oxygen (dashed). The error bars denote the standard error (which falls within the line width for the lipid atoms). (a) MSD. (Inset) 10-point running average of the power-law exponent α in 〈[r(t) – r(0)]²〉 ∼ t^α as a function of time t. (b) Time-dependent diffusion coefficient (Eq. 1). These graphs highlight the anomalous surface diffusion of a proton on a DMPC membrane.

The average proton transfer rate is significantly reduced from 0.42 ps⁻¹ in the water phase (18) to 0.082 ± 0.024 ps⁻¹ at the membrane surface. Furthermore, Fig. 5 a shows that, at the membrane, proton transfer occurs in bursts, whereas proton transfer in water is a continuous process. We identified two distinct phases for proton transfer on the surface:

• 1.A stall phase characterized by virtually no transfer events (see plateau regions in Fig. 5 a), and
• 2.A transfer phase where the transfer rate approaches the one observed in the water phase.

Figure 5.

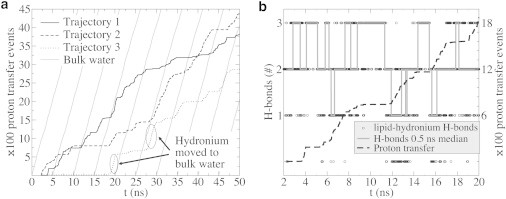
Proton transfer events at the membrane surface. (a) Comparison between the cumulative number of transfer events on the surface (three representative trajectories) and in the water phase (shaded). For convenient comparison, the latter is shown multiple times, shifted 5 ns along the x axis. (b) The correlation between proton transfer rate and lipid-hydronium hydrogen bonds. The correlation is most clear when the number of lipid-hydronium hydrogen bonds reaches its maximum, which is accompanied by almost absent proton transfer (plateau regions). The result of a 0.5-ns median of the lipid-hydronium hydrogen bonds, used for further analysis, is shown. For clarity, only 20 ns are displayed.

Fig. 5 b shows that the stall phase arises from a state, in which the hydronium forms three hydrogen bonds with lipids (see Methods for hydrogen-bond definitions). Moreover, as the number of lipid hydronium hydrogen bonds decreases, the probability of proton transfer increases (see Table 1). The average proton transfer rate in a state with zero, one, two, or three lipid-hydronium hydrogen bonds is 0.42, 0.23, 0.079, and 0.0012 ps⁻¹, respectively. The transfer rate of a proton at the surface without lipid-hydronium hydrogen bonds is similar to that in bulk water. However, with a probability of 0.035, 0.12, 0.41, and 0.43 to be in a state with zero, one, two, or three lipid-hydronium hydrogen bonds, respectively, the overall transfer rate is dominated by the states that exhibit slow transfer rates (states with two and three lipid-hydronium hydrogen bonds).

Table 1.

Probability that a number x of proton transfer events takes place within 1 ps

		Probability of x transfer ps−1
		None	1	2	3
Number of lipid-H3O+ hydrogen bonds	0	0.70	0.21	0.070	0.017
	1	0.85	0.094	0.044	0.010
	2	0.95	0.028	0.017	0.003
	3	1.00	0.001	0.000	0.000

Because of fast fluctuations in the number of hydronium-lipid hydrogen bonds, we used a 0.5-ns median (shaded line in Fig. 5 b) to extract trajectories that correspond to zero, one, two, or three hydronium-lipid hydrogen bonds, respectively, for further analysis of the proton surface diffusion. Fig. 5 b shows that the length of the stall phase agrees very well to a continuous stretch of median three hydrogen bonds, suggesting that the 0.5-ns median is an appropriate measure. The proton transfer rate, with 0.38, 0.22, 0.097, and 0.0058 ps⁻¹, and the occupancy, with 0.02, 0.10, 0.46, and 0.41, extracted from the trajectory parts with a median of zero, one, two, or three lipid-hydronium hydrogen bonds are also close to the values obtained in a direct analysis (previous paragraph). From now on, we will refer to the ensembles of trajectory parts that correspond to zero, one, two, or three (x) median hydronium-lipid hydrogen bonds as hb0, hb1, hb2, or hb3 (hbx).

A representative trajectory illustrating the proton transfer stall phase (Fig. 5) shows that the lifetime of a specific number of hydrogen bonds can be in the order of nanoseconds. Analysis of the lifetime distribution revealed a half-life for the existence of zero, one, two, or three lipid-hydronium hydrogen bonds of 0.63, 0.37, 0.69, and 0.87 ns, respectively. In addition, two and especially three lipid-hydronium hydrogen bonds exhibited a very long tail in the lifetime distribution, with >10% having a lifetime that exceeded 4 ns.

Further analysis of the hbx ensembles revealed that the MSD of hb3 was, within statistical error, equal to the lipid phosphor (Fig. 6 a), reaching an MSD after 300 ps of 0.13 ± 0.05 nm² and 0.10 ± 0.01 nm², respectively. A larger difference was found for hb2 and hb1, with 0.18 ± 0.01 and 0.62 ± 0.06 nm², respectively. Without hydronium-lipid hydrogen bonds, the MSD is larger still with 7.8 ± 0.6 nm². Thus, only hydroniums that have three hydrogen bonds to lipids follow the lipid diffusion.

Figure 6.

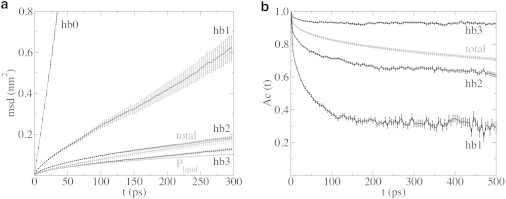
Restricted diffusion of an excess proton hydrogen-bonded to a lipid. Properties of the hbx ensembles, demonstrating the importance of the number of hydrogen bonds for the dynamics of the proton. (a) Lateral MSD. For comparison, the total hydronium and the lipid phosphor MSD is displayed. (b) Autocorrelation function of the hydronium-lipid hydrogen bonds, which remarkably decays to a plateau.

Although the hydronium remains bound to a median of one or two lipids in the hb1 or hb2 ensemble, respectively, the autocorrelation of the hydronium lipid contact (see Methods for details), shown in Fig. 6 b, indicates that the hydronium moves between different lipids. In the hb3 ensemble, >90% of the hydronium-lipid hydrogen bonds still exist after 500 ps. In contrast, for the hb1, and to a lesser extent the hb2 ensemble, the autocorrelation function drops significantly for the first 100–200 ps, indicating hydrogen-bond interactions with different lipids. However, the decay in the autocorrelation reaches a plateau after ∼250 ps (Fig. 6 b). For the timespan shown in Fig. 6 b, we can exclude a finite size effect as a cause (31,32), because the probability that the hydronium-lipid hydrogen bond is restored by an interaction with a periodic image is negligible (see the Supporting Material). Instead, the hydronium-lipid interaction switches between only a few lipids.

Because the proton is mainly located on water molecules in direct contact with lipid oxygens, we analyzed the connectivity of these waters by extracting the cluster-size distribution of all water molecules within the first solvation shell and 1.5 water solvation shell, respectively (see inset in Fig. 7). Water molecules were considered part of a cluster if the distance to any member of the cluster is within 0.35 nm. Fig. 7 shows that, when considering only the first solvation shell around lipid oxygens, many small clusters were present, demonstrating a low connectivity of these water molecules. In contrast, when one additional water layer was considered (1.5 water solvation shell), the dominant cluster size was close to the maximum cluster size, suggesting one large water network. Because proton transfer to a second shell water molecule already results in a severe free-energy penalty (Fig. 3), the small clusters of first-shell water molecules create small free-energy wells, in which the proton freely diffuses but only rarely escapes. As a result, the proton repeatedly revisits the lipids around the free-energy well.

Figure 7.

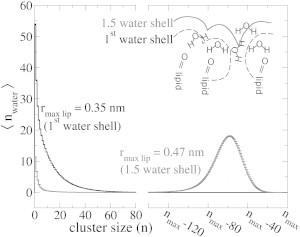
Connectivity of the water molecules at various distances around lipid oxygens. Cluster-size distribution for water molecules within 0.35 and 0.47 nm from a lipid hydrogen-bond acceptor, corresponding to first solvation shell and 1.5 water solvation shell, respectively. The n_max is the total number of water molecules within the considered water shell. (Inset) Schematic representation of the water shells considered in the cluster analysis.

Despite the free-energy barrier between these small water clusters, we observed occasional transitions of the proton between adjacent free-energy wells (see Fig. 9 for representative trajectory), providing an on-surface diffusion pathway. The low transition rate and relatively long dwell-time inside the free-energy wells closely resembles diffusion near the percolation threshold, which yields subdiffusive behavior (33).

Figure 9.

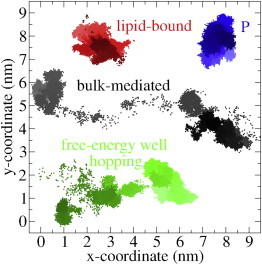
Representative trajectories of the displacement of the excess proton when it is bound to a lipid, hopping between free-energy wells and in bulk. For comparison, a typical lipid phosphor trajectory is shown. The time intervals are from 2 ns (light) to 50 ns (dark). To see this figure in color, go online.

Finally, the proton occasionally leaves the bilayer, diffuses along the outermost boundary of the surface or even through the water phase, before readsorbing onto the bilayer. Fig. 8 shows that the dynamics of a proton in this non-surface-bound state approaches that of a proton in bulk, both with respect to diffusion coefficient and transfer rate.

Figure 8.

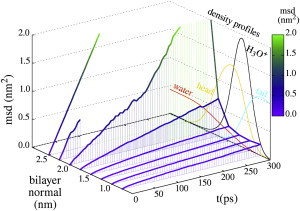
Lateral MSD of the excess proton at various membrane penetration depths shows that the diffusion rate increases as the proton leaves the membrane. The MSD at 2.5 nm is the average lateral MSD in bulk water and we could only obtain the MSD at 2.25 nm over 50 ps due to sampling problems. To illustrate the excess protons penetration depth the density profiles normal to the membrane surface of the hydronium, water, lipid tails, and lipid headgroups are plotted in the background (also shown in Fig. 1). To see this figure in color, go online.

Thus, we identified three modes for proton diffusion, as follows:

• 1.Bound directly to a lipid,
• 2.Shuttling inside the small water clusters within the headgroup region with occasional hops to nearby clusters, and
• 3.Through the bulk.

The two lipid-bound diffusion pathways have also been identified in MS-EVB simulations (8,9). The three diffusion modes are illustrated in Fig. 9. A lipid-bound proton exhibited the same restricted diffusive behavior as the lipid phosphor and, as a result, the diffusion coefficient at short timescale is very low. In contrast, both a proton that hopped between adjacent free-energy wells and a proton that moved through the bulk covered considerably larger distances. Although proton desorption (from the lipid membrane) and hopping (between free-energy wells) are rather infrequent events, the much larger diffusion coefficient associated with these diffusion modes causes an increase of the overall diffusion coefficient at larger timescale (a superdiffusive regime).

The MSD in Fig. 4 indeed shows a superdiffusive regime, but only for a very short timespan. For bulk-mediated surface diffusion, however, the diffusion coefficient is expected to increase asymptotically toward the bulk diffusion coefficient, due to the growing contribution of the bulk-mediated diffusion pathway in time. In our simulations, the small solvent volume restricts this growing contribution, because the protons that reach the periodic image membrane are effectively removed from the bulk. To address the contribution of the reduced solvent volume, we numerically solved the two-dimensional diffusion equation for a proton released on a membrane surface that consisted of periodic low-free-energy wells, schematically shown in Fig. 10. Parameters for this model were derived from our atomistic simulations (see the Supporting Material for details).

Figure 10.

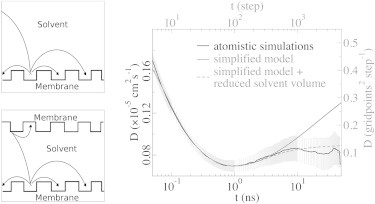
Schematic representation of our simplified model with infinite solvent volume (upper left) and a reduced solvent volume (lower left). In the right graph, the time dependence of the surface-diffusion coefficient as derived by the simplified model (gray) shows the expected increasing diffusion coefficient at long timescale for infinite solvent volume (solid) and the effect of a reduced volume (dashed). The latter is in agreement with the result of our atomistic simulations (black). The lower and left axis corresponds to the atomistic simulations and the upper and right axis corresponds to the simplified model. For simplified model details, see the Supporting Material.

Fig. 10 shows that the mean-square surface displacement of a proton in this simplified system displays an initial subdiffusive regime, in agreement with our atomistic simulations. As expected for bulk-mediated diffusion, at long timescales an extended superdiffusive regime that approaches bulk diffusion asymptotically appears. When we reduced the volume in our simplified model by introducing a second membrane (Fig. 10), the timespan of the superdiffusive regime is significantly reduced, in agreement with the atomistic simulations. The short superdiffusive regime in our atomistic simulations is thus a result of the small periodic system, and not a typical property of proton diffusion on a membrane surface.

Discussion and Conclusion

We have performed MD simulations of an excess proton near a DMPC membrane to analyze surface affinity and surface diffusion, which are key aspects of the steady-state theory put forward to explain the protonmotive force in the cellular energy machinery (4,5).

Equilibrium distributions

We found that the excess proton binds to the DMPC surface with an affinity of −13.0 ± 0.5 kJ mol⁻¹. Previous simulation studies have reported affinities of −21, −3, and 42 kJ mol⁻¹ at a DOPC, DMPC, and DLPE bilayer, respectively (8,9,34). However, these simulations were performed at a different temperature (300 K) than ours (323 K). Therefore, a direct comparison, even in the case of DMPC, is difficult. Moreover, different force fields and different approaches to model the excess protons were used. With these differences in mind, we consider our results in reasonable agreement with the MS-EVB simulations from Smondyrev and Voth (8).

A comparison with experiments is even more complicated, because direct measurement of the proton surface concentration [H⁺] is a formidable challenge. Recently, the local proton exchange dynamics at DOPC and DOPG lipid vesicle surfaces in thermodynamic equilibrium has been measured. Although the membrane was different in these experiments, it was found that the proton surface concentration is 100-fold larger than the bulk concentration, corresponding to a proton surface affinity of −11.5 kJ mol⁻¹ (6,7), in line with our result.

In our simulations the excess proton interacted strongly with the lipid’s oxygens in the headgroup phosphate and linker carbonyl. Strong interactions have also been observed between the lipid oxygens and adjacent water molecules (35–39). If we assume that an excess proton associated with such a water molecule experiences a similar strong lipid interaction, association of the proton with a water molecule adjacent to a lipid oxygen will be preferred over a bulk water molecule, which could (partly) explain the high surface affinity. We speculate that this preference of the proton for a water molecule interacting with the lipid oxygen over a bulk water molecule is a general feature of lipid membranes, because of the following:

• 1.A strong proton surface affinity has been found for other lipid bilayers, both in measurements (7,6,14) and simulations (8,9); and
• 2.Water molecules that interact strongly with lipids have been observed in other lipid membranes as well (35).

Dynamics

Movement of the proton on the membrane surface is not the two-dimensional equivalent of proton diffusion in bulk water. Instead, the diffusion in presence of a membrane surface is anomalous, characterized by a short subdiffusive regime (1 ns) and a subsequent superdiffusive regime.

The anomalous diffusion is due to presence of three different diffusion processes (Fig. 11), each with a distinct diffusion coefficient:

• 1.In the first process, the hydronium is tightly bound to the lipid and follows the diffusion of the lipid, which is subdiffusive at short timescales (40).
• 2.In the second process, protons are less tightly bound inside small water clusters within the lipid headgroup region and occasionally jump from one cluster to another. Although the distance between the clusters is small (approximately one water molecule, in agreement with experiment (17)), the transition frequency is rather low due to a significant barrier separating the clusters. Within these clusters, the proton shuttles between the water molecules, experiencing a local caging effect. This caging, in combination with occasional jumps between clusters, generates a percolation effect that leads to a subdiffusive regime on short timescales and normal diffusion at long timescales (33,40). These two diffusion modes, in which the proton’s movement is correlated with the movement of the lipids, have also been identified by Smondyrev and Voth (8) and Yamashita and Voth (9), who attributed the overall diffusion of an excess proton to a slow diffusion of protons trapped within the headgroup region and a slightly faster diffusion of protons in the shallow interface region before bulk water.
• 3.In the third process, the proton resides on the outer edge of the headgroup region and escapes into the bulk, where the diffusion constant approaches that of a free excess proton in water. For bulk-surface systems that exhibit strong surface adsorption, the adsorption-desorption kinetics frequently provide the primary mechanism of surface diffusion, which, in case of a surface diffusion that is slower than bulk diffusion, gives rise to a superdiffusive regime (41). The superdiffusive regime therefore exists due to the strong surface adsorption of the proton in combination with the severely restricted diffusion in the surface-bound states.

Figure 11.

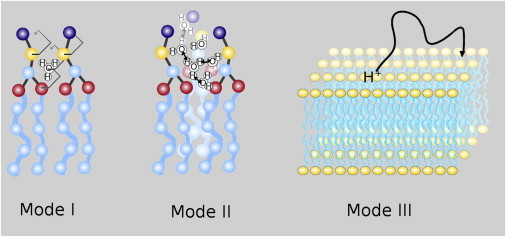
Schematic representation of the three observed diffusion modes for a proton on a membrane surface. In Mode I, the hydronium is bound to the lipids. Proton transfer is absent and diffusion is determined by the lipid, to which it is bound. In Mode II, the proton is captured within a free-energy well composed of a small lipid-enclosed cluster of water molecules. Within this well, the proton can transfer freely, and diffusion is a superposition of the proton diffusion within the well, and the diffusion of the whole well. In Mode III, the proton desorbs from the membrane. The proton migrates freely over the surface or through the bulk before the proton readsorbs onto the membrane, leading to large-scale surface diffusion. To see this figure in color, go online.

An important consequence of the sub- and superdiffusive regime is that the diffusion coefficient is not constant. Yet, previous reports on diffusion coefficients of protons at membranes surfaces have assumed a constant value corresponding to Fickian diffusion (8–11,13,14,17). Interestingly, the measured diffusion coefficients (0.02–12 × 10⁻⁵ cm² s⁻¹) cover a similar range as the time-dependent diffusion coefficient in our simulations (0.069–9 × 10⁻⁵ cm² s⁻¹). However, leaving out the proteinaceous systems from the comparison worsens the agreement, because the diffusion constants reported for pure phosphatidylcholine systems are typically much higher (13,14).

To compare our results to previous computations, we extracted a constant diffusion coefficient from a 1–10-ps time interval as in Smondyrev and Voth (8) and Yamashita and Voth (9), and obtained a value of 0.32 × 10⁻⁵ cm² s⁻¹. Because we performed the simulation at 323 K, rather than at 300 or 298 K, at which most experiments and MS-EVB simulations were carried out, we cannot directly compare the diffusion constants. Because tunneling does not play a dominant role near room temperature, we can assume Arrhenius behavior and expect the diffusion to be lower at room temperature. However, because our results were obtained under periodic boundary conditions, the diffusion is underestimated due to finite-size artifacts (42), which are not easily corrected in a nonhomogeneous system, such as ours.

Although the correction may affect the diffusion through bulk and on the membrane surface differently because of the larger hydrodynamic radius of the phospholipids compared to water, we consider it highly unlikely that the anomalous character of the diffusion would disappear after correction. Nevertheless, even with these issues in mind, the diffusion constant is in line with the MS-EVB result of 0.15–0.23 × 10⁻⁵ cm² s⁻¹ (8,9). We remark at this point that despite the apparent agreement with previous MS-EVB results, our approach underestimates proton delocalization, which affects solution structure (43,44) (see Fig. S6 in the Supporting Material) and may also have an impact on the diffusion process. At present, the MS-EVB3 approach by Wu et al. (45) is presumably the most suitable approach to take into account the effect of charge delocalization in classical MD simulations of protons.

Experimental support for the existence of bulk-mediated long-range proton surface diffusion is ambiguous. On the one hand, fast proton surface diffusion in systems with low aqueous buffer concentration is incompatible with predominant bulk-mediated long-range surface diffusion via the buffer molecules (14,15). In addition, an H/D kinetic isotope effect of five shows that hydrogen-bond breaking is rate-limiting rather than a water rearrangement, suggesting on-surface diffusion via water-wires as the dominant diffusion mode (14,15). Furthermore, faster proton on-surface than surface-to-bulk displacement (6) and the slow detection of protons appearing in the bulk after release on a purple membrane surface, as opposed to the fast detection of the proton appearing at a new surface site (10–12), indicates fast on-surface diffusion and no significant contribution of bulk-mediated diffusion.

On the other hand, a theoretical assessment shows that protons desorb and readsorb onto the surface thousands of times before equilibration into the bulk, giving rise to coupled surface bulk diffusion (46). If the rate-limiting step for desorption is breaking of a hydrogen bond to escape the free-energy well, the many desorption events will induce an H/D kinetic isotope effect between 2.5 and 7, providing an alternative explanation for the observed isotope effect. In addition, in fluorescence measurements at high aqueous buffer concentrations, the diffusion rate is compatible with bulk-mediated proton diffusion via the buffer molecules (13,14). Finally, lateral on-surface proton diffusion on DPPC bilayers could not be detected by scanning electrochemical microscopy proton feedback (47).

We suspect the existing conundrum on the existence of the bulk-mediated diffusion pathway originates from the fact that the competing on-surface pathway is very sensitive to the membrane conditions. On the one hand, in our simulations, the low connectivity of the first shell water molecules severely limits long-range on-surface diffusion of the proton, promoting the bulk-mediated diffusion pathway. On the other hand, the protein content in a purple membrane, for example, may promote the on-surface diffusion mode over bulk-mediated long-range surface diffusion, as observed in experiments (10–12). On Langmuir films, a similar promotion may be achieved by compression (48).

In fact, we expect that the overall proton surface diffusion is sensitive to factors that influence any of the observed diffusion modes, either in diffusion behavior or relative population. For example, conditions that influence the well-depth associated with the isolated water clusters, for instance by competition of other ions, might have a significant impact on the proton surface dwell-time. In this respect, we note that the cations present in the buffer solution may be relevant, because sodium is attracted to the lipid bilayer surface, occupying the same water clusters as the proton (49–59), whereas potassium has no significant affinity for the membrane surface or at least less than sodium (51,54,56,58). These observations suggest that the membrane composition as well as the constituents of the solution medium could also strongly affect proton surface diffusion.

To validate proton anomalous surface diffusion experimentally, the relation between time and MSD is required, particularly within the time- and length-scales, in which the sub- and superdiffusive regime are clearly identifiable. Therefore, the experimental time- and length-scales should be within a few tens of nanoseconds and nm², which corresponds to a distance between a proton source and a proton sensor of at maximum a few tens of lipids.

To control the distance between a proton source and a proton sensor on the nanometer length scale, we propose a rigid linker. Clearly, the linked source and sensor cannot be allowed to interact with other linked pairs, which requires very low concentrations and careful design of the linker to avoid aggregation, presenting a considerable challenge. Yet, with the linker the existence of a superdiffusive regime can be tested by varying the length of the linker within the relevant length-scale. If the linker distance falls within the superdiffusive regime, a superlinear relation between the square of the linker distance and the time of maximum sensor activity should be observed.

Alternatively, in an ensemble of single molecule experiments, in which a single proton is released on a membrane, the ensemble-averaged travel distance to a sensor depends on the sensor concentration. Normal and anomalous diffusion will then induce a different response of the time to maximum sensor activity to variation of the concentration, which may, for instance, be probed by super-resolution imaging techniques (60,61). As an example, we calculated this response in our simplified model with the proton source distributed on an evenly spaced grid (for details, see the Supporting Material). Fig. 12 shows that the predominant on-surface diffusion can be clearly distinguished from the predominant bulk-mediated diffusion in this way.

Figure 12.

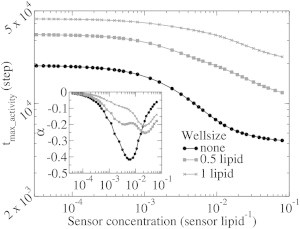
Time to maximum sensor activity after proton release on the surface as a function of the sensor concentration. The log-log scale revealed a power law relation in the well systems (shaded), which is absent for free surface diffusion (solid). The plot of the power-law exponent α shows that the power-law relation is only approximate.

Implications for the cellular energy machinery

To explain why the protonmotive force exceeds the osmotic force, the steady-state theory requires that protons are retained on the surface. The high affinity for the membrane surface fulfills this criterion. Furthermore, the minimum-diffusion coefficient of 0.069 ± 0.005 × 10⁻⁵ cm² s⁻¹ at 1 ns is sufficient for the energy machinery to function. Assuming an ATPase density of 1.5 × 10¹² cm⁻² (62,63), it would take on average 480 ns for a proton to reach an ATPase. Because the diffusion coefficient increases with time, the actual travel time will be shorter. In addition, other effects in a functional cell membrane can reduce the time even further, such as the density of proton pumps, protein clustering (64), cristae formation, or the antenna effect of proteins (65).

Because the bulk-mediated proton diffusion will cause proton loss into the bulk, increasing the on-surface diffusion coefficient would increase the efficiency of the energy machinery. In DMPC, the on-surface diffusion is slow because the low connectivity between the water clusters prevents proton transfer between these clusters. Because the low connectivity is due to the bulky headgroups, we speculate that incorporating lipids with smaller headgroups, such as phosphatidylethanolamines and cardiolipin, which are abundant in membranes involved in the energy machinery (66–68), could enhance proton diffusion. This could result in a more efficient energy machinery and allow the cell to withstand harsher conditions.

Supporting Citations

Reference (69) appears in the Supporting Material.