A G-Protein Subunit Translocation Embedded Network Motif Underlies GPCR Regulation of Calcium Oscillations

Abstract

G-protein βγ subunits translocate reversibly from the plasma membrane to internal membranes on receptor activation. Translocation rates differ depending on the γ subunit type. There is limited understanding of the role of the differential rates of G_βγ translocation in modulating signaling dynamics in a cell. Bifurcation analysis of the calcium oscillatory network structure predicts that the translocation rate of a signaling protein can regulate the damping of system oscillation. Here, we examined whether the G_βγ translocation rate regulates calcium oscillations induced by G-protein-coupled receptor activation. Oscillations in HeLa cells expressing γ subunit types with different translocation rates were imaged and quantitated. The results show that differential G_βγ translocation rates can underlie the diversity in damping characteristics of calcium oscillations among cells. Mathematical modeling shows that a translocation embedded motif regulates damping of G-protein-mediated calcium oscillations consistent with experimental data. The current study indicates that such a motif may act as a tuning mechanism to design oscillations with varying damping patterns by using intracellular translocation of a signaling component.

Introduction

The concentration of cytoplasmic calcium ions is known to change with specific patterns of periodicity in response to a variety of stimuli. These oscillations are thought to constitute an essential part of information processing involved in cell signaling (1,2). Calcium oscillations play a crucial role in regulating cellular functions such as secretion and contraction (3,4). Activation of G-protein-coupled receptors (GPCRs) is known to trigger calcium oscillations (5,6). It has been suggested that both amplitude and temporal characteristics of calcium spiking encode signaling information (1,7,8). Various attempts have been made to understand such oscillatory behavior, using both mathematical modeling and experimental studies (6,9–12).

Although interplay between a fast positive and a slow negative feedback has been identified as one of the key motifs mediating these oscillations (9–11), the molecular mechanisms involved in tuning oscillation characteristics have not been fully identified. For instance, it is unclear how, in the presence of a continuous stimulus, postactivation oscillations shift to a damped response, eventually tapering off. Furthermore, there is limited information about mechanisms that are at the basis of cell-to-cell variability in calcium oscillation behavior. Because βγ-mediated phospholipase C-β (PLC-β) activation is a primary event in Gi-mediated calcium oscillations (13), we investigated whether the receptor stimulated translocation of the βγ complex between the plasma membrane and internal membranes plays a role in modulating these oscillations.

On activation by extracellular signals, heterotrimeric G-proteins were thought to be localized to the plasma membrane. However, more recent evidence suggests that on activation, G-protein βγ subunit types translocate from the plasma membrane to intracellular membranes at differential rates (14,15). The rate of translocation of different βγ types varies, depending on the affinity of the γ subunit for membranes (16). There is however, limited knowledge about the role that this translocation plays in regulating signaling network properties and cellular functions.

To study the role of a translocation module in a calcium oscillatory network, we developed an ODE (ordinary differential equation) mathematical model of an oscillatory circuit, with and without reversible translocation of the principal signaling component. Dynamical analysis of the network suggested that translocation can influence oscillation characteristics. Our studies on α2 adrenergic receptor (α2AR)-induced calcium oscillations in HeLa cells provide experimental support for such a prediction. The ability to introduce γ subunit types or knockdown a specific γ subunit type in a cell allowed the proportion of fast versus slow translocating subunit types to be varied in these cells. The results suggested a role for differential translocation rates in tuning the damping of receptor-mediated calcium oscillations.

Because most cells express multiple γ subunits types (15), a two subunit model (slow and fast translocating) of Gαi-mediated calcium oscillations was developed through incorporation of γ subunits with different translocation rates. The model was also used to predict cell-to-cell heterogeneity in a population by invoking parametric distribution. Our model captured the experimentally observed statistical distribution of oscillation characteristics in a cell population and indicated that the relative proportion of differentially translocating γ subunits can play a role in regulating cell-to-cell variability in calcium oscillations.

Materials and Methods

Mathematical modeling and simulation

We used an ODE model and bifurcation and Eigenvalue analysis to identify the role of translocation of a component in calcium oscillation circuit. Furthermore, we constructed another model with two γ subunits (two subunit model) to capture the role of spatiotemporal modulation of Gβγ in regulating calcium oscillations. Mainly, we used kinetics of reactions and transportation of signaling components, to develop a system of ODEs. The set of ODEs were solved using the subroutine ode23s in MATLAB (The MathWorks, Natick, MA) to obtain the simulated time course of calcium oscillations. Eigenvalue analysis was performed to characterize the damping and frequency of oscillations.

Cell culture and transfection

HeLa cells were cultured in MEM medium (Cellgro, Manassas, VA) supplemented with 10% dialyzed fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA) and antibiotics. 0.2 × 10⁶ cells were seeded on 29 mm glass bottom dishes (In Vitro Scientific, Sunnyvale, CA) and maintained in culture until 70–80% confluency. All transfections were performed using 2 μl Lipofectamine 2000 per dish (Invitrogen, Life Technologies, Grand Island, NY) as per manufacturer’s protocol.

Constructs, small hairpin RNA (shRNA), and cell lines

HeLa cells (ATCC, Manassas, VA) were transfected with mCherry tagged fast (γ11) and slow (γ3) translocating γ subunit (15). The γ11-3 chimera was made by substitution of the last 9 amino acids of the C-terminus of γ11 with those of γ3. PH-mCh (17) was used to detect inositol trisphosphate (IP3) production during Gi activation in HeLa cells. A γ11 knockdown stable HeLa cell line was used where γ11 was knocked down using shRNA in a lentivirus resulting in ∼70–80% reduction of γ11 expression (34). Another stable HeLa cell line was created using the non-Target shRNA control virus.

Live cell imaging

Transfected cells on 29 mm glass bottom dishes were imaged using a Leica-Andor spinning disc confocal imaging system, which consists of an Andor FRAP-PA device and EM-CCD camera. To avoid anomalies due to confocal plane changes, an adaptive focus control was used. Imaging was performed using a 63X objective. Calcium imaging was performed in Hank’s Balanced Salt Solution (HBSS) (Invitrogen, Life Technologies, Grand Island, NY). Cell cultures were loaded with 2 μM Fluo-4 (Molecular Probes, Life Technologies, Grand Island, NY) for 30 min in HBSS. The cells were then washed with HBSS after which Fluo-4 images (Excitation: 488nm; Emission: 510 nm) were acquired at 2–3 s intervals at 37°C. Cells expressing mCh-tagged γ11, γ11-3, and γ3 were selected by mCh fluorescence (Excitation: 595 nm; Emission: 610 nm). Norepinephrine (Sigma, St. Louis, MO) in HBSS was used to activate the α2AR at different concentrations (in the range of 0.05–100 μM).

Image analysis and quantification of cell-to-cell variability in calcium oscillations

Time-lapse movies were acquired every 2–3 s, for 2 min before agonist addition and 15 min after agonist addition. Raw image data were analyzed with Andor software to obtain the time course of fluorescence levels in single cells. For a single cell, cytosolic calcium increase was measured by quantifying the fold change of the fluorescence level with respect to the basal level. For each single cell of a population, (size ∼80–100 cells) the number of calcium spikes (N) and the duration of calcium spiking (T) was quantified using MATLAB (The MathWorks) and OriginPro 8.0 peak analyzer. Histograms of the previous parameters were obtained using a routine written in MATLAB.

Statistical modeling and analysis

Assuming a Gamma distribution function in upstream activation, a MATLAB subroutine was written to simulate the calcium spiking characteristics in a cell population. The response for each single cell in the population is based on the two γ subunit ODE model. For comparison between the groups with different genotypes (for live cell imaging experiment and simulation), kernel-density function was fitted to the distribution of calcium oscillation characteristics using MATLAB.

Results

Cell-to-cell variability in damping of calcium oscillations

Translocation of Gβγ between plasma membrane and internal membranes regulates the concentration of Gβγ at the plasma membrane. This can potentially have an effect on the activity of effectors downstream of Gβγ. Consistent with this notion, differential rates of translocation of different Gβγ subunits have distinct effects on the activation of PLC-β and IP3 release at the plasma membrane (17). Because intracellular calcium release is mediated by IP3, we examined whether the translocation rate of Gβγ can influence cytosolic calcium oscillation characteristics.

First, we chose an experimental framework to investigate the effect of G-protein subunit translocation on receptor-mediated calcium oscillation. Activating endogenous α2AR with norepinephrine stimulated Gi-mediated calcium oscillations in HeLa cells (Fig. 1, a, c, and e). The oscillatory response was monitored by time lapse imaging of Fluo-4 intensity. Oscillations were inhibited by an antagonist, yohimbine (Fig. 1, b, d, and f). PLCβ activation and IP3 generation was confirmed through increase in the IP3 sensor PLCδ−PH-mCh (17) intensity in the cytosol and decrease at the plasma membrane (Fig. S1 in the Supporting Material). We found that cytosolic calcium release was abolished in HeLa cells in the presence of thapsigargin, a blocker of sarcoplasmic reticulum calcium-ATPase pump (Fig. S2 a). Additionally, we found that HeLa cells show calcium oscillations even without calcium in the medium (Fig. S2 b), which is consistent with observations reported in the literature (4). However, the frequency and amplitude is slightly different compared to cells in medium containing calcium. These results clearly show that the stimulation through norepinephrine induces intracellular calcium release in HeLa cells.

Figure 1.

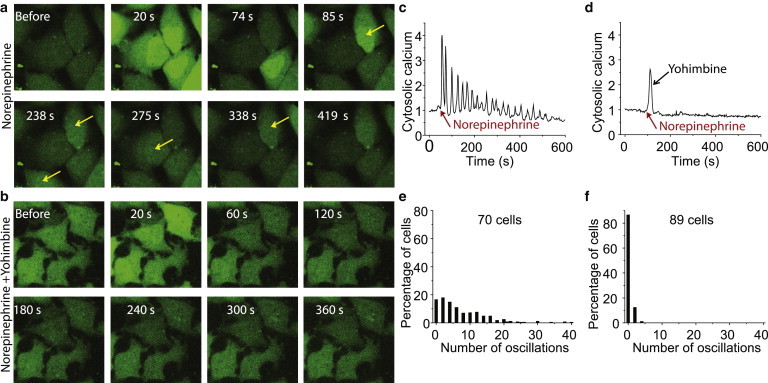
Calcium oscillation induced by α2AR. (a) Representative images of HeLa cells showing Ca²⁺ response in the continuous presence of norepinephrine (agonist, dose = 100 μM). (b) Representative HeLa cell showing Ca²⁺ response after addition of agonist (norepinephrine, dose = 100 μM) followed by antagonist (yohimbine, dose = 50 μM). Times shown are period elapsed after agonist addition. Antagonist was added at 25 s. Arrows point to cells that show increases in calcium over basal state cells. Cells exposed to antagonist do not show such an increase in any cell over basal state cells. (c) Time course of Ca²⁺ oscillations in the presence of norepinephrine in a single cell. Red arrow indicates addition of norepinephrine. (d) Time course of Ca²⁺ oscillations after addition of norepinephrine (red arrow) followed by yohimbine (black arrow). (e and f) Frequency distribution of the number of Ca²⁺ spikes in cells from (a and b). Number of independent experiments (N_exp) = 5. To see this figure in color, go online.

We analyzed calcium oscillations through quantification of the number of calcium spikes and duration of oscillations in single cells with norepinephrine. We performed a detailed dose response analysis of norepinephrine stimulated HeLa cells at concentrations ranging from 0.005 to 200 μM. We found that cells showed calcium oscillations between 0.5 and 100 μM and performed our experimental analysis within that range.

Oscillatory responses were grouped into three categories, low, medium, and high based on agonist concentration (Fig. 2, a–c). At low doses, most of the cells with limited spiking showed rapid damping (Fig. 2 a). The variability in dampening and number of spikes at medium and high dose was higher (see Fig. 2, b and c). Because calcium oscillations in a cell population showed a wide variation in spiking pattern when activated at a high dose, mean analysis was not suited for quantification of population behavior. Hence, cell-to-cell variability in calcium oscillations in populations of cells was measured by fitting probability density function to the frequency distribution of responses.

Figure 2.

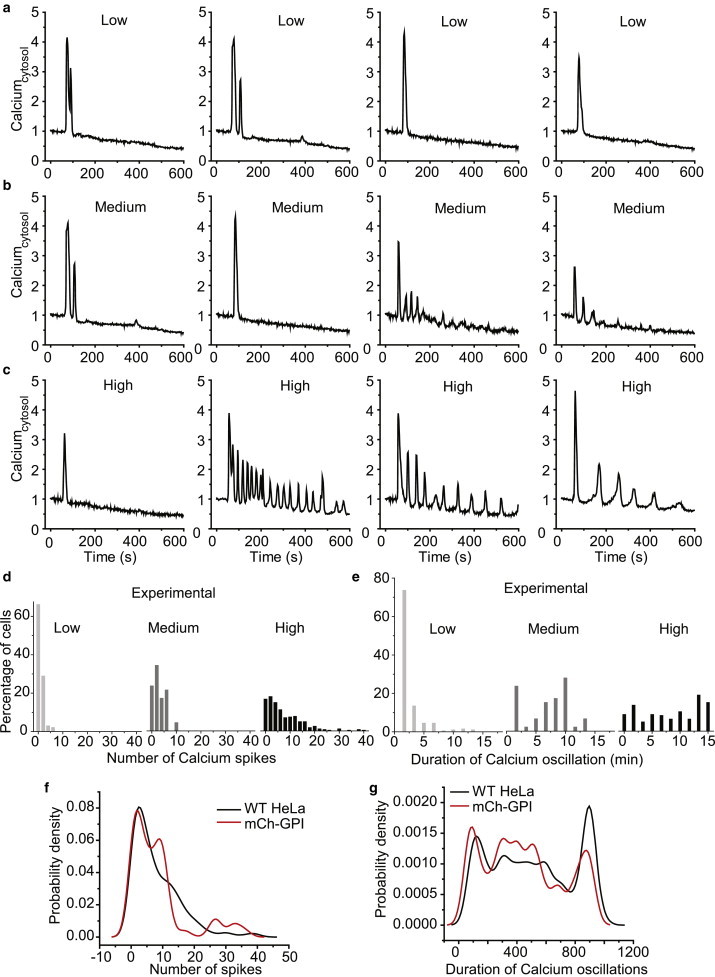
Cell-to-cell variability in α2AR-induced Ca²⁺ oscillation characteristics in a HeLa cell population for a range of drug doses. Representative time course of Ca²⁺ oscillation in HeLa cells at increasing doses of norepinephrine: (a) low (0.5 μM); (b) medium (5 μM); (c) high (100 μM). (d and e) Experimentally obtained frequency distribution of number (d) and duration (e) of Ca²⁺ spiking at different drug doses. Nonparametric kernel-density function fitted to (f) number and (g) duration of Ca²⁺ spiking at high drug dose, 100 μM norepinephrine (n = 250), (N_exp = 3). To see this figure in color, go online.

To categorize the oscillatory behavior in a cell population, cells exhibiting different numbers of calcium spikes and duration of oscillations were binned. The frequency distribution histograms indicate that with increasing doses, the population shifts from a lower number and duration of spiking toward a higher number and longer duration (Fig. 2, d and e). A nonparametric kernel density function fit to the previous probability distribution reemphasizes that oscillatory behavior is heterogeneous at high doses (Fig. 2, f and g).

Calcium oscillations in cells with multiple G-protein γ subunit types

We then examined the impact of different proportions of fast (γ_fast) and slow (γ_slow) translocating γ subunits on receptor stimulated calcium oscillation characteristics in HeLa cells. The quantitative real-time polymerase chain reaction profile of γ subunit types in HeLa cells revealed that they contain γ5, γ10, γ11, and γ12 (15). γ11 is a rapidly translocating subunit (t_1/2 ∼10 s), whereas the others are slower (t_1/2 >50 s) (15,16).

Based on this, the fraction of γ_fast was varied by transfecting HeLa cells with the γ11 subunit. Similarly, to alter the fraction of γ_slow, HeLa cells were transfected with a γ3 subunit (t_1/2 ∼200 s) (15,16). Additionally, to rule out the possibility that any differences in effects between γ11 and γ3 are not peculiar to the subunit types but reflect their translocation characteristics, we constructed a chimeric γ11-3 molecule by substituting the C-terminal domain of γ11 with the corresponding domain of the γ3 subunit. The C-terminal domain is known to determine translocation rates (14) and the comparison of translocation characteristics of chimeric γ11-3, γ3, and γ11 shows that as anticipated, γ11-3 translocates similar to γ3 (Fig. S3 a). We first characterized the effect of agonist (norepinephrine) on the translocation rate of the γ subunit types and plotted the translocation profiles for overexpressed γ11 or γ3 (Fig. S3 c–e). Because we observed cell-to-cell variation in translocation rates, we performed a distribution analysis for γ11 and γ3 translocation rates at different agonist concentrations (Fig. S3 f).

Next, we performed live cell imaging of a cell population transfected with three different γ subunit types, γ3, γ11, and γ11-3 (Movies S1–S3). Because a larger fraction of HeLa cells in a population showed an oscillatory response at a higher agonist concentration (Fig. 2, c–e), experiments were performed using 100 μM norepinephrine. Although100 μM norepinephrine may appear to be a relatively high concentration, there is little information about the actual effective physiological concentrations that a receptor senses in a native tissue. It is clear based on the ability of yohimbine to inhibit the extended oscillations detected with 100 μM norepinephrine (Fig. 1 d) that the calcium oscillations are stimulated specifically by the α2AR. Overall, this suggests that the experiments and results described below using 100 μM concentration of norepinephrine are likely to be physiologically relevant.

Fig. 3, a–i, shows translocation properties of mCh-γ11, mCh-γ3, and mCh-γ11-3 and their corresponding calcium spiking profiles. γ11, γ3, and γ11-3 translocation rates from the plasma membrane to internal membranes were consistent with known differences in the translocation rates of γ11 (∼10 s) and γ3 (∼200 s) (15) and with the known role of the C-terminus in translocation (Fig. 3, b, e, and h). The corresponding calcium oscillations in these cells showed distinctly different characteristics (Fig. 3, c, f, and i). The results suggest that translocation rates of γ subunits affect oscillatory dynamics.

Figure 3.

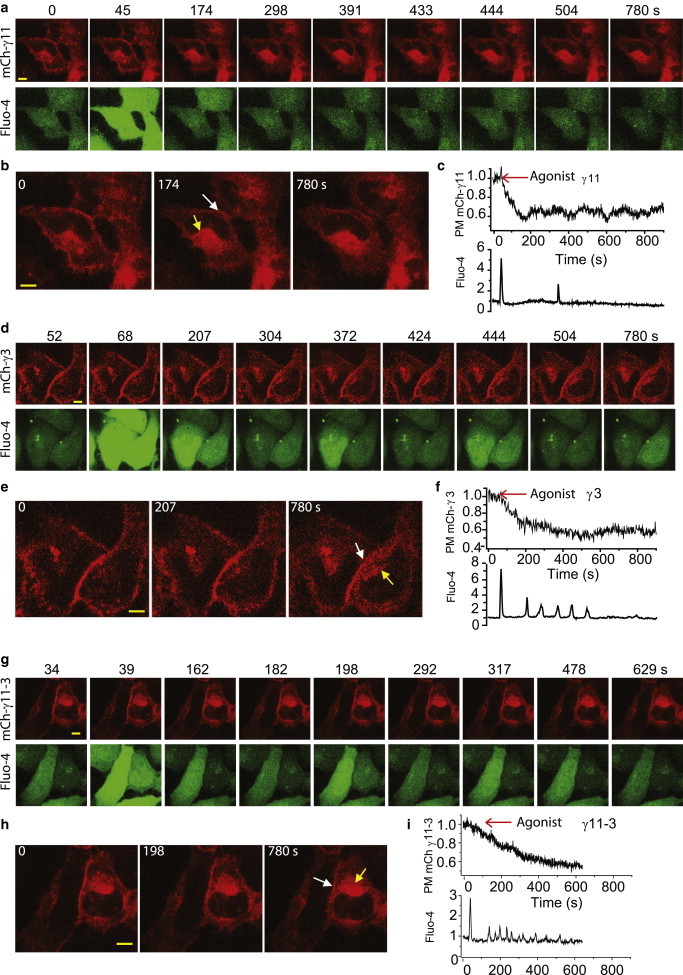
Effect of G-protein γ subunits with differential translocation rates on Ca²⁺ oscillations. γ translocation and Ca²⁺ oscillations induced by α2AR activation with 100 μM norepinephrine were imaged in live cells. (a) Simultaneous monitoring of γ translocation and Ca²⁺ oscillation in two representative HeLa cells expressing mCh-γ11 subunit and loaded with Fluo-4. Upper panel: mCh-γ11 fluorescence. γ distribution on the plasma membrane (white arrow), and internal membranes (yellow arrow). γ subunit redistribution occurs after GPCR activation. Lower panel: Fluo-4 intensity. (b) Time course of γ11 subunit depletion from plasma membrane in one representative cell. (c) Time course of Ca²⁺ oscillation for the corresponding cell. (d) Similar simultaneous monitoring of γ subunit translocation and Ca²⁺ oscillation in two representative HeLa cells expressing mCh-γ3 subunit and loaded with Fluo-4. (e and f) Time course of γ3 subunit depletion from PM and Ca²⁺ oscillation in a representative cell. (g) Similar results from cells expressing mCh-γ11-3. (h and i) Time course of γ11-3 subunit depletion from PM and Ca²⁺ oscillation from a representative cell. Scale bar = 10 μm. Number of cells studied in each case ≥45. N_exp = 3. To see this figure in color, go online.

The relative proportion of fast versus slow translocating γ subunit in a cell determines calcium oscillation characteristics

Cell-to-cell variability in calcium oscillations (Fig.S4) in populations of cells transfected with mCh-γ11, mCh-γ3, and mCh-γ3-11 was characterized by fitting a probability density function to the frequency distribution of responses. Fig. 4, a and b, shows frequency distribution (histograms) of the number of spikes and duration of calcium oscillations in the previous populations. To compare across two populations, the histograms obtained for the three cell types were fitted with a nonparametric kernel distribution (Fig. 4, c–f). Cell populations transfected with mCh-γ11 show a higher frequency for a lower number of calcium spikes (Fig. 4, c and d, red trace), and with shorter duration of oscillations (Fig. 4, e and f, red trace), whereas cell populations transfected with mCh-γ3 (Fig. 4, c and e, black trace), and mCh-γ11-3 (Fig. 4, d and f, black trace), shows a distribution with more cells exhibiting a higher number of calcium spikes and duration.

Figure 4.

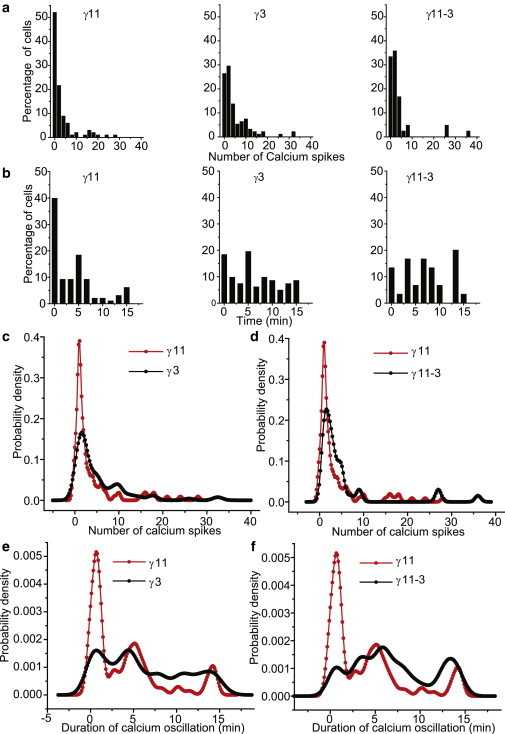
Introduction of γ subunit with differential translocation rates yields distinct patterns of α2AR-induced Ca²⁺ oscillations in HeLa cells (100 μM agonist). (a) Frequency distribution of number of Ca²⁺ spikes in mCh-γ11, mCh-γ3, and mCh-γ11-3 transfected cell populations. (b) Frequency distribution of the duration of Ca²⁺ oscillations in mCh-γ11, mCh-γ3, and mCh-γ11-3 transfected cell populations (c–f) Comparison of the distribution of number and duration of Ca²⁺ spikes in different cell populations as denoted. For comparison, nonparametric kernel density fitted to the distribution of number and duration of Ca²⁺ spiking in mCh-γ11, mCh-γ3, and mCh-γ11-3 transfected cells. All activation with 100 μM norepinephrine. Number of cells studied: mCh-γ11 = 100, mCh-γ3 = 94, mCh-γ11-3 = 45). (N_exp=3). To see this figure in color, go online.

A control experiment with cells transfected with a plasma membrane marker, mCh-GPI (18) showed calcium oscillation characteristics similar to untransfected HeLa cells (Fig. 2, f and g), so the effects seen were not due to the expression of a heterologous protein.

Our experimental results reveal an inverse correlation between the fraction of γ_fast and corresponding number of calcium spikes in cells that belong to populations expressing different γ subunit types (Table S1). The probability density of cells with calcium spikes <3 (highest damping) is higher in γ11 transfected cells than in γ11-3 or γ3 transfected cells (Fig.4, c and d) (Table S1). Additionally, the duration of calcium oscillations shows a similar relationship with the proportion of γ_fast in a cell. Cells with shorter durations of oscillations (0–100 s) are present more frequently in γ11 expressing populations than γ3 or γ11-3 expressing populations (Fig. 4, e and f) (Table S1). The consistent behavior of γ11-3 and γ3 in these experiments showed that their effect on oscillatory behavior was likely due to translocation kinetics and less likely due to any peculiarity that is subtype specific. Overall, the results suggest that the proportion of fast translocating γ subunits in a cell can tune calcium oscillatory behavior in terms of number and duration of spiking.

G_βγ reaction-translocation model exhibits regulation of calcium oscillations through G_βγ redistribution among plasma membrane and internal membranes

To rationalize the experimental observations as noted previously, we developed a dynamic model of GPCR-mediated calcium oscillations by incorporating the basic framework from Kummer et al. (9). The reaction schematic of Gi-mediated calcium oscillation is presented in Fig. 5 a. The model was modified to consider interactions specific to the Gi pathway and translocation of a βγ complex with a specific γ subtype. The model incorporates negative and positive feedbacks in the core motif to capture oscillatory behavior. The core model uses the following components of the signaling network: i), active βγ concentration at the plasma membrane (βγ_PM); ii), βγ concentration in internal membranes (βγ_IM); iii), activated PLC- β concentration (PLC- β); iv), calcium in the cytosol (Ca_cyt); and v), calcium in intracellular sources (Ca_ER). Details of the model are in the Supporting Material (section 1) and model parameters are in Table S2.

Figure 5.

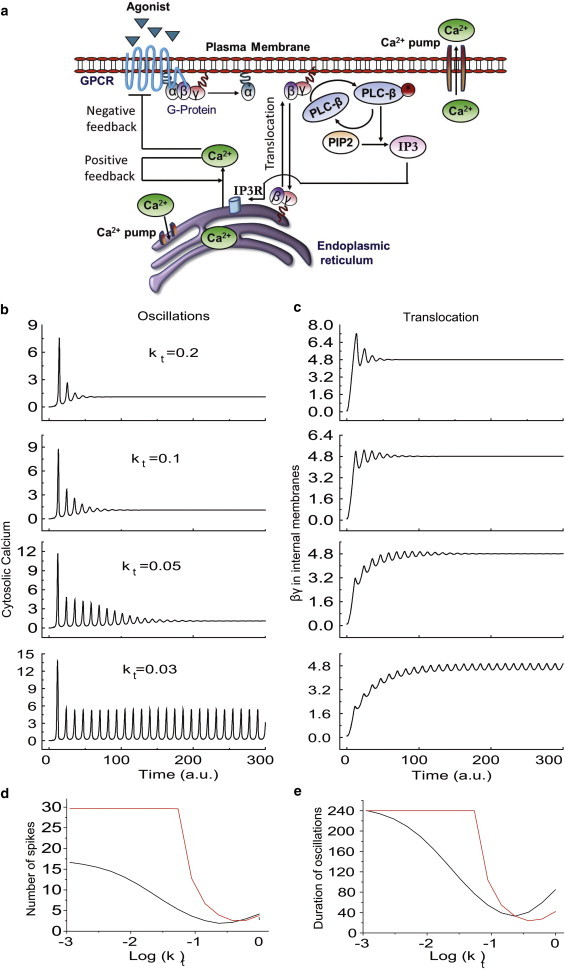
The role of translocation dynamics in regulation of Gi-mediated Ca²⁺ oscillation (in silico analysis from a single γ subunit model) (a) Simplified biochemical reaction schematic of the Gi coupled GPCR activated signaling network that induces Ca²⁺ oscillations in the presence of βγ translocation between plasma membrane and internal membranes. (b) Simulation of the time course of the Ca²⁺ oscillation pattern for different γ translocation rates (k_t). (c) Simulation of the corresponding kinetics of γ translocation to internal membrane. (d) Increasing the translocation rate leads to a decreased number of Ca²⁺ spikes measured over a fixed time period (240 s). (e) Increasing the translocation rate leads to earlier switching off and shorter duration of Ca²⁺ oscillation (black: low; red: high dose). To see this figure in color, go online.

We performed numerical simulations to obtain the patterns of calcium oscillations and the profile of βγ subunit translocation to internal cell membranes when varying translocation rates (k_t) (Fig. 5, b and c). Simulation results show that the rate of G_βγ translocation can modulate the number and duration of calcium spikes in a cell (Fig. 5, d and e). These results show that even though eventually the same fraction of fast and slow Gβγ goes to internal membranes, in the case of Gβγ_fast, the oscillations are totally damped, whereas in the case of Gβγ_slow, calcium oscillations continue even after translocation has reached steady state (e.g., compare kt = 0.2 and 0.03 at t = 200). At this time, in both cases the concentration of Gβγ in intracellular membranes is the same, but calcium oscillations are sustained only in the case of βγ_slow. This suggests that the rate at which Gβγ translocate can have a striking impact on calcium oscillation characteristics.

Eigenvalue analysis of the Gi-mediated calcium oscillation model (single γ-subunit model) shows that both damping and frequency of calcium oscillations are dependent on βγ the translocation rate (Fig. S5). Overall, results reveal an inverse dependence of the number of calcium spikes and their duration on the rate of γ subunit translocation (Fig. 5, d and e).

Bifurcation analysis of the single-subunit calcium model

To characterize the effect of translocation on calcium oscillations, we performed bifurcation analysis for the previous calcium model (Fig. 5) with and without translocation of the Gβγ subunit. Fig. 6 a shows a bifurcation plot with respect to agonist concentration for four different values of translocation rates (k_t). Results show that a minimum amount of agonist is necessary to induce oscillations via Hopf bifurcations. For example with k_t = 0, a minimum agonist concentration of 1.3 AU will induce oscillations. The maximum and minimum values of the amplitude attained during calcium oscillation are also depicted in Fig. 6 a. Furthermore, on increasing the agonist concentration, the maximum value of the amplitude increases, whereas the minimum remains the same. On increasing the translocation rate k_t, the Hopf bifurcation point shifts to the right indicating that higher agonist concentration is required to induce oscillations. Note that the steady-state value of the cytosolic calcium is independent of the translocation rate. However, the maxima of oscillation decrease with increase in the value of k_t, whereas the minima remain unaltered. The Hopf bifurcation point can also be visualized by obtaining the leading Eigen value. As seen in Fig. 6 b, the real part of the Eigen value changes from a negative to a positive value at Hopf bifurcation and is a function of the translocation rate as discussed previously. The stable steady state is observed for the negative and the positive real part of the Eigen value indicating the loss of stability leading to oscillation as shown through simulations (see Fig. 5, b and c). The phase plane plot (for various k_t value) showing dynamic cytosolic calcium versus βγ concentrations for a fixed agonist dose shows a limit cycle in the absence of translocation (Fig. 6 c). Results show that, on increasing the translocation rate, the space enclosed by the limit cycle shrinks. On further increasing the translocation rate, the limit cycle loses its stable focus leading to a damped response. This aspect is depicted in Fig. 6 d, wherein for a given agonist dose, the cytosolic calcium concentration is plotted versus the translocation rate, k_t. In the absence of translocation, the system oscillates and on introducing translocation the amplitude of the oscillation decreases before shifting to a damped response. For a given agonist concentration there exists a critical translocation rate beyond which the system loses oscillatory behavior.

Figure 6.

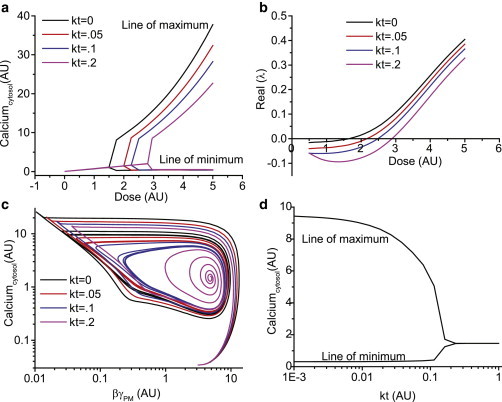
Bifurcation analysis of the single subunit calcium model (a) Steady-state cytosolic calcium concentration (arbitrary units) as a function of agonist dose for different translocation rates (kt). The upper lines as depicted by Line of maximum indicates maximum of the oscillations. The lower lines as depicted by Lines of minimum indicates minimum of oscillations. (b) Real part of Eigen values as a function of agonist dose (for different kt) (c) Dynamic phase response in terms of cytosolic calcium concentration versus βγ subunit concentration at the plasma membrane for different values of kt. (d) Steady-state calcium concentration as a function of translocation rate constant kt for an agonist dose. The line of maximum and minimum indicates as mentioned in (a). The single subunit calcium model was simulated for various translocation rates to obtain the previous results. In (a–c), kt values used are kt = 0 (black), kt = 0.05 (red), kt = 0.1(blue), kt = 0.2 (purple). To see this figure in color, go online.

The previous analysis of the Gi-mediated calcium oscillation model demonstrates that both damping and frequency of calcium oscillations are dependent on the βγ translocation rate. Overall, the results reveal an inverse dependence of the number of calcium spikes and their duration on the rate of γ subunit translocation (Fig. 5, d and e), over a certain range of translocation rate constant k_t. The results from the single subunit model here are consistent with the experimental observations in HeLa cells (Figs. 3 and 4). Although the calcium model presented here does not account for the receptor endocytosis, incorporating such effects will not affect the relation between translocation rate constant and the shift of the Hopf bifurcation point (Fig. S6 a and b). Additionally, simulations indicated that varying individual parameters by ±20% (result shown for two parameters in Fig. S7) does not influence the trend observed in the property of bifurcation (as in Fig. 6 a).

Two-subunit model - simulations of oscillations in cells with different proportions of γ subunit types

Because HeLa cells contain multiple γ subunits with differential translocation rates (γ5, γ10, γ11, and γ12) rather than a single γ subunit (15), we constructed a two-subunit model for Gi-mediated calcium oscillations containing two types of γ subunits with distinct translocation kinetics (Supporting Material 2.1, 2.2). Using this model, we then simulated the calcium response in the presence of differing proportions of two types of γ subunits, namely, slow translocating (γ_slow, k_t = 0.02 S⁻¹) and fast translocating (γ_fast, k_t = 0.2 S⁻¹). The number of calcium spikes (Fig. 7 a) and the total duration of oscillations (Fig. 7 b) decrease with increasing proportion of the faster translocating subunit (γ_fast/γ_total) due to damped oscillation for both low and high input stimulus values (corresponding to low and high dose). However, the shift from sustained to damped oscillation with increasing γ_fast/γ_total is steeper for a higher dose of agonist (Fig. 7, a and b). Simulation results show that the dependence between number of spikes and duration of oscillation with γ_fast/γ_total follows an inverse function (Fig. 7, a and b), as seen in experiments with HeLa cells (Figs. 3 and 4).

Figure 7.

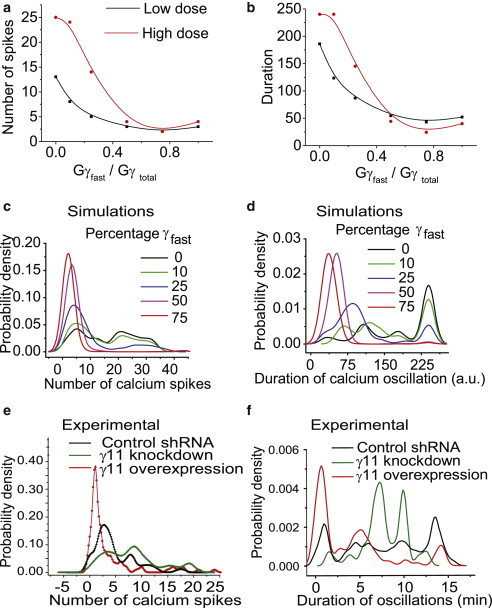
Two γ-subunit model (γ_fast and γ_slow) shows that the ratio of γ_fast:γ_slow regulates the distribution of Ca²⁺ oscillation characteristics in a cell population. We invoked different ratios of fast and slow γ subunits by varying m1 and m2 values in the model from 0 to 1 (model description in the Supporting Material). Changes in number (a) and duration (b) of Ca²⁺ spikes in response to increasing the fraction of γ_fast at different input doses (black: low; red: high dose). Increasing the fraction of γ_fast induces a shift in distribution of Ca²⁺ oscillation pattern in a HeLa cell population. (c and d) Simulated distribution of Ca²⁺ spikes in a cell population containing different percentages of γ_fast. (e and f) Experimentally observed distribution of Ca²⁺ spikes in γ11 knockdown, control shRNA, and γ11 cell populations. n_control = 150, n_{γ11-knockdown} = 90, n = number of cells studied. For both experiment and simulation, nonparametric kernel density function was fitted to the distribution of the number and duration of Ca²⁺ spiking in a cell population. (N_exp = 3). Details about the simulation of population response is in the Supporting Material, section 2.3. To see this figure in color, go online.

To obtain the calcium response in a cell population, we used a distribution of the activation rate of βγ (rate at which active βγ is generated after GPCR activation) at the plasma membrane in the two-subunit model. Such an approach has been used to model cell-to-cell variability in other biological systems (19–22). In this model, we assumed a Gamma distribution $\left(\mathrm{F}\left(\mathrm{R},\mathrm{k},\theta \right)=1/{\theta }^{k}1/\Gamma \left(k\right)R^{\left(k-1\right)}{e}^{-\left(R/\theta \right)}\right)$, where, θ = scale factor; k = shape factor) in G-protein activation, which may arise due to a variable expression level (Supporting Material 2.3). The Gamma distribution in protein expression level has been computationally and experimentally shown to exist in cell populations (23,24). We simulated calcium oscillations in a cell population for various proportions of fast versus slow translocating subunits (γ_fast:γ_slow) (Fig. 7, c and d). In cells containing only slow γ subunits (γ_fast:γ_slow - 0:100), the damping of oscillations showed wide cell-to-cell variability (Fig. 7, c and d). This is similar to the experimental observations for cells transfected with γ3 or γ11-3 subunit (Fig. 4, c–f, black traces). Introduction of a higher proportion of a fast subunit (γ_fast:γ_slow - 100:0) reduced this variability in oscillation characteristics such that most of the cells showed a relatively short period of oscillations. This result is consistent with experimental observations for cell populations overexpressing the γ11 subunit (Fig. 4, c–f, red traces).

Experiments and simulations: relative proportion of γ_fast regulates cell-to-cell variability in calcium oscillation in a population

The two-subunit model predicts that the increase in the proportion of fast translocating γ subunits would increase the fraction of cells having damped calcium oscillation and reduce cell-to-cell variability (Fig. 7, a and b). To test this prediction, we then compared the calcium spiking characteristics of γ11 knockdown HeLa cells with cells expressing either control shRNA, γ11 or γ3 (Fig. 7, e and f). Movie S4 and Movie S5 show α2AR-induced calcium oscillations in control shRNA and γ11 knockdown HeLa cells. A nonparametric kernel distribution fitted to the experimental (Fig. 7, e and f), and simulated distributions (Fig. 7, c and d), depicts the continuous shift in distribution of number of spikes and duration of calcium oscillation with increasing percentage of γ_fast.

The transiently transfected cells show an intrinsic variation in the expression levels of γ subunits. When calculated from mCherry intensity, moving from low expression of introduced γ11 to high, the probability of cells having a low number of calcium spikes increases and this is reflected in the simulation (Fig. S8, a and b). Furthermore, our results show that agonist concentrations do not have a significant effect on γ_fast:γ_slow dependency of Gi coupled GPCR-mediated calcium oscillation distribution in a cell population (Fig. S9). Overexpression of γ11 increases the proportion of cells with a lower number of calcium spikes (∼70% cells with spike number<3). In contrast, if γ11 is below native levels, it decreases the fraction of cells with a low number of calcium spikes (∼17% cells with spike number<3) (Table S3). This is consistent with the trend predicted from model simulations for different γ_fast:γ_slow ratios (Fig. 7, c and d).

Discussion

Systems level properties of signaling networks cannot be understood intuitively from the molecular interaction map of the network (25–28). This is especially true for properties that may emerge as a result of dynamic signaling events that show spatiotemporal variation in a cell. Although the components of many signaling networks and their individual activities have been identified, there is less information about the role of the spatiotemporal dynamics of signaling molecules in regulating the properties of these networks. Here, we perform dynamic analysis using a model to examine the effect of translocation of Gβγ subunits on oscillatory behavior of cytosolic calcium.

Dynamic properties of a system, such as oscillations, are achieved through a structural motif consisting of components with specific parametric values. Such dynamic behavior can be analyzed through bifurcation analysis (26).

The bifurcation analysis of a single subunit model suggested that higher amounts of agonist concentrations are required to achieve oscillation for a network motif with translocation. Thus, for a given agonist concentration a critical translocation rate constant will determine the Hopf bifurcation point beyond which the oscillations will damp over time. This allows oscillations to be terminated even in the presence of a stimulus. This theoretical framework also suggests that such a signaling motif can be used as a tuning mechanism to regulate system oscillations through differential translocation of a signaling component of a network.

Using genetic perturbation and live cell imaging, this prediction was tested experimentally by focusing on the receptor-mediated translocation of the Gβγ complex. Our results suggest that the relative proportion of different γ types expressed in a cell can play a role in regulating extracellular signal-induced calcium oscillation characteristics. Variability in IP3 production, GIRK potassium channel responses, and Golgi breakdown have been observed in response to the differential translocation rates of Gβγ subunits (15,17,29). Results show that Gβγ translocation can regulate critical network-level properties such as calcium oscillations.

In the current work, we specifically focus on the effect of translocation on norepinephrine-stimulated calcium oscillation. However, we did not analyze the effect of oscillation on translocation. This is a question of interest for future focus. Similar studies can also be performed to investigate for translocation embedded motif for other agonists and receptors. The oscillations observed in experiments are stochastic in nature. Multiple sources of noise in the oscillatory network may give rise to such stochastic responses. Furthermore, deterministic chaotic oscillations may also give rise to such a response (8). A general problem in addressing such stochasticity is to distinguish deterministic chaos from oscillations superimposed by the stochastic noise.

Heterogeneity in cell signaling responses to GPCR activation has been noted (5,19,30). Our data suggest that cell-to-cell variability in calcium oscillations in a population is regulated by the relative proportion of γ subunit types in the cell. We show that cells expressing predominantly slow translocating subunits will show wide variability in the duration of oscillations, whereas cells expressing predominantly fast translocating subunits show oscillations for relatively short durations before damping. Thus, the physiological output of a cell can be influenced by its γ subunit profile and by gene expression or posttranslational changes in this profile.

Engineering systems are designed by setting specific parametric values for components of a motif to yield a desired dynamic property. A classical engineering analogy is the RLC circuit composed of a resistor (R), an inductor (L), and a capacitor (C) in series to yield an oscillatory response in circuit current. Although the capacitance and inductance quantify the frequency and amplitude of the sustained oscillation, the resistance characterizes the damping property. In such a circuit, energy is transferred back and forth from the inductor to the capacitor, whereas the resistor causes the decay of oscillations. Thus, the desired rate of damping and frequency of oscillations can be designed by varying the parametric value of the resistance.

Here, by drawing an analogy from the electrical RLC circuit, we performed a similar analysis to characterize the damping behavior of calcium oscillations in HeLa cells. A combination of theoretical analysis and experimental evidence suggests that translocation of the signaling protein is part of an oscillatory network (Fig. 8). The network model here contains fast and slow feedback loops in the signaling motif and yields sustained oscillations similar to inductance and capacitance in the RLC circuit, whereas βγ translocation characterizes this damping behavior akin to the role of resistor. Thus, translocation rates decide the decay of amplitude and change in the frequency of calcium oscillations and can be used specifically to design desired oscillatory characteristics.

Figure 8.

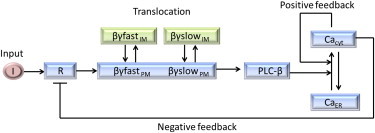
Schematic of G-protein γ subunit translocation embedded motif that regulates GPCR-induced calcium oscillation. Presence of two γ subunit types with different translocation rates is assumed. In the signaling pathway the positive and negative feedbacks yield sustained oscillations similar to the inductor and capacitor in a RLC circuit. The translocation of the βγ subunit offers resistance to the oscillations, which dampens the response analogous to the electrical circuit. To see this figure in color, go online.

Known desensitization mechanisms predominantly involve the phosphorylation of a receptor and its internalization resulting in GPCR signaling activity being terminated for relatively long periods of time (31). The results here suggest that GPCR-mediated βγ translocation in a cell can dynamically damp a critical signaling output. There is evidence that other signaling proteins such as Ras are not confined to specific cell compartments as originally thought, but are capable of extracellular signal directed spatial redistribution between cell membranes (32,33). Translocation embedded motifs may thus play a general role in regulating signaling pathways by acting as a simple desensitizing mechanism that is capable of rapid recovery. The computational and experimental framework used here can be applied to probe the role of other signal triggered protein movement in regulating cell function.