Abstract
The feasibility of using subharmonic aided pressure estimation (SHAPE) to noninvasively estimate interstitial fluid pressure (IFP) was studied. In vitro, radiofrequency signals, from 0.2 ml/l of Definity (Lantheus Medical Imaging, N Billerica, MA) were acquired within a water-tank with a Sonix RP ultrasound scanner (Ultrasonix, Richmond, BC, Canada; fT/R=6.7/3.35 MHz and fT/R =10/5 MHz) and the subharmonic amplitudes of the signals were compared over 0–50 mmHg. In vivo, five swine with naturally occurring melanomas were studied. Subharmonic signals were acquired from tumours and surrounding tissue during infusion of Definity and compared to needle-based pressure measurements. Both in vitro and in vivo, an inverse linear relationship between hydrostatic pressure and subharmonic amplitude was observed with r2=0.63–0.95; p<0.05, maximum amplitude drop 11.36 dB at 10 MHz and −8 dB, and r2 as high as 0.97; p<0.02 (10 MHz and −4/−8 dB most promising), respectively, indicating that SHAPE may be useful in monitoring IFP.
Keywords: Pressure estimation, Contrast agents, Subharmonic signals, Breast cancer, Ultrasound imaging
1. Introduction
Neoadjuvant chemotherapy (systemic preoperative chemotherapy) of breast cancer is often given before primary surgical treatment as it can offer considerable benefits to the patient by shrinking the tumour and even in some cases offer complete pathologic response, i.e. no tumor was detected [1, 2]. Neoadjuvant chemotherapy can also offer an early indication of a patient’s response to chemotherapy, thereby distinguishing responders and non-responders and allowing for further personalization of treatment. Consequently, monitoring breast cancer response to neoadjuvant therapy provides the possibility of adjusting the treatment if the patient is responding poorly or not at all [1, 3].
One of the indicators that have been suggested for monitoring neoadjuvant chemotherapy is interstitial fluid pressure (IFP) [4]. Generally, IFP is 10 to 30 mmHg higher in cancerous tissue than in normal tissue, although values up to 107 mmHg have been recorded in melanoma [4, 5]. This increase is attributed to leaky and collapsed vessels, fibrosis, high cell density and a defective lymphatic system in the tumour [5-7]. Due to the abnormal vasculature, tumour microvascular pressure (MVP) has been shown to be equal to IFP [8, 9]. Currently, IFP can only be measured with invasive wick-in-needle or micropuncture techniques [5]. IFP studies using the wick-in-needle technique have been conducted in cancers of the breast, cervix, head, neck, skin, lymph nodes and more [4, 7, 10-12]. Moreover, high IFP in tumours may lead to reduced drug delivery to the tumour and, therefore, it has been suggested that using IFP lowering drugs can further improve neoadjuvant chemotherapy [12].
Vascular ultrasound contrast agents are gas-filled microbubbles (diameter generally less than 8 μm) that improve the depiction of vascularity in ultrasound images by enhancing the difference in reflectivity between tissue and the agent [13]. Due to their small size, these microbubbles can traverse the entire capillary bed [13]. The idea of using microbubbles to monitor pressure was first suggested by Fairbank and Scully [14]. Given the difference in compressibility between the surrounding medium and a microbubble any changes in hydrostatic pressure induce changes in the size of the microbubble [15]. This in turn affects the reflectivity and resonance frequency of the bubble [15, 16]. The methods studied to date for pressure measurements with microbubbles include (1) utilizing changes in resonance frequency [14, 16], (2) employing the disappearance time of the microbubbles [17, 18] and (3) using the pulse echo amplitude of a single bubble [19]. However, these methods have not been tested for in vivo use due to lack of accuracy (errors > 10 mmHg) under ideal, in vitro conditions.
At higher acoustic pressures (>200 kPa) ultrasound contrast agents act as nonlinear oscillators producing harmonics, ultra- and subharmonics in the received signals. In subharmonic imaging pulses are transmitted at a frequency f0 and the echoes are received at half that frequency (f0/2). Subharmonic imaging has been shown to be a feasible option for contrast enhanced breast imaging due to marked subharmonic generation by contrast agents relative to limited subharmonic generation in tissues [20]. Our group developed a novel technique termed subharmonic aided pressure estimation (SHAPE; U.S. Patent 6,302,845) utilizing the subharmonic amplitude of the scattered signal from the microbubbles for pressure tracking [15]. Using the contrast agent Levovist (Schering AG, Berlin, Germany) and a pulse-echo setup with single-element transducers in a water tank, we demonstrated that the relationship between subharmonic amplitude and acoustic pressure can be described by a characteristic sigmoidal curve with 3 different stages of subharmonic generation depending on the acoustic power: i.e., occurrence, growth and saturation. The occurrence and saturation stages are not favourable for pressure estimation as the subharmonic response to hydrostatic pressure changes is weak in these stages. However, in the growth stage there was an inverse linear relationship (9.6 dB decrease in subharmonic amplitude over 0 to 186 mmHg, r = 0.98, p < 0.05) between the hydrostatic pressure and the subharmonic amplitude that can be used as a scale to estimate the hydrostatic pressure [15]. This inverse linear relationship has also been confirmed for other contrast agents and over different frequencies (2.5 – 6.6 MHz) and acoustic pressures (0.35 - 0.60 MPa) showing a decrease of 10-14 dB over a pressure range of 0 to 186 mmHg for all agents (r2 > 0.97, p < 0.05) [21].
Furthermore, our group has also looked at a variety of pressure estimation applications. An in vivo proof of concept for cardiac SHAPE was established by measuring the aortic pressure of two dogs (using two single element transducers to implement SHAPE) [22]. As that setup is not clinically acceptable, a Sonix RP scanner (Ultrasonix, Richmond, BC, Canada) was modified for SHAPE and initial studies in canines showed that left ventricular pressures could be estimated in vivo with errors as low as 0.19 mmHg [23]. Moreover, a Logiq 9 scanner (GE Healthcare, Milwaukee, WI) was modified for portal vein studies in canines (n = 14). These studies confirmed the inverse linear relationship (r2 > 0.90; p ≤ 0.01) between the subharmonic amplitude and the pressure in the portal vein [24]. Cardiovascular applications for SHAPE are conducted at a lower transmission frequency than would be needed for tumor SHAPE on or close to the surface of the skin and therefore the method needed to be developed further for this application.
Our group has proposed that SHAPE can potentially be used to estimate the IFP in tumours, thus making it possible to noninvasively monitor the tumour response to neoadjuvant chemotherapy. Hence, this method would be a considerable improvement over the wick-in-needle method currently used for IFP measurements and would potentially increase the use of IFP as a biomarker for neoadjuvant chemotherapy. Ultimately, tumor SHAPE would be used to monitor cancer therapy and therefore absolute pressure values are not needed, only a relative value to the baseline taken at the beginning of treatment. To test this hypothesis, the feasibility of using SHAPE to noninvasively estimate tumour IFP was studied in vitro in a water tank pressurized to simulate the IFP range in tumours. Furthermore, an in vivo proof of concept investigation of IFP measurements with SHAPE in swine melanoma was conducted. In this paper we report, first the in vitro water tank experiments designed to optimize the frequency and acoustic output for SHAPE over a hydrostatic pressure range of 50 mmHg and then move on to an in vivo proof of concept, or feasibility study, of the SHAPE method using these optimized acoustic parameters in swine melanoma.
2. Materials and methods
2.1. In vitro experiments
Two different sets of experiments were conducted in vitro; a) the acoustic power levels were varied and the hydrostatic pressure held constant at 0 mmHg to establish the optimal acoustic power levels for pressure estimation (in the growth zone; [15]) and b) the hydrostatic pressure was varied from 0 to 50 mmHg at the optimal power levels selected in the previous experiments.
An acrylic water-tank (inner dimensions after lining: 11.75 cm × 8.26 cm × 8.26 cm) that can withstand pressures up to 100 mmHg was custom-built and used to investigate SHAPE at the IFP levels encountered in breast tumours (Figure 1 a) – b)). The tank was lined with 25.4 mm of Sorbothane (McMaster-Carr, Atlanta, GA) to eliminate effects from standing waves and 9.5 mm of gum rubber (McMaster-Carr) was used to couple the Sorbothane to the isotonic diluent used for the experiments. A digital pressure gauge (OMEGA Engineering, Stamford, CT) was used to monitor the pressure values. A commercial ultrasound scanner, Sonix RP (Ultrasonix, Richmond, BC, Canada; Software version 3.2.2) operating in the Research mode with a high frequency linear array probe L14-5 (nominal BW 5-14 MHz; actual BW 3- 12MHz ), was positioned at a 45° angle to a thin plastic acoustic window (0.1 mm) in the tank. The water-tank was filled with isotonic diluent (800 ml) and immersed in a larger water-bath also filled with isotonic diluent. Measurements were made at room temperature (25°C). The contrast agent Defnity (Lantheus Medical Imaging, N Billerica, MA) was injected through an inlet on the tank (dose: 0.2 ml/l) and kept in suspension using a magnetic stirrer. To ensure an even concentration of agent within the tank, 30 s of mixing was allowed before starting measurements. Two transmission frequencies, 6.7 MHz and 10 MHz (subharmonic signals received at subharmonic frequencies 3.35 and 5 MHz, which are around 10 and 12 dB down from peak intensity respectively) were considered. These frequencies were selected as they fall within the frequency band of the transducer and can be used for clinical breast imaging, since ultimately the goal is to employ SHAPE for human breast cancer IFP estimation. Pulse inversion was implemented on the scanner to minimize scatter from tissue and increase sensitivity to bubble signals [13] and each measurement was taken with the scanning depth fixed at 6 cm (frame rate 9 Hz) and the focus at 4.25 cm (positioned approximately 1.5 cm within the water tank; Figure 1 c)).
Figure 1.
a) – b) Water tank and acoustic setup with the L14-5 transducer. Notice the digital pressure gauge on the top of the tank and the syringe to alter the hydrostatic pressure. c) B-mode image of the water tank. The region of interest used for SHAPE is indicated with a red square.
In order to establish the optimal acoustic power setting for pressure measurements, the hydrostatic pressure was kept at 0 mmHg and the acoustic power varied with a step size of 2 dB from −20 dB to 0 dB (relative levels - full range of the system), equivalent to 0.24 to 2.05 MPa peak to peak, measured with a 0.2 mm needle hydrophone (Precision Acoustics, Dorchester, Dorset, UK). The subharmonic signals were plotted as a function of acoustic power. The acoustic power levels within the growth zone (of the characteristic sigmoidal curve) were then selected for further SHAPE investigation with varying hydrostatic pressure.
The hydrostatic pressure within the tank was varied from 0 to 50 mmHg (in steps of 10 mmHg, n = 3) by pumping air with a 100 ml syringe through a one-way valve attached to an inlet on the tank (Figure 1 a) – b)). Pressure values were then compared using linear regression to the radiofrequency (RF) data acquired with the Sonix RP.
The RF data were extracted using programs obtained from Ultrasonix and processed offline on a PC computer using Matlab (Mathworks, Natick, MA) programs developed by our group. A region-of-interest (ROI) of 4 by 4 mm was selected (Figure 1 c)). The Fourier Transform of each vector within the ROI was computed and the subharmonic amplitude extracted from the spectra over a 1 MHz bandwidth around the subharmonic peak. The subharmonic amplitude was then averaged over all the vectors in the ROI and in frames corresponding to 2 seconds to eliminate effects from noise. Then linear regression analysis was used to determine the relationship between the hydrostatic pressure and the change in subharmonic amplitude. All statistical analyses were conducted using Stata 9.0 (Stata Corporation, College Station, TX).
2.2. In vivo experiments
As an initial proof-of-concept, SHAPE was tested on five Sinclair swine (weight: 9.5 ± 4.1 kg; Sinclair Bio Resources, Columbia, MO), with naturally occurring melanomas (similar to malignant melanomas in humans) [25, 26]. Tumour volume was estimated using the formula for an ellipsoid where length, width and height were measured from B-mode images of the melanoma.
The animals were sedated with an intramuscular injection of 0.04 mg/kg of Atropine (Med-Pharmex Inc, Pomona, CA) and 5 mg/kg of Telazol (Tiletamine/Zolezepam, Pfizer, New York, NY). General anaesthesia was then maintained with 2-4% of Isoflurane (Iso-thesia; Abbott Laboratories, Chicago, IL) through an endotracheal tube during the procedure. Body temperature was kept steady with a heating pad and after the procedure the animals were euthanized with an intravenous injection of 0.25 ml/kg of Beuthanasia. All experiments were supervised by the Laboratory Animal Services Department and conducted in agreement with a protocol approved by Thomas Jefferson University’s Institutional Animal Care and Use Committee.
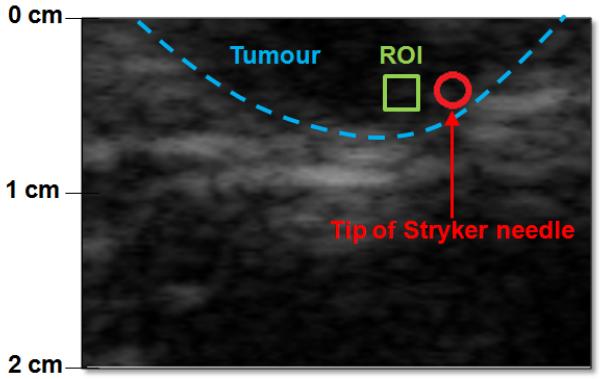
To ensure constant concentration of microbubbles throughout the experiment, 3 ml of Definity were injected into a 50 ml saline bag and the agent-saline mix was then infused through an ear vein at a rate of 6.25 ml/min. The presence of Definity in the melanomas was confirmed visually by a radiologist before data acquisition. A needle based pressure monitor system (Stryker, Berkshire, UK) was used as a reference standard to measure IFP within the tumours and 3 to 5 cm from the tumour periphery in the surrounding normal tissue (Figure 2). For this pressure monitor, 1 ml of saline is injected into the tissue and then the monitor stabilizes at the IFP level of the tissue (stabilization time < 30 s). Pressure measurements were taken in triplicate both in normal tissue and in the melanoma (one after the other), while simultaneously acquiring ultrasound RF data. Field of view varied from 2.0 to 4.0 cm depending on tumour size and location (frame rate 12-13 Hz depending on depth). Two transmission frequencies 6.7 MHz and 10 MHz were considered (subharmonic frequency at 3.35 and 5 MHz, respectively). The optimal acoustic power setting could not be determined in vivo due to time constraints, but acoustic power levels of −4 dB, −8 dB and −12 dB were used as they showed the most promise in vitro. Moreover, the melanomas were on the skin surface so ultrasound attenuation was, therefore, assumed to have minimal impact on results.
Figure 2.
An example B mode image from one of the swine melanomas. Tumour periphery is indicated by a blue dashed line, ROI for SHAPE with a green box and the location of the Stryker pressure monitor needle is indicated with a red circle
RF data were processed offline using the same algorithms as in vitro with the ROI selected close to the tip of the pressure monitor needle. The location of the needle tip was verified by a radiologist (Figure 2). Frame rate was 9 fps, pulse length of 5 and the number of scan lines within the ROI was 22. Linear regression analysis was conducted with Stata 9.0 (Stata Corporation, College Station, TX) to compare the subharmonic amplitude extracted from the RF data with the pressure values acquired with the Stryker pressure monitoring system. We used the regress command in STATA to make a linear regression model of the data. The regress command gives the p-value from the F-test that is used to determine the statistical significance of the model and r2 as well as the results of the t-test for the data.
3. Results
3.1. In vitro experiments
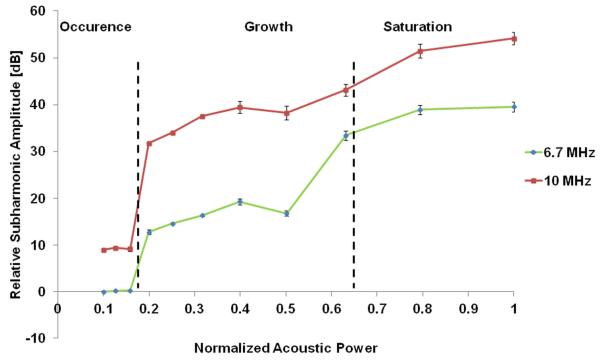
An approximate sigmoidal curve for the relationship between the subharmonic amplitude and the acoustic power showed the three stages of subharmonic generation: i.e., occurrence (−20 dB to −16 dB) where there was minimal change in the subharmonic amplitude; growth (−16 dB to −4 dB) where there was a sharp rise in subharmonic amplitude and the subharmonic is most sensitive to pressure changes, and finally saturation (−4 dB to 0 dB) where again there is minimal subharmonic amplitude change (Figure 3). Based on this relationship four acoustic power levels covering the growth stage and its boundaries were chosen for further investigation of hydrostatic pressure estimation using SHAPE; −16, −12, −8 and −4 dB (corresponding to 0.33, 1.06, 1.33, 1.68 MPa and 0.24, 1.21, 1.52 and 1.78 MPa peak to peak for 6.7 MHz and 10 MHz, respectively). No fundamental peak was observed as it was cancelled out by the pulse inversion implemented. Normalised acoustic power is scaled so that 1.0 refers to the highest acoustic power level and the remaining power levels are normalized to that value as such: normalized acoustic power level = acoustic power level/highest acoustic power level.
Figure 3.
Subharmonic response to changes in acoustic power with the occurrence, growth and saturation phases. The relative subharmonic amplitude is scaled so that 0 dB refers to the lowest measured subharmonic amplitude and the remaining values are then scaled to that point as such: relative subharmonic amplitude = measured subharmonic amplitude – lowest measured subharmonic amplitude .
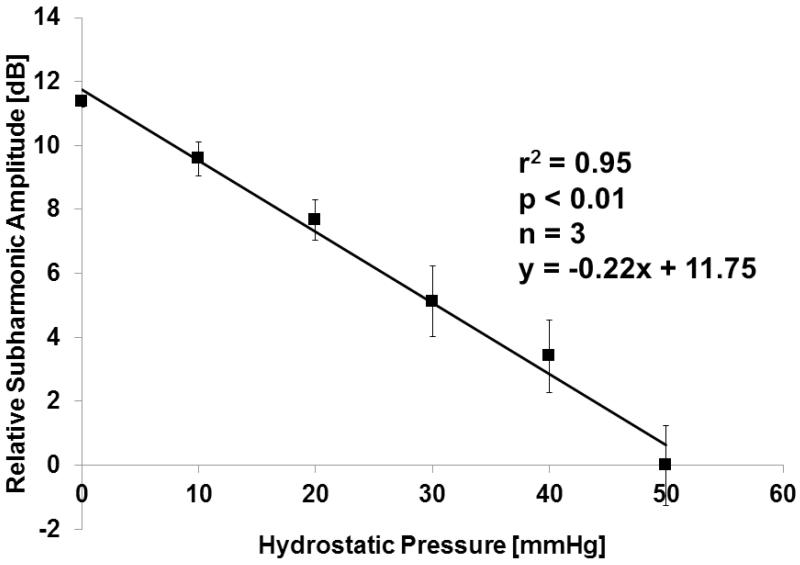
In the water-tank an inverse relationship was seen over a pressure change from 0 to 50 mmHg at both 6.7 MHz and 10 MHz transmission frequencies and all acoustic power levels −16 dB to −4 dB (r2 ≥ 0.63; p < 0.05; Figure 4). The r2 values from the linear regression analysis were consistently higher for a transmission of 10 MHz (receiving the subharmonic at 5 MHz) than for 6.7 MHz (receiving at 3.35 MHz). Moreover, pressure estimates obtained at −16 dB (start of the growth phase) showed limited sensitivity compared to the higher acoustic power settings likely due to a lack of subharmonic generation (still in the occurrence phase). The largest drop in subharmonic amplitude (corresponding to the maximum sensitivity for pressure estimation), 11.4 dB over 50 mmHg, was seen at 10 MHz and −8 dB (r2 = 0.95; p < 0.01; Figure 5).
Figure 4.
Decrease in subharmonic signal amplitude for Definity as a function of frequency and acoustic power (n = 3) when hydrostatic pressures were varied from 0 to 50 mmHg.
Figure 5.
Inverse linear relationship between pressure and subharmonic signal amplitude for Definity at 10 MHz and −8 dB acoustic output power (n = 3).
3.2. In vivo experiments
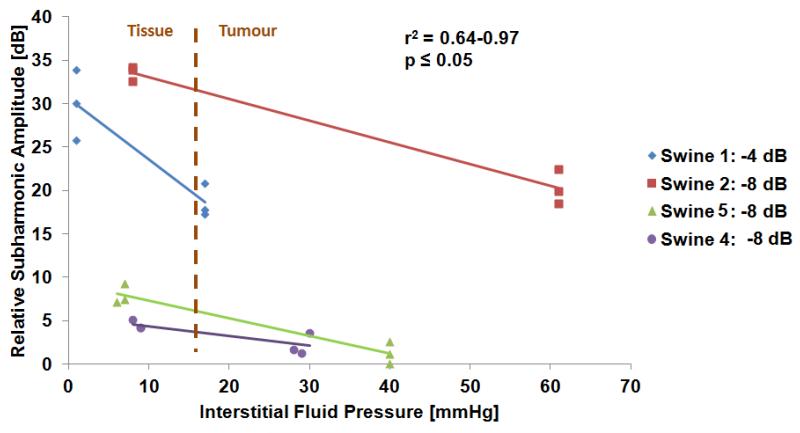
For the swine the IFP was always lower than 21 mmHg in normal tissue and in the melanomas IFP was higher than 16 mmHg (Figure 6). No significant relationship was observed between tumour volume and tumour IFP (r2=0.08, p=0.07).
Figure 6.
Best fit in vivo measurements showing SHAPE results compared to the pressure monitor for 10 MHz. The difference between tissue and tumour IFP is clearly captured by SHAPE. Note that for a clearer comparison of best fit results, relative values for subharmonic amplitude (0 dB corresponding to the lowest dB value and then subharmonic amplitude difference relative to that value is reported) are used in the figure whereas actual values are used in table 1.
Table 1 lists the results of all the measurements taken in vivo. In all cases but one an inverse linear relationship was observed. In the case where the subharmonic amplitude increased with higher IFP there was no statistically significant relationship (Tumour 4, 10 MHz, −8 dB; p=0.054). Only one melanoma showed statistically significant results for IFP at the transmission frequency of 6.7 MHz (at −8 dB acoustic power; −2.88 dB over 40 mmHg change, r2 = 0.91, p = 0.02), presumably due to the subharmonic frequency (3.35 MHz) lying at the lower end of the linear array’s bandwidth. However, for 10 MHz transmission frequency the relationship between the subharmonic amplitude and the IFP had a higher correlation for all animals. Data from one swine were eliminated due to technical difficulties with the Stryker pressure monitor. Due to time limitations imposed by the infusion of Definity (only 2 vials were available to use for each swine allowing less than 8 minutes of infusion) not all frequency/acoustic power settings were evaluated for each swine. However, the slope for three of the four swine was very similar to each other (−0.19 ± 0.07 dB/mmHg) and to the in vitro slope (−0.22 dB/mmHg) whereas one melanoma showed a large spread within the normal tissue IFP subharmonic amplitude. In vivo, the best acoustic parameters for SHAPE using Definity in this parameter space were 10 MHz and acoustic power settings of −4 or −8 dB (Figure 6). An infusion was employed to minimize any timing effects and no trend as a function of time was seen in the signals. The subharmonic signals were steady during the in vivo measurements (average standard deviation 0.39 dB; Range: 0.25 – 0.69 dB, data not shown). There is a statistically significant difference (p<0.01) in slopes and offsets between tumours and for the offset depending on power level (p=0.05). However, there was not a significant difference in slopes with power level (p=0.16) nor a significant difference between the slopes and offsets and frequency (p>0.05).
Table 1.
A summary of in vivo measurements showing SHAPE results compared to the pressure monitor. One animal was eliminated due to technical difficulties with the pressure monitor and not all conditions were considered for all animals due to time constraints.
| Tumour (Swine) |
Frequency [MHz] |
Acoustic Output [dB] |
Subharmonic amplitude in tissue [dB] |
St. dev [dB] |
Subharmonic amplitude in tumour [dB] |
St. dev [dB] |
Change in subharmonic amplitude [dB] |
Tissue IFP [mmHg] |
Tumour IFP [mmHg] |
Change in IFP [mmHg] |
(r2, p) | Slope [dB/mmHg] |
Intercept [dB] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | −4 | 66.52 | 4.08 | 55.27 | 1.90 | −11.26 | 1 | 17 | 16 | 0.82, 0.012 | −0.70 | 67.23 | |
| 1(1) | −8 | 66.90 | 2.22 | 57.19 | 1.69 | −9.71 | 1 | 17 | 16 | 0.90, 0.004 | −0.61 | 67.51 | |
| 6.7 | −4 | 67.45 | 2.75 | 60.31 | 7.03 | −7.14 | 2 | 17 | 15 | 0.40, 0.177 | −0.48 | 68.40 | |
| −8 | 67.92 | 0.86 | 60.67 | 8.24 | −7.25 | 2 | 17 | 15 | 0.37, 0.207 | −0.48 | 68.89 | ||
|
| |||||||||||||
| 2(2) | 10 | −4 | 67.87 | 2.17 | 60.52 | 0.67 | −7.35 | 8 | 61 | 53 | 0.89, 0.005 | −0.14 | 68.98 |
| −8 | 70.18 | 0.90 | 56.90 | 2.01 | −13.28 | 8 | 61 | 53 | 0.97, 0.001 | −0.25 | 72.19 | ||
|
| |||||||||||||
| 4(4) | 10 | −8 | 35.94 | 0.57 | 39.21 | 1.09 | 3.27 | 20 | 69 | 33 | 0.64, 0.056 | 0.07 | 34.61 |
| −12 | 36.13 | 0.93 | 35.53 | 4.19 | −0.60 | 18 | 71 | 32 | 0.17, 0.425 | −0.01 | 36.33 | ||
|
| |||||||||||||
| 10 | −8 | 44.56 | 1.13 | 37.84 | 1.27 | −6.72 | 7 | 40 | 30 | 0.92, 0.003 | −0.20 | 45.98 | |
| 5(3) | −12 | 42.50 | 2.27 | 38.89 | 0.37 | −3.61 | 8 | 40 | 0 | 0.63, 0.058 | −0.11 | 43.40 | |
| 6.7 | −8 | 49.36 | 0.87 | 46.48 | 0.42 | −2.88 | 10 | 40 | 0 | 0.91, 0.003 | −0.10 | 50.31 | |
| −12 | 43.94 | 2.24 | 43.79 | 2.89 | −0.15 | 10 | 40 | 0 | 0.10, 0.542 | −0.01 | 43.99 | ||
4. Discussion
An inverse linear relationship between changes in hydrostatic pressure and subharmonic amplitude (r2 as high as 0.97, p < 0.05) over the IFP pressure range found in tumours (0 – 50 mmHg) was confirmed in vitro. This study has established that for the contrast agent Definity and the acoustic parameters tested, a transmission frequency of 10 MHz (receiving at 5 MHz) and acoustic power of −8 dB offer the greatest sensitivity for pressure estimation. In addition, in vivo proof-of-concept for SHAPE as a noninvasive monitor of IFP has been provided in four swine with naturally occurring melanoma. In vivo the IFP was always lower than 21 mmHg in normal tissue and in the melanomas IFP was higher than 16 mmHg, as expected from the literature [4, 7, 10-12]. SHAPE showed excellent correlation with IFP values obtained in normal tissues and in the tumour using the Stryker needle-based pressure measurements (r2 = 0.67 – 0.96, p < 0.01) with optimal sensitivity at a transmission frequency of 10 MHz and acoustic power settings −4 or −8 dB. These results suggest that SHAPE may be useful as a noninvasive pressure monitor of IFP in tumours. Due to attenuation and differences there will not be one global relationship between IFP and the subharmonic amplitude applicable to all animals. However, from the in vitro study it is clear that an inverse linear relationship can be arrived at and in vivo the slopes and offsets give an indication that this holds true even with individual differences between animals. In clinical practice a calibration method would need to be implemented alongside the IFP pressure estimation. As this is a proof of concept study no such method was employed for this project. We are currently exploring what method can be used for calibration in IFP measurements.
The main limitation of this study is the small sample size in vivo (only four swine). Nonetheless, this still constitutes a proof of concept for SHAPE for estimating tumour IFP and studies in a nude athymic rat model with human breast cancer xenografts are currently being performed to further investigate the ability of SHAPE to monitor treatment response. Furthermore, correlation between IFP and subharmonic amplitude was generally lower when transmitting at 6.7 MHz and this setup may have been pushing the bandwidth limitations of the probe as the subharmonic received at 3.35 MHz is at the lower end of the probe’s bandwidth (5 - 14 MHz). Additionally, a potential criticism is that only one location within each melanoma was considered. However, studies by Jain et al. [12] show that tumour pressure is typically homogenous in the tumour itself, but rapidly drops at its periphery so this should not affect SHAPE (Less et al. 1992). The subharmonic signal in vivo did not vary greatly with time (maximum standard deviation 0.7 dB). This suggests that SHAPE is independent of the concentration within the ROI, as was also shown by Shi et al. (1999).
Taghian et al. [27] used a wick-in-needle technique to monitor the IFP of breast cancer before and after neoadjuvant chemotherapy with two drugs used consecutively. When used as a first drug, paclitaxel decreased the IFP by 36 % (p = 0.02) whereas with doxorubicin as the first drug there was only an 8 % reduction (p = 0.41). As this was a hypothesis-generating study they did not show any outcome related to the relationship between IFP and therapy response [27]. However, the level of IFP has been shown to predict disease free survival (DFS) for cervical cancer (34 % DFS if IFP > 19 mmHg, 68% DFS if IFP < 19 mmHg; p = 0.002) [10]. Boucher and Jain’s (1991) group successfully concluded that the wick in needle technique can be used for IFP measurements in human melanomas. Thus, the level of IFP in tumours could potentially be used to monitor the response to neoadjuvant chemotherapy and offer early adjustment of therapy for non-responders. Moreover, Less and colleagues (1992) have suggested that IFP could be helpful for localization of tumours as there is a sharp drop in IFP at the tumour periphery.
Several other groups have reported a relationship between subharmonic amplitude and hydrostatic pressure, using both single-element transducers and commercial ultrasound scanners in vitro [28-30]. One group studied the response of the subharmonic, fundamental and second harmonic signals to a change in hydrostatic pressure with the contrast agent Optison (GE Healthcare, Princeton, NJ). They showed that an increase in hydrostatic pressure leads to a time-dependent decrease in subharmonic amplitude (r > 0.71) [28-30]. Andersen and Jensen [31] investigated the ratio between the energy of the subharmonic and the fundamental amplitudes to estimate pressure using the contrast agent SonoVue (Bracco, Milan, Italy) and determined that there was an inverse linear relationship between this ratio and hydrostatic pressure changes; albeit with a high standard deviation. Frinking and colleagues [32] have shown that depending on the acoustic power level the subharmonic amplitude either decreases with increasing hydrostatic pressure (as determined by our group and others), or increases with hydrostatic pressure. As an example, at 50 kPa an increase of 18.9 dB in the subharmonic amplitude was seen over a 40 mmHg increase in hydrostatic pressure, but at 400 kPa a decrease of 9.6 dB was seen over 185 mmHg. However, they used an experimental phospholipid shell agent and our setup has not been able to distinguish a subharmonic response from noise at acoustic pressures lower than 100 kPa using commercial agents [21]. Faez et al. (2011) observed both an increase and a decrease in the subharmonic amplitude with increasing hydrostatic pressure using BR14 microbubbles (Bracco Research S.A., Geneva, Switzerland). They reported a maximum of 8 dB increase in subharmonic amplitude over 15 kPa when transmitting at 10 MHz and 240 kPa acoustic pressure. Potentially, these discrepancies are due to differences in experimental setup or the properties of the contrast agents used.
5. Conclusions
Results from this study demonstrate that SHAPE may be useful for the noninvasive monitoring of IFP. If proven viable, SHAPE has the potential to provide benefits for cancer therapy as it is noninvasive and thus, there is less risk and more comfort for the patient than with the wick-and-needle method. Moreover, it would make it easier to customize individual patient treatment if SHAPE were found to be able to monitor neoadjuvant treatment response throughout the chemotherapy cycles.
Subharmonic aided pressure estimation of interstitial tumor pressure is verified
Inverse relationship between hydrostatic/tumor pressure and subharmonic amplitude
Maximum drop in amplitude in vitro 11.36 dB at 10 MHz and −8 dB
Most promising acoustic parameters in vivo 10 MHz and −4/−8 dB
Subharmonic aided pressure estimation may be useful in monitoring cancer treatment
Acknowledgements
This work was supported by the U.S. Army Medical Research Material Command under grant W81XWH-08-1-0503, National Institute of Health R21 CA137733, R21 HL081892 and RC1 DK087365 (supporting JRE).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Guarneri V, Frassoldati A, Giovannelli S, Borghi F, Conte P. Primary systemic therapy for operable breast cancer: A review of clinical trials and perspectives. Cancer Letters. 2007;248:175–185. doi: 10.1016/j.canlet.2006.07.001. [DOI] [PubMed] [Google Scholar]
- [2].Mauri D, Pavlidis N, Ioannidis JPA. Neoadjuvant versus adjuvant systemic treatment in breast cancer: a meta-analysis. Journal of the National Cancer Institute. 2005;97:188–194. doi: 10.1093/jnci/dji021. [DOI] [PubMed] [Google Scholar]
- [3].McMasters KM, Hunt KK. Neoadjuvant chemotherapy, locally advanced breast cancer, and quality of life. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 1999;17:441–444. doi: 10.1200/JCO.1999.17.2.441. [DOI] [PubMed] [Google Scholar]
- [4].Curti BD, Urba WJ, Gregory Alvord W, Janik JE, Smith JW, Madara K, Longo DL. Interstitial Pressure of Subcutaneous Nodules in Melanoma and Lymphoma Patients: Changes during Treatment. Cancer Research. 1993;53:2204–2207. [PubMed] [Google Scholar]
- [5].Heldin CH, Rubin K, Pietras K, Ostman A. High interstitial fluid pressure - an obstacle in cancer therapy, Nature reviews. Cancer. 2004;4:806–813. doi: 10.1038/nrc1456. [DOI] [PubMed] [Google Scholar]
- [6].Ferretti S, Allegrini PR, Becquet MM, McSheehy PMJ. Tumor interstitial fluid pressure as an early-response marker for anticancer therapeutics. Neoplasia (New York, NY) 2009;11:874. doi: 10.1593/neo.09554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Less JR, Posner MC, Boucher Y, Borochovitz D, Wolmark N, Jain RK. Interstitial hypertension in human breast and colorectal tumors. Cancer Res. 1992;52:6371–6374. [PubMed] [Google Scholar]
- [8].Boucher Y, Jain RK. Microvascular pressure is the principal driving force for interstitial hypertension in solid tumors: implications for vascular collapse. Cancer Research. 1992;52:5110. [PubMed] [Google Scholar]
- [9].Boucher Y, Leunig M, Jain RK. Tumor angiogenesis and interstitial hypertension. Cancer Research. 1996;56:4264. [PubMed] [Google Scholar]
- [10].Milosevic M, Fyles A, Hedley D, Pintilie M, Levin W, Manchul L, Hill R. Interstitial fluid pressure predicts survival in patients with cervix cancer independent of clinical prognostic factors and tumor oxygen measurements. Cancer Res. 2001;61:6400–6405. [PubMed] [Google Scholar]
- [11].Gutmann R, Leunig M, Feyh J, Goetz AE, Messmer K, Kastenbauer E, Jain RK. Interstitial hypertension in head and neck tumors in patients: correlation with tumor size. Cancer Research. 1992;52:1993. [PubMed] [Google Scholar]
- [12].Jain RK, Tong RT, Munn LL. Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: insights from a mathematical model. Cancer Research. 2007;67:2729. doi: 10.1158/0008-5472.CAN-06-4102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Goldberg BB, Raichlen JS, Forsberg F. Ultrasound contrast agents: basic principles and clinical applications. Informa Healthcare. 2001 [Google Scholar]
- [14].Fairbank WM, Jr., Scully MO. A new noninvasive technique for cardiac pressure measurement: resonant scattering of ultrasound from bubbles. IEEE transactions on bio-medical engineering. 1977;24:107–110. doi: 10.1109/TBME.1977.326112. [DOI] [PubMed] [Google Scholar]
- [15].Shi W, Forsberg F, Raichlen J, Needleman L, Goldberg B. Pressure dependence of subharmonic signals from contrast microbubbles. Ultrasound in Medicine & Biology. 1999;25:275–283. doi: 10.1016/s0301-5629(98)00163-x. [DOI] [PubMed] [Google Scholar]
- [16].Ishihara K, Kitabatake A, Tanouchi J, Fujii K, Uematsu M, Yoshida Y, Kamada T, Tamura T, Chihara K, Shirae K. New approach to noninvasive manometry based on pressure dependent resonant shift of elastic microcapsules in ultrasonic frequency characteristics. Japanese Journal of Applied Physics Supplement. 1988;27:125–127. [Google Scholar]
- [17].Bouakaz A, Frinking PJA, de Jong N, Bom N. Noninvasive measurement of the hydrostatic pressure in a fluid-filled cavity based on the disappearance time of micrometer-sized free gas bubbles. Ultrasound in Medicine & Biology. 1999;25:1407–1415. doi: 10.1016/s0301-5629(99)00109-x. [DOI] [PubMed] [Google Scholar]
- [18].Postema M, Bouakaz A, de Jong N. Noninvasive microbubble-based pressure measurements: a simulation study. Ultrasonics. 2004;42:759–762. doi: 10.1016/j.ultras.2003.12.007. [DOI] [PubMed] [Google Scholar]
- [19].Hök B. A new approach to noninvasive manometry: Interaction between ultrasound and bubbles. Medical and Biological Engineering and Computing. 1981;19:35–39. doi: 10.1007/BF02443844. [DOI] [PubMed] [Google Scholar]
- [20].Forsberg F, Piccoli CW, Merton DA, Palazzo JJ, Hall AL. Breast Lesions: Imaging with Contrast-enhanced Subharmonic US—Initial Experience1. Radiology. 2007;244:718–726. doi: 10.1148/radiol.2443061588. [DOI] [PubMed] [Google Scholar]
- [21].Halldorsdottir VG, Dave JK, Leodore LM, Eisenbrey JR, Park S, Hall AL, Thomenius K, Forsberg F. Subharmonic Contrast Microbubble Signals for Noninvasive Pressure Estimation under Static and Dynamic Flow Conditions. Ultrasonic imaging. 2011;33:153–164. doi: 10.1177/016173461103300301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Forsberg F, Ji-Bin L, Shi WT, Furuse JAFJ, Shimizu MASM, Goldberg BBAGBB. In vivo pressure estimation using subharmonic contrast microbubble signals: proof of concept. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on. 2005;52:581–583. doi: 10.1109/tuffc.2005.1428040. [DOI] [PubMed] [Google Scholar]
- [23].Dave JK, Halldorsdottir VG, Eisenbrey JR, Raichlen JS, Liu JB, McDonald ME, Dickie K, Wang S, Leung C, Forsberg F. Noninvasive LV Pressure Estimation Using Subharmonic Emissions From Microbubbles. JACC Cardiovascular Imaging. 2012;5:87. doi: 10.1016/j.jcmg.2011.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Dave J, Halldorsdottir V, Eisenbrey J, Liu JB, Lin F, Zhou JH, Wang HK, Thomenius K, Forsberg F. IEEE. 2010. In vivo subharmonic pressure estimation of portal hypertension in canines; pp. 778–781. [Google Scholar]
- [25].Hook R, Jr, Berkelhammer J, Oxenhandler R. Melanoma: Sinclair swine melanoma. The American Journal of Pathology. 1982;108:130. [PMC free article] [PubMed] [Google Scholar]
- [26].Goldberg BB, Merton DA, Liu JB, Forsberg F, Zhang K, Thakur M, Schulz S, Schanche R, Murphy GF, Waldman SA. Contrast-Enhanced Ultrasound Imaging of Sentinel Lymph Nodes After Peritumoral Administration of Sonazoid in a Melanoma Tumor Animal Model. Journal of Ultrasound in Medicine. 2011;30:441–453. doi: 10.7863/jum.2011.30.4.441. [DOI] [PubMed] [Google Scholar]
- [27].Taghian AG, Abi-Raad R, Assaad SI, Casty A, Ancukiewicz M, Yeh E, Molokhia P, Attia K, Sullivan T, Kuter I, Boucher Y, Powell SN. Paclitaxel decreases the interstitial fluid pressure and improves oxygenation in breast cancers in patients treated with neoadjuvant chemotherapy: clinical implications. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 2005;23:1951–1961. doi: 10.1200/JCO.2005.08.119. [DOI] [PubMed] [Google Scholar]
- [28].Adam D, Burla E. Blood pressure estimation by processing of echocardiography signals. Computers in Cardiology. 2001;2001:609–612. [Google Scholar]
- [29].Adam D, Sapunar M, Burla E. On the relationship between encapsulated ultrasound contrast agent and pressure. Ultrasound in Medicine & Biology. 2005;31:673–686. doi: 10.1016/j.ultrasmedbio.2005.01.005. [DOI] [PubMed] [Google Scholar]
- [30].Ganor Y, Adam D, Kimmel E. Time and pressure dependence of acoustic signals radiated from microbubbles. Ultrasound in Medicine & Biology. 2005;31:1367–1374. doi: 10.1016/j.ultrasmedbio.2005.06.014. [DOI] [PubMed] [Google Scholar]
- [31].Andersen KS, Jensen JA. Impact of acoustic pressure on ambient pressure estimation using ultrasound contrast agent. Ultrasonics. 2010;50:294–299. doi: 10.1016/j.ultras.2009.09.016. [DOI] [PubMed] [Google Scholar]
- [32].Frinking PJA, Gaud E, Brochot J, Arditi M. Subharmonic scattering of phospholipid-shell microbubbles at low acoustic pressure amplitudes, Ultrasonics, Ferroelectrics and Frequency Control. IEEE Transactions on. 2010;57:1762–1771. doi: 10.1109/tuffc.2010.1614. [DOI] [PubMed] [Google Scholar]