Computational Morphodynamics: A modeling framework to understand plant growth

Abstract

Computational morphodynamics utilizes computer modeling to understand the development of living organisms over space and time. Results from biological experiments are used to construct accurate and predictive models of growth. These models are then used to make novel predictions providing further insight into the processes in question, which can be tested experimentally to either confirm or rule out the validity of the computational models. This review highlights two fundamental issues: (1.) models should span and integrate single cell behavior with tissue development and (2.) the necessity to understand the feedback between mechanics of growth and chemical or molecular signaling. We review different approaches to model plant growth and discuss a variety of model types that can be implemented, with the aim of demonstrating how this methodology can be used, to explore the morphodynamics of plant development.

Introduction

System biology has emerged as a field that attempts to integrate large-scale datasets obtained from genomic, gene expression, proteomic, metabolomic, and imaging studies into a global framework to explain cellular or organismal function (73). These systems approaches integrate the biological sciences with the quantitative approaches of applied mathematics, physics, and engineering to explicitly model biological processes computationally. A computational model is an explicit formulation of a hypothesis that allows the computer to simulate and generate a visualization of a biological process based on the available data. The creation of models to explain biological systems is in no way a new concept in biology. However, most biological models created to date are intuitive, non-quantitative, and can be understood in cartoon form. While those models are perfectly acceptable, certain processes in developmental biology, such as plant growth, involve a two-way interaction between geometry and cellular molecular function over space and time that is nearly impossible to visualize, let alone comprehend, with static models. To address this deficiency, the field of computational morphodynamics has emerged to explain complex temporal and spatial interactions of growth and signaling through the use of computational modeling integrated with biological imaging.

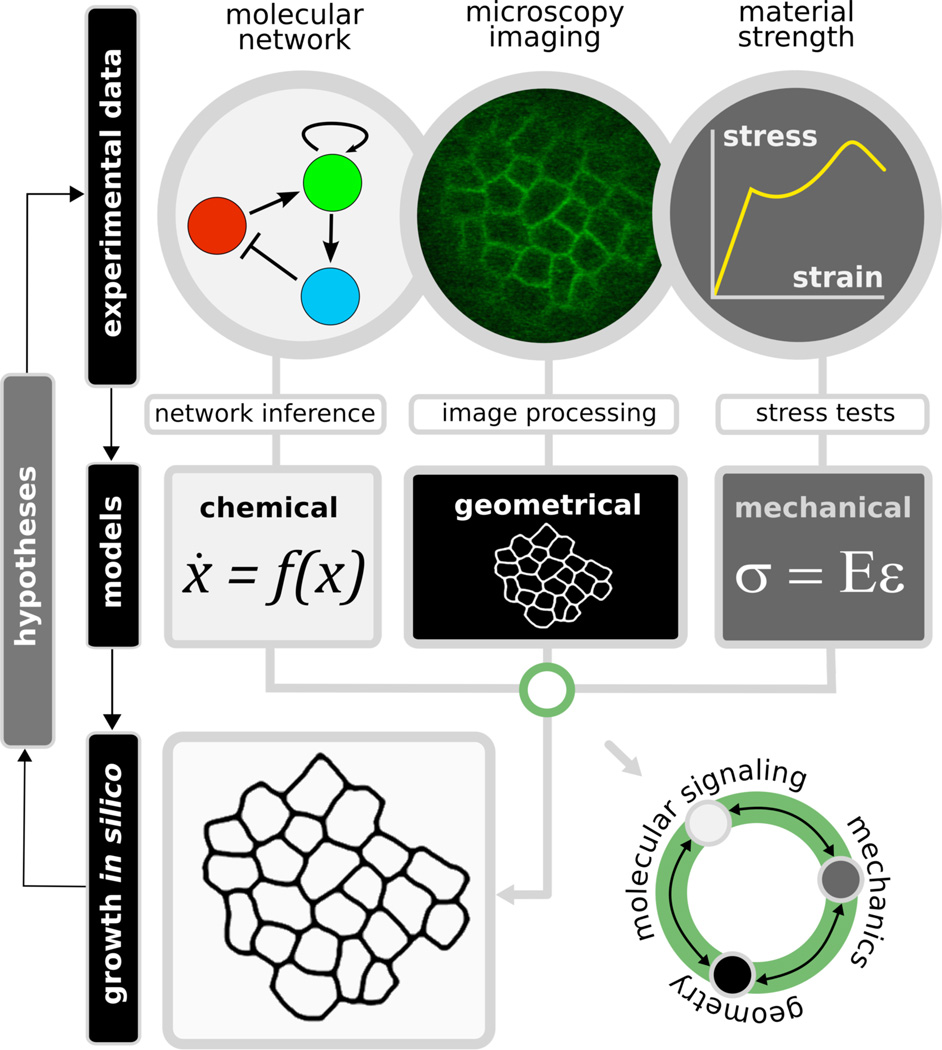
Plant growth takes place on several levels beginning at the cellular scale, to the tissue level, all the way to a consideration of the whole plant, where the emergence of organs dictates overall form. Two key challenges to modeling plant growth are creating multicellular models that describe single cell dynamics based on high resolution cellular live imaging data and integrating chemical or molecular models with mechanical models to create a self organized growing template. A computational morphodynamic study begins by extracting a mechanical cellular template from a biological image (Figure 1). Genetic, biochemical, cell/molecular biology, and imaging experiments form the basis for inferring the biochemical network controlling developmental signaling processes. The model is constructed such that the biochemical network lives inside each cell, directing interactions between those cells. A feedback loop ensues between the mechanical properties of single cells and the biochemical network within each cell. Through this loop signaling can influence cell growth and cell growth can feed back to influence the signaling processes. Finally, from the model dynamic predictions are made that are used to generate new hypotheses that can be tested experimentally (Figure 1).

Figure 1. Schematic of a proposed computational morphodynamics experiment.

A hypothesis is tested by the experimental flow illustrated above. Data is collected from experiments to parameterize the molecular, geometrical, and mechanical parameters of a computational model. Each of the three components is interdependent upon each other. Finally, the model is used to make new predictions to further modify the initial hypothesis, which can be retested experimentally.

The use of mathematical equations to explicitly describe biological processes in model form allows for a greater exploration of intuitive ideas and generation of computer models that are easier to visualize. Computational morphodynamics seeks to uncover general principles by exploring mathematical models based upon experimental observations. To achieve this, we believe that models should have the following characteristics: (1.) models should be biologically based and explicit—the variables described in the model should have counterparts observed in the experimental data that the model will be calibrated against, (2.) models should be parameterized realistically, (3.) models should be built such that they can make key predictions that are experimentally testable. Models are organized based on one of two methodologies, bottom up or top down. The bottom up approach puts together key players such as interacting genes, proteins, and metabolites to build mathematical models of reasonably small networks through loss or gain of function perturbation experiments (47). On the other hand, a top down approach integrates available data at the genome level to construct large networks (59). Nonetheless, both approaches use some common modeling methodologies. In this review we first describe the current models that explain plant growth and mention the methodologies used in these models. Next we take an in depth look at the challenges of computational morphodynamics and progress that is being made toward meeting these challenges. Finally, we look forward and discuss some future directions for the role of computational morphodynamics in developmental biology.

Modeling Approaches

Plant growth has been examined on all levels, from the single cell to the whole plant and corresponding models have been created. These models employ different approaches at various levels of complexity. Here we illustrate some of these through examples.

Kinematical approach to dynamics

A kinematic approach describes the overall growth of a plant organ or tissue through a computer model, while abstracting such details as activities of cells and the molecular framework underlying the growth decisions (91). The models are parameterized by measurements of organ growth and serve to reproduce growth realistically. There are two major classes of kinematic models.

The first class attempts to replicate the growth of the plant as a whole. Two such models describe the growth of Arabidopsis and rice plants (82, 122). Extensive measurements of growth were used to fit parameters to models based upon L systems, which are a set of formal grammars that describe the reiterative nature of plant growth (93) The plant models are divided into modules e.g., leaf, meristem, internode, and flower, and are produced iteratively according to the observed development of the plant. These models are able to reproduce Arabidopsis and rice plants that bear a striking resemblance to those found in nature.

Whole plant models are useful for predicting how environmental factors such as nutrient availability or crowding will affect the overall growth of the plant (53). When applied to crop plants, kinematic models have agronomic value in predicting optimal growth conditions. For example, Hiller et al. used models and measurements of maize leaves to show that the reduction in leaf growth in the upper leaves of densely grown plants is due to a reduction in the duration of linear expansion phase, not a change in the growth rate (53).

The second class of kinematic models takes measurements of growth in different regions of the organ and predicts the resulting shape of the organ. These models are often based on the inference of growth from the analysis of clonal sectors induced at different times during development. For example, Rolland-Lagan et al. used sectors in snapdragon (Antirrhinum majus) induced at early stages of development to infer the growth rates in the petal lobe (100, 101). The growth model is parameterized by the growth rate, anisotropy (differences in growth rate between one direction and another), and direction with respect to an external grid. All of these can vary in space and time. Based upon the measurements, Rolland-Lagan et al. constructed a spring model for the growth of the petal lobe to show that the crucial parameter in generating the asymmetry of the lobe is the growth direction. Their model led them to hypothesize the existence of a long-range signal that acts to orient growth vertically throughout the petal.

Kinematic models will lay the groundwork for future models in which growth and proliferation of individual cells, regulated by molecular signaling networks, recreate the growth of the plant. As a starting point, molecular decision making networks can control the developmental decisions that were initially hard wired into these descriptive models. For example, Prusinkiewicz et al. took a step in this direction by adding a gene regulatory network including the key regulators LEAFY (LFY) and TERMINAL FLOWER (TFL) to an L-systems model to control the decision of whether a meristem becomes a shoot or a flower (92). They show that by varying LFY and TFL activity they can reproduce the inflorescence architecture of wild type, mutant, and overexpression plants. Similarly, Coen et al. expanded their model of snapdragon petal growth (see above) to associate differences in the growth patterns with regional identities that correlate with the expression patterns of genes such as CYCLOIDEA (CYC) and DICHOTOMA (DICH) (13). This 2D finite element model correctly reproduces the petal shape of both wild type and petals in which CYC is overexpressed. However, neither of these models incorporates cellular mechanics, which is one of the challenges for the future.

Biomechanics of single cells

In contrast to the kinematic models, single cell models focus exclusively on individual cells as the basis for growth. These models of plant growth assume that wall loosening leads to a drop in turgor pressure that causes the movement of water into the cell to maintain the turgor pressure leading to irreversible cell expansion (72, 109). However, anisotropic growth as discussed by Baskin et al., depends on cellulose microfibril orientation since the orientation of the fibrils ultimately determines the stiffness of the cell wall (3). An early model proposed by Veytsman et al. described extension of cell walls due to interactions between wall polymers (120). The deposition of cellulose fibrils in the cell walls is oriented by the cortical microtubules; therefore, dynamics of microtubules are an essential consideration in models of cell growth (16, 88, 121).

Dumais et al. studied the tip expansion in Medicago truncatula root hairs using measurements of wall expansion rates in conjunction with a mechanical model of the elastic properties of a pressurized thin shell (26). The expansion patterns obtained from the model led to the conclusion that the observed anisotropic tip expansion was due to anisotropy of the mechanical properties of the cell wall. While models of this type are able to help us understand single cell morphodynamics, if we want to comprehend macroscopic plant patterns, multicellular models are needed.

Mechanics of Tissues

Plant tissues are composed of connected cells, with the constraint that cells cannot slide past each other (63). Growth of individual cells occurs through the mechanisms discussed above and over short time scales where forces between cells get balanced such that all of the stresses are located at the cell walls. These stresses can be modified by mechanical signaling that can lead to local rearrangement of the underlying microtubules, which modifies the direction of cellulose deposition and lead to anisotropic growth (3, 48).

The appearance of primordia in the peripheral zone of the shoot apical meristem has been hypothesized to arise as a result of buckling (24, 111). Using a pressurized shell model Dumais et al. combined the observations made from gapping patterns due to cuts in the sunflower SAM, with predictions of stress patterns to conclude that primordia could be initiated in the generative zone by buckling due to compressive stresses (28).

Recent models have also discussed the emergence of the venation pattern due to mechanical instabilities between cells (8, 66). Alternative models describe vein patterning due to the distribution of the phytohormone auxin in tissues (23, 112). The role of the mechanical properties of plant tissue has also been used to explain the rapid dynamics of the venus fly trap and twining of plants (33, 43, 54).

Examples of chemical or molecular signaling and gene regulatory network models

Numerous signaling components and gene regulatory networks govern plant growth and development but few have been modeled computationally. The following is a discussion of those chemical and molecular signaling pathways and gene regulatory networks that have been modeled highlighting the usefulness of predictions obtained from those models.

One of the most extensively modeled systems in plant development has focused on the transport and signaling of the phytohormone auxin. Auxin is an essential regulator of plant development controlling cell identity, cell division, and cell expansion, which is primarily dependent on its distribution in plant tissues. The predominant naturally occurring auxin, indole-3-acetic acid (IAA), is a weak acid that is subject to ion trapping upon entering cells. The PIN-FORMED (PIN) gene family of auxin efflux facilitators is responsible for the directional transport of the auxin anion throughout tissues, by providing channels, asymmetrically distributed in the plasma membrane of plant cells, through which auxin can exit the cells (99). Modeling auxin transport at the tissue level has provided important insights into the role of this hormone in several biological processes.

Patterning of the plant vasculature is dependent on the flow of auxin. Experiments conducted by Sachs led him to propose that plant veins form along auxin flow paths due to positive feedback between auxin flux and auxin transport capacity (103). Sachs’s model suggested cells with increased capacity for transport would act as sinks. This was subsequently modeled by Mitchison who proposed that if the concentration within a transport route decreased with increasing flux auxin would move into these cells forming the transport route (78). However, experimental data shows that the auxin concentration in developing vascular tissues is higher than in the surrounding tissues, which is required for vascular development (103). In response to this criticism, Mitchison proposed that cellular auxin concentrations need only be low during the initial stages of vascular canalization when cells are acting as sinks. As development proceeds, the presence of an auxin anion channel localized to one end of the cell while being depleted from the other end could maintain the flux of auxin through a cell even if the cellular concentration was high. Two recent modeling studies lend support to this hypothesis demonstrating that auxin could accumulate under the conditions proposed by Mitchison (32, 34). Imaging studies on the localization of PIN1 (the PIN isoform found in developing vein cells) in developing veins have confirmed several aspects of PIN polarity predicted by the flux model. The orientation of PIN1 during the initiation of tertiary veins resembles the localization of PIN1 in simulations based on the flux model in which a new vein forms from the sink towards the source (106). Experimental results show that PIN1 expression is initially in a cell adjacent to the secondary vein and subsequently expressed in the next adjacent cell down further from the source. In these cells the localization of PIN1 is directed towards the pre-existing secondary vein as supported by the flux model. A separate modeling study found that simulations run with a simplified flux model that incorporated auxin sources could generate realistic patterns of vein formation (39, 76, 102).

In the shoot apical meristem auxin plays an important role in initiation of new organs, as high auxin concentration both predicts and causes the location of appearance of new leaf and floral primordia (86, 98, 99). Several mathematical models have been proposed based on experimental data to predict auxin flux and PIN1 polarity patterns during organ initiation. Live imaging studies on developing inflorescence meristems demonstrated that PIN1 is largely confined to the epidermal layer of cells in the shoot apical meristem and is initially polarized towards the area of tissue with the highest auxin concentration, where the incipient primordium is located. However, as that primordium becomes established, PIN polarity reverses in cells at the edge of the primordium and reorients toward the next primordium (52, 79). Several new computational models have been developed to understand the patterning of PIN1 polarity during primordial induction and are suggestive of a positive feedback between cellular auxin concentrations and direction of auxin transport as new primordia are specified (20, 57, 113). These models all suggest cell-cell signaling as a way to coordinate PIN1 polarity towards the cell with the highest auxin concentration, thereby specifying new floral primordia. Another predication made by one of the models was the presence of an auxin maximum at the apex of the meristem (20). This was shown experimentally by the strongest immunolocalization signal of an auxin responsive reporter to the central zone of the shoot apex and developing primordia and the presence of the auxin influx mediator, AUX1, in the epidermal layer of the shoot apical meristem (20, 99). These data suggest a situation where auxin is initially transported apically into the meristem such that a maximum forms in the central zone of the epidermis and subsequently auxin is transported outward and basally through the action of the PIN1 efflux mediator in the specification of new organ primordia.

In development cell identity can be specified by two non-exclusive mechanisms, cell linage specification by genetic determination and positional information perceived by molecular or other signals non-uniformly distributed throughout the organism. In plants, interpretation of the cues signaling positional information is often the predominant mechanism for acquiring cell identity (107). The leaf and root epidermis in Arabidopsis bears specialized hairs that form in distinct patterns throughout the leaf epidermis and in the root epidermal cell files. In the leaf, hairs (trichomes) are spaced in dotted patterns with no clustering, whereas the root epidermis is divided into alternating cell files of trichoblasts (hair cells) and atrichoblasts (non-hair cells). Patterning of hair cells in the Arabidopsis epidermis is controlled by a genetic network involving the regulation of the GLABRA1/GLABRA3/ENHANCER OF GLABRA3 genes in the leaf and WEREWOLF/GLABRA3/ENHANCER OF GLABRA3 in the root. These activator complexes are inhibited by the function of two genes, TRIPTYCHON (TRY) and CAPRICE (CPC) (67, 108). Two recent papers have computationally modeled this genetic pathway, which provided useful predictions about its structure that were experimentally verified.

Benítez et al., developed an activation-inhibitor system, a type of Turing reactiondiffusion system to model the GLABARA1 (GL1I) and WEREWOLF (WER) genetic networks (89). They found that despite the presence of GL1 in the leaf and WER in the root the activator complex formed with GLABRA3 (GL3)/ENHANCER OF GLABRA3 (EGL3) in both genetic networks functioned essentially the same in their model simulations. This model was able to produce a pattern of spaced, not clustered, trichomes similar to that observed in the leaf epidermis. This activation-inhibition system was based on a reaction-diffusion system that specifies local self-activation and lateral inhibition. In the root, the epidermal cells that overlie two cortical cell layers develop into trichoblasts while those that are above one cortical layer develop into atrichoblasts (35). Genetic evidence points to the function of a membrane receptor protein kinase, SCRAMBLED (SCM), in sensing a signal derived from the cortical layer in epidermal cell specification (64). Benítez et al. updated their reaction-diffusion model to include a signal from the cortical layer that would specify epidermal cell identity. Model simulations were only able to produce the observed pattern of alternating hair and non-hair cell files when the signal from the cortical layer was modeled to induce the WER activator complex. This suggested that the signal from the cortical layer has an important function in inducing epidermal cell fate through induction of the WER activator complex.

Recently Savage et al. challenged the activation-inhibition system as the underlying mechanism for patterning in the root epidermis (105). The assumption made by Benítez et al. had been that WER was self-activated, which had not been determined experimentally. Savage et al. proposed two different models that centered on the mode of regulation of WER in an epidermal interaction network based on a stochastic Boolean formalism. The first assumed local WER self-activation with CPC repressing WER indirectly (local WER self-activation model), while the second model did not include WER self-activation but assumed uniform WER transcription that was repressed by both CPC and SCM activity (mutual support model). In model simulations run in a cpc mutant background the mutual support model closely matched the experimental observation of increased WER expression in cpc trichoblast cells (67). The authors then experimentally determined that WER expression was the same in a wild type or wer background ruling out local WER self-activation. The mutual support model also correctly predicted the wild type WER expression pattern in the gl3/egl3 double mutant background. These data provided direct experimental support for the mutual support model ruling out WER self-activation as a mechanism for epidermal patterning in the root and highlights how computational model predictions can guide the formulation of new experiments to elucidate the function of biological pathways.

Combining Signaling and Mechanics

The coupling of molecular signaling models with mechanical models is a challenge that has provided insight into a number of different aspects of plant growth and development. Two of the systems that have been considered from this perspective are phyllotaxis and pollen tube growth.

The phyllotaxis model presented by Shipman et al. is an example of a model that combines biochemistry with growth mechanics (84). Rather than placing auxin in discrete compartments to approximate the properties of cells, this model described auxin concentration in a continuum throughout the meristem. In terms of the mechanics involved, the meristem was modeled as a compressed sheet that buckles to minimize energy similar to a previous model by Shipman and Newell (111). The results of this hybrid model show that in some cases the auxin concentration is predominantly responsible for dictating the phyllotactic pattern, in some scenarios the compressive stress dominates, and still in other cases both the biochemistry and the mechanical buckling work cooperatively to pattern the meristem.

Pollen tube development is another area that has received ample of attention by modelers. Molecular signaling was modeled by the diffusion of morphogens in the pollen tube by Denet et al., while the mechanical aspect of pollen tube growth was modeled as finite elements by Bolduc et al. and as a viscoplastic system by Dumais et al. (9, 21, 27). These models considered biochemistry and mechanics separately, but a model created by Kroeger et al. is an example of the combination of both concepts in the same model (62). In this model the pollen tube is represented as two fluids separated by a curved interface simulating the cytoplasmic membrane. The growth of this interface is related to the relative internal pressure as well as the elastic properties of the wall with a hydrodynamic equation. A unique element to this model is the inclusion of calcium diffusion. Calcium diffusion is coupled to the properties of the membrane by a diffusion equation that changes in response to the elasticity of the membrane, simulating a stretch-activated ion gate. This close coupling of mechanics and molecular signaling was able to generate the oscillatory pollen tube growth observed in nature, presenting a plausible model that further experiments may prove to be accurate.

So far these computational amalgamations of biochemistry and mechanics have provided useful insight into the morphodynamical processes of plant development. We hope that as the field progresses models will continue this trend.

Examples of Model Types

We next turn to the methodology of describing molecular network dynamics as well as a description of the physical growing cellular template within which such networks exist and interact.

Molecular Modeling

Molecular models exist in a wide variety of mathematical representations including differential equation models, stochastic models, Boolean models, Petri-nets, cellular automata and event-based models (18, 77).

The choice of the model depends to some extent on the available type of data. The description of biochemical networks in terms of ordinary differential equations (ODE) is a common approach in systems biology (116). Examples of ODE models in Arabidopsis include models of circadian clock dynamics and ethylene signaling (22, 71, 127). Differential equations describe the evolution in the concentration levels of participating species such as mRNAs, proteins, and small molecules assuming a well-stirred mixture. Models are constructed based upon known or assumed interactions and require experimental parameters such as the stoichiometry and reaction rates. While reactions can be described in terms of mass action kinetics, simplifying assumptions based upon the speed of reactions as well as the concentrations of the participating species can be made that result in Michaelis-Menton type of kinetics. The Hill coefficients in these reaction rates are indicators of the co-operativity of the system. For example, some models of gene regulatory networks assume that binding and unbinding of transcription factors to DNA is rapid, compared to other processes, this allows a thermodynamic approach that has been used to map out gene regulatory function, which is essential for understanding how inputs from transcription factors at each gene are integrated to build a network (7, 61). Analysis of the network dynamics reveals several features of the system including the existence of multiple steady states for protein levels, or oscillations in protein levels, and the time it takes for the system to settle down after perturbation. These features can be addressed by application of nonlinear dynamics techniques such as bifurcation theory and by traditional engineering techniques such as perturbation analysis (114). Biological networks are replete with interacting negative and positive feedback loops and these methods can be used to extract useful properties of the dynamics that informs us about the functionality of the network (119). Networks can be searched for motifs (a sub-network which has particular dynamical properties) that can often impact the functionality of the whole network (74).

The differential equation approach can be extended to model spatial dynamics by using reaction-diffusion equations (83). We assume that individual cells are tiny compared to the dimensions over which the reacting species diffuse. These equations are then solved in continuous space with the appropriate boundary conditions. As originally hypothesized by Turing, pattern formation can occur by an activator-inhibitor interaction (37, 118). The activator induces itself and a second molecular species. The second molecule feeds back to inhibit the original activator. Both the inhibitor and activator are produced in the same location. However, if the inhibitor diffuses rapidly away from the activator then a peak of activator can form. This was the approach taken in the trichome and root hair models proposed by Benítez et al. (see above) (6). Such an approach has also been used to describe the pattern of WUSCHEL expressing in the shoot apical meristem where the authors extracted data from confocal imaging to parameterize their model (56). The reaction-diffusion approach is a good approximation if transport of network components occurs through passive diffusion. However, a compelling reason to adopt a cellular framework for plants is the polar transport of auxin out of a cell by PIN proteins localized to specific domains of the plasma membrane making a cellular description necessary (104). Results from such a description are easily compared to experimental data if the simulations are performed on extracted cellular templates from imaging providing another compelling advantage for the use of models that explicitly include cells (57).

Stochastic fluctuations in molecule numbers due to the inherent randomness of transcription/translation, degradation events (intrinsic noise), and environmental signals (extrinsic noise) has an effect on the dynamics of the underlying genetic network (58, 94, 115). There are now numerous examples of networks that either utilize noise or are adversely affected by it. Although such an approach has yet to find broad use in the plant biology community, it is nonetheless important since a theoretical treatment could potentially uncover novel functionality of a network in terms of its ability to filter out or amplify noise.

Boolean models are used for large networks where we often have incomplete information (2). In this case the simplest assumption to make about the activity of a gene is that it is either on or off. At each node (gene), all the inputs into that node are integrated into a logical rule with examples being OR, AND, or more complicated regulation. For a network of interacting genes that is initialized at the start, a synchronous update is done to give the state at the next time step. Asynchronous updates simulate differences in temporal biological processes (1). The dynamical behavior of such networks can be stable, critical, or chaotic. Using this framework it is possible to study the stability of the network in terms of the gene regulatory rules that occur at every gene. For large networks where little information is available about the components, such an approach is computationally feasible as compared to an ODE model. Recent models of Arabidopsis gene regulatory and signaling networks using this formalism discuss the ABC model of flower development, abscisic acid regulation of stomata closure, and the patterning of the root epidermis (30, 69, 105).

Mechanical framework

A proper mechanical description of cells must be sought to provide an accurate description of growth. In these weak spring models each cell has walls (shared by neighboring cells) that are comprised of weak springs joined at the vertices (80, 110). The springs are under tension due to the turgor pressure within a cell as well as due to the turgor pressure from surrounding cells. This equilibrium is maintained over very short time scales. However over longer time scales the springs, which are modeled as viscoelastic elements, gradually increase their resting lengths due to the turgor pressure. Hence, growth occurs quasi-statically due to increasing resting length. Division is modeled by introducing a new cell wall, so as to partition a cell when it reaches approximately twice its starting volume. Spring models have been used to describe cell growth and proliferation during phyllotaxis, auxin induced growth, growth of cells in the SAM, and leaf venation due to mechanical forces (14, 15,29, 57).

Alternatively, growth of cells can be described by a continuum approximation in terms of stress and strain relationships using the theory of elasticity. Specifically, Dumais et al. used the theory of a thin shell with the mechanical property of anisotropic viscoplasticity to describe tip growth in plants cells including root hairs and pollen tubes (27).

A third approach is to use finite-element method (FEM), which is a commonly used method in engineering (4, 85). FEM involves solving the partial differential equations of elastic media by first partitioning the domain of interest into smaller elements, each having a simple polyhedral shape. Within each element one assumes a uniform stress-strain relationship that allows one to solve for the displacement, and to impose continuity of solutions across element boundaries. In regions where the stress and strain gradients are high, more elements are required to accurately capture the rapidly changing behavior of the system. Recently, Hamant et al. used the FEM to model stress-strain in the L1 layer of the shoot apical meristem, and correlated this to the behavior of the cortical microtubule arrays of these cells (48).

Another method to study growth and proliferation of cells, using a stochastic framework, is the cellular Potts model (5, 38, 45). A given configuration of cells is defined by an energy function in terms of the shape and size of its cells. The energy is minimized when a cell grows up to its target area, and is made to increase if the cell increases its cell wall perimeter. Grieneisen et al. used such a formalism to describe growth and division of cells in the root as a function of varying levels of auxin by making the area of cell a function of the auxin concentration (46).

There are several other multiscale computational frameworks each of which can serve as a substrate for modeling regulatory networks within each cell in addition to intercellular communication. These frameworks deal with individual reactions at the smallest scale and organ growth at the largest scale. Recent examples of computational frameworks include L-Studio simulation, OpenAlea software platform for virtual plants, CellModeller software, and Dynamical Grammars (80, 90, 93). The Dynamical Grammars framework can represent discrete entities like cells with mechanical attributes allowing for growth and division (80). Within each cell exist gene regulatory networks either described by ODE’s or by stochastic processes. Furthermore, diffusion of molecules allows for intercellular communication. The grammars are basically the rules that allow for transitions of various types, such as cell growth, biochemical reactions within cells, movement of molecules from a cell to a neighboring cell, and cell division.

Computational morphodynamics–two challenges

The first challenge of the field of computational morphodynamics is to determine how the sum of the behaviors of individual cells culminates in the overall size, shape, and form of each organ in the plant. The second challenge is to understand how local molecular signaling interacts with mechanical growth processes to change the behaviors of individual cells. In the following sections, we will discuss these challenges and the tools necessary to meet them in the coming years.

Challenge One-- Single Cell to organism

We will start with the first challenge of translating the actions of individual cells to the cumulative morphology of the whole plant. As discussed in the preceding sections, most of the current models generally address either the whole plant or only a small population of cells with the goal being to bridge this gap. The supracellular kinematic growth models that mimic growth of the tissue quite realistically need to be matched with mechanical models describing growth and gene regulatory networks of the constituent cells. If we succeed in integrating these models into a single understanding, we will be able to predict how changing the subcellular signaling within the cell will alter the morphology of the organ and test this prediction with experiments.

The bridge we need between single cells and the plant is the dynamic actions of cells in vivo. The necessary capabilities include imaging of living cells, computationally extracting information from these 4D (3D plus time) images, using this information to build realistic cellular templates for models, building the models, and then again use imaging to test the predictions of the models.

Live imaging—capturing growth as it occurs

Imaging growing plants and modeling go hand in hand. Imaging data can be used to generate the hypotheses expressed in the models (48). Likewise, the predictions made by the model often are testable only by imaging living plants and determining the effects of experimental manipulations.

Live imaging is simply the repeated imaging of a living sample over time (97). Some examples of tissue scale live images are scanning electron micrographs of impressions made from living shoot apical meristems (25, 65). These images beautifully show the growth of epidermal cells and the changes in curvature of the meristem as primordia emerge. However, these images are limited to showing the shapes of cells in the surface. To visualize both subcellular structures and underlying cells, live imaging has been conducted with confocal laser scanning microscopy (10, 51, 95). In confocal imaging, transgenic plants expressing fluorescently tagged proteins can be imaged. Ubiquitous nuclear or plasma membrane markers and stains are useful for determining the cell division and growth patterns (10, 50, 95). Likewise, the dynamics of gene expression patterns and protein localization can be correlated in space and time with live imaging (52). We expect additional microscope technologies such as multi-photon microscopy, allowing greater imaging depth, and digital scanned light sheet fluorescence microscopy, allowing rapid imaging with low phototoxicity, will bring added resolution and power to plant live imaging experiments in the future (31, 60).

The difficulty in the live imaging technique is several fold. The first problem is accessing the tissue of interest. For exposed tissues, such as roots, this is not a problem, but for tissues that are covered such as the shoot apical meristem, accessibility can be a major issue. In the case of the inflorescence meristem the overlying floral buds are delicately dissected away prior to imaging (97). Alternatively, primordia can be removed from the meristem by treating the plants with the polar auxin transport inhibitor NPA. When the plants are removed from NPA, they recover, initiate primordia, and can be imaged (44).

The second challenge is fitting the living plant under the microscope. In some cases, such as the imaging of a moss, this is straightforward because the plant can happily grow mounted in water on a slide (50). In other cases, the part of the plant of interest is attached to a slide and mounted with a cover slip, while the rest of the plant grows normally (Figure 2A). Alternatively, the whole plant can be grown in a plastic box, submerged in water, and imaged with a water dipping lens (97).

Figure 2.

Live imaging and image processing. (a) To live image the sepals, the inflorescence (arrow) was taped to a slide and mounted under a cover slip in water. The whole plant was tipped on its side in a covered pot such that the inflorescence was positioned to observe the side of the sepal. (b–e) Live imaging was used to examine the cell division pattern in loss of giant cells from organs (lgo) mutant sepals. The epidermal nuclei (ATML1::H2B-mYFP) and cell walls (Propidium iodide) were fluorescently labeled. The sepal was imaged every 6 hours for 78 hours. The cells from the pink lineage were outlined in yellow in all images. (b) A projection view of the lgo-1 mutant sepal at the 36-hour time-point was made using the Zeiss LSM microscope software. Nuclei are shown in green and cell walls in red. Note that the surrounding flower buds are also visible. (c) Volume rendering of the same 36-hour image in Amira®. Nuclei are shown in gold and cell walls in green. Note that the adjacent flowers have been cropped and the rotation of the sepal has been changed slightly through registration with the other sepals in the time series. (d–e)The cell lineages were manually tracked from the 30-hour (d) to the 36-hour (e) time point. Cells in a lineage were marked with the same colored dot. Daughter cells immediately after division were circled in white. Note that the pink cell at 30 hours divides horizontally to make two daughters at 36 hours. (f–k) Cells were segmented (h–i) from plasma membranes of a projection of sepal epidermal cells (f) and a confocal section of a shoot meristem (g). The segmented cells can be analyzed to determine their area (j light colors for larger cells) and their connections (k). Scale bar in A: 1 cm, B–E: 20 µm, F: 50 µm, and G: 20 µm. (Unpublished data AHKR, Marcus Heisler, AC, and EMM)

The third problem is keeping the plant alive and healthy while imaging. Restricting the amount of laser light to which they are exposed is crucial. Various tissues and particular fluorescent markers have differential sensitivity and generally this is experimentally determined. Not only does photobleaching affect the marker being imaged, phototoxicity will often kill cells. Staining the tissue with a vital die such as Propidium iodide can mark the occurrence of dead cells. The plants being imaged should be inspected after imaging to make sure they are still growing at normal rates (10, 97). In addition, most plants must be removed from the water, dried, and placed back in the growth room in the normal vertical orientation between imaging sessions to allow normal growth. Some plants will die in the process and those data are eliminated from consideration. The clones of cells and division patterns observed in live imaging match with the clones generated in sectoring studies indicating that the live imaging is not altering the normal growth of the plant (50, 95).

The selection of the time interval for imaging depends on the speed required to capture the process as it is changing. For example, imaging every six hours is sufficient to catch the cell divisions in the shoot apical meristem and track the cell lineages but longer timeframes are not. PIN protein localization tends to be more dynamic and two-hour intervals are more appropriate (52, 95). In contrast the events taking place during the regeneration of new meristems from callus can often be tracked over daily intervals (42). The selection of the interval also depends on the requirements of the system to keep the laser light low because imaging too often damages the plants.

Biologists may wonder whether live imaging is necessary given its labor-intensive nature and its difficulty. For decades, biologists have been inferring processes that happen in time from dead and fixed samples taken from multiple plants at different times. These images can be beautiful and are ideal for automated image processing (117). Although this dead imaging approach has certainly been successful in answering static questions, it cannot show the dynamics of the process. One example of the value of live imaging comes from the fundamental question of how the size of the meristem is controlled. Although it had long been known that clavata3 (clv3) mutants have enlarged meristems, it was not known whether the enlargement was due to proliferation or incorrect cell fate specification (12). Through live imaging of plants while transiently knocking down CLV3 activity Reddy et al. show that cells are first incorrectly respecified and only subsequently is proliferation altered (96). This experiment shows both the advantages of live imaging and the value of transient interventions in determining the function of genes. The results have been incorporated into a recent model describing the homeostasis of meristem size (36).

Image processing

The primary role of image processing and analysis is to reveal the shape and size of objects of interest present in microscope images and to identify the spatio-temporal relationship between them. Image processing produces quantitative data that ultimately serves as empirical evidence in the design, validation, and optimization of growth models. With accurate measurements one can build realistic computational representations mimicking the geometry of cells and their network of connections that can form the basis for mechanical molecular models (Figure 1). Furthermore, image processing provides a detailed geometric description of cells, tissues, and organs necessary for the resizing and reshaping of cells as they divide and grow, which can form the basis for growth in the model. The procedures in image processing include: (1.) visualization of the data (2.) segmentation (3.) registration (4.) tracking (5.) creating a realistic geometry for a mechanical model.

1. Visualization of 4D data

Visualizing the 4D dataset produced by live imaging generally requires specialized software. While useful, the projections generated by the confocal microscope software packages or image J are insufficient (Figure 2B). Image analysis packages with volume rendering capabilities such as Amira (Visage GmbH), Paraview, and Imaris (Bitplane AG) allow the creation of 3D visualizations that can be rotated freely and cropped (Figure 2C) (49). Contrast enhancement, reduction of noise, deblurring, and similar procedures can enhance images in preparation for segmentation (extraction of features) and provide a richer visualization experience.

2. Segmentation—extraction of features from images

The computation of shape and size follows from a deterministic image-processing pipeline in which segmentation plays a major role. Image segmentation is the process of partitioning an image into distinct regions each representing a single homogeneous object (40). It is a fundamental step in the quantification of morphology as it generates digital masks from which one can calculate volume, area, length, and shape properties for each segmented object (Figure 2, F–K). Segmentation is also called upon when computing the connectivity (topology) between objects, as we first need to detect them before finding their neighbors. Topology gives us the adjacency of cells for any given cell in a tissue, which is essential information when investigating cell-to-cell communication.

Extracting meaningful information from an image is not a straightforward task. Very often one need to craft image-processing pipeline to analyze the images at hand. There are practical and theoretical limitations of image formation, acquisition, and algorithm development that prevent us from having universal image processing solutions. For example, images of plant tissues generated using a confocal microscope might have a diverse range of characteristics that would make the design of a general and robust (error-free) processing algorithm very challenging, if not impossible. This is in accordance with the No Free Lunch ideas that state that a general-purpose, universal optimization strategy is impossible and that specialization is necessary (123). Non-homogeneous illumination patterns, presence of different levels of noise throughout, missing signal in crucial areas, bad alignment of time lapse frames, mismatch during image mosaicing of pieces of a larger image, are a few problematic issues difficult to be automatically detected and repaired. There are an unaccountable number of other possibilities leading to unpredictable image qualities and aberrations that directly impact the design of robust image processing algorithms.

A little human intervention in correcting the automatic segmentation results is often advantageous since there is never enough knowledge built in the algorithms to tackle all possible variability. This semi-automated approach is not to be confused with manually generating a solution (e.g. completely segmenting a cell by hand) but is rather a minimum intervention to provide the computer with missing information.

Segmentation has been used in roots and shoots to extract cells. In Marcuzzo et al. the authors propose an automatic 2D cell segmentation method applied to the Arabidopsis root (75). They apply the watershed segmentation algorithm followed by a classification step to discard segmented regions that are not cells. Their SVM (Support Vector Machine) based classifier is trained using a cell contour descriptor. Results show a reduced false-positive rate of segmented cells as compared to the pure watershed segmentation results. The work of de Reuille et al. proposes a cell segmentation and reconstruction protocol to extract cell geometry and topology in the L1 surface layer of the Arabidopsis SAM (19). They reconstruct the outer surface of the L1 layer such that only cell walls visible from outside the meristem are present in the projection image. Junction vertices where cell walls meet are then manually marked and grouped for each cell. An automatic procedure then determines the polygonal cell topology and maps the 2D sheet of cells to the 3D surface of the meristem.

3. Registration—Alignment of images and computation of growth

In a live imaging session, often the experimenter physically moves the sample, or the growth of the tissue changes the orientation, such that images from different time points do not directly align. For example, when imaging growing roots, keeping the quiescent center as the static reference point, involves significantly moving the stage between images (10). While every effort should be made to preserve the alignment between imaging sessions, subsequent computational registration, or alignment of the images is generally required. In its essence, a registration method computes the geometrical transformation that is necessary to completely align (superimpose) two consecutive images of the same growing object. This transformation can be done without allowing the image to be stretched to produce a time series to visualize growth (Figure 2D–E) (50). Alternatively the images can be warped to align object boundaries. This warping gives how much stretching is need to deform the object so its shape is the same in both images, providing the biologist a measure of growth rate. Image registration thus offers a measure of absolute growth and preferential growth direction (81).

4. Tracking—determining the lineage of cells

Segmentation is often the primary step in the computation of cell lineage, as we first need to exactly locate and enumerate the cells present in each frame of a time-lapse image before associating mother and daughter cells. Human tracking of cell lineages is an extremely laborious and time-consuming process. (Figure 2D–E). Therefore several programs have been designed to track the lineage of the cells automatically (41, 55,68, 70). This may be another good case for the semi-automated approach where the computer offers a plausible solution, which is verified by the user and if necessary corrected by the biologist.

5. Translating imaging to realistic geometry for models

The reconstruction of cell geometry and topology from images enables us to build finite element meshes needed for plant tissue simulation. The transition of cells represented as a collection of unlabeled pixels in images to cells represented as finite element meshes is transforming the way we do image-based analysis for predictive simulation (125, 126, 128). We can now, with varying levels of difficulty, reconstruct cells from images and carry on complicated simulations with their geometry. Efforts exist to bring this methodology to the computational studies of plant development (48).

Challenge Two–The Mechanical-Molecular Nexus

Tremendous progress has been made in the last few years in addressing the challenge of combining molecular signaling with the mechanics of the cell growth in plants. The advent of live imaging techniques (covered in the previous section) allows us to build more detailed mathematical models connecting single cells that live together on an extracted template. The next few studies highlight the role of experimentation in the formulation and subsequent validation of the model.

Two recent papers have demonstrated a role for mechanical signaling in the morphogenesis of the shoot apical meristem in Arabidopsis during development (15, 48). In Hamant et al, the authors utilized both physical and mathematical approaches to demonstrate that SAM morphogenesis is dependent on the orientation of the microtubule cytoskeleton, which is regulated by mechanical stress on the cell walls in the epidermal cell layer. Live imaging of cell morphology by laser confocal microscopy following depolymerization of the microtubule cytoskeleton with oryzalin revealed that cellular differentiation and patterning of new primordia were not dramatically affected. However, loss of the microtubule cytoskeleton blocks cytokinesis resulting in the formation of giant polyploid cells with a geometry that resembled two-dimensional foams that are isotropic in nature. The notable effect of these changes is the absence of the crease that forms between the meristem and primordia and suggests that while microtubules are not required for developmental patterning, such as phyllotaxis, they are required for morphogenetic effects such as tissue folding. Further analysis of microtubule orientations revealed that at the meristem apex microtubule orientations are highly dynamic while those at the base and periphery of the meristem primarily align in circumferential radial arrays. At the boundary between the flower primordia and the meristem microtubules are aligned in supracellular orthoradial arrays along the boundary domain.

Previous studies provided a link between maximal stress directions and orientation of cortical microtubules (124). The anisotropy of stress across a plant cell wall is due to the direction of the rigid cellulose microfibrils laid down during cell wall synthesis and since this often parallels the direction of cortical microtubule orientation it is thought cellulose microfibril synthesis is guided by cortical microtubule tracks (11, 17, 87). To determine the relationship between stress on the cell walls and the orientation of microtubules a mechanical model was developed to calculate the direction of principle stresses in different domains of the meristem. The meristem was modeled as a shell inflated by internal pressure that depends on three assumptions: (1.) the elastic nature of the tissue and the role of the outer wall in the epidermal cell layer in supporting turgor pressure, (2.) limiting growth, and (3.) being under uniform pressure from the inside. The principle stresses calculated from this model were found to be parallel to the cortical microtubule orientations observed in the live images from meristem tissue. The authors went a step further and designed a 3D cell- and wall-based tissue model with the same assumptions but added elastic wall mechanics, wall growth, microfibrils indicating the direction of cellular mechanical anisotropy, stress feedback, growth and proliferation. This model reproduced the observed microtubule orientation in living tissue on all templates tested, including the orthoradial cortical microtubule orientation at the boundary between the floral primordia and meristem. The model also reproduced the loss of the crease between the boundary of the primordia and meristem and ballooning of cells in the pin-shaped template when the anisotropy was removed for the parameters of the model simulating oryzalin treatment.

As a final test as to whether the orientation of microtubules along the principle direction of maximal stress can alter the orientation of cell wall synthesis and thereby regulate morphogenesis two approaches were taken. The first approach utilized laser ablation of a single cell or multiple cells to locally eliminate turgor pressure that would induce changes to the stress and strain on the cell walls in the central zone of the L1 layer of the meristem, where cortical microtubule orientations and growth patterns suggest cells walls are mechanically isotropic. Theoretical predictions, obtained by modeling the L1 layer using the finite-element method and ablation simulated by a loss of turgor pressure and reduction of the elastic properties of the ablated cell walls, indicated that a rearrangement in principle stress directions occurs following cell ablation such that principle stress directions shifts gradually from radial to circumferential around the wound site. Confirmation of these model predictions was obtained by laser ablation studies of cells in the central zone of the L1 layer followed by live imaging, where is was observed that microtubules reorient circumferentially around the ablation site. As a second and final approach, the authors applied force directly to the meristem tissue and observed orientation of the microtubules by live imaging. Upon meristem squeezing, cells at the apex of the meristem either stabilized or aligned their cortical microtubules toward the axis that is parallel to the maximal stress direction. These results indicate stress control of microtubule controlled anisotropy of cell wall synthesis, which in turn reinforces cells against the principle stress directions, and is required for certain morphological events like tissue folding and maintenance of a cylindrical stem uncoupled from control of differentiation and growth.

In a separate study Corson et al. observed isotropic cell growth following microtubule depolymerization in a growing shoot apical meristem similar to the results of Hamant et al. (15). Under these isotropic growth conditions they also observed that the angle distribution between the cell walls, where they meet at a vertex, was similar to the angles observed between vertices of soap films, indicating that cells were at mechanical equilibrium with each other. In addition, the authors observed that cell having < 6 sides have convex cell walls while those cells with > 6 sides have concave cell walls in oryzalin treated meristems. They next performed simulations of a simplified two dimensional model of growing cells, each of which is maintained in elastic equilibrium over short time scales against turgor pressure, by cell walls, modeled as viscoelastic rods.

When the simulations of the mathematical model were done assuming uniform turgor pressure in all cells the cell shapes did not match the experimental data obtained by live confocal imaging of oryzalin treated meristems. The authors show through the exploration of a model assuming turgor is correlated to the size of the cell correctly predicts the geometry of the observed cell shapes. Some of the larger cells with a higher number of cell walls have concave shape, whereas the smaller cells are often convex, which fits the live confocal imaging data from oryzalin treated meristems. This suggests a link between cell size and turgor pressure, which the authors hypothesize is a general feature of plant tissues that maintains a level of homogeneity of cell size to generate a template for other patterning mechanisms to operate.

Two recent studies implicate a molecular to mechanical connection in roots. Grieneisen et al. used a Potts framework to describe the mechanics of a growing root, in which auxin transport due to PIN is simulated (46). Confocal imaging of PIN protein patterning was used to build a mathematical model of auxin transport on a geometrical template of cells. The regulated auxin transport patterns the growing root to have a maximum of auxin located in the stem cell region. The authors showed that the auxin maximum occurs due to the change of direction of auxin flow, when basal flow through the vasculature towards the root tip, turns around to flow back up apically through the epidermal cells. The auxin maximum was shown to be robust to the transport parameters of the model, auxin production/decay as well as to tissue ablation. A link between the mechanics and signaling is hypothesized, such that cells in the neighborhood of the auxin maximum proliferate rapidly, whereas further away from this center, where the auxin gradient decreases, cells grow longer. The faster growing cells which sense a shallower gradient of auxin, move away from the rapidly proliferating center, thereby giving rise to a sharp delineation of the meristematic and elongation zones, agreeing well with the observations

Summary

As we have discussed in this review, there are two key challenges to producing predictive computational morphodynamic models of plant growth. The first challenge is translating from single cell to tissue scale growth. To meet this challenge we propose using live imaging data to follow single cells and their contributions to whole tissues. Following the detailed dynamics of cells allows us to extract a cellular template, which one can form the basis of a computational model. The second challenge is integrating molecular models with the mechanics of growth to create a self-organized growing tissue. To meet this challenge we first must perform biological experiments to discover the key molecular components that determine the growth phenomenon being studied, i.e. the relevant genes, hormones and the interaction network. Then we need to couple the parameters that influence growth with the molecular network. Although innovative steps toward both challenges have already been taken, more advances are needed to reach the ideal experimental-modeling framework (Figure 1).

Future Issues.

1. Image analysis needs to be 4D. A step in this direction will involve advances in the live imaging technique, either in the optical configuration or in the way the sample is imaged, to get better resolution in the deeper parts of the tissue. Once we can truly track all of the cells, we can begin to match their growth with their spatio-temporal gene expression patterns to gain insights into the molecular mechanical feedback loop.

2. Models also need to be 4D. These models should be built using finite elements (FEM) to model the whole tissue of growing and dividing cells. For this, finite element software needs to be made more adaptive so that it can describe cell division. To calibrate the FEM wall properties we need to extend our analysis of cell wall growth. In addition, FEM software needs to interact with molecular modeling software such that the molecular network can modify the properties of the cell walls and the structure of the cellular framework. For example, each cell should include a molecular cell cycle model that can regulate spatially dependent cell division rates.

3. We need to develop a single simulation framework in which we can iteratively add many different types of models to describe the progression of several developmental processes. As many groups contribute to the increasing the pool of available mathematical models, such a modeling framework would serve as a platform for integrating and exchanging models.

4. Successful computational morphodynamics studies require the assembly of multidisciplinary teams including biologists, image processing experts, and modelers. We believe computational morphodynamics will provide just such a platform for future collaborations between biology and the computational sciences to uncover the beautiful mysteries of plant growth.