Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates

Significance

High-temperature superconductivity emerges when holes are introduced into the antiferromagnetic, insulating CuO₂ plane of the cuprates. Intervening between the insulator and the superconductor is the mysterious pseudogap phase. Evidence has been accumulating that this phase supports an exotic density wave state that may be key to its existence. By introducing visualization techniques that discriminate the electronic structure at the two oxygen sites with each CuO₂ unit cell, we demonstrate that this density wave consists of periodic modulations maintaining a phase difference of π between every such pair of oxygen sites. Therefore, the cuprate pseudogap phase contains a previously unknown electronic state—a density wave with a d-symmetry form factor.

Abstract

The identity of the fundamental broken symmetry (if any) in the underdoped cuprates is unresolved. However, evidence has been accumulating that this state may be an unconventional density wave. Here we carry out site-specific measurements within each CuO₂ unit cell, segregating the results into three separate electronic structure images containing only the Cu sites [Cu(r)] and only the x/y axis O sites [O_x(r) and O_y(r)]. Phase-resolved Fourier analysis reveals directly that the modulations in the O_x(r) and O_y(r) sublattice images consistently exhibit a relative phase of π. We confirm this discovery on two highly distinct cuprate compounds, ruling out tunnel matrix-element and materials-specific systematics. These observations demonstrate by direct sublattice phase-resolved visualization that the density wave found in underdoped cuprates consists of modulations of the intraunit-cell states that exhibit a predominantly d-symmetry form factor.

Understanding the microscopic electronic structure of the CuO₂ plane represents the essential challenge of cuprate studies. As the density of doped holes, p, increases from zero in this plane, the pseudogap state (1, 2) first emerges, followed by the high-temperature superconductivity. Within the elementary CuO₂ unit cell, the Cu atom resides at the symmetry point with an O atom adjacent along the x axis and the y axis (Fig. 1A, Inset). Intraunit-cell (IUC) degrees of freedom associated with these two O sites (3, 4), although often disregarded, may actually represent the key to understanding CuO₂ electronic structure. Among the proposals in this regard are valence-bond ordered phases having localized spin singlets whose wavefunctions are centered on O_x or O_y sites (5, 6), electronic nematic phases having a distinct spectrum of eigenstates at O_x and O_y sites (7, 8), and orbital-current phases in which orbitals at O_x and O_y are distinguishable due to time-reversal symmetry breaking (9). A common element to these proposals is that, in the pseudogap state of lightly hole-doped cuprates, some form of electronic symmetry breaking renders the O_x and O_y sites of each CuO₂ unit cell electronically inequivalent.

Fig. 1.

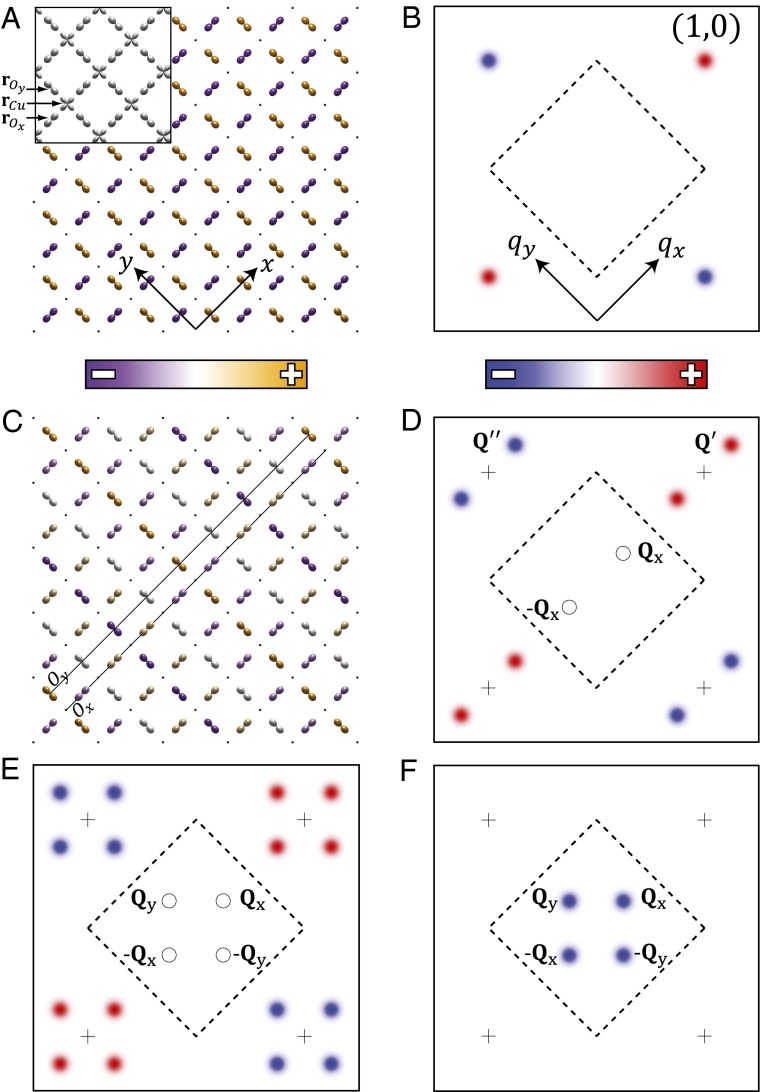
Intraunit-cell electronic structure symmetry in the CuO₂ plane. (A) Schematic of translationally invariant electronic structure pattern with opposite-sign density on O_x and O_y (d symmetry), as discussed in refs. 12, 13, and 32. The inactive Cu sites are indicated by gray circles. Inset shows elementary Cu, O_x, and O_y orbitals, on the three sublattices in the CuO₂ plane; r_Cu sublattice contains only the Cu sites, ${\mathit{r}}_{{\text{O}}_x}$ sublattice contains only the O_x sites, and ${\mathit{r}}_{{\text{O}}_y}$ sublattice contains only the O_y sites. Referring to this arrangement as having “d symmetry” does not, at this stage, imply any specific relationship to the d-symmetry Cooper pairing of the superconducting state. (B) Fourier transform of the Q = 0 C₄-breaking pattern of opposite-sign density on O_x and O_y in A. The Bragg peaks have the opposite sign, indicating the IUC states have d symmetry (12, 32). (C) Schematic of a d-form factor DW ${\rho }_D\left(\mathit{r}\right)=D\hspace{0.17em}\mathrm{Cos}\left({\mathit{Q}}_{\mathit{x}}\cdot \mathit{r}+{\varphi }_D\left(\mathit{r}\right)\right)$ with the origin chosen at a Cu site and modulating only along the x axis. The colors represent the density ${\rho }_D\left(\mathit{r}\right)$ at every oxygen site. Two thin lines are shown; one labeled O_x traverses parallel to ${\mathit{Q}}_{\mathit{x}}$ and passes only through oxygen sites oriented along the x axis, and the second one labeled O_y again traverses parallel to ${\mathit{Q}}_{\mathit{x}}$ but passes only through oxygen sites oriented along the y axis. The color scale demonstrates how the amplitude of the DW is exactly π out of phase along these two trajectories. (D) The real component of the Fourier transform of the pattern in C. For this d-form factor DW, the Bragg-satellite peaks at Q′ and Q′′ exhibit opposite sign. More profoundly, because they are out of phase by π, the modulations of O_x and O_y sites cancel, resulting in the disappearance of the DW modulation peaks at ±Q within the BZ (dashed box). (E) The real component of the Fourier transform of a d-form factor DW having modulations at Q = (Q,0);(0,Q) (SI Text, section 3); the DW satellites of inequivalent Bragg peaks at Q′ and Q′′ exhibit opposite sign, and the basic DW modulation peaks at Q have disappeared from within the BZ, as indicated by open circles. (F) The real component of the Fourier transform of an s′-form factor DW having modulations at Q = (Q,0);(0,Q) (SI Text, section 3); the DW satellites of inequivalent Bragg peaks at Q′ and Q′′ now cancel whereas the basic DW modulation peaks at Q are robust within the BZ.

Electronic Inequivalence at the Oxygen Sites of the CuO₂ Plane in Pseudogap State

Experimental electronic structure studies that discriminate the O_x from O_y sites do find a rich phenomenology in underdoped cuprates. Direct oxygen site-specific visualization of electronic structure reveals that even very light hole doping of the insulator produces local IUC symmetry breaking, rendering O_x and O_y inequivalent (10), that both Q ≠ 0 density wave (11) and Q = 0 C₄-symmetry breaking (11, 12, 13) involve electronic inequivalence of the O_x and O_y sites, and that the Q ≠ 0 and Q = 0 broken symmetries weaken simultaneously with increasing p and disappear jointly near p_c = 0.19 (13). For multiple cuprate compounds, neutron scattering reveals clear intraunit-cell breaking of rotational symmetry (14, 15, 16). Thermal transport studies (17) can likewise be interpreted. Polarized X-ray scattering studies reveal the electronic inequivalence between O_x and O_y sites (18) and that angular dependent scattering is best modeled by spatially modulating their inequivalence with a d-symmetry form factor (19). Thus, evidence from a variety of techniques indicates that Q = 0 C₄ breaking (electronic inequivalence of O_x and O_y) is a key element of underdoped-cuprate electronic structure. The apparently distinct phenomenology of Q ≠ 0 incommensurate density waves (DW) in underdoped cuprates has also been reported extensively (20–27). Moreover, recent studies (28, 29) have demonstrated beautifully that the density modulations first visualized by scanning tunneling microscopy (STM) imaging (30) are indeed the same as the DW detected by these X-ray scattering techniques. However, although distinct in terms of which symmetry is broken, there is mounting evidence that the incommensurate DW and the IUC degrees of freedom are somehow linked microscopically (13, 16, 19, 31, 32).

Density Waves That Modulate the CuO₂ Intraunit-Cell States

One possibility is a density wave that modulates the CuO₂ IUC states. Proposals for such exotic DWs in underdoped cuprates include charge density waves with a d-symmetry form factor (33–35) and modulated electron-lattice coupling with a d-symmetry form factor (35, 36). Modulations of the IUC states having wave vectors Q = (Q,Q);(Q,−Q) have been extensively studied (37–41) but little experimental evidence for such phenomena exists. Most recently, focus has sharpened on the models (35, 36, 41–43) yielding spatial modulations of IUC states that occur at incommensurate wave vectors Q = (Q,0);(0,Q) aligned with the CuO₂ plane axes. The precise mathematical forms of these proposals have important distinctions, and these are discussed in full detail in SI Text, section 1.

Density waves consisting of modulations on the O_x sites that are distinct from those on the O_y sites can be challenging to conceptualize. Therefore, before explaining their modulated versions, we first describe the elementary symmetry decomposition of the IUC states of CuO₂. There are three possibilities (SI Text, section 2): a uniform density on the copper atoms with the O_x and O_y sites inactive (s symmetry), a uniform density on the oxygen atoms with the copper sites inactive (s′ symmetry), and a pattern with opposite-sign density at the O_x and O_y sites with the copper sites inactive (d symmetry). The latter state is shown in Fig. 1A. As these three IUC arrangements are spatially uniform, they correspond to specific representations of the point group symmetry of the lattice. Phase-resolved Fourier transforms of each arrangement could reveal their point group symmetry from the relative signs of the Bragg amplitudes. The s- and s′-symmetry cases both share 90°-rotational symmetry in their Bragg amplitudes (SI Text, section 2), whereas the Bragg amplitudes for a d-symmetry case change sign under 90° rotations as shown in Fig. 1B. Thus, by studying the magnitude and sign of the Bragg amplitudes in phase-resolved site-specific electronic structure images, one can extract the degree to which any translationally invariant IUC arrangement has an s, an s′, or, as in our previous work (12, 13, 31, 32, 44), a d symmetry (SI Text, section 2).

Next we consider periodic modulations of the IUC states with wave vector $\mathit{Q}$, as described by

$$\rho \left(\mathit{r}\right)\mathrm{=}\left[S\left(\mathit{r}\right)\mathrm{+}{S}^{\prime }\left(\mathit{r}\right)\mathrm{+}D\left(\mathit{r}\right)\right]\mathrm{Cos}\left(\mathit{Q}\mathrm{\cdot }\mathit{r}\mathrm{+}\varphi \left(\mathit{r}\right)\right).$$ [1]

Here $\rho \left(\mathit{r}\right)$ is a generalized density representing whatever electronic degree of freedom is being modulated; S, S′, and D are the coefficients of the DW form factors with s, s′, and d symmetry, respectively; and ϕ(r) is an overall phase [that might be spatially disordered (31, 32)]. A simple way to understand these DW form factors is in terms of the three CuO₂ sublattices: ${\mathit{r}}_{\mathrm{Cu}},\hspace{0.17em}{\mathit{r}}_{{\mathrm{O}}_x},\hspace{0.17em}{\mathit{r}}_{{\mathrm{O}}_y}$ (Fig. 1A, Inset). By definition, $S\left(\mathit{r}\right)=A_S$ if $\mathit{r}\in {\mathit{r}}_{\mathrm{Cu}}$ and otherwise zero; $S\prime \left(\mathit{r}\right)=A_{S\prime }$ if $\mathit{r}\in {\mathit{r}}_{{\mathrm{O}}_x}$ or ${\mathit{r}}_{{\mathrm{O}}_y}$ and otherwise zero; and $D\left(\mathit{r}\right)=A_D$ if $\mathit{r}\in {\mathit{r}}_{{\mathrm{O}}_x}$ and $D\left(\mathit{r}\right)=-A_D$ if $\mathit{r}\in {\mathit{r}}_{{\mathrm{O}}_y}$ and otherwise zero. This last case is a d-form factor density wave (dFF-DW) as shown schematically in Fig. 1C. In cuprates, a generic DW can actually have S, S′, and D all nonzero because the directionality of modulation wave vector Q breaks rotational symmetry (SI Text, section 2). Therefore, to identify a predominantly dFF-DW one should consider the structure of its Fourier transform, which exhibits several distinctive features. Fig. 1C shows a schematic dFF-DW that modulates along Q_x. In this state, by considering the two trajectories parallel to Q_x marked O_x and O_y, we see that the amplitude of the wave along O_x is exactly π out of phase with that along the adjacent trajectory O_y. For this reason, when its Fourier transform is determined (Fig. 1D), no primary modulation peaks occur at ±Q_x inside the first Brillouin zone (BZ). The second effect is that the Bragg satellite peaks at Q′ = (1,0) ± Q_x and Q′′ = (0,1) ± Q_x have opposite sign as shown in Fig. 1D (SI Text, section 3). Note that if an equivalent dFF-DW occurred only along Q_y $(\perp$ Q_x), the effects would correspond to those in Fig. 1D but with the Bragg satellite peaks then occurring at Q′ = (1,0) ± Q_y and Q′′ = (0,1) ± Q_y and again having opposite sign (SI Text, section 3).

Sublattice Phase-Resolved Fourier Transform STM

With the recent development of STM techniques to image IUC electronic structure (10–13, 32) while simultaneously achieving high-precision phase-resolved Fourier analysis (12, 13, 31, 32), it was suggested by one of us (S. Sachdev) that a practical approach to determining the form factor of underdoped cuprate DWs would be to partition each such image of the CuO₂ electronic structure into three separate images. The first image contains only the measured values at Cu sites (Cu(r)) and the other two images O_x(r) and O_y(r) contain only the measurements at the x/y-axis oxygen sites. The latter are key because two types of DW, ${\rho }_{S^{\prime }}\left(\mathit{r}\right)=S^{\prime }\hspace{0.17em}\mathrm{Cos}\left(\mathit{Q}\cdot \mathit{r}+{\varphi }_{S^{\prime }}\left(\mathit{r}\right)\right)$ and ${\rho }_D\left(\mathit{r}\right)=D\hspace{0.17em}\mathrm{Cos}\left(\mathit{Q}\cdot \mathit{r}+{\varphi }_D\left(\mathit{r}\right)\right)$, are both actually formed by using only phenomena from the O_x/O_y sites (Fig. 1C). Once the original electronic structure image is thus separated, the phase-resolved Fourier transform of O_x(r) and O_y(r), ${\tilde{O}}_x\left(\mathit{q}\right)$and ${\tilde{O}}_y\left(\mathit{q}\right)$, may, in principle, be used to reveal the form factor of these two types of DW.

A dFF-DW with modulations along both x and y axes at Q = (Q,0);(0,Q) should then exhibit two key characteristics exemplified by Fig. 1E whose equivalent experimental information is contained in $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ (SI Text, section 3). The first is that modulation peaks at Q should disappear in $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ whereas the Bragg-satellite peaks at Q′ = (1,0) ± Q and at Q′′ = (0,1) ± Q should exist with opposite sign as shown in Fig. 1E [the same being true for $Im{\tilde{O}}_x\left(\mathit{q}\right)+Im{\tilde{O}}_y\left(\mathit{q}\right)$]. The second predicted characteristic is that the primary DW peaks at Q should exist clearly in $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ whereas their Bragg-satellite peaks at Q′ = (1,0) ± Q and Q′′ = (0,1) ± Q should disappear [the same being true for $Im{\tilde{O}}_x\left(\mathit{q}\right)-Im{\tilde{O}}_y\left(\mathit{q}\right)$]. This is required because, if all O_y sites are multiplied by −1 as when we take the difference $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$, a dFF-DW is converted to an s′-form factor DW. For this reason, the signature of a dFF-DW in $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ is that it should exhibit the characteristics of Fig. 1F (SI Text, section 3).

Experimental Methods

To search for such phenomena, we use spectroscopic imaging STM (32) to measure both the differential tunneling conductance $dI/dV\left(\mathit{r},E=eV\right)\equiv g\left(\mathit{r},E\right)$ and the tunnel-current magnitude $I\left(\mathit{r},E\right)$, at bias voltage V and on samples of both Bi₂Sr₂CaCu₂O_8+x (BSCCO) and Ca_2−xNa_xCuO₂Cl₂ (NaCCOC). Because the electronic density-of-states $N\left(\mathit{r},E\right)$ always enters as $g\left(\mathit{r},E\right)\mathrm{\propto }\left[e{I}_S/{\displaystyle {\int }_0^{e{V}_S}N\left(\mathit{r},E^{\prime }\right)d{E}^{\prime }}\right]N\left(\mathit{r},E\right)$, where I_s and V_s are arbitrary parameters, the unknown denominator ${\displaystyle {\int }_0^{e{V}_S}N\left(\mathit{r},E^{\prime }\right)d{E}^{\prime }}$ always prevents valid determination of $N\left(\mathit{r},E\right)$ based only upon $g\left(\mathit{r},E\right)$ measurements. Instead, $Z\left(\mathit{r},\left|E\right|\right)=g\left(\mathit{r},E\right)/g\left(\mathit{r},-E\right)$ or $R\left(\mathit{r},\left|E\right|\right)=I\left(\mathit{r},E\right)/-I\left(\mathit{r},-E\right)$ is used (11–13, 31, 32) to suppress the otherwise profound systematic errors. This approach allows distances, wavelengths, and phases of electronic structure to be measured correctly. Physically, the ratio $R\left(\mathit{r},V\right)\propto {\displaystyle {\int }_0^{eV}N\left(\mathit{r},E\right)dE}/{\displaystyle {\int }_{-eV}^{0}N\left(\mathit{r},E\right)dE}$ is measured using an identical tip-sample tunnel junction formed at $\mathit{r}$ but using opposite bias voltage ±V; it is a robust measure of the spatial symmetry of electronic states in the energy range |E| = eV. Additionally for this study, measurements at many pixels within each unit-cell are required (to spatially discriminate every O_x, O_y, and Cu site) while simultaneously measuring in a sufficiently large field of view (FOV) to achieve high resolution in phase definition (11, 12, 32, 44).

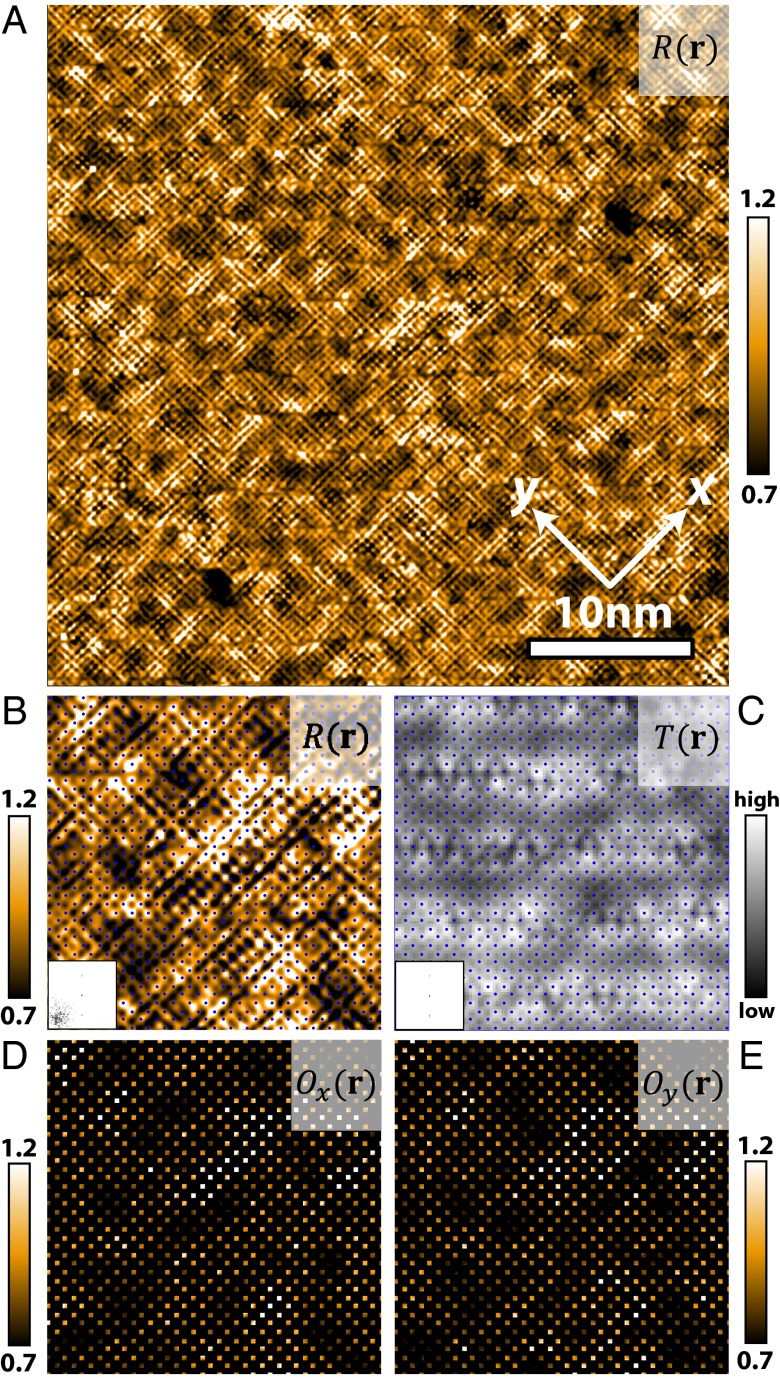
Data acquired under these circumstances are shown in Fig. 2A, the measured R(r, |E| = 150 meV) for a BSCCO sample with p ∼ 8 ± 1%. This FOV contains ∼15,000 each of individually resolved Cu, O_x, and O_y sites. Fig. 2B shows a magnified part of this R(r) with Cu sites indicated by blue dots; Fig. 2C is the simultaneous topographic image showing how to identify the coordinate of each Cu, O_x, and O_y site in all of the images. Using the Lawler–Fujita phase-definition algorithm that was developed for IUC symmetry determination studies (12, 32, 44), we achieve a phase accuracy of ∼0.01π (44) throughout. Fig. 2 D and E shows the partition of measured $R\left(\mathit{r}\right)$ into two oxygen site-specific images O_x(r) and O_y(r) determined from Fig. 2B (segregated Cu site-specific image is shown in SI Text, section 5). Larger FOV O_x(r);O_y(r) images partitioned from $R\left(\mathit{r}\right)$ in Fig. 2A and their Fourier transforms are shown in SI Text, section 5.

Fig. 2.

Oxygen site-specific imaging and segregation of R(r). (A) Measured R(r) with ∼16 pixels within each CuO₂ unit cell and ∼45 nm square FOV for a BSCCO sample with p ∼ 8 ± 1%. This R(r) electronic structure image reveals the extensive local IUC C₄ breaking (12, 13) (SI Text, section 5). (B) Smaller section of R(r) in FOV of A, now showing the location of the Cu lattice as blue dots. The well-known (11–13, 32) breaking of C₄ rotational symmetry within virtually every CuO₂ unit cell and the modulations thereof are obvious. (C) Topographic image of FOV in B showing Cu lattice sites as identified from the Bi atom locations as blue dots. By using the Lawler–Fujita algorithm (12, 44) spatial-phase accuracy for the CuO₂ plane of ∼0.01π is achieved throughout. (D) In the same FOV as B, we measure the value of R at every O_x site and show the resulting function O_x(r). (E) In the same FOV as B, we measure the value of R at every O_y site and show the resulting function O_y(r).

Direct Measurement of the DW Form Factor from Sublattice Phase-Resolved Images

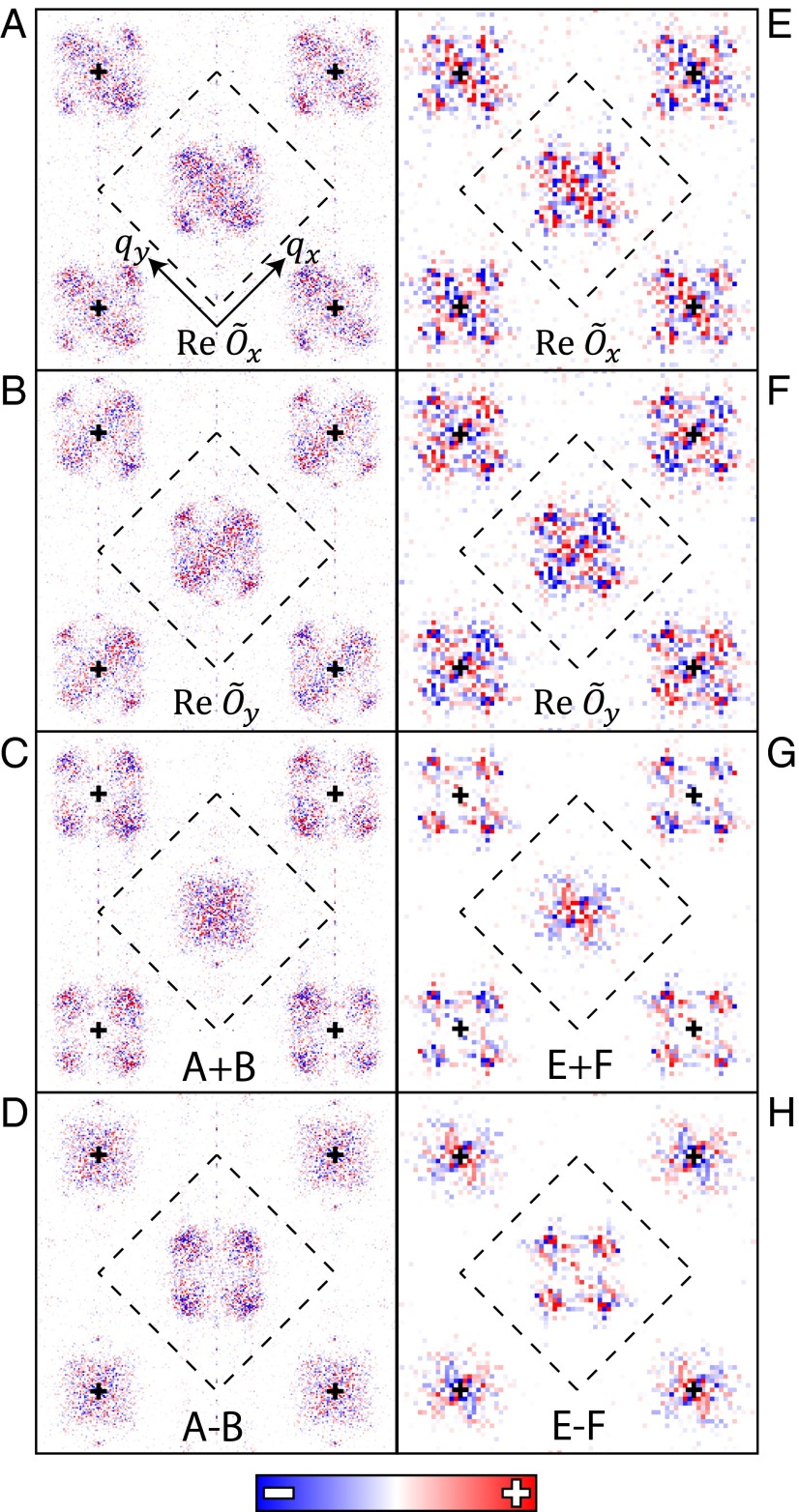
Now we consider the complex Fourier transforms of $O_x\left(\mathit{r}\right)$ and $O_y\left(\mathit{r}\right)$, ${\tilde{O}}_x\left(\mathit{q}\right)$ and ${\tilde{O}}_y\left(\mathit{q}\right)$, as shown in Fig. 3 A and B. We note that the use of $R\left(\mathit{r},V\right)$ or $Z\left(\mathit{r},V\right)$ is critically important for measuring relative phase of O_x/O_y sites throughout any DW, because analysis of $g\left(\mathit{r},V\right)$ shows how the tip–sample junction establishment procedure (11, 32) scrambles the phase information irretrievably. Upon calculating the sum $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ as shown in Fig. 3C, we find no DW modulation peaks in the vicinity of Q. Moreover, there is evidence for a $\pi$-phase shift between much sharper peaks at Q′ and Q′′ (albeit with phase disorder). Both of these effects are exactly as expected for a dFF-DW (Fig. 1 E and F). Further, the modulation peaks at Q inside the first BZ that are weak in Fig. 3 A and B and absent in Fig. 3C are clearly visible in $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ as shown in Fig. 3D. Hence the absence of this feature in $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ cannot be ascribed to broadness of the features surrounding $\mathit{q}=0$; rather, it is due to a high-fidelity phase cancelation between the modulations on O_x and O_y occurring with q ∼ Q. Finally, the Bragg-satellite peaks at Q′ = (1,0) ± Q and Q′′ = (0,1) ± Q that were clear in $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ are absent in $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$. Comparison of all these observations with predictions for a dFF-DW in Fig. 1 E and F demonstrates that the modulations at Q maintain a phase difference of approximately π between O_x and O_y within each unit cell and therefore predominantly constitute a d-form factor DW.

Fig. 3.

Sublattice phase-resolved analysis revealing d-form factor DW. (A) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)$ from R(r) in Fig. 2A. The four DW peaks at Q and the DW Bragg-satellite peaks exist but are all poorly resolved. (B) $Re{\tilde{O}}_y\left(\mathit{q}\right)$ from Fig. 2A; again, the four DW peaks at Q and the DW Bragg-satellite peaks exist but are all poorly resolved. (C) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ from A and B. The four DW peaks at Q are not detectable whereas the DW Bragg-satellite peaks are enhanced and well resolved. Compared to Fig. 1E, these are the expected phenomena of a d-form factor DW (with spatial disorder in ϕ_D). (D) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ from A and B. The primary DW peaks at Q are strongly enhanced whereas the DW Bragg-satellite peaks have disappeared. Compared to Fig. 1F, these are once again the expected phenomena of a dFF-DW. (E) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)$ for an NaCCOC sample with p ∼ 12 ± 1%. The DW peaks at Q, and the DW Bragg-satellite peaks exist but are poorly resolved. (F) Measured $Re{\tilde{O}}_y\left(\mathit{q}\right)$ for NaCCOC. The DW peaks at Q, and the DW Bragg-satellite peaks exist but are poorly resolved. (G) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$ from E and F. The four DW peaks at Q are no longer detectable whereas the DW Bragg-satellite peaks are enhanced and well resolved. Importantly (modulo some phase noise) the Bragg-satellite peaks at inequivalent Q′ and Q′′ exhibit opposite sign. Compared to Fig. 1E, these are the expected phenomena of a dFF-DW. (H) Measured $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ from E and F. The four DW peaks at Q are enhanced whereas the DW Bragg-satellite peaks have disappeared. Compared to Fig. 1F, these confirm the dFF-DW conclusion.

To demonstrate that these phenomena are not a specific property of a given tip–sample tunnel matrix element, crystal symmetry, surface termination layer, or cuprate material family, we carry out the identical analysis on data from NaCCOC samples with p ∼ 12 ± 1% (SI Text, section 5). For this compound, Fig. 3 E and F shows the measured $Re{\tilde{O}}_x\left(\mathit{q}\right)$ and $Re{\tilde{O}}_y\left(\mathit{q}\right)$. Again, the absence of DW peaks at Q in Fig. 3G, which shows $Re{\tilde{O}}_x\left(\mathit{q}\right)+Re{\tilde{O}}_y\left(\mathit{q}\right)$, is due to cancelation between O_x and O_y contributions, as these peaks are visible in $Re{\tilde{O}}_x\left(\mathit{q}\right)$ and $Re{\tilde{O}}_y\left(\mathit{q}\right)$ (Fig. 3 E and F). Moreover, the sign change between the Bragg satellites Q′ = (1,0) ± Q and Q′′ = (0,1) ± Q in Fig. 3G is another hallmark of a dFF-DW. Finally, $Re{\tilde{O}}_x\left(\mathit{q}\right)-Re{\tilde{O}}_y\left(\mathit{q}\right)$ reveals again that the modulation peaks at Q inside the first BZ that are invisible in Fig. 3G become vivid in Fig. 3H, whereas the Bragg satellites disappear. One can see directly that these results are comprehensively consistent with observations in Fig. 3 A–D, meaning that the DW of NaCCOC also exhibits a robust d-symmetry form factor. This observation rules out experimental/materials systematics as the source of the dFF-DW signal and therefore signifies that this state is a fundamental property of the underdoped CuO₂ plane.

Cuprate d-Form Factor DW Is Both Predominant and Robust

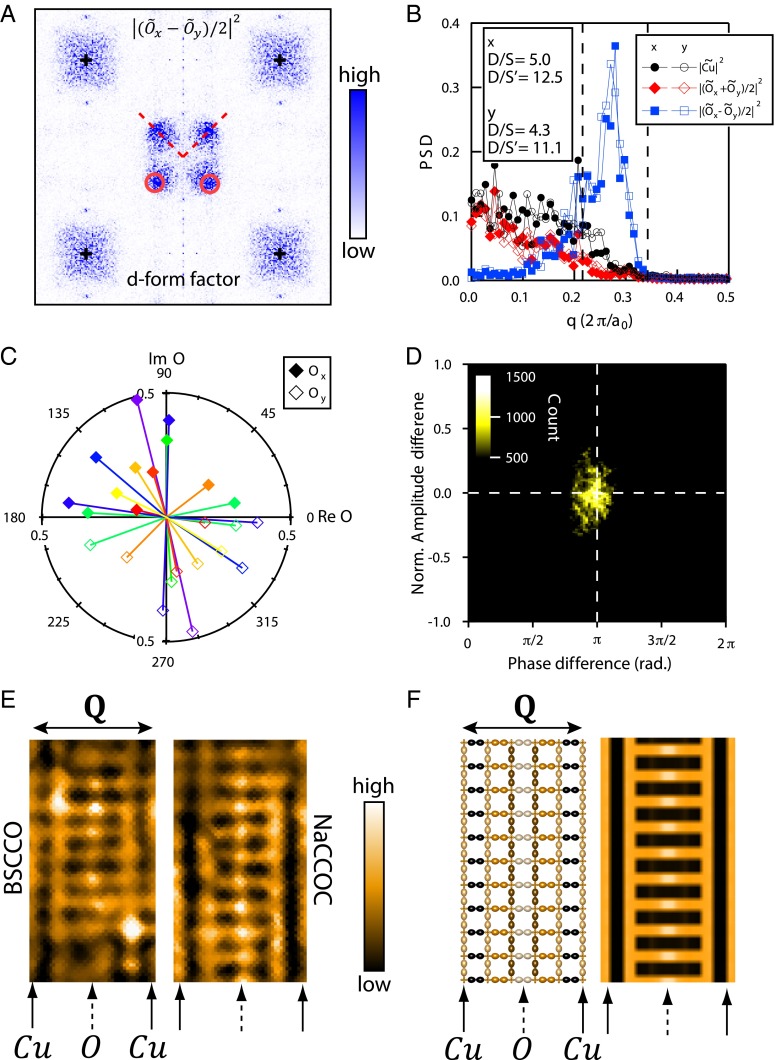
One can quantify the preponderance of the dFF-DW by measuring the magnitude of the s-, s′-, and d-symmetry form factors of the observed DW near Q inside the first BZ (SI Text, section 2). In Fig. 4A we show the power spectral density Fourier transform analysis |$\left({\tilde{O}}_x\left(\mathit{q}\right)-{\tilde{O}}_y\left(\mathit{q}\right)\right)/2$|² yielding the d-form factor magnitude D, with the equivalent results for only the Cu sites $|{\tilde{C}}_u\left(\mathit{q}\right){|}^2$ to determine the s-form factor magnitude S, and |$\left({\tilde{O}}_x\left(\mathit{q}\right)+{\tilde{O}}_y\left(\mathit{q}\right)\right)/2$|² for the s′-form factor magnitude S′, shown in SI Text, section 5. In Fig. 4B, the measured values S, S′, and D are plotted along the dashed lines through Q in Fig. 4A and show that the d-form factor component is far stronger than the others for both modulation directions. This is also the case in the NaCCOC data. Fig. 4C shows examples of measured complex-valued ${\tilde{O}}_x\left(\mathit{q}\right)\equiv Re{\tilde{O}}_x\left(\mathit{q}\right)+iIm{\tilde{O}}_x\left(\mathit{q}\right)$ and compares them to ${\tilde{O}}_y\left(\mathit{q}\right)\equiv Re{\tilde{O}}_y\left(\mathit{q}\right)+iIm{\tilde{O}}_y\left(\mathit{q}\right)$ for each of a series of representative q within the DW peaks surrounding Q (all such data are from Figs. 2 and 3). Fig. 4D is a 2D histogram showing both the magnitude difference and the phase difference between all such pairs of Fourier-filtered ${\tilde{O}}_x\left(\mathit{r}\right):{\tilde{O}}_y\left(\mathit{r}\right)$ within the same broad DW peaks (SI Text, section 5). These data reveal the remarkably robust nature of the d-form factor of the DW and that the strong spatial disorder in DW modulations (e.g., Fig. 2A and ref. 44) has little impact on the phase difference of π between O_x and O_y within every CuO₂ unit cell. Finally, focusing on specific regions of the R(r) images, one can now understand in microscopic detail the well-known (11, 13, 31, 32) but unexplained spatial patterns of CuO₂ electronic structure when detected with subunit-cell resolution (e.g., Fig. 4E). In fact, the virtually identical electronic structure patterns in BSCCO and NaCCOC (Fig. 4E and ref. 11) correspond to the instance in which a unidirectional dFF-DW occurs with Q = (0.25,0) and with amplitude peaked on the central O_x sites (Fig. 4E, dashed vertical arrow). A model of a dFF-DW with this choice of spatial phase is shown in Fig. 4F (SI Text, section 1) with the calculated density adjacent; the agreement between data (Fig. 4E) and the dFF-DW model (Fig. 4F) gives a clear visual confirmation that the patterns observed in real space R(r) data (10, 11, 13, 32) are a direct consequence of a locally commensurate, unidirectional, d-form factor density wave.

Fig. 4.

d-form factor DW: predominance and robustness. (A) Power spectral-density (PSD) Fourier transforms of R(r) measured only at the O_x/O_y sites yielding |$\left({\tilde{O}}_x\left(\mathit{q}\right)-{\tilde{O}}_y\left(\mathit{q}\right)\right)/2$|². This provides the measure of relative strength of the d-form factor in the DW. (B) Measured PSD is plotted along the dashed line through Q in A and shows the d-form factor component predominates greatly. The measured ratios within the DW peaks surrounding Q are D/S > 5 and D/S′ > 12. (C) ${\tilde{O}}_x\left(\mathit{q}\right)\equiv Re{\tilde{O}}_x\left(\mathit{q}\right)+iIm{\tilde{O}}_x\left(\mathit{q}\right)$ compared with ${\tilde{O}}_y\left(\mathit{q}\right)\equiv Re{\tilde{O}}_y\left(\mathit{q}\right)+iIm{\tilde{O}}_y\left(\mathit{q}\right)$ for each of a series of representative q within the DW peaks surrounding Q. This shows how, wherever the CuO₂ unit cell resides in the disordered DW (Fig. 2A), the relative phase between the O_x and O_y sites is very close to π whereas the differences in magnitudes are close to zero. (D) Two-axis histogram of difference in normalized magnitude (vertical) and phase (horizontal) between all pairs ${\tilde{O}}_x\left(\mathit{r},\mathit{Q}\right)$ and ${\tilde{O}}_y\left(\mathit{r},\mathit{Q}\right)$ that are obtained by Fourier filtration of O_x(r) and O_y(r) to retain only q ∼ Q (SI Text, section 5). This represents the measured distribution of amplitude difference, and phase difference, between each pair of O_x/O_y sites everywhere in the DW. It demonstrates directly that their relative phase is always close to π and that their magnitude differences are always close to zero. (E) Measured R(r) images of local electronic structure patterns that commonly occur in BSCCO and NaCCOC (11). The Cu and O_x sites (labeled by solid and dashed arrows, respectively) were determined independently and directly from topographic images (11). (F) (Left) dFF-DW model with Q = (0.25,0) and amplitude maximum on the central O_x site (dashed arrow). (Right) The calculated density-wave pattern from this model. Therefore, a dFF-DW model with this particular spatial phase provides an excellent explanation for the observed density patterns shown in E and reported previously in refs. 11–13 and 32.

Conclusions and Discussion

By generalizing our technique of phase-resolved intraunit-cell electronic structure imaging at Cu, O_x, and O_y (11–13, 31, 32, 44), to include segregation of such data into three images [Cu(r), O_x(r), and O_y(r)], sublattice-phase–resolved Fourier analysis yielding $\widetilde{Cu}\left(\mathit{q}\right)$, ${\tilde{O}}_x\left(\mathit{q}\right)$, and ${\tilde{O}}_y\left(\mathit{q}\right)$ becomes possible. Then, by comparing predicted signatures of a dFF-DW in Fig. 1 E and F with the equivalent measurements $Re{\tilde{O}}_x\left(\mathit{q}\right)\pm Re{\tilde{O}}_y\left(\mathit{q}\right)$ in Fig. 3 C and D and Fig. 3 G and H, respectively, we find them in excellent agreement for both BSCCO and NaCCOC. In their X-ray observations on underdoped Bi₂Sr₂CuO₆ and YBa₂Cu₃O₇, Comin et al. (19) used a model of the scattering amplitudes of the Cu and O atoms in the presence of charge-density modulations and showed that a density wave that modulates with a d-form factor between O_x and O_y sites provides a significantly better fit to the measured cross section than s- or s′-form factors. In our complementary approach, we demonstrate using direct sublattice phase-resolved visualization that the cuprate density waves involve modulations of electronic structure (not necessarily charge density) that maintain a relative phase of ∼π between O_x and O_y or equivalently that exhibit a d-symmetry form factor.

New challenges are revealed by the detection of the dFF-DW state in the cuprate pseudogap phase. The first is to determine its relationship to the Q = 0 C₄-breaking phenomena that are widely reported in underdoped cuprates (12–18). In this regard, a potentially significant observation is that coupling between a DW with both s′- and d-form factor components and a Q = 0 nematic state is allowed by symmetry at the level of Ginzburg–Landau theory, so that their coexistence is not unreasonable. Nevertheless, the specifics of that coupling (31) and how the phase diagram is arranged (13) in terms of the dFF-DW and Q = 0 states remain to be determined and understood. Another challenge is to understand the microscopic physics of the dFF-DW itself. The fidelity of the π-phase difference within each unit cell (Fig. 4) despite the intense spatial disorder (Fig. 2) implies that there must be a powerful microscopic reason for inequivalence of electronic structure at the O_x and O_y sites in underdoped cuprates. One may ask whether, in addition to antiferromagnetic interactions (36–43), the Coulomb interactions between holes on adjacent O_x and O_y sites that play a key role in theories for the Q = 0 nematic (7, 8, 40) may be an important factor in formation of the dFF-DW. Finally, finding the microscopic relationship of the dFF-DW to the d-wave high-temperature superconductivity and to the pseudogap state now emerges as an issue of primary importance.