Learning of Spatial Relationships between Observed and Imitated Actions allows Invariant Inverse Computation in the Frontal Mirror Neuron System

Abstract

It has been suggested that the human mirror neuron system can facilitate learning by imitation through coupling of observation and action execution. During imitation of observed actions, the functional relationship between and within the inferior frontal cortex, the posterior parietal cortex, and the superior temporal sulcus can be modeled within the internal model framework. The proposed biologically plausible mirror neuron system model extends currently available models by explicitly modeling the intraparietal sulcus and the superior parietal lobule in implementing the function of a frame of reference transformation during imitation. Moreover, the model posits the ventral premotor cortex as performing an inverse computation. The simulations reveal that: i) the transformation system can learn and represent the changes in extrinsic to intrinsic coordinates when an imitator observes a demonstrator; ii) the inverse model of the imitator’s frontal mirror neuron system can be trained to provide the motor plans for the imitated actions.

I. Introduction

BRAIN-IMAGING studies have provided evidence suggesting that the human mirror neuron system (MNS) is involved in learning by imitation of an observed action [1]–[3]. Traditionally, it was suggested that the MNS is composed of two main components designated as the frontal and parietal MNSs respectively in the ventral premotor cortex (PMv) and the inferior parietal lobule (IPL) [4], [5]. Besides these MNS components, an assisting component characterized as mirror-like system includes the superior temporal sulcus (STS) [2].

Generally, the functional properties and roles of the MNS in learning by visually guided imitation can be examined by considering the neural or behavioral responses of an imitator during the following two-phase study for the imitator [6]. First, during an observation phase, the imitator observes an action (e.g., an arm reaching for an object) performed by the demonstrator. In this phase, the MNS responses of the imitator are typically compared against a rest condition. Second, during an action execution phase, the imitator reproduces the action observed in the first phase. The imitator’s MNS responses and kinematics recorded in this phase are generally compared with the corresponding data during observation or execution alone. Based on these two-phase experiments, brain-imaging studies have revealed that intraconnections and interconnections between and within the inferior frontal cortex (IFC), the posterior parietal cortex (PPC), and the superior temporal cortex (STC) would constitute a large neural architecture for action imitation [7].

Since the internal model framework could bridge the gap between neural mechanisms and computations necessary for understanding the MNS, various modeling approaches have been proposed [7]–[11]. These models commonly suggested that the pathway from the STS to the frontal MNS via the parietal MNS would serve as an inverse model, whereas the reverse pathway would correspond to a forward model [7]. However, these models focused only on the functioning of the MNS associated with the forward computation without explicitly investigating the inverse computation. Moreover, they did not explicitly integrate a biologically plausible frame of reference transformation (FORT) system, although it is critical to learn visually guided actions performed by other individuals since the demonstrator and the imitator perform and imitate the action in their own frames of reference, respectively [12]. Recently, it was suggested that neural substrates such as the superior parietal lobule (SPL) [13], [14] as well as the intraparietal sulcus (IPS, specifically in the anterior and lateral parts) [13], [15] could implement the transformation system.

Therefore, this paper aims to propose a biologically plausible and behaviorally realistic MNS model based on internal model concepts, which incorporates both the transformation of a frame of reference and the inverse computation through two-phase learning including action observation and imitation. It will deepen our understanding of the basic neurophysiological and computational mechanisms by investigating functional relationships between neural structures and sensorimotor transformations that underlie adaptive MNS computations during action observation and imitation. Also, this model could be employed for learning by imitation in humanoid robotics.

II. The Model Overview

The currently proposed model extends the anatomical and conceptual architecture proposed in our previous model based on Miall’s model [9], [14] (Fig. 1).

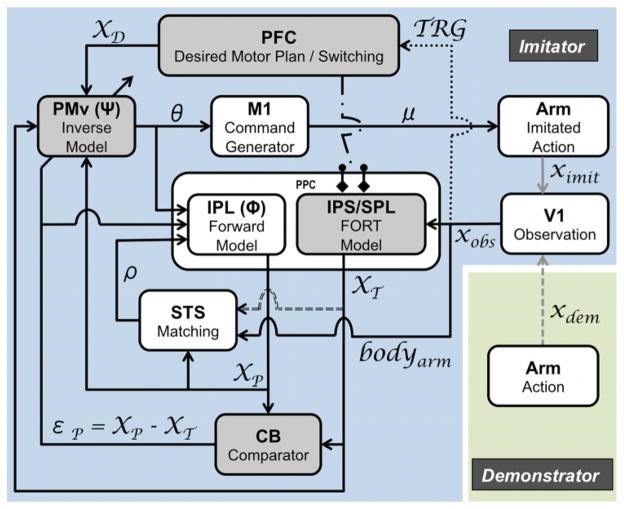
Fig. 1.

The model overview for the human MNS based on a forward and an inverse model framework during learning by imitation for reaching action. Functional roles and computations are described in the boxes and the links, respectively. The proposed pathway from the IPS/SPL (including the FORT system) to the STS is represented with a dashed gray line. The dark gray boxes (PFC, PMv, IPS/SPL, and CB) are currently implemented. x_dem: demonstrator’s action; x_imit: imitator’s own action; x_obs: observed action; TRG: trigger; body_arm: corresponding body limbs; X_T: transformed action; X_P: predicted action; ε_P: prediction error; ρ: cross correlation; X_D: desired motor plan; θ: motor plan; μ: motor command.

During the observation phase, the demonstrator’s action is encoded into kinematic visual information in the primary visual cortex (V1). The encoded information is sent to the STS as well as the IPS/SPL, and triggers the prefrontal cortex (PFC). Subsequently, the STS provides an abstract visual representation of the familiar biological motion (e.g., reaching) and corresponding body limbs (e.g., arm) [9], [16]; the IPS/SPL (i.e., the FORT system) transforms the observed information in the viewpoint of the imitator’s intrinsic coordinate system [13]; the PFC initiates the whole system by providing the intentions to imitate [10].

In particular, the recruitment of the FORT system may be mediated by means of the switching mechanism applying the stimulus-response mapping rules in the PFC [17], [18]. For example, the PFC would switch to the translation, scaling, and rotation modes when observing the actions performed by other individuals, whereas it would switch to the identity mode (i.e., no transformation in this case) when processing the visual feedback of one’s own actions. Afterwards the transformed observed actions would update the PMv to change the encoded information to the motor plan (i.e., inverse computation), which is required to reproduce the observed action. Although no action is performed during observation, the efference copy of the motor plan is still available and sent to the IPL, which in turn predicts the sensory consequences of the corresponding action (i.e., forward computation) that are transferred to the STS and the cerebellum (CB) [9]. Then, the STS compares the expected and observed actions to enhance the retrieval of the familiar actions when the match is successful [16]. In addition, the CB generates the prediction error that can be used to update the inverse and forward model in the PMv and the IPL, respectively.

During the subsequent action execution phase, where the observed action is actually imitated, the neural processes between and within the PMv, the IPL, the STS, and the CB will remain as similar to those previously described in the observation phase. However, contrary to observation, the neural drive will be also sent to the musculoskeletal system through the primary motor cortex (M1) to perform actual actions. The imitator can then observe one’s own actions with the identity transformation since the frame of reference is identical. Finally, when the imitator observes one’s own motor output, the actual feedbacks (e.g., somatosensory and visual) are available, thus the error between the actual sensory consequences of the action and the observed prior action can be compared to update the PMv, the IPL, and the STS.

III. Methods

Currently, two separate radial basis function (RBF) networks [19], [20] serve as both the FORT and the adaptive inverse model systems mapping f : 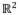→ 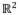according to:

$$f(x)={\kappa }_0+{\sum }_{i=1}^n{\kappa }_i\varphi (\Vert x-c_i\Vert )$$ (1)

$$\varphi (u)=exp(-0.5u^2/{\sigma }^2)$$ (2)

where x ∈ 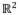is the input vector, f (x) ∈ 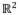is the output vector, ϕ (·) is the Gaussian basis function, || · || denotes the Euclidean norm, n is the number of RBFs, κ_i (0 ≤ i ≤ n)are the synaptic weights, $c_i\in {ℝ}_D^2$(1 ≤ i ≤ n) are the RBF centers, and σ is known as the RBF width parameter.

Learning in the model involves changing synaptic connection weights between nodes in the hidden and output layers by the orthogonal least squares algorithm [20]. Currently, the forward model was supposed to be known a priori by employing the exact mathematical model.

A. Frame of Reference Transformation System

The FORT system assumed to be in the IPS/SPL aims to help the imitator to solve and generalize the mapping $f_T:{ℝ}_D^2\to {ℝ}_I^2$ using (1) and (2), where ${ℝ}_D^2$ and ${ℝ}_I^2$ are two-dimensional workspaces in a demonstrator-centered (D) and an imitator-centered (I) frame of reference, respectively.

In general, the mapping includes various combinations of translation, rotation, scaling, and reflection procedures, and each of them can be specifically described as following [21], [22]: i) Translation is a mechanism for the imitator to refer to the demonstrator’s actions in the same position by shifting the origin of the imitator’s frame of reference; ii) Rotation allows the imitator facing the same direction with the demonstrator by rotating the orientation of the axial frame of the imitator; and iii) Scaling and Reflection are so-called personalization methods for the imitator in the understanding of the observed actions by changing the ratio and shape of the body (i.e., scaling) or the handedness (i.e., reflection).

The current FORT neural network combining translation, rotation, and scaling transformations was trained by using only 25 uniformly spaced reference points regardless of the size of the demonstrator’s workspace. Based on this approach, the network could approximate the whole workspace, leading to the efficient network. As a first step, the network was trained before the inverse model system while the demonstrator and the imitator faced each other.

B. Adaptive Inverse Model System

The adaptive inverse model system is assumed to be in the frontal MNS and can be simply described by the mapping $f_I:{ℝ}_V^2\to {ℝ}_M^2$ using (1) and (2). Namely, ${ℝ}_V^2$ and ${ℝ}_M^2$ are two-dimensional spaces specifying the observed action and the motor plan respectively in the visual (V) and the motor (M) domain.

As previously mentioned, the inverse model was acquired by using a two-phase learning process (i.e., learning by action observation and again by action execution). This learning approach is behaviorally realistic since learning by imitation in ecological conditions generally requires continuously repeating these two phases in a sequential manner. Two-phase learning was repeated until reaching the threshold (1.0×10⁻⁶ m). Performance of the right upper limb in the horizontal plane was simulated with a geometrical model including 2 degrees of freedom. Predictive performance and model accuracy were assessed by comparing the similarity of the observed and the executed action in the geometric shape (here, a triangle) of reaching trajectories.

IV. Results

The anthropometric data and the functional range of motion in the performance of the right upper limb arm for the demonstrator and the imitator are shown in Table I.

TABLE I.

Anthropometric Data and Functional Range of Motion

Dimension name	Demonstrator	Imitator
Upper Arm Length	0.33 m	0.16 m
Forearm Length	0.27 m	0.12 m
Shoulder Horizontal Adduction (θ1)†	0° to 120°	0° to 120°
Elbow Horizontal Flexion (θ2)†	0° to 120°	0° to 120°

^†The 0° start position for establishing the degrees of each motion is 90° shoulder abduction and 90° elbow extension, respectively (Fig. 2a).

A. Frame of Reference Transformation System

The results revealed that the observed demonstrator’s workplace (green) was successfully transformed (red) and mapped onto the imitator’s workplace (blue) (Fig. 2). The performance of the FORT system was evaluated comparing the errors measured by the normalized Euclidean distance with respect to the length of the imitator’s upper limb between the observed-and-scaled demonstrator’s workspace (red) and the imitator’s workspace (blue) (Fig. 2b), where the mean and standard deviation of the errors is 0.033 and 0.021, respectively. Besides, the standardized dissimilarity measure (SDM) using procrustes analysis, where values near 0 and 1 respectively indicate more similarity and dissimilarity between two shapes, is only 8.14×10⁻⁴ [23].

Fig. 2.

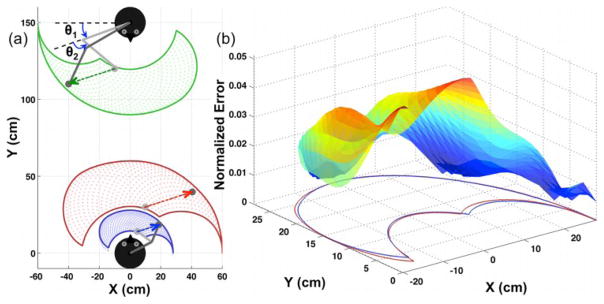
The FORT system includes translation, rotation, and scaling. (a) The demonstrator and the imitator are facing each other at the top (the demonstrator) and the bottom (the imitator). The demonstrator’s workspace (green) was transformed into the observed workspace (red) by the imitator. This observed workspace would be scaled into the imitator’s own workspace (blue), where the imitation is performed. The imitator could reproduce (blue arrow) the action that was performed (green arrow) by the demonstrator. (b) The normalized Euclidean distance error between the scaled red area and the original blue area is represented at the XY plane.

B. Adaptive Inverse Model System

The results supported that the inverse model can adaptively learn and reproduce the action in the imitator’s frame of reference (Fig. 3).

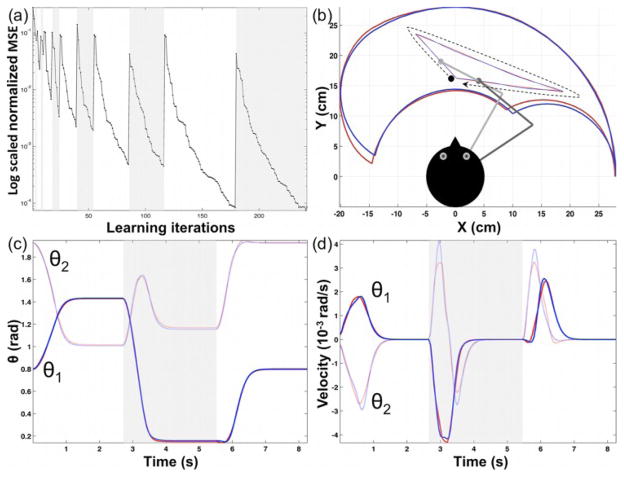
Fig. 3.

Adaptive inverse model performance. (a) The log scaled normalized MSE curve represents 6 sequentially repeating adaptive learning by observation (white bands) and by action execution (gray bands). (b) The imitator reproduces (blue) the observed (red) triangular kinematics in a clockwise direction (black dotted arrow). The red and blue bean-shaped areas represent the demonstrator and imitator’s workspaces, respectively. (c)–(d) The three white and gray bands represent each linear segment of the triangular shape. Generally, the joint angles displacements were sigmoid and the velocity profiles were single-peaked bell shapes although sometimes these classical kinematics were slightly distorted due to cumulative residual errors from the FORT and the inverse model.

Specifically, it was found that the normalized mean squared error (MSE) showed a tendency to decrease exponentially throughout learning and that, compared to learning by observation, learning by execution required about 5.2% less time to reach the same performance (Fig. 3a). These findings suggest that prior knowledge obtained during the observation phase helped the imitator to acquire more rapidly the action during actual performance. Once the inverse kinematic was learned, a triangular reaching action was used to assess the performance of the overall neural model during action imitation (Fig. 3b–3d). The SDM between the observed and imitated action is 2.64×10⁻⁵.

V. Discussion

We proposed a biologically plausible human MNS model for action imitations through two-phase learning combining action observation and execution. Three novel results emerged from the simulation. First, the frontal MNS could learn the inverse dynamic computation to reproduce the observed kinematics. This learning was based on the performance and prediction error; it thus expands previous works that were mainly conducted in motor control [24]. Second, an ecological two-phase learning mechanism could make the inverse model more behaviorally realistic by sequentially repeating both observation and action execution phases. In this context, the PFC would work as a neural basis for the switching system between two transformation modes (i.e., self-observation and other-observation) in the IPS/SPL. Finally and more importantly, the IPS/SPL could acquire the FORT system to transform the demonstrator to the imitator’s frame of reference [13]–[15]. Although other models did not explicitly examine such a transformation system, this could be another important assisting component for the MNS in imitation. For instance, it was reported in monkeys that the responses of the mirror neurons in the PMv would be similar independently of the demonstrator’s position [8], [25]. Our model offers a possible explanation of the neurophysiological findings. Specifically, the IPS/SPL would transform the information from the extrinsic visual space into the intrinsic sensorimotor space. Then, the information expressed in the transformed frame of reference corresponding to the imitator would be sent to the frontal MNS and thus result in the demonstrator’s position independent activity in the frontal MNS. Based on the rationale, the FORT system could make the imitator perceive both other and own actions in a common frame of reference.

The current model also contains several limitations that need to be considered. For instance, the implementation of the PFC is relatively succinct and should be further developed. Also, the forward model was assumed as known a priori; however, various neural modeling approaches can be employed to learn the forward model [19], [24]. Another limitation is that the IPS/SPL (or FORT system) must be trained when the demonstrator and imitator are facing each other (i.e., their position is spatially symmetric), and its learning must precede the acquisition of the inverse model. Therefore, future works aim i) to extend the PFC model, ii) to examine the coordination of learning between the frontal (inverse model) and parietal (forward model) MNS, and iii) to investigate the capabilities of the transformation system incorporated in the IPS/SPL.