Multi-Material Decomposition Using Statistical Image Reconstruction for Spectral CT

Abstract

Spectral CT provides information on material characterization and quantification because of its ability to separate different basis materials. Dual-energy (DE) CT provides two sets of measurements at two different source energies. In principle, two materials can be accurately decomposed from DECT measurements. However, many clinical and industrial applications require three or more material images. For triple-material decomposition, a third constraint, such as volume conservation, mass conservation or both, is required to solve three sets of unknowns from two sets of measurements. The recently proposed flexible image-domain (ID) multi-material decomposition (MMD) method assumes each pixel contains at most three materials out of several possible materials and decomposes a mixture pixel by pixel. We propose a penalized-likelihood (PL) method with edge-preserving regularizers for each material to reconstruct multi-material images using a similar constraint from sinogram data. We develop an optimization transfer method with a series of pixel-wise separable quadratic surrogate (PWSQS) functions to monotonically decrease the complicated PL cost function. The PWSQS algorithm separates pixels to allow simultaneous update of all pixels, but keeps the basis materials coupled to allow faster convergence rate than our previous proposed material-and pixel-wise SQS algorithms. Comparing with the ID method using 2D fan-beam simulations, the PL method greatly reduced noise, streak and cross-talk artifacts in the reconstructed basis component images, and achieved much smaller root-mean-square (RMS) errors.

I. INTRODUCTION

X-ray computed tomography (CT) images the spatial distribution of attenuation coefficients of the object being scanned. Attenuation maps have many applications both in medical diagnosis and treatment and in industry for nondestructive evaluation. A conventional CT scanner measures a single sinogram at single X-ray source potential. Conventional image reconstruction methods process such measurements to produce a scalar-valued image of the scanned object.

In practice the scanned object always contains multiple materials. For example, the organs and tissues of human body under CT scans contain typical basis materials of blood, fat, muscle, water, cortical bone, air and contrast agent [1], [2]. Material attenuation coefficients depend on the energy of the incident photons. An X-ray beam in clinical practice is usually composed of individual photons with a wide range of energies, and each photon energy is attenuated differently by the materials in the object. If uncorrected, this energy dependence causes artifacts in images reconstructed by conventional methods, such as beam-hardening artifacts [3]. This energy dependence also allows the possibility of basis-material decomposition [1], [4]–[8]. Numerous applications of two-material decomposition have been explored, including CT-based attenuation correction for positron emission tomography (PET) [7], [9], beam-hardening artifacts correction [10], [11], and virtual un-enhancement (VUE) CT [1], [8].

Dual-energy (DE) CT methods, pioneered by Alvarez and Macovski et al. [4], [12]–[15], are the most predominant approaches for reconstructing two basis materials (e.g., soft-tissue and bone). They decomposed the energy dependence of attenuation coefficients into two components, one approximated the photoelectric interaction and another approximated Compton scattering, and separated these two components from two sets of measurements at two different source energies. Although DECT methods were originally proposed in the late 1970s and early 1980s, DECT scanners became clinically available only recently with technological developments, such as fast kVp-switching, dual-source CT and dual-layer detectors. These new techniques have brought renewed interest in DECT [6], [7], [9], [16]–[18], [18]–[26].

Several methods have been developed for reconstructing two basis materials from one CT scan with a single tube voltage setting. Ritchings and Pullan [27] described a technique for acquiring spectrally different data by filtering alternate detector elements. Taschereau et al. [28] retrofitted a preclinical microCT scanner with a filter wheel that alternates two beam filters between successive projections. One filter provides a low energy beam while the other filter provides a high energy beam. We [29] proposed a statistical penalized weighted least-squares (PWLS) method for reconstructing two basis materials from a single-voltage CT scan, exploiting the incident spectra difference of rays created by filtration, such as split [30] and bow-tie filters. One major limitation of decomposition methods based on single-voltage CT is the significant overlap in the two spectra that are generated by different filters.

Many clinical and industrial applications desire three or more component images [1], [22], [31], [32]. Quantifying liver fat concentration requires images of four constitute materials, liver tissue, blood, fat and contrast agent [1], [32]. Multi-material decomposition (MMD) can generate VUE images by removing the effect of contrast agents from contrast-enhanced CT exams without needing an additional contrast-free scan, reducing patient dose [1]. For radiotherapy, it is also useful to know the distributions of materials besides bone and soft tissue, such as calcium, metal (e.g., gold) and iodine-based contrast agent.

Typically, spectral CT methods reconstruct images of L₀ = M₀ basis materials from M₀ sets of measurements with M₀ different spectra [5]. Sukovic and Clinthorne [5] separated L₀ = 3 basis materials from M₀ = 3 sinograms acquired using M₀ = 3 distinct source voltages, one of which was near the K-edge of one basis material. Generally, spectral CT requires multiple scans or specialized scanner designs, such as quasi-monochromatic sources [33] or energy-resolved photon-counting detectors [34]. In this paper, we focus on MMD using DECT which is currently the only commerically available version of spectral CT. However, the general formulation is applicable to a variety of spectral CT approaches.

A third criteria, such as volume conservation [21], mass conservation [22] or both [1], can enable reconstructing three basis materials from DECT measurements. Volume (mass) conservation assumes the sum of the volumes (masses) of the three constituent materials is equivalent to the volume (mass) of the mixture. To reconstruct L₀ > 3 materials from DECT, solving this ill-posed problem requires additional assumptions. Mendonca et al. [1] proposed an image-domain (ID) method to reconstruct multiple materials pixel by pixel from a DECT scan. In addition to both volume and mass conservation assumptions, that method assumes that each pixel contains a mixture of at most three materials where the material types can vary between pixels. It establishes a material library containing all the possible triplets of basis materials for a specific application. It obtains a dual-material-density pair through projection-based decomposition approach from DECT measurements, and then generates a linear-attenuation-coefficient (LAC) pair for each pixel at two selected distinct energies (e.g.. 70 and 140 keV). Given a LAC pair, a material triplet and the sum-to-one constraint that was derived using both the volume and mass conservation assumption, triple material decomposition is solved for each pixel. This method sequentially decomposes each pixel into different triplets in the material library in a prioritized order, and collects solutions of volume fractions that satisfy a box ([0, 1]) constraint and sum-to-one constraint. If there is a solution, it moves on to the next pixel and skips material triplets with lower priorities. If there is no feasible solution for all the material triplets, it relaxes the box constraints and accepts the volume fractions corresponding to the triplet with minimal Hausdorff distance to the LAC pair over all possible triplets.

Inspired by the ID method [1], [35] we proposed a penalized-likelihood (PL) method [36] with an edge-preserving regularizer to reconstruct multi-material images. It is well known that statistical image reconstruction methods based on physical models of the CT system and scanned object and statistical models of the measurements can obtain lower noise images with higher quality. The proposed PL method considers each material image as a whole, instead of pixel by pixel, so prior knowledge, such as piecewise smoothness, can help solve the reconstruction problem.

The cost function of the PL method is minimized under the constraints that each pixel contains at most three materials, the volume fractions of basis materials sum to one, and the fractions are in the box [0, 1]. It is difficult to minimize the PL cost function directly. The preliminary PL method [36] applied optimization transfer principles to develop a series of pixel- and material-wise separable quadratic surrogates to monotonically decrease the cost function. The separability both in the pixel and material made the curvatures of surrogate functions large, causing slow convergence. In this paper, we propose an optimization transfer method with pixel-wise separable quadratic surrogates (PWSQS) that keep the materials coupled. The coupling in materials results in faster convergence. The maintained separability in pixels makes the PWSQS algorithm simultaneous and constrained optimization on each pixel easy.

We evaluated the proposed PL method on a modified NCAT chest phantom [37] containing fat, blood, omnipaque300 (iodine-based contrast agent), cortical bone, and air. Comparing with the ID method, the PL method was able to reconstruct component images with lower noise, greatly reduced streak artifacts, and alleviated the cross-talk phenomenon where a component of one material appearing in the image of another material. The RMS errors of the PL method were about 60% lower for fat, blood, omnipaque300 and cortical bone, compared to the filtered ID method.

The organization of this paper is as follows. Section II introduces the physical models, including the measurement and object model. Section III describes the PL method. Section IV derives the PWSQS algorithm. Section V shows the results. Section VI presents conclusions.

II. Physical Models

A. Measurement Model

We use the following general model to describe the measurement physics for X-ray CT. The detector measures X-ray photons emerging from the object at M₀ ≥ 1 different incident spectra. Based on current technologies, different incident spectra can be realized by either scanning with different X-ray spectra, such as fast kVp-switching [16] or dual-source CT [18], or by energy-resolved photon-counting detectors [34]. Let Y_im denote the measurement for the ray ℒ_im which is the ith ray for the mth energy scan, where m = 1, …, M₀, i = 1, …, N_d, and N_d is the number of rays. For notational simplicity we assume that the same number of rays are measured for each incident spectrum, but the physics model and methods presented in this paper can be easily generalized to cases where different incident spectra have different number of recorded rays. For a ray ℒ_im of infinitesimal width, the mean of the projection measurements can be expressed as:

$${ȳ}_{im}\triangleq \int I_{im}(ℰ)\text{exp}(-{\int }_{{ℒ}_{im}}\mu (\overrightarrow{x},ℰ)\mathrm{d}\ell )\mathrm{d}ℰ+r_{im},$$ (1)

where μ(x⃗, ℰ) denotes the 3D unknown spatially- and energy-dependent attenuation distribution, ∫_ℒim · dℓ denotes the “line integral” function along line ℒ_im, and the incident X-ray intensity I_im(ℰ) incorporates the source spectrum and the detector gain. In reality, the measurements suffer from background signals such as Compton scatter, dark current and noise. The ensemble mean of those effects (for the ray ℒ_im) is denoted as r_im. We treat each I_im(ℰ) and r_im as known nonnegative quantities. In practice, I_im(ℰ) can be determined by careful calibration [38], and r_im are estimated by some preprocessing steps prior to iterative reconstruction [39]–[41].

B. Object Model for Basis Material Decomposition

We describe the object model for basis material decomposition as

$$\mu (\overrightarrow{x},ℰ)=\sum _{l=1}^{L_0}{\mu }_l(ℰ)\sum _{j=1}^{N_{\mathrm{p}}}{b}_j(\overrightarrow{x})x_{lj,}$$ (2)

where μ_l(ℰ) denotes the energy-dependent LAC of the lth material type, b_j(x⃗) denotes spatial basis functions (e.g., pixels), and x_lj denotes the volume fraction of the lth material in the jth pixel. Conventionally, one reconstructs L₀ = M₀ sets of basis materials from M₀ sets of measurements with M₀ different spectra [42].

Volume conservation [21], mass conservation [22] and combinations [1] have been used to provide extra information for solving L₀ = M₀ + 1 sets of unknowns from M₀ sets of independent measurements. Volume (mass) conservation assumes the sum of the volumes (masses) of the three constituent materials is equivalent to the volume (mass) of the mixture. Mendonca et al. [1] pointed out that any reasonable method for material decomposition already makes an implicit assumption of mass conservation. They used both volume and mass conservation to produce a model for the LAC of a mixture of materials. In this paper we adopt their model where the volume fractions x_lj should satisfy the following sum to one and box constraints:

$$\{\begin{array}{cc}{\sum }_{l=1}^{L_0}{x}_{lj}=1,\hfill & \forall j,\hfill \\ a_l\le x_{lj}\le b_l,\hfill & \forall l,j.\hfill \end{array}$$ (3)

We relax the lower limit of the box constraint to be slightly smaller than 0, and the upper limit to be slightly greater than 1, i.e., $a_l=-{\epsilon }_l^a$ where ${\epsilon }_l^a\ll 1/2$, and $b_l=1+{\epsilon }_l^b$ where ${\epsilon }_l^b\ll 1/2$. This relaxation is similar to the work in [43], where negative values are allowed for the reconstructed densities of basis materials, such as water and iodine. This is because the estimated volume fractions are just coefficients for combining the linear attenuation coefficients of basis materials to produce the equivalent attenuation of a mixture. The sum to one constraint in (3) provides an extra criteria for solving L₀ = M₀ + 1 sets of unknowns from M₀ sets of measurements.

Additional assumptions are needed to estimate L₀ > M₀ + 1 sets of unknowns from M₀ sets of measurements [1]. We assume that each pixel contains at most (M₀ + 1) types of materials and the material types can vary between pixels, i.e.

$$\sum _{l=1}^{L_0}{\mathrm{𝟙}}_{\{x_{lj}\ne 0\}}\le M_0+1,\forall j.$$ (4)

Let Ω be a (M₀ + 1)-tuple library containing all tuples formed from L₀ pre-selected materials of interest. Given a tuple ω in Ω, there are only (M₀ + 1) unknowns for each pixel, which are solvable from M₀ sets of measurements with the help of the box and sum-to-one constraints given in (3). Note that air must be included as one basis material type even if it is typically not of primary interest. This is because there are always locations with LACs of zeros in the field of view (FOV) of the scanner and only the LAC of air is zero.

C. Combining Measurement and Object Model

Let x denote the image vector x = (x₁, …, x_l, …, x_L0) ∈ ℝ^N_p×L₀ for x_l = (x_l1, …, x_lj, …, x_lNp) ∈ ℝ^N_p of the lth material. Combining the general measurement model (1) and the object model (2), the mean of the projection measurement ȳ_im(x) can be represented as follows,

$${ȳ}_{im}(\mathit{x})=z_{im}({\mathit{s}}_{im}(\mathit{x}))+r_{im},$$ (5)

for m = 1, …, M₀ and i = 1, …, N_d where

$$z_{im}({\mathit{s}}_{im}(\mathit{x}))\triangleq \int I_{im}(ℰ){\mathrm{e}}^{-\mathit{\mu }(ℰ)·{\mathit{s}}_{im}(\mathit{x})}\mathrm{d}ℰ.$$ (6)

The linear attenuation vector μ(ℰ) and the sinogram vector s_im(x) are defined as

$$\mathit{\mu }(ℰ)\triangleq ({\mu }_1(ℰ),\dots ,{\mu }_{L_0}(ℰ))$$ (7)

$${\mathit{s}}_{im}(\mathit{x})\triangleq (s_{im1}(\mathit{x}),\dots ,s_{im{L}_0}(\mathit{x}))$$ (8)

$$s_{iml}(\mathit{x})\triangleq {[{\mathit{A}}_m{\mathit{x}}_l]}_i=\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{x}_{lj},$$ (9)

where A_m denotes the N_d × N_p system matrix with entries

$$a_{mij}\triangleq {\int }_{{ℒ}_{im}}{b}_j(\overrightarrow{x})\mathrm{d}\ell .$$ (10)

As usual, we ignore the exponential edge gradient effects caused by the nonlinearity of Beer’s law [44], [45].

III. Penalized-Likelihood (PL) Reconstruction

For the case of normal clinical exposures, the X-ray CT measurements are often modeled as independently Poisson random variables with means (1), i.e.

$$Y_{im}~\text{Poisson}\{{ȳ}_{im}(\mathit{x})\}.$$

The corresponding negative log-likelihood for independent measurements Y_im has the form

$$\mathrm{L̄}(\mathit{x})\equiv \sum _{m=1}^{M_0}\sum _{i=1}^{N_{\mathrm{d}}}{t}_{im}({\mathit{s}}_{im}(\mathit{x})),$$ (11)

where ≡ means “equal to within irrelevant constants independent of x”, and

$$t_{im}({\mathit{s}}_{im})\triangleq {ȳ}_{im}({\mathit{s}}_{im})-Y_{im}{h}_{im}({\mathit{s}}_{im})$$ (12)

$$h_{im}({\mathit{s}}_{im})\triangleq \text{log}({ȳ}_{im}({\mathit{s}}_{im})).$$ (13)

We estimate component fraction images x from the noisy measurements Y_im by minimizing a Penalized-Likelihood (PL) cost function subject to constraints given in (3) and (4) on the elements of x as follows:

$$\mathit{x̂}=\underset{\mathit{x}\text{subject to}(3)\&(4)}{\text{arg min}}\mathrm{\Psi }(\mathit{x})$$ (14)

$$\mathrm{\Psi }(\mathit{x})\triangleq \mathrm{L̄}(\mathit{x})+R(\mathit{x}).$$ (15)

The edge-preserving regularization term R(x) is

$$R(\mathit{x})=\sum _{l=1}^{L_0}{\beta }_l{R}_l({\mathit{x}}_l),$$ (16)

where the regularizer for the lth material is

$$R_l({\mathit{x}}_l)=\sum _{j=1}^{N_{\mathrm{p}}}\sum _{k\in {𝒩}_{lj}}{\kappa }_{lj}{\kappa }_{lk}{\psi }_l(x_{lj}-x_{lk}),$$ (17)

where the potential function Ψ_l is a hyperbola

$${\psi }_l(t)=\frac{{\delta }_l^2}{3}(\sqrt{1+3{\left(\frac{t}{{\delta }_l}\right)}^2}-1),$$ (18)

and where κ_lj and κ_lk are parameters encouraging uniform spatial resolution [46] and 𝒩_lj is some neighborhood of voxel x_lj. The regularization parameters β_l and δ_l can be chosen differently for different materials according to their properties.

Since the LAC of air is zero there is no contribution of air component to the data fitting term L̄(x) in (11), but the regularizer term R(x) in (16) should include the air component because its image is piecewise smooth like other components. One could generalize the regularizer to consider joint sparsity of the component images [47], [48].

IV. Optimization Algorithm

Because the cost function Ψ(x) in (15) is difficult to minimize directly, we apply optimization transfer principles (OTP) [49]–[52] to develop an algorithm that monotonically decreases Ψ(x) each iteration. We find a pixel-wise separable quadratic surrogate (PWSQS) ϕ⁽ⁿ⁾ (x) of the cost function, and then minimize ϕ⁽ⁿ⁾ (x) under constraints given in (3) and (4) on each pixel. We loop over all tuples in the pre-determined material library Ω, minimize the surrogates under box and sum-to-one constraints in (3), and determine the optimal tuple for each pixel as the one minimizing the surrogate of that pixel.

A. Optimization Transfer Principles

The optimization transfer method [49], [50] replaces the cost function Ψ(x) that is difficult to minimize with a surrogate function ϕ⁽ⁿ⁾ (x) that is easier to minimize at the nth iteration. The next estimate x⁽ⁿ⁺¹⁾ is the minimizer of the surrogate function, i.e.,

$${\mathit{x}}^{(n+1)}\triangleq \underset{\mathit{x}}{\text{arg min}}{\varphi }^{(n)}(\mathit{x}).$$ (19)

Repeatedly choosing a surrogate function and minimizing it at each iteration, one obtains a sequence of vectors {x⁽ⁿ⁾} that monotonically decrease the original cost function Ψ(x). The monotonicity is guaranteed by the following surrogate conditions:

$$\begin{array}{cc}\hfill {\varphi }^{(n)}\left({\mathit{x}}^{(n)}\right)& =\mathrm{\Psi }\left({\mathit{x}}^{(n)}\right),\hfill \\ \hfill {\varphi }^{(n)}(\mathit{x})& \ge \mathrm{\Psi }(\mathit{x}),\forall \mathit{x}\in {ℝ}^{N_{\mathrm{p}}\times L_0}.\hfill \end{array}$$ (20)

To derive surrogate functions for Ψ(x) in (15), we consider the data fidelity term (11) and regularizer term (16) separately.

B. Surrogate of the Data Fidelity Term

1. First Surrogate: Non-Separable Convex Surrogate: The first step is to derive a convex surrogate as a function of the sinogram vector s_im. Since h_im(s_im) is convex (See Appendix A-A), it is bounded below by its tangent plane:

   $$h_{im}({\mathit{s}}_{im})\ge h_{im}({\mathit{s}}_{im}^{(n)})+{\nabla ̵}_{{\mathit{s}}_{im}}{h}_{im}({\mathit{s}}_{im}^{(n)})(s_{im}-{\mathit{s}}_{im}^{(n)}),$$ (21)

   where ${\mathit{s}}_{im}^{(n)}\triangleq {\mathit{s}}_{im}({\mathit{x}}^{(n)})$. This inequality and the nonnegativity of Poisson random variable Y_im lead to our first surrogate for the data fidelity term L̄(x):

   $$\mathrm{L̄}(\mathit{x})\le L_1^{(n)}(\mathit{x})\triangleq \sum _{m=1}^{M_0}\sum _{i=1}^{N_{\mathrm{d}}}{f}_{1,im}^{(n)}({\mathit{s}}_{im}(\mathit{x})),$$ (22)

   where

   $$f_{1,im}^{(n)}({\mathit{s}}_{im})\triangleq {ȳ}_{im}({\mathit{s}}_{im})-Y_{im}(h_{im}({\mathit{s}}_{im}^{(n)})+{\nabla ̵}_{{\mathit{s}}_{im}}{h}_{im}({\mathit{s}}_{im}^{(n)})({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)})).$$ (23)

   If the source is monoenergetic and if r_im = 0, then h_im is linear and the first surrogate $L_1^{(n)}(\mathit{x})$ exactly equals the original negative log-likelihood data fidelity term L̄(x), so it should be a “reasonably tight” surrogate function.

2. Second Surrogate: Non-Separable Quadratic Surrogate: The second step is to find a quadratic surrogate of the first convex surrogate given in (22) and (23). We rewrite $f_{1,im}^{(n)}({\mathit{s}}_{im})$ as follows,

   $$f_{1,im}^{(n)}({\mathit{s}}_{im})={ȳ}_{im}({\mathit{s}}_{im})-Y_{im}{\nabla ̵}_{{\mathit{s}}_{im}}{h}_{im}({\mathit{s}}_{im}^{(n)}){\mathit{s}}_{im}+C={ȳ}_{im}({\mathit{s}}_{im})-\frac{Y_{im}}{{ȳ}_{im}({\mathit{s}}_{im}^{(n)})}{\nabla ̵}_{{\mathit{s}}_{im}}{ȳ}_{im}({\mathit{s}}_{im}^{(n)}){\mathit{s}}_{im}+C=C+\int I_{im}(ℰ){\mathrm{e}}^{-\mathit{\mu }(ℰ)·{\mathit{s}}_{im}}\mathrm{d}ℰ+\int Y_{im}^{(n)}{I}_{im}(ℰ){\mathrm{e}}^{-\mathit{\mu }(ℰ)·{\mathit{s}}_{im}^{(n)}}\mathit{\mu }(ℰ)·{\mathit{s}}_{im}\mathrm{d}ℰ=\int I_{im}(ℰ)f(\mathit{\mu }(ℰ)·{\mathit{s}}_{im};Y_{im}^{(n)}{\mathrm{e}}^{-\mathit{\mu }(ℰ)·{\mathit{s}}_{im}^{(n)}})\mathrm{d}ℰ+C,$$ (24)

   where $Y_{im}^{(n)}\triangleq \frac{Y_{im}}{{ȳ}_{im}({\mathit{s}}_{im}^{(n)})}$, and

   $$f(x;\alpha )\triangleq {\mathrm{e}}^{-x}+\alpha x,$$ (25)

   and C denotes the constants in (23) that are irrelevant to s_im.
   Let c̆(·; α) given in (55) denote the optimal curvature for f(x; α) given in [52, Eqn. (28)]. We form the optimal quadratic surrogate of f(x; α) using c̆(·; α), and substitute it into (24) to obtain a quadratic surrogate of $f_{1,im}^{(n)}({\mathit{s}}_{im})$ as follows (See Appendix A-B),

   $$f_{2,im}^{(n)}({\mathit{s}}_{im})=f_{1,im}^{(n)}({\mathit{s}}_{im}^{(n)})+{\nabla ̵}_{{\mathit{s}}_{im}}{f}_{1,im}^{(n)}({\mathit{s}}_{im}^{(n)})({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)})+\frac{1}{2}({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)})\prime {\mathit{C̆}}_{im}^{(n)}({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)}),$$ (26)

   where the L₀ × L₀ curvature matrices are given by

   $${\mathit{C̆}}_{im}^{(n)}\triangleq \int I_{im}(ℰ){\mathrm{c̆}}_{im}^{(n)}(ℰ)\mathit{\mu }(ℰ)\mathit{\mu }\prime (ℰ)\mathrm{d}ℰ,$$ (27)

   $${\mathrm{c̆}}_{im}^{(n)}(ℰ)\triangleq \mathrm{c̆}(\mathit{\mu }(ℰ)·{\mathit{s}}_{im}^{(n)};Y_{im}^{(n)}{\mathrm{e}}^{-\mathit{\mu }(ℰ)·{\mathit{s}}_{im}^{(n)}}).$$ (28)
   Summing this quadratic surrogate leads to the following non-separable quadratic surrogate for the first convex surrogate $L_1^{(n)}(\mathit{x})$:

   $$L_1^{(n)}(\mathit{x})\le L_2^{(n)}(\mathit{x})\triangleq \sum _{m=1}^{M_0}\sum _{i=1}^{N_{\mathrm{d}}}{f}_{2,im}^{(n)}({\mathit{s}}_{im}(\mathit{x})),$$ (29)

   where $f_{2,im}^{(n)}({\mathit{s}}_{im}(\mathit{x}))$ is given in (26).

3. Third Surrogate: Pixel-Wise Separable Quadratic Surrogate: Define pixel vector as x_j ≜ (x_1j, …, x_L0j). The surrogate function $L_2^{(n)}(\mathit{x})$ is a non-separable quadratic function of x_j. Non-separable surrogates are inconvenient for simultaneous update algorithms and for enforcing the constraint in (3) and (4) on each pixel. To derive a simple simultaneous update algorithm that is fully parallelizable and suitable for ordered-subsets implementation [53], [54], we find next a pixel-wise separable quadratic surrogate $L_3^{(n)}(\mathit{x})$ of the non-separable quadratic surrogate $L_3^{(n)}(\mathit{x})$ by applying De Pierro’s additive convexity trick [50], [53]. This novel pixel-wise separable quadratic surrogate remains non-separable with respect to the basis materials.

   Appendix A-C derives $L_3^{(n)}(\mathit{x})$ in detail. It is defined as

   $$L_2^{(n)}(\mathit{x})\le L_3^{(n)}(\mathit{x})\triangleq \sum _{j=1}^{N_{\mathrm{p}}}{f}_{3,j}^{(n)}({\mathit{x}}_j),$$ (30)

   where

   $$f_{3,j}^{(n)}({\mathit{x}}_j)\triangleq \sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{\pi }_{mij}{f}_{2,im}^{(n)}(b_{mij}({\mathit{x}}_j))$$ (31)

   $$b_{mij}({\mathit{x}}_j)\triangleq \frac{a_{mij}}{{\pi }_{mij}}({\mathit{x}}_j-{\mathit{x}}_j^{(n)})+\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j^{(n)}.$$ (32)

   The π_mij values are non-negative and are zero only when a_mij is zero, and satisfy ${\sum }_{j=1}^{N_{\mathrm{p}}}{\pi }_{mij}=1$. For our empirical results, we use the following typical choice for π_mij [53],

   $${\pi }_{mij}\triangleq \frac{|a_{mij}|}{a_{mi}},a_{mi}\triangleq \sum _{j=1}^{N_{\mathrm{p}}}|a_{mij}|.$$ (33)
4. Pixel-Wise Separable Quadratic Surrogate in Matrix-Vector Formation: We have designed three surrogate functions sequentially having relationships

   $$\mathrm{L̄}(\mathit{x})\le L_1^{(n)}(\mathit{x})\le L_2^{(n)}(\mathit{x})\le L_3^{(n)}(\mathit{x}).$$ (34)

   Therefore, $L_3^{(n)}(\mathit{x})$ is a surrogate function of L̄(x). It is much easier to minimize the the surrogate $L_3^{(n)}$ under the proposed constraints since it is quadratic and separable with respect to pixels.

Combining the function value (60), gradient (61) and Hessian (62) derived in Appendix A-C, the pixel-wise separable quadratic surrogate has the following matrix-vector form

$$L_3^{(n)}(\mathit{x})=\mathrm{L̄}({\mathit{x}}^{(n)})+\nabla ̵\mathrm{L̄}({\mathit{x}}^{(n)})(\mathit{x}-{\mathit{x}}^{(n)})+\frac{1}{2}(\mathit{x}-{\mathit{x}}^{(n)})\prime {\mathit{D}}_{\mathrm{L̄}}^{(n)}(\mathit{x}-{\mathit{x}}^{(n)}),$$ (35)

where ${\mathit{D}}_{\mathrm{L̄}}^{(n)}$ is a block diagonal matrix over j = 1, …, N_p, i.e.,

$${\mathit{D}}_{\mathrm{L̄}}^{(n)}\triangleq \text{diag}\left\{{\mathit{D}}_{\mathrm{L̄},j}^{(n)}\right\},$$ (36)

$${\mathit{D}}_{\mathrm{L̄},j}^{(n)}\triangleq \sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}\frac{a_{mij}^2}{{\pi }_{mij}}{\mathit{C̆}}_{im}^{(n)},$$ (37)

and ${\mathit{C̆}}_{im}^{(n)}(ℰ)$ is defined in (27). The L₀ × L₀ matrix ${\mathit{D}}_{\mathrm{L̄},j}^{(n)}$ is not diagonal due to the outer products in (27).

C. Surrogate of the Penalty Term

To derive a SQS function for the penalty term, we apply De Pierro’s additive convexity trick [50], [53], [55] in a similar fashion and use Huber’s optimal curvature [56, p. 185] for the potential function Ψ_l. The SQS function has the following matix-vector form

$$R^{(n)}(\mathit{x})=R({\mathit{x}}^{(n)})+\nabla ̵R({\mathit{x}}^{(n)})(\mathit{x}-{\mathit{x}}^{(n)})+\frac{1}{2}(\mathit{x}-{\mathit{x}}^{(n)})\prime {\mathit{D}}_R^{(n)}(\mathit{x}-{\mathit{x}}^{(n)}),$$ (38)

where ${\mathit{D}}_R^{(n)}$ is a diagonal matrix, i.e.,

$${\mathit{D}}_R^{(n)}\triangleq \mathtt{\text{diag}}\{{\mathit{D}}_{R,j}^{(n)}\},$$ (39)

$${\mathit{D}}_{R,j}^{(n)}\triangleq \mathtt{\text{diag}}\left\{4{\beta }_l\sum _{k\in {𝒩}_{lj}}{\kappa }_{lj}{\kappa }_{lk}{\omega }_{{\psi }_l}\right(x_{lj}^{(n)}-x_{lk}^{(n)}\left)\right\},$$ (40)

where ω_Ψ(t) ≜ Ψ̇(t) /t.

D. Pixel-Wise Separable Quadratic Surrogate (PWSQS)

Combining the surrogates for the data fidelity term (35) and penalty term (38), the PWSQS function for the cost function Ψ(x) is

$${\varphi }^{(n)}(\mathit{x})=L_3^{(n)}(\mathit{x})+R^{(n)}(\mathit{x}).$$ (41)

It is easier to minimize ϕ⁽ⁿ⁾ (x) than the original cost function Ψ(x) because it is quadratic and separable with respect to pixels by construction. For the sake of optimization under constraints on each pixel, we rewrite ϕ⁽ⁿ⁾ (x) in terms of j as

$${\varphi }^{(n)}(\mathit{x})\equiv \sum _{j=1}^{N_{\mathrm{p}}}{\varphi }_j^{(n)}({\mathit{x}}_j),$$ (42)

where

$${\varphi }_j^{(n)}({\mathit{x}}_j)\equiv {\nabla ̵}_{{\mathit{x}}_j}\mathrm{\Psi }\left({\mathit{x}}^{(n)}\right){\mathit{x}}_j+\frac{1}{2}{\Vert {\mathit{x}}_j-{\mathit{x}}_j^{(n)}\Vert }_{{\mathit{D}}_j^{(n)}}^2,$$ (43)

where ∇̵_xj denotes the gradient with respect to x_j, and the L₀ × L₀ Hessian matrix of ${\varphi }_j^{(n)}$ is

$${\mathit{D}}_j^{(n)}\triangleq {\mathit{D}}_{\mathrm{L̄},j}^{(n)}+{\mathit{D}}_{R,j}^{(n)}.$$ (44)

E. Optimization With Material Constraints

After designing the surrogate (42), the next step of the optimization transfer algorithm is to minimize ϕ⁽ⁿ⁾ (x) under constraints given in (3) and (4) on each pixel. Because ϕ⁽ⁿ⁾ (x) is pixel-wise separable, one can minimize ${\varphi }_j^{(n)}({\mathit{x}}_j)$ for all pixels simultaneously. We now focus on the problem of minimizing ${\varphi }_j^{(n)}({\mathit{x}}_j)$ under the proposed constraints.

Let ω denote a tuple in the material library Ω, i.e., ω ∈ Ω. The optimization problem on the jth pixel is

$$({\mathit{x̂}}_j,\mathrm{\omega ̂})=\underset{{\mathit{x}}_j,\omega \in \mathrm{\Omega }}{\text{arg min}}{\varphi }_j^{(n)}({\mathit{x}}_j)\mathrm{s}.\mathrm{t}.\{\begin{array}{cc}{\sum }_{l=1}^{L_0}{x}_{lj}=1,\hfill & \hfill \\ a_l\le x_{lj}\le b_l,\hfill & l\in \omega ,\hfill \\ x_{lj}=0,\hfill & l\notin \omega ,\hfill \end{array}$$ (45)

where

$${\varphi }_j^{(n)}({\mathit{x}}_j)\triangleq \frac{1}{2}{\mathit{x}}_j^{\prime }\mathit{H}{\mathit{x}}_j+\mathit{p}\prime {\mathit{x}}_j,$$ (46)

$$\mathit{H}\triangleq {\mathit{D}}_j^{(n)},$$ (47)

$$\mathit{p}\triangleq {\nabla ̵}_{{\mathit{x}}_j}\mathrm{\Psi }\left({\mathit{x}}^{(n)}\right)-({\mathit{x}}_j^{(n)})\prime {\mathit{D}}_j^{(n)}.$$ (48)

The goal of this optimization is to estimate x_j and material types ω. We solve it as follows.

1. For each ω ∈ Ω, find the optimal x̂_j(ω) and the corresponding function values ${\varphi }_j^{(n)}({\mathit{x̂}}_j(\omega ))$. Without loss of generality, we consider the case where a given ω = (1, …, L) for some L between 1 and L₀, then the optimization problem is

   $${\mathit{x̂}}_j(\omega )=\underset{{\mathit{x}}_j(\omega )}{\text{arg min}}{\varphi }_j^{(n)}({\mathit{x}}_j(\omega )){\varphi }_j^{(n)}({\mathit{x}}_j(\omega ))\equiv \frac{1}{2}{\mathit{x}}_j^{\prime }(\omega )\mathit{H}(\omega ){\mathit{x}}_j(\omega )+\mathit{p}\prime (\omega ){\mathit{x}}_j(\omega )\mathrm{s}.\mathrm{t}.\{\begin{array}{c}{\sum }_{l=1}^L{x}_{lj}=1,\hfill \\ a_l\le x_{lj}\le b_l,\hfill \end{array}$$ (49)

   where ${\mathit{x}}_j(\omega )\triangleq (x_{1j},\dots ,x_{Lj}),{\mathit{x}}_j^{(n)}(\omega )\triangleq (x_{1j}^{(n)},\dots ,x_{Lj}^{(n)})$, and H(ω) and p(ω) are formed from elements in H and p with indexes corresponding to ω = (1, …, L) respectively.
2. Determine the best tuple ω̂ by comparing all ${\varphi }_j^{(n)}(\mathit{x̂}(\omega ))$, i.e.,

   $$\mathrm{\omega ̂}=\underset{\omega \in \mathrm{\Omega }}{\text{arg min}}{\varphi }_j^{(n)}({\mathit{x̂}}_j(\omega )).$$

3. Obtain x̂_j ≡ x̂_j(ω̂) with padded zeros for l ∉ ω.

Given material types, i.e., given ω, the optimization problem defined in (49) is a typical convex quadratic programming problem. We used the Generalized Sequential Minimization Algorithm (GSMO) [57] to solve (49), and parallelized GSMO to update all pixels simultaneously. The pseudo-code of GSMO for solving the quadratic optimization problem with constraints in (49) is summarized in the supplementary material. One can use other quadratic programming methods to solve (49).

F. Ordered-Subset PWSQS Algorithm Outline

We use the ordered subsets approach to accelerate the “convergence” to a good local minimum [52] by replacing the gradient in (43) with a subset gradient scaled by the total number of subsets.

The overall ordered-subset pixel-wise separable quadratic surrogate (OS-PWSQS) algorithm for minimizing the PL cost function with constraints given in (14) is outlined in Table I.

TABLE I.

Ordered-subset pixel-wise separable quadratic surrogate (OS-PWSQS) algorithm outline.

1) Choose πmij factors using (33).

2) Initialize x(0) using the results of the image-domain method [1].

3) For each iteration d = 1, …, Diter

a) For each subset (subiteration) q = 1, …, Qiter

i) n = d + q/Qiter

ii) Compute gradient of the data fidelity term L̇qj.

$${\mathrm{L̇}}_{qj}=\sum _{i\in {𝒮}_q}\sum _{m=1}^{M_0}{a}_{mij}{\nabla ̵}_{{\mathit{s}}_{im}}{t}_{im}({\mathit{s}}_{im}^{(n)}),{\nabla ̵}_{{\mathit{s}}_{im}}{t}_{im}({\mathit{s}}_{im}^{(n)})={\nabla ̵}_{{\mathit{s}}_{im}}{ȳ}_{im}({\mathit{s}}_{im}^{(n)})-Y_{im}{\nabla ̵}_{{\mathit{s}}_{im}}{h}_{im}({\mathit{s}}_{im}^{(n)}),$$

where ∇̵simȳim and ∇̵sim him are given in (50) and (52) respectively, and

$${\mathit{s}}_{im}^{(n)}=(s_{im1}({\mathit{x}}^{(n)}),\dots ,s_{im{L}_0}({\mathit{x}}^{(n)})),s_{iml}({\mathit{x}}^{(n)})=\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_l^{(n)},l=1,\dots ,L_0.$$

iii) Compute gradient of penalty term Ṙqj.

$${Ṙ}_{qj}=\frac{1}{Q}\left({\beta }_1\frac{\partial }{\partial x_{1j}}{R}_1({\mathit{x}}_1){|}_{{\mathit{x}}_1={\mathit{x}}_1^{(n)}},\dots ,{\beta }_{L_0}\frac{\partial }{\partial x_{L_{0}j}}{R}_L({\mathit{x}}_{L_0}){|}_{{\mathit{x}}_{L_0}={\mathit{x}}_{L_0}^{(n)}}\right)$$

$$\frac{\partial }{\partial x_{lj}}{R}_l({\mathit{x}}_l){|}_{{\mathit{x}}_l={\mathit{x}}_l^{(n)}}=\sum _{k\in {𝒩}_{lj}}{\kappa }_{lj}{\kappa }_{lk}{\mathrm{\psi ̇}}_l(x_{lj}^{(n)}-x_{lk}^{(n)}),l=1,\dots ,L_0$$

iv) Compute L0 × L0 curvature matrices ${\mathit{D}}_{qj}^{(n)}$.

$${\mathit{D}}_{qj}^{(n)}={\mathit{D}}_{\mathrm{L̄},qj}^{(n)}+\frac{1}{Q}{\mathit{D}}_{R,j}^{(n)},{\mathit{D}}_{\mathrm{L̄},qj}^{(n)}=\sum _{i\in {𝒮}_q}\sum _{m=1}^{M_0}\frac{a_{mij}^2}{{\pi }_{mij}}{\mathit{C̆}}_{im}^{(n)},$$

where ${\mathit{C̆}}_{im}^{(n)}$ and ${\mathit{D}}_{R,j}^{(n)}$ are defined in (27) and (40) respectively.

v) Compute H and p using (47) and (48), i.e.,

$$\mathit{H}={\mathit{D}}_{qj}^{(n)},\mathit{p}={\mathrm{L̇}}_{qj}+{Ṙ}_{qj}-({\mathit{x}}_j^{(n)})\prime {\mathit{D}}_{qj}^{(n)}.$$

vi) For each tuple ω ∈ Ω

A) Form ${\mathit{x}}_j^{(n)}(\omega )$, H(ω), p(ω) by extracting elements in ${\mathit{x}}_j^{(n)}$, H and p with indexes corresponding to ω respectively.

B) Obtain minimizer x̂j(ω) of the QP problem in (49) using GSMO.

C) Compute and store minimal surrogate function value ${\varphi }_j^{(n)}({\mathit{x̂}}_j(\omega ))$ using (49).

End

vii) Determine optimal ω̂ by comparing all ${\varphi }_j^{(n)}({\mathit{x̂}}_j(\omega ))$, i.e.,

$$\mathrm{\omega ̂}=\underset{\omega \in \mathrm{\Omega }}{\text{arg min}}{\varphi }_j^{(n)}({\mathit{x̂}}_j(\omega )).$$

viii) Obtain x̂j ≡ x̂j(ω̂) with padded zeros for l ∉ ω.

ix) Update all pixels x(n+1/Qiter) = x̂ = (x̂1, …, x̂j, …, x̂Np).

End

x(n+1) = x(n+Qiter/Qiter).

End

V. Results

To evaluate the proposed PL method for MMD and to compare it with the ID method [1], we simulated a DECT scan and reconstructed volume fractions of a modified NCAT chest phantom [37] containing fat, blood, omnipaque300 (iodine-based contrast agent), cortical bone and air. We generated virtual un-enhancement (VUE) images from the reconstructed volume fractions using these two methods.

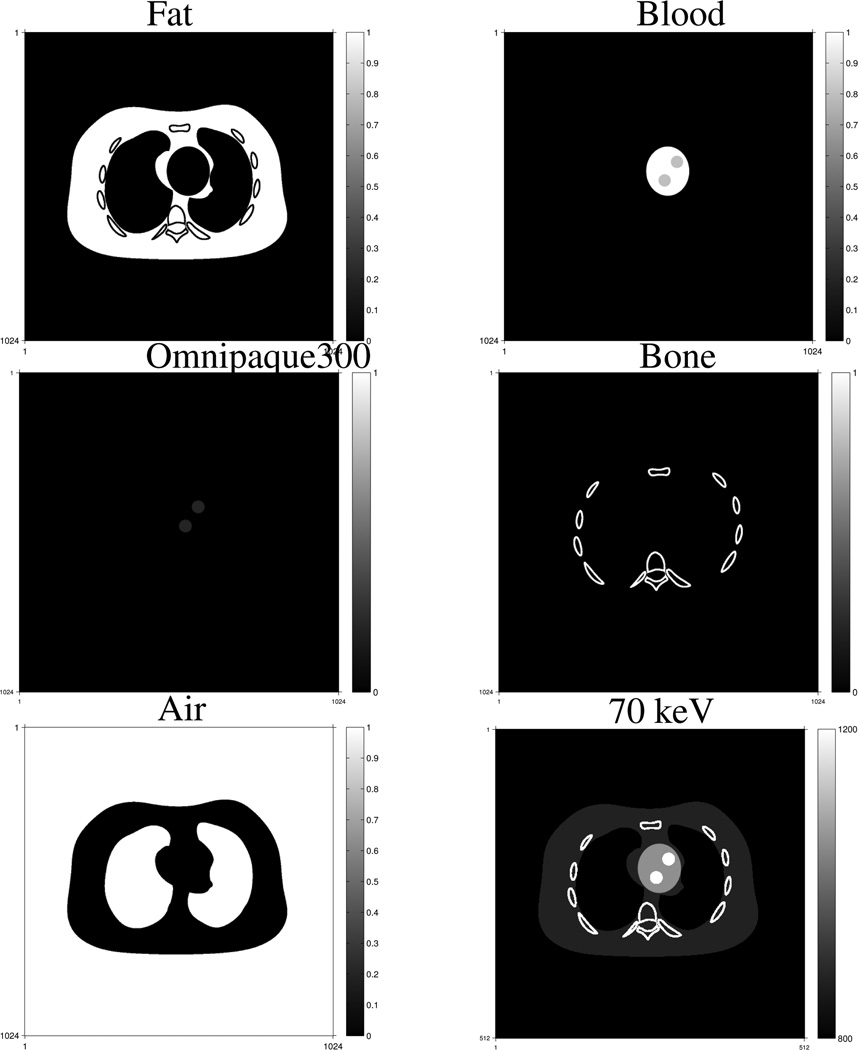
Fig. 1 shows true volume fractions and monoenergetic image at 70 keV of the simulated NCAT chest phantom. The simulated true images were 1024 × 1024 and the pixel size was 0.49 mm, while the reconstructed images were 512 × 512 and the pixel size was 0.98 mm. We introduced this model mismatch deliberately to test the MMD methods. We down-sampled the simulated true component images to the sizes of the reconstructed images by linearly averaging, and used these down-sampled images for comparisons with the reconstructed images.

Fig. 1.

True volume fractions and the monoenergetic image at 70 keV of the NCAT chest phantom. The volume fractions are in the range of [0, 1] and the monoenergetic image is displayed over [800, 1200] with the shifted Hounsfield unit (HU) scale where air is 0 HU and water is 1000 HU.

We simulated the geometry of a GE LightSpeed X-ray CT fan-beam system with an arc detector of 888 detector channels by 984 views over 360°. The size of each detector cell was 1.0239 mm. The source to detector distance was D_sd = 949.075mm, and the source to rotation center distance was D_s0 = 541mm. We included a quarter detector offset to reduce aliasing. We used the distance-driven (DD) projector [58] to generate projections of the true object. We simulated two incident spectra of X-ray tube voltages at 140 kVp and 80 kVp, and normalized them by their corresponding total intensities by summing the intensities over all energy bins. We generated noiseless measurements ȳ_im of the simulated NCAT phantom using (1) and the normalized spectra. To add Poisson distributed noise to the noiseless measurements ȳ_im, we first chose 2 × 10⁵ incident photons per ray for the 140 kVp measurements, and then determined the value of incident photons per ray for the 80 kVp measurements according to the ratio of total intensities of the originally simulated spectra at high and low energies. The incident photons per ray for the 80 kVp measurements was 2 × 10⁵ · I_i2/I_i1 = 6 × 10⁴ where I_i1 and I_i2 denote the total intensity of the ith ray for the 140 kVp and 80 kVp spectrum respectively.

For this simulation we let the triplet material library Ω contain five triplets selected from five materials: fat, blood, omnipaque300, cortical bone and air, excluding the combination of omnipaque300 and cortical bone and the combination of omnipaque300 and fat. (This material library is based on the fact that contrast agent does not spread into the cortical bone area and fat area.) We implemented the ID method with several different priority lists of material triplets as described in [1]. We found that the performance of the ID method depends on the priorities of material triplets in the list. We selected the priority list that produces the best ID image quality in terms of noise, artifacts and crosstalk of component images. To initialize the PL iteration, we applied a 3 × 3 median filter to the ID images to decrease noise, especially salt-and-pepper noise due to crosstalk among component images. (See Fig. 1 in the supplementary material for the ID images.) A priority list is not used in the PL method as it determines the optimal triplet as the one that minimizes the PWSQS function in (46) for each pixel.

We used the conventional projection-domain dual-material decomposition method with polynomial approximation [4] followed by FBP to reconstruct water-iodine density images and chose 70 keV and 140 keV to yield LAC pairs for the ID method. We also tried a more sophisticated dual-material decomposition method, the statistical sinogram restoration method proposed in [9], but the final reconstructed component images were very similar to those of using poly-nominal approximation. For the PL method we chose β_l = 2⁸, 2¹¹, 2¹¹, 2⁸, 2⁴ and δ_l = 0.01, 0.01, 0.005, 0.01, 0.1 for fat, blood, omnipaque300, cortical bone and air, respectively. We ran 500 iterations of the optimization transfer algorithm in Table I with 41 subsets to accelerate the convergence. Because (14) is a nonconvex problem, the algorithm finds a local minimum.

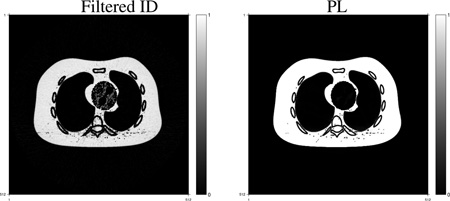
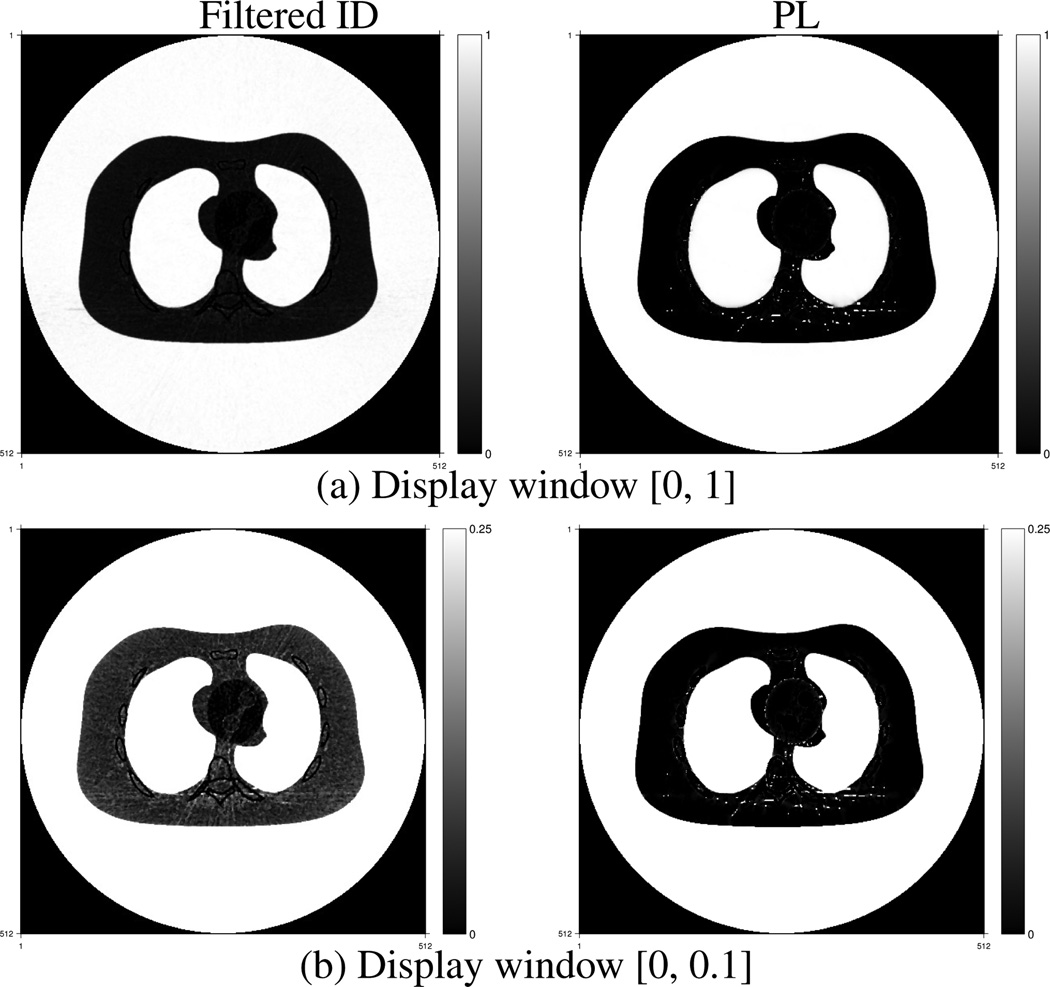
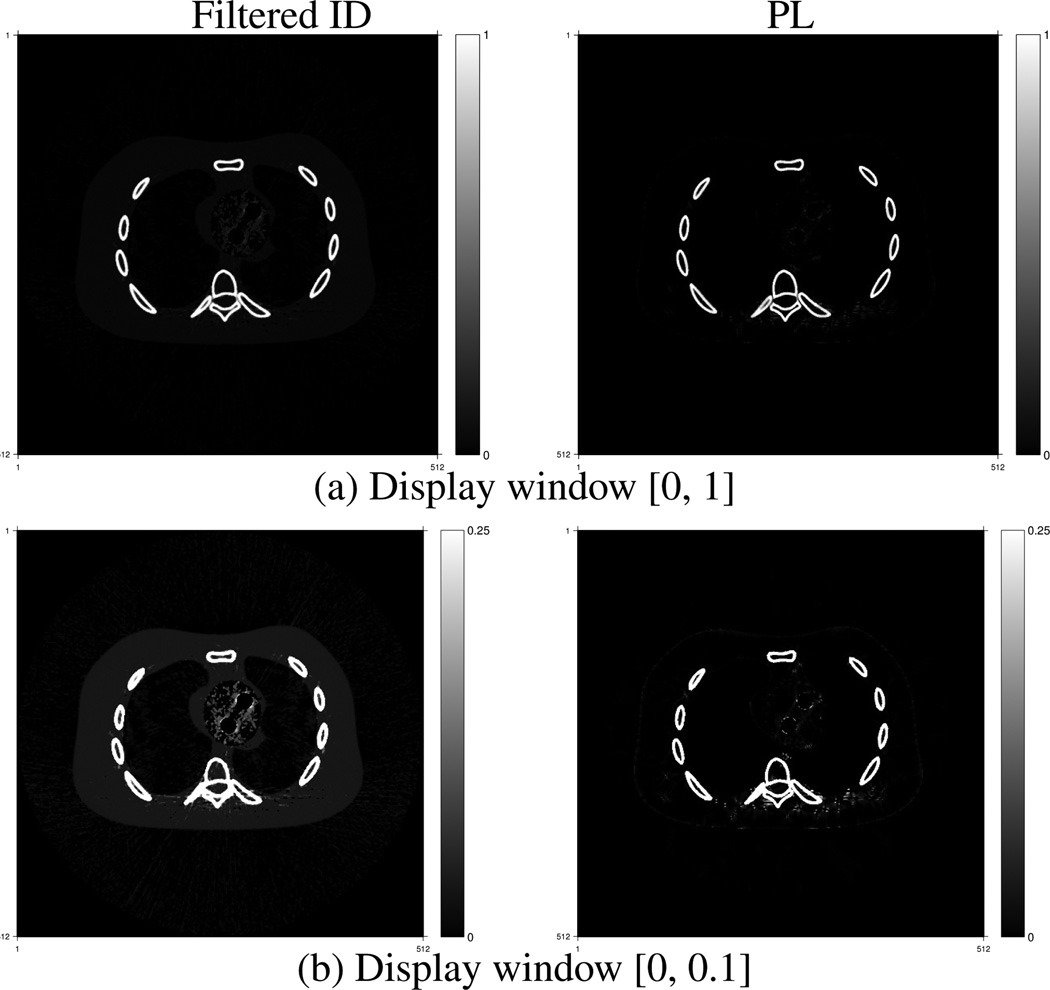
Fig. 2–Fig. 6 show estimated volume fractions of the five materials reconstructed by the PL method and the filtered ID method. The grayscale values represent volume fractions of each material. The big white disks in Fig. 6 are due to the circular reconstruction support. The streak-like artifacts in the reconstructed images by the filtered ID method are very similar to those in Figure 4 in [35] and Fig. 6 in [1]. The PL method greatly reduces these streak-like artifacts. Material cross talk is evident in the filtered ID results. Blood went into the fat image in Fig. 2, especially in the heart region. Cortical bone presented in the blood image in the upper left image in Fig. 3. Fat appeared in the cortical bone image, as evident in the lower left image in Fig. 5. The PL method alleviated this cross-talk phenomenon very effectively. In addition, the PL method reconstructed component images with lower noise.

Fig. 2.

Fat component fraction images reconstructed by the filtered ID method (left) and the PL method (right).

Fig. 6.

Air component fraction images reconstructed by the filtered ID method (left) and the PL method (right).

Fig. 4.

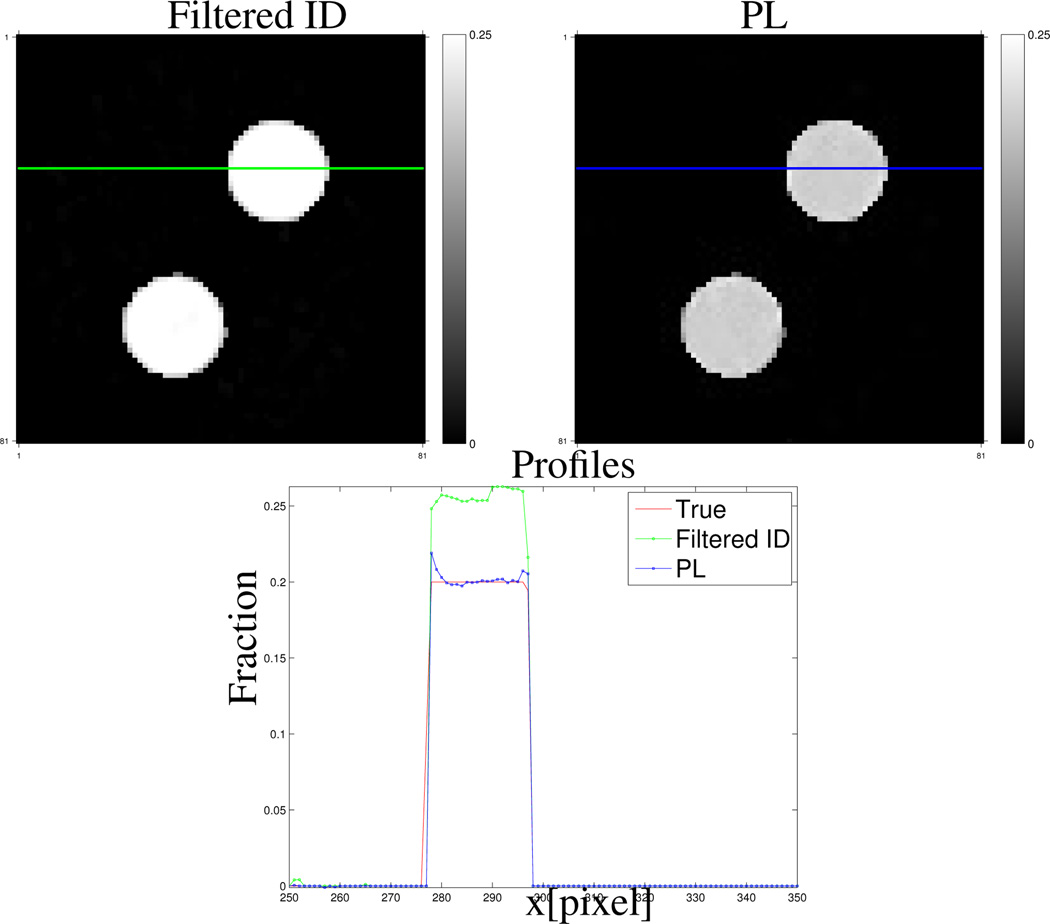
Zoomed-in omnipaque300 component fraction images reconstructed by the filtered ID method (upper left) and the PL method (upper right). The lower image shows the horizontal profiles.

Fig. 3.

Blood component fraction images reconstructed by the filtered ID method (left) and the PL method (right).

Fig. 5.

Cortical bone component fraction images reconstructed by the filtered ID method (left) and the PL method (right).

Fig. 4 shows the profiles of the down-sampled true and reconstructed omnipaque300 component images by the PL and filtered ID method respectively in the lower image. The locations of the profiles are indicated as a blue line and green line in the PL and filtered ID images. The PL method corrected the bias introduced by the filtered ID method. Profiles of reconstructed other component images are provided in the supplementary material.

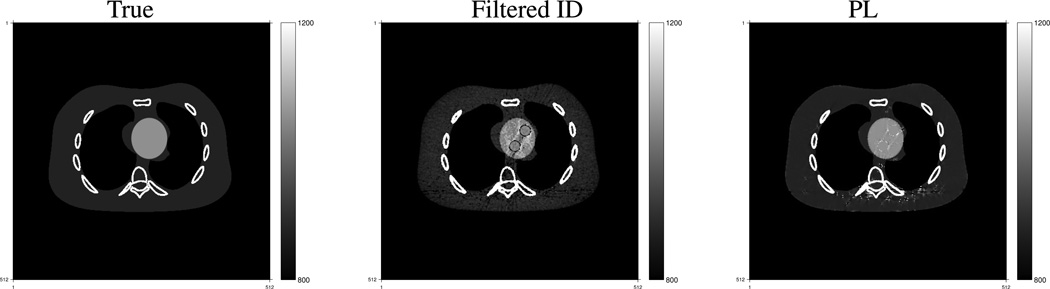
We constructed the virtual un-enhancement (VUE) images by replacing the volume of contrast agent (omnipaque300) in each pixel by the same amount of blood according to the method introduced in [1], [35]. Fig. 7 shows true and constructed VUE images at 70 keV using the component images reconstructed by the filtered ID and PL method. The images are displayed in a window of [800, 1200] with the shifted Hounsfield unit (HU) scale where air is 0 HU and water is 1000 HU. Having more accurate contrast agent and blood component images, the PL method produced a VUE image that is closer to the truth, while the VUE image using the filtered ID method has more obvious residuals of contrast agent. The PL method decreased beam-hardening artifacts in the monochromatic VUE image.

Fig. 7.

True and estimated virtual un-enhancement (VUE) images at 70 KeV. The display window is [800, 1200] HU where the HU scale is shifted by 1000 HU, i.e., air is 0 HU and water is 1000 HU.

We calculated the root-mean-square (RMS) errors of the component fractions $\sqrt{\frac{1}{N_{\mathrm{p}}}{\sum }_{j=1}^{N_{\mathrm{p}}}({\mathrm{x̂}}_{lj}-x_{lj})}$ within the reconstruct support for each material based on the down-sampled true images. Table II shows RMS errors of the component images reconstructed by the ID method, filtered ID method and the PL method. The errors of the component images were scaled by 10³ for easy comparison. Table II also shows the RMS errors of the VUE images using the ID, filtered ID and PL method. The median filtering greatly decreased the RMS errors of the ID images, especially for the fat and blood basis materials. Comparing with the filtered ID method, the PL method lowered the RMS errors by about 60% for fat, blood, omnipaque300 and cortical bone component images, 2% for air image, and 20% for the monochromatic VUE image at 70 keV.

TABLE II.

RMS error comparison of the reconstructed component fraction images by the ID method, filtered ID method and the PL method. The errors of component fraction images are unitless and enlarged by 10³. The errors of the VUE images are in HU unit.

Method	Fat	Blood	Omnipaque	Bone	Air	VUE
ID	156.3	134.7	4.0	38.1	49.5	54.6
Filtered ID	101.6	62.5	3.3	34.9	42.0	54.3
PL	51.3	19.4	1.4	16.6	41.2	43.6

VI. Conclusions

We proposed a statistical image reconstruction method for multi-material decomposition (MMD) using DECT measurements. We used a PL cost function containing a negative log-likelihood term and an edge-preserving regularization term for each basis material. We adopted the mass and volume conservation assumption and assumed each pixel contains at most three basis materials to help solve this ill-posed problem of estimating multiple sets of unknowns from two sets of sinograms. Comparing with the ID method [1], [35] that uses the same assumptions, the proposed PL method reconstructed component and monochromatic VUE images with reduced noise, streak artifacts and cross-talk. The PL method was able to lower the RMS error by about 60% for fat, blood, omnipaque300 and cortical bone basis material images, and 20% for the monochromatic VUE image at 70 keV, compared to the filtered ID method.

Due to the complexity and non-convexity of the PL cost function it is difficult to minimize the cost function directly. We previously introduced an optimization transfer method [36] with a series of material- and pixel-wise separable quadratic surrogate functions to monotonically decrease the PL cost function. The separability in both pixel and material caused the curvature of each surrogate function to be small. The smaller the curvature, the slower the convergence rate. The constraints on each pixel couple the estimates of material fractions, so even if we used a surrogate function that is separable across materials, the minimization step would not be separable due to the constraints. In this paper, we proposed a PWSQS optimization transfer method with separable quadratic surrogate functions that decouples pixels only. The PL cost function decreases faster with the PWSQS method (results not shown). However, iterative methods for MMD are computationally expensive. In each iteration, a MMD method requires one forward projection and one back-projection for each basis-material image, solving a constrained quadratic programming problem for each physically meaningful material tuple, and comparing results of all material tuples to determine the optimal tuple for each pixel. The simulations in this paper used 2D fan-beam data; to apply the PWSQS method to 3D data, more future work on accelerating the optimization process is needed. One potential accelerating method is combining OS-PWSQS with spatially non-uniform optimization transfer [59].

The PL cost function has two parameters, one regularizer coefficient β_l and one edge-preserving parameter δ_l for each material. We found that the choice of parameters for one material component influenced the reconstructed image of another component. An appropriate combination of parameters needs to be carefully determined for each application. Huh and Fessler [60] used a material-cross penalty for DECT reconstruction. This penalty used the prior knowledge that different component images have common edges; this idea could be used for MMD as well. Choosing regularizers for the PL method and optimizing the parameters needs further investigation.

Since the PL cost function is non-convex, good initialization is important. We used the results of the ID method followed by median filtering as the initialization of the PL method. The median filtering decreased noise and RMS errors of the ID images, but did not preserve the sum-to-one constraint that the ID images satisfied. Even with this initialization the PL method was able to converge to a good local minimum that is close to the truth. As future work we will investigate image-domain “statistical” reconstruction methods that are computationally more practical than the PL method. Such methods could also serve to initialize the PL method.

We used the contrast agent, omnipaque300, as a basis material in this paper. Alternatively one can use diluted contrast agent or iodine as basis materials. Future work would investigate the effects of using various basis materials. Future work also includes applying the PL method to real spectral CT data, e.g., from fast-kVp switching DE scans, dual-source scans, or dual-layer detectors, to decompose materials as needed by the application.

Appendix A

Surroagte Function Derivations

This section describes derivation details of the surrogate design in Section IV.

A. Convexity Proof

This section proves the convexity of h_im(s_im). The gradient of ȳ_im(s_im) with respect to s_im is

$${\mathrm{\nabla ⃓}}_{{\mathit{s}}_{im}}{ȳ}_{im}({\mathit{s}}_{im})=-\int I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}\mathit{\mu }(\epsilon )\mathrm{d}\epsilon ,$$ (50)

and the Hessian is

$${\nabla }_{{\mathit{s}}_{im}}^2{ȳ}_{im}({\mathit{s}}_{im})=\int I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}\mathit{\mu }(\epsilon )\mathit{\mu }\prime (\epsilon )\mathrm{d}\epsilon .$$ (51)

Since the Hessian matrix is positive-semidefinite, i.e. ${\nabla }_{{\mathit{s}}_{im}}^2{ȳ}_{im}({\mathit{s}}_{im})⪰\mathbf{0}$, the function ȳ_im(s_im) is convex.

The gradient of h_im(s_im) with respect to s_im is

$${\mathrm{\nabla ⃓}}_{{\mathit{s}}_{im}}{h}_{im}({\mathit{s}}_{im})=\frac{1}{{ȳ}_{im}({\mathit{s}}_{im})}{\mathrm{\nabla ⃓}}_{{\mathit{s}}_{im}}{ȳ}_{im}({\mathit{s}}_{im}).$$ (52)

The Hessian of h_im(s_im) is,

$${\nabla }_{{\mathit{s}}_{im}}^2{h}_{im}({\mathit{s}}_{im})=\frac{1}{{ȳ}_{im}({\mathit{s}}_{im})}\int I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}\mathit{\mu }(\epsilon )\mathit{\mu }\prime (\epsilon )\mathrm{d}\epsilon -\frac{1}{{ȳ}_{im}^2({\mathit{s}}_{im})}(\int I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )·(\int I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )\prime =\frac{z_{im}({\mathit{s}}_{im})}{{ȳ}_{im}({\mathit{s}}_{im})}\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathit{\mu }\prime (\epsilon )\mathrm{d}\epsilon -\frac{z_{im}^2({\mathit{s}}_{im})}{{ȳ}_{im}^2({\mathit{s}}_{im})}(\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )·(\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )\prime ⪰\frac{z_{im}^2({\mathit{s}}_{im})}{{ȳ}_{im}^2({\mathit{s}}_{im})}\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathit{\mu }\prime (\epsilon )\mathrm{d}\epsilon -\frac{z_{im}^2({\mathit{s}}_{im})}{{ȳ}_{im}^2({\mathit{s}}_{im})}(\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )·(\int q_{im}(\epsilon )\mathit{\mu }(\epsilon )\mathrm{d}\epsilon )\prime =\frac{z_{im}^2({\mathit{s}}_{im})}{{ȳ}_{im}^2({\mathit{s}}_{im})}\text{Cov}\{\mathit{\mu }(\epsilon )\}⪰\mathbf{0},$$ (53)

where we define the following “probability density function”

$$q_{im}(\epsilon )\triangleq \frac{I_{im}(\epsilon ){\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}(\mathit{x})}}{z_{im}({\mathit{s}}_{im})},$$ (54)

and used the fact that z_im(s_im) ≤ ȳ_im(s_im) for the first inequality. Since the Hessian matrix of h_im(s_im) is positive-semidefinite, h_im(s_im) is a convex function of s_im.

B. Derivation of Non-Separable Quadratic Surrogate

The section derives the non-separable quadratic surrogate in Section IV-B2 in details.

The optimal curvature c̆(·; α) for f(x; α) derived in [52] is

$$\mathrm{c̆}(x;\alpha )=\{\begin{array}{cc}{\left[2\frac{1-{\mathrm{e}}^{-x}-x{\mathrm{e}}^{-x}}{x^2}\right]}_{+},\hfill & x>0\hfill \\ 1,\hfill & x=0.\hfill \end{array}$$ (55)

Thus the optimal quadratic surrogate for f(x; α) is

$$q(x;x_0,\alpha )\triangleq f(x_0;\alpha )+ḟ(x_0;\alpha )(x-x_0)+\frac{1}{2}\mathrm{c̆}(x_0;\alpha ){(x-x_0)}^2,$$ (56)

where q(x; x₀, α) ≥ f(x; α).

Substituting (56) into (24) leads to a non-separable quadratic surrogate $f_{2,im}^{(n)}({\mathit{s}}_{im})$ of $f_{1,im}^{(n)}({\mathit{s}}_{im})$, i.e.,

$$f_{2,im}^{(n)}({\mathit{s}}_{im})\triangleq C+\int I_{im}(\epsilon )\left(f\right(\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}^{(n)};Y_{im}^{(n)}{\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}^{(n)}})+ḟ(\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}^{(n)};Y_{im}^{(n)}{\mathrm{e}}^{-\mathit{\mu }(\epsilon )·{\mathit{s}}_{im}^{(n)}})\mathit{\mu }(\epsilon )·({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)})+\frac{1}{2}{\mathrm{c̆}}_{im}^{(n)}(\epsilon ){(\mathit{\mu }(\epsilon )·({\mathit{s}}_{im}-{\mathit{s}}_{im}^{(n)}\left)\right)}^2)\mathrm{d}\epsilon ,$$ (57)

where ${\mathrm{c̆}}_{im}^{(n)}(ℰ)$ is defined in (28). Because $f_{2,im}^{(n)}({\mathit{s}}_{im})$ is a quadratic function of s_im, one can rewrite it as (26).

C. Derivation of Pixel-Wise Separable Quadratic Surrogate

This section derives the pixel-wise separable quadratic surrogate in Section IV-B3.

We rewrite the sinogram vector as

$${\mathit{s}}_{im}(\mathit{x})=\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j=\sum _{j=1}^{N_{\mathrm{p}}}{\pi }_{mij}(\frac{a_{mij}}{{\pi }_{mij}}({\mathit{x}}_j-{\mathit{x}}_j^{(n)})+\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j^{(n)}),$$ (58)

provided ${\sum }_{j=1}^{N_{\mathrm{p}}}{\pi }_{mij}=1$ and π_mij is zero only if a_mij is zero. If the π_mij’s are nonnegative, then we can apply the convexity inequality to the quadratic function $f_{2,im}^{(n)}({\mathit{s}}_{im}(\mathit{x}))$ defined in (26) to write

$$f_{2,im}^{(n)}({\mathit{s}}_{im}(\mathit{x}))=f_{2,im}^{(n)}\left(\sum _{j=1}^{N_{\mathrm{p}}}{\pi }_{mij}\right(\frac{a_{mij}}{{\pi }_{mij}}({\mathit{x}}_j-{\mathit{x}}_j^{(n)})+\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j^{(n)}\left)\right)\le \sum _{j=1}^{N_{\mathrm{p}}}{\pi }_{mij}{f}_{2,im}^{(n)}(b_{mij}({\mathit{x}}_j)),$$ (59)

where b_mij is defined in (32).

The value of $L_3^{(n)}$ evaluated at x⁽ⁿ⁾ is

$${L_3^{(n)}(\mathit{x})|}_{\mathit{x}={\mathit{x}}^{(n)}}=\sum _{j=1}^{N_{\mathrm{p}}}{f}_{3,j}^{(n)}\left({\mathit{x}}_j^{(n)}\right)=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{f}_{2,im}^{(n)}\left({\mathit{s}}_{im}\right({\mathit{x}}^{(n)}\left)\right)=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{t}_{im}\left({\mathit{s}}_{im}\right({\mathit{x}}^{(n)}\left)\right)=\mathrm{L̄}(\mathit{x}){|}_{\mathit{x}={\mathit{x}}^{(n)}}.$$ (60)

The column gradient of $L_3^{(n)}$ has elements x_lj

$${\frac{\partial }{\partial x_{lj}}{L}_3^{(n)}(\mathit{x})|}_{{\mathit{x}}_j={\mathit{x}}_j^{(n)}}={\frac{\partial }{\partial x_{lj}}{f}_{3,j}^{(n)}({\mathit{x}}_j)|}_{{\mathit{x}}_j={\mathit{x}}_j^{(n)}}=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{a}_{mij}{ḟ}_{2,im}^{(n)}\left(\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j^{(n)}\right)=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{a}_{mij}{ṫ}_{im}\left(\sum _{j=1}^{N_{\mathrm{p}}}{a}_{mij}{\mathit{x}}_j^{(n)}\right)={\frac{\partial }{\partial x_{lj}}\mathrm{L̄}(\mathit{x})|}_{{\mathit{x}}_j={\mathit{x}}_j^{(n)}}.$$ (61)

The “matched function value” and “matched derivative” properties are inherent to optimization transfer methods [51]. The Hessian ${\mathit{D}}_{\mathrm{L̄},j}^{(n)}\triangleq {\nabla }^2{f}_{3,j}^{(n)}(\mathit{x})$ has elements

$${\left[{\mathit{D}}_{\mathrm{L̄},j}^{(n)}\right]}_{lk}=\frac{{\partial }^2}{\partial x_{lj}\partial x_{kj}}{f}_{3,j}^{(n)}({\mathit{x}}_j)=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}{a}_{mij}\frac{{\partial }^2}{\partial x_{lj}\partial x_{kj}}{f}_{2,im}^{(n)}(b_{mij}({\mathit{x}}_j))=\sum _{i=1}^{N_{\mathrm{d}}}\sum _{m=1}^{M_0}\frac{a_{mij}^2}{{\pi }_{mij}}{\left[{\mathit{C̆}}_{im}^{(n)}\right]}_{lk},$$ (62)

where ${\mathit{C̆}}_{im}^{(n)}$ is defined in (28).