Abstract
Motivation: RNA folding is a complicated kinetic process. The minimum free energy structure provides only a static view of the most stable conformational state of the system. It is insufficient to give detailed insights into the dynamic behavior of RNAs. A sufficiently sophisticated analysis of the folding free energy landscape, however, can provide the relevant information.
Results: We introduce the Basin Hopping Graph (BHG) as a novel coarse-grained model of folding landscapes. Each vertex of the BHG is a local minimum, which represents the corresponding basin in the landscape. Its edges connect basins when the direct transitions between them are ‘energetically favorable’. Edge weights endcode the corresponding saddle heights and thus measure the difficulties of these favorable transitions. BHGs can be approximated accurately and efficiently for RNA molecules well beyond the length range accessible to enumerative algorithms.
Availability and implementation: The algorithms described here are implemented in C++ as standalone programs. Its source code and supplemental material can be freely downloaded from http://www.tbi.univie.ac.at/bhg.html.
Contact: qin@bioinf.uni-leipzig.de
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Much of RNA’s functional complexity is rooted not only in the details of its intricate 3D structure but also in its ability to adaptively acquire distinct conformations on its own or in response to specific cellular signals including the recognition of proteins, nucleic acids, metal ions, metabolites, vitamins, changes in temperature and even RNA biosynthesis itself. These conformational transitions are spatially and temporally tuned to achieve a variety of functions. The most obvious examples are riboswitches (Baumstark et al., 1997; Perrotta and Been, 1998; Schultes and Bartel, 2000) and RNA thermometers (Klinkert and Narberhaus, 2009; Narberhaus et al., 2006).
The intricate structures of RNAs are typically modeled to a reasonable approximation in terms of secondary structures (Thirumalai et al., 2001). This is because the thermal melting data (thermodynamic free energy model) of secondary structures have been interpreted by a nearest-neighbor model (Mathews et al., 1999, 2004) and form the basis for widely used structure prediction algorithms that predict secondary structure with reasonable accuracy (Hofacker, 2003; Zuker, 2003; Zuker and Sankoff, 1984). In particular, the partition function of the Boltzmann ensemble of secondary structures for a given RNA sequence can be computed in cubic time using a well-known dynamic programming approach (McCaskill, 1990). Thus, a stochastic backtracking algorithm (Ding and Lawrence, 2003) can be used to produce representative structures and to generate Boltzmann-weighted samples to assess complex structural features like base pair probabilities.
The inclusion of pseudoknots and other tertiary contacts into RNA structure prediction remains time-consuming and technically challenging (Das and Baker, 2007; Rivas and Eddy, 1999; Rother et al., 2011; Smit et al., 2009). In its most general form, the problem is NP-complete (Maňuch et al., 2011). Furthermore, free energy models for pseudoknots are based on sparse experimental data and hence are crude at best. Nevertheless, secondary structures with pseudoknots can be important for the dynamics of folding (Isambert and Siggia, 2000). Owing to the journal’s length restrictions, we focus on the Boltzmann ensemble of secondary structures in the main text and relegate the extension to structures with pseudoknots to Supplementary Material Part H. For brevity, we will speak of the ‘energy’ instead of ‘free energy’ of a secondary structure.
The kinetic process of RNA folding can be described as a dynamic process in the molecule’s energy landscape (Flamm et al., 2002). The energy landscape is a particular network whose vertices represent all the possible structures and whose edges connect structures that can be interconverted by elementary rearrangements, typically the opening or closing of individual base pairs. For each structure as a vertex in the landscape, its energy is evaluated based on the thermodynamic energy model (Mathews et al., 1999) for characterizing its dynamical state. Thus, the transition rates between adjacent secondary structures can be estimated by the Metropolis rule (Flamm et al., 2000; Xayaphoummine et al., 2007). In this setting, the RNA folding process is viewed as a Markov chain, and the transition rates between two adjacent structures in the landscape are related with their energy differences. Typically, different structural transitions are of different rates as observed by Smit et al. (2007), which is consistent with the thermodynamic picture: the equilibrium distribution of this Markov process coincides with the Boltzmann distribution of the secondary structures.
The number of different secondary structures, however, makes it impossible to enumerate the entire landscape except for short sequences, so that one has to resort to coarse-grained approximations. The barrier tree of the landscape, Figure 1B, encodes the local minima and their connecting energy barriers. The idea to elucidate the basin structure of a landscape by means of a barrier tree has been developed independently in different contexts, including potential energy surfaces for protein folding (Garstecki et al., 1999; Wales, 2011), spin glasses (Klotz and Kobe, 1994) and molecular clusters (Doye et al., 1999). The exact computation of barrier trees in general requires the enumeration of the landscape. For RNA secondary structures, a modification of the backtracking step in the dynamic programming folding algorithm can be used to enumerate only the lowest-lying fraction of the landscapes (Wuchty et al., 1999). However, even within this favorable setting, barrier trees are accessible only for RNA molecules with up to ∼100 nt.
Fig. 1.
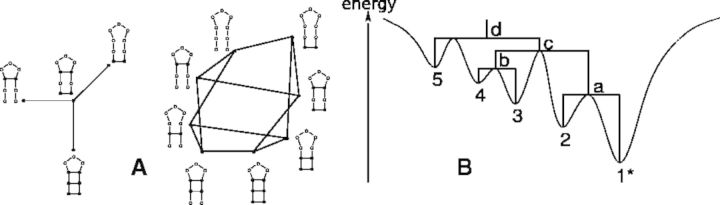
(A) Adjacency in an RNA folding landscape is encoded by insertion or deletion of a single base pair. The underlying graph of an RNA folding landscape is connected owing to the existence of the particular valid secondary structure that contains no base pair (open structure). (B) Schematics representation of an energy landscape and its associated barrier tree. Local minima are labeled with numbers (1–5), saddle points with lowercase letters (a–d). The global minimum is marked with an asterisk
An alternative to the exact construction of barrier trees is the use of heuristic approaches. For example, Tang et al. (2008) adopted computational techniques for motion planning in robotics to obtain an approximated representation of the RNA folding landscape. A different type of coarse graining can be obtained by conditioning the folding algorithms on the distances from two reference points, resulting in a kind of 2D ‘projection’ of the landscape (Lorenz et al., 2009). Heuristic methods are also used to (locally) navigate the optimal folding path between two given structures. For instance, findpath (Flamm et al., 2000) is a fast algorithm that produces excellent quality direct pathways based on the Morgan–Higgs algorithm (Morgan and Higgs, 1998). Furthermore, RNAtabupath (Dotu et al., 2010) and its related web server, RNApathfinder, used a tabu semi-greedy heuristic to determine nearly optimal folding pathways between two given secondary structures. Lorenz et al. (2009) developed a heuristic algorithm PathFinder based on their 2D ‘projection’ of the landscape.
The difficult part in computing coarse graining models such as barrier trees is to determine the saddle points. The local minima, on the other hand, can be obtained efficiently by means of modified dynamic programming algorithms. This was demonstrated first by Clote (2005) with respect to the Nussinov–Jacobson energy model and later extended to the Turner energy model by Lorenz and Clote (2011). Their extension of McCaskill’s algorithm can be used to generate Boltzmann-weighted samples of local minima. Empirically, they find that the number of local optima is roughly the square root of the number of secondary structures, i.e. it grows exponentially with chain length. Exact combinatorial results have been derived by Fusy and Clote (2012) for the base stacking energy model, which is a variant of the Nussinov model, where each stacked base pair contributes −1 toward the energy of the structure.
Hence, for large RNAs, one still has to resort to sampling. Boltzmann-weighted samples are not necessarily the most efficient way to explore the basin structure of the landscape because they are strongly biased toward usually small fraction of low energy structures. Sahoo and Albrecht (2012) thus considered a stochastic sampling method to obtain local minima within a prescribed distance of a reference structure: random structures are iteratively improved by gradient (down-hill) walks until local minima are reached. Such samples can be used to estimate the total number of local minima following the arguments of Garnier and Kallel (2000).
The remainder of this contribution is organized as follows. In Sections 2.1 and 2.2, we first introduce the basic concepts and existing results in the field of RNA folding landscapes. In Section 2.3, we introduce the ‘Basin Hopping Graph’ (BHG) as a new coarse graining model of the energy landscape and then describe algorithms for its construction. In Section 3, we present and discuss our experimental results. Section 4 summarizes the article and suggests directions for future work.
2 THEORY
2.1 RNA folding landscapes
Given an RNA sequence σ, let 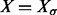 denote the set of all secondary structures that can be formed by σ assuming that (i) only canonical (GC, AU and GU) base pairs are formed, (ii) base pairs do not cross, i.e. pseudoknots are not formed, and (iii) hairpin loops have a minimum length of 3. These conditions define the ensemble of structures implemented in the most commonly used RNA folding tools including mfold (Zuker and Sankoff, 1984) and the ViennaRNA Package (Hofacker et al., 1994; Lorenz et al., 2011). It is well known that the cardinality
denote the set of all secondary structures that can be formed by σ assuming that (i) only canonical (GC, AU and GU) base pairs are formed, (ii) base pairs do not cross, i.e. pseudoknots are not formed, and (iii) hairpin loops have a minimum length of 3. These conditions define the ensemble of structures implemented in the most commonly used RNA folding tools including mfold (Zuker and Sankoff, 1984) and the ViennaRNA Package (Hofacker et al., 1994; Lorenz et al., 2011). It is well known that the cardinality 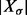 grows exponentially with the length of σ [(Hofacker et al., 1996) and the references therein] provided the stickiness of σ, i.e. the probability that two arbitrarily chosen nucleotides in σ can form a base pair, is relatively large. This is true for most biological RNA sequences, as the values of stickiness for RNAs are around 0.375 (Hofacker et al., 1994).
grows exponentially with the length of σ [(Hofacker et al., 1996) and the references therein] provided the stickiness of σ, i.e. the probability that two arbitrarily chosen nucleotides in σ can form a base pair, is relatively large. This is true for most biological RNA sequences, as the values of stickiness for RNAs are around 0.375 (Hofacker et al., 1994).
This set of discrete conformations is arranged as a graph by defining a ‘move set’, i.e. by specifying which pairs of secondary structures can be interconverted in a single step [(Reidys and Stadler, 2002) and the references therein]. Figure 1A gives a simple example. Each vertex of the RNA folding landscape, i.e. each RNA secondary structure x, is associated with an energy f(x). A well-established energy model allows us to explicitly compute f(x) for every structure x in terms of additive contributions for base pair stacking as well as hairpin loops, interior loops, bulges and multiloops (Mathews et al., 1999).
2.2 Local minima, saddles and basins
A secondary structure 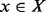 is a local minimum (LM) of the landscape if it does not have neighbors with lower energy. In particular, x is a global minimum or a minimum free energy structure (MFE) if its energy is minimal within X. For each LM x, we define its gradient basin
is a local minimum (LM) of the landscape if it does not have neighbors with lower energy. In particular, x is a global minimum or a minimum free energy structure (MFE) if its energy is minimal within X. For each LM x, we define its gradient basin
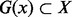 as the set of structures
as the set of structures 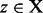 so that the unique gradient walk with starting point in z ends in x. We note for later reference that the gradient basins of all the LMs in the RNA folding landscape forms a partition of its configuration space X. This partitioning forms an intuitive coarse-grained model of the landscape.
so that the unique gradient walk with starting point in z ends in x. We note for later reference that the gradient basins of all the LMs in the RNA folding landscape forms a partition of its configuration space X. This partitioning forms an intuitive coarse-grained model of the landscape.
An important concept for our own approach is the direct saddle. A direct saddle between two LMs x and y is a structure 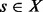 with minimal energy so that both x and y are reachable from s by means of an adaptive walk. We call
with minimal energy so that both x and y are reachable from s by means of an adaptive walk. We call 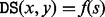 the direct saddle height between x and y. Not every pair of LMs is connected by direct saddles. However, the graph consisting of LMs and their connections by direct saddles is always connected (Supplementary Material Part A; Klemm et al., 2014).
the direct saddle height between x and y. Not every pair of LMs is connected by direct saddles. However, the graph consisting of LMs and their connections by direct saddles is always connected (Supplementary Material Part A; Klemm et al., 2014).
The cycle
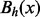 of x at energy level h can be defined as a maximal connected subset of
of x at energy level h can be defined as a maximal connected subset of 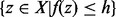 that contains x. In other words,
that contains x. In other words, 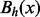 is the set of structures found by a flooding algorithm starting at x (Flamm et al., 2000, 2002; Sibani et al., 1999). In particular, the basin
is the set of structures found by a flooding algorithm starting at x (Flamm et al., 2000, 2002; Sibani et al., 1999). In particular, the basin 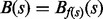 of s (Flamm et al., 2002) is the set of all points in X that can be reached from s by a path whose elevation never exceeds f(s).
of s (Flamm et al., 2002) is the set of all points in X that can be reached from s by a path whose elevation never exceeds f(s).
The saddle height
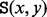 between any two vertices x and y is the minimal value h for which
between any two vertices x and y is the minimal value h for which 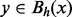 . In other words,
. In other words, 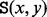 is the level at which two cycles
is the level at which two cycles 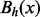 and
and 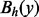 ‘merge’. If x and y are LMs connected by a direct saddle point, then
‘merge’. If x and y are LMs connected by a direct saddle point, then 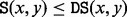 . A structure
. A structure 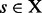 is called a saddle between
is called a saddle between 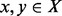 if (i)
if (i) 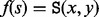 and (ii) there is a path P connecting x and y so that
and (ii) there is a path P connecting x and y so that 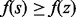 for all
for all 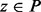 . A path
. A path 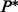 connecting x and y in the landscape is energetically optimal if
connecting x and y in the landscape is energetically optimal if 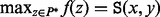 . Energetically optimal paths are not necessarily unique (Supplementary Material Part C). For RNA folding landscapes, the problems of computing saddle heights, saddle points and the energetically optimal path are NP-hard (Maňuch et al., 2011).
. Energetically optimal paths are not necessarily unique (Supplementary Material Part C). For RNA folding landscapes, the problems of computing saddle heights, saddle points and the energetically optimal path are NP-hard (Maňuch et al., 2011).
It has been proven in (Flamm et al., 2002) that for any two saddles 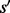 and
and 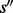 ,
, 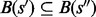 ,
, 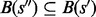 or
or 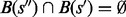 is satisfied, i.e. the basins below saddles of a landscape form a hierarchy with respect to set inclusion order (Supplementary Material Part B). Because the landscape is connected, this hierarchical structure is naturally represented by a tree called barrier tree (Flamm et al., 2002; Wolfinger et al., 2004). The leaves and interior nodes of this tree correspond to the LMs and their saddle points, respectively.
is satisfied, i.e. the basins below saddles of a landscape form a hierarchy with respect to set inclusion order (Supplementary Material Part B). Because the landscape is connected, this hierarchical structure is naturally represented by a tree called barrier tree (Flamm et al., 2002; Wolfinger et al., 2004). The leaves and interior nodes of this tree correspond to the LMs and their saddle points, respectively.
The barrier tree can be computed using a flooding algorithm (Flamm et al., 2000; Sibani et al., 1999) implemented, e.g. in the program barriers (Flamm et al., 2002). It takes an energy sorted list of structures as input. This list may contain either all structures or only the structures below some threshold energy. The only part of barriers that relies on the geometric properties of the configuration space is the routine that generates all neighbors of each structure in the list. Therefore, barriers has a time complexity of 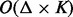 , where Δ denotes the maximum number of neighbors for a structure in the landscape, and K denotes the number of structures in the input list. For the technical complications arising from degeneracy in the landscape, see Flamm et al. (2002).
, where Δ denotes the maximum number of neighbors for a structure in the landscape, and K denotes the number of structures in the input list. For the technical complications arising from degeneracy in the landscape, see Flamm et al. (2002).
The barrier tree abstraction has two major disadvantages: (i) It neglects much of the geometric information of the folding landscape because the neighborhood relation between basins is ignored as illustrated in Figure 2. (ii) The high computational cost makes it unfeasible in practice for RNA molecules with a length >100 nt.
Fig. 2.
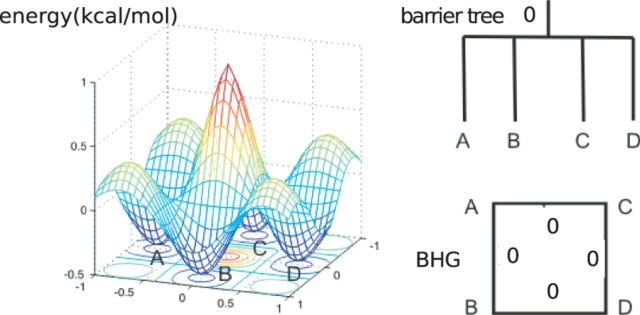
A landscape with four local minima (A, B, C, and D) is illustrated in the left hand side. Its corresponding barrier tree (top) and BHG (bottom) are shown on the right hand side with saddle heights annotated inside. For any pair of local minima, their corresponding saddle heights are all equal to 0 kcal/mol. Regarding direct saddle heights, except 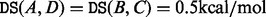 , the rest are all of value 0 kcal/mol. One key difference is that the energetically favorable neighborhood relation between the basins can be displayed in the BHG but not in the barrier tree
, the rest are all of value 0 kcal/mol. One key difference is that the energetically favorable neighborhood relation between the basins can be displayed in the BHG but not in the barrier tree
2.3 The Basin Hopping Graph
2.3.1 Definition
The BHG has been devised to overcome these shortcomings. The basic idea is to incorporate additional neighborhood information by considering LMs as adjacent if the transition between their corresponding basins is ‘energetically optimal’. For two given LMs x and y, the condition energetically optimal requires that their direct saddle height is equal to their saddle height, i.e. 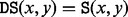 . A schematic diagram of the BHG for a toy landscape is illustrated in Figure 2, in which, the transition from A to B on Figure 2 is energetically optimal, as
. A schematic diagram of the BHG for a toy landscape is illustrated in Figure 2, in which, the transition from A to B on Figure 2 is energetically optimal, as 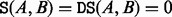 , but the transition from A to D is not, as
, but the transition from A to D is not, as 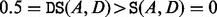 .
.
We focus on the energetically optimal transitions because, on one hand as proven in Supplementary Material Lemma S1, the energetically optimal paths connecting two local minima x and y can be represented as a concatenation of energetically optimal transitions between neighboring basins. In Figure 2, for example, there are two energetically optimal paths between A and D: 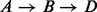 and
and 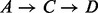 . Both paths are composed of optimal transitions between neighbored basins
. Both paths are composed of optimal transitions between neighbored basins 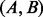 ,
, 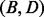 ,
, 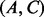 and
and 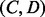 .
.
On the other hand, a key observation is that the ‘energetically optimal’ transitions are usually rare and hence the BHG is a fairly sparse graph. Therefore, the BHG may be the minimal ‘information container’ that is able to track the energetically optimal paths between any two local minima in the RNA landscape. We have shown in Figure 2 that the barrier tree fails to track the optimal path between A and D. In Supplementary Material Part C, we further prove inductively that the barrier tree is equivalent to the dendrogram obtained from the BHG by single linkage clustering.
The BHG could be constructed by enumeration and flooding in a manner similar to the barrier tree. Instead, we describe an efficient heuristic that allows us to overcome the stringent length restrictions imposed by enumerative approaches. The procedure consists of two largely independent components: (i) The RNAlocmin program generates a sample set of LMs within a user-defined energy range above the MFE. This component replaces the exhaustive enumeration of all low energy states. (ii) The BHGbuilder algorithm is then used to estimate direct saddle points and to determine the BHG adjacency on the input set of LMs. As we show below, the vertex and edge weights can be estimated along the way.
2.3.2 RNAlocmin
The basic idea of RNAlocmin is straightforward: it samples a start structure and then uses a gradient walk to determine the corresponding LM. The main technical difficulty is to make the sampling part efficient. Boltzmann sampling, as implemented in RNAsubopt -p or sfold (Ding and Lawrence, 2003; Ding et al., 2004), predominantly yields structures close to the MFE, which are frequently transported to the global minimum or one of the other local optima with low energy.
To avoid this kind of oversampling, we resort to the idea underlying Simulated Annealing and modify the Boltzmann weights by an extra scaling factor ξ that artificially increases the sample temperature:
| (1) |
where 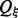 the correspondingly modified partition function and
the correspondingly modified partition function and 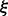 serves as a normalization factor. A change of the thermodynamic temperature T also affects the RNA energy parameters, which are free energy contributions (Mathews et al., 1999), and hence affects f(s) in a biased manner. It is necessary, therefore, to be able to vary the thermodynamic temperature and the sample temperature ξ independently. For
serves as a normalization factor. A change of the thermodynamic temperature T also affects the RNA energy parameters, which are free energy contributions (Mathews et al., 1999), and hence affects f(s) in a biased manner. It is necessary, therefore, to be able to vary the thermodynamic temperature and the sample temperature ξ independently. For 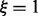 we obtain regular Boltzmann ensembles, for
we obtain regular Boltzmann ensembles, for 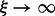 we approach uniform sampling of X. The implementations of the partition function algorithms of the ViennaRNA Package have been modified to provide this option from version 2.0.3 on.
we approach uniform sampling of X. The implementations of the partition function algorithms of the ViennaRNA Package have been modified to provide this option from version 2.0.3 on.
Because we are interested in the LMs within a prescribed energy increment above the MFE, it pays to adjust ξ accordingly. Instead of a fixed optimal ξ, we use an adaptive ξ-schedule, which prefers LMs with relatively low energies. As the thermodynamic energy model of RNAs is strongly dependent on the input sequence, we first estimate the expected energies as a function of ξ. To this end, we obtain a set of LMs from 1000 sampled structures and tabulate the average energy of the LMs for each 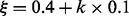 in which an integer k ranges over the interval [0, 21], Figure 3 (top). From these values we obtain an estimate
in which an integer k ranges over the interval [0, 21], Figure 3 (top). From these values we obtain an estimate 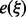 for the expected free energy by linear interpolation. In principle, one could precompute these tables for various sequence compositions. We found, however, that the computational overhead to estimate these values for each input is tolerable in practice. Alternatively, one could also estimate the
for the expected free energy by linear interpolation. In principle, one could precompute these tables for various sequence compositions. We found, however, that the computational overhead to estimate these values for each input is tolerable in practice. Alternatively, one could also estimate the 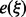 ‘on the fly’ from the already sampled LMs.
‘on the fly’ from the already sampled LMs.
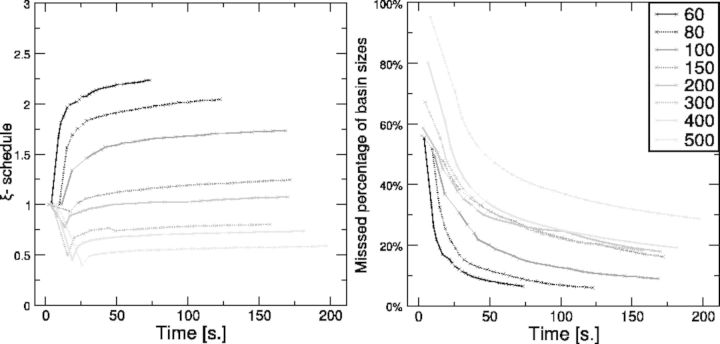
Fig. 3.
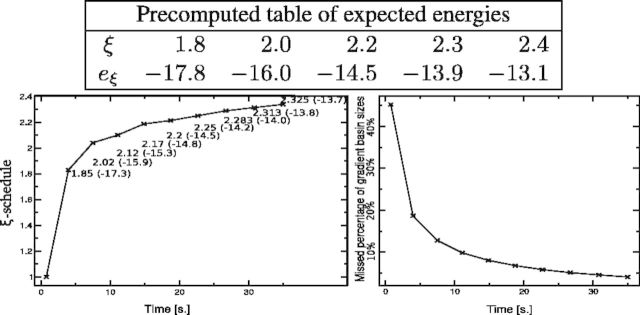
Computation of LMs for Melitaea cinxia U6 snRNA JX878560.1 (107 nt) with RNAlocmin. (Left) Adaptive ξ schedule as a function of run time. For each sampling epoch we show the values of e and ξ as 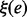 . The precomputed
. The precomputed 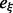 table is shown at the top. (Right) Size-weighted fraction of undiscovered LMs compared with exhaustive enumeration with RNAsubopt and barriers. Basin sizes are estimated from the 106 structures with the lowest energies
table is shown at the top. (Right) Size-weighted fraction of undiscovered LMs compared with exhaustive enumeration with RNAsubopt and barriers. Basin sizes are estimated from the 106 structures with the lowest energies
From each sampled structure s, we obtain the corresponding LM x via a gradient walk starting from s. In practice, the implementation does not completely evaluate candidate structures but considers the energy increments for opening and closing individual base pairs, each of which can be obtained by three lookups from the tabulated energy model. For each LM x, the number q(x) of gradient walks terminating in x is recorded to keep track of sampling efficiency. Sahoo and Albrecht (2012) introduced a heuristic criterion designed to avoid reaching the same LM too many times from different initial random starting points. They propose that the sampling is sufficient when most of the minima have been seen at least twice. We modify this rule and stipulate that sampling is sufficient up to energy level e if 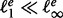 , where
, where 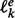 denotes the number of minima with an energy less than e that have been detected at least once and at most k times (
denotes the number of minima with an energy less than e that have been detected at least once and at most k times (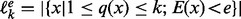 ). The rule of (Sahoo and Albrecht, 2012) and its energy-dependent variants are empirically well supported (see also Section 3) but so far lack a good theoretical justification.
). The rule of (Sahoo and Albrecht, 2012) and its energy-dependent variants are empirically well supported (see also Section 3) but so far lack a good theoretical justification.
To turn the rule into an operational criterion, we determine, at a given step of the sample procedure, the smallest energy cutoff e so that 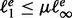 , where the so-called convergence parameter μ is a user-defined threshold, set to
, where the so-called convergence parameter μ is a user-defined threshold, set to 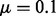 by default. The energy e is then interpreted as the desired expected energy for the next sampling epoch. The corresponding value of ξ is obtained from the precomputed table mentioned above. RNAlocmin continues until the energy e exceeds the user-defined upper bound or if the requested number of iterations have been done.
by default. The energy e is then interpreted as the desired expected energy for the next sampling epoch. The corresponding value of ξ is obtained from the precomputed table mentioned above. RNAlocmin continues until the energy e exceeds the user-defined upper bound or if the requested number of iterations have been done.
The time complexity of RNAlocmin is composed of two parts. First, samples have to be gathered by RNAsubopt, and then gradient walks have to be constructed for each sample. The time complexity of an average gradient walk is 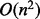 , where n is the length of the sequence. We are dealing mainly with highly folded structures and they tend to only have small number of insertions possible, and therefore, these structures have O(n) neighbors. Recomputing their energy is in O(1) steps as mentioned earlier, and the gradient walk has at most O(n) steps on RNA landscapes. For each value of ξ, we have a setup cost of
, where n is the length of the sequence. We are dealing mainly with highly folded structures and they tend to only have small number of insertions possible, and therefore, these structures have O(n) neighbors. Recomputing their energy is in O(1) steps as mentioned earlier, and the gradient walk has at most O(n) steps on RNA landscapes. For each value of ξ, we have a setup cost of 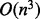 for the forward recursion of McCaskill’s algorithms and
for the forward recursion of McCaskill’s algorithms and 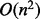 to generate a sample. The complexity of the latter step could be reduced to
to generate a sample. The complexity of the latter step could be reduced to  using the Boustrophedon method (Ponty, 2008). As the sampling step is already dominated by the effort for the gradient walk, we retained the simpler implementation. The total time complexity is then
using the Boustrophedon method (Ponty, 2008). As the sampling step is already dominated by the effort for the gradient walk, we retained the simpler implementation. The total time complexity is then 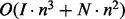 , where I is the number of ξ-sampling epochs and N is the total number of sampled structures.
, where I is the number of ξ-sampling epochs and N is the total number of sampled structures.
For performance evaluation, we generated samples of 10 randomly generated RNA sequences with uniform nucleotide composition for each length from 60 to 500 (Supplementary Material Part D Fig. S2). For each sequence, LMs are generated from at most 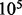 start structures for each value of ξ. Computations were performed on an Intel Xeon CPU E5450 3.00 GHz.
start structures for each value of ξ. Computations were performed on an Intel Xeon CPU E5450 3.00 GHz.
2.3.3 BHGbuilder
BHGbuilder aims to determine the BHG adjacency and the corresponding edge weights (saddle heights) between these adjacent LMs. Initially, all pairs of LMs are arranged in a priority queue 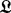 by increasing base pair distance. Then BHGbuilder uses an iterative procedure to determine the BHG-adjacent LMs: for each pair of LMs in
by increasing base pair distance. Then BHGbuilder uses an iterative procedure to determine the BHG-adjacent LMs: for each pair of LMs in 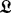 , (i) an initial path
, (i) an initial path 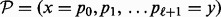 is computed with some existing heuristic path-finding algorithm. Our implementation uses findpath (Flamm et al., 2000) provided by the ViennaRNA Package as the default underlying algorithm (alternatives such as Pathfinder could be used as well); (ii) an iterative re-evaluation procedure (Fig. 4) is used to improve
is computed with some existing heuristic path-finding algorithm. Our implementation uses findpath (Flamm et al., 2000) provided by the ViennaRNA Package as the default underlying algorithm (alternatives such as Pathfinder could be used as well); (ii) an iterative re-evaluation procedure (Fig. 4) is used to improve 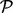 . At each
. At each 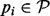 , we start a gradient walk and determine its end points vi. If all vi coincide with x or y, then
, we start a gradient walk and determine its end points vi. If all vi coincide with x or y, then 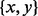 is a candidate BHG edge. Otherwise, each pair of distinct consecutive (w.r.t. to
is a candidate BHG edge. Otherwise, each pair of distinct consecutive (w.r.t. to 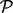 ) LMs is reinserted into the priority queue. The process ends when
) LMs is reinserted into the priority queue. The process ends when 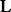 is empty and returns an approximation of the BHG graph. Its vertex set consists of both the LMs provided as input (e.g. by RNAlocmin) and the additional LMs obtained in the path-construction step. Its edges are the BHG adjacencies as outlined above. Finally, a double-sided flooding procedure (optional) is called to further improve the edge weights between two BHG-adjacent vertices. Here, an exact saddle can be discovered by enumerating the structures in these two adjacent basins if the number of structures enumerated does not overcome a certain threshold.
is empty and returns an approximation of the BHG graph. Its vertex set consists of both the LMs provided as input (e.g. by RNAlocmin) and the additional LMs obtained in the path-construction step. Its edges are the BHG adjacencies as outlined above. Finally, a double-sided flooding procedure (optional) is called to further improve the edge weights between two BHG-adjacent vertices. Here, an exact saddle can be discovered by enumerating the structures in these two adjacent basins if the number of structures enumerated does not overcome a certain threshold.
Fig. 4.
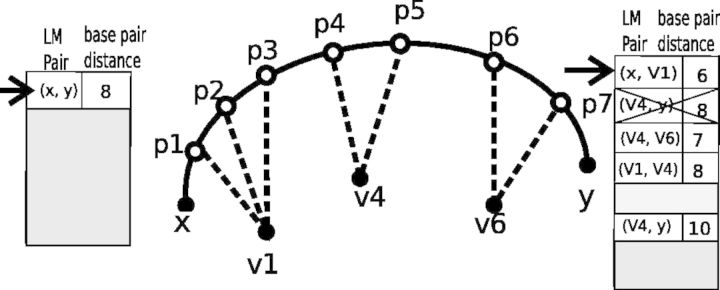
Iterative path construction in BHGbuilder. First, an initial path 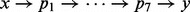 is computed with findpath for the first pair of LMs
is computed with findpath for the first pair of LMs 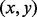 in the priority queue
in the priority queue 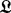 . The base pair distance between x and y is 8. Next, the gradient walks starting from
. The base pair distance between x and y is 8. Next, the gradient walks starting from 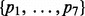 determine three consecutive LMs v1, v4 and v6. Thus, the adjacent pairs
determine three consecutive LMs v1, v4 and v6. Thus, the adjacent pairs 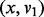 ,
,  ,
, 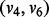 and
and 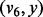 are inserted into
are inserted into 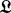 for the next iteration
for the next iteration
BHGbuilder has a time complexity of 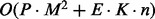 , where terms capture the above described algorithm and the flooding of the resulting pairs of LMs: P is the time complexity of one run of the underlying path-finding algorithm,
, where terms capture the above described algorithm and the flooding of the resulting pairs of LMs: P is the time complexity of one run of the underlying path-finding algorithm, 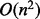 in the case of findpath; M is number of LMs in the input,
in the case of findpath; M is number of LMs in the input, 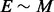 denotes the number of edges in the BHG as an output; K denotes the maximal number of additional structures appearing in the flooding procedure and O(n) is the average time complexity to compute the neighborhood for each structure. Therefore, the time complexity of BHGbuilder with findpath is
denotes the number of edges in the BHG as an output; K denotes the maximal number of additional structures appearing in the flooding procedure and O(n) is the average time complexity to compute the neighborhood for each structure. Therefore, the time complexity of BHGbuilder with findpath is 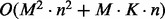 .
.
3 RESULTS AND DISCUSSION
3.1 RNAlocmin
Figure 5 summarizes the sampling schedule and the size-weighted fraction of undetected basins as a function of invested CPU time. Not surprisingly, the sampling times to reach a given level of coverage of the landscape increase with sequence length. This is an obvious consequence of the exponential increase in the number of LMs. Nevertheless, the adaptive ξ schedule is effective because for different RNA lengths, the speed of finding new LMs remains stable, i.e. the number of detected LMs grows linearly with respect to the running time (shown in the Supplementary Material Part D Fig. S2).
Fig. 5.
Average performance of RNAlocmin for random generated RNA sequences of lengths 60–500. The crosses annotate the time points when ξ get updated
Figure 5 (right) shows that for sequence lengths up to 500 nt, RNAlocmin is able to find a collection of LMs whose combined basin sizes cover more than two-thirds of the search space within 200 s. For sequences shorter than 300 nt, this fraction increases to 80%. Similar results are obtained from biological RNA sequences and collected in Supplementary Material Part E Figures S3–S11.
To compare the performance of RNAlocmin with RNAlocopt (Lorenz and Clote, 2011), we allocate the same CPU time to both programs and evaluate the total number of detected LMs and the size-weighted fraction of undiscovered basins. Both Figure 6 and the additional benchmarks summarized in the Supplementary Material Part E Figures S3–S11 show that RNAlocmin consistently outperforms its competitor with respect to both measures.
Fig. 6.
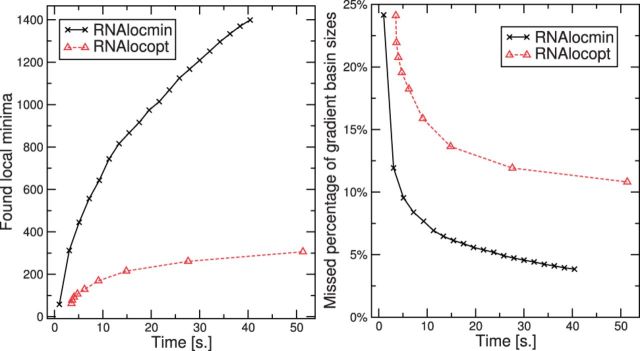
Comparison between RNAlocmin and RNAlocopt for the SV11 RNA switch L07337_1 (115 nt), see Section 3.2.4. The sample size for RNAlocmin was limited to N = 4000 000 structures. The fraction of undetected basins was estimated by enumeration of 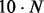 suboptimal structures with RNAsubopt -e and subsequent evaluation of the gradient basins with barriers
suboptimal structures with RNAsubopt -e and subsequent evaluation of the gradient basins with barriers
3.2 BHGbuilder
3.2.1 Approximated BHG versus Barrier tree
In Figure 7, we compared the BHG (top) and the barrier tree (bottom) for the RNA molecule 5′-GUGUCGCUUUCGAUUAAGGACCUACAACAGGCU-3′. To highlight the difference between the barrier tree and the BHG, we consider the refolding pathway between (i) the MFE and (ii) the next-lowest LM. Both structures readily allow us to read off the saddle height as 1.9 kcal/mol. The BHG shows that there are two alternative optimal pathways 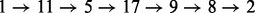 and
and 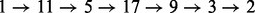 . The barrier tree provides a much more ambiguous picture. It suggests a refolding pathway climbing to the saddle separating LM 1 and LM 2 but does not provide any indication of the intermediate states. The path backtracking procedure implemented in barriers can identify the first folding pathway. Owing to the inherent tree topology, however, it is not possible to also find the alternative connection. We note here, this path backtracking procedure is limited to RNA molecules
. The barrier tree provides a much more ambiguous picture. It suggests a refolding pathway climbing to the saddle separating LM 1 and LM 2 but does not provide any indication of the intermediate states. The path backtracking procedure implemented in barriers can identify the first folding pathway. Owing to the inherent tree topology, however, it is not possible to also find the alternative connection. We note here, this path backtracking procedure is limited to RNA molecules 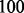 nt only, as the number of optimal paths is usually too big.
nt only, as the number of optimal paths is usually too big.
Fig. 7.
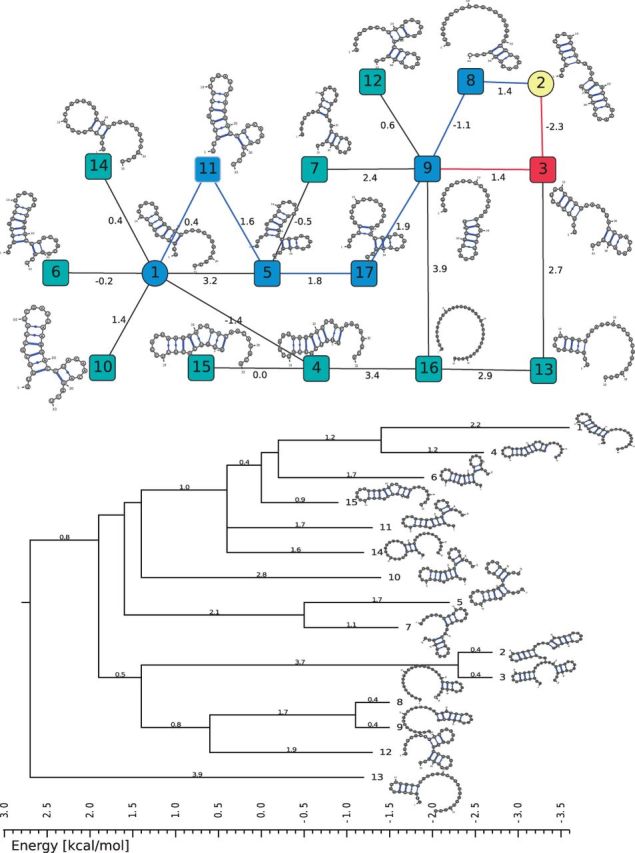
Comparison of the BHG and the barrier tree for a small RNA molecule. The vertex set of the BHG (top) comprises the 15 LMs of the input and two additional LMs 16 and 17 discovered by BHGbuilder. The barrier tree generated with barriers (below) contains only the 15 input LMs. Secondary structure drawings were produced with VARNA (Darty et al., 2009)
There are pairs of LMs that are not connected by an energetically optimal path but are still BHG adjacent. An example is LM 1 and LM 5 in Figure 7, which are adjacent in the BHG while  . These cases appear when the underlying path-searching algorithm misses the optimal solution for the initial path. In practice, these ‘energetically suboptimal’ paths rarely hurt the computation of the saddle height, which is calculated only after the entire BHG, and hence the competing indirect paths, have been determined. As these paths usually reduce the graph distance at the expense of a small energy penalty, such paths may still be relevant for the folding kinetics. One might want to consider an optimization criterion that involves both path length and energy instead of just peak energy along the path as we do here.
. These cases appear when the underlying path-searching algorithm misses the optimal solution for the initial path. In practice, these ‘energetically suboptimal’ paths rarely hurt the computation of the saddle height, which is calculated only after the entire BHG, and hence the competing indirect paths, have been determined. As these paths usually reduce the graph distance at the expense of a small energy penalty, such paths may still be relevant for the folding kinetics. One might want to consider an optimization criterion that involves both path length and energy instead of just peak energy along the path as we do here.
3.2.2 Approximation of saddle heights
BHGbuilder is a heuristic algorithm and thus will in general only find upper bounds of saddle heights. For moderate-size RNAs, a direct comparison with exact values obtained from barriers is possible. For larger molecules, we compare with other heuristics. In particular, it is interesting to check whether the construction of the BHG brings a further improvement of the saddle heights compared with the path construction heuristic findpath alone. Because BHGbuilder uses findpath for its initial estimates of saddle heights, it is of course guaranteed that 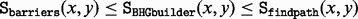 . The improvements of BHGbuilder over findpath are mostly a consequence of the inclusion of additional LMs such as (17) in Figure 7 (top), which is necessary for the optimal path. In Figure 8, we use two snRNAs as examples, the 107 nt U6 snRNA of Melitaea cinxia and the 166 nt U1 snRNA of the mouse. For U6, we sample 1000 LMs and determine the exact saddle heights between all pairs by flooding with RNAsubopt/barriers. The saddle point estimates are similar in this case, with BHGbuilder obtaining the exact values and only small errors of up to 0.1 kcal/mol in ∼7.4% of the pairs for findpath. For the 166 nt mouse U1 snRNA, however, an exact computation with barriers already exceeds our hardware limitations. The direct comparison of BHGbuilder and findpath yields a moderate improvement of on average 0.8 kcal/mol for almost half of the pairs of LMs.
. The improvements of BHGbuilder over findpath are mostly a consequence of the inclusion of additional LMs such as (17) in Figure 7 (top), which is necessary for the optimal path. In Figure 8, we use two snRNAs as examples, the 107 nt U6 snRNA of Melitaea cinxia and the 166 nt U1 snRNA of the mouse. For U6, we sample 1000 LMs and determine the exact saddle heights between all pairs by flooding with RNAsubopt/barriers. The saddle point estimates are similar in this case, with BHGbuilder obtaining the exact values and only small errors of up to 0.1 kcal/mol in ∼7.4% of the pairs for findpath. For the 166 nt mouse U1 snRNA, however, an exact computation with barriers already exceeds our hardware limitations. The direct comparison of BHGbuilder and findpath yields a moderate improvement of on average 0.8 kcal/mol for almost half of the pairs of LMs.
Fig. 8.
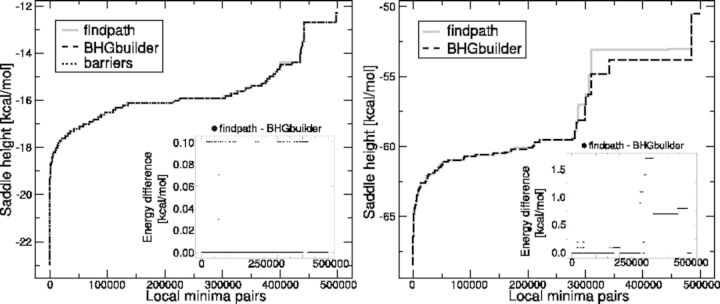
Comparison of the saddle height estimates of BHGbuilder and findpath for Melitaea cinxia U6 snRNA JX878560.1 (107 nt) and the Mus musculus U1 snRNA NR_004413.2 (166 nt). Here, the x-axes denote the indices of LM-pairs, which are sorted according to their saddle heights in an increasing order and the y-axes are the corresponding saddle heights (kcal/mol) estimations derived from different methods. The inset shows the difference in saddle heights between BHGbuilder and findpath
BHGbuilder performs equally well or better than findpath in all 10 examples of Supplementary Material Part F Figures S12–S21. For three cases, we find substantial improvements of the saddle point energies that can help to derive more exact RNA kinetic parameters. In seven cases, only small or no improvements were obtained. Still, the adjacency information generated by BHGbuilder, can add further accuracy to kinetic parameters in all cases because it provides information on alternative connections between LMs; see Supplementary Material Part F for details.
3.2.3 Prediction of folding pathways
BHGbuilder can also be used to predict the optimal folding path between a pair of user-prescribed LMs. Here we make use of the iterative path improvement step to elaborate on underlying folding path prediction software such as findpath (Flamm et al., 2000), RNAtabupath (Dotu et al., 2010) and Pathfinder (Lorenz et al., 2009). In Table 1, we compare BHGbuilder with findpath, RNAtabupath and Pathfinder on 100 randomly generated instances with n = 200, i.e. well beyond the reach of exact enumeration. Interestingly, the computationally expensive flooding step brings no improvement for this task. Pathfinder nearly always obtains the path with the lowest peak height but is more than two orders of magnitude slower.
Table 1.
Performance comparison with different folding path prediction algorithms for the refolding paths between the MFE structure and a randomly selected LM
| Algorithm | Number of best runs |
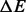 (kcal/mol) (kcal/mol) |
Time (s) |
|---|---|---|---|
| RNAtabupath | 14 | 3.0598 | 4617.7 |
| BHGbuild | 34 | 1.1028 | 7.6674 |
| BHGbuild -noF | 34 | 1.1028 | 0.6824 |
| Pathfinder | 95 | 0.0367 | 113.01 |
| findpath | 12 | 1.5104 | 0.6397 |
Note: Values are averages over 100 RNA sequences of length 200 nt. 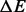 is the average difference in the energy from the best run. BHGbuild -noF is the BHG algorithm without the optional flooding step. Pathfinder was run with option -M DB-MFE, and for findpath we used depth
=
1000.
is the average difference in the energy from the best run. BHGbuild -noF is the BHG algorithm without the optional flooding step. Pathfinder was run with option -M DB-MFE, and for findpath we used depth
=
1000.
3.2.4 SV11 RNA: a hard case
The SV11 sequence is a particularly hard test case for landscape-oriented algorithms because it features a functional metastable state with high energy and a high energy barrier. The 115 nt SV11 RNA was discovered in in vitro selection experiments as an excellent substrate for Qβ replicase (Biebricher and Luce, 1992). It features a nearly palindromic sequence with an extremely stable hairpin-like MFE structure. Pulse-chase experiments showed that the active conformation is a metastable structure formed during replication, while the MFE serves as a template for the Qβ replicase. Melting experiments indicated that the metastable conformation comprises two distinct stems (Biebricher and Luce, 1992).
The energy difference between the MFE and the metastable conformation is 28.5 kcal/mol, well beyond the reach of exhaustive enumeration. Boltzmann sampling is also inefficient for such large energy differences as well, hence RNAlocopt is still trapped in the vicinity of the MFE after 1 h at a sample size of 108. During the same wall clock time, RNAlocmin (convergence parameter 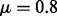 ) found the metastable in a sample of
) found the metastable in a sample of 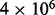 structures.
structures.
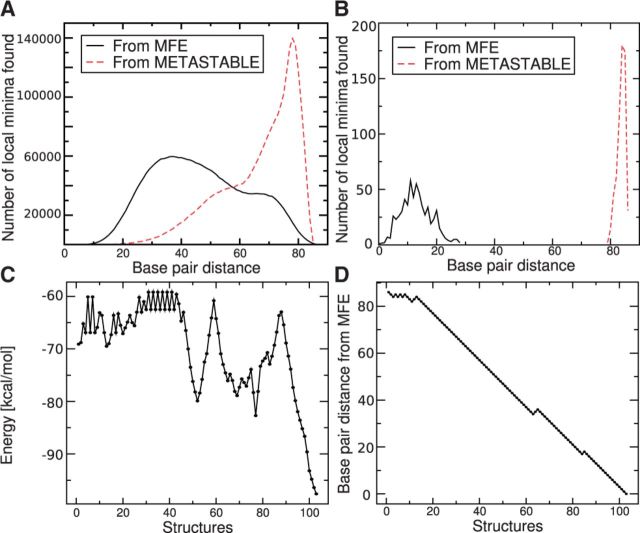
Figure 9A and B summarize the differences between RNAlocopt and RNAlocmin in the base pair distance distributions of the LMs. While RNAlocopt found only 620 distinct LMs, we obtained 2 619 305 with RNAlocmin using a much smaller sample size. Importantly, RNAlocmin covers not only LMs near to MFE but also, due to the adaptive schedule, those more distant LMs in energy and base pairing pattern. RNAlocmin found the metastable stable state as the 365172th LM w.r.t. energy.
Fig. 9.
Energy landscape of the SV11 RNA. The distribution of base pair distances from MFE and metastable structure are shown for a sample of 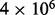 structures for RNAlocmin (A) and 108 structures for RNAlocopt (B). The metastable basin is missed completely by RNAlocopt. Panels (C) and (D) record the folding energy and base pair distance from the MFE structure along the optimal (re)folding path from the MFE to the metastable state as computed by BHGbuilder. The x-axis is the number of structures along the path
structures for RNAlocmin (A) and 108 structures for RNAlocopt (B). The metastable basin is missed completely by RNAlocopt. Panels (C) and (D) record the folding energy and base pair distance from the MFE structure along the optimal (re)folding path from the MFE to the metastable state as computed by BHGbuilder. The x-axis is the number of structures along the path
BHGbuilder cannot process an input set of this size within reasonable time. Most of the LMs, however, are not persistent. They are either shallow or just ‘transition’ LMs with only two neighbors in the final BHG. Therefore, we selected from the initial input set those that remains LM with respect to an expanded move set that includes base pair shifts (Wuchty et al., 1999). Now the metastable has rank ∼6700 w.r.t. energy. Starting from the 7000 lowest LMs w.r.t. to the expanded move set and removing shallow LMs whose gradient basin has an escape barrier <1.0 kcal/mol leaves an initial set of 2665 non-shallow LMs as input. BHGbuilder constructs a BHG with 110593 vertices and 224666 edges in <20 h. The optimal folding path connecting MFE to metastable state in the BHG has a saddle height of 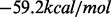 . This is a 3.1 kcal/mol improvement over both findpath and Pathfinder. We visualized the optimal path by monitoring how the free energies and the base pair distances (with MFE) vary along this path in Figure 9C and D, respectively. With few exceptions, the base pair distance monotonically decreases along the pathway. Interestingly, most of these detours appear in close vicinity of high energy peaks, which is potentially necessary to circle around the high energy barriers.
. This is a 3.1 kcal/mol improvement over both findpath and Pathfinder. We visualized the optimal path by monitoring how the free energies and the base pair distances (with MFE) vary along this path in Figure 9C and D, respectively. With few exceptions, the base pair distance monotonically decreases along the pathway. Interestingly, most of these detours appear in close vicinity of high energy peaks, which is potentially necessary to circle around the high energy barriers.
4 CONCLUDING REMARKS
The BHG introduced here is a conceptually rigorous coarse graining of a landscape comprising the LMs and those direct saddle points between them that are also globally the most favorable connections. At the same time it is a refinement of the barrier tree, which can be obtained from the BHG by single linkage clustering. It is not specific to RNA folding, which we used as a concrete application here, but can be computed in principle for any landscape.
The focus on the BHG adjacency captures the most likely transitions between basins. Thus, when the BHG serves as a basis for computing folding dynamics, one-step transition rate 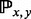 between any two given local minima x and y is approximated by an Arrhenius rule as
between any two given local minima x and y is approximated by an Arrhenius rule as 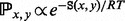 if x and y are adjacent in the BHG and 0 otherwise. This improves on the Arrhenius approximation for the barrier tree in which
if x and y are adjacent in the BHG and 0 otherwise. This improves on the Arrhenius approximation for the barrier tree in which 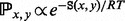 for each pair of local minima. Using Figure 2 as an example, in the BHG, any pathway from A to D needs to pass through either B or C, and thus, it requires two steps to refold from A to D. However, in a barrier tree, this is approximated as a one-step transition because it omits the geometric information between two basins. This approximation will be less accurate than the macro-state transition rates model outlined by Wolfinger et al. (2004). For instance, the direct transition between A and D in Figure 2 is neglected in the BHG model. A toy kinetic example comparing the three discussed approaches is presented in Supplementary Material Part G. The exponential relation between energies and rates suggests that energetically non-optimal direct transitions will play only a minor role compared with pathways with multiple intermediates that all have strictly smaller peak energies. This is true only for differences larger than a few kT. To accommodate this point, we can replace energetic optimality by a relaxed condition of the form
for each pair of local minima. Using Figure 2 as an example, in the BHG, any pathway from A to D needs to pass through either B or C, and thus, it requires two steps to refold from A to D. However, in a barrier tree, this is approximated as a one-step transition because it omits the geometric information between two basins. This approximation will be less accurate than the macro-state transition rates model outlined by Wolfinger et al. (2004). For instance, the direct transition between A and D in Figure 2 is neglected in the BHG model. A toy kinetic example comparing the three discussed approaches is presented in Supplementary Material Part G. The exponential relation between energies and rates suggests that energetically non-optimal direct transitions will play only a minor role compared with pathways with multiple intermediates that all have strictly smaller peak energies. This is true only for differences larger than a few kT. To accommodate this point, we can replace energetic optimality by a relaxed condition of the form 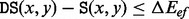 , which includes some suboptimal direct transitions between basins to the BHG. It will be interesting to see how the threshold
, which includes some suboptimal direct transitions between basins to the BHG. It will be interesting to see how the threshold 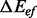 affects the folding kinetics. It is computationally feasible to keep suboptimal transitions as long as
affects the folding kinetics. It is computationally feasible to keep suboptimal transitions as long as 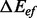 is a small multiple of kT.
is a small multiple of kT.
The BHG has been introduced with the explicit purpose of allowing for an efficient high-quality heuristic approximation so as to overcome the stringent size limitations of the exact algorithms. Empirically we find that the combination of improved sampling of low-energy local LMs with RNAlocmin, fast construction of initial candidate saddles with findpath and the construction of the BHG by iterative path improvement with BHGbuilder comes close to the exact solutions for small systems. At the same time, it extends the range at which RNA folding landscapes can be studied to at least 300 nt, thus including most structured RNAs of biological interest, such as RNAs shown in Supplementary Material Part E and F. BHGbuilder is also capable of exploring partial landscapes determined by the input set of LMs. Therefore, it allows us to ‘zoom-in’ and focus on the region of particular biological interest. The methods are readily extended to pseudoknotted RNAs as shown in Supplementary Material Part H. However, they become computationally much more demanding.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Martin Mann and Fenix Huang for helpful discussion, Peter Kerpedjiev for proofreading and Ronny Lorenz, main caretaker and programmer of the ViennaRNA package, for implementing the ξ-scaling technique into RNAsubopt.
Funding: In part by Deutsche Forschungsgemeinschaft (STA 850/15); Austrian Science Fund (FWF): [M1618-N28]; and IK Computational Science funded by the University of Vienna.
Conflict of Interest: none declared.
REFERENCES
- Baumstark T, et al. Viroid processing: Switch from cleavage to ligation is driven by a change from a tetraloop to a loop E conformation. EMBO J. 1997;16:599–610. doi: 10.1093/emboj/16.3.599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biebricher CK, Luce R. In vitro recombination and terminal elongation of RNA by Qβ replicase. EMBO J. 1992;38:5129–5135. doi: 10.1002/j.1460-2075.1992.tb05620.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clote P. An efficient algorithm to compute the landscape of locally optimal RNA secondary structures with respect to the Nussinov-Jacobson energy model. J. Comput. Biol. 2005;1:83–101. doi: 10.1089/cmb.2005.12.83. [DOI] [PubMed] [Google Scholar]
- Darty K, et al. VARNA: interactive drawing and editing of the RNA secondary structure. Bioinformatics. 2009;25:1974–1975. doi: 10.1093/bioinformatics/btp250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R, Baker D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl Acad. Sci. USA. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y, Lawrence C. A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res. 2003;31:7280–7301. doi: 10.1093/nar/gkg938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y, et al. Sfold web server for statistical folding and rational design of nucleic acids. Nucleic Acids Res. 2004;32:W135–W141. doi: 10.1093/nar/gkh449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dotu I, et al. Computing folding pathways between RNA secondary structures. Nucleic Acids Res. 2010;38:1711–1722. doi: 10.1093/nar/gkp1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doye JP, et al. Evolution of the potential energy surface with size for Lennard-Jones clusters. J. Chem. Phys. 1999;111:8417–8429. [Google Scholar]
- Flamm C, et al. RNA folding kinetics at elementary step resolution. RNA. 2000;6:325–338. doi: 10.1017/s1355838200992161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flamm C, et al. Barrier trees of degenerate landscapes. Z. Phys. Chem. 2002;216:155–173. [Google Scholar]
- Fusy É, Clote P. Combinatorics of locally optimal RNA secondary structures. J. Math. Biology, 2012;68:341–375. doi: 10.1007/s00285-012-0631-9. [DOI] [PubMed] [Google Scholar]
- Garnier J, Kallel L. Efficiency of local search with multiple local optima. SIAM J. Discrete Math. 2000;15:122–141. [Google Scholar]
- Garstecki P, et al. Energy landscapes, supergraphs, and “folding funnels” in spin systems. Phys. Rev. E. 1999;60:3219–3226. doi: 10.1103/physreve.60.3219. [DOI] [PubMed] [Google Scholar]
- Hofacker I. Vienna RNA secondary structure server. Nucleic Acids Res. 2003;31:3429–3431. doi: 10.1093/nar/gkg599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofacker I, et al. Combinatorics of RNA secondary structures. Discrete Appl. Math. 1996;88:207–237. [Google Scholar]
- Hofacker IL, et al. Fast folding and comparison of RNA secondary structures. Monatsh. Chem. 1994;125:167–188. [Google Scholar]
- Isambert H, Siggia ED. Modeling RNA folding paths with pseudoknots: application to hepatitis delta virus ribozyme. Proc. Natl Acad. Sci. USA. 2000;97:6515–6520. doi: 10.1073/pnas.110533697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klemm K, et al. Recent Advances in the Theory and Application of Fitness Landscapes. Vol. 6. Berlin, Germany: Springer; 2014. pp. 153–176. [Google Scholar]
- Klinkert B, Narberhaus F. Microbial thermosensors. Cell. Mol. Life Sci. 2009;66:2661–2676. doi: 10.1007/s00018-009-0041-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klotz T, Kobe S. “Valley Structures” in the phase space of a finite 3D Ising spin glass with ±i interactions. J. Phys. A Math. Gen. 1994;27:L95–L100. [Google Scholar]
- Lorenz R, et al. 2D projections of RNA folding landscapes. In: Grosse I, et al., editors. GCB.LNI. Vol. 157. 2009. pp. 11–20. [Google Scholar]
- Lorenz R, et al. ViennaRNA Package 2.0. Alg. Mol. Biol. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz W, Clote P. Computing the partition function for kinetically trapped RNA secondary structures. PLoS One. 2011;6:e16178. doi: 10.1371/journal.pone.0016178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathews D, et al. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- Mathews DH, et al. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl Acad. Sci. USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maňuch J, et al. NP-completeness of the energy barrier problem without pseudoknots and temporary arcs. Nat. Comput. 2011;10:391–405. [Google Scholar]
- McCaskill JS. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
- Morgan S, Higgs P. Barrier heights between ground states in a model of RNA secondary structure. J. Phys. A Math. Gen. 1998;31:3153–3170. [Google Scholar]
- Narberhaus F, et al. RNA thermometers. FEMS Microbiol. Rev. 2006;30:3–16. doi: 10.1111/j.1574-6976.2005.004.x. [DOI] [PubMed] [Google Scholar]
- Perrotta AT, Been MD. A toggle duplex in hepatitis delta virus self-cleaving RNA that stabilizes an inactive and a salt-dependent pro-active ribozyme conformation. J. Mol. Biol. 1998;279:361–373. doi: 10.1006/jmbi.1998.1798. [DOI] [PubMed] [Google Scholar]
- Ponty Y. Efficient sampling of RNA secondary structures from the Boltzmann ensemble of low-energy: the boustrophedon method. J. Math. Biol. 2008;56:107–127. doi: 10.1007/s00285-007-0137-z. [DOI] [PubMed] [Google Scholar]
- Reidys CM, Stadler PF. Combinatorial landscapes. SIAM Rev. 2002;44:3–54. [Google Scholar]
- Rivas E, Eddy SR. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 1999;285:2053–2068. doi: 10.1006/jmbi.1998.2436. [DOI] [PubMed] [Google Scholar]
- Rother K, et al. RNA and protein 3D structure modeling: similarities and differences. J. Mol. Model. 2011;17:2325–2336. doi: 10.1007/s00894-010-0951-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahoo S, Albrecht AA. Approximating the set of local minima in partial RNA folding landscapes. Bioinformatics. 2012;28:523–530. doi: 10.1093/bioinformatics/btr715. [DOI] [PubMed] [Google Scholar]
- Schultes EA, Bartel DP. One sequence, two ribozymes: implications for the emergence of new ribozyme folds. Science. 2000;289:448–452. doi: 10.1126/science.289.5478.448. [DOI] [PubMed] [Google Scholar]
- Sibani P, et al. The lid method for exhaustive exploration of metastable states of complex systems. Comput. Phys. Commun. 1999;116:17–27. [Google Scholar]
- Smit S, et al. RNA structure prediction from evolutionary patterns of nucleotide composition. Nucleic Acids Res. 2009;37:1378–1386. doi: 10.1093/nar/gkn987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smit S, et al. Evolutionary rates vary among rRNA structural elements. Nucleic Acids Res. 2007;35:3339–3354. doi: 10.1093/nar/gkm101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang X, et al. Simulating RNA folding kinetics on approximated energy landscapes. J. Mol. Biol. 2008;381:1055–1067. doi: 10.1016/j.jmb.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Thirumalai D, et al. Early events in RNA folding. Annu. Rev. Phys. Chem. 2001;52:751–762. doi: 10.1146/annurev.physchem.52.1.751. [DOI] [PubMed] [Google Scholar]
- Wales DJ. Decoding the energy landscape: extracting structure, dynamics and thermodynamics. Phil. Trans. R. Soc. A. 2011;370:2877–2899. doi: 10.1098/rsta.2011.0208. [DOI] [PubMed] [Google Scholar]
- Wolfinger MT, et al. Exact folding dynamics of RNA secondary structures. J. Phys. A Math. Gen. 2004;37:4731–4741. [Google Scholar]
- Wuchty S, et al. Complete suboptimal folding of RNA and the stability of secondary structures. Biopolymers. 1999;49:145–165. doi: 10.1002/(SICI)1097-0282(199902)49:2<145::AID-BIP4>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- Xayaphoummine A, et al. Encoding folding paths of RNA switches. Nucleic Acids Res. 2007;35:614–622. doi: 10.1093/nar/gkl1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker M, Sankoff D. RNA secondary structures and their prediction. Bull. Math. Biol. 1984;46:591–621. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.