Sodium MRI: Methods and applications

Abstract

Sodium NMR spectroscopy and MRI have become popular in recent years through the increased availability of high-field MRI scanners, advanced scanner hardware and improved methodology. Sodium MRI is being evaluated for stroke and tumor detection, for breast cancer studies, and for the assessment of osteoarthritis and muscle and kidney functions, to name just a few. In this article, we aim to present an up-to-date review of the theoretical background, the methodology, the challenges and limitations, and current and potential new applications of sodium MRI.

1. Background

1.1. Introduction

Sodium is the most abundant cation present in the human body, and performs a number of vital body functions. The balance between intra- and extra-cellular sodium concentration is particularly crucial for insuring the proper functioning of a cell, and disturbances of this balance are often signs of disorders (e.g. in stroke or in tumors). In addition, sodium takes part in such processes as nerve signal transmission and muscle action. A further frequent function is the regulation of osmotic pressure. For example, in cartilage and in intervertebral disk tissue, sodium ions balance the negative charges of glycosaminoglycans, which leads to an uptake of water into the tissue. Measuring the sodium concentration directly in the tissues of interest or in vivo hence is of great interest for providing additional biochemical information about both normal and abnormal body functions.

Although proton MRI has been highly successful, very often the information from standard MRI cannot provide direct biochemical markers for cell integrity and tissue viability, or for following changes in tissue viability upon treatment. Sodium MRI could provide some of this complementary information in a quantitative and non-invasive manner. A fact often overlooked is that ²³Na also yields the second strongest nuclear magnetic resonance (NMR) signal among all nuclei present in biological tissues, after proton ¹H spins.

Due to the increase of the available magnetic fields for MRI scanners (1.5 T, 3 T, 7 T, 9.4 T), hardware capabilities such as strong gradient strengths with high slew rates, and new double-tuned radiofrequency (RF) coils, sodium MRI is now possible within reasonable measurement times (~10–15 min) with a resolution of a few millimeters and has already been applied in vivo in many human organs such as brain, cartilage, kidneys, heart, as well as in muscle and breast.

The majority of current sodium MRI applications can be understood without much sophisticated theory beyond assuming the study of a nucleus with very short T₂ relaxation. On the other hand, contrast and quantification can in many situations be significantly affected by the underlying spin dynamics which is governed either by a residual or a fluctuating quadrupolar interaction, which leads to line splittings in the former, and to biexponential relaxation in the latter case. In tissues, a complex mix of the two cases often persists, including the confounding factors of inhomogeneities and exchange. Taking full stock of all underlying phenomena and the information content available from advanced methods both ex vivo and in vivo can allow one to extract further tissue parameters and provide opportunities for new imaging contrast.

In this review article we focus on regimes ranging from liquids to semi-solids, thereby specifically excluding applications in the solid state. For applications in solids, we wish to refer the reader to other review articles that cover those fields, their methodology and applications [1–6].

Also, we wish to emphasize that ²³Na NMR and MRI applications in semi-solids are certainly not limited to health-related fields, and studies have appeared in fields related to materials science as well [7,8]. In this review article, however, we put an emphasis on health-related and physiologically relevant applications.

A number of excellent review articles focusing on ²³Na NMR in semi-solids and ²³Na MRI should be highlighted here as well [9–16].

1.2. Sodium in biological tissues

Sodium is a vital component of the human body. It is an important electrolyte that helps maintain the homeostasis of the organism through osmoregulation (maintaining blood and body fluid volume) and pH regulation [17]. It is also involved in cell physiology through the regulation of the transmembrane electrochemical gradient, thus partaking in heart activity, in the transmission of nerve impulses, and in muscle contractions. Sodium concentrations are very sensitive to changes in the metabolic state of tissues and to the integrity of cell membranes.

The intra-cellular fraction makes up approximately 80% of the tissue volume with a sodium concentration of 10–15 mM, and the extra-cellular volume fraction (including the vascular compartment) accounts for the rest, with a sodium concentration of 140–150 mM. Cells in healthy tissues maintain this large sodium concentration gradient between the intra-cellular and extra-cellular compartments across the cell membrane, and any impairment of the energy metabolism or disruption of the cell membrane integrity leads to an increase of the intra-cellular sodium concentration. The sodium flux in and out of cells can occur by several mechanisms. Examples of these include voltage- and ligand-gated Na⁺ channels, Na⁺/Ca⁺ exchangers (NCX), Na⁺/H⁺ exchangers (NHE), Na⁺/bicarbonate ( ${\text{HCO}}_3^{-}$) cotransporters, Na⁺/K⁺/2Cl⁻ cotransporters, Na⁺/Mg⁺ exchangers and most importantly the Na⁺/K⁺-ATPase [18].

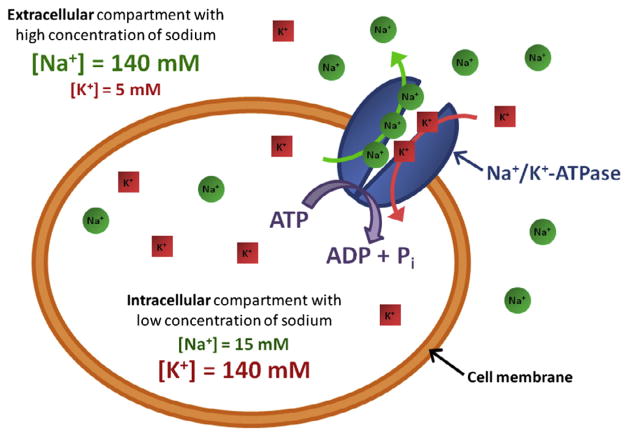
The Na⁺/K⁺-ATPase (also called sodium–potassium pump, or just sodium pump) is present within the membrane of every animal cell [19,20]. It is a plasma membrane-associated protein complex that is expressed in most eukaryotic cells, whose main function is to maintain the sodium and potassium gradients across the membrane. It therefore participates in the resting potential of the cell, by pumping three sodium ions out of the cell while pumping two potassium ions into the cell (see Fig. 1).

Fig. 1.

Schematics of the sodium–potassium pump (Na⁺/K⁺-ATPase).

The ion transport is performed against the electrochemical Na⁺ and K⁺ gradients existing across the cell membrane and therefore requires energy provided by adenosine triphosphate (ATP) hydrolysis. This large electrochemical gradient is essential to protect the cell from bursting as a result of osmotic swelling and also creates a potential that is used for transmitting nerve impulses and for pumping ions (such as protons, calcium, chloride, and phosphate) and metabolites and nutrients (such as glucose and amino acids) or neurotransmitters (such as glutamate) across the cell membrane. ATPase activity and ion transport are intimately linked and are two aspects of the same function. Regulation of Na⁺/K⁺-ATPase therefore plays a key role in the etiology of some pathological processes. For example, when the demand for ATP exceeds its production, the ATP supply for the Na⁺/K⁺-ATPase will be insufficient to maintain the low intra-cellular sodium concentration and thus an increase of intra-cellular sodium concentration can be observed [18,19].

1.3. Beginnings of biological sodium NMR

Biological tissues were already investigated with sodium NMR spectroscopy in the early 1970s [21,22] and with sodium MRI in the early 1980s [23–25], first on animals in vivo and then on human brain [26] and human heart and abdomen [27]. Sodium MRI was thereafter applied to brain tumor and ischemia detection in the late 1980s [28]. In the 1990s there was an increase of interest in sodium MRI, due to the increase of the magnetic fields in scanners, improvements of electronics and RF coils, and new rapid sequences that allowed one to acquire sodium images within a few minutes with millimeter resolution [29]. New contrasts such as triple quantum filtering [30–32] provided further promise of tissue discrimination and characterization. This trend continued and intensified through the 2000s until today.

1.4. Sodium NMR properties

The NMR-active isotope of sodium is ²³Na with close to 100% natural abundance. Its Larmor frequency is approximately 5% larger than the one of ¹³C, and ~26% of the proton frequency. ²³Na has a nuclear spin of 3/2, and hence exhibits a quadrupolar interaction. The NMR sensitivity of sodium is 9.2% of the proton sensitivity and the concentration in vivo is approximately 2000 times lower than the water proton concentration. As a consequence, sodium MRI has on average a signal-to-noise (SNR) ratio which is 3000–20,000 times lower than the proton MRI SNR (depending on its concentration and visibility in organs or tissues).

The nuclear quadrupolar moment Q interacts with the electric field gradients (EFG) generated by the electronic distribution around the nucleus [3,33,34]. In liquids this interaction is often averaged to zero. In the intermediate (semi-solid) regime, e.g. in biological tissues, the quadrupolar interaction results in a biexponential relaxation behavior, and with anisotropic motion, line splittings may appear. The dominance of the quadrupolar relaxation mechanism for NMR signals can allow a sensitive characterization of the molecular environment of the sodium ions. A short T₂ component T_2,fast = 0.5–5 ms generally contributes to 60% of the signal, and a long component T_2,slow = 15–30 ms corresponds to 40% of the signal. In order to detect both T₂ components, imaging techniques with ultrashort echo times (UTE) of less than 0.5 ms are required. Typical ranges of sodium concentrations and relaxation times in some human tissues in vivo are given in Table 1. It has been shown that in the slow-motion regime, where biexponential relaxation is observed, multiple quantum coherences (MQC) can be created and selectively detected with multiple quantum filtered (MQF) sequences [35], thereby providing additional opportunities for the identification of intra-cellular sodium.

Table 1.

Ranges of sodium concentrations and relaxation times in some human tissues in vivo (T₁ and the fast and slow components of T₂, i.e. T_2,fast, and T_2,slow, respectively). These ranges are based on Refs. [11,36–42] and references therein. WM – white matter, GM – grey matter, CSF – cerebrospinal fluid.

Tissue	[Na+] (mM)	T1 (ms)	T2,fast (ms)	T2,slow (ms)
Brain
WM	20–60	15–35	0.8–3	15–30
GM	30–70	15–35	0.8–3	15–30
CSF	140–150	50–55	–	55–65
Cartilage	250–350	15–25	0.5–2.5	10–30
Blood	140–150	20–40	2–3	12–20
Muscle	15–30	12–25	1.5–2.5	15–30

2. Theoretical formalism and pulse sequences

2.1. Tensors and hamiltonians

2.1.1. Irreducible spherical tensor operators (ISTOs)

The ensemble spin-states of a spin 3/2 system can be described by a 4 × 4 density matrix

$$\rho =({\rho }_{ij})=\sum _{ij}{\rho }_{ij}\mid i\rangle \langle j\mid =\left(\begin{array}{cccc}{\rho }_{11}& {\rho }_{12}& {\rho }_{13}& {\rho }_{14}\\ {\rho }_{21}& {\rho }_{22}& {\rho }_{23}& {\rho }_{24}\\ {\rho }_{31}& {\rho }_{32}& {\rho }_{33}& {\rho }_{34}\\ {\rho }_{41}& {\rho }_{42}& {\rho }_{43}& {\rho }_{44}\end{array}\right),$$

where the spin-states |i〉 ∈ {|1〉, |2〉, |3〉, |4〉} correspond to the eigen-states of the z-component of the spin angular momentum operator, I_z, with the magnetic quantum numbers $\frac{3}{2},\frac{1}{2},-\frac{1}{2},-\frac{3}{2}$, respectively. While in $\text{spin}-\frac{1}{2}\text{NMR}$ it is common to use the Cartesian tensor operators or product operators [43–45], irreducible spherical tensor operators (ISTOs) are more suitable for expanding the matrix into individual components for a spin ≥ 1/2. The ISTOs for the spin 3/2 case are made up of a set of 16 operators T_lm with rank l = 0, 1, 2, 3 and order m = −l, …,+l [46–48], allowing a complete and orthogonal expansion of the form

$$\rho =\sum _{l,m}{c}_{lm}{T}_{lm},$$ (1)

with c_lm being complex numbers. Several tensor normalizations are in use, which differ by a pre-factor which depends on l and the spin number I. The most common normalization is the one listed in [46,47], which provides the spin-independent relationship $I_{\pm }=\mp \sqrt{2}{T}_{1\pm 1}$, and also allows one to couple tensors using Clebsch–Gordan factors without any additional conversion factors. With this convention, the ISTOs have the matrix representations as listed in Table 2. The ISTOs can also be written in the form of linear combinations of Cartesian or raising and lowering operators (I_± and I_± = I_x ± iI_y) as shown in Table 3.

Table 2.

Matrix expressions of the irreducible spherical tensors T_l,m in the |i〉 basis. The expressions for T_l,−m are found by $T_{l,-m}={(-1)}^m{T}_{l,m}^{†}$, where † means hermitian conjugation (i.e. simple transposition in the case of real entries of these matrices).

$T_{0,0}=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$

$T_{1,0}=\left(\begin{array}{cccc}\frac{3}{2}& 0& 0& 0\\ 0& \frac{1}{2}& 0& 0\\ 0& 0& -\frac{1}{2}& 0\\ 0& 0& 0& -\frac{3}{2}\end{array}\right)T_{1,1}=\left(\begin{array}{cccc}0& -\sqrt{\frac{3}{2}}& 0& 0\\ 0& 0& -\sqrt{2}& 0\\ 0& 0& 0& -\sqrt{\frac{3}{2}}\\ 0& 0& 0& 0\end{array}\right)$

$T_{2,0}=\left(\begin{array}{cccc}\sqrt{\frac{3}{2}}& 0& 0& 0\\ 0& -\sqrt{\frac{3}{2}}& 0& 0\\ 0& 0& -\sqrt{\frac{3}{2}}& 0\\ 0& 0& 0& \sqrt{\frac{3}{2}}\end{array}\right)T_{2,1}=\left(\begin{array}{cccc}0& -\sqrt{3}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& \sqrt{3}\\ 0& 0& 0& 0\end{array}\right)T_{2,2}=\left(\begin{array}{cccc}0& 0& \sqrt{3}& 0\\ 0& 0& 0& \sqrt{3}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$

$T_{3,0}=\left(\begin{array}{cccc}\frac{3}{2\sqrt{10}}& 0& 0& 0\\ 0& -\frac{9}{2\sqrt{10}}& 0& 0\\ 0& 0& \frac{9}{2\sqrt{10}}& 0\\ 0& 0& 0& -\frac{3}{2\sqrt{10}}\end{array}\right)T_{3,1}=\left(\begin{array}{cccc}0& -\frac{3}{\sqrt{10}}& 0& 0\\ 0& 0& 3\sqrt{\frac{3}{10}}& 0\\ 0& 0& 0& -\frac{3}{\sqrt{10}}\\ 0& 0& 0& 0\end{array}\right)T_{3,2}=\left(\begin{array}{cccc}0& 0& \frac{3}{2}& 0\\ 0& 0& 0& -\frac{3}{2}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)T_{3,3}=\left(\begin{array}{cccc}0& 0& 0& -\frac{3}{\sqrt{2}}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$

Table 3.

Relationship between irreducible spherical tensor (ISTO) and Cartesian operators (spin-independent).

ISTO	Cartesian decomposition	Description
T00	1	Identity
T10	Iz	Longitudinal magnetization
T1±1	$\mp \frac{1}{\sqrt{2}}{I}_{\pm }$	Rank 1 SQC
T20	$\frac{1}{\sqrt{6}}\left(3I_z^2-I(I+1)\right)$	Quadrupolar order
T2±1	$\mp \frac{1}{2}{[I_z,I_{\pm }]}_{+}$	Rank 2 SQC
T2±2	$\frac{1}{2}{I}_{\pm }^2$	Rank 2 DQC
T30	$\frac{1}{\sqrt{10}}\left(5I_z^3-(3I(I+1)-1)I_z\right)$	Octupolar order
T3±1	$\mp \frac{1}{4}\sqrt{\frac{3}{10}}{\left[5I_z^3-I(I+1)-\frac{1}{2},I_{\pm }\right]}_{+}$	Rank 3 SQC
T3±2	$\frac{1}{2}\sqrt{\frac{3}{4}}{\left[I_z,I_{\pm }^2\right]}_{+}$	Rank 3 DQC
T3±3	$\mp \frac{1}{2\sqrt{2}}{I}_{\pm }^3$	Rank 3 TQC

SQC, DQC and TQC stand for single, double, and triple quantum coherences. The anticommutator for the operators A and B is defined as [A, B]₊ = AB + BA.

2.1.2. The Zeeman term and the equilibrium density matrix

The Zeeman Hamiltonian in angular frequency units (or units of J/ħ) is given by

$${\mathcal{H}}_z=-{\omega }_0{I}_z=-{\omega }_0{T}_{10},$$ (2)

with ω₀ = γ_NaB₀ the Larmor angular frequency, γ_Na = 70.808493 × 10⁶ rad T⁻¹ s⁻¹ the sodium gyromagnetic ratio, and B₀ the magnetic field. The chemical shift range of ²³Na is very small, and its contribution is therefore ignored in this equation and for much of the rest of this article (a notable exception is the discussion of dynamic frequency shifts and paramagnetic shifts which will be mentioned later).

The Zeeman interaction is by far the most dominant interaction in most ²³Na NMR applications, In this case, one can write the equilibrium density matrix via the Boltzmann distribution as

$${\rho }_{eq}=\frac{exp(\hslash {\omega }_0{I}_z/kT)}{Z}\approx \frac{1}{Z}\mathbf{1}+\hslash {\omega }_0{I}_z/kT,$$ (3)

where Z = Tr{exp(ħω₀I_z/kT)}, 1 is the identity matrix, and the last step is made by use of the high-temperature approximation. Since 1 does not lead to any observables, and does not participate in the evolution, one typically omits this term and writes

$${\rho }_{eq}={aI}_z,$$ (4)

where the Boltzmann factor a = ħγB₀/kT is likewise frequently omitted.

2.1.3. The quadrupolar Hamiltonian (H_Q)

The quadrupolar interaction arises from the electrostatic energy term involving the charge distribution of the nucleus and the electric field gradient around the nucleus [3,33,34]. The quadrupolar term is the first non-vanishing term in a series expansion, with higher order terms (hexadecapole) being negligibly small.

Since the nuclear quadrupole moment can be assumed to be constant, the nuclear quadrupole interaction is determined by the orientation, magnitude and temporal average of the electric field gradient (EFG) generated by the electronic configuration of the molecular environment surrounding the nucleus. If V(x, y, z) is the electrostatic potential produced by the electrons at the point (x, y, z), the EFG can be described by the tensor V_αβ with the components:

$$V_{\alpha \beta }=\frac{{\partial }^{2}V}{\partial \alpha \partial \beta },(\text{with}\alpha ,\beta =x,y,\text{or}z).$$ (5)

If we choose the principal axes of the symmetric tensor V_αβ as coordinate axes, the cross-terms vanish, i.e. V_xy = V_xz = V_yz = 0. It is common to label the remaining components such that |V_zz| ≥ |V_yy| ≥|V_xx|, and to define V_zz = eq (where e is the unit electric charge, and q the field gradient per unit charge) and to define the anisotropy parameter

$$\eta =\frac{V_{xx}-V_{yy}}{V_{zz}},0\le \eta \le 1.$$ (6)

The quadrupolar interaction is then represented by the quadrupolar Hamiltonian

$${\mathcal{H}}_Q={\omega }_Q\sum _{m=-2}^2{(-1)}^M{F}_{2,-m}{T}_{2m},$$ (7)

where the quadrupolar coupling angular frequency is

$${\omega }_Q=\frac{e^{2}qQ}{6\hslash },$$ (8)

with Q the nuclear quadrupole moment. The spatial tensors F_lm in the principal axis frame (PAS) of V_αβ take the form

$$\begin{array}{l}{F}_{2,0}^{\mathit{PAS}}=\sqrt{\frac{3}{2}},\\ F_{2,\pm 1}^{\mathit{PAS}}=0,\\ F_{2,\pm 2}^{\mathit{PAS}}=\frac{\eta }{2}.\end{array}$$ (9)

The dependence of the interaction on orientation of the PAS with respect to the magnetic field can be described via

$$F_{lm}=\sum _{m^{\prime },m}{D}_{m^{\prime },m}^l(\alpha ,\beta ,\gamma )F_{l{m}^{\prime }}^{\mathit{PAS}}$$ (10)

using the Wigner rotation matrices ( $D_{m^{\prime },m}^l$) [49].

2.1.4. The effect of a residual quadrupolar interaction

We may consider two cases here, with very similar outcomes: (1) H_Z ≫ H_Q and no motion or (2) partial averaging and downscaling of the quadrupolar interaction such that H_Z ≫ 〈H_Q 〉. In both cases one can truncate the quadrupolar Hamiltonian to the secular component,

$${\mathcal{H}}_Q={\omega }_Q\sqrt{\frac{3}{2}}{T}_{20}=\frac{{\omega }_Q}{2}[3I_z^2-I(I+1)].$$ (11)

This interaction then predicts the appearance of three resonance lines with distance 3ω_Q/2π between them as shown schematically in Fig. 2,, type-a. The relative intensity of the lines is 3:4:3, which originates from the observable signal as determined by $\text{Tr}\{I_{-\rho }^{†}\}$. The relative ratio then amounts to the relative values of the squares of the off-diagonal elements of the T_1,−1 tensor. The outer transitions are typically called the satellite transitions, and the inner one is called the central transition.

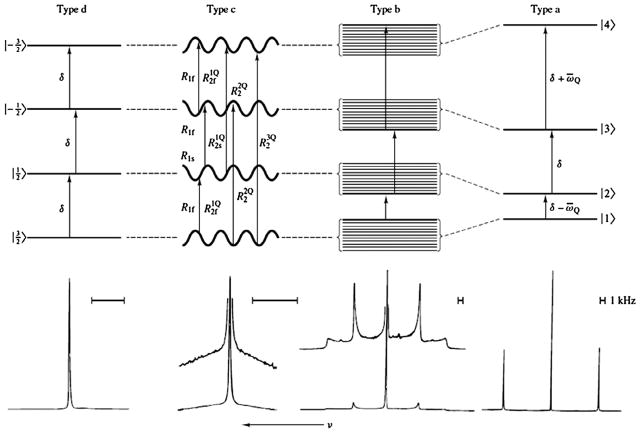
Fig. 2.

Typical energy levels and corresponding NMR spectra of sodium nuclei in different environments. Four types of motionally narrowed SQ spectra are possible (a, b, c, and d). The type-a (crystal-like) and type-b (powder-like) spectra are shown of Na⁺ in aqueous suspensions of oriented and unoriented dodecyl sulfate micelles, respectively. The type-c (homogeneous, biexponential, super-lorentzian-like) spectrum is that of Na⁺ in an aqueous solution that has a high concentration of micelle-solubilized gramicidin channels. The type-d (liquid-like) spectrum is from NaCl in H₂O. We can make the correspondence $\overline{{\omega }_Q}=3{\omega }_Q$ in type-a. Reproduced with permission from Ref. [12].

In the second case, where the quadrupolar coupling is the result of some downscaled coupling via reorientation motion, ω_Q would represent the temporally and spatially averaged coupling constant 〈ω_Q F_2,0〉 in Eq. (11). Strictly speaking, ω_Q would also contain the term from the anisotropy factor, $\sqrt{1+\frac{{\eta }^2}{3}}$, but since this factor can rarely be measured independently in motionally averaged systems, we will not carry it along here.

In solids, situations may arise when the secular approximation is no longer justified. It is common to include the second order perturbation term in the overall Hamiltonian. We neglect this component here, as this case is not relevant to tissues or semi-solids as considered here.

Fig. 2 shows different motional regimes that can be observed, and their ensuing spectra. The effect described here corresponds to the ‘type-a’ category as classified by Rooney and Springer [12–14]. ‘Type-b’ spectra arise when the sample is inhomogeneous and contains regions with a distribution of quadrupolar couplings, leading to a distribution of level shifts as indicated in Fig. 2. The effect of a fluctuating quadrupolar interaction is illustrated with the ‘type-c’ regime and leads to biexponential relaxation as discussed later. Finally, if the fluctuations are very fast, or in the absence of a quadrupolar interaction one recovers the spectrum of ‘type-d’ where all transitions are equivalent. In such a case, the spin transitions do not differ from those of a spin 1/2 nucleus.

2.2. Evolution and conversion between tensors

In this section we first provide a general overview of the effects and conversions that typically occur in experiments, and provide a full solution later. The evolution of a ²³Na nuclear spin can be described by the master equation given as

$$\frac{d}{dt}\rho (t)=-i[\mathcal{H},\rho (t)]-\widehat{\widehat{\mathit{\Gamma }}}\{\rho (t)-{\rho }^{th}\},$$ (12)

where ρ^th is the density operator in the thermal equilibrium state, 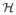the spin Hamiltonian, and $\widehat{\widehat{\mathit{\Gamma }}}$ the relaxation superoperator.

The total Hamiltonian 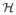can for most practical purposes in ²³Na NMR of tissues and liquids be assumed to be equal to 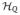(one may wish to allow for inhomogeneous broadening, in which case a distribution of 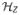terms would be added).

In order to follow the sequence of events in experiments at high magnetic fields, one can follow these simple rules: [3,48].

1. A non-selective radiofrequency (RF) pulse changes the coherence order m within the limits of |m|italic> l. The amplitude induced by the rotation is given by the corresponding Wigner rotation element, so a rotation with flip angle θ and phase ϕ of T_l,m to T_l,m′ gives rise to a factor $exp(-i\varphi (m^{\prime }-m))d_{m,m^{\prime }}^l(\theta )$, where $d_{m,m^{\prime }}^l(\theta )$ is the reduced Wigner rotation matrix element.

2. The quadrupolar coupling Hamiltonian can only change the rank l.

3. Quadrupolar relaxation can only change the rank l.

After a ${90}_y^{°}$ pulse acting on equilibrium magnetization, one obtains $\rho =I_x=\frac{1}{\sqrt{2}}(T_{1,-1}-T_{1,1})$. A constant residual quadrupolar coupling (type-d) would lead to evolution within the following subspaces

$$\{T_{1,1},T_{2,1},T_{3,1}\}\text{and}\{T_{1,-1},T_{2,-1},T_{3,-1}\}$$ (13)

due to the commutation relationships

$$\begin{array}{l}[T_{2,0},T_{1,\pm 1}]=\pm \sqrt{3}{T}_{2,\pm 1}\\ [T_{2,0},T_{2,\pm 1}]=\pm \frac{6\sqrt{3}}{5}{T}_{1,\pm 1}+\frac{4}{\sqrt{5}}{T}_{3,\pm 1}\\ [T_{2,0},T_{3,\pm 1}]=\pm \frac{3}{\sqrt{5}}{T}_{2,\pm 1}.\end{array}$$ (14)

On the other hand, if only quadrupolar relaxation were active, the double-commutators [T_2,0,[T_2,0, ρ]], [T_2,±1, [T_2,∓1, ρ]], and [T_2,±2, [T_2,∓2, ρ]] in the Redfield relaxation expressions that make up $\widehat{\widehat{\mathit{\Gamma }}}$ can only connect operators within the following subspaces

$$\{T_{1,1},T_{3,1}\},\{T_{1,-1},T_{3,-1}\},\{T_{1,0},T_{3,0}\}.$$ (15)

Hence, in isotropic liquids only odd rank tensors T_3±1 can be formed under the influence of quadrupolar relaxation. In anisotropic media, where the residual quadrupolar interaction does not average to zero, rank 2 tensors T_2±1 can be also formed.

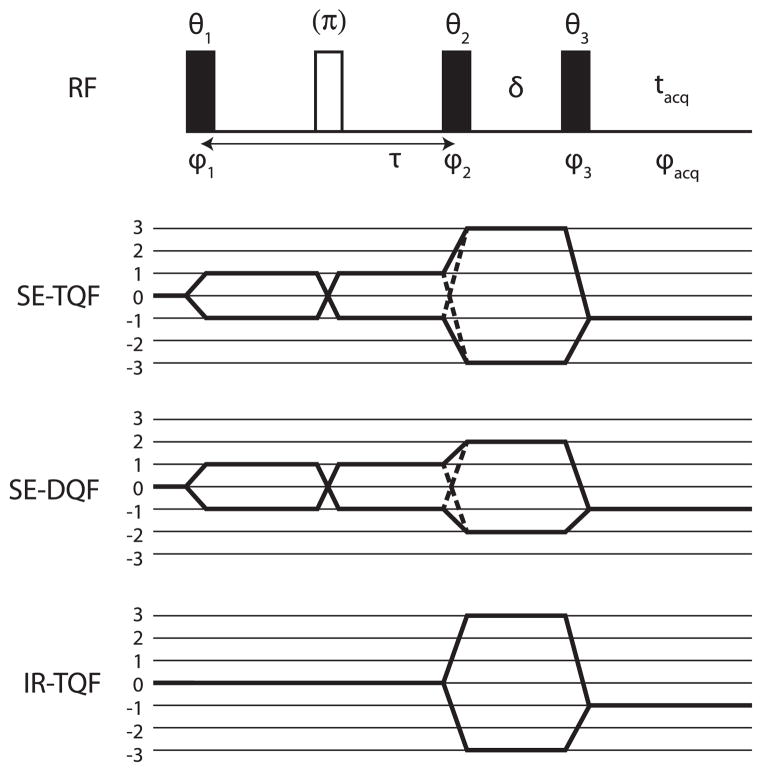
A multiple-quantum filtered (MQF) experiment can be used to distinguish between the two cases [35,50–52]. For example, the T_2,±1 term generated in the first case can be converted to a double-quantum coherence (DQC) term T_2,±2 by another pulse, while this term is not available due to relaxation alone. The corresponding pulse sequence is shown in Fig. 3, along with the different phase cycles that would be used for the experiments.

Fig. 3.

Multiple quantum filter (MQF) pulse sequence. For the triple quantum filter (TQF), θ₁ = θ₂ = θ₃ = 90°, and a typical phase cycle is ϕ₁ = 30°, 90°, 150°, 210°, 270°, 330°, ϕ₂ = ϕ₁, ϕ₃ = 90°, ϕ_acq = 0, 180°. For the double quantum filter (DQF) a typical phase cycle is θ₁ = θ₂ = θ₃ = 90°, ϕ₁ = 0°, 90°, 180°, 270°, ϕ₂ = ϕ₁ − 90°, ϕ₃ = 90°, ϕ_acq = 0, 180°. For DQF with magic angle pulses (DQF-MA), θ₁ = 90°, θ₂ = θ₃ = 54.7°, and the phase cycling is the same as for DQF. For the IR-TQF sequence, θ₁ = 180°, θ₂ = θ₃ = 90°, and no additional 180° pulse is used. The phase cycle is ϕ₁ = 30°, 90°, 150°, 210°, 270°, 330°, ϕ₂ = ϕ₁ − 90°, ϕ₃ = 90°, ϕ_acq = 0, 180°. The delay δ is kept as short as possible to avoid signal decay. These minimal phase cycles could be augmented by an independent 2-step cycle on the first pulse (with an accompanying 0, 180° cycle on the receiver), and a 2-step cyclec on the 180° pulse, giving a 12 or a 24-step cycle for the TQF/IR-TQF experiments, and 8 or 16-step cycle for DQF.

One can also separate the regimes to some degree using a triple-quantum filtered (TQF) experiment by a judicious choice of pulse flip angles, as discussed in more detail below.

Since multiple quantum coherences (MQCs) cannot be detected directly, the final RF pulse converts the MQCs into single quantum coherences (SQCs), T_1±1, T_2±1, T_3±1, which then evolve under the action of relaxation and the residual quadrupolar interaction (RQI) into detectable SQC (T_1,−1) during the acquisition time t_acq. A 180° RF pulse can be applied in the middle of the preparation time τ in order to refocus any chemical shifts, or more typically magnetic field inhomogeneities. Since MQFs are very sensitive to RF imperfections, it has been shown that filters without this refocusing pulse generate a better signal and are more robust to RF inhomogeneities for in vivo MQF MRI [53]. Recently, procedures have been published for avoiding B₀ inhomogeneities by separately acquiring and storing the individual phase cycling steps and subsequent post-processing before co-adding the individual signals [54–56]. Specific absorption rate (SAR) considerations also favor the sequence without the 180° pulse. The formation of DQC and TQC is detected separately by choosing the appropriate RF pulse flip angles and phase cycling. Typical phase cycles and choices of RF pulse flip angles are given in the caption of Fig. 3. DQF can detect the contribution of two tensors, T_2±2, T_3±2, due to the slow motion regime or/and RQI in anisotropic media. If θ₁ = θ₂ = θ₃ = 90°, contributions from both T_2±1 and T_3±1 can be detected. If θ₁ = 90° and θ₂ = θ₃ = 54.7° (magic angle), only the contribution of T_2±2 is detected, which arises only from the anisotropic RQI. Only T_3±3 due to the slow motion regime can be detected by the TQF sequence.

2.3. Full solution of the evolution equations

In this section we provide the complete solution of the evolution equation, Eq. (12), based on residual quadrupolar coupling of the form of Eq. (11) and a fluctuating quadrupolar interaction of the form of Eq. (7) with the definitions in Eqs. (8) and (9) as the relaxation mechanism.

Using the Redfield formalism, one can write the action of the relaxation superoperator as

$$\widehat{\widehat{\mathit{\Gamma }}}\{\rho -{\rho }^{th}\}=A\sum _{m=-2}^2{(-1)}^m[T_{2,m},[T_{2,-m},\rho -{\rho }^{th}]](J(m\omega )-iK(m\omega )),$$ (16)

where J(ω) is the spectral density function, and iK(ω) is the imaginary portion arising in the Fourier Transform from the integration of the autocorrelation function from 0 to ∞(rather than from −∞ to ∞) [33], and A a constant used for conversion between different conventions as explained below. The K term gives rise to a small frequency shift, called the dynamic frequency shift. For the typical case of exponential autocorrelation functions, the relationship K(ω) = ωτ_cJ(ω) holds. The shift is rarely observable [57], since it is small (typically within the linewidth of the transitions [58]). We therefore neglect it for the rest of this treatment.

The convention used in our article is characterized by A = 1 and has the advantage that all quadrupolar-coupling-related expressions are included in J(ω). As a result, the expressions as listed below can be used directly for all fluctuation regimes, including direct fluctuations of electric field gradients, for example due to ion solvation or due to motion near a polyelectrolyte. For ease of comparison between different conventions, we list here the following definitions of the spectral density functions and conversion factors A for an isotropic tumbling model:

$$\text{Convention}\mathrm{I},$$ (17)

$$A=1,$$ (18)

$$J(\omega )=\frac{{(2\pi )}^2}{60}\frac{C_Q^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}.$$ (19)

Here C_Q is the ‘quadrupole coupling constant’ and has the usual definition C_Q = e²qQ/h (as noted before, the term from the anisotropy factor, $\sqrt{1+\frac{{\eta }^2}{3}}$, would be contained in here as well, which we drop for simplicity). Convention I is the one used in this article, as well as, for example in Refs. [10,59–61].

Other conventions are in use, of which two popular ones are

$$\text{Convention}\text{II},$$ (20)

$$A=\frac{1}{3},$$ (21)

$$J(\omega )=\frac{{(2\pi )}^2}{20}\frac{C_Q^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}$$ (22)

used for example in Refs. [48,62], and

$$\text{Convention}\text{III}.$$ (23)

$$A=\frac{1}{3}\frac{{(2\pi )}^2}{40}{C}_Q^2,$$ (24)

$$J(\omega )=\frac{2{\tau }_c}{1+{(\omega {\tau }_c)}^2},$$ (25)

which is used for example in [35,63]. Note that for C given in Refs. [35,63], the relationship C = 3A holds.

Closed solutions can be obtained by using the tensor operator basis or the single transition basis. There is no obvious advantage of one vs. the other. Eventually, it is most useful to represent the final evolution expressions in the form of spherical tensor transformations. The results are easy to interconvert from one basis to another. The right hand side of Eq. (12) can be evaluated in the tensor basis as summarized in Table 4. Note, that these results are completely equivalent to those given in other works [48,62] when considering that there Convention II for scaling J(ω), and normalized tensors with symmetric and antisymmetric linear combinations ( $T_{lm}(s)=\frac{1}{\sqrt{2}}[T_{lm}+T_{l,-m}]$, and $T_{lm}(a)=\frac{1}{\sqrt{2}}[T_{lm}-T_{l,-m}]$) were used. From these expressions, one can then derive full analytical solutions to the evolution for a number of special cases. The complete solution is given in Appendix A, and we highlight some of the main results in the text below.

Table 4.

Conversion amplitudes in the equation of motion, Eq. (12), from a tensor T_l2,m to a tensor T_l1/,m. The expressions for the negative orders m are identical except for complex conjugation. For brevity, we use the notation J_m = J(mω) here.

m	l1	l2	amplitude
0	1	1	$-\frac{6}{5}(J_1+4J_2)$
0	1	3	$-\frac{18}{5}\sqrt{\frac{2}{5}}(J_1-J_2)$
0	2	2	−6(J1 + J2)
0	3	1	$-4\sqrt{\frac{2}{5}}(J_1-J_2)$
0	3	3	$-\frac{6}{5}(4J_1+J_2)$
1	1	1	$-\frac{3}{5}(3J_0+5J_1+2J_2)$
1	1	2	$-\frac{9}{5}i\sqrt{2}\omega Q$
1	1	3	$-\frac{9}{5}\sqrt{\frac{3}{5}}(J_0-J_2)$
1	2	1	$-\frac{3}{\sqrt{2}}i{\omega }_Q$
1	2	2	−3(J0 + J1 + 2J2)
1	2	3	$-3i\sqrt{\frac{3}{10}}{\omega }_Q$
1	3	1	$-2\sqrt{\frac{3}{5}}(J_0-J_2)$
1	3	2	$-2i\sqrt{\frac{6}{5}}{\omega }_Q$
1	3	3	$-\frac{3}{5}(2J_0+5J_1+3J_2)$
2	2	2	−3(J0 + 2J1 + J2)
2	2	3	$-i\frac{3}{2}\sqrt{3}{\omega }_Q$
2	3	2	$-2i\sqrt{3}{\omega }_Q$
2	3	3	−3(J0 + J2)
3	3	3	−3(J1 + J2)

2.4. Biexponential decay of the free induction decay (FID)

The free-induction decay after single pulse excitation in the absence of quadrupolar coupling (f_Q = 0) can be found from Eq. (A.29) to be biexponential

$$\frac{2}{5}{e}^{-R_{2,\text{slow}}t}+\frac{3}{5}{e}^{-R_{2,\text{fast}}t}=\frac{2}{5}{e}^{-[3J({\omega }_0)+3J(2{\omega }_0)]t}+\frac{3}{5}{e}^{-[3J(0)+3J({\omega }_0)]t}.$$ (26)

The origin of the biexponential relaxation can be understood as arising from the faster relaxation of the satellite transitions compared to the central transition, because they experience larger fluctuations from the instantaneous quadrupolar interactions.

2.5. TQF buildup behavior

According to Eq. (A.29), a free evolution delay τ after a single pulse gives rise to the appearance of a third-rank tensor with an amplitude proportional to

$$e^{-R_{2,\text{slow}}\tau }-e^{-R_{2,\text{fast}}\tau }=e^{-[3J({\omega }_0)+3J(2{\omega }_0)]\tau }-e^{-[3J(0)+3J({\omega }_0)]\tau }.$$ (27)

The third-rank component, when converted into triple-quantum coherences is filtered out using a TQF element (Fig. 3). Recording the buildup behavior of this component can be used to extract relaxation properties, or to filter out slow motion sodium.

2.6. Relaxation behavior of populations, third-rank tensor buildup after inversion pulse – IR-TQF experiment

One can observe the relaxation behavior of the −I_z-term by following the populations after a 180° inversion pulse as a function of the delay τ. The Zeeman term also has a biexponential relaxation behavior according to Eq. (A.11):

$$e^{-R_{1,\text{fast}}\tau }+4e^{-R_{1,\text{slow}}\tau }=e^{-6J({\omega }_0)\tau }+4e^{-6J(2{\omega }_0)\tau }.$$ (28)

In an IR-TQF (Fig. 3) experiment, one first generates the non-equilibrium state ρ = −I_z = −T₁₀ by a 180° pulse and then the third-rank component builds up as a function of τ, which can subsequently be filtered out by a TQF element. The T₃₀ term builds up according to Eq. (A.11) with an amplitude proportional to

$$e^{-R_{1,\text{fast}}\tau }-e^{-R_{1,\text{slow}}\tau }=e^{-6J({\omega }_0)\tau }-e^{-6J(2{\omega }_0)\tau }.$$ (29)

The buildup of the third rank component can again be thought of as arising from the faster relaxation of the populations in the outer energy levels due to larger fluctuations.

2.7. Analysis of biexponential decays and optimal settings

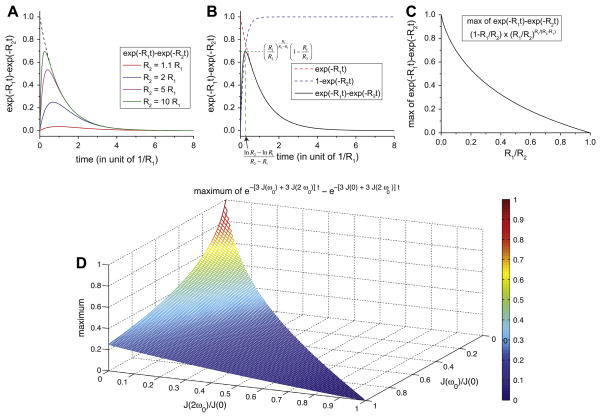
The buildup of the third-rank component as measured by the TQF and IR-TQF experiments can be analyzed as illustrated in Fig. 4. Fig. 4b illustrates the optimal setting for the delay τ based on the two relaxation rates R₂ and R₁ in the curve. Fig. 4c can be used to determine the maximum achievable signal at the optimal delay setting. It is clear that this signal goes to zero as the relaxation rates become equal to each other, indicating that no third-rank components were built up. Fig. 4d shows how the maximum achievable signal depends on the ratios J(ω₀)/J(0) and J(2ω₀)/J(0) in the TQF experiment. The largest amplitudes are achieved in the cases where the ratios go to zero (for example in the very slow motion regime, as discussed below).

Fig. 4.

(A) Plots of a biexponential function e^−R₁t − e^−R₂t with R₂ = 1.1R₁ (red), 2R₁ (blue), 5R₁ (purple), and 10R₁ (green). The dashed line is the plot of the function e^−R₁t alone. (B) Plot of a biexponential function e^−R₁t − e^−R₂t with R₂ = 10R₁. As visual guides, the two functions, e^−R₁t and 1 − e^−R₂t were plotted (red and blue dashed lines, respectively). The biexponential function reaches its maximum ${\left(\frac{R_1}{R_2}\right)}^{\frac{R_1}{R_2-R_1}}\left(1-\frac{R_1}{R_2}\right)$ when $t=\frac{ln{R}_2-ln{R}_1}{R_2-R_1}$. (C) Plot of the maximum of the biexponential function e^−R₁t − e^−R₂t as a function of the ratio R₁/R₂ (0 < R₁ ≤ R₂). This ratio is equal to J(2ω₀)/J(ω₀) for longitudinal relaxation and [J(ω₀) + J(2ω₀)]/[J(0) + J(ω₀)] for transverse relaxation. (D) Plot of the maximum of the biexponential function e^−R₁t − e^−R₂t for the transverse relaxation: R₁ = 3J(ω₀) + 3J(2ω₀) and R₂ = 3J(0) + 3J(2ω₀) with J(0) ≥ J(ω₀) ≥ J(2ω₀) > 0. With a ≡ J(ω₀)/J(0) and b ≡ J(2ω₀)/J(ω0), the maximum is given as ${\left(\frac{a+b}{1+a}\right)}^{\frac{a+b}{1-b}}\left(\frac{1-b}{1+a}\right)$ with 0 < b ≤ a ≤ 1.

2.8. Notes on phase cycling and pulse flip angles

One can distinguish between the TQF, IR-TQF, and DQF experiments on the basis of a suitable combination of flip angles with appropriate phase cycles [15,64,65]. At the core of the selection process is a 6-step cycle (with 60° intervals) for the first two pulses in the TQF/IR-TQF experiments (selecting ± triple quantum coherences), and a 4-step cycle with 90° intervals for the DQF experiment (selecting ± double quantum coherences), as illustrated in Fig. 3.

For the TQF experiments, the flip angles of the second and third pulses should be 90° to maximize the signal intensities (see a complete list of the flip-angle dependencies of different pathways in Appendix A). For the DQF experiment, suppose that the coherence pathways involving the second-rank tensors T_2,±1 need to be exclusively selected, the existence of which will show whether there is a residual quadrupolar coupling or not. By setting the flip angle of either the second or the third pulse (θ₂ and/or θ₃) to the magic angle, the coherence pathways involving the third-rank tensors T_3,±2 will be suppressed, since they have a sin θ₂ sin θ₃(1 − 3 cos² cos θ₂)(1 − 3 cos² cos θ₃) dependence (see Appendix A). By changing both flip angles from 90° to the magic angle, the signal from the coherence pathways involving the second-rank tensors T_2,±1 is reduced by sin θ₂ sin θ₃. Such a sequence is also typically called DQF-MA (with MA short for magic angle).

The flip-angle-based selections mentioned here represent special cases of rank-selection procedures, which is in principle extendible to any spin value [66,67].

There is one important requirement on the phases of the second and third pulses in the TQF and IR-TQF sequences that are needed to choose the correct coherent pathways. The phase of the second pulse in the TQF sequence should be same as the phase of the first pulse in order to convert T_3,±1 to T_3,±3. If the phase of the second (non-180°) pulse is shifted by 90° relative to the phase of the first pulse, no triple quantum coherences are generated from T_3,±1. One can find an analogy with the spin-1/2 case, where x magnetization can be converted to z magnetization by a y pulse, but not by an x pulse. Similar considerations apply for the conversion of T_3,±3 to T_3,−1, and from T₃₀ to T_3,±3. The different pathways and the acquired phase factors are listed in Appendix A. As a result, in a minimal 6-step phase cycle in the TQF and IR-TQF experiments, one can in principle distinguish between these experiments by a simple 90° phase shift of the second (non-180°) pulse. Details are given in Appendix A, and the minimal 6-step cycle is listed in the caption of Fig. 3.

In the presence of B₁ inhomogeneities and other possible flip-angle errors, however, a clean separation between TQF and IR-TQF is not possible on this basis alone, and it is best to augment the phase cycle by at least an additional two-step cycle on the first pulse (with accompanying 0, 180° shifts for the receiver, and another on the 180° pulse (giving a minimum of 12 or 24 steps for TQF/IR-TQF or 8 and 16 for DQF). This precise separation between TQF and IR-TQF is required when the respective buildup curves are to be analyzed and fitted. In vivo, such a separation is, however, not always necessary, as one is most concerned with a separation between a normal single-quantum and a triple-quantum behavior (for example, for fluid or extra-cellular suppression, as discussed below), which is guaranteed regardless. Therefore, a minimal 6-step cycle could work well for TQF/IR-TQF, and a 4-step cycle for DQF. Considerations regarding B₁ inhomogeneity suppression may require longer cycles, to suppress additional coherence pathways as mentioned above and described in Refs. [54–56].

2.9. Triexponential relaxation

Triexponential relaxation can be observed when cross-correlated relaxation mechanisms are included in the calculations. These could arise from an interference between paramagnetic and quadrupolar interactions [68,69] (or between chemical shift and quadrupolar interactions), but are not common. Other manifestations of these mechanisms are the buildup of a second rank component, which complicates analyses which rely on the clean separation between a quadrupolar coupling and relaxation effects. Paramagnetic-quadrupolar cross-correlation has been observed for sodium in solutions with high concentrations of paramagnetic molecules [68,69].

3. Summary of motional regimes and their effects on spectra

Depending on the motional regime of the system, its energy levels and relaxation rates change, giving one or many NMR peaks in a spectrum, as shown on Fig. 2 [12]. We summarize below several of the possible motional regimes and their effects on the spectra [12,14,15] for a single type of sodium, where the motion could be characterized by a single correlation time τ_c. This case would either describe reorientation motion, or also the case where EFG fluctuations are characterized by such a correlation time. Following this section, we provide an overview of exchange models for describing exchange between compartments, which can be super-imposed on the motional classification as laid out here.

3.1. Isotropic motion with motional narrowing (ω₀τ_c ≪ 1)

In a system of rapid motion such as a fluid, the quadrupolar interaction is averaged to zero on a time scale of $\frac{2\pi }{{\omega }_0}$ and the four energy levels of the spin $\frac{3}{2}$ are equally spaced by the angular frequency ω₀. The ²³Na spectrum is then composed of a single resonance line at ω₀, as shown in the type-d spectrum in Fig. 2 (a spectrum shown of NaCl in aqueous solution). Both transverse and longitudinal relaxation proceed as monoexponential decays. Such spectra can be obtained, for example, from synovial fluids in the body. In this regime, the three transitions behave exactly in the same way, and the spin 3/2 nucleus can be treated as a pseudo 1/2 spin, simply with a fast T₁ and T₂ relaxation rate.

3.2. Isotropic motion in the intermediate to slow motion regime (ω₀τ_c ~ 1), (ω₀τ_c > 1)

The satellite and central transitions have different longitudinal and transverse relaxation rates as outlined earlier.

This situation can correspond to a biological-like type-c spectrum in Fig. 2, which was obtained from solubilized micelles in an aqueous solution. It is a “homogeneous” (“biexponential”, “super-Lorentzian”) spectrum, in which the satellite peaks have essentially coalesced into a single, broad, homogeneous peak. The relaxation rates are:

$$R_{1,\text{fast}}=6J(0),$$ (30)

$$R_{1,\text{slow}}=6J({\omega }_0),$$ (31)

$$R_{2,\text{fast}}=3J(0)+3J({\omega }_0),$$ (32)

$$R_{1,\text{slow}}=3J({\omega }_0)+3J(2{\omega }_0),$$ (33)

with the spectral density function given as

$$J(\omega )=\frac{{(2\pi )}^2}{60}\frac{C_Q^2{\tau }_c}{1+{(\omega {\tau }_c)}^2}$$ (34)

under Convention I (Eq. (19)).

3.3. Partial alignment and slow motion (ω₀τ_c > 1)

In this regime, the quadrupolar interaction is not completely averaged to zero, and a residual quadrupolar interaction (RQI) has to be considered. The single-quantum (SQ) relaxation rates are

$$\begin{array}{l}{\lambda }_{1,0}=3(J_1+J_2),\\ {\lambda }_{1,\pm 1}=3(J_0+J_1+J_2)\pm 3\sqrt{J_2^2-{({\omega }_Q)}^2}\end{array}$$ (35)

as shown in Eq. (A.23).

Depending on the magnitude of J₂, three situations can occur:

1. If ω_Q bold> J₂, the relaxation rates are real and there is no line splitting despite the presence of the RQI. The single-pulse spectrum is the sum of three Lorentzians. The RQI influences the linewidths and amplitudes of the components. This case can be still described by a type-c spectrum in Fig. 2. In this case, the DQF signal due to even rank coherence T_2±2 can be used to detect and measure ω_Q.

2. If ω_Q > J₂, the relaxation eigenvalues corresponding to the outer transitions are complex and the satellite transitions are shifted by $\pm 3\sqrt{{({\omega }_Q)}^2-J_2^2}$ from the central transition. This case corresponds to a powder-like type-b spectrum in Fig. 2, which was acquired from unoriented micelles in aqueous solution (unoriented liquid crystal). The DQF signal from T_2±2 can also be used to measure ω_Q.

3. If ω_Q ≫ J₂, the energy levels are all shifted by the RQI resulting in three distinct peaks in the spectrum. The central transition and the two satellite transitions are separated by 3ω_Q. This frequency separation between the lines provides therefore indirect information about the RQI and the magnitude of ordering in the system. This case can be described by a crystal-like type-a spectrum in Fig. 2 (the spectrum in the Figure was obtained from sodium ions in aqueous solution with oriented micelles). The relative areas of the peaks are 3:4:3 as also discussed earlier.

Anisotropic molecular tumbling may also require the incorporation of one or two additional correlation times into the spectral density expressions [70], to account for the principal axis motion.

3.4. Compartment models

In tissues, Na⁺ aquo cations exist in compartmentalized spaces (intra- and extra-cellular compartments for example) and encounter an abundance of charged macromolecules. The nature of tissue is such that most of the sodium spectra are likely to be of type c or type b, or intermediates or superpositions of these. Several models were therefore developed in order to interpret sodium spectra in biological tissues and are described in more details in Refs. [12–14] and references therein. The single-compartment model is also known as the Debye Model (DM). Further models are summarized below.

3.5. Discrete Exchange Model (DEM)

The DEM is a more complex model based on equilibrium chemical exchange between distinct sites that have different quadrupolar properties. These individual sites can each be characterized by a Debye model (single τ_c). For example, the James–Noggle exchange occurs between two different type-d sites and can yield only a resultant type-d spectrum. Bull exchange happens between a type-d site and a type-c site and can yield either type of resultant spectrum, depending on the lability of the exchange on the time-scale determined by the properties of the two sites. Chan exchange occurs between a type-d site and a type-a site and can produce all kinds of resultant spectra, depending on the lability of the exchange or the random orientation distribution of the type-a sites. A two-site DEM model, however, has at least six (or even eight, if temperature is included) independent parameters to describe the resulting spectra, and a three-site exchange model requires at least 13 independent parameters. Analyzing the tissue with a realistic DEM is therefore very difficult.

3.6. Berendsen-Edzes Model (BEM)

The BEM seems is a more realistic model which focuses on the EFG tensor projection fluctuations caused by motions of the inner hydration shell of the ion Na⁺(aq), that are very powerful and very rapid. Slower modulations also occur, usually of lower amplitudes, and are generated as the aquo ion diffuses and encounters macro-molecules. The BEM mechanism is based on the concept of a sample domain, as experienced by diffusing aquo ions, which must be at least as large as the average volume sampled by the diffusional excursions during the lifetime of an NMR coherence. The BEM can therefore be useful for describing spectra by modeling domains with the same (type-a) or random (type-b) orientations. A type-c spectrum can also be described using BEM for Na⁺ in blood plasma, for example, where rapid modulations of the inner hydration sphere domain happen together with isotropic slow fluctuations of the EFG by diffusion.

3.7. Other models

Some other more complex models such as continuous diffusion models, models with distributions of τ_c values, or Debye models with a distribution of ω_Q values were also developed in order to describe more accurately sodium spectra in biological tissues. The Augustine model [71–73], for example, also describes the important case of sodium ions in the vicinity of polyelectrolytes. In this case, relaxation is induced by the diffusion motion of the ions within the EFG generated by the polyelectrolytes.

4. Pulse sequences for compartment and fluid suppression

The most popular sequences currently in use for in vivo sodium MRI are the single-pulse and the inversion recovery (IR) sequence. Others, such as TQF have, with notable exceptions, mostly been used in animal imaging, due to their generally large SAR requirements, especially at high fields when sodium MRI is more sensitive. In many pathological states, the sodium concentration increase is detected, which can be caused by either an increase of intra-cellular sodium concentration, the increase of extra-cellular volume with a constant concentration (140 mM) or an increase of vascularization. It is widely believed that the most accurate approach to study the health of tissues in vivo should be taken by isolating the sodium NMR signal from the intra-cellular compartment. intra-cellular sodium concentration and relaxation properties should give access to some more useful information on cell viability (homeostasis, energetic state and sodium pump function) [74]. In other cases, it is of interest to separate out the immobile sodium fraction in extra-cellular space (such as in osteoarthritis). These techniques can be broadly classified as techniques for compartment and fluid separation, and we summarize them here.

4.1. Techniques based on shift reagents

These techniques are based on the use of a ₂₃Na chemical shift reagent based on lanthanide chelates, such as Tm (DOTP)⁵⁻, $\text{Dy}{(\text{PPP})}_2^{7-}$ or Dy (TTHA)³⁻ [75–77]. These compounds are thought to not penetrate the cell membrane and therefore create a frequency offset for the sodium nuclei in the extra-cellular space. Depending on concentration, the shift can be as large as 20–40 ppm (the largest ones are typically seen for the Tm and Dy compounds). These compounds do not cross the blood–brain barrier. Furthermore, they are moderately toxic and thus cannot be used in humans.

4.2. Diffusion

Diffusion-based techniques can separate the sodium signal from the intra-cellular and extra-cellular compartments based on the differences between the motional properties of the ions in these two compartments [78–80]. The fast relaxation rates and the low gyromagnetic ratio of sodium require the use of very large magnetic field gradients and fast switching, which is challenging but not impossible in clinical MRI scanners. Other ex vivo studies have used a TQF diffusion filter experiment to separate compartments. For TQF, the action of the gradient is larger by a factor 3 than for SQ coherences. The diffusion attenuation is hence larger by a factor 9. This technique, in combination with 1D spectroscopy, allowed one to distinguish several compartments in the optic nerve ex vivo [81].

4.3. Inversion recovery (IR)

The IR technique can be employed simply based on the difference in the T₁ relaxation of the sodium nuclei in different compartments. As the T₁ relaxation time of the extra-cellular sodium or free sodium in fluids can be significantly longer than the T₁ of the intra-cellular sodium, IR can be used to eliminate the signal contribution from either environment [82–89].We discuss sodium quantification issues with this technique in the next section.

4.4. Multiple quantum filters

Since only slow-motion sodium leads to the generation of triple-quantum coherences, a TQF or IR-TQF experiment allows one in principle to separate out the slow-moving sodium [12,14,30,35,57,90–97]. extra-cellular fluids typically provide for a fast motion regime, where no significant TQF buildup can be observed. As a result, a TQF experiment can therefore be used for the selective detection of intra-cellular sodium. One drawback is the relatively low sensitivity of this method (~10% of the single-pulse intensity is a typical in vivo value), and of course another is the need for a relatively long phase cycle. Nonetheless, the technique provides for a very clean separation of the signals.

Several reports estimate that the TQF NMR signal in biological tissues comes primarily from the intra-cellular sodium [95,98–102], but this statement is still controversial and studies on physiological samples have shown a significant contribution of the extra-cellular sodium in MQ-filtered spectra [74,103,104]. DQF experiments can also be used to select signals from ordered environments (such as cartilage) [105–107], by exploiting the appearance of a residual quadrupolar interaction.

4.5. Optimal control pulse shape design

Pulse optimization strategies based on optimal control theory (OCT) have been used to design rf pulses with enhanced performance in spin 1/2 systems [108]. Recently, this approach has also been implemented for ²³Na NMR and MRI. In particular, it has been applied to the problem of optimal excitation of the central transition under quadrupolar coupling and relaxation [61], the selective detection of ordered sodium ions [109], and for the differentiation between fast and slow sodium ions [60]. The results demonstrated that OCT can be quite successful in improving the performance of ²³Na NMR and MRI in terms of sensitivity and contrast.

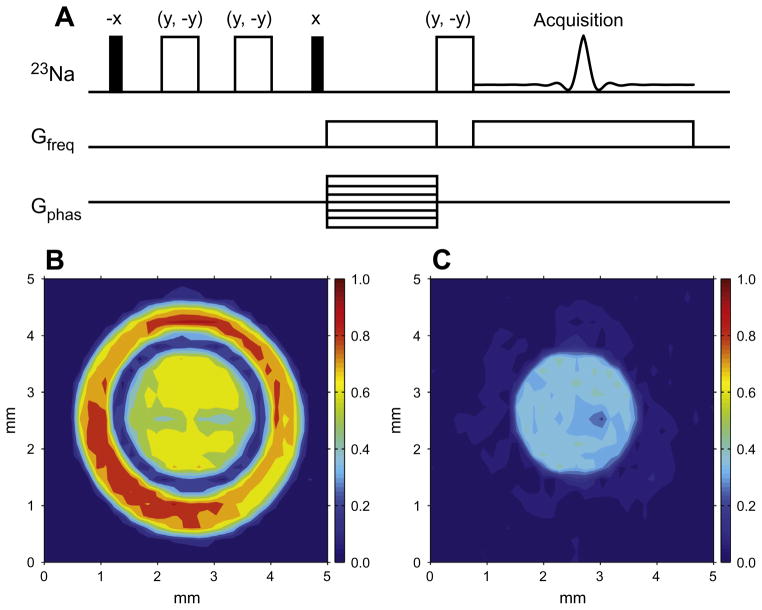
The first application of OCT to ²³Na NMR was the optimal excitation of the central transition under quadrupolar coupling [110]. It led to the discovery of a simple excitation sequence with the central transition reaching the theoretical maximum in the absence of relaxation [109]. The sequence resembles a pulse sequence consisting of two pulses with opposite phases and separated by a delay. By setting the flip angles of the two pulses to the same value, the signals from the sodium ions with no quadrupolar couplings are automatically suppressed. Furthermore, if the flip angle for both pulses is set to the magic angle ~ 54°, the satellite signals disappear, while the signal of the central transition is proportional to sin²(πf_Qτ). Here f_Q = 3ω_Q/2π is the quadrupolar splitting (in Hz) between the resonance lines and τ is the duration of the delay between two magic-angle pulses. When the quadrupolar coupling constant and the delay are matched, the signal from the central transition can reach 94% of the theoretical maximum. Therefore, the pulse sequence, named the quadrupolar jump-and-return sequence [109], can be used to selectively excite the sodium ions in ordered environments (Fig. 5). 180° pulses during the delay can be used to remove unwanted effects due to static field inhomogeneities.

Fig. 5.

2D ²³Na images obtained with the pulse sequences shown in (A) – the quadrupolar jump-and-return (QJR) sequence. (B) The signal is excited by a hard 90° pulse. (C) The QJR sequence with a delay of 2.5 ms was used to excite the signal. The phantom consists of two concentric tubes (3 mm and 5 mm od, respectively), the inner tube filled with Pf1 bacteriophage solution (f_Q = 205 Hz) and an outer with 50 mM NaCl solution. Reproduced with permission from Ref. [109].

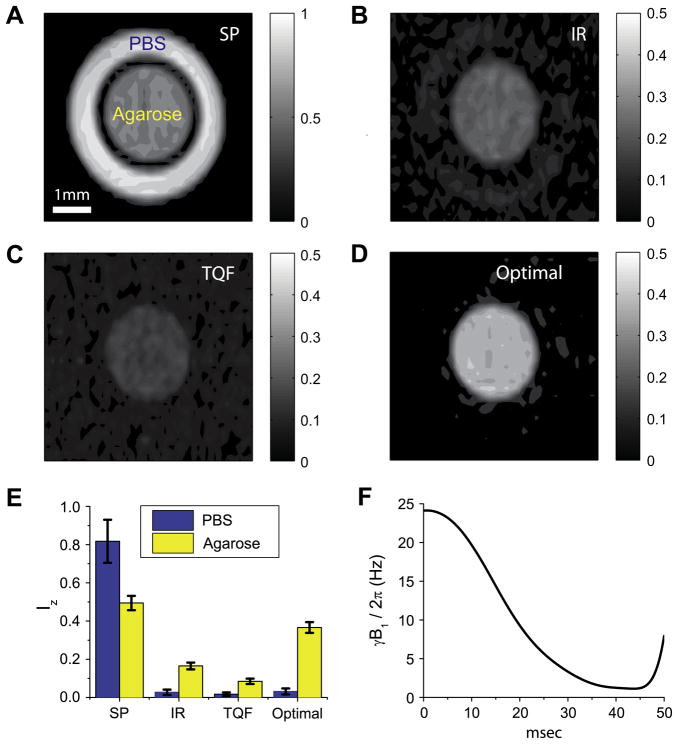
For situations where quadrupolar relaxation is the dominant evolution mechanism (without a residual line splitting due to quadrupolar coupling), IR and the TQF can be used to selectively detect such slowly-tumbling sodium ions by exploiting the difference in the relaxation times or the accessible states. IR is a more sensitive technique, while TQF is a cleaner one. An optimal shape was derived via OCT, which was more efficient than both of these for generating contrast (Fig. 6), thus showing that there is still considerable potential in improving sodium excitation sequences. The optimal shapes were further optimized for robustness in the presence of variations of static and rf magnetic fields [60].

Fig. 6.

²³Na images of a phantom consisting of an inner 3 mm tube filled with 20% agarose gel (T_1,slow = 31.5 ms, T_1,fast = 30.3 ms, T_2,slow = 28.5 ms, and T_2,fast = 3.1 ms) and an outer 5 mm tube filled with PBS (T₁ = T₂ = 56.4 ms). The images were recorded by using (A) a hard 90° pulse, (B) inversion recovery with a delay of 35.5 ms, (C) spin-echo TQF, and (D) an optimal pulse. The intensities were scaled with respect to the pixel of the highest intensity from the image (A). (E) Comparison of averaged intensities of PBS and agarose gel in the images (A–D). (F) The waveform of the optimal pulse used to get the image (D). Parts of the figures are reproduced with permission from Ref. [60].

5. MRI implementation

5.1. Image readout sequences

Due to the short (biexponential) T₂ relaxation of sodium in tissues and in vivo, ultrashort TE (UTE) sequences are recommended to acquire the images. The first sodium images were acquired with 3D gradient echo sequences [111] where the echo time (TE) was minimized by using a non-selective hard pulse, thus avoiding the use of a slice refocusing gradient, and by applying read and phase gradients with the maximum slew rates and magnitudes. TE as short as 2–3 ms can be achieved with this method, although longer delays are more typical. The shortest TEs (<1 ms) can generally be obtained by acquiring the data from the center of k-space in a radial or spiral fashion. The most common type of this kind of sequence is the 3D radial sequence which has been used widely for sodium MRI [112]. This method can be further improved with respect to signal-to-noise ratio (SNR) and time efficiency by modifying the density of acquisition points along the projections and also by twisting the radial projection in the outer k-space in an optimal manner in order to fill k-space more homogeneously and thus to improve the point spread function of the acquisition method. This is done in sequences such as the density adapted radial sequence [113], the twisted projection imaging (TPI) and its variations [29,114,115], the 3D cones [116] and in the FLORET sequences [117]. Examples of k-space trajectories from 3D radial and TPI sequences are shown in Fig. 7. These latter sequences now represent the de facto standard for sodium MRI. Other UTE sequences, which include SPRITE [118,119], SWIFT [120], ZTE [121], and PETRA [122] are still under investigation for their use for in vivo sodium MRI. The data acquired with all these non-Cartesian sequences are reconstructed using different methods, such as regridding [123–125], non-uniform fast Fourier transform (NUFFT) algorithms [126,127], or other iterative methods [128,129]. Under-sampled data can further be processed by compressed sensing [130].

Fig. 7.

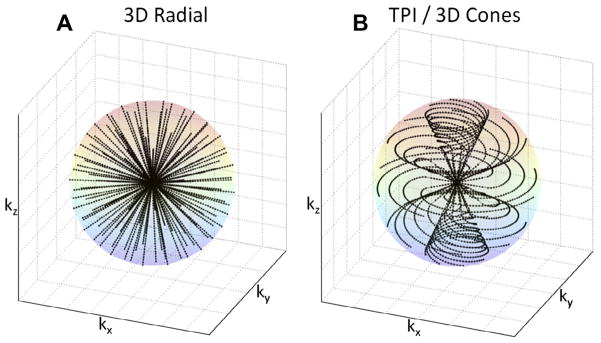
k-Space trajectories for different UTE sequences. (A) 3D radial sequence. (B) Twisted projection imaging (TPI) or 3D cones types of sequences.

5.2. Sodium quantification

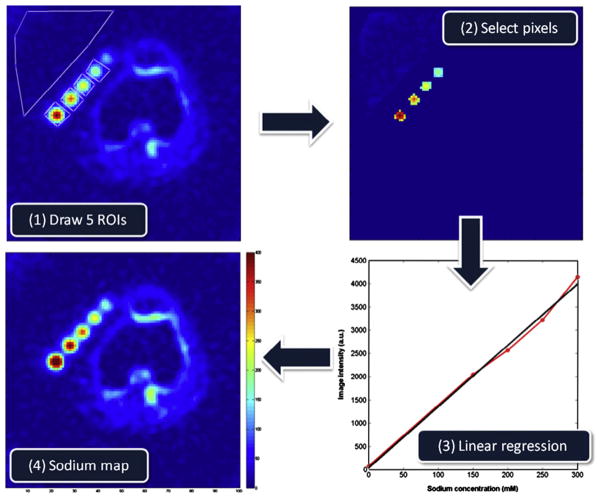
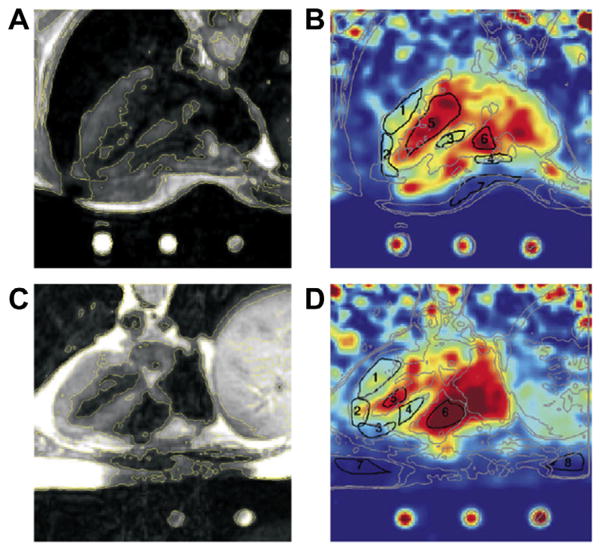
Sodium concentration quantification is generally performed by placing phantoms of known sodium concentration and known relaxation times within the field-of-view of the images. It is best to use phantoms with relaxation times that match approximately the relaxation times of the investigated tissue in order to reduce uncertainties in the quantification. A linear regression from the phantom signals, corrected for relaxation, is then used to produce the tissue sodium concentration (TSC) map. For example, reference phantoms for brain or muscle imaging are typically composed of 2–3% agar gel with sodium concentrations within the range of TSC usually found in these tissues (10 mM up to 150 mM). For cartilage, 4–6% agar gels can be used, with sodium concentrations between 100 and 350 mM. Fig. 8 shows an example of the TSC quantification procedure in cartilage.

Fig. 8.

Example of a tissue sodium map (TSC) calculation in articular cartilage. (A) ROIs are drawn over the noise background (which serve as the 0 mM sodium concentration reference) and over reference phantoms (here, 150, 200, 250 and 300 mM). (B) The same number of voxels with higher signal intensity is selected from each ROI on each phantom, and all voxels from the noise background are selected. (C) The mean signal intensity is calculated for the noise and for each phantom, and plotted versus their known sodium concentrations. Simple linear regression is then performed for fitting the points with a function I = a × TSC + b, with I the image intensity, and TSC the tissue sodium concentration of the phantoms (in mM), a and b the unknown constants to be found by regression. (D) The TSC map calculated by TSC = (I − b)/a.

6. Biomedical applications

We present here an overview of recent biomedical applications of sodium MRI for assessing diseases and therapies non-invasively and quantitatively in vivo, sorted by the targeted organs or diseases. In this overview, we also focus mostly on human in vivo MRI, which best illustrate the breadth of applications that newer methodology has enabled.

6.1. Brain

Since the first experiments on sodium MRI, many studies have been performed on brain, first to show the feasibility of quantitative brain sodium MRI, and then to evaluate its possible use for assessing diseases such as tumors, stroke, multiple sclerosis (MS), Alzheimer’s disease (AD) or Huntington’s disease (HD).

The strategies employed in these areas are to use sodium MRI as a probe for the changes in cellular integrity and viability through changes in intra-cellular sodium concentration and/or extra-cellular volume due to these pathologies [11,26,28,131–133].

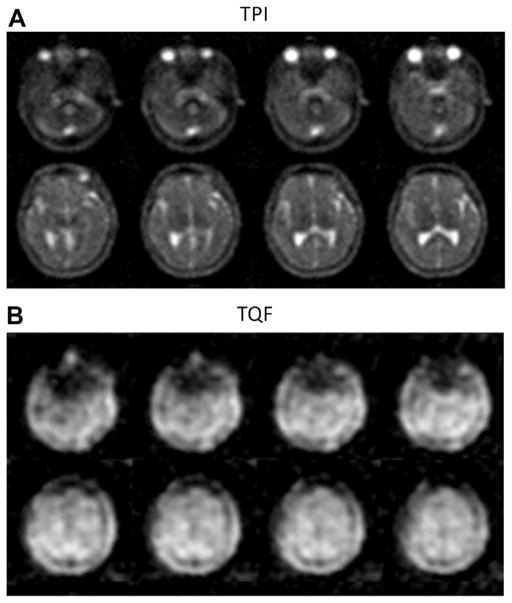
Examples of single pulse and TQF brain sodium images are shown in Fig. 9A and B. Other examples of sodium images with new TQF schemes can be found in Refs. [37,54,134] and with IR in Refs. [82,135].

Fig. 9.

Examples of sodium brain images. (A) Twisted projection imaging (TPI) at 3 T of a healthy brain. (B) Triple-quantum filtered (TQF)-TPI at 3 T of a healthy brain. Courtesy of Professor F. Boada, New York University Medical Center/University of Pittsburgh Medical Center.

Thulborn et al. [136] proposed to measure tissue sodium concentration (TSC) via ²³Na MRI (along with proton MRI) and cell volume fraction (CVF) for assessing diseased tissues in the brain (tumor, stroke). TSC is the volume fraction weighted mean of the intra-cellular sodium concentration ([Na]_in = 10–15 mM) and the extra-cellular sodium concentration ([Na]_ex = 140–150 mM). Therefore TSC = CVF × [Na]_in + (1 − CVF) × [Na]_ex. CVF is around 0.8 in normal brain tissues. After correction of the fractional average water content in normal brain (~0.8), the average TSC in brain is calculated as 45–55 mM, which is the range of values usually measured experimentally. An increase of TSC indicates a loss of tissue viability. TSC maps can be obtained directly from quantitative sodium MRI where reference phantoms with known sodium concentrations and relaxation times are placed within the FOV. CVF can be estimated from TSC through knowledge of [Na]_in and [Na]_ex, obtained from TQF sodium MRI, for example [137].

Brain sodium images have been acquired at fields of up to 9.4 T in vivo [138,139].

6.1.1. Stroke

Stroke is the third largest cause of death in the USA and a leading cause of long-term disability. Stroke can be classified into two subtypes: ischemic and hemorrhagic. Most of the strokes are ischemic (around 87%). It is very important to intervene as early as possible after symptom onset in order to reperfuse viable tissues and minimize tissue loss in order to improve recovery. The usual treatment is thrombolysis by intravenous injection of recombinant tissue plasmogen (tPA) within a 3-h window after onset [140], which induces recanalization of blocked arteries and potentially reperfusion of ischemic tissues. There is a risk, however, also of hemorrhagic transformation or edema formation due to reperfusion in non-viable tissues which can reverse the expected outcome of thrombolysis. It is therefore important to assess the viability of tissues and their likelihood of recovery before the treatment is applied.

A combination of proton diffusion weighted imaging (DWI) and perfusion weighted imaging (PWI) [142] has been proposed to help identify patients with more probable improvement in outcome after thrombolysis: ADC maps from DWI can identify regions of cerebral ischemia (water restriction) within minutes after ischemic onset, reflecting cytotoxic edema, and PWI can detect regions with perfusion deficits (regions at risk) within seconds of ischemic on-set. It has been proposed that the mismatch area between a larger abnormal PWI region and a smaller lesion in the ADC map can represent the ischemic penumbra, where the tissue is at risk for infarction but still viable, and could therefore be saved [143–145]. It has been found, however, that DWI does not necessarily represent ischemic tissue damage, that the limit of salvageable tissue is not limited to the volume of the DWI–PWI mismatch, and that PWI and DWI do not provide information on the duration of the acute period of ischemia, and cannot establish the time of symptom onset. As a result, patients would be excluded from thrombolysis treatment based on this analysis [141,146].

A more direct method, such as quantitative sodium MRI, that could give accurate spatial information on the tissue viability and also time information about stroke onset could prove to be very useful for stoke management. TSC is very sensitive to cell homeostasis and any loss of cellular energy production will impair the Na⁺/K⁺-ATPase and induce loss of ion balance across the cell membrane. An increase in TSC can be associated with an increase of intra-cellular sodium due to the loss of integrity of the cell, and also with an increase of extra-cellular volume when cells are dying. Studies in animal models and humans have shown that sodium MRI can measure increases in TSC over the first few hours and days after induction of cerebral ischemia, and that sodium MRI could have a potential utility for stroke management [141,146–149]. These studies have further shown that an elevation of 50% in TSC above the TSC value in the homologous region in the contralateral brain hemisphere was consistent with completed infarction (corresponding to 70 mM in humans). This value could therefore serve as a threshold for tissue viability and help decision making about which treatment should be more suitable for the patient. It is also suggested that the different rates of loss of tissue viability are reflected in the different rates of change in TSC values between cortex and basal ganglia. Therefore, clinical decisions to use thrombolytic agents may use different time windows depending on the location of stroke. These studies showed that sodium MRI can be used as a useful complement to DWI and PWI for managing patients with acute and subacute stroke and that TSC evolution can help guide the thrombolysis protocol outside the 3-h time window currently used for treatment decision making.

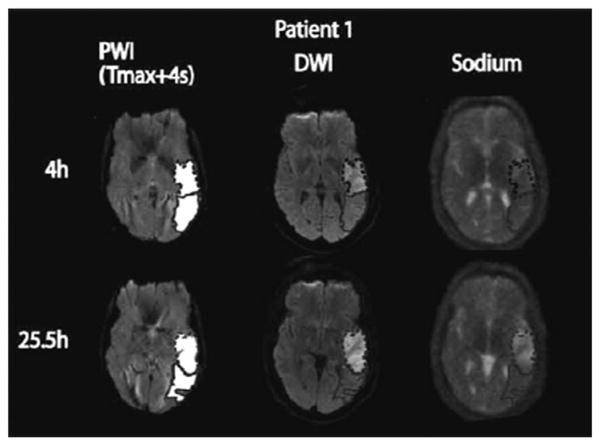
Some examples of sodium images in human stroke are shown in Fig. 10C. In this study, Tsang et al. [141] showed that sodium signal intensity cannot be predicted by PWI and that it was not altered within the PWI-DWI mismatch tissue, irrespective of the interval between symptom onset and image acquisition, indicating pre-served viable tissue in this region. A combination of DWI, PWI and sodium MRI could therefore provide useful information on tissue viability in patients with stroke, despite an unknown symptom onset time. Further studies could include optimized sodium acquisitions, perhaps based on TQF or IR preparation for increasing the weighting of the images towards the intra-cellular sodium content, and thus providing help for stroke management in a quantitative and non-invasive manner.

Fig. 10.

Representative perfusion weighted imaging (PWI), diffusion weighted imaging (DWI) at 1.5 T and sodium TPI at 4.7 T of the brain of a patient with acute ischemic stroke. These images show the hypoperfused (Tmax + 4s) perfusion maps, the DWI hyperintense region (core) in dotted outline and the PWI-DWI mismatch tissue (penumbra) in solid outline, and corresponding sodium images, acquired 4 h and 25.5 h after symptom onset. Reproduced with permission from From Ref. [141].

6.1.2. Tumors

Tumor malignancy can be characterized by angiogenesis and cell proliferation [150], among other effects. Unregulated cell division, leading to tumor growth, can be initiated by changes in Na⁺/H⁺ exchange kinetics and therefore changes in intra-cellular and extra-cellular pH [151]. This mechanism, associated with reduced Na⁺/K⁺-ATPase activity [152] leads to increased intra-cellular sodium concentration that can therefore also be associated with tumor malignancy [38,153]. Most likely, the increase in total sodium concentration in malignant tumors depends on both changes in extra-cellular volume fraction and in intra-cellular sodium content. Similarly, tumor neovascularization and increase in interstitial space both lead to an increased extra-cellular volume fraction and are also associated with the potential for tumor proliferation [154]. Overall, total sodium concentration levels in malignant tumors are likely to be elevated, and therefore could perhaps be measured by quantitative single pulse sodium MRI non-invasively. Implementing TQF or IR in the sodium acquisition could also provide information more specific to changes in the intra-cellular sodium content by reducing the weight of fluids (from edema) and/or extra-cellular sodium in image contrast.

The conventional MRI protocol for brain tumor scanning is based on T₂-, and T₁-weighted ¹H images in combination with DWI and PWI. T₂-weighted and T₁-weighted images with and without gadolinium enhancement are used for detecting the location and dimension of the tumor. DWI gives information on the extent of vasogenic edema while excluding cytotoxic edema, and PWI can detect the regions of the tumor with high vascularity, which are consistent with high-grade tumors [136]. All these changes, however, are generally late events in tumor development. Adding sodium MRI to the protocol would therefore provide direct and more rapid biochemical information on the tumor metabolism, and also help monitor the immediate effects of therapy. Further applications could include a study of the effects of cancer therapies over time.

Ouwerkerk et al. [38] combined proton and sodium MRI at 1.5 T to measure the TSC in brain and to determine how TSC is altered in malignant tumors. Sodium images were acquired with a UTE TPI sequence. Mean TSC (in mmol/kg wet weight) was measured as 60 for grey matter (GM), 70 for white matter (WM), 135 for cerebrospinal fluid (CSF), 115 for vitreous humor, 100 for tumor, 70 for unaffected contralateral tissue, and 100 for regions surrounding the tumors (detected with FLAIR hyperintense proton image). Significant differences in TSC were demonstrated for both tumors and surrounding FLAIR hyperintense tissues versus GM, WM, CSF, and contralateral brain tissue. This work shows that UTE sodium MRI can be used to quantify absolute TSC in patients with brain tumors and shows increased sodium concentration of 50–60% in tumors relative to that in normal brain regions. These measurements cannot, however, define whether TSC increases are due to changes in extra-cellular volume, intra-cellular sodium content or neovascularization.

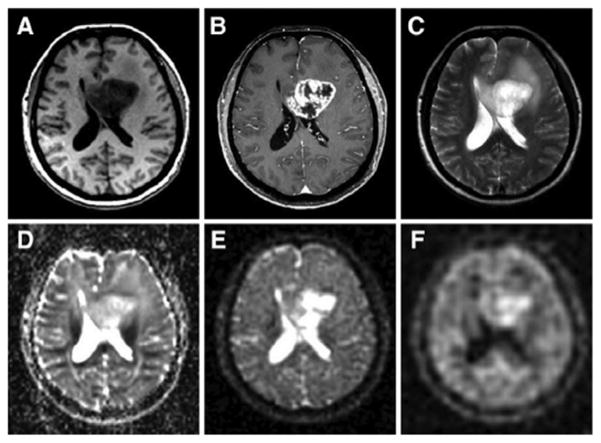
Nagel et al. [135] recently applied sodium MRI with and without IR to 16 patients with brain tumors of different grades (WHO grades I–IV) at 7 T. Some examples of proton and sodium images are presented in Fig. 11. The authors found that TSC increased in 15 of 16 brain tumors before therapy and that IR imaging enabled further differentiation of these lesions by suppressing CSF and edema signal. Further, all glioblastomas (grade IV) demonstrated higher IR sodium signal intensities as compared with WHO grade I–III tumors. It was also noted that contrary to total TSC signal, the IR sodium signal correlated with the histologic MIB-1 proliferation rate of tumor cells. This study shows that a combination of sodium MRI with and without T₁ relaxation weighting through IR can reveal important physiological tissue characteristics and help characterize and grade tumors.

Fig. 11.

Proton and sodium images from a patient with glioblastoma (WHO grade IV) of the left medial frontal lobe. (A) T₁ weighted MRI, (B) T₁ weighted MRI with contrast medium (rim enhancement), (C) T₂ weighted MRI showing cystic and solid portions of the lesion and perifocal brain edema, (D) DWI showing elevated ADC values in the center of the tumor, (E) sodium MRI showing increased sodium signal in the tumor, (F) sodium MRI with fluid suppression by inversion recovery (IR), also showing increased sodium signal mainly at the center of the tumor. Proton images (A–D) were acquired at 3 T while sodium images (E and F) were acquired at 7 T. Reproduced with permission from Ref. [135]. Coyright 2011, Wolters Kluwer Health.

Very recently Fiege et al. [134] combined single pulse and TQF sodium imaging in a single acquisition scheme and applied this new sequence to 6 healthy brains and 3 brains with tumors at 4 T. In this very preliminary work, the authors detected a decrease of signal in tumor regions on the TQF images compared to normal tissue, probably due to suppression of edema around the tumors. Due to the very low resolution of the images (10 mm isotropic) and low SNR of the TQF images, it is difficult to reach definitive conclusions yet.

6.1.3. Multiple sclerosis

Another interesting application of sodium MRI in the brain is the assessment of multiple sclerosis (MS). MS is an inflammatory neurological disease characterized by focal and diffuse inflammation in white matter (WM) and grey matter (GM), by demyelination of the axons and by neuroaxonal injury and loss, but the cellular and molecular mechanisms contributing to neurodegeneration are still poorly understood [155]. Studies have shown that the accumulation of sodium in axons through non-inactivating sodium channels can promote the reverse action of the Na⁺/Ca²⁺ exchanger, which leads to a metabolic cascade, and results in an overload with intra-axonal calcium and axon degeneration [156,157].

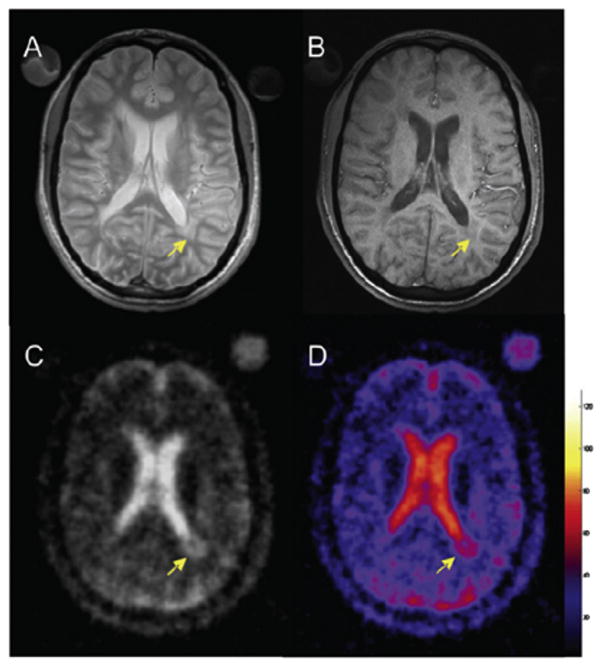
The first application of sodium MRI to MS at 3 T was demonstrated recently [158] in 17 patients with relapsing–remitting MS (rrMS) and 13 normal subjects (Fig. 12). The main results are shown in Fig. 11G and H. Images were acquired at 3 T with a 3D radial sequence and a birdcage coil. The absolute TSC was measured in lesions and in several areas of normal-appearing white and grey matter in patients (NAWM and NAGM in proton MRI), and corresponding areas of white and grey matter in controls. Mean sodium concentrations were 20 and 30 mM in WM and GM in controls, and 27 and 36 mM in corresponding NAWM and NAGM in MS patients. In this preliminary study, TSC in MS patients was therefore elevated in acute and chronic lesions compared to areas of NAWM. The TSC in areas of NAWM was significantly higher than in corresponding WM regions in healthy controls. TSC averaged over lesions and over regions of NAWM and NAGM matter was positively associated with T₂-weighted and T₁-weighted lesion volumes from proton MRI. The expanded disability status scale score showed a mild, positive association with the mean TSC in chronic lesions, in regions of NAWM and NAGM. More studies need to be performed to understand the pathophysiological mechanisms involved in tissue injury in MS and their link to sodium images. Separation of intra-cellular and extra-cellular sodium by TQF [137] or IR could prove to be useful for this purpose. This work shows that abnormal values of TSC measured non-invasively with sodium MRI in patients with rrMS might reflect changes in the composition of the lesions and/or changes in metabolic integrity.

Fig. 12.

Example of brain sodium image on a patient with multiple sclerosis (MS). (A) Proton density MRI, (B) T₁ weighted MRI, (C) sodium MRI, and (D) corresponding TSC map. Reproduced with permission from Ref. [158].

Another recent study by Zaaraoui et al. [159] expanded the method to patients with early and advanced rrMS. It was found that TSC increased inside demyelinated lesions in both groups of patients. TSC was also increased in NAMW and NAGM of advanced rrMS patients, but not in early rrMS.

6.1.4. Alzheimer’s disease (AD)

Finding biomarkers for detecting early signs of AD and tracking response to treatments is the subject of intense research. Methods such as sampling the cerebrospinal fluid (CSF) for biochemical analysis of biomarkers, positron emission tomography (PET), and MR imaging (through regional volumetric analysis) or spectroscopy (N-acetylaspartate with ¹H NMR or glutamate with ¹³C NMR) have been proposed.

A first study on the applicability of sodium MRI to Alzheimer’s disease (AD) was performed by Mellon et al. [160]. The hypothesis here is that alterations of the sodium levels in brain due to cell death or loss of viability characteristics of AD could be measured with sodium MRI non-invasively and could give useful complementary information for the assessment of early AD. In these studies, a small increase (7.5%) of the relative sodium signal intensity was found in the brains of patients with AD compared to controls. Further, it was found that this signal intensity enhancement was moderately inversely correlated with hippocampal volume measured from T₁ weighted inversion recovery proton images. No conclusive explanation on a physiological basis can be provided at the moment for this sodium content increase. Possible explanations are that the extra-cellular volume increases due to cell death and fluid invasion, the intra-cellular sodium concentration increases due to an impairment of the Na⁺/K⁺-ATPase due to amyloid beta channels in the membrane, or perhaps that a combination of some of these effects is at play. More studies that allow fluid suppression and/or intra-cellular sodium isolation (IR, TQF) need to be performed in order to selectively study these possible aspects of AD progression.

6.1.5. Huntington’s disease

A very recent preliminary study [161] showed that patients with Huntington’s disease (n = 13) also present increased TSC in the whole brain compared to healthy controls (n = 13), in structurally affected regions of the brain, but also in some non-affected regions. Similar to the AD case, no satisfying explanation of these TSC increases could be proposed due to the limited data, low resolution and lack of differentiation between intra-cellular and extra-cellular sodium content. Further studies may help explain these observed TSC variations which are generally linked to changes in cellular and metabolic integrity that leads up to structural degeneration.

6.2. Breast

Treatments for breast cancer such as prophylactic mastectomy or chemoprevention are more effective when the disease is detected at an early stage. Mammography is the standard method for breast cancer screening [162] with high specificity (>90%) but has a very variable sensitivity (30–60%) due to difficult lesion detection in dense breast tissue [163–165]. Ultrasound (US) is a supplemental method for women with high-risk and dense breast tissue that can increase screening sensitivity, but can also lead to higher false-positive rates [166]. Standard proton MRI has a higher sensitivity (75–90%) and is less affected by the breast tissue density, but has lower specificity (70–90%) [163,166]. False-positive diagnoses from these screening methods result in increased patient anxiety, overdiagnosis and unnecessary biopsy, or overtreatment [167].

Sodium MRI could improve this situation by adding more information about the physiology and metabolism of suspicious lesions, such as cellular integrity and energy metabolism. As proliferating tumors may cause increases in the sodium content of tissues due to disruption of the sodium–potassium pump in cell membranes, quantitative sodium MRI would be a good candidate to detect tumors in the breast and also assess the degree of malignancy and follow-up chemotherapy. To test this hypothesis, Ouwerkerk et al. [168] applied quantitative sodium MRI at 1.5 T and TPI acquisition to patients with benign and malignant breast tumors before biopsy. T₂ and T₁ weighted contrast-enhanced proton MRI were also acquired. Sodium and proton images were co-registered to allow quantification of TSC in normal and suspicious tissues based on ¹H MRI contrast enhancement, with histology confirmed by biopsy. The measured TSC were on average higher by 60% in histologically proven malignant lesions compared to glandular tissue. TSC in benign tumors was significantly higher than in adipose tissue but at the same level as in glandular tissue (34 mM). An example of these results is shown in Fig. 13.

Fig. 13.

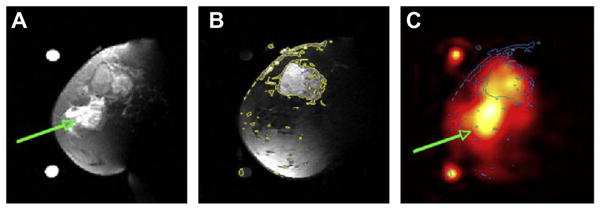
Examples of breast cancer images from a patient with 5.5 cm infiltrating poorly differentiated ductal carcinoma (T3) at the 12 o’clock position in the left breast. (A) Fat suppressed T₂ weighted MRI showing a mass with T₂ intermediate signal and edematous T₂ bright retroareolar glandular tissue (arrow). (B) Fat suppressed T₁ weighted MRI post-Gd injection with contour levels in yellow, showing enhancement of the mass at 12 o’clock but not in the retroareolar glandular tissue. (C) Sodium MRI with contours from B superimposed in blue. The region with edema is indicated by the green arrow. Reproduced with permission from Ref. [168].

Increased TSC can arise from an increase of the extra-cellular volume fraction (EVF) due to changes in cellular organization, from an increase of the vascular volume, or from increases in the intracellular sodium concentration due to impaired energy metabolism and Na⁺/K⁺-ATPase activity, or a combination of all these factors. Further studies based on fluid suppressed ²³Na MRI, combined with sensitive proton MRI techniques such as DWI or T₁ contrast enhancement, could further help in assessing biochemical information in breast cancer.

A multiparametric multinuclear combination of MRI techniques could prove to be useful for grading benign and malignant tumors, and also for monitoring the response to chemotherapy [169]. It was even shown by Jacobs et al. [170] that a multimodal combination of ¹H+²³Na MRI with computed tomography (CT) and proton emission tomography (PET) was feasible and could help to evaluate the complex tumor micro-environment by examining the changes in morphology, sodium concentrations and glucose metabolism in response to therapy.

6.3. Heart

Acute myocardial infarction (MI) can lead to an increase in the intra-cellular sodium concentration due to loss of ionic homeostasis and due to an enlarged extra-cellular volume as a consequence of myocardial edema formation or scar formation [171,172]. Quantitative sodium MRI appears therefore to be a good candidate to try to detect cardiac infarction by measuring localized increased sodium content in cardiac tissues and thereby help to differentiate viable from non-viable tissue. Some preliminary studies using surface coils were performed over the years to test the feasibility of cardiac sodium MRI for assessing infarction [111,173–176].

Ouwerkerk et al. [174] measured the myocardial TSC of healthy volunteers. Mean TSC was approximately 43 mM in the left ventricular (LV) free wall, 53 mM in the septum and 17 mM in adipose tissue. The same team then applied the method to twenty patients with nonacute MI (Fig. 14). Mean TSC for MI was measured to be higher by 30% than for noninfarcted tissues in LV regions (significant difference). The mean TSC in regions adjacent to MI regions was intermediate between MI and normal tissue sodium content. The study also concludes that TSC increase was not related to infarct age, size or global ventricular function. The measured sodium TSC or pixel intensity changes may be attributable to loss of cellular integrity, inhibition of the Na⁺/K⁺-ATPase function due to energy depletion and changes in the sodium concentration gradient between intra-cellular and extra-cellular volumes, and possibly also changes in the molecular environment of the sodium ions.

Fig. 14.

Comparison between ¹H and ²³Na cardiac images at 1.5 T of healthy volunteers. Registered axial ¹H MRI FSE images (A and C), cardiac-gated at 60–70 bpm, echo train length = 8, effective TE = 17 ms. Coil sensitivity adjusted axial slices from three-dimensional ²³Na TPI data sets of the heart (B and D) with TR/ TE = 100/0.17 ms, and adiabatic half passage (AHP) excitation from healthy human volunteers. The ²³Na image intensity was adjusted for the coil receiving sensitivity using a computer-generated B₁ field estimate of the coil. The ¹H image data were interpolated in three dimensions so that images (A and C) match the spatial positions of the images (B and D). The resulting in-plane resolution was 128 × 128, at the same slice spacing as the ²³Na data. The three-dimensional ²³Na image data were interpolated to 128 × 128 pixels in-plane to facilitate copying of contours and ROI. Yellow contours are drawn in the ¹H images (A and C) and copied to the ²³Na images (B and D) (shown as gray lines) to guide placement of the ROIs (black lines in the ²³Na images). ROIs were placed in the lateral LV wall, anterior LV wall, and septum (ROI numbers 1–3 or 1–4 in all images). Additional ROIs were placed in the left ventricle for LV blood (ROI number 5) and in the right ventricle for RV blood (ROI number 6). Reproduced with permission from Ref. [174].

Future studies might include imaging at higher fields for increasing the SNR and spatial resolution for better identification of infarcted tissues and adjacent areas, and the use of sequences that could separate intra-cellular from extra-cellular sodium and/ or relaxation times weighted (TPI associated with TQF or IR), for a better estimation of intra-cellular TSC, which is likely to be more sensitive to cell energy impairment and viability.

6.4. Skeletal muscle

Sodium MRI has the potential to provide insights into muscle physiology and disorders. In muscle tissues, the electrochemical gradient across the cell membrane is maintained by the Na⁺/K⁺-ATPase mechanism, but when an action potential is generated, there is a rapid influx of sodium ions and efflux of potassium ions via the sodium and potassium channels, leading to muscle contraction. During intense contractile activity, the persistent influx and efflux of ions, which degrades the transmembrane Na⁺ and K⁺ gradients, can lead to a loss of membrane excitability and muscle contractility [177], which is believed to represent one of the main mechanisms of muscle fatigue [178].

It has already been shown that many disease states, such as diabetes, starvation and hypothyroidism, can be linked to a decrease in Na⁺/K⁺-ATPase activity in skeletal muscle [177]. Therefore sodium MRI has the potential to play a role in imaging of these disorders. For example, Bansal et al. [39] studied the change of sodium concentration and relaxation in muscle after voluntary muscle contractions. The authors showed that the sodium intensity in the images increased by ~34% in the exercised muscle and then diminished with a half-life time of 30 min. At the same time, the calculated sodium concentration did not change significantly, while the long T₂ component of the sodium relaxation increased. This work therefore suggests that the change in intensity in the sodium images is mainly due to a change in the sodium-macromolecule interaction rather than a change in TSC. We describe below a few examples of sodium MRI studies of different muscular diseases.

6.4.1. Diabetes

Sodium MRI has been studied recently in diabetic patients. Some results from the study by Chang et al. [179] are presented in Fig. 15. Pre- and post-exercise sodium intensity was measured in sodium images in healthy volunteers and in patients with diabetes, in the tibialis anterior (TA) as control muscle, in the soleus (S) and the gastrocnemius (G) muscles. It was found that the muscle sodium signal intensities (in S and G) increase significantly immediately after exercise and that afterwards this sodium signal recovers down to baseline more slowly in diabetics than in healthy subjects.

Fig. 15.

Sodium images in the muscle at rest (A) and post-exercise (B). 3D FLASH proton MRI (C) was performed after sodium MRI to delineate muscle anatomy: TA is tibialis anterior, S is soleus and G is gastrocnemius. In healthy subjects (D), the sodium signal intensity increases significantly in S and G just after exercise, but not in the control muscle TA. The sodium intensity then decreases to near baseline in both S and G with a half-time of around 22 min. In diabetic subjects (E), sodium signal intensity increases significantly in S and G just after exercise, but not in the control muscle TA. The sodium intensity then decreases to near baseline with half-times of around 37 min in S and 27 min in G. Reproduced with permission from Ref. [179].

The increase in sodium signal intensity could be due to two main factors: (1) an increase in total muscle sodium content due to an increase in the volumes of both the intra-cellular and extra-cellular compartments after exercise as well as an increase of intra-cellular concentration by muscle cell depolarization and (2) alterations in the macromolecular environment and therefore changes in T₂ relaxation times or in the proportions of the long and short T₂ components. Na⁺/K⁺-ATPase preserves the muscle membrane excitability by maintaining the Na⁺ and K⁺ concentration gradients across the cell membrane and therefore helps protect muscles against fatigue [177]. Diabetics, however, have a decreased Na⁺/K⁺-ATPase activity and decreased numbers of Na⁺ and K⁺ pumps on the muscle cell membrane, which has been attributed to insulin resistance [180]. This effect would result in a decreased ability to extrude intra-cellular sodium ions into the extra-cellular space and leads to elevated intra-cellular sodium content in muscle with a slower recovery to baseline.

This preliminary study shows that sodium MRI could therefore be applied to patients with diabetes in order to evaluate those who are at risk of diabetic muscle infarction. Moreover, fluid and/or extra-cellular sodium suppression by TQF or IR, along with T₂ relaxation measurements, could prove to be useful to assess the origin of the sodium intensity decrease observed in this study.

6.4.2. Muscular channelopathy

Patients with hypokalemic periodic paralysis (hypoPP) or paramyotonia congenita (PC), two different kinds of muscular channelopathies, were scanned with sodium MRI in a study by Nagel et al. [40]. These rare diseases are considered to be caused by genetic mutations of the voltage-gated sodium channels in muscular cells, which can also be characterized by elevated myoplasmic sodium at rest and after cooling (for provoking PC pathology effects).

Three sodium techniques were used to assess the disease: total tissue sodium concentration (²³Na-TSC), T₁-weighted sodium imaging (²³Na-T₁) and inversion recovery (²³Na-IR). The latter was used to suppress most of the extra-cellular and vascular sodium and vasogenic edema. All ²³Na sequences showed significantly higher signal intensities in hypoPP compared with PC patients and healthy subjects, and provocation in PC induced a significant increase (> 20%) in the ²³Na-IR signal and a corresponding decrease of muscle strength. Signal intensities from ²³Na-T₁ and ²³Na-TSC also have a non-significant tendency to be higher after provocation in PC. This study indicates that ²³Na-IR could provide a stronger weighting toward intra-cellular sodium than ²³Na-T₁ or ²³Na-TSC, and therefore may allow a better visualization of changes in the intra-cellular sodium content. A combined application of ²³Na-TSC and ²³Na-IR could therefore improve the analysis of pathophysiological changes in muscles of patients with muscular channelopathies by measuring the changes in intra-cellular concentration and T₁ relaxation time.

The same kind of study was also performed on patients with hyperkalemic periodic paralysis (hyperPP) by Amarteifio et al. [181]. They showed that sodium MRI can detect increased myoplasmic sodium content in HyperPP patients with permanent weakness, as they are affected by an incomplete inactivation of muscular sodium channels [182]. In this case too, ²³Na-IR is more sensitive to intra-cellular changes than ²³Na-TSC and ²³Na-T₁. In conclusion, sodium overload may cause muscle degeneration developing with age and sodium MRI could therefore help monitoring medical treatments that reduce this overload.

6.4.3. Myotonic dystrophy

Myotonic dystrophy has been linked to alterations in sodium channel conductance regulation, which can cause elevated muscle fiber concentrations that correlate with disease severity [183].

Constantinides et al. [184] have found in their study that the mean TSC measured with sodium MRI after exercise was elevated by 16% and 22% in two healthy volunteers, and 47% and 70% in two dystrophic muscles compared with those at normal resting levels. These results in patients with myotonic dystrophy are consistent with the known imbalance in sodium homeostasis in dystrophic muscle fibers [185]. Quantitative sodium imaging could be a valuable tool for characterizing the early onset, pathogenesis, and monitoring of pharmacologic treatment of dystrophic muscle, but more data need to be acquired to confirm these findings.

6.4.4. Hypertension

Another possible application of quantitative sodium MRI in muscle is to measure the increase of body sodium content due to hypertension, which is linked to a disturbed total body sodium regulation. Kopp et al. [186] measured the sodium content in the triceps surea of healthy volunteers and of patients with primary aldosteronism, before and after treatment. They found a 29% increase in muscle Na⁺ content in patients with aldosteronism compared with normal women and men. This tissue Na⁺ content was then reduced to normal levels (20–25 mM) after successful treatment without accompanying weight loss. The authors suggest that sites such as muscle (and also skin) could serve to store Na⁺ nonosmotically by binding of the Na⁺ ions to proteoglycans within the extra-cellular compartment without apparent accompanying fluid retention or changes in serum Na⁺ concentration in patients with primary aldosteronism.

In a subsequent study [187], Kopp et al. measured the sodium in muscle and skin of 57 patients with hypertension and 56 control subjects at 3 T. Representative images are shown in Fig. 16. The authors noticed an increase of Na⁺ deposition in skin in both men and women with increasing age, and an age-dependent increase of sodium content in muscle in men, but not women. A slight increase of sodium concentration in both muscle and skin was detected in men and women with refractory hypertension, compared to age-matched controls. These studies show promise for hypertension assessment by sodium MRI. These techniques could also help testing the role of Na⁺ for assessing long-term cardiovascular risk in populations.

Fig. 16.

Examples of sodium images (row A) and proton images (row B) of the lower leg of a young healthy volunteer (left column) and of an older volunteer with hypertension (right column). Tubes with solutions containing 10, 20, 30, and 40 mmol/L of NaCl are arranged below the extremity, and used as calibration standards for quantification of the tissue sodium concentration. Tissue Na⁺ content increased in the old subject compared to the young subject. No significant difference in muscle water content is visible (B). Reproduced with permission from Ref. [187].

6.5. Cartilage

Cartilage is a dense connective tissue that can be found in many parts of the body such as articular joints between bones (hyaline cartilage), in the ear and nose (elastic cartilage) or in intervertebral disk (fibrocartilage).

Here, we will mainly focus on articular hyaline cartilage, which consists of a small population of chondrocytes (5% of volume) within a large extra-cellular matrix (ECM) made of type II collagen fibers (15–20% of the volume), proteoglycans (PG; 3–10%) and water (65–80%) and does not contain blood vessels. PGs further consist of a protein core and negatively charged glycosaminoglycan (GAG) side chains, which endow cartilage with a negative fixed charge density (FCD). This FCD attracts free-floating positive counter-ions, such as Na⁺, which in turn attract water molecules within the cartilage through osmotic pressure. The negative charge from the GAG side chains also provides a strong electrostatic repulsive force between the PG molecules and is responsible for the compressive stiffness of cartilage. The collagen fibers serve to immobilize the PG and provide a tensile force opposing the tendency of the PG to expand the cartilage. Due to these properties, articular cartilage can provide synovial joints with lubrication and can also serve to absorb mechanical shocks and to distribute load over the underlying bone [36,188].

6.5.1. Osteoarthritis

Osteoarthritis (OA) is the most common form of arthritis in synovial joints and a leading cause of chronic disability, mainly in the elderly population. From the biochemical point of view, OA is a degenerative disease of the articular cartilage, characterized by a reduction of FCD (or GAG) concentration, possible changes of size and organization of the collagen fibers, and aggregation of the PG. These changes lead to an alteration of the mechanical properties of the cartilage, which can therefore lose its load-and shear-bearing functions. At present, there does not exist either a known cure or a preventive treatment for OA, and present treatments focus mainly on pain management with analgesics and quality of life (e.g., exercise and weight loss). If these methods are ineffective, joint replacement surgery may be considered. Early detection of OA, prior to irreversible morphological changes, and an accurate method for quantifying the effects of potential treatments are therefore of fundamental importance.

Radiography is the standard method used to detect gross loss of cartilage by measuring joint space narrowing, but does not image cartilage directly. Proton MRI, such as T₁-weighted, T₂-weighted and proton density imaging, can provide morphological information on damage of cartilage, such as fissuring and partial- or full-thickness cartilage defects, but does not give any information on the GAG content within the ECM or the structure of the collagen fiber network. New methods for functional proton MRI of cartilage are under development, such as T_1ρ mapping [189], T₂ mapping [190], GAG chemical exchange saturation transfer (gagCEST) [191–193], delayed gadolinium enhanced MRI of cartilage (dGEM-RIC) [194] and diffusion weighted imaging (DWI) [195]. T₂ mapping and DWI can give information about collagen fiber and water mobility, while the other methods can provide information on the FCD or GAG content, indirectly through the use of contrast agents (dGEMRIC), or directly (T_1ρ mapping, gagCEST). All these methods are still under investigation for assessing their specificities and sensitivities for detecting early OA.

It has been shown that sodium concentration has a strong correlation with FCD and GAG content in cartilage [196–198], therefore quantitative sodium MRI could also be useful for detecting directly GAG loss in early OA [199,41,200]. Several studies have already been performed on healthy and OA cartilage, and show that in general TSC in healthy cartilage is in the range of 250–350 mM, while it is typically lower than 250 mM in OA cartilage [200]. Because of the low resolution of the sodium images (>3 mm), due to the presence of synovial fluid or joint effusion and also possible cartilage thickening, the sensitivity of the method to measure small changes of TSC within the cartilage should include fluid suppression by either TQF [31,201] or IR [83] to suppress signals from surrounding fluids.

An example of quantitative sodium MRI of cartilage at 7 T in presented in Fig. 17, where fluid suppression was obtained by IR with an adiabatic inversion pulse [83]. The images were acquired with a 3D radial sequence. It is shown that fluid suppression allows a better differentiation between control and OA patient. This work is still preliminary but it is reproducible and repeatable [88]. Further information could be obtained from sodium T₁ and T₂ rates, which are expected to be very sensitive to any changes of their environment, such as GAG depletion or collagen fiber rupture. Some reviews on the potential of sodium MRI and OA are presented in Refs. [36,89].

Fig. 17.

Cartilage sodium concentration maps from a healthy volunteer (control) and a patient with osteoarthritis (OA). Images were acquired with a 3D radial sequence (R3D) and IR WURST (IRW). IR WURST was used to suppress fluids through inversion recovery (IR) with an adiabatic WURST pulse in order to increase the sensitivity of the method to a change of sodium concentration within the cartilage only. MED = femorotibial medial and LAT = femorotibial lateral cartilage. Reproduced with permission from [86].

The quadrupolar interaction itself has been shown to increase with degradation in cartilage ex vivo [16,197,202], and this effect has also been shown to occur in osteoarthritic and osteoporotic cartilage [202]. These interactions could, in principle be used for producing alternative image contrast (quadrupolar contrast [61,109,110,203,204]), but its implementation in imaging has not been explored yet.

6.5.2. Cartilage repair

Sodium MRI could also prove to be useful for assessing cartilage repair [87,205–207]. For example, Zby`ň et al. [205] compared sodium and proton images at 7 T from 9 subjects who underwent reparative bone marrow stimulation (BMS) procedures (micro fracture and subchondral drilling) and 9 matched subjects who underwent restorative cell-based procedures (MACT). No sodium quantification was performed, but a sodium normalized mean signal intensity (NMSI) was calculated. For comparison between different subjects, a repair-to-reference ratio was also calculated for each subject. Significantly lower average sodium NMSI were found in repair tissue compared to native healthy cartilage, from both MACT and BMS repair procedures. Higher sodium NMSI were measured in MACT subjects compared to BMS subjects, which were interpreted as resulting from a better quality of repair from MACT due to higher GAG content. As no fluid suppression was performed in the sodium acquisition, this increase of sodium signal within the repair region could also arise from partial fluid invasion of the scaffold in MACT. It is noticed that higher sodium NMSI in repair cartilage did not result in better clinical outcome of the MACT patients, which could then corroborate the hypothesis that the increase of signal might not originate only from GAG content but also from fluids. The absence of fluid suppression and of TSC quantification make the results of this study difficult to interpret and reproduce in other research labs. As a short TR of 10 ms was used, the contribution from fluid signal is expected to be strongly attenuated, but still present. The long TE (3.77 ms) for sodium acquisition might also lead to a significant loss of signal in native and repair cartilage (which might have different T₂ relaxation behavior – generally biexponential and very short in cartilage). Histological measurements from biopsies from repair cartilage have shown that more fibrocartilage (with less GAG) is present in BMS repair regions [208,209], and more hyaline-like cartilage is present in MACT regions [210], which could be correlated with the results of this study.

Chang et al. [87] evaluated the feasibility of fluid-suppressed sodium imaging with inversion recovery (IR) at 7 T for detecting cartilage repair in the knee of eleven patients. These patients had undergone different reparative and restorative cartilage repair procedures. Images were acquired during follow-up after several weeks (range: 12–151 weeks) after surgery. Selected T₂-weighted proton and TSC maps from sodium images are shown in Figs. 18A and B, with and without fluid suppression, respectively. These images were obtained from a person who had undergone osteochondral allograft transplantation, and one with juvenile cartilage cell implantation. In all cases, the area of cartilage repair was more easily detectable on fluid-suppressed TSC maps, visible as a ‘hole’, thus indicating that GAG is not present in those areas. This pilot study shows the feasibility of fluid-suppressed sodium MRI for cartilage repair imaging and indicates that sodium MRI could prove useful for detecting the evolution of GAG content during follow-up of the repair procedure. More data from more subjects and overmore time points need to be acquired for evaluating the utility of this imaging technique to assess cartilage repair in the knee joint. For best quantification results, further studies could also take into account the changes in T₁ and T₂ sodium relaxation times within the repair and adjacent regions in cartilage, as they may also vary due to changes in the cartilage matrix structure and GAG concentrations.

Fig. 18.

A. Sagittal T₂-weighted ¹H MR image (left) of the right knee with an osteochondral allograft transplantation (arrowhead) at the weight-bearing aspect of the medial femoral condyle. There is synovial fluid at the articular surface (arrows) in the conventional ²³Na TSC map (middle). Hyperintense signal is seen from synovial fluid at the articular surface (arrows) and to a lesser extent in a subchondral location at the repair site (arrowhead). On the TSC map from ²³Na-IR MRI (right), there is a visible suppression of signal from free sodium within synovial fluid (arrows) and also in the subchondral location (arrowhead). B. Axial T₂-weighted ¹H MR image (left) of the right knee, with a juvenile cartilage cell implantation (arrowhead) at the medial facet of the patella. Structures containing free sodium, such as synovial fluid and popliteal vessels, are indicated by arrows. On the conventional ²³Na TSC map (middle), hyperintense signal is seen from synovial fluid at the articular surface and within the popliteal vessels (arrows). On the ²³Na-IR TSC map (right panel), a suppression of signal from free sodium within synovial fluid and within popliteal vessels is visible (arrows). The calibration phantoms are seen at top left of the sodium images. Reproduced with permission from Ref. [87].

Two other preliminary studies have compared sodium MRI with dGEMRIC and gagCEST for evaluating cartilage in patients after repair procedures. Schmitt et al. [207] scanned 12 MACT patients with both sodium MRI at 7 T and dGEMRIC at 3 T. A significant correlation (R² = 0.7, p = 0.001) was found between the results from these two methods after MACT procedure. Trattnig et al. [206] scanned 12 patients (5 MFX and 7 MACT) at 7 T with sodium MRI and gagCEST. A moderate correlation (R² = 0.49, p not given) was found between the results from these two methods after repair procedures.

6.5.3. Intervertebral disk

The processes governing GAG and sodium concentration are very similar in the intervertebral disk. Ex vivo studies have demonstrated that sodium concentrations could also be used to report on GAG conditions in the disk [198]. Insko et al. [211] demonstrated the feasibility of sodium MRI of the intervertebral disk (IVD) in vivo at 4 T using a surface coil and a 3D gradient echo sequence. This technique could be used to measure the proteoglycan content in fibrocartilage and help detect early degenerative changes in IVD. In a subsequent recent study, Wang et al. [212], showed that sodium MRI can correlate with loss of proteoglycans in the spine.

6.6. Abdomen

Quantitative sodium MRI could also prove to be useful for assessing cell viability in abdominal organs for the purposes of detecting and diagnosing diseases in liver, gallbladder, pancreas, kidney, spleen, prostate, uterus and others [213]. Very few studies have been performed for the moment on the abdomen, mainly due to the lack of suitable body sodium coils and the necessity for the acquisition sequences to take into account the cardiac and respiratory movements of the body, which can seriously perturb the quality of the images. We survey here some preliminary work on the kidney, prostate and uterus.

6.6.1. Kidney

The kidneys are essential in regulating homeostatic functions in the body such as extra-cellular fluid volume, acid–base equilibrium (pH), electrolyte concentrations, and blood pressure (via maintaining salt and water balance). This role depends tightly on the regulation of extra-cellular sodium in the kidney, which builds up a concentration gradient from the cortex to the medulla. Thus, renal function is tightly dependent on this corticomedullary gradient and mapping this gradient with sodium MRI could help assess kidney impairments.

A first study in humans by Maril et al. [214] presented sodium MRI of kidneys before and after water deprivation, as shown in Fig. 19. This work was performed at 3 T with a surface coil and data were acquired with a 3D gradient echo sequence. The results show that the sodium signal intensity increased linearly from the cortex to each of the medullae with a mean slope of 1.6 (in arbitrary units per mm) and then decreased towards the renal pelvis. After 12 h water deprivation, this gradient increased significantly by 25%. The sodium gradient change in the kidney may reflect changes in the concentration in each kidney compartment (cortex, medulla), but also within micro-compartments therein (intra-cellular, extra-cellular, vascular compartments). Differences in the relaxation times of sodium within the tissues also contribute to the overall measurements.

Fig. 19.

Examples of kidney images. (A) Scheme of a human kidney. Central coronal slices of the 3D sodium images of a human kidney under normal conditions (B) and after 12-h water deprivation (C). The sodium gradient increases significantly by 25% after water deprivation. Reproduced with permission from Ref. [214].

A following study by Rosen et al. [215] showed sodium MRI at 3 T on a patient with a transplanted kidney, who was previously diagnosed with end-stage hypertensive nephropathy, to measure the corticomedullary sodium gradient and to assess the quality of the new kidney. The kidney was imaged 4 months after transplantation. The measured mean medulla/cortex SNR ratio was 1.8, and the gradient slope was 1.1 (arbitrary units/mm), which was lower than the gradient observed in the healthy kidney in the previous study. This difference was interpreted as being due to the effects of the recent transplantation. Although resolution and SNR were low and the physiology/biochemistry involved is not fully known, such findings are encouraging for possible applications of quantitative sodium MRI for assessing renal functions in different diseases such as nephropathy, renal failure as well as in kidney transplantation.

6.6.2. Prostate

Sodium MRI of the human prostate was recently tested in vivo at 3 T [216,217] and compared with diffusion MRI. The prostate and its different compartments were identifiable, with measured TSC of around 60 mM in the central zone and 70 mM in the peripheral zone. This method could be a potential radiological biomarker of prostate cancer and of treatment response.

6.6.3. Uterus

Uterine leiomyomata (fibroids) were investigated by diffusion weighted imaging (DWI) and quantitative sodium MRI by Jacobs et al. [218] at 1.5 T. Uterine leiomyomata are solid masses arising from the muscle of the uterus (myometrium) and can be associated with menstrual pain and loss of reproductive function. The goal was to monitor the treatment of fibroids on patients that were treated using MRI guided high-intensity focused ultrasound surgery (MRg-HIFUS). Regions where the tissue was treated were clearly identified on both DWI and sodium images. The TSC in normal myometrium tissue was approximately 36 mM with an apparent diffusion coefficient (ADC) of 2.2 mm²/s. The TSC was 28 mM in untreated fibroids and increased to 42 mM in treated tissues while ADC was 1.75 mm²/s in untreated fibroids and decreased to 1.3 mm²/s in treated tissues.

The mechanisms involved in the changes in ADC and TSC in treated uterine tissue are still unknown but these changes may provide an empirical measure of the efficacy of the treatment. DWI is sensitive to translational motion and changes in the intra- and extra-cellular compartments available for diffusion of water molecules and can reveal disruptions or restrictions to the movement of these molecules within a tissue. Sodium MRI is more sensitive to the gradient of ion concentration between the intra- and extra-cellular compartments, which depends on the Na⁺/K⁺-ATPase activity within the cell membrane and its energy consumption. Thermal ablation disrupts the cell membrane and alters the cellular integrity and perfusion of the tissue. The ADC and sodium changes within the diseased uterine tissue before and after treatment may therefore reflect a combination of complex changes in tissues such as modification of the water environment, disruption of Na⁺/K⁺-ATPase function, decreased vascularization or cytotoxic edema. This preliminary study suggests that DWI (ADC map) coupled with quantitative sodium concentration images may provide non-invasive biomarkers for the uterine leiomyomata response to therapy or for the investigation of malignant tumors by probing biochemical changes that can give information beyond the usual anatomical imaging parameters.

6.7. Whole body

Most human body parts have been scanned with sodium MRI separately for the moment, and recently a study by Wetterling et al. [219] demonstrated whole body sodium MRI in vivo at 3 T. A new asymmetrical birdcage coil was used to acquire the data in 5 segments of 10 min acquisitions each with a 3D radial sequence, and a nominal isotropic resolution of 6 mm. The resulting composite image of the 5 acquisitions is shown in Fig. 20. Despite the low resolution, one can easily detect many different organs such as the brain, the left and right ventricles of the heart, the liver, the bladder, the spine or articular cartilage. Possible applications of whole body sodium imaging could be for example the detection and malignancy assessment of cancer with metastases, and monitoring the response to chemotherapy.

Fig. 20.

Whole body sodium MRI of a volunteer. Reproduced with permission from Ref. [219].

6.8. Cancer and chemotherapeutic response

Although the following studies were not performed on humans but on rats or mice in vivo, it is useful to mention these here as they represent important preliminary work in preparation for potential human applications on cancer and chemotherapeutic response assessment [84,220,221]. The goal of cancer therapy is to eliminate neoplastic cells, but the assessment of the therapeutic efficiency in vivo may be difficult. Different functional imaging modalities such as PET (rate of glycolysis), DWI MRI (extra-cellular volume) or sodium MRI (intra-cellular sodium) could prove to be useful for this purpose.

6.8.1. Chemotherapy assessment

It has already been demonstrated that DWI is highly sensitive to microscopic changes in cellular structure and can be useful for the quantitative assessment of tumor response to therapeutic insult by observing the microscopic changes in water diffusion due to cellular destruction [222]. These microscopic changes generally precede macroscopic changes in tumor volume, which occur at much later stages after therapeutic insult. On the other hand, quantitative sodium MRI can give direct information on the intra-cellular and extra-cellular sodium concentrations, which depend on the intact- ness of the sodium channels and the Na⁺/K⁺-ATPase mechanism in the cell membrane as well as on the cellular energy consumption. Therefore, any disruption in cellular integrity can lead to abnormal imbalances that are detectable using sodium MRI.

Schepkin et al. [223] studied the possibility of using DWI and sodium MRI for assessing non-invasively the effect of chemotherapeutic treatment of tumors in vivo. The study was performed on 9L gliosarcomas implanted in rats and then treated with varying doses of BCNU. MRI images were acquired at 21.1 T. The main results are shown in Fig. 21A and B. This study demonstrated a very good correlation between DWI and sodium MRI, and thus indicated that sodium MRI may help to reveal the efficacy of tumor therapy within a few days following treatment in a dose-dependent manner.

Fig. 21.

Examples of sodium MRI and proton DWI studies on tumor and chemotherapeutic response in a rat glioma. (A) Sodium images (top) and proton ADC maps (bottom) of a BCNU-treated 9L rat glioma acquired at days 0, 7, and 23 (left to right). BCNU injection is performed at day 17 after tumor implantation. The central sodium image at day 7 shows a dramatic increase of sodium concentration throughout the entire tumor area. Image at day 23 shows tumor regrowth after tumor shrinking started at day 9 and its maximum regression at day 16. (B) Correlation of tumor sodium concentration and ADC in rat glioma obtained at various points following a single dose of BCNU. (C) Time course after tumor implantation of sodium (left) and ADC (right) variations for a naive type 9L glioma. Sodium and ADC data are given in percent relative to normal contralateral brain. All data are presented as mean ± standard deviation. Sodium concentration steadily increased in the naive tumor at a rate of 2.4% per day while ADC was practically unchanged (1.4% per day). (D) Time course after tumor implantation of sodium (left) and ADC (right) variations for a glioma created from a resistant 9L cell line. Sodium concentration steadily increased in the resistant tumor at a rate of 5.8% per day while ADC was practically unchanged (1.2% per day). Sodium values were corrected for partial volume effects. Figures A and B were reproduced with permission from Ref. [221]. Figures C and D were reproduced with permission from Ref. [224].

Babsky et al. [220] implanted fibrosarcoma (RIF-1) tumors in mice and monitored the effects of 5-fluorouracil (5FU) treatment with proton DWI, single pulse and TQF sodium MRI and also PET for measuring fluorodeoxyglucose (FDG) uptake in the tumor. Tumor volumes significantly decreased in treated animals and slightly increased in control tumors one, two, and three days post-treatment. Single-pulse sodium signal intensity (SI) and water ADC increased in treated tumors but not in control tumors during the same period. TQF sodium SI and FDG uptake were significantly lower in treated tumors compared with control tumors 3 days after 5FU treatment. The authors concluded that the correlated increases in single pulse sodium SI and water ADC following chemotherapy might reflect an increase in extra-cellular space, while the lower TQF sodium signal and FDG uptake in treated tumors compared with control tumors suggested a shift in tumor metabolism from glycolysis to oxidation and/or a decrease in cell density. A multiparametric approach using ¹H+²³Na MRI, PET and histology could therefore provide a clearer understanding of the relationship between metabolic and ionic changes in tumors caused by chemotherapy.

Kline et al. [84] used sodium MRI with IR to monitor the response to chemotherapy of mouse xenograft tumors propagated from human prostate cancer cell lines, in order to increase the weighting of the images toward intra-cellular sodium content. A 37% increase in sodium signal intensity was observed between images before and 24 h after administration of antineoplastics, which may be due to an increase of intra-cellular sodium in the treated tumors. These findings can be matched with experiments with these same drugs and cells treated in culture, where a significant intra-cellular sodium elevation (10–20 mM) was detected using a ratiometric fluorescent dye. Flow cytometry also showed that this intra-cellular sodium increase preceded cell death by apoptosis. Sodium MRI with IR seems to increase the weight of the images to intra-cellular sodium and could help monitoring apoptosis of tumor cells induced by chemotherapy in a non-invasive manner.

6.8.2. Tumor resistance to therapy

Schepkin et al. [224] also studied the capability of sodium MRI and DWI for monitoring tumor resistance to chemotherapy in intracranial rat 9L gliomas, in order to see if these methods could be used as biomarkers for drug resistance. It was first determined that implanted resistant 9L cells created tumors with significantly reduced TSC (57 mM) compared with nonresistant (naive) 9L cells (78 mM) and that corresponding differences in ADC were less pronounced but still statistically significant.

The main results are presented in Fig. 21C–D which shows the time course evolution of sodium content and ADC in naive and resistant tumors after chemotherapeutic injection (BCNU). Both sodium and ADC can differentiate resistant from naive tumors. It is shown that sodium content and ADC vary at very different rates in the two kinds of tumors after treatment and thus must depend on different mechanisms. Many parameters are involved, such as tumor volume change, increased extra-cellular volume, increased intra-cellular sodium concentration due to deficit in ATP production, increase of blood supply, and lactate overproduction (indicator of increased glycolysis). As lactate production tends to correlate with tumor aggressiveness, the increasing intra-cellular sodium content could be an indicator of growing tumor malignancy. The increase in intra-cellular sodium is likely the main mechanism involved in the detected increase of the sodium signal.

This study shows that TSC measured with sodium MRI could give important information about the level of drug resistance before chemotherapy and that it is more sensitive than DWI for detecting small changes in tumor resistance.

7. Conclusion

We have reviewed here the theoretical basis of ²³Na NMR and MRI, different pulse sequences, as well as in vivo MRI applications. The detection of sodium signals in vivo is challenging, and sodium images typically have low SNR (around 20–40), low resolution (2–10 mm) and long acquisition times (10–30 min). Such constraints, however, are often outweighed by the improved diagnostic information that can be obtained from measuring sodium concentrations, such as is the case in osteoarthritis, stroke, and muscle disorders, for example. Pioneering work in these areas has already demonstrated unique contrast, in complement to existing ¹H techniques.

Due the low gyromagnetic ratio of the sodium nuclei (26% of the proton gyromagnetic ratio), strong magnetic field gradients need to be used for acquiring images with higher resolution, which can therefore be limited by the hardware capabilities of clinical scanners (currently around 40 mT/m) and physiological constraints on gradient slew rates (200 T/(m s)). There are definite advantages to sodium MRI at high static fields (≥3 T), although important data have been acquired even at 1.5 T.

New methodological advances, such as multichannel capabilities [225,226] with parallel data acquisition using array coils and parallel reconstruction algorithms [227], and also new reconstruction schemes such as compressed sensing (CS), that allow rapid undersampled data acquisitions [228,130] have provided significant speed up and sensitivity boosts. An optimized combination of parallel-CS-NUFFT reconstruction associated with optimized sequences such as TPI at high field could therefore allow one to significantly reduce the acquisition time to a few minutes and still generate images of good resolution (1–2 mm) and maintain reasonable SNR. Such a procedure would position sodium MRI well within the realm of practical clinical imaging techniques. Assessing the intra-cellular sodium content is more challenging, as the intra-cellular sodium concentration is significantly lower. Recent pulse excitation techniques based on optimal control theory [60,61] could also provide additional sensitivity and contrast enhancements. Given the many promising pilot studies that have already been performed, one can expect many new applications and studies with of ²³Na MRI to emerge in the near future.

Highlights.

• Sodium MRI gives new biochemical information as a complement to proton MRI.

• Sodium MRI is sensitive to loss of ion homeostasis and cell viability.

• Sodium ions are sensitive to their environment through the quadrupolar relaxation and the residual quadrupolar interaction.

• Sodium MRI can be applied to all parts of the body for assessing diseases.

Glossary

AD

Altzheimer’s disease

ADC

apparent diffusion coefficient

BMS

bone marrow stimulation

CEST

chemical exchange saturation transfer

CSF

cerebrospinal fluid

CVF

cell volume fraction

DWI

diffusion weighted imaging

DQC

double quantum coherence

DQF

double quantum filter

ECM

extra-cellular matrix

EFG

electric field gradient

FCD

fixed charge density

FID

free induction decay

FOV

field of view

GAG

glycosaminoglycan

GM

grey matter

IR

inversion recovery

ISTO

irreducible spherical tensor operator

LvN

Liouville–von Neumann

MA

magic angle

MACT

matrix-associated autologous chondrocyte transplantation

MI

myocardial infarction

MQC

multiple quantum coherence

MQF

multiple quantum filter

MS

multiple sclerosis

NMSI

normalized mean signal intensity

OA

osteoarthritis

OCT

optimal control theory

PBS

phosphate buffered saline

PG

proteoglycan

PWI

perfusion weighted imaging

RF

radio frequency

ROI

region of interest

SAR

specific absorption rate

SNR

signal-to-noise ratio

SQC

single quantum coherence

TE

echo time

TPI

twisted projection imaging

TQC

triple quantum coherence

TR

repetition time

TQF

triple quantum filter

TSC

tissue sodium concentration

UTE

ultrashort TE (echo time)

WM

white matter

Appendix A

The full solution for the evolution in the presence of both relaxation and residual quadrupolar interaction is developed here in the single transition basis. The connection to the tensor conversions is given as well.

In the single transition basis, we can write the Liouville–von Neumann (LvN) Equation (Eq. (12)) in terms of the elements of the density operator ρ_rs as

$$\frac{d}{dt}{\rho }_{rs}=-i\sum _k({\mathcal{H}}_{rk}{\rho }_{ks}-{\rho }_{rk}{\mathcal{H}}_{ks})-\sum _{tu}{\mathit{\Gamma }}_{\mathit{rstu}}\{{\rho }_{tu}-{\rho }_{tu}(0)\}$$ (A.1)

$$=-i\sum _{tu}{\mathcal{H}}_{\mathit{rstu}}{\rho }_{tu}-\sum _{tu}{\mathit{\Gamma }}_{\mathit{rstu}}\{{\rho }_{tu}-{\rho }_{tu}(0)\},$$ (A.2)

where 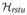= 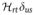δ_us − δ_rt .

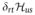If one arranges the elements of the density operator ρ according to

$$({\rho }_{11},{\rho }_{22},{\rho }_{33},{\rho }_{44},{\rho }_{12},{\rho }_{23},{\rho }_{34},{\rho }_{21},{\rho }_{32},{\rho }_{43},{\rho }_{13},{\rho }_{24},{\rho }_{31},{\rho }_{42},{\rho }_{14},{\rho }_{41}),$$

where ${\rho }_{kl}=\mid \frac{5}{2}-k\rangle \langle \frac{5}{2}-l\mid$ and |a〉 is an eigenstate of the z component of the spin angular momentum with the eigenvalue a, i.e. I_z|a〉 = a|a〉, the relaxation superoperator $\widehat{\widehat{\mathit{\Gamma }}}$ becomes block-diagonal, and each block conserves the magnetic quantum number m = l − k. In the same representation, the chemical shift and the quadrupolar interaction are diagonal. Therefore, one can solve the free evolution by examining the individual m subspaces separately.

All spectral density functions listed here follow Convention I (Eq. (19)).

A.1. Subspace independent of quadrupolar coupling

There are 3 subspaces in which the quadrupolar interaction does not contribute to the spin evolution: m = 0, ±3.

A.1.1. m = ±3 subspaces

This is the simplest subspace with the single dimensionality. The relevant equation is:

$$\begin{array}{l}\frac{d}{dt}{\rho }_{14}=-3[J({\omega }_0)+J(2{\omega }_0)]{\rho }_{14}\text{and}\\ \frac{d}{dt}{\rho }_{41}=-3[J({\omega }_0)+J(2{\omega }_0)]{\rho }_{41}.\end{array}$$ (A.3)

Therefore, the solution is

$$\begin{array}{l}{\rho }_{14}(t)=e^{-3[J({\omega }_0)+J(2{\omega }_0)]t}{\rho }_{14}(0)\text{and}\\ {\rho }_{41}(t)=e^{-3[J({\omega }_0)+J(2{\omega }_0)]t}{\rho }_{41}(0).\end{array}$$ (A.4)

The triple quantum coherences decay exponentially with a decay constant 3[J(ω₀) + J(2ω₀)], which is equal to R_2,long as will be seen below.

A.1.2. m = 0 subspace

The dimensionality of the m = 0 subspace is 4, and the corresponding part of the LvN equation is given by

$$\frac{d}{dt}\left(\begin{array}{c}{\rho }_{11}\\ {\rho }_{22}\\ {\rho }_{33}\\ {\rho }_{44}\end{array}\right)=-\left(\begin{array}{cccc}3[J({\omega }_0)+J(2{\omega }_0)]& -3J({\omega }_0)& -3J(2{\omega }_0)& 0\\ -3J({\omega }_0)& 3[J({\omega }_0)+J(2{\omega }_0)]& 0& -3J(2{\omega }_0)\\ -3J(2{\omega }_0)& 0& 3[J({\omega }_0)+J(2{\omega }_0)]& -3J({\omega }_0)\\ 0& -3J(2{\omega }_0)& -3J({\omega }_0)& 3[J({\omega }_0)+J(2{\omega }_0)]\end{array}\right)\times \left[\left(\begin{array}{c}{\rho }_{11}\\ {\rho }_{22}\\ {\rho }_{33}\\ {\rho }_{44}\end{array}\right)-\left(\begin{array}{c}{\rho }_{11}^{th}\\ {\rho }_{22}^{th}\\ {\rho }_{33}^{th}\\ {\rho }_{44}^{th}\end{array}\right)\right],$$ (A.5)

where $({\rho }_{11}^{th},{\rho }_{22}^{th},{\rho }_{33}^{th},{\rho }_{44}^{th})=(3/2,1/2,-1/2,-3/2)$. Since the matrix is real and symmetric, one can easily diagonalize it:

$$\begin{array}{r}-\left(\begin{array}{cccc}3[J({\omega }_0)+J(2{\omega }_0)]& -3J({\omega }_0)& -3J(2{\omega }_0)& 0\\ -3J({\omega }_0)& 3[J({\omega }_0+J(2{\omega }_0))]& 0& -3J(2{\omega }_0)\\ -3J(2{\omega }_0)& 0& 3[J({\omega }_0)+J(2{\omega }_0)]& -3J({\omega }_0)\\ 0& -3J(2{\omega }_0)& -3J({\omega }_0)& 3[J({\omega }_0)+J(2{\omega }_0)]\end{array}\right)=\frac{1}{2}\left(\begin{array}{cccc}1& -1& -1& 1\\ 1& 1& -1& -1\\ 1& -1& 1& -1\\ 1& 1& 1& 1\end{array}\right)\\ \times \left(\begin{array}{cccc}0& 0& 0& 0\\ 0& -6J({\omega }_0)& 0& 0\\ 0& 0& -6J(2{\omega }_0)& 0\\ 0& 0& 0& -6[J({\omega }_0)+J(2{\omega }_0)]\end{array}\right)\times \frac{1}{2}\left(\begin{array}{cccc}1& 1& 1& 1\\ -1& 1& -1& 1\\ -1& -1& 1& 1\\ 1& -1& -1& 1\end{array}\right)\end{array}$$ (A.6)

and the matrix exponentiation gives the evolution operator:

$$e^{{\mathcal{L}}_{0}t}\equiv \frac{1}{4}\left(\begin{array}{cccc}1+\alpha +\beta +\alpha \beta & 1-\alpha +\beta -\alpha \beta & 1+\alpha -\beta -\alpha \beta & 1-\alpha -\beta +\alpha \beta \\ 1-\alpha +\beta -\alpha \beta & 1+\alpha +\beta +\alpha \beta & 1-\alpha -\beta +\alpha \beta & 1+\alpha -\beta -\alpha \beta \\ 1+\alpha -\beta -\alpha \beta & 1-\alpha -\beta +\alpha \beta & 1+\alpha +\beta +\alpha \beta & 1-\alpha +\beta -\alpha \beta \\ 1-\alpha -\beta +\alpha \beta & 1+\alpha -\beta -\alpha \beta & 1-\alpha +\beta -\alpha \beta & 1+\alpha +\beta +\alpha \beta \end{array}\right),$$ (A.7)

where α ≡ e^−6J₁t and β ≡ e− ^6J₂t. Note that Eq. (A.5) is inhomogeneous, so 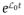should be applied as follows:

$$\left(\begin{array}{c}{\rho }_{11}(t)\\ {\rho }_{22}(t)\\ {\rho }_{33}(t)\\ {\rho }_{44}(t)\end{array}\right)-\left(\begin{array}{c}{\rho }_{11}^{th}\\ {\rho }_{22}^{th}\\ {\rho }_{33}^{th}\\ {\rho }_{44}^{th}\end{array}\right)-e^{{\mathcal{L}}_{0}t}\left[\left(\begin{array}{c}{\rho }_{11}(0)\\ {\rho }_{22}(0)\\ {\rho }_{33}(0)\\ {\rho }_{44}(0)\end{array}\right)-\left(\begin{array}{c}{\rho }_{11}^{th}\\ {\rho }_{22}^{th}\\ {\rho }_{33}^{th}\\ {\rho }_{44}^{th}\end{array}\right)\right].$$ (A.8)

A.1.3. Example: inversion recovery

After applying an inversion pulse to the thermal equilibrium state, the diagonal elements of the density operator can be obtained by setting (ρ₁₁(0), ρ₂₂(0), ρ₃₃(0), ρ₄₄(0)) = (−3/2,−1/2, 1/2, 3/2) in Eq. (A.8):

$$\begin{array}{l}\left(\begin{array}{c}{\rho }_{11}(t)\\ {\rho }_{22}(t)\\ {\rho }_{33}(t)\\ {\rho }_{44}(t)\end{array}\right)-\left(\begin{array}{c}{\rho }_{11}^{th}\\ {\rho }_{22}^{th}\\ {\rho }_{33}^{th}\\ {\rho }_{44}^{th}\end{array}\right)=e^{{\mathcal{L}}_{0}t}\left[\left(\begin{array}{c}-3/2\\ -1/2\\ 1/2\\ 3/2\end{array}\right)-\left(\begin{array}{c}{\rho }_{11}^{th}\\ {\rho }_{22}^{th}\\ {\rho }_{33}^{th}\\ {\rho }_{44}^{th}\end{array}\right)\right]\\ =\alpha \left(\begin{array}{c}-1\\ 1\\ -1\\ 1\end{array}\right)+2\beta \left(\begin{array}{c}-1\\ -1\\ 1\\ 1\end{array}\right).\end{array}$$ (A.9)

For the m = 0 subspace, one can set up the following states corresponding to the zeroth-order spherical tensors (indicated in the subscript),

$$\begin{array}{l}{\widehat{u}}_{T_{0,0}}=\left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right),{\widehat{u}}_{T_{1,0}}=\frac{1}{2}\left(\begin{array}{c}3\\ 1\\ -1\\ -3\end{array}\right),{\widehat{u}}_{T_{2,0}}=\sqrt{\frac{3}{2}}\left(\begin{array}{c}1\\ -1\\ -1\\ 1\end{array}\right),\text{and}\\ {\widehat{u}}_{T_{3,0}}=\frac{3}{2\sqrt{10}}\left(\begin{array}{c}1\\ -3\\ 3\\ -1\end{array}\right).\end{array}$$ (A.10)

In terms of these vectors, the result in Eq. (A.9) is given as

$$\left(\begin{array}{c}{\rho }_{11}\\ {\rho }_{22}\\ {\rho }_{33}\\ {\rho }_{44}\end{array}\right)={\widehat{u}}_{T_{1,0}}-\frac{2}{5}[e^{-6j({\omega }_0)t}+4e^{-6J(2{\omega }_0)t}]{\widehat{u}}_{T_{1,0}}-\frac{2}{5}[e^{-6J({\omega }_0)t}-e^{-6J(2{\omega }_0)t}]\frac{2\sqrt{10}}{3}{\widehat{u}}_{T_{3,0}},$$ (A.11)

which describes the recovery of the longitudinal magnetization back to the thermal equilibrium and the buildup of octupolar order (T₃₀). The recovery and buildup are governed by two exponentially decaying functions with the decay constants 6J(ω₀) and 6J(2ω₀). After a reading pulse applied at time t, the first point of the FID or the integration of the Fourier-transformed spectrum gives the size of the longitudinal magnetization, which is proportional to $1-\frac{2}{5}[e^{-6J({\omega }_0)t}+4e^{-6J(2{\omega }_0)t}]$. To measure the buildup of the octupolar order, a multiple-quantum filtering technique can be applied, which usually consists of two π/2 pulses with a phase cycle. For example, the first π/2 pulse excites the triple-quantum coherences T_3,±3 from octupolar order, the phase cycle selects only the triple-quantum coherence, and the second π/2 pulse converts the triple-quantum coherences into the single-quantum coherence T_3,±1, which is subsequently converted into observable magnetization through quadrupolar coupling or quadrupolar relaxation. The intensity at the resonance frequency should be proportional to a function e^{−6J(ω₀)t} − e^{−6J(2ω₀)t}.

A.2. Subspace depending on quadrupolar coupling

The remaining four subspaces with m = ±1,±2 are affected by the residual quadrupolar interaction. The following two-dimensional expressions will be useful for calculating the free evolution in these subspaces.

A two-dimensional coupled ordinary linear differential equation is given by

$$\frac{d}{dt}\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)=Ly=\left(\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right).$$ (A.12)

The general solution can be written as

$$\left(\begin{array}{c}{y}_1(t)\\ y_2(t)\end{array}\right)={Ae}^{-{\lambda }_{1}t}\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right)+{Be}^{-{\lambda }_{2}t}\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right),$$ (A.13)

and the initial condition should satisfy

$$\left(\begin{array}{c}{y}_1(0)\\ y_2(0)\end{array}\right)=A\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right)+B\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right).$$ (A.14)

The general solution can also be expressed as:

$$\left(\begin{array}{c}{y}_1(t)\\ y_2(t)\end{array}\right)=R\left(\begin{array}{c}{y}_1(0)\\ y_2(0)\end{array}\right)=\left(\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right)\left(\begin{array}{c}{y}_1(0)\\ y_2(0)\end{array}\right).$$ (A.15)

By equating Eqs. (A.13) and (A.15) and using the expression of Eq. (A.14), we get

$$R_{11}=\frac{1}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}(e^{-{\lambda }_{1}t}{\alpha }_1{\beta }_2-e^{-{\lambda }_{2}t}{\alpha }_2{\beta }_1),$$ (A.16)

$$R_{12}=-\frac{{\alpha }_1{\beta }_1}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}(e^{-{\lambda }_{1}t}-e^{-{\lambda }_{2}t}),$$ (A.17)

$$R_{21}=\frac{{\alpha }_2{\beta }_2}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}(e^{-{\lambda }_{1}t}-e^{-{\lambda }_{2}t}),$$ (A.18)

$$R_{22}=-\frac{1}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}(e^{-{\lambda }_{1}t}{\alpha }_2{\beta }_1-e^{-{\lambda }_{2}t}{\alpha }_1{\beta }_2),$$ (A.19)

or in a simpler form,

$$R=\frac{1}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}\left(\begin{array}{cc}{e}^{-{\lambda }_{1}t}{\alpha }_1{\beta }_2-e^{-{\lambda }_{2}t}{\alpha }_2{\beta }_1& -{\alpha }_1{\beta }_1(e^{-{\lambda }_{1}t}-e^{-{\lambda }_{2}t})\\ {\alpha }_2{\beta }_2(e^{-{\lambda }_{1}t}-e^{-{\lambda }_{2}t})& -(e^{-{\lambda }_{1}t}{\alpha }_2{\beta }_1-e^{-{\lambda }_{2}t}{\alpha }_1{\beta }_2)\end{array}\right)$$ (A.20)

$$=\frac{1}{{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1}\left[e^{-{\lambda }_{1}t}\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\end{array}\right)({\beta }_2-{\beta }_1)+e^{-{\lambda }_{2}t}\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right)(-{\alpha }_2{\alpha }_2)\right].$$ (A.21)

A.2.1. m = ±1 subspaces

The m = ±1 subspaces are each three-dimensional. The LvN equation for the m = 1 subspace is given as

$$\frac{d}{dt}\left(\begin{array}{c}{\rho }_{12}\\ {\rho }_{23}\\ {\rho }_{34}\end{array}\right)=\left(\begin{array}{ccc}-3[J(0)+J({\omega }_0)+J(2{\omega }_0)]-2\pi {if}_Q& 0& 3J(2{\omega }_0)\\ 0& -3[J(\omega )+J(2\omega )]& 0\\ 3J(2{\omega }_0)& 0& -3[J(0)+J({\omega }_0)+J(2{\omega }_0)]+2\pi {if}_Q\end{array}\right)\left(\begin{array}{c}{\rho }_{12}\\ {\rho }_{23}\\ {\rho }_{34}\end{array}\right),$$ (A.22)

where f_Q is the distance in Hz from the central peaks to the satellite peaks. This three-dimensional subspace breaks down to a single and a two dimensional subspaces.

The eigenvalues of the matrix are

$$\begin{array}{l}{\lambda }_{1,0}=-3[J(\omega )+J(2{\omega }_0)]\text{and}{\lambda }_{1,\pm }\\ =-3[J(0)+J({\omega }_0)+J(2{\omega }_0)]\pm \sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2},\end{array}$$ (A.23)

and the corresponding eigenvectors are

$$\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)\text{and}\left(\begin{array}{c}-2\pi {if}_Q\pm \sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}\\ 0\\ 3J(2{\omega }_0)\end{array}\right).$$ (A.24)

Therefore, by using Eq. (A.21) for the two-dimensional sub- space, the free evolution in the m = 1 subspace becomes

$$\left(\begin{array}{c}{\rho }_{12}(t)\\ {\rho }_{23}(t)\\ {\rho }_{34}(t)\end{array}\right)=\left(\begin{array}{ccc}{R}_{11}& 0& R_{13}\\ 0& R_{22}& 0\\ R_{31}& 0& R_{33}\end{array}\right)\left(\begin{array}{c}{\rho }_{12}(0)\\ {\rho }_{23}(0)\\ {\rho }_{34}(0)\end{array}\right),$$ (A.25)

where

• $R_{11}=\frac{1}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}\times \left[e^{{\lambda }_{1,+}t}\left(-2\pi {if}_Q+\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)+e^{{\lambda }_{1,-}t}\left(2\pi {if}_Q+\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)\right]$

• $R_{13}=\frac{3J(2{\omega }_0)}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}(e^{{\lambda }_{1,+}t}-e^{{\lambda }_{1,-}t})$

• R₂₂ = e^λ_1,0t

• $R_{31}=\frac{3J(2{\omega }_0)}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}(e^{{\lambda }_{1,+}t}-e^{{\lambda }_{1,-}t})$

• $R_{33}=\frac{1}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}\left[e^{{\lambda }_{1,+}t}\left(2\pi {if}_Q+\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)+e^{{\lambda }_{1,-}t}\left(-2\pi {if}_Q+\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)\right]$

The expression for the m = −1 subspace can be obtained by replacing f_Q with −f_Q.

A.3. Example: FID when f_Q = 0

After applying a 90° pulse to the thermal equilibrium state, the single-quantum coherences T_1,1 and T_1,−1 are excited. The free evolution for T_1,−1 is given as

$$\left(\begin{array}{c}{\rho }_{21}(t)\\ {\rho }_{32}(t)\\ {\rho }_{43}(t)\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{2}(e^{{\lambda }_{1,+}t}+e^{{\lambda }_{1,-}t})& 0& \frac{1}{2}(e^{{\lambda }_{1,+}t}-e^{{\lambda }_{1,-}t})\\ 0& e^{{\lambda }_{1,0}t}& 0\\ \frac{1}{2}(e^{{\lambda }_{1,+}t}-e^{{\lambda }_{1,-}t})& 0& \frac{1}{2}(e^{{\lambda }_{1,+}t}+e^{{\lambda }_{1,-}t})\end{array}\right)\left(\begin{array}{c}\sqrt{3/2}\\ \sqrt{2}\\ \sqrt{3/2}\end{array}\right)$$ (A.26)

$$=\sqrt{\frac{3}{2}}{e}^{{\lambda }_{1,+}t}\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+\sqrt{2}{e}^{{\lambda }_{1,0}t}\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right).$$ (A.27)

These three vectors can be decomposed into corresponding vectors for the first-order spherical tensors,

$$\begin{array}{l}{\widehat{u}}_{T_{1,-1}}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}\sqrt{3}\\ 2\\ \sqrt{3}\end{array}\right),{\widehat{u}}_{T_{2,-1}}=\sqrt{3}\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right),\text{and}\\ {\widehat{u}}_{T_{3,-1}}=\frac{3}{\sqrt{10}}\left(\begin{array}{c}1\\ -\sqrt{3}\\ 1\end{array}\right).\end{array}$$ (A.28)

The solution can then be written as

$$\left(\begin{array}{c}{\rho }_{21}(t)\\ {\rho }_{32}(t)\\ {\rho }_{43}(t)\end{array}\right)=\left(\frac{2}{5}{e}^{{\lambda }_{1,0}t}+\frac{3}{5}{e}^{{\lambda }_{1,+}t}\right){\widehat{u}}_{T_{1,-1}}+\left(-\frac{2}{\sqrt{15}}{e}^{{\lambda }_{1,0}t}+\frac{2}{\sqrt{15}}{e}^{{\lambda }_{1,+}t}\right){\widehat{u}}_{T_{3,-1}},$$ (A.29)

which describes the monotonic decay of the transverse magnetization and the buildup of the single-quantum coherence of the third-rank component, governed by two exponentially decaying functions with the time constants −λ_1,0 = 3J(ω₀) + 3J(2ω₀) and −λ_1,+t = 3J(0) + 3J(ω₀). Only the transverse magnetization is directly observable, so the FID should be proportional to the coefficient of û_T1,−1 in Eq. (A.29) or 2e^{−[3J(ω₀)+3J(2ω₀)]t} + 3e^{−[3J(0)+3J(ω₀)]t}. The buildup of the single-quantum coherence of the octupolar order may be observed through the triple-quantum filter technique, giving a signal proportional to e^{−[3J(ω₀)+3J(2ω₀)]t} − e^{−[3J(0)+3J(ω₀)]t}.

A.4. m = ±2 subspaces

Each of the m = ±2 subspaces is two-dimensional. The LvN equation for the m = 2 subspace is given as

$$\frac{d}{dt}\left(\begin{array}{c}{\rho }_{13}\\ {\rho }_{24}\end{array}\right)=\left(\begin{array}{cc}-3[J(0)+J({\omega }_0)+J(2{\omega }_0)]-2\pi {if}_Q& -3J({\omega }_0)\\ -3J({\omega }_0)& -3[J(0)+J({\omega }_0)+J(2{\omega }_0)]+2\pi {if}_Q\end{array}\right)\left(\begin{array}{c}{\rho }_{13}\\ {\rho }_{24}\end{array}\right).$$ (A.30)

The eigenvalues of the matrix are

$${\lambda }_{2,\pm }=-3[J(0)+J({\omega }_0)+J(2{\omega }_0)]\pm \sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2},$$ (A.31)

and the corresponding eigenvectors are

$$\left(\begin{array}{c}2\pi {if}_Q\pm \sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}\\ 3J({\omega }_0)\end{array}\right).$$ (A.32)

Therefore, the free evolution in the m = 2 subspace is described by

$$\left(\begin{array}{c}{\rho }_{13}(t)\\ {\rho }_{24}(t)\end{array}\right)=\left(\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right)\left(\begin{array}{c}{\rho }_{13}(0)\\ {\rho }_{24}(0)\end{array}\right),$$ (A.33)

where

• $R_{11}=\frac{1}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}\times \left[e^{{\lambda }_{2,+}t}\left(2\pi {if}_Q+\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)-e^{{\lambda }_{2,-}t}\left(2\pi {if}_Q-\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)\right]$

• $R_{12}=\frac{3J({\omega }_0)}{2\sqrt{9J{(2{\omega }_0)}^2-4{\pi }^2{f}_Q^2}}(e^{{\lambda }_{2,+}t}-e^{{\lambda }_{2,-}t})$

• $R_{21}=\frac{3J({\omega }_0)}{2\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}}(e^{{\lambda }_{2,+}t}-e^{{\lambda }_{2,-}t})$

• $R_{22}=\frac{-1}{2\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}}\left[e^{{\lambda }_{2,+}t}\left(2\pi {if}_Q+\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)+e^{{\lambda }_{2,-}t}\left(-2\pi {if}_Q+\sqrt{9J{({\omega }_0)}^2-4{\pi }^2{f}_Q^2}\right)\right]$

The propagator for a m = −2 subspace can be obtained by substituting f_Q with −f_Q.

A.5. Summary of decay constants

Some of the results of this section are summarized in the table below.

Observables	Experiment	Decay constant
T3,0	Inversion recovery with TQF	6J(2ω0) ≡ 1/T1,slow
		6J(ω0) ≡ 1/T1,fast
T3,1	Spin echo with TQF, when fQ = 0	3[J(ω0) + J(2ω0)] ≡ 1/T2,slow
		3[J(0) + J(ω0)] ≡ 1/T2,fast
T3,2	Delay after DQF, when fQ = 0	3[J(0) + J(2ω0)]
T3,3	Delay after TQF	3[J(ω0) + J(2ω0)] = 1/T2,slow
Central transition	Spin echo, when 2πfQ > 3J(2ω0)	3[J(ω0) + J(2ω0)] = 1/T2,slow
Satellite transition	Spin echo, when 2πfQ > 3J(2ω0)	3[J(0) + J(ω0) + J(2ω0)]
T2,2 and T3,2	Delay after DQF, when 2πfQ > 3J(ω0)	3[J(0) + J(ω0) + J(2ω0)]

A.6. Triple quantum filter coherence pathways, flip angle, and phase dependence

The coherence pathways of interest are T_3,0 → T_3,±3 → T_3,±1 and T_3,±1 → T_3,±3 → T_3,±1. Using the Wigner coefficients, the transition matrix elements of two consecutive pulses with the flip angles θ₂ and θ₃ and their corresponding phases ϕ₂ and ϕ₃ can be calculated (note, θ_2,3, and ϕ_2,3 refer to the definitions in the pulse sequence in Fig. 3). First, for the case starting with T_3,0, the transition matrix elements are given in the following table.

Coherence pathway	$D_{\pm 1,\pm 3}^3({\varphi }_3,{\theta }_3,-{\varphi }_3)D_{\pm 3,0}^3({\varphi }_2,{\theta }_2,-{\varphi }_2)$
T3,0 → T3,3 → T3,1	$-\frac{5\sqrt{3}}{16}{e}^{i(2{\varphi }_3-3{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^2{\theta }_3{sin}^2{\theta }_2$
T3,0 → T3,−3 → T3,1	$\frac{5\sqrt{3}}{16}{e}^{i(-4{\varphi }_3+3{\varphi }_2)}{sin}^2\frac{{\theta }_3}{2}{sin}^2{\theta }_3{sin}^2{\theta }_2$
T3,0 → T3,3 → T3,−1	$-\frac{5\sqrt{3}}{16}{e}^{i(4{\varphi }_3-3{\varphi }_2)}{sin}^2\frac{{\theta }_3}{2}{sin}^2{\theta }_3{sin}^2{\theta }_2$
T3,0 → T3,−3 → T3,−1	$\frac{5\sqrt{3}}{16}{e}^{i(-2{\varphi }_3+3{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^2{\theta }_3{sin}^2{\theta }_2$

For the combination of 0 and π/2 phases of the two pulses one has for the amplitudes:

ϕ2	ϕ3	Final state
0	0	$-\frac{5\sqrt{3}}{4}{sin}^2{\theta }_3{sin}^2{\theta }_{2}cos{\theta }_3(T_{3,1}-T_{3,-1})$
0	$\frac{\pi }{2}$	$\frac{5\sqrt{3}}{4}{sin}^2{\theta }_3{sin}^2{\theta }_2(T_{3,1}-T_{3,-1})$
$\frac{\pi }{2}$	0	$-i\frac{5\sqrt{3}}{4}{sin}^2{\theta }_3{sin}^2{\theta }_2(T_{3,1}+T_{3,-1})$
$\frac{\pi }{2}$	$\frac{\pi }{2}$	$i\frac{5\sqrt{3}}{4}{sin}^2{\theta }_3{sin}^2{\theta }_{2}cos{\theta }_3(T_{3,1}+T_{3,-1})$

From this table, one can see that the coherence pathway can be suppressed when (ϕ₂,ϕ₃) = (0, 0) and (π/2,π/2) with θ₃ = π/2. On the other hand, one can maximize the signal intensity by choosing θ₂ = θ₃ = π/2 with (ϕ₂,ϕ₃) = (0,π/2) or (0,π/2). The phase of the acquisition should be π/2 when (ϕ₂,ϕ₃) = (0,π/2) and 0 when (ϕ₂,ϕ₃) = (π/2, 0) to obtain the absorption-like signal. (This is because T_3,1 − T₃₋₁ and i(T_3,1 + T₃₋₁) are hermitian.)

For the single quantum coherences T_3,±1,

Coherence pathway	$D_{\pm 1,\pm 3}^3({\varphi }_3,{\theta }_3,-{\varphi }_3)D_{\pm 3,\pm 1}^3({\varphi }_2,{\theta }_2,-{\varphi }_2)$
T3,1 → T3,3 → T3,1	$15e^{i(2{\varphi }_3-2{\varphi }_2)}{cos}^4\frac{{\theta }_3}{2}{sin}^2\frac{{\theta }_3}{2}{cos}^4\frac{{\theta }_2}{2}{sin}^2\frac{{\theta }_2}{2}$
T3,−1 → T3,3 → T3,1	$15e^{i(2{\varphi }_3-4{\varphi }_2)}{cos}^4\frac{{\theta }_3}{2}{sin}^2\frac{{\theta }_3}{2}{cos}^2\frac{{\theta }_2}{2}{sin}^4\frac{{\theta }_2}{2}$
T3,1 → T3,−3 → T3,1	$15e^{i(4{\varphi }_3+4{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^4\frac{{\theta }_3}{2}{cos}^2\frac{{\theta }_2}{2}{sin}^4\frac{{\theta }_2}{2}$
T3,−1 → T3,−3 → T3,1	$15e^{i(4{\varphi }_3+2{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^4\frac{{\theta }_3}{2}{cos}^4\frac{{\theta }_2}{2}{sin}^2\frac{{\theta }_2}{2}$
T3,1 → T3,3 → T3,−1	$15e^{i(4{\varphi }_3-2{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^4\frac{{\theta }_3}{2}{cos}^4\frac{{\theta }_2}{2}{sin}^2\frac{{\theta }_2}{2}$
T3,−1 → T3,3 → T3,−1	$15e^{i(4{\varphi }_3-4{\varphi }_2)}{cos}^2\frac{{\theta }_3}{2}{sin}^4\frac{{\theta }_3}{2}{cos}^2\frac{{\theta }_2}{2}{sin}^4\frac{{\theta }_2}{2}$
T3,1 → T3,−3 → T3,−1	$15e^{i(-2{\varphi }_3+4{\varphi }_2)}{cos}^4\frac{{\theta }_3}{2}{sin}^2\frac{{\theta }_3}{2}{cos}^2\frac{{\theta }_2}{2}{sin}^4\frac{{\theta }_2}{2}$
T3,−1 → T3,−3 → T3,−1	$15e^{i(-2{\varphi }_3-2{\varphi }_2)}{cos}^4\frac{{\theta }_3}{2}{sin}^2\frac{{\theta }_3}{2}{cos}^4\frac{{\theta }_2}{2}{sin}^2\frac{{\theta }_2}{2}$

For the initial states T_3,1 − T_3,−1 and i(T_3,1 + T_3,−1), which are Hermitian, the final states are given for the cases with ϕ₂ and ϕ₃ being 0 and π/2 as

ϕ2	ϕ3	T3,1 − T3,−1	i(T3,1 + T3,−1)
0	0	(T3,1 − T3,−1) cos θ3 cos θ2	i(T3,1 + T3,−1)
0	$\frac{\pi }{2}$	−(T3,1 − T3,−1) cos θ2	− i(T3,1 + T3,−1) cos θ3
$\frac{\pi }{2}$	0	−(T3,1 − T3,−1) cos θ3	− i(T3,1 + T3,−1) cos θ2
$\frac{\pi }{2}$	$\frac{\pi }{2}$	(T3,1 − T3,−1)	i(T3,1 + T3,−1)cos θ3 cos θ2

after taking out the common factor $\frac{15}{6}{sin}^2{\theta }_3{sin}^2{\theta }_2$. When θ₂ = θ₃ = π/2, there is only one combination of ϕ₂ and ϕ₃ depending on the initial state, which can produce any signal.

A.7. Double quantum filter coherence pathways, flip angle, and phase dependence

The coherence pathways of interest are

• T_2,±1→T_2,±2→T_2,±1 and

• T_3,±1→T_3,±2→T_3,±1.

For the second-order spherical tensors T_2,±1, the transition matrix elements are

Coherence pathway	$D_{\pm 1,\pm 2}^2({\varphi }_3,{\theta }_3,-{\varphi }_3)D_{\pm 2,\pm 1}^2({\varphi }_2,{\theta }_2,-{\varphi }_2)$
T2,1 → T2,2 → T2,1	$-4e^{i({\varphi }_3-{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}sin\frac{{\theta }_2}{2}$
T2,1 → T2,−2 → T2,1	$-4e^{i(-3{\varphi }_3+3{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,−1 → T2,2 → T2,1	$-4e^{i({\varphi }_3-3{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,−1 → T2,−2 → T2,1	$-4e^{i(-3{\varphi }_3+{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}sin\frac{{\theta }_2}{2}$
T2,1 → T2,2 → T2,−1	$-4e^{i(3{\varphi }_3-{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}sin\frac{{\theta }_2}{2}$
T2,1 → T2,−2 → T2,−1	$-4e^{i(-{\varphi }_3+3{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,−1 → T2,2 → T2,−1	$-4e^{i(3{\varphi }_3-{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,−1 → T2,−2 → T2,−1	$-4e^{i(-{\varphi }_3+{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}sin\frac{{\theta }_2}{2}$

For the initial states T_2,1 − T_2,−1 and i(T_2,1 + T_2,−1), which are Hermitian, the final states are given for the cases with ϕ₂ and ϕ₃ being either 0 or π/2 as

ϕ2	ϕ3	T2,1 − T2,−1	i(T2,1 + T2,−1)
0	0	(T2,1 − T2,−1) cos θ3 cos θ2	i(T2,1 + T2,−1)
0	$\frac{\pi }{2}$	i(T2,1 + T2,−1) cos θ3 cos θ2	−(T2,1 − T2,−1)
$\frac{\pi }{2}$	0	−i(T2,1 + T2,−1)	(T2,1 − T2,−1) cos θ3 cos θ2
$\frac{\pi }{2}$	$\frac{\pi }{2}$	(T2,1 − T2,−1)	i(T2,1 + T2,−1) cos θ3 cos θ2

after taking out the common factor −sin θ₃ sin θ₂. When θ₂ = θ₃ = π/2, ϕ₂ is important to observe the signal, depending on the initial state.

For the third-order spherical tensors T_3,±1, the transition matrix elements are

Coherence pathway	$D_{\pm 1,\pm 2}^3({\varphi }_3,{\theta }_3,-{\varphi }_3)D_{\pm 2,\pm 1}^3({\varphi }_2,{\theta }_2,-{\varphi }_2)$
T3,1 → T3,2 → T3,1	$\begin{array}{l}-\frac{5}{2}{e}^{i({\varphi }_3-{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}(-1+3cos{\theta }_3)\\ sin\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}(-1+3cos{\theta }_2)sin\frac{{\theta }_2}{2}\end{array}$
T3,1 → T3,2 → T3,−1	$\begin{array}{l}-\frac{5}{2}{e}^{i(3{\varphi }_3-{\varphi }_2)}cos\frac{{\theta }_3}{2}(1+3cos{\theta }_3)\\ {sin}^3\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}(-1+3cos{\theta }_2)sin\frac{{\theta }_2}{2}\end{array}$
T3,1 → T3,−2 → T3,1	$\begin{array}{l}-\frac{5}{2}{e}^{i(-3{\varphi }_3+3{\varphi }_2)}cos\frac{{\theta }_3}{2}(1+3cos{\theta }_3)\\ {sin}^3\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}(1+3cos{\theta }_2){sin}^3\frac{{\theta }_2}{2}\end{array}$
T3,1 → T3,−2 → T3,−1	$\begin{array}{l}-\frac{5}{2}{e}^{i(-{\varphi }_3+3{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}(-1+3cos{\theta }_3)\\ sin\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}(1+3cos{\theta }_2){sin}^3\frac{{\theta }_2}{2}\end{array}$
T3,−1 → T3,2 → T3,1	$\begin{array}{l}-\frac{5}{2}{e}^{i({\varphi }_3-3{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}(-1+3cos{\theta }_3)\\ sin\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}(1+3cos{\theta }_2){sin}^3\frac{{\theta }_2}{2}\end{array}$
T3,−1 → T3,2 → T3,−1	$\begin{array}{l}-\frac{5}{2}{e}^{i(3{\varphi }_3-3{\varphi }_2)}cos\frac{{\theta }_3}{2}(1+3cos{\theta }_3)\\ {sin}^3\frac{{\theta }_3}{2}cos\frac{{\theta }_2}{2}(1+3cos{\theta }_2){sin}^3\frac{{\theta }_2}{2}\end{array}$
T3,−1 → T3,−2 → T3,1	$\begin{array}{l}-\frac{5}{2}{e}^{i(-3{\varphi }_3+{\varphi }_2)}cos\frac{{\theta }_3}{2}(1+3cos{\theta }_3)\\ {sin}^3\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}(-1+3cos{\theta }_2)sin\frac{{\theta }_2}{2}\end{array}$
T3,−1 → T3,−2 → T3,−1	$\begin{array}{l}-\frac{5}{2}{e}^{i(-{\varphi }_3+{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}(-1+3cos{\theta }_3)\\ sin\frac{{\theta }_3}{2}{cos}^3\frac{{\theta }_2}{2}(-1+3cos{\theta }_2)sin\frac{{\theta }_2}{2}\end{array}$

As before, for the initial states T_3,1 − T_3,−1 and i(T_3,1 + T_3,−1), the final states are given as

ϕ2	ϕ3	T3,1 −T3,−1	i(T3,1 + T3,−1)
0	0	(T3,1 − T3,−1)(1 − 3cos2θ3)(1 − 3cos2θ2)	i(T3,1 + T3,−1) 4cosθ3cosθ2
0	$\frac{\pi }{2}$	i(T3,1 + T3,−1)(1 − 3cos2θ3)(1 − 3cos2θ2)	−(T3,1 − T3,−1)4cosθ3cosθ2
$\frac{\pi }{2}$	0	i(T3,1 + T3,−1)4cosθ3cosθ2	−(T3,1 − T3,−1)(1 − 3cos2θ3)(1 − 3cos2θ2)
$\frac{\pi }{2}$	$\frac{\pi }{2}$	(T3,1 − T3,−1)4cosθ3cosθ2	i(T3,1 + T3,−1)(1 − 3cos2θ3)(1 − 3cos2θ2)

after taking out the common factor $-\frac{5}{8}sin{\theta }_{3}sin{\theta }_2$. The phase ϕ₂ of the first pulse controls the visibility of the signal depending on the initial state when θ₂ = θ₃ = π/2 or when either of θ₂ and θ₃ is set to the magic angle.

Normally it is not necessary to consider the evolution of T_2,0, but for completeness, it is:

Coherence pathway	$D_{\pm 1,\pm 2}^2({\varphi }_3,{\theta }_3,-{\varphi }_3)D_{\pm 2,0}^2({\varphi }_2,{\theta }_2,-{\varphi }_2)$
T2,0 → T2,2 → T2,1	$\sqrt{\frac{3}{2}}{e}^{i({\varphi }_3-2{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,0 → T2,2 → T2,−1	$\sqrt{\frac{3}{2}}{e}^{i(3{\varphi }_3-2{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,0 → T2,−2 → T2,1	$-\sqrt{\frac{3}{2}}{e}^{i(-3{\varphi }_3+2{\varphi }_2)}cos\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_2}{2}$
T2,0 → T2,−2 → T2,−1	$-\sqrt{\frac{3}{2}}{e}^{i(-{\varphi }_3+2{\varphi }_2)}{cos}^3\frac{{\theta }_3}{2}sin\frac{{\theta }_3}{2}{sin}^3\frac{{\theta }_2}{2}$

The final state can be found when ϕ₂ and ϕ₃ are either 0 or π/2:

ϕ2	ϕ3	Final State
0	0	T2,1 − T2,−1
0	$\frac{\pi }{2}$	i(T2,1 + T2,−1) cosθ3
$\frac{\pi }{2}$	0	−(T2,1 − T2,−1)
$\frac{\pi }{2}$	$\frac{\pi }{2}$	−i(T2,1 + T2,−1)cosθ3

after taking out the common factor $\frac{1}{2}\sqrt{\frac{3}{2}}sin{\theta }_3{sin}^3\frac{{\theta }_2}{2}$. Hence, the signal can be suppressed when ϕ₃ = π/2 and θ₃ = π/2.

A.8. Summary of pulse phase choices in MQF sequences

The table below summarizes the choice of the phases of the pulses to obtain absorption-like signal without changing the phase of the acquisition.

Coherence pathway	(ϕ2,ϕ3)
T3,0 → T3,±3 → T3,±1	(0,π/2)
T3,1 → T3,±3 → T3,±1	(0, 0)
T2,1 → T2,±2 → T2,±1	(0, 0)
T3,1 → T3,±2 → T2,±1	(π/2,π/2)

The spectral densities J(0), J(ω₀), and J(2ω₀) can be estimated by observing the build-up of T_3,0 and T_3,1 during inversion recovery and spin echo sequences, respectively. Measuring the decays of the double-quantum and triple-quantum coherences can be useful to validate the biexponential fitting curves on the build-up of T_3,0 and T_3,1, or to increase accuracy. See the main text for a discussion of the main results of Appendix A.