A Rare Variant Association Test Based on Combinations of Single-Variant Tests

Abstract

Next generation sequencing technologies make directly testing rare variant associations possible. However, the development of powerful statistical methods for rare variant association studies is still underway. Most of existing methods are burden and quadratic tests. Recent studies show that the performance of each of burden and quadratic tests depends strongly upon the underlying assumption and no test demonstrates consistently acceptable power. Thus, combined tests by combining information from the burden and quadratic tests have been proposed recently. However, results from recent studies (including this study) show that there exist tests that can outperform both burden and quadratic tests. In this article, we propose three classes of tests that include tests outperforming both burden and quadratic tests. Then, we propose the optimal combination of single-variant tests (OCST) by combining information from tests of the three classes. We use extensive simulation studies to compare the performance of OCST with that of burden, quadratic and optimal single-variant tests. Our results show that OCST either is the most powerful test or has similar power with the most powerful test. We also compare the performance of OCST with that of the two existing combined tests. Our results show that OCST has better power than the two combined tests.

Introduction

Recent studies show that complex diseases are caused by both common and rare variants [Pritchard, 2001; Pritchard and Cox, 2002; Walsh and King, 2007; Stratton and Rahman, 2008; Bodmer and Bonilia, 2008; Ng et al., 2009; Teer and Mullikin, 2010]. To detect disease associated common variants, indirect mapping methods based on tagging SNPs can be used. However, to detect disease associated rare variants, direct association mapping methods in which all variants must be identified should be used because rare variants are essentially independent of other variants. Next-generation sequencing technology allows sequencing of the whole genome of large groups of individuals, and thus makes direct association mapping feasible [Andre’s et al., 2007; Metzker, 2010].

Statistical methods for common variant association studies have been well developed. However, the variant by variant methods for common variant association studies may not be optimal for rare variant association studies due to allelic heterogeneity as well as the extreme rarity of individual variants [Li and Leal, 2008]. Recently, statistical methods for rare variant association studies by summarizing genotype information from multiple variants have been developed. These methods can be roughly divided into three groups: burden tests, quadratic tests, and combined tests.

Burden tests include the cohort allelic sums test (CAST) [Morgenthaler and Thilly, 2007], the combined multivariate and collapsing (CMC) method [Li and Leal, 2008], the weighted sum (WS) method [Madsen and Browning, 2009], the variable minor allele frequency threshold (VT) method [Price et al., 2010], and the cumulative minor-allele test (CMAT) [Zawistowski et al., 2010], among others. Burden tests collapse rare variants in a genomic region into a single burden variable and then regress the phenotype on the burden variable to test for the cumulative effects of rare variants in the region [Lee et al., 2012]. Let x_im denote the genotype (number of minor alleles) of the i^th individual at the m^th variant. As shown by Sha et al. [2012], the burden variables of the aforementioned methods are all the weighted combination of variants, Σ_mw_mx_im, or its function with different ways to model the weights w_m. Let s_m denote the score test statistic from a linear model or a logistic model for the m^th variant. Linear test statistics with the form Σ_mW_ms_m are also based on the burden variable Σ_mw_mx_im. Thus, from the way of collapsing genotypes, burden tests and linear tests are equivalent. So, burden tests are also called linear tests [Derkach et al., 2012].

Quadratic tests with test statistics in the form ${\Sigma }_m{W}_m{s}_m^2$ include C-alpha test [Neale et al., 2011], sequence kernel association test (SKAT) [Wu et al., 2011], and the test for testing the effects of the optimally weighted combination of variants TOW [Sha et al., 2012]. Recently developed adaptive weighting methods for rare variant association studies [Han and Pan, 2010; Hoffmann et al., 2010; Lin and Tang, 2011; Yi and Zhi, 2011; Sha et al., 2013], as pointed out by Derkach et al., [2012], are operationally similar to quadratic tests. Combined tests include the test using Fisher’s method to combine information from the linear and quadratic statistics (Fisher-CT) [Derkach et al., 2012] and the optimal linear combination of the burden test and SKAT (SKAT-O) [Lee et al., 2012].

Burden tests and quadratic tests perform quite differently. Burden tests or linear tests implicitly assume that all the rare variants are causal and directions of effects are all the same. If these assumptions are true, burden tests can outperform quadratic tests; otherwise, burden tests can perform poorly and quadratic tests can outperform burden tests [Wu et al., 2011; Lee et al., 2012; Sha et al., 2012; Derkach et al., 2012]. Ladouceur et al. [2012] showed that the performance of each of burden and quadratic tests depends strongly upon the underlying assumption and no test demonstrates consistently acceptable power despite the large sample size. To increase the robustness of the test, both SKAT-O and Fisher-CT combine a burden and a quadratic test aiming to have advantages of both burden and quadratic tests. However, burden and quadratic tests cannot cover all situations. Kinnamon et al. [2012] demonstrated that the single-variant test with statistic ${\max }_m{s}_m^2$ can outperform both burden and quadratic tests when there are a large number of neutral variants and small number of causal variants. Results of this study show that the tests with statistics ${\Sigma }_m\mid s_m{\mid }^p(p\ge 4),{\Sigma }_m{\left(s_m{I}_{\{s_m\ge 0\}}\right)}^2,\mathrm{or}{\Sigma }_m{(-s_m{I}_{\{s_m\le 0\}})}^2$ can outperform both burden and quadratic tests in some situations.

In this article, through the optimal combination of single-variant tests under different criteria, we first obtain three classes of tests that are well beyond burden and quadratic tests. Then, we propose the optimal combination of single-variant tests (OCST) by combining information from tests of the three classes. Using extensive simulation studies, we compare the performance of OCST with that of the burden, quadratic, and the optimal single-variant tests. Our results show that, in a wide range of scenarios, OCST either is the most powerful test or has similar power with the most powerful test. We also compare power of OCST with that of the two existing combined tests: Fisher-CT and SKAT-O. We are able to demonstrate that OCST has better power than both Fisher-CT and SKAT-O.

Method

Consider a sample of n individuals. Each individual has been genotyped at M variants in a genomic region (a gene or a pathway). Denote y_i as the trait value of the i^th individual for either a quantitative trait or a qualitative trait (1 for cases and 0 for controls for a qualitative trait) and denote x_im as the genotypic score of the i^th individual at the m^th variant, where x_im∈{0,1,2} is the number of minor alleles. If there are no covariates, we use the generalized linear model [Nelder and Wedderburn, 1972]

$$g\left(E(y_i\mid x_{im})\right)={\beta }_0+{\beta }_1{x}_{im}$$

to model the relationship between trait values and genotypes at the m^th variant, where g() is a monotone “link” function. Under the generalized linear model, the score test statistic to test the null hypothesis H₀:β₁ = 0 is given by [Sha et al., 2011]

$$s_m=\frac{U_m}{\sqrt{V_m}},$$ (1)

where $U_m={\Sigma }_{i=1}^n(y_i-\stackrel{‒}{y})(x_{im}-{\stackrel{‒}{x}}_m)\mathrm{and}{V}_m=\frac{1}{n}{\Sigma }_{i=1}^n{(y_i-\stackrel{‒}{y})}^2{\Sigma }_{i=1}^n{(x_{im}-{\stackrel{‒}{x}}_m)}^2$. The statistic s_m asymptotically follows the standard normal distribution. If there are covariates, we use the method proposed by Sha et al. [2012] to adjust the effect of the covariates. Let (z_i1,…,z_ip)^T denote covariates of the i^th individual. We adjust both trait value y_i and genotypic score x_im for the covariates by applying linear regressions. That is,

$$y_i={\alpha }_0+{\alpha }_1{z}_{i1}+\dots +{\alpha }_p{z}_{ip}+{\epsilon }_i\mathrm{and}{x}_{im}={\alpha }_{0m}+{\alpha }_{1m}{z}_{i1}+\dots +{\alpha }_{pm}{z}_{ip}+{\tau }_{im}.$$ (2)

Let ỹ_i and x̃_im denote the residuals of y_i and x_im, respectively. With covariates, we replace y_i and x_im by ỹ_i and x̃_im in s_m.

Let $S_m=s_m^2$. Current quadratic tests for rare variant association studies are combinations of S_m. The statistic of TOW [Sha et al., 2012] $T_{TOW}={\Sigma }_{m=1}^M{S}_m$ and the statistic of SKAT [Wu et al., 2011] $T_{SKAT}={\Sigma }_{m=1}^M{w}_m{S}_m$, where w_m = V_mW_m and W_m is the weight used by SKAT. Since ${\Sigma }_{m=1}^M{s}_m={\Sigma }_{i=1}^n(y_i-\stackrel{‒}{y})x_i$, where $x_i={\Sigma }_{m=1}^M{w}_m{x}_{im}\mathrm{and}{w}_m=1∕\sqrt{V_m}$ is asymptotically equivalent to the weights used by Weighted Sum (WS) method [Madsen and Browning, 2009], ${\Sigma }_{m=1}^M{s}_m$ is a burden test and is similar to WS method. These observations motivate us to consider combinations of S_m and combinations of s_m.

First, we consider the optimal combinations of S₁,…,S_M under different criteria, that is, $T_a^{\mathring{a}}\left(p\right)=\underset{u_1,\dots ,u_M}{\max }{\Sigma }_{m=1}^M{u}_m{S}_m$ under the condition ${\Sigma }_{m=1}^M{u}_m^p=1$ for p∈(1,∞). By solving the maximization problem, we have $T_a^{\mathring{a}}\left(p\right)={\left({\Sigma }_{m=1}^M{S}_m^{p∕(p-1)}\right)}^{(p-1)∕p}$. The class of tests $\{T_a^{\mathring{a}}\left(p\right):p∊(1,\infty )\}$ is equivalent to {T_a(z):z∈(1,∞)}, where $T_a\left(z\right)={\left({\Sigma }_{m=1}^M{S}_m^z\right)}^{1∕z}$. We further extend {T_a(z):z∈(1,∞)} to A_a = {T_a(z):z∈(1,∞)}, where we define $T_a\left(\infty \right)=\underset{z\to \infty }{\lim }{T}_a\left(z\right)=\underset{1\le m\le M}{\max }{S}_m\mathrm{and}{T}_a\left(1\right)={\Sigma }_{m=1}^M{S}_m$. Each test in A_a can be more powerful than other tests in A_a in some scenarios. No test can be consistently more powerful than other tests in A_a (see Figures S1 and S2). Note that TOW (T_a(2)) belongs to A_a. In most cases, there is another test in A_a that is more powerful than TOW (Figures S1 and S2).

All tests in A_a are robust to the directions of the effects of causal variants. From the literature [Sha et al., 2012; Wu et al., 2011], we learn that tests being robust to directions of the effects of causal variants are less powerful than burden tests when directions of the effects of causal variants are all the same and there are not many neutral variants. This observation leads us to consider the optimal combination of s₁,…,s_M besides the class of tests A_a. To consider the optimal combination of s₁,…,s_M, we propose to use either $T_b^{\mathring{a}}\left(p\right)=\underset{w_1,\dots ,w_M}{\max }{\sum }_{m=1}^M{w}_m{s}_m$ under the condition ${\sum }_{m=1}^M{w}_m^p=1$ and w_m≥0 for m = 1,…,M or $T_c^{\mathring{a}}\left(p\right)=\underset{w_1,\dots ,w_M}{\max }{\sum }_{m=1}^M{w}_m{s}_m$ under the condition ${\sum }_{m=1}^M{(-w_m)}^p=1$ and w_m≤0 for m = 1,…,M. Using the same argument for A_a, we have that $T_b^{\mathring{a}}\left(p\right)$ lead to the class of tests A_b={T_b(z):z∈[1,∞]}, where $T_b\left(z\right)={\left({\sum }_{m=1}^M{\left(s_m{I}_{\{s_m\ge 0\}}\right)}^z\right)}^{\frac{1}{z}}\mathrm{and}{T}_c^{\mathring{a}}\left(p\right)$ lead to the class of tests A_c={T_c(z):z∈[1,∞]}, where $T_c\left(z\right)={\left({\sum }_{m=1}^M{(-s_m{I}_{\{s_m\le 0\}})}^z\right)}^{\frac{1}{z}}$.

Each of the three test classes A_a, A_b, and A_c has its own favorite scenario. The favorite scenario of A_a is that both risk and protective variants are present. The favorite scenario of A_b is that all causal variants are risk variants while the favorite scenario of A_c is that all causal variants are protective variants (see Figures S3 and S4). Let P_a(z), P_b(z), and P_c(z) denote the p-values of T_a(z), T_b(z) and T_c(z), respectively. Our proposed Optimal Combination of Single-variant Tests (OCST) is defined as

$$T_{OCST}=\underset{z∊[1,\infty ]}{\min }(P_a\left(z\right),P_b\left(z\right),P_c\left(z\right)).$$

T_OCST can be obtained by a simple grid search across a range of z. For a given grid 1≤z₁<…<z_k≤∞ , the test statistic $T_{OCST}=\underset{1\le k\le K}{\min }(P_a\left(z_k\right),P_b\left(z_k\right),P_c\left(z_k\right))$.

We use a permutation test to evaluate the p-value of OCST. In each permutation, we randomly shuffle the trait values. Suppose that we perform B times of permutations. Let $s_m^{\left(b\right)}$ denote the values of s_m based on the b^th permuted data, where b=0 represents the original data. Based on $s_m^{\left(b\right)}(b=0,1,\dots ,B)$, we can calculate $T_s^{\left(b\right)}\left(z_k\right)$ for s = a, b, or c. Then, we transfer $T_s^{\left(b\right)}\left(z_k\right)\mathrm{to}{P}_s^{\left(b\right)}\left(z_k\right)$ by

$$P_s^{\left(b\right)}\left(z_k\right)=\frac{1}{B+1}\sum _{d=0}^{B}I(T_s^{\left(d\right)}\left(z_k\right)\ge T_s^{\left(b\right)}\left(z_k\right)),\mathrm{for}s=a,b,\mathrm{and}c.$$

Let $P^{\left(b\right)}=\underset{1\le k\le K}{\min }(P_a^{\left(b\right)}\left(z_k\right),P_b^{\left(b\right)}\left(z_k\right),P_c^{\left(b\right)}\left(z_k\right))$. Then, the p-value of OCST is given by

$$\frac{1}{B}\sum _{b=1}^{B}I(P^{\left(b\right)}<P^{\left(0\right)}).$$

For a simulation study with R replicates, the above procedure will be rather computationally expensive. In our simulation studies, we use the pooling permutation method proposed by Guo and Lin [2009] to evaluate p-values. In the pooling permutation method, permuted samples from all the replicates are pooled together to form a joint sample from the null distribution. Suppose that we have R replicates and we perform B permutations for each replicate. Let $T_s^{(b,r)}\left(z_k\right)$ denote the value of T_s(z_k) based on the b^th permuted data in the r^th replicate for s=a,b, or c, where b=0 represents original data. Then, we transfer $T_s^{(b,r)}\left(z_k\right)$ to the corresponding p-value $P_s^{(b,r)}\left(z_k\right)$ by

$$P_s^{(b,r)}\left(z_k\right)=\frac{1}{(B+1)R}\sum _{l=1}^R\sum _{d=0}^{B}I(T_s^{(d,l)}\left(z_k\right)\ge T_s^{(b,r)}\left(z_k\right)),\mathrm{for}s=a,b,\mathrm{and}c.$$

Let $P^{(b,r)}=\underset{1\le k\le K}{\min }(P_a^{(b,r)}\left(z_k\right),P_b^{(b,r)}\left(z_k\right),P_c^{(b,r)}\left(z_k\right))$. Then, the p-value of OCST in the r^th replicate is given by

$$\frac{1}{BR}\sum _{l=1}^R\sum _{b=1}^{B}I(P^{(b,l)}<P^{(0,r)}).$$

Since the permutation samples are pooled across all replicates to form a sample from the null, B can be set to be much smaller than the situation when only one sample is analyzed.

Comparison of Tests

We compare the performance of the proposed test with that of (1) the weighted sum (WS) method [Madsen and Browning, 2009], (2) the sequence kernel association test (SKAT) [Wu et al., 2011], (3) $T_a\left(\infty \right)=\underset{1\le m\le M}{\max }{S}_m$ that is called maximum single-variant test (MAXST), and (4) $T_a\left(2\right)={\sum }_{m=1}^M{s}_m^2$ that is the same as TOW [Sha et al., 2012]. The rank sum test used by WS is replaced with the score test based on residuals ỹ_i and x̃_im. We also compare the performance of the proposed method with two combined tests: Fisher-CT and SKAT-O [Derkach et al., 2012; Lee et al., 2012].

Simulation

The empirical Mini-Exome genotype data provided by the 17^th genetic analysis workshops (GAW17) are used for simulation studies. This dataset contains genotypes of 697 unrelated individuals on 3205 genes. We choose six genes: AHNAK (gene1), AKAP13 (gene2), COL6A3 (gene3), FREM2 (gene4), MDN1 (gene5), and TG (gene6) with 231, 163, 187, 143, 187, and 146 variants, respectively. We merge the six genes to form a super gene (Sgene) with 1057 variants. We use Sgene because the distributions of the minor allele frequencies (MAFs) in the 1057 variants in the Sgene and in the 24487 variants in all the 3205 genes are very similar (Figure S5). In our simulation studies, we generate genotypes based on the genotypes of 697 individuals in the Sgene. The genotypes of the GAW17 data set are extracted from the sequence alignment files provided by the 1000 Genomes Project for their pilot3 study (http://www.1000genomes.org). We use the program fastPHASE [Scheet and Stephens, 2006] to infer haplotypic phase for the 697 individuals and calculate haplotype frequencies. To generate the genotype of an individual, we generate two haplotypes according to the haplotype frequencies. To generate a qualitative disease affection status, we use a liability threshold model based on a continuous phenotype (quantitative trait). An individual is defined to be affected if the individual’s phenotype is at least one standard deviation larger than the phenotypic mean. This yields a prevalence of 16% for the simulated disease in the general population. In the following, we describe how to generate a quantitative trait.

To evaluate type I error, we generate trait values independent of genotypes by using the model:

$$y=0.5X_1+0.5X_2+\epsilon ,$$ (3)

where X₁ is a continuous covariate generated from a standard normal distribution, X₂ is a binary covariate taking values 0 and 1 with a probability of 0.5, and ε follows a standard normal distribution.

To evaluate power, we assume that there are M variants in total and there are n_cau causal variants, where M is determined by n_cau and the percentage of neutral variants. When M and n_cau are given, we randomly choose M variants from 1057 variants of Sgene as total variants and randomly choose n_cau rare variants (MAF<0.01) from M variants as causal variants. Denote n_r and n_p as the number of risk variants and protective variants, respectively, where n_r + n_p = n_cau. For an individual, let $x_i^r$ and $x_j^p$ denote the genotypic scores of the i^th risk variant and the j^th protective variant, respectively. The disease model is given by

$$y=0.5X_1+0.5X_2+\sum _{i=1}^{n_r}{\beta }_i^r{x}_i^r-\sum _{j=1}^{n_p}{\beta }_j^p{x}_j^p+\epsilon ,$$

where X₁, X₂, and ε are the same as those in equation (3); ${\beta }_i^r$ and ${\beta }_j^p$ are constants and their values depend on the heritability of each causal variant. We have two models to determine the heritability of each causal variant. Let h_i denote the heritability of the i^th causal variant and let $h_T={\sum }_{i=1}^{n_{cau}}{h}_i$ denote the total heritability. In Model 1, let r₁,…,r_ncasu be random numbers between 0 and 1, then, $h_i=h_T{r}_i∕{\sum }_{j=1}^{n_{cau}}{r}_j\mathrm{for}i=1,\dots ,n_{cau}$. In model 2, h₁=0.5h_T. Let r₂,…,r_ncasu be random numbers between 0 and 1, then, $h_i=h_T{r}_i∕\left(2{\sum }_{j=2}^{n_{cau}}{r}_j\right)\mathrm{for}i=2,\dots ,n_{cau}$. Under Model 1, all causal variants have the same expected heritability. Under Model 2, the heritability of one of the causal variants is much larger than that of other causal variants.

Results

In simulation studies, p-values are estimated using a pooling permutation method [Guo and Lin, 2009] in which permuted samples from all the replicates are pooled together to form a joint sample from the null distribution. In each replicate, we perform 20 permutations. Type I error rates are evaluated using 10,000 replicated samples, while powers are evaluated using 1,000 replicated samples.

For type I error evaluation, we consider different kinds of traits, different haplotype structures (different genes), and different significance levels. For 10,000 replicated samples, the 95% confidence intervals (CIs) for type I error rates of nominal levels 0.05, 0.01, and 0.001 are (0.046, 0.054), (0.008, 0.012), and (0.0004, 0.0016), respectively. The estimated type I error rates of the five tests are summarized in Table 1. As shown in this table, more than 95% estimated type I error rates are within the 95% CIs, which indicates that the estimated type I error rates are not significantly different from the nominal levels. Thus, all the five tests are valid tests.

Table 1.

Estimated type I error rates (in percentage) of the five tests.

		Quantitative Traits					Qualitative Traits
α	Gene	WS	MAXST	TOW	SKAT	OCST	WS	MAXST	TOW	SKAT	OCST
5%	Gene1	5.21	5.11	4.82	5.18	4.96	5.04	5.26	5.04	5.04	5.20
	Gene3	5.06	5.06	5.12	5.10	5.14	4.72	5.37	4.97	4.93	5.07
	Gene5	4.92	5.37	4.88	4.54	5.08	4.98	5.37	5.14	5.03	4.97
	Sgene	5.23	5.09	4.74	5.18	4.73	4.77	4.98	4.68	4.90	5.03
1%	Gene1	0.96	0.86	0.89	1.08	0.77	1.09	1.05	1.09	0.91	0.97
	Gene3	1.09	1.09	1.09	1.06	1.14	0.99	1.06	0.97	1.06	0.90
	Gene5	0.93	1.12	0.98	0.84	0.93	0.85	1.22	1.01	1.15	1.04
	Sgene	0.89	1.04	1.12	1.02	1.02	0.98	1.08	0.92	0.94	0.99
0.1%	Gene1	0.11	0.06	0.10	0.05	0.13	0.13	0.08	0.09	0.10	0.09
	Gene3	0.07	0.11	0.12	0.08	0.07	0.07	0.08	0.11	0.10	0.08
	Gene5	0.12	0.15	0.06	0.03	0.12	0.10	0.10	0.12	0.14	0.16
	Sgene	0.13	0.13	0.13	0.07	0.18	0.06	0.11	0.11	0.14	0.13

Note: α denotes the significance level. In this set of simulations, sample size is 1000.

For power comparisons, we conduct two sets of simulations. In simulation set 1, we compare the power of OCST with that of burden (WS), quadratic (SKAT and TOW), and optimal single-variant (MAXST) tests. In simulation set 2, we compare the power of OCST with that of two combined tests (SKAT-O and Fisher-CT). For simulation set 1, we compare the power of the five tests for power as a function of the percentage of neutral variants (Figures 1, 2, S6, S7) and as a function of the percentage of protective variants (Figures 3, S8). The power of TOW and the power of SKAT have similar patterns in all the simulation scenarios, but TOW is consistently more powerful than SKAT. In the following discussion of power comparisons, we omit SKAT.

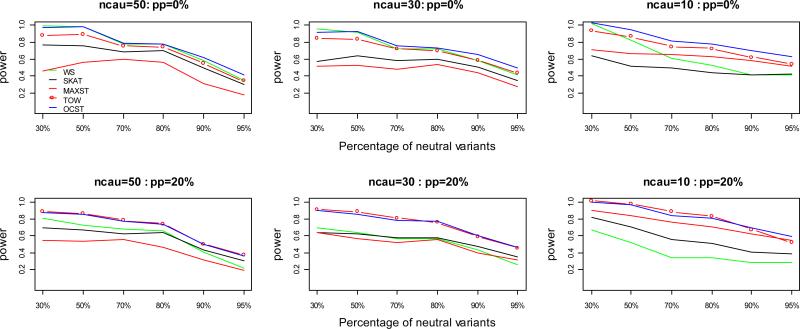
Figure 1.

Power comparisons of the five tests for power as a function of the percentage of neutral variants under model 1 for quantitative traits. ncau represents the number of causal variants. pp represents the percentage of protective variants. In this set of simulations, sample size is 1000; significance level is 0.001; total heritability is 0.05. Tn=ncau/(1−pn), where Tn represents the total number of variants and pn represents the percentage of neutral variants, and the Tn variants are randomly chosen from the 1057 variants of Sgene.

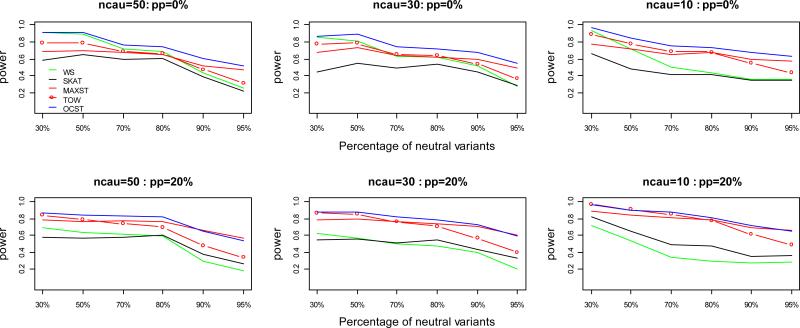
Figure 2.

Power comparisons of the five tests for power as a function of the percentage of neutral variants under model 2 for quantitative traits. ncau represents the number of causal variants. pp represents the percentage of protective variants. In this set of simulations, sample size is 1000; significance level is 0.001; total heritability is 0.05. Tn=ncau/(1−pn), where Tn represents the total number of variants and pn represents the percentage of neutral variants, and the Tn variants are randomly chosen from the 1057 variants of Sgene.

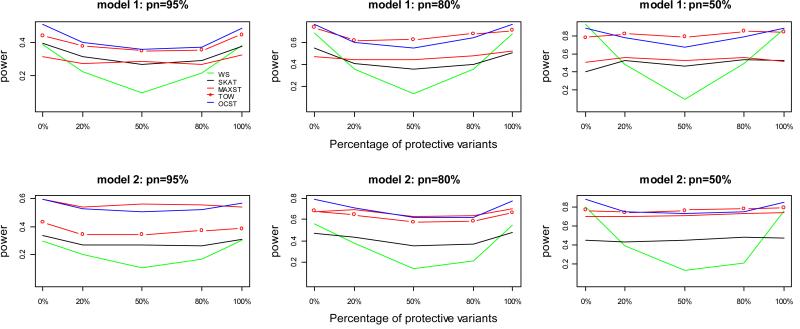
Figure 3.

Power comparisons of five tests for power as a function of the percentage of protective variants for quantitative traits. The number of causal variants is 20. pn represents the percentage of neutral variants. In this set of simulations, sample size is 1000; significance level is 0.001; total heritability is 0.05. Tn=ncau/(1−pn), where Tn represents the total number of variants and ncau represents the number of causal variants, and the Tn variants are randomly chosen from the 1057 variants of Sgene.

As shown by the power comparisons for power as a function of the percentage of neutral variants (Figures 1, 2), in all the cases, OCST either is the most powerful test or has similar power with the most powerful test. WS is the most powerful test and OCST has similar power with WS when there are no protective variants and the percentage of neutral variants is small; TOW is the most powerful test and OCST has similar power with TOW under model 1 when both protective and risk variants are present; MAXST is the most powerful test and OCST has similar power with MAXST under model 2 when both protective and risk variants are present and the percentage of neutral variants is large; OCST is the most powerful test otherwise. With the increase of neutral variants, power of all the tests decreases while the power of WS decreases the fastest and power of MAXST decreases the slowest. With the decrease of number of causal variants, power of all the tests increases while the power of WS increase the slowest and power of MAXST increases the fastest. The reason that the power of MAXST decreases the slowest with the increase of neutral variants and increases the fastest with the decrease of causal variants is that MAXST essentially only depends on the variant with the largest heritability. This reason can also explain why the power of MAXST is higher under model 2 than that under model 1.

The power comparisons for power as a function of the percentage of protective variants are given in figure 3. As shown by figure 3, again, OCST either is the most powerful test or has similar power with the most powerful test. TOW is the most powerful test and OCST has similar power with TOW when the percentage of neutral variants is small; MAXST is the most powerful test and OCST has similar power with MAXST under model 2 when the percentage of neutral variants is large; OCST is the most powerful test otherwise. When both protective and risk variants are present, the power of WS decreases dramatically, while the power of OCST decreases slightly and the power of TOW and MAXST doesn’t decrease at all.

Power comparisons based on a qualitative trait have similar patterns to those based on a quantitative trait (Figures S6-S8). However, the power of TOW and MAXST decreases in the presence of both risk and protective variants, although decreases not as fast as that of WS (Figure S8). As pointed out by Wu et al. [2011] and Sha et al. [2012], decrease in power of TOW and MAXST in the presence of both risk and protective variants is due to the fact that protective variants lower MAFs in cases and thus make observing rare variants in cases more difficult.

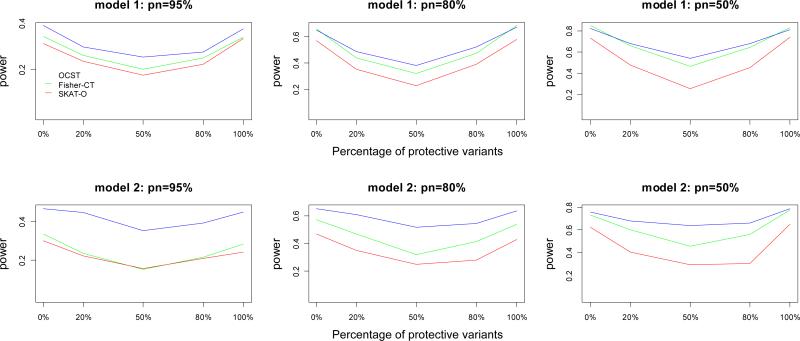
In simulation set 2, we compare the power of OCST, Fisher-CT, and SKAT-O for power as a function of percentage of protective variants. Results are summarized in Figure 4. This figure shows that OCST is consistently more powerful than Fisher-CT and Fisher-CT is consistently more powerful than SKAT-O. Power simulation results based on a qualitative trait yield the same conclusions, but differences in power between the three tests are smaller than those based on a quantitative trait (Figure S9).

Figure 4.

Power comparisons of three tests (OCST, Fisher-CT, and SKAT-O) for power as a function of the percentage of protective variants for quantitative traits. The number of causal variants is 20. pn represents the percentage of neutral variants. In this set of simulations, sample size is 1000; significance level is 0.001; total heritability is 0.05. Tn=ncau/(1−pn), where Tn represents the total number of variants and ncau represents the number of causal variants, and the Tn variants are randomly chosen from the 1057 variants of Sgene.

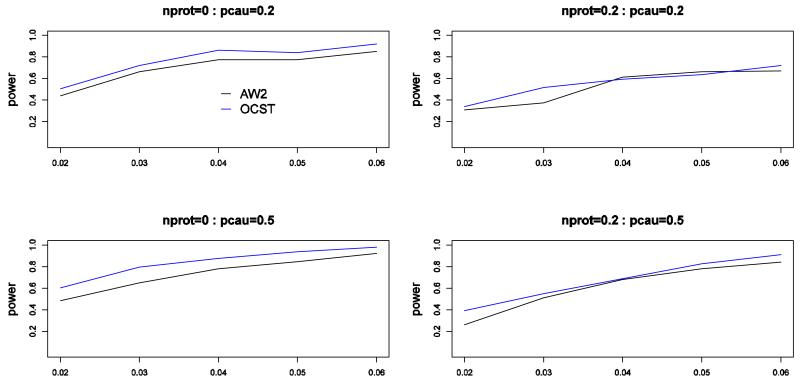
We also perform simulation studies to compare the power of the proposed test (OCST) with the Adaptive Weighting test (AW2) proposed by Sha et al. [2013]. The power comparisons of these two tests for power as a function of the heritability for quantitative traits are given in Figure 5. This figure shows that OCST is consistently more powerful than AW2.

Figure 5.

Power comparisons of the proposed test (OCST) and AW2 proposed by Sha et al. [2013] for power as a function of the heritability for quantitative traits. The number of causal variants is 30. nprot represents the percentage of protective variants. pcau represents the percentage of causal variants. In this set of simulations, sample size is 1000; significance level is 0.001.

Discussion

There is increasing interest to detect associations between rare variants and complex traits. Reasons are that (1) the common variants identified through genome-wide association studies (GWAS) account for only a small portion of the presumed phenotypic variation and (2) the development of next-generation sequencing technology has made directly testing all rare variants feasible. Several statistical methods for rare variant association studies have been developed recently. However, recent studies show that the performance of each of these methods depends strongly upon the underlying assumption and no method demonstrates consistently acceptable power [Ladouceur et al. 2012]. More recently, Derkach et al., [2012] and Lee et al., [2012] proposed combined tests by combining information from the burden and quadratic tests. However, results from this study and from Kinnamon et al. [2012] show that there exist tests that can outperform both burden and quadratic tests in some situations. In this article, we propose a novel combined test OCST by combining information from tests of the three classes that are well beyond burden and quadratic tests. Our results show that, comparing with burden and quadratic tests, OCST either is the most powerful test or has similar power with the most powerful test. Our results also show that OCST has better power than the two combined tests: Fisher-CT and SKAT-O.

All the existing methods discussed in this article are for unrelated individuals only. Although our proposed method is also described using unrelated individuals, our method can be applied to family-based data as long as there is a single-variant test. As an example, we consider the within-family test T_WFT and admixture between-family test T_adBFT proposed by Fang et al. [2012] for family-based rare variant association studies. We can use either T_WFT or T_adBFT as the single-variant test s_m and then our method can be applied to family-based data through this s_m.

Using formula (2) to adjust for the effect of covariates for binary traits may look strange. Previous researches showed that using formula (2) to adjust for the effect of covariates for binary traits works well. To control for population stratification, Price et al. [2006] used formula (2) to adjust for the effect of covariates (eigenvectors) for binary traits and they showed that this method works fine. In rare variant association studies, Sha et al. [2012] used formula (2) to adjust for the effect of covariates for binary traits and their results also showed that this method works very well.