Abstract
A quantitative description of allosteric transition remains a significant science challenge. Many allosteric enzymes contain a central β-sheet in their catalytic domain. When an allosteric protein undergoes the transition between T (tense) and R (relaxed) allosteric states, this central β-sheet undergoes a conformational change. A traditional method of measuring this change, the root mean square deviation (RMSD), appears to be inadequate to describe such changes in meaningful quantitative manner. We designed a novel quantitative method to demonstrate this conformational transition by measuring the change in curvature of the central β-sheet when enzymes transition between allosteric states. The curvature was established by calculating the semiaxes of a 3-D hyperboloid fitted by least squares to the Cα atomic positions of the β-sheet. The two enzymes selected for this study, fructose 1,6-bisphosphatase (FBPase) from pig kidney and aspartate carbamoyltransferase (ATCase) from E. coli, showed while transitioning between the allosteric states (T ⇔ R) a notable change in β-sheet curvature (∼5%) that results in a large lateral shift at the sheet's edge, which is necessary to convey the signal. The results suggest that the β-sheet participates in storing elastic energy associated with the transition. Establishing a tentative link between the energetics of the β-sheet in different allosteric states provides a more objective basis for the naming convention of allosteric states (tense or relaxed), and provides insight into the hysteretic nature of the transition. The approach presented here allows for a better understanding of the internal dynamics of allosteric enzymes by defining the domains that directly participate in the transition.
Keywords: Allosteric transition, β-sheet, Conformational change, Nonlinear fitting, Fructose 1, 6-bisphosphatase, Aspartate transcarbamylase, Global optimization
Introduction
Allostery is an important regulatory mechanism that allows biochemical processes to be controlled at the individual protein level. Allosteric proteins usually control the metabolic flows of biochemical pathways by being strategically placed at crucial junctions of individual pathways. Allosteric regulation is accomplished by proteins that change their activity level by interacting with small molecule effectors. In the classical definition of allostery, a protein has two levels of chemical activity that correspond to two different conformational states: T (inactive or tense), and R (active or relaxed), which is based on a traditional naming convention. Therefore, a small molecule changes the protein's physical characteristics by interacting with an allosteric protein. The conformational changes involved in allostery range from very small to very large, including major rearrangements of the secondary, tertiary, and quaternary structures of a protein. One classical example of such regulatory behavior is ATP activation and CTP inhibition of E. coli aspartate transcarbamoylase, a crucial enzyme in the bacterium's pyrimidine biosynthesis pathway [1].
Although the unique character of allosteric enzymes was recognized at the end of the nineteenth century, a description of its kinetics had to wait until the mid-twentieth century, when the concerted model (MWC) [2] and the sequential model (KNF) [3] were proposed. Now, in the twenty-first century, we are just beginning to gain an understanding of their mechanistic–physical roles. Protein-folding principles led to understanding allosteric transitions in terms of both free-energy changes [4] and dynamical rearrangement of the conformational ensemble [5, 6]. Several key theoretical approaches attempt to explain allostery quantitatively: (i) the Corex formalism [7–9]; (ii) the Los Alamos group approach based on the dynamics of individual proteins [10], and; (iii) the mechanism based on insights into the protein-folding problem [11] and relieving structural frustration [12]. Unfortunately, these methods neither allow conformational change to be directly measured nor do they predict the structures of alternative allosteric states once a single conformational state is known. Only recently has a more quantitative approach to reviewing and summarizing the allosteric transition been undertaken [13].
Consequently, we decided to construct a quantitative method to measure conformational changes associated with the allosteric transition based on our extensive experience with several allosteric enzymes [14, 15]. This effort was aided by insights gained from allosteric structures present in the Protein Data Bank (PDB) [16]. Approximately 25 allosteric proteins with both structural states are deposited in the PDB. The majority of these have α/β architecture with a central β-sheet (with notable exceptions like hemoglobin), which suggests that β-sheets play a special role in allosteric enzymes. Despite their closely packed protein interiors, β-sheets possess intrinsic flexibility, with a natural right-handed twist [17]. Experimental evidence of the importance of the β-sheet's flexibility in allosteric regulation has been provided [18].
The β-sheets can form closed-ended β-barrels or open-ended β-sheets [17]. An inspection of the β-sheets from a variety of protein structures suggests that β-sheets with fewer strands are more curved than more extended sheets with many strands. We hypothesize that the twisting of β-sheets results in a low-energy state. Therefore, a change in β-sheet curvature associated with structural transition should accumulate strain. The idea of storing elastic energy in β-sheets has been explored previously [19].
To quantitatively describe β-sheet changes in allosteric enzymes, we adopted an approach proposed by Novotny, Bruccoleri, and Newell [20] that was developed after a comprehensive review of β-sheet properties [21–23] had been published. Novotny et al. proposed a hyperboloid of one sheet (strophoid) as a mathematical model to represent β-barrels. We suggest that the hyperboloid model [20] is applicable to all β-sheets in proteins [24], not only to the β-barrels to which it was originally applied. This approach successfully explored previously proposed numerical relationships between the number of strands and the twist angle in β-sheets, so it may also reveal further insights into the connection between the energetics and conformational states. When the backbone of an individual strand is twisted, the remaining strands suffer considerable tension, resulting in concerted rearrangement. Once this tension has been released, the strands relax [25]. The repetitive cycle of tension and relaxation may constitute the basis for the allosteric transition.
For our study, we selected FBPase and ATCase proteins, as both of these enzymes have been used as models to study allosteric transitions for many years [1, 26]. Both enzymes are built around a structural theme of β-sheets surrounded by helices. Both enzymes are multi-subunit ensembles (Fig. 1) that undergo a global conformational change that involves a rotation of the complex's crucial elements by approximately 17°. Despite significant insight into how these two enzymes function, questions about how the individual domains participate in the transition states remain.
Fig. 1.
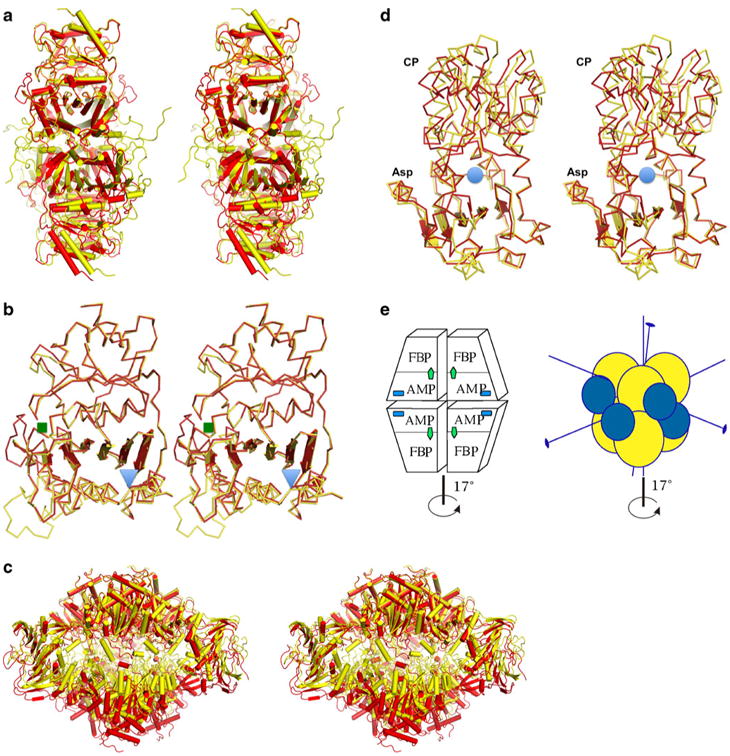
Stereo diagram of the allosteric transition showing both the T-and the R-state models as determined by X-ray crystallography, with the T state in yellow and the R state in red for both enzymes. a FBPase tetrameric structures representing both states. b Superposition of the FBPase monomers showing the distortion of the β-sheet; the regulatory site is marked with a blue triangle, while the active site is marked with a green square. c ATCase dodecamer representing a global conformational transition marked by vertical expansion and the rotation of the lower trimer of catalytic subunits bridged by regulatory subunits. d ATC catalytic subunit with Asp and CP binding domains and the active site marked by a blue circle, showing the distortion of the β-sheet of the Asp domain and the resulting conformational transition. e Schematic representation of the quaternary structures of both enzymes, with the main axis of symmetry indicated. The FBPase is composed of four identical subunits that form two dimers rotating around the main axis during the allosteric transition (left panel). The active site is labeled FBP (green arrow), and the regulatory site is labeled AMP (blue square). The ATCase (right panel) is a dodecamer with two catalytic trimers represented by yellow spheres and three regulatory dimers represented by blue spheres. The conformational change in both enzymes is the rotation of the upper dimer (trimer) against the lower dimer (trimer) by ∼17°
We combined the nonlinear fitting of the hyperboloid parameters with energy calculations and showed that allosteric transition was associated with changes in the curvature of the central β-sheet. We postulated that the flatter the β-sheet becomes (larger values of a, b, c), the higher the energy to which it corresponds. This idea was based on observations that β-sheets with a smaller number of participating strands were usually more twisted (characterized by higher curvature), suggesting that a more curved β-sheet is in a lower energy state. We propose that associating global energy states of the β-sheet with their curvature constitutes a better convention for naming the allosteric states.
Materials and methods
Protein models
Two protein models were selected to test the general methodology of the nonlinear fitting of the hyperboloid to positions of the Cα atoms representing β-sheets. In order to examine β-sheet conformational changes observed during allosteric transition, we selected the models of fructose 1,6-bisphosphatase from pig kidney (FBPase) and aspartate carbamoyltransferase from E. coli (ATCase). These models were selected for several reasons. Firstly, both enzymes are functionally important in cell survival and have been extensively studied [1, 26]. Secondly, our direct involvement in the structural determinations rendered us able to appropriately judge the quality of individual structures. Thirdly, both of the models for the T and R states have been determined, and their structures are known to a resolution of ∼2 Å. For FBPase, we selected the PDB [16] models 1RDZ [14] and 1CNQ [26] to represent the T and R states, respectively (Fig. 1a,b). For aspartate transcarbamoyltransferase, we selected 1ZA1 [27] and 1D09 [28] to represent the T and R states, respectively (Fig. 1b,c).
Additionally, in a control experiment, we used an eight-stranded (TIM) β-barrel enzyme because this protein motif has been previously investigated [20] by the hyperboloid method. The TIM barrel is a good system on which to test our approach since it provides a sufficient number of Cα positions. The structure of triose phosphate isomerase from Plasmodium falciparum (1LYX) [29] was selected since it corresponded well to the protein used in a prior study [20]. Additionally, we evaluated the structure of one subunit of tryptophane synthase (2CLH) [30] because it appears to have a rounder barrel. A comparison of the resulting parameters illustrates the changes in the curvature of the hyperboloid and provides a visual representation of those changes.
Nonlinear fitting
In the original paper [20], β-barrel structures were studied by fitting the hyperboloids to their general shapes. To improve the fit, a helical squeeze of the hyperboloid was introduced and was represented by an additional parameter, D. The authors claimed that this model described β-barrels better than the classical hyperboloid. In general, however, an increased number of model parameters may improve the fit but they also hide the physical origin of the distortion. Consequently, we used a classical three-parameter hyperboloid model, without the D parameter, to provide a clearer interpretation. We developed a nonlinear fitting procedure to search for an optimal set of hyperboloid parameters to describe the β-sheet. Three of those parameters (a, b, c) described the curvature of the β-sheet in three dimensions, while the remaining six parameters described the three-dimensional orientation of the hyperboloid. Since the nonlinear nature of the fitting procedure did not guarantee solution consistency, the procedure was repeated several times using different sets of initial guess parameters, and then statistically evaluated. We developed linear and nonlinear methods to obtain hyperboloid parameters. Results from the nonlinear method (discussed below) were reliable; results from the linear method were not. The set of Cα atoms for the TIM structure, defined formally using the SHEET record in the PDB structure, contained 40 Cα points for the 1LYX structure and 42 Cα points for the 1CLH structure.
Coordinates of the β-sheet domains for both the T and R states were extracted from the ATOM records of the PDB file. β-Strand extent was determined based on SHEET records listed in the PDB record. The structures were inspected using crystallographic visualization programs such as Protein Explorer [31]. The set of α-carbon atoms selected for hyperboloid fitting was visually inspected and confirmed to belong to the β-sheet region of the enzyme. Before fitting, the three-dimensional models of both allosteric states were superposed to avoid the use of vastly different starting points for the nonlinear optimization procedure.
The coordinates (x, y, z) for the α-carbon atoms that belonged to the β-strands were extracted from the PDB files using a semiautomated procedure. We used a Matlab (MathWorks, Natick, MA, USA) script to generate a list of the three-dimensional coordinates. Mapping the selected coordinates onto the hyperboloid involved determining Euler rotation angles (φ, θ, ψ), translation (tx, ty, tz), and calculating the best hyperboloid parameters (a, b, c). The latter parameters generate a direct geometrical interpretation of the curvature of the surface in the x, y, and z directions. This feature can be best understood in two dimensions. Assuming that a = b results in an equation that describes a circle with a radius equal to the a parameter.
The following single-sheet hyperboloid equation is used to fit the position of the Cα atoms in the β-sheet:
| (1) |
The hyperboloid is defined by nine parameters. In addition to the three canonical parameters (a, b, c) used to describe the general shape, the method calculates rotational (φ, θ, ψ) (defined by Euler angles) and translational (tx, ty, tz) parameters. Thus, mapping was defined as a nonlinear least-squares problem, where the residual function R(w) = [R1(w),R2(w),…,Rm(w)]T is given by the following:
 |
(2) |
where w = (φ, θ, ψ, a, b, c, tx, ty, tz) is a vector with nine unknown parameters, m is the number of atoms being considered, and (x̃i,ỹi,z̃i) is the new atom position, calculated as follows:
| (3) |
where
| (4) |
Thus, this is an unconstrained problem where we wish to find the global minimum w* by minimizing the differentiable objective function
| (5) |
such that f(w*) >0, and f(w*) ≤f(w) for any W ∈ ℝn. The residual can be interpreted as a combined deviation of the fitted Cα atom positions away from the surface of the hyperboloid.
The data were entered into a program that combines the Levenberg-Marquardt minimization method with a multi-start strategy [32, 33]. The basic scheme for the code was described previously [33]. The most significant innovation is the perturbation of the Hessian by μk = fk, which differs from the popular choice of μk = ‖∇ fk‖2.
While a classical multi-start strategy is simple and easily implemented in global optimization (combining random sampling with a local minimization algorithm), the proposed method used in this study involved random sampling combined with a selective search. The local minima can then be bypassed, and a global minimum can eventually be attained [32, 33].
Nonlinear fitting algorithms quite often tend to diverge, so an arbitrary convergence criterion had to be established. Ideally, the convergence criterion for the ideal data fitted to the function would lead to 0. A functional value was needed to serve as a convergence criterion for all of the enzymatic runs. We heuristically determined this criterion to be equal to 0.00544, a value selected as a compromise between the number of steps needed to reach minimal error and yet still reach convergence. In nonlinear optimization procedures, the continuation of minimization beyond a certain threshold usually leads to divergence.
Energy calculation
To establish the connection between conformational states of the molecule and the energy landscape of the transition, we used a well-established method of molecular mechanics that uses a classical force field, as encoded in the program Amber. First, we retrieved X-ray models for both the T and R states of the FBPase and ATCase from the PDB. Both models representing the two allosteric states are visualized in Fig. 1a–d, with a schematic representation of the enzymes and their changes during allosteric transition given in Fig. 1e. To quantify the conformational changes, we employed energy optimization for models of both allosteric states using Amber 10 in its parallel version [34]. The PDB structures initially downloaded were stripped of water molecules and ligands. The models were modified to have identical amino acid sequences (6–337 for FBPase), and hydrogen atoms were generated using Amber 10. Subsequently, we performed energy minimization on models of both allosteric states to achieve a small gradient change from cycle to cycle (<0.001 kcal mol−1), which took between 10,000 and 20,000 minimization steps. The computations were performed with a parm99SB force field [35] using the generalized Born implicit solvation model [36] on a 128-node Linux cluster.
Next, we introduced the ligands (i.e., AMP) to both FBPase (T and R states) structures by docking them with known coordinates of these moieties found in homologous structures. AMP is known to stabilize the T state of the enzyme and serves as a feedback inhibitor. In the case of ATCase, we introduced PALA, which causes the molecule to attain the R-state conformation. We subjected the structures of both states containing ligands to the same minimization procedure as used for FBPase using the generalized Born implicit solvent model for both states and both protein models. Afterwards, we estimated the contribution to the total energy that comes from the β-sheet by partitioning the calculated energy into the internal energy (intra) represented by the β-sheet atoms, the remaining protein atoms, and the interaction energy (inter) between the β-sheet and the rest of the molecule. Calculations for the ATCase structure required substantial hardware resources to carry out the optimization because of its size (∼2700 amino acids, ∼44,000 atoms).
Results and discussion
Measuring conformational changes quantitatively in allosteric enzymes is a difficult task. Even when the change is pronounced, choosing an arbitrary “reaction coordinate” is a difficult task. We hypothesized that allosteric transitions in enzymes containing a central β-sheet may be quantified by calculating the curvature of the β-sheet in the R and T states. This conformational change is quantified by measuring the change in hyperboloid parameters (curvature) that are obtained from a fit to the positions of the Cα atoms of the β-sheet. We used a nonlinear fitting procedure (as described in “Materials and methods”) to search for an optimal set of hyperboloid parameters to describe the β-sheet. The method was tested on two selected enzymes, FBPase and ATCase. To illustrate the power of the method, we selected a previously described case, TIM barrel enzymes.
TIM
To verify our computational approach, we performed hyperboloid fitting for two structures containing the eight-stranded β-barrel (TIM). The first was triosephosphate isomerase from P. falciparum (TIM-1LYX), and the second was tryptophan synthase (TS-1CLH). Results from the method applied to the TIM barrel architecture were compared to those reported in the literature [20, 37], and constituted a control experiment. Though our method differed in details from that previously used, we obtained similar results to Novotny et al. (Table 1). Since the PDB structure of the TIM barrel used by Novotny et al. was not available, we used a similar enzyme model. To better visualize the significance of these results and differences in the hyperboloid curvature, we investigated tryptophane synthase, a related enzyme with a rounder TIM barrel.
Table 1. Comparison of the (a, b, c) hyperboloid parameters for TIM barrels taken from the literature with those obtained by the nonlinear method.
| TIM data from Novotny et al. | TIM data obtained from nonlinear fitting** of 40 pts erms=3.5259 | TS* data obtained from nonlinear fitting** of 40 pts erms=3.5259 | |
|---|---|---|---|
| Minor semiaxis (a) | 5.8 | 6.5 | 8.3 |
| Major semiaxis (b) | 8.6 | 8.9 | 8.8 |
| Canonical parameter c | 13.4 | 32.1 | 27.8 |
Data for tryptophane synthase TS model 1CLH
For this fitting procedure, the starting seed number was 8, 5, 20, which was run for 1,000 iterations
A set of 40 Cα atoms was used in the fitting. The atoms were defined by the SHEET cards in the PDB file (see “Materials and methods”). The results for the a and b parameters (∼7 Å and ∼9 Å, respectively) agreed with those obtained by Novotny et al. (Table 1). The results for the two enzymes containing the TIM barrel are presented in Table 1, and show a different curvature for each enzyme. The values of the a, b, and c parameters are easily verified by comparing them to the β-barrel dimensions presented in Fig. 2. The c parameter is much more difficult to verify directly, and it is the most difficult to estimate correctly. This is due to two reasons. Firstly, it depends on the algorithm used for its estimation. For example, with the simplified method of Novotny et al. [20], the distance in the xy plane is calculated without taking into account the tilt of the hyperboloid surface from the normal to the xy plane. Secondly, the results are dependent on the content of the fitting set of Cα atoms (i.e., how many are used). To avoid ambiguity, we used only the atoms that were assigned by PDB records to the β-sheet.
Fig. 2.
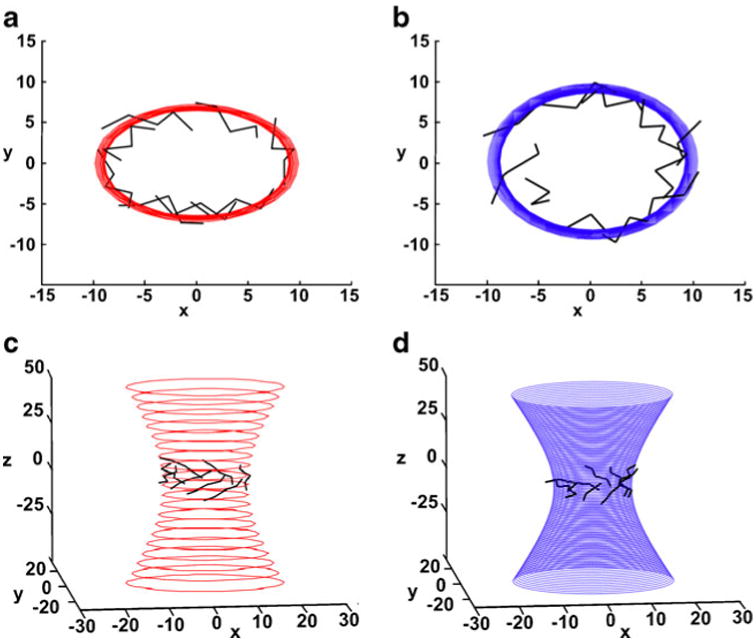
Schematic representation of the hyperboloids fitted to the Cα atoms of the β-barrel of (a and c) the triosephosphate isomerase model (TIM-1LYX; hyperboloid in red), and (b and d) the tryptophane synthase (TS-1CXH; hyperboloid in blue). Two views (along the hyperboloid axis and a side view) are shown. The TS barrel is rounder, and the curvature differs by approximately 16%, as seen by viewing along the hyperboloid axis
To visualize changes in hyperboloid parameters and illustrate the usefulness of our method, we compared the results for the original TIM barrel with those for the second TIM barrel found in the rounder tryptophan synthase (Fig. 2; Table 1); the differences in both a and b parameters were approximately 2–20% of their original values (Fig. 2).
FBPase
We applied our method to the open β-sheets of FBPase and ATCase. For both enzymes, a stereo representation of the structure is shown for both allosteric states (Fig. 1a–d). We fitted the hyperboloid to the β-sheet Cα atoms derived from the FBPase T and R states and compared the results. As expected, for a less folded and flatter β-sheet (i.e., for the R state of FBPase and the T state of ATCase), the results exhibited much larger values for the largest hyperboloid a parameter (Table 2) compared to the more twisted β-sheet (T state of FBPase and R state of ATCase). The two smaller parameters b and c (describing the highest curvature) were ∼50 Å, while the largest parameter (a) was ∼200 Å. The nonlinear method gave consistent results and indicated that there was a small difference between the curvatures, as measured by the change in the a parameter of the β-sheet in both states. Table 2 shows the parameters obtained by the nonlinear method, including statistical errors for both enzymes derived from multiple runs.
Table 2. The hyperboloid parameters for FBPase and ATCase derived by the nonlinear fitting method.
| FBPase | AVG(stdv) a (largest) | AVG(stdv) b (medium) | AVG(stdv) c (smallest) | trials used In estimation* |
| T state (1rdz) | 179.85(0.08) | 57.23(0.04) | 55.67(0.01) | 5 |
| R state (1cnq) | 189.28(0.08) | 56.47(0.04) | 56.19(0.01) | 5 |
| Difference | -9.43 | 0.76 | -0.52 | |
| % change | -4.98 | 1.33 | -0.92 | |
| ATCase | ||||
| ASP domain | AVG(stdv) a (largest) | AVG(stdv) b (medium) | AVG(stdv) c (smallest) | trials used in estimation* |
| T state (1za1) | 88.28(0.05) | 49.35(0.18) | 31.59(0.03) | 4 |
| R state (1d09) | 83.59(0.05) | 48.51(0.35) | 31.48(0.06) | 4 |
| Difference | 4.69 | 0.84 | 0.10 | |
| % change | 5.31 | 1.70 | 0.03 | |
| CP domain | ||||
| T state (1za1) | 132.91(0.02) | 56.05(0.26) | 39.91(0.06) | 4 |
| R state (1d09) | 132.10(0.03) | 57.15(0.02) | 39.39(0.01) | 4 |
| Difference | 0.81 | -1.10 | 0.52 | |
| % change | 0.60 | -1.96 | 1.30 | |
| reg domain | ||||
| T state (1za1) | 261.54(0.01) | 90.88(0.01) | 73.87(0.01) | 4 |
| R state (1d09) | 257.19(0.01) | 95.34(0.14) | 71.90(0.05) | 4 |
| Difference | 4.35 | -4.46 | 1.96 | |
| % change | 1.66 | -4.90 | 2.66 |
In most cases, the range of error was rather small, so that numerous runs were unnecessary. We determined heuristically that 4–6 calculations were sufficient to obtain reliable parameter values. Convergence was reached with an F value of 0.0054 where F=fi+1–fi is the convergence between cycles when improving the fit
The nonlinear method of fitting, which incorporates the first and approximated second derivatives, provided consistent solutions and gave different parameters for the active and inactive states. Figure 3 shows the superposition of the Cα atoms of both β-sheets in the T and R states fitted to hyperboloids obtained for FBPase. Figure 3b shows a small but consistent difference in the curvature of the hyperboloids fitted to the allosteric states. The a parameter of the hyperboloid is directly related to the transition from the T to the R state (Table 2). This parameter is larger for the R state and becomes (upon binding with AMP) smaller for the T state. In FBPase, the T state corresponds to a more twisted conformation of the β-sheet. Changes in other canonical parameters (b and c) are within expected error levels, as measured by the assumed variability produced by crystallographic errors. The expected positional accuracy of x, y, z data at 2 Å resolution is ∼0.2 Å, which should account for a <0.1% change in the hyperboloid parameter. The ∼5% change in the largest canonical parameter is significant in comparison to the expected error derived from the accuracy of the XYZ positions of individual atoms, and was larger than expected from simple RMSD calculations. The effect of the curving of the β-sheet, which would have been averaged out in the RMSD computation, is captured by the method presented above.
Fig. 3.
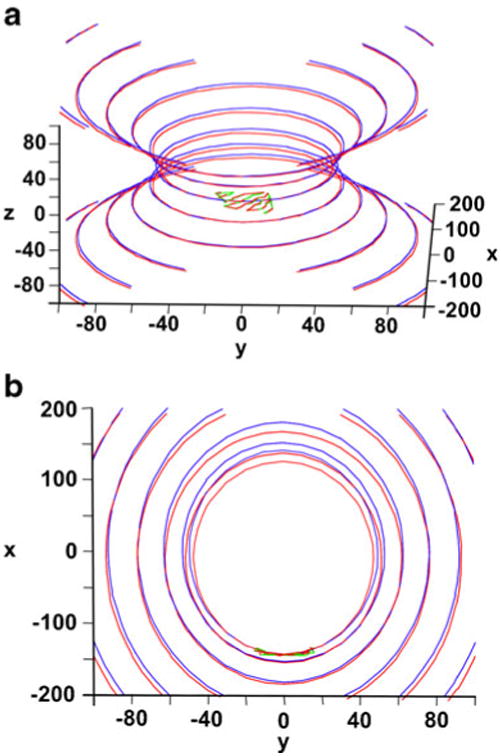
The Cα coordinates of the FBPase β-sheet superposed on the optimized hyperboloids (R state of enzyme in red; T state in green/blue): a general view; b view along a major axis, showing a small difference in the canonical parameters of the hyperboloids fitted to both states
Besides a major change in quaternary arrangement, as defined by the rotation between the upper and lower dimers (Fig. 1e, left panel), there are numerous other conformational changes. Two loops change their conformation by closing on the substrate binding site (70's loop) and the AMP binding site (20's loop). Those changes are coupled to a small internal reorganization of each subunit. When only β-sheets of the T and R states were superposed, the RMSD resulted in a 0.4 Å displacement. When the loops were included, the RMSD measured ∼4.5 Å. When the β-sheet strands are aligned by tangent, the divergence on the other side of the sheet exceeds 1.5 Å. Therefore, such a change is sufficient to dislodge the metal ions and cause the decreased activity of the T state.
FBPase: the energy calculation
To evaluate the relationship between the curvature and the internal energy of the β-sheet, we carried out molecular mechanical calculations. According to our hypothesis, the smaller the value of the canonical parameter, the less strained and more twisted the β-sheet should be. However, the amount of free energy stored in those distorted structures must be small. The estimated difference between the allosteric states is around ∼3.5 kcal [4]. A distorted β-sheet can probably store a fraction of this amount. However, since the global energy change is associated with such a large structural change (the ends of the β-sheet can move significantly), the relation of the curvature to the energy can differentiate allosteric states and, in doing so, possibly establish a more objective energy-based naming convention for allosteric states.
We carried out molecular mechanical calculations using the molecular modeling package Amber 10 and the param99SB force field (see “Materials and methods”) using the generalized Born approximation for the solvent contribution. We performed energy minimization for both allosteric states of the FBPase and ATCase structures taken from the PDB. The results of this optimization are presented in Table 3. The AMP is known to be an inhibitor and stabilizer of the T state. Optimization of the FBPase structures with and without ligand (AMP) leads to a reversal of the ground state and lower R-state energies without the ligand and a lower T-state energy with the AMP bound. When the other ligands are bound (F6P, PO4, and two or three metal ions), all of these moieties stabilize the R state with or without the AMP. Thus, only ligand (AMP) binding shifts the equilibrium of the FBPase towards the T state by 87 kcal mol−1 (26 + 61 kcal mol−1; Table. 3). This change can be traced back to the VdW and nonbonded electrostatic energy contributions.
Table 3. Results from the energy optimization of T- and R-state models of the FBPase averaged over four subunits (kcal mol−1).
| Total final energy (all subunits) | ||||||||
| FBPase (tetramer)a | ATCase (dodecamer)b | |||||||
| No ligand | Ligand (AMP) | No ligand | Ligand (PALA) | |||||
| T state | -45523 | -46870 | -111070 | -114270 | ||||
| R state | -45549 | -46809 | -111340 | -114850 | ||||
| Difference | 26 | -61 | 270 | 580 | ||||
| The energy of the β-sheet of relevant domainsc | ||||||||
| No ligand | Ligand (AMP) | No ligand | Ligand (PALA) | |||||
| Intra | Inter | Intra | Inter | Intra | Inter | Intra | Inter | |
| T state | -499.15 | -1251.68 | -494.36 | -1364.52 | -406.95 | -1122.4 | -404.85 | -1475.49 |
| (SD)e | (3.04) | (3.61) | (3.82) | (18.5) | (1.24) | (10.03) | (0.72) | (7.16) |
| R state | -478.75 | -1279.15 | -466.97 | -1425.31 | -413.35 | -1146.12 | -409.00 | -1496.53 |
| (SD)e | (0.01) | (0.01) | (0.01) | (0.06) | (3.46) | (2.96) | (4.11) | (0.74) |
| Difference | -20.4 | 27.79 | -29.25 | 60.79 | 6.4 | 23.72 | 4.15 | 21.04 |
| Diff of relevant statesd | -15.61 | -85.37 | 2.05 | 374.13 | ||||
| Diff of total (Intra+Inter) | -100.98 | 376.18 | ||||||
In the FBPase calculations, the AMP was present as a ligand that stabilizes the T state
In the ATCase calculations, PALA was present as a ligand that stabilizes the R state
In FBPase, the β-sheet of the AMP-binding domain was selected for computation; in ATCase, the ASP domain was selected
For FBPase (T + AMP) − R, for ATCase T − (R + PALA)
Standard deviation calculated over the subunits participating in an assembly: 4 in FBPase and 6 in ATCase
We then calculated β-sheet internal energy and its interaction energy with the rest of the molecule. This resulted in a lowering of the T-state internal energy for the β-sheet by ∼20 kcal mol−1 (or the total energy of the β-sheet by 104 kcal mol−1). The interaction energy between different subcomponents (β-sheet atoms and the rest of the molecule) clearly indicates that the β-sheet is responsible for lowering not only the total T-state energy but that of the remaining part of the molecule as well. However, the total energy contained in the β-sheet distortion was still lower in the T state by ∼104 kcal mol−1 compared to the R state (Table 3). This clearly supports the notion that the energy state of the entire molecule is controlled by binding ligands, which drive the system between the different allosteric states. Hence, we confirmed our hypothesis that the more twisted β-sheet present in the T-state structure (cf. Table 2: T-state (1rdz) structure with a parameter 179.9 vs. R-state (1cnq) with a=189.3) has a lower energy state compared to the R state regardless of the total energy exhibited by the model with or without ligands (i.e., the differences in the internal energies of the β-sheets between the T and R states are −29.3 or −20.4 for the model with or without ligand, respectively). This result confirms our expectation that energy is partially stored in the distorted β-sheet and that the more curved state has a lower energy regardless of the presence of ligands. This is in surprising agreement with the observations of sheet curvature done by Chothia [23]. Work is currently being carried out in our laboratory to design state-of-the-art calculations to establish a more reliable absolute energy scale so as to determine the real energy content associated with internal stress of the β-sheet.
The results imply that changes in the hyperboloid parameters relate to changes in β-sheet energy. Therefore, we postulate establishing an energy-based naming convention for the T and R states. If a larger review of allosteric enzymes confirms this initial observation, it would be possible to associate the lower free-energy state (or the relaxed state) of the β-sheet with the more twisted state. This generalized state corresponds to the T state for FBPase and to the R state in ATCase (see below).
ATCase
The E. coli ATCase enzyme is a complex system that exhibits homotropic as well as heterotropic allosteric regulation and contains several β-sheet domains. The enzyme has twelve subunits organized into three catalytic trimers connected by three regulatory dimers. Every domain of every subunit is arranged around a central β-sheet. As all of the β-sheets need to be taken into consideration, the three β-sheet regions of the carbamyl phosphate (CP), aspartate (ASP), and regulatory (CTP-binding) domains were studied. Interestingly, the CP domain showed no significant change, whereas the ASP domain showed behavior similar to FBPase. The behavior of the regulatory domain is more complex, as discussed below.
a. ATCase ASP domain
As with FBPase, the Cα atoms belonging to the β-sheet of the ASP domain were selected and the hyperboloid model was fitted to them. The results indicated that the β-sheet is in a state that is more curved than that in FBPase. The values of the a, b, c parameters are close to 80 Å, 50 Å, and 30 Å, respectively (Table 2). The a parameter changes significantly between both allosteric states (∼88 Å for the T state and ∼83 Å for the R state), with the change representing approximately 5% of the larger value. However, in contrast to FBPase, the a parameter is larger in the T state (1az1) of the enzyme and smaller in the R state (1d09). This result suggests that, in this domain, the T state represents the state with higher free-energy content (more tense, and therefore a less twisted state), while R is truly the relaxed state. This corresponds well to our postulated mechanical interpretation whereby the enzyme in the more relaxed (lower energy) state has higher curvature, which is associated with a smaller a parameter. It is interesting that this interpretation can also be tied to the kinetic interpretation of the allosteric regulation of aspartate transcarbamylase where the resting state is T and this is converted to the R state upon the binding of substrates or allosteric effectors. In contrast, the FBPase enzyme must bind AMP to be converted to the T state. It seems that, in both enzymes, the binding of a small molecule effector leads to more curved β-sheet. The sheet of the ASP domain in ATCase is more curved than that in FBPase. At a structural level, the transition in the ATCase can be traced to the conversion of the 240's loop from a helical to a more open extended form, which is needed to create the binding site for substrates, especially aspartate. This conformational transformation is responsible for the curving of the β-sheet.
b. ATCase CP domain
The Cα atoms that compose the β-sheet region of the CP domain were examined to determine whether they are affected by the allosteric transition. After fitting our hyperboloid model, the values of all three parameters were larger than those in the ASP domain and close to 130 Å, 60 Å, and 40 Å, respectively. The changes in the canonical parameters between both states were small, suggesting that this domain is not significantly influenced by the allosteric transition. The domain contains a mobile 80's loop. In transitioning between the T and R states, this loop does not influence the curvature of the central β-sheet of the CP domain. This contrasts with the influence of the 240's loop in the ASP domain, which changes the curvature of the β-sheet upon the allosteric transition.
c. The ATCase regulatory domain
The ATCase regulatory domains form a dimer created by the complementation of the five-stranded β-sheets present in both subunits. The hyperboloid was fitted to the Cα atoms of the regulatory subunit using two different methods. Initially, the calculations were carried out using all ten strands from both domains spanning the B/D subunits of the enzymes. However, the representation of two subunits by a single β-sheet may not be justified, so we performed fitting calculations for only five strands of the β-sheet in an individual domain (single regulatory subunit). In both cases, the results were similar and they will be discussed together for simplicity.
For the regulatory subunit, all three hyperboloid canonical parameters change upon transition from the T to the R state. The largest a parameter measures ∼250 Å, which represents an exceptionally flat β-sheet (Table 2). Two other parameters are also large and compare with the largest β-sheet parameters of the CP and ASP subunits (∼90 Å and ∼70 Å). Interpreting these changes is not easy because, unlike in the ASP domain, the two smaller parameters change the most (∼4% and ∼2.5%) and move in a divergent manner (e.g., if the curvature increases in one direction, the curvature decreases in the other direction). This suggests that the β-sheet that is located in the ATCase regulatory domain is controlled in a more complex fashion and does not follow the simple one-dimensional transformation pattern found for both FBPase and ATCase.
Therefore, the homotropic allosteric transition may be universally controlled by a single parameter associated with β-sheet curvature, but the heterotropic allosteric transition could be more complex and may require β-sheet changes in two dimensions. Further studies to clarify this observation are needed.
ATCase: the energy calculation
Encouraged by the success of the energy calculations for FBPase that showed the switching effect of the allosteric inhibitor AMP and the R-state-stabilizing influence of natural ligands (F6P and the metal ions), we carried out energy minimization of the entire dodecamer of ATCase. This is a large system containing more than 2700 amino acids and in excess of 44,000 atoms. The computation was performed on a Linux cluster with 128 processors. Approximately 15,000 cycles of minimization were needed to obtain convergence. The obtained energies are presented in Table 3. As in the case of FBPase, the energy stabilization was influenced by the presence of the R-state stabilizer PALA. PALA is an inhibitor that mimics a transition state. Even though we did not obtain the switching behavior, the direction of energy stabilization was correct. The presence of PALA stabilized (lowered) the R state of the enzyme by almost 250 kcal mol−1. The internal energy of the β-sheet was also stabilized in the R state by several (∼4–6) kcal mol−1, while the total energy of the sheet was stabilized by ∼376 kcal mol−1 (2 + 374 kcal mol−1). Those results, in combination with the results obtained for FBPase, provide support for the switching mechanism that is schematically sketched out in Fig. 4, and for the energy storage mechanism postulated above.
Fig. 4.
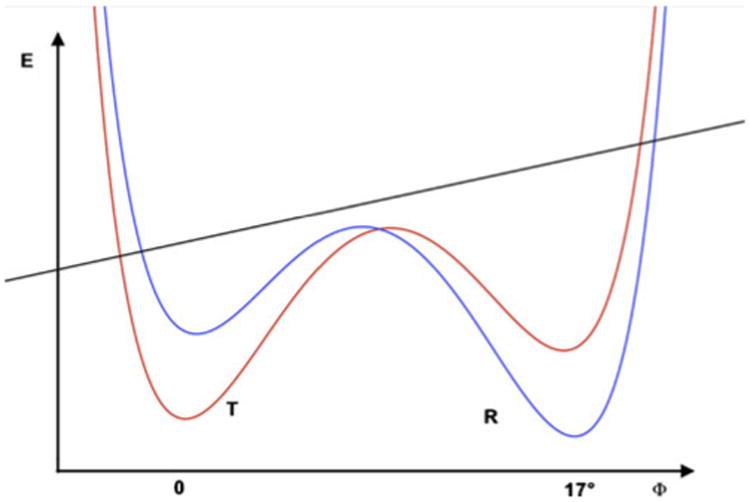
Schematic representation of the free-energy behavior of the allosteric systems (FBPase) in which the bistable potential serves as a model for switching behavior that is caused by the binding of small molecule ligands. The dark straight line represents the internal energy of the β-sheet (different energy scale), while the red and blue curves correspond to the free energy of the total system in the T and R states, respectively. In both systems (FBPase and ATCase), the reaction coordinate is a twist angle between the subunits (Fig. 1c) that characterizes the allosteric states. The slope of the energy change of the β-sheet would be the opposite in ATCase (R state has lower energy and a higher curvature) compared to FBPase (Table 3). After renaming the states according to the proposed convention, the schematic would become universal, with the T state having higher β-sheet energy and lower curvature (a flatter β-sheet)
Conclusions
We have presented a method for detecting and monitoring the structural changes observed in two allosteric enzymes during the transition between the T and R states. One enzyme was smaller (FBPase) and showed simple allosteric behavior. The second enzyme was larger and exhibits more complex allosteric behavior (ATCase). We constructed a computational tool to quantitatively describe the geometry and energy of the β-sheet in two endpoint allosteric states. The hyperboloid was fitted to the Cα atoms of the β-sheet in both the T and the R allosteric states. The difference in the canonical parameters of the hyperboloid was used to detect curvature changes of the β-sheet. The change in β-sheet backbone conformation was used to determine the extent of allosteric transition and to differentiate between allosteric states. For FBPase, the change in β-sheet conformation of the crucial domain was limited to one dimension. This curvature, as measured by the value of the largest hyperboloid semiaxis, changed by ∼5%. A similar result was obtained for the homotropic allosteric transition in the ASP domain of ATCase. Such a change in the conformation of the β-sheet is significant, as it causes a shift by a few Å at the edge of the sheet.
We compared the roles of the β-sheets during allosteric transition in different ATCase domains and subunits. The ASP domain of ATCase undergoes a major change, while the CP domain remains mostly unchanged. This corresponds to the presence of the 240's loop in the ASP domain, which undergoes a required conformational change during the allosteric transition in order to create an active site positioned at the interface between the catalytic subunits. The change in the hyperboloid a parameter of the β-sheet in the ASP domain is similar to the analogous parameter change for the FBPase (Table 2). This observation suggests a tentative generalization. In a simple (homotropic) allosteric transition, the curvatures of the β-sheets in the domains that participate directly in the transition result in a ∼5% change.
The direction of the change was clearly correlated with the binding of small molecule effectors and corresponded to the energy change in the β-sheet (see the comparison between the colored fields in Tables 2 and 3). Our results suggested that the T state in FBPase is more curved and has a lower energy. This lower energy suggests, contrary to our expectations, a less stressed T state than R state. In the ATCase, the R-state β-sheet curvature is smaller, and the R-state energy is lower (more relaxed) compared to the T state. The sign of the curvature change coincides with the sign change in the total energy of the β-sheet in both enzymes. When comparing the naming conventions used in both enzymes to the results presented here, there is surprising inconsistency. Historically and somewhat arbitrarily, the states in FBPase correspond to their respective expected energy contents in reversed order compared to ATCase. In FBPase, the T/R-state naming convention is inconsistent with the curvature and energy content of the β-sheet. Our results suggest that a more consistent convention needs to be introduced that is based on the internal interactions within the protein (Tables 2 and 3). We propose that the nomenclature should be unified by taking into account the energy component, and hence the β-sheet curvature of the particular state. This new convention would require that the names of the allosteric states in the FBPase (T–R) are switched (replaced).
Our results also suggest that the participation of the β-sheets in the allosteric mechanism may be more complex than was originally thought. While α-helices may be the primary structure affected by the allosteric transition in many proteins (e.g., hemoglobin), the β-sheet may provide a guide to the extent and the energy content of this transition in many others. Further study is needed to determine the relative roles of α-helices and β-sheets in allosteric transition and to establish how they store the distortion energy.
In summary, the enzymes studied here exhibited a significant change in their β-sheet domains upon the allosteric transition. If the β-sheets were unrestricted, the observed change would be minimal. However, since the change was greater than expected, we can conclude that β-sheets involved in the allosteric transition are affected by the binding of small molecule effectors in a systematic and predictable manner, leading to the possibility of being able to predict the conformation of the other allosteric state in the absence of specific structural information.
Acknowledgments
M. Argáez, B. Bueno, and L. Velázquez were supported in part by the U.S. Department of the Army Grant DAAD19-01-1-0741, DAAD19-02-1-0243, and NIH 3T34GM008048. BS acknowledges partial support from NIH GM064481.
Contributor Information
Ellen Tolonen, Department of Chemistry, University of Texas at El Paso, El Paso, TX 79968, USA.
Brenda Bueno, Department of Mathematical Sciences, University of Texas at El Paso, El Paso, TX 79968, USA.
Sanjeev Kulshreshta, Department of Chemistry, University of Texas at El Paso, El Paso, TX 79968, USA.
Piotr Cieplak, Sanford-Burnham Medical Research Institute, 10901 N. Torrey Pines Rd, La Jolla, CA 92037, USA.
Miguel Argáez, Department of Mathematical Sciences, University of Texas at El Paso, El Paso, TX 79968, USA.
Leticia Velázquez, Department of Mathematical Sciences, University of Texas at El Paso, El Paso, TX 79968, USA.
Boguslaw Stec, Email: bstec@burnham.org.
References
- 1.Stevens RC, Lipscomb WN. A molecular mechanism for pyrimidine and purine nucleotide control of aspartate transcarbamoylase. Proc Natl Acad Sci USA. 1992;89:5281–5285. doi: 10.1073/pnas.89.12.5281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions:a plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 3.Koshland DE, Nemethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1996;6:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 4.Schachman HK. Can a simple model account for the allosteric transition of aspartate transcarbamoylase. J Biol Chem. 1988;263:18583–18586. [PubMed] [Google Scholar]
- 5.Gunasekaran K, Ma B, Nussinov R. Is allostery an intrinsic property of all dynamic proteins? Proteins Struct Funct Bioinf. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 6.Kumar S, Ma B, Tsai CJ, Sinha N, Nussinov R. Folding and binding cascades: dynamic land-scapes and population shifts. Protein Sci. 2000;9:10–19. doi: 10.1110/ps.9.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hilser VJ, Freire E. Structure-based calculation of the equilibrium folding pathway of proteins: correlation with hydrogen exchange protection factors. J Mol Biol. 1996;262:756–772. doi: 10.1006/jmbi.1996.0550. [DOI] [PubMed] [Google Scholar]
- 8.Hilser VJ, Dowdy D, Oas TG, Freire E. The structural distribution of cooperative interactions in proteins: analysis of the native state ensemble. Proc Natl Acad Sci USA. 1998;95:9903–9908. doi: 10.1073/pnas.95.17.9903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Freire E. The propagation of binding interactions to remote sites in proteins: analysis of the binding of the monoclonal antibody D1.3 to lysozyme. Proc Natl Acad Sci USA. 1999;96:10118–10122. doi: 10.1073/pnas.96.18.10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ming D, Wall ME. Quantifying allosteric effects in proteins. Proteins Struct Funct Bioinf. 2005;59:697–707. doi: 10.1002/prot.20440. [DOI] [PubMed] [Google Scholar]
- 11.Anfinsen CB. Studies of the principles that govern the folding of protein chains (Nobel Lecture) Norstedt & Sons; Stockholm: 1972. [DOI] [PubMed] [Google Scholar]
- 12.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 13.Daily MD, Gray JJ. Local motions benchmark allosteric proteins. Proteins. 2007;67:385–399. doi: 10.1002/prot.21300. [DOI] [PubMed] [Google Scholar]
- 14.Stec B, Abraham R, Giroux E, Kantrowitz ER. Crystal structures of the active site mutant (Arg-243→Ala) in the T and R allosteric states of pig kidney fructose-1,6-bisphosphatase expressed in Escherichia coli. Protein Sci. 1996;5:1541–1545. doi: 10.1002/pro.5560050810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stieglitz K, Stec B, Baker DP, Kantrowitz ER. Monitoring the transition from the T to the R state in E. coli aspartate transcarbamoylase by X-ray crystallography: crystal structures of the E50A mutant enzyme in four distinct allosteric states. J Mol Biol. 2004;341:853–868. doi: 10.1016/j.jmb.2004.06.002. [DOI] [PubMed] [Google Scholar]
- 16.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucl Acid Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Murzin AG, Lesk AM, Chothia C. Principles determining the structure of beta-sheet barrels in proteins. I. A theoretical analysis. J Mol Biol. 1994;236(5):1369–1381. doi: 10.1016/0022-2836(94)90064-7. [DOI] [PubMed] [Google Scholar]
- 18.Liu L, Wales ME, Wild JR. Conversion of the allosteric regulatory patterns of aspartate transcarbamoylase by exchange of a single beta-strand between diverged regulatory chains. Biochemistry. 1997;36:3126–3132. doi: 10.1021/bi962065d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sun S, Chandler D, Dinner AR, Oster G. Elastic energy storage in beta-sheets with application to F1-ATPase. Eur Biophys J. 2003;32:676–683. doi: 10.1007/s00249-003-0335-6. [DOI] [PubMed] [Google Scholar]
- 20.Novotny J, Bruccoleri RE, Newell J. Twisted hyperboloid (strophoid) as a model of β-barrels in proteins. J Mol Biol. 1984;177:567–573. doi: 10.1016/0022-2836(84)90301-2. [DOI] [PubMed] [Google Scholar]
- 21.Salemme FR, Weatherford DW. Conformational and geometrical properties of β-sheets in proteins I. J Mol Biol. 1981;146:101–117. doi: 10.1016/0022-2836(81)90368-5. [DOI] [PubMed] [Google Scholar]
- 22.Salemme FR, Weatherford DW. Conformational and geometrical properties of β-sheets in proteins II. J Mol Biol. 1981;146:119–141. doi: 10.1016/0022-2836(81)90369-7. [DOI] [PubMed] [Google Scholar]
- 23.Chothia CJ. Conformation of twisted beta-pleated sheets in proteins. Mol Biol. 1973;75:295–302. doi: 10.1016/0022-2836(73)90022-3. [DOI] [PubMed] [Google Scholar]
- 24.Stec B, Kreinovich V. Geometry of the protein structures. Why hyperbolic surfaces are a good approximation for beta-sheets. Geombinatorics. 2005;XV:18–27. [Google Scholar]
- 25.Kellermayer MS, Smith MS, Granzier HL, Bustamante C. Folding–unfolding transitions in single titin molecules characterized with laser tweezers. Science. 1997;276:1112–1116. doi: 10.1126/science.276.5315.1112. [DOI] [PubMed] [Google Scholar]
- 26.Choe JY, Poland BW, Fromm HJ, Honzatko RB. Role of a dynamic loop in cation activation and allosteric regulation of recombinant porcine fructose-1,6-bisphosphatase. Biochemistry. 1998;37:11441–11445. doi: 10.1021/bi981112u. [DOI] [PubMed] [Google Scholar]
- 27.Wang J, Stieglitz KA, Cardia JP, Kantrowitz ER. Structural basis for ordered substrate binding and cooperativity in aspartate transcarbamoylase. Proc Natl Acad Sci USA. 2005;102:8881–8886. doi: 10.1073/pnas.0503742102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jin L, Stec B, Lipscomb WN, Kantrowitz ER. Insights into the mechanisms of catalysis and heterotropic regulation of Escherichia coli aspartate transcarbamoylase based upon a structure of the enzyme complexed with the bisubstrate analogue N-phosphonacetyl-l-aspartate at 2.1 Å. Proteins Struct Funct Bioinf. 1999;37:729–742. [PubMed] [Google Scholar]
- 29.Velanker SS, Ray SS, Gokhale RS, Suma S, Balaram H, Balaram P, Murthy P. Triosephosphate isomerase from Plasmodium falciparum: the crystal structure provides insights into antimalarial drug design. Structure. 1997;5:751–761. doi: 10.1016/s0969-2126(97)00230-x. [DOI] [PubMed] [Google Scholar]
- 30.Ngo H, Harris R, Kimmich N, Casino P, Niks D, Blumenstein L, Barends TR, Kulik V, Weyand M, Schlichting I, Dunn MF. Synthesis and characterization of allosteric probes of substrate channeling in the tryptophan synthase bienzyme complex. Biochemistry. 2007;46:7713–7727. doi: 10.1021/bi700385f. [DOI] [PubMed] [Google Scholar]
- 31.Guex N, Diemand A, Peitsch MC, Schwede T. Deep View Swiss-Pdb Viewer. GlaxoSmithKline R&D/Swiss Institute of Bioinformatics; Basel: 2003. [Google Scholar]
- 32.Velázquez L, Phillips GN, Jr, Tapia RA, Zhang Y. Selective search for global optimization of zero or small residual least-squares problems: a numerical study. Comput Optim Appl. 2001;20:299–315. [Google Scholar]
- 33.Velázquez L, Argáez M, Bueno B, Stec B. Proceedings of the 2005 Conference on Diversity in Computing (TAPIA '05) ACM Press; New York: 2005. On a global optimization technique for solving a nonlinear hyperboloid least squares problem; pp. 1–3. [Google Scholar]
- 34.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Wang B, Pearlman DA, Crowley M, Brozell S, Tsui V, Gohlke H, Mongan J, Hornak V, Cui G, Beroza P, Schafmeister C, Caldwell JW, Ross WS, Kollman PA. AMBER 8. University of California; San Francisco: 2004. [Google Scholar]
- 35.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct Funct Bioinf. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Srinivasan J, Miller J, Kollman PA, Case DA. Continuum solvent studies of the stability of RNA hairpin loops and helices. J Biomol Struct Dyn. 1998;16:671–82. doi: 10.1080/07391102.1998.10508279. [DOI] [PubMed] [Google Scholar]
- 37.Lasters I, Wodak SW, Alard P, Van Cutsem E. Structural principles of parallel 8-barrels in proteins. Proc Natl Acad Sci USA. 1988;85:3338–3342. doi: 10.1073/pnas.85.10.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]


