Knowledge-fused differential dependency network models for detecting significant rewiring in biological networks

Abstract

Background

Modeling biological networks serves as both a major goal and an effective tool of systems biology in studying mechanisms that orchestrate the activities of gene products in cells. Biological networks are context-specific and dynamic in nature. To systematically characterize the selectively activated regulatory components and mechanisms, modeling tools must be able to effectively distinguish significant rewiring from random background fluctuations. While differential networks cannot be constructed by existing knowledge alone, novel incorporation of prior knowledge into data-driven approaches can improve the robustness and biological relevance of network inference. However, the major unresolved roadblocks include: big solution space but a small sample size; highly complex networks; imperfect prior knowledge; missing significance assessment; and heuristic structural parameter learning.

Results

To address these challenges, we formulated the inference of differential dependency networks that incorporate both conditional data and prior knowledge as a convex optimization problem, and developed an efficient learning algorithm to jointly infer the conserved biological network and the significant rewiring across different conditions. We used a novel sampling scheme to estimate the expected error rate due to “random” knowledge. Based on that scheme, we developed a strategy that fully exploits the benefit of this data-knowledge integrated approach. We demonstrated and validated the principle and performance of our method using synthetic datasets. We then applied our method to yeast cell line and breast cancer microarray data and obtained biologically plausible results. The open-source R software package and the experimental data are freely available at http://www.cbil.ece.vt.edu/software.htm.

Conclusions

Experiments on both synthetic and real data demonstrate the effectiveness of the knowledge-fused differential dependency network in revealing the statistically significant rewiring in biological networks. The method efficiently leverages data-driven evidence and existing biological knowledge while remaining robust to the false positive edges in the prior knowledge. The identified network rewiring events are supported by previous studies in the literature and also provide new mechanistic insight into the biological systems. We expect the knowledge-fused differential dependency network analysis, together with the open-source R package, to be an important and useful bioinformatics tool in biological network analyses.

Background

Biological networks are context‐specific and dynamic in nature [1]. Under different conditions, different regulatory components and mechanisms are selectively activated or deactivated [2],[3]. One example is the topology of underlying biological network changes in response to internal or external stimuli, where cellular components exert their functions through interactions with other molecular components [4],[5]. Thus, in addition to asking “which genes are differentially expressed”, the new question is “which genes are differentially connected” [6],[7]. Studies on network-altering events will shed new light on whether network rewiring is a general principle of biological systems regarding disease progression or therapeutic responses [2],[3]. Moreover, due to inevitable experimental noise, snapshots of dynamic expression, and post-transcriptional or translational/post-translational modifications, systematic efforts to characterize biological networks must effectively distinguish significant network rewiring from random background fluctuations [1].

Almost exclusively using high-throughput gene expression data and focusing on conserved biological networks, various network inference approaches have been proposed and tested [1], including probabilistic Boolean networks [8], state‐space models [9],[10], and probabilistic graphical models [11]. However, since these methods often assume that there is a static network structure, they overlook the inherently dynamic nature of molecular interactions, which can be extensively rewired across different conditions. Hence, current network models only present a conserved cellular network averaging across all samples. To explicitly address differential network analysis [3],[5],[12], some initial efforts have been recently reported [1]. In our previous work, Zhang et al. proposed to model differential dependency networks between two conditions by detecting network rewiring using significance tests on local dependencies across conditions [13],[14], which is a substantially different method from the one proposed in this paper where experimental data and prior knowledge are jointly modeled. The approach was successfully extended by Roy et al. to learn dynamic networks across multiple conditions [15], and by Gill et al. to assess the overall evidence of network differences between two conditions using the connectivity scores associated with a gene or module [16]. Pioneered and reported in [17], correlation and partial correlation are used to construct network graphs, and differential pathway analysis is developed based on graph edit distance. The temporal evolution of network structures is examined with a fused penalty term to encode relationship between adjacent time points in [18]. Furthermore, recent efforts have also been made to incorporate existing knowledge about network biology into data-driven network inference [19]. Wang et al. proposed to incorporate prior knowledge into the inference of conserved networks in a single condition by adjusting the Lasso penalties [20]. Yet, the inherently dynamic wiring of biological networks remains under-explored at the systems level, as interaction data are typically reported under diverse and isolated conditions [1].

There are at least five unresolved issues concerning differential network inference using data-knowledge integrated approaches: (1) the solution (search) space is usually large while sample sizes are small, resulting in potential overfitting; (2) both conserved and differential biological networks are complex and lack closed-form or efficient numerical solutions; (3) “structural” model parameters are assigned heuristically, leading to potentially suboptimal solutions; (4) prior knowledge is imperfect for inferring biological networks under specific conditions, e.g., false positive “connections”, biases, and non-specificity; and (5) most current methods do not provide significance assessment on the differential connections and rigorous testing of the type I error rate.

To address these challenges, we formulated the inference of differential dependency networks that incorporate both conditional data and prior knowledge as a convex optimization problem, and developed an efficient learning algorithm to jointly infer the conserved biological network and the significant rewiring across different conditions. Extending and improving our work on Gaussian graphical models [21],[22], we designed block-wise separable penalties in the Lasso-type models that permit joint learning and knowledge incorporation with an efficient closed-form solution. We estimated the expected error rate due to “random” prior knowledge via a novel sampling scheme. Based on that scheme, we developed a strategy to fully exploit the benefit of this data-knowledge integrated approach. We determined the values of model parameters that quantitatively correspond to the expected significance level, and evaluated the statistical significance of each of the detected differential connections. We validated our method using synthetic datasets and comprehensive comparisons. We then applied our method to yeast cell line and breast cancer microarray data and obtained biologically plausible results.

Methods

Formulation of knowledge-fused differential dependency network (kDDN)

We represent the condition‐specific biological networks as graphs. Suppose there are p nodes (genes) in the network of interest, and we denote the vertex set as V. Let G⁽¹⁾ = (V, E⁽¹⁾) and G⁽²⁾ = (V, E⁽²⁾) be the two undirected graphs under the two conditions. G⁽¹⁾ and G⁽²⁾ have the same vertex set V, and condition‐specific edge sets E⁽¹⁾ and E⁽²⁾. The edge changes indicated by the differences between E⁽¹⁾ and E⁽²⁾ are of particular interest, since such rewiring may reveal pivotal information on how the organisms respond to different conditions. We label the edges as common edges or specific to a particular condition in graph G = (V, E) to represent the learned networks under the two conditions.

Prior knowledge on biological networks is obtained from well-established databases such as KEGG [19] and is represented as a knowledge graph G _W  = (V, E _W ), where the vertex set V is the same set of nodes (genes) and the edge set E_W over V is translated from prior knowledge. There are many alternatives to extract existing domain knowledge, e.g., STRING, HPRD, or manual construction. The adjacency matrix of G_W, W ∈ ℜ ^p × p , is used to encode the prior knowledge. The elements of W are either 1 or 0, with X _ji  = 1 indicating the existence of an edge from the j^th gene to the i^th gene (or their gene products), where i, j = 1, 2, ⋯, p, i ≠ j. W is symmetric if the prior knowledge is not directed.

The main task in this paper is to infer from data and prior knowledge G_W the condition‐specific edge sets E (both E⁽¹⁾ and E⁽²⁾). The method is illustrated in Figure 1.

Figure 1.

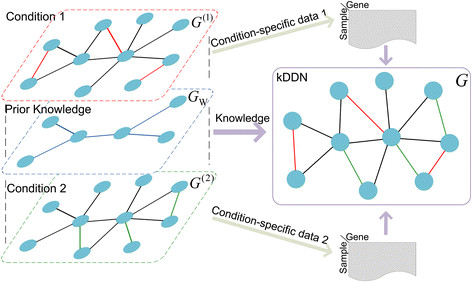
Knowledge-fused differential dependency network learning. The algorithm takes condition-specific data and prior knowledge as input and infers condition-specific networks. Black edges are common edges. Red and green edges are differential edges specific to conditions.

We consider the p nodes in V as p random variables, and denote them as X₁, X₂, ⋯, X _p . Suppose there are N₁ samples under condition 1 and N₂ samples under condition 2. Without loss of generality, we assume N₁ = N₂ = N. Under the first condition, for variable X _i , we have observations ${\mathbf{x}}_i^{\left(1\right)}={\left[x_{1i}^{\left(1\right)},x_{2i}^{\left(1\right)},\cdots ,x_{\mathit{Ni}}^{\left(1\right)}\right]}^{\mathrm{T}}$, while under the second condition, we have ${\mathbf{x}}_i^{\left(2\right)}={\left[x_{1i}^{\left(2\right)},x_{2i}^{\left(2\right)},\cdots ,x_{\mathit{Ni}}^{\left(2\right)}\right]}^{\mathrm{T}}$, i = 1,2,⋅⋅⋅,p. Further, let ${\mathbf{X}}^{\left(1\right)}=\left[{\mathbf{x}}_1^{\left(1\right)},{\mathbf{x}}_2^{\left(1\right)},\cdots ,{\mathbf{x}}_p^{\left(1\right)}\right]$ be the data matrix under condition 1 and ${\mathbf{X}}^{\left(2\right)}=\left[{\mathbf{x}}_1^{\left(2\right)},{\mathbf{x}}_2^{\left(2\right)},\cdots ,{\mathbf{x}}_p^{\left(2\right)}\right]$ be the data matrix under condition 2.

Denote

$${\mathbf{y}}_i=\left[\begin{array}{c}\hfill {\mathbf{x}}_i^{\left(1\right)}\hfill \\ \hfill {\mathbf{x}}_i^{\left(2\right)}\hfill \end{array}\right],\mathbf{X}=\left[\begin{array}{cc}\hfill {\mathbf{X}}^{\left(1\right)}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{X}}^{\left(2\right)}\hfill \end{array}\right],$$ (1)

and

$${\mathbf{\beta }}_i=\left[\begin{array}{c}\hfill {\mathbf{\beta }}_i^{\left(1\right)}\hfill \\ \hfill {\mathbf{\beta }}_i^{\left(2\right)}\hfill \end{array}\right]={\left[{\beta }_{1i}^{\left(1\right)},{\beta }_{2i}^{\left(1\right)},\cdots ,{\beta }_{\mathit{pi}}^{\left(1\right)},{\beta }_{1i}^{\left(2\right)},{\beta }_{2i}^{\left(2\right)},\cdots ,{\beta }_{\mathit{pi}}^{\left(2\right)}\right]}^{\mathrm{T}},$$ (2)

with the non‐zero elements of ${\mathbf{\beta }}_i^{\left(1\right)}$ indicating the neighbours of the i^th node under the first condition and the non‐zero elements of ${\mathbf{\beta }}_i^{\left(2\right)}$ indicating the neighbours of the i^th node under the second condition.

The problem of simultaneously learning network structures and their changes under two conditions is formulated as a regularized linear regression problem with sparse constraints and solved by convex optimization. For each node (variable) X _i , i = 1,2,⋅⋅⋅,p, we solve the optimization with the objective function

$$f\left({\mathbf{\beta }}_i\right)=\frac{1}{2}{‖{\mathbf{y}}_i-\mathsf{X}{\mathbf{\beta }}_i‖}_2^2+{\lambda }_1{\displaystyle {\sum }_{j=1}^P}\left(1-W_{\mathit{ji}}\theta \right)\left(\left|{\beta }_{\mathit{ji}}^{\left(1\right)}\right|+\left|{\beta }_{\mathit{ji}}^{\left(2\right)}\right|\right)+{\lambda }_2{‖{\mathbf{\beta }}_i^{\left(1\right)}-{\mathbf{\beta }}_i^{\left(2\right)}‖}_1$$ (3)

The non‐zero elements in W introduce knowledge to the objective function (3), and θ is a ℓ₁ penalty relaxation parameter taking value in [0, 1].

The solution is obtained by minimizing (3),

$$\begin{array}{l}{\mathbf{\beta }}_i=arg{min}_{{\mathbf{\beta }}_i}f\left({\mathbf{\beta }}_i\right)\\ =arg{min}_{{\mathbf{\beta }}_i^{\left(1\right)},{\mathbf{\beta }}_i^{\left(2\right)}}\frac{1}{2}{‖{\mathbf{y}}_i-\mathbf{X}{\mathbf{\beta }}_i‖}_2^2+{\lambda }_1{\displaystyle \sum _{j=1}^p\left(1-W_{\mathit{ji}}\theta \right)\left(\left|{\beta }_{\mathit{ji}}^{\left(1\right)}|+|{\beta }_{\mathit{ji}}^{\left(2\right)}\right|\right)}+{\lambda }_2{‖{\mathbf{\beta }}_i^{\left(1\right)}-{\mathbf{\beta }}_i^{\left(2\right)}‖}_1\\ \mathrm{s}.\mathrm{t}.{\beta }_{\mathit{ii}}^{\left(1\right)}=0,{\beta }_{\mathit{ii}}^{\left(2\right)}=0.\end{array}$$ (4)

Both the cost function $\frac{1}{2}{‖{\mathbf{y}}_i-\mathbf{X}{\mathbf{\beta }}_i‖}_2^2$ and two regularization terms ${\displaystyle \sum _{j=1}^p\left(1-W_{\mathit{ji}}\theta \right)\left(\left|{\beta }_{\mathit{ji}}^{\left(1\right)}|+|{\beta }_{\mathit{ji}}^{\left(2\right)}\right|\right)}$ and $‖{\mathbf{\beta }}_i^{\left(1\right)}-{\mathbf{\beta }}_i^{\left(2\right)}‖$ co-existed in the objective function are convex, and this convex formulation leads to an efficient algorithm. The structures of the graphical model under two conditions are obtained jointly by solving (4) sequentially for all nodes. The inconsistency between ${\mathbf{\beta }}_i^{\left(1\right)}$ and ${\mathbf{\beta }}_i^{\left(2\right)}$ highlights the structural changes between two conditions, and the collection of differential edges form the differential dependency network.

Given the vast search space and complexity in both conserved and differential networks, it is crucial for kDDN to identify statistically significant network changes and filter the structural and parametric inconsistencies due to noise in the data and limited samples. This objective is achieved by selecting the proper model specified by λ₁ and λ₂ that best fits the data and suffices the statistical significance. λ₁ is determined by controlling the probability of falsely joining two distinct connectivity components of the graph [23] and λ₂ is found by setting differential edges to a defined significance level. We refer readers to Additional file 1: S4.1 for a detailed discussion of model parameter-setting approaches.

With parameters specified, problem (4) can be solved efficiently by the block coordinate descent algorithm presented in Additional file 1: S4.3, Algorithm S1.

Incorporation of prior knowledge

The prior knowledge is explicitly incorporated into the formulation by W _ji and θ in the block-wise weighted ℓ₁ -regularization term. W _ji  = 1 indicates that the prior knowledge supports an edge from the j^th gene to the i^th gene and 0 otherwise. A proper θ will reduce the penalty applied to ${\beta }_{\mathit{ji}}^{\left(c\right)}$, c = 1, 2, corresponding to the connection between X _j and X _i with W _ji  = 1. As a result, the connection between X _j and X _i will more likely be detected.

θ is a weighting parameter on the influence of prior knowledge, determining the degree of the knowledge incorporation in the network inference. When θ = 0, the algorithm ignores all knowledge information and gives solely data-based results; conversely, when θ = 1, the edge between X _j and X _i will always be included if such an edge exists in the prior knowledge. Therefore, the prior knowledge incorporation needs to find a proper balance between the experimental data and prior knowledge to achieve effective incorporation, as well as limit the adverse effects caused by any spurious edges contained in imperfect prior knowledge.

Here we propose a strategy to control the adverse effects incurred in the worst‐case scenario under which the given prior knowledge is totally random. In this case, the entropy of the knowledge distribution over the edges is maximized and the information introduced to the inference is minimal. Incorporating such random knowledge, the inference results will deviate from the purely data-driven result. We want to maximize the incorporation of relevant prior knowledge, while at the same time making sure the potential negative influence of irrelevant prior knowledge is under control so that the expected deviation is confined within an acceptable range in the worst‐case scenario. To properly set the value of θ, we assess the actual influence of prior knowledge for each value that θ may take, and developed Theorem 1 to determine the best degree of prior knowledge incorporation. This approach guarantees robustness even when the prior knowledge is highly inconsistent with the underlying ground truth.

To quantify the effects of prior knowledge incorporation, we use graph edit distance [24] between two adjacency matrices as a measurement for the dissimilarity of two graphs. Let G_T = (V, E_T) denote the ground‐truth graph with edge set E _T , G_X = (V, E_X) denote the graph learned purely from data, i.e., W = 0, and $G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }=\left(V,E_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)$ denote the graph learned with prior knowledge. W_R indicates that the prior knowledge is “random”. Let d(G₁, G₂) denote the graph edit distance between two graphs. Further, let |E| be the number of edges in the graph G.

Our objective is to bound the increase of inference error rate associated with the purely data-driven result, $d\left(G_{\mathrm{T}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)/\left|E_{\mathrm{T}}\right|-d\left(G_{\mathrm{T}},G_{\mathrm{X}}\right)/\left|E_{\mathrm{T}}\right|$, within an acceptable range δ even if the prior knowledge is the worst case by finding a proper θ.

Since G_T is unknown, we instead control the increase in the error rate indirectly by evaluating the effect of random knowledge against G_X, the purely data‐driven inference result. Specifically, we use a sampling‐based algorithm to find the empirical distribution of $d\left(G_{\mathrm{X}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)$, and choose the largest θ ∈ [0, 1] that satisfies:

$$\begin{array}{l}\widehat{\theta }=\mathit{max\theta }\\ \mathrm{s}.\mathrm{t}.E\left[d\left(G_{\mathrm{X}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)\right]/\left|E_{\mathrm{X}}\right|\le \delta ,\end{array}$$ (5)

where E[d(G₁, G₂)] is the expectation of the graph edit distance between graphs G₁ and G₂, with respect to its empirical distribution.

A natural question is whether using G_X instead of G_T to control the increase in the error rate induced by random knowledge is legitimate. To answer this question, we show in Theorem 1 (proof included in Additional file 1: S2) that the θ obtained in (5) in fact controls an upper bound of $E\left[d\left(G_{\mathrm{T}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)\right]/\left|E_{\mathrm{T}}\right|$, i.e. the increase in the network inference error rate induced by random prior knowledge (the worst‐case scenario), under the assumption that the number of false negatives (FN) in the data-driven result G_X is smaller than the number of false positives (FP). As we adopt a strategy to control the probability of falsely joining two distinct connectivity components [23], this assumption generally holds.

Theorem 1 establishes the relationship between prior knowledge incorporation θ and the adverse effects of prior knowledge on network inference, quantified by δ, under the worst-case scenario (when the prior knowledge is completely irrelevant). For example, δ = 0.1 indicates that the user can accept at most 10% performance degradation if the prior knowledge is completely noise. With the estimate of θ at δ = 0.1, even the prior knowledge is totally random, the performance will decrease no more than 10%, while the relevant portion of the real prior knowledge (better than random noise) can greatly improve the overall network inference performance.

Theorem 1

For a given δ ∈ [0, 1), if the prior knowledge incorporation parameter θ satisfies the inequality

$$\frac{E\left[d\left(G_{\mathrm{X}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)\right]}{\left|E_{\mathrm{X}}\right|}\le \delta ,$$ (6)

then the increase in the error rate induced by incorporating random prior knowledge is bounded by δ, more specifically,

$$\frac{E\left[d\left(G_{\mathrm{T}},G_{\mathrm{X},{\mathbf{W}}_{\mathrm{R}},\theta }\right)\right]}{\left|E_{\mathrm{T}}\right|}\le \frac{d\left(G_{\mathrm{T}},G_{\mathrm{X}}\right)}{\left|E_{\mathrm{T}}\right|}+\delta$$ (7)

Given the number of edges specified in the prior knowledge, procedures to compute θ are detailed in Algorithm S2 in Additional file 1: S4.3.

Results and discussion

We demonstrated the utility of kDDN using both simulation data and real biological data. In the simulation study, we tested our method on networks with different sizes and compared with peer methods the performance of overall network structure recovery, differential network identification and tolerance of false positives in the prior knowledge.

In a real data application, we used kDDN to learn the network rewiring of the cell cycle pathway of budding yeast in response to oxidative stress. A second real data application was the study of the differential apoptotic signaling between recurring and non-recurring breast cancer tumors. Applications to study muscular dystrophy and transcription factor binding schemes are included in Additional file 1: S6.

Simulation study

We constructed a Gaussian Markov random field with p = 100 nodes and 150 samples following the approach used in [23], and then randomly modified 10% of the edges to create two condition‐specific networks with sparse changes. The details of simulation data generation procedure are provided in Additional file 1: S5.1. The number of edges in prior knowledge M was set to be the number of common edges in the two condition‐specific networks, and δ was set to 0.1.

To assess the effectiveness of prior knowledge incorporation and robustness of kDDN when false positive edges were present in prior knowledge, we examined the network inference precision and recall of the overall network and the differential network at different levels of false positive rate in the prior knowledge.

Both false positives and false negatives in the prior knowledge here are with respect to the condition-specific ground truth from which the data are generated. Thus, although false positives in prior knowledge may contribute more learning errors, false negatives will not worsen network learning performance (results shown in Additional file 1: S5.5).

Starting from prior knowledge without any false positive edges, we gradually increased the false positive rate in prior knowledge until all prior knowledge was false. At each given false positive rate in the prior knowledge, we randomly created 1,000 sets of prior knowledge, and compared the performance of kDDN in terms of precision and recall with two baselines: (1) a purely data-driven result, corresponding to kDDN with θ=$0$, i.e., without using any prior knowledge in the network inference (using only data for network inference); and (2) a naïve baseline of knowledge incorporation by superimposing (union) the prior knowledge network and the network inferred purely from the data.

The results of the overall network (both common and differential edges) learning are shown in Figure 2(a) and (b). The dot-connected lines are averaged precision or recall of the network learned with 1,000 sets of prior knowledge. The box plot shows the first, second and third quartiles of precision or recall at each false positive rate in prior knowledge (with the ends of the whiskers extending to the lowest datum within a 1.5 interquartile range of the lower quartile, and the highest datum within a 1.5 interquartile range of the upper quartile). The blue squared lines, brown circle lines, and red diamond lines indicate the mean performance of kDDN, purely data-driven baseline, and naïve baseline, respectively. Narrower lines with the same colors and line styles mark the one standard deviation of the performance of the corresponding approach.

Figure 2.

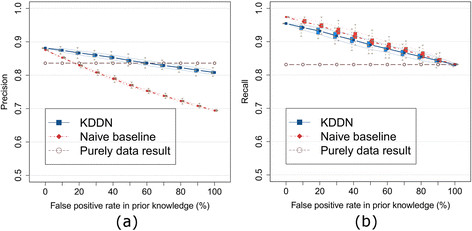
Effects of false positive rates in prior knowledge on inference of the overall network. (a) Precision of overall network inference. (b) Recall of overall network inference. The experiments show that true knowledge improves both precision and recall of overall network inference, and the maximum degradation of inference results is bounded when the prior knowledge is imperfect.

Precision reflects the robustness to the false positive edges and efficiency of utilizing the information in prior knowledge. Figure 2(a) shows that, as expected, the false positive rate in prior knowledge has a limited effect on the precision of kDDN (blue squared lines). With more false positives in the prior knowledge, the precision decreases but is still around the purely data-driven baseline (brown circle lines) and much better than the naïve baseline (red diamond lines). The naïve baseline suffers significantly from the false positives in prior knowledge, because it indiscriminately accepts all edges in prior knowledge without considering evidence in the data. This observation corroborates the design of our method: to control the false detection incurred by the false positives in the prior knowledge. At the point where the false positive rate in the prior knowledge is 100%, the decrease of precision compared with the purely data-based result is bounded within δ.

Recall reflects the ability of prior knowledge in helping recover missing edges. Figure 2(b) shows that when the prior knowledge is 100% false, the recall is the same as that of the purely data-driven result, because in this case the prior knowledge brings in no useful information for correct edge detection. When the true positive edges are included in the prior knowledge, the recall becomes higher than that of the purely data-based result, because more edges are correctly detected by harnessing the correct information in the prior knowledge. The naïve baseline is slightly higher in recall, since it calls an edge as long as knowledge contains it, while kDDN calls an edge only when both knowledge and data evidence are present. The closeness between kDDN and naïve baseline demonstrates the high efficiency of our method in utilizing the true information in prior knowledge.

We then evaluated the effect of knowledge incorporation solely on the identification of differential networks following the same protocol. The results are shown in Figure 3 with the same color and line annotations.

Figure 3.

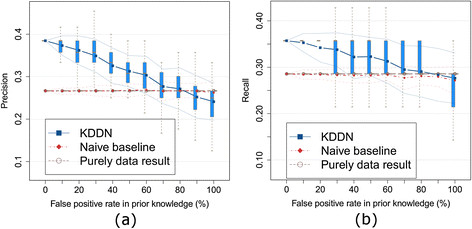
Effects of false positive rates in prior knowledge on inference of the differential network. (a) Precision of differential network inference. (b) Recall of differential network inference. The experiments show that true knowledge improves both precision and recall of differential network inference. The maximum degradation of inference results is bounded when the prior knowledge is imperfect.

For differential network recovery, the naïve baseline is almost identical to purely data-driven results because the prior knowledge seldom includes a differential edge in a large network with sparse changes. While similar advantages of kDDN apply, our method has better precision and recall, and bounds the performance degradation when knowledge is totally wrong. Unlike the naïve baseline where knowledge and data are not linked, we model the inference with knowledge and data together, so knowledge is also able to help identify differential edges. Performance evaluation results in Additional file 1: S5.3 studied networks with varying sizes, reaching consistent conclusions.

Depending on specific conditions, false positives in prior knowledge may not distribute uniformly, but tend to aggregate more towards certain nodes. Experiments with biased knowledge distribution shown in Additional file 1: S5.4, Figures S10-S13 indicate no difference or little improvement compared to random knowledge, confirming that random knowledge represents the worst-case scenario and the bound according to random knowledge is sufficient.

Performance comparisons with peer methods

We compared our joint learning method kDDN with four peer methods: 1) DDN (independent learning) [13], 2) csLearner (joint learning) [15], 3) Meinshausen’s method (independent learning) [23], and 4) Tesla (joint learning) [18]. csLearner can learn more than two networks but we restricted the condition to two. Meinshausen’s method learns the network under a single condition, and we combined the results learned under each condition to get conserved network and differential network. Tesla learns a time-evolving network, but can be adapted to two-condition learning as well. Only kDDN can assign edge-specific p-values to differential edges.

Parameters in kDDN are automatically inferred from data as described in Additional file 1: S4.1. For the competing methods in the comparison, we manually tested and tuned their parameters to obtain their best performance. We set DDN to detect pair-wise dependencies. The number of neighbors in csLearner is set to “4” (the ground truth value). Meinshausen’s method uses the same λ₁ as inferred by kDDN, as it is a special case of kDDN under one condition without prior knowledge. Tesla uses the empirically-determined optimal parameter values, since the parameter selection was not automatic but relies on user input.

To assess the impact of prior knowledge, we ran kDDN under three scenarios: data-only (kDDN.dt), data plus true prior knowledge (kDDN.tk), and data plus “random” prior knowledge (kDDN.fk). Only kDDN is able to utilize prior knowledge.

The ground truth networks consisted of 80, 100, 120, 140 and 160 nodes, respectively, and correspondingly 120, 150, 200, 200 and 240 samples. For each network size, 100 replicate simulation networks were generated. We evaluated the performance of inferring both overall and differential edges of the underlying networks using the F-score (harmonic mean of precision and recall, $2\frac{\mathrm{precision}*\mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}$) and precision-recall averaged over all datasets under each network size.

The results are presented in Figure 4 using bar plots. The color annotations are: orange-csLearner, golden-DDN, olive green-kDDN.dt, aquamarine-kDDN.fk, blue-kDDN.tk, purple-Meinshausen, magenta-Tesla. We used one-sided t-tests to assess whether kDDN performs better than the peer methods across all network sizes. The null hypothesis is that there is no difference between the mean of F-score of kDDN and the peer methods. The alternative hypothesis is that kDDN has the greater mean of F-score. The detailed results are included in Tables S1 and S2 in Additional file 1: S5.7, which shows that kDDN.tk performs significantly better than peers in all cases, and kDDN.dt and kDDN.fk performs better than peers in 118 of 120 cases.

Figure 4.

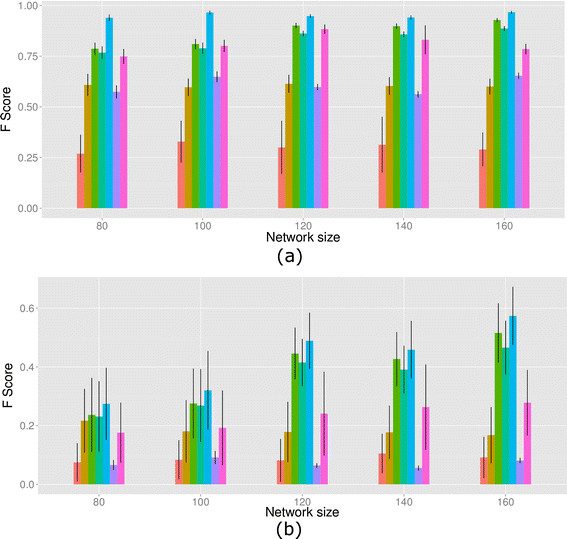
Performance comparison in F score. (a) Inference of overall network. (b) Inference of differential network. Legend (from left to right): orange-csLearner, golden-DDN, olive green-kDDN.dt, aquamarine-kDDN.fk, blue-kDDN.tk, purple-Meinshausen, magenta-Tesla. The experimental results show that kDDN outperforms the peer methods in both overall network learning and differential network inference.

Figure 4(a) compares the ability of recovering overall networks. We see kDDN.tk consistently outperforms all peer methods, and kDDN.dt and kDDN.fk performs comparably to Tesla (best-performing peer method). The independent learning methods, DDN and Meinshausen’s method, place third due to their inability to jointly use data.

Figure 4(b) shows the comparison of performance on recovering differential edges. kDDN consistently outperforms all peer methods under all scenarios. While kDDN and Tesla share some commonalities, they use different formulations. Where Tesla uses logistic regression, kDDN adopted linear regression to model the dependency. Such a difference also has implications for the subsequent solutions and outcomes. The fact that kDDN determines λ₂ according to the statistical significance of differential edges helps kDDN outperform Tesla in differential edge detection. It is also clear that a single-condition method cannot find the differential edges correctly and has the worst performance.

In Figures S17 and S18 in Additional file 1: S5.7, the performance of these methods is compared in terms of precision and recall; we reached the same conclusions.

Through these comparisons, we show that kDDN performs better than peer methods in both overall and differential network learning. High-quality knowledge further improves kDDN performance, while kDDN is robust enough even to totally random prior knowledge. Joint learning, utilization of prior knowledge, and attention to statistical significance all helped kDDN outperform the other methods.

Pathway rewiring in yeast uncovers cell cycle response to oxidative stress

To test the utility of kDDN using real biological data, we applied the kDDN to the public data set GSE7645. This data set used budding yeast Saccharomyces cerevisiae to study the genome-wide response to oxidative stress imposed by cumene hydroperoxide (CHP). Yeast cultures were grown in controlled batch conditions, in 1L fermentors. Three replicate cultures in mid-exponential phase were exposed to 0.19mM CHP, while three non-treated cultures were used as controls. Samples were collected at t = 0 (immediately before adding CHP) and at 3,6,12,20,40,70 and 120 min after adding the oxidant. Samples were processed for RNA extraction and profiled using Affymetrix Yeast Genome S98 arrays. There were 48 samples in total, evenly divided between the treated and the non-treated groups.

We analyzed the network changes of cell cycle-related genes with structural information from the KEGG yeast pathway as prior knowledge. We added the well-studied yeast oxidative stress response gene Yap1[25]-[28] to the knowledge network and related connections gathered from the Saccharomyces Genome Database [29]. The learned differential network result is shown in Figure 5, in which nodes represent genes involved in the pathway rewiring, and edges show the condition-specific connections. Red edges are connections in control and green edges are connections under stress.

Figure 5.

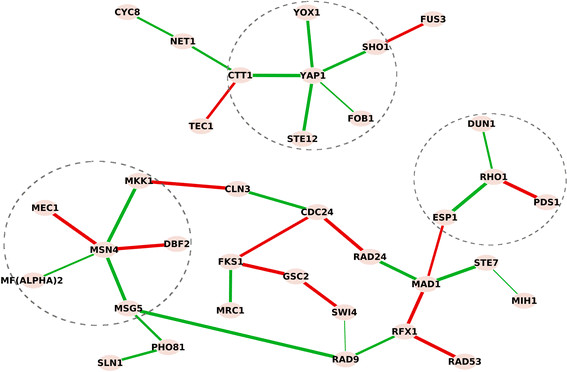
Differential dependency network in budding yeast reflects the cell cycle response to oxidative stress. Red edges are connections in control and green edges are connections under stress, mutually and exclusively. Yap1, Rho1 and Msn4, the three known responders to stress response, are at the center of the inferred networks in response to oxidative stress. They are activated under oxidative stress and many connections surrounding them are activated (green edges). Acting as an antioxidant in response to oxidative stress, Ctt1 coordinate with Yap1 to protect cells from oxidative stress.

Oxidative stress is a harmful condition in cells, due to the failure of the antioxidant defense system to effectively remove reactive oxygen molecules and other oxidants. The result shows that Yap1, Rho1 and Msn4 are at the center of the network response to oxidative stress; they are activated under oxidative stress and many connections surrounding them are created (green edges). Yap1 is a major transcription factor that responds to oxidative stress [25]-[28]. Msn4 is considered as a general responder to environmental stresses including heat shock, hydrogen peroxide, hyper-osmotic shock, and amino acid starvation [30],[31]. Rho1 is known to resist oxidative damage and facilitate cell survival [32]-[34]. The involvement of these central genes captured the dynamic response of how yeast cells sense and react to oxidative stress. The edge between Yap1 and Ctt1 under stress grants more confidence to the result. Ctt1 acts as an antioxidant in response to oxidative stress [35], and the coordination between Yap1 and Ctt1 in protecting cells from oxidative stress is well established [36]. This result depicted the dynamic response of yeast when exposed to oxidative stress and many predictions are supported by previous studies. This real data study validated the effectiveness of the methods in revealing underlying mechanisms and providing potentially novel insights. These insights would be largely missed by conventional differential expression analysis as the important genes Rho1, Msn4, Yap1 and Ctt1 ranks 13, 20, 64 and 84 among all 86 involved genes based on t-test p-values. In a comparison with data-only results in Additional file 1: S6.1, 14 different differential edges are found. We also applied a bootstrap method in [37] to assess the robustness of the findings as detailed in Additional file 1: S6.2.

Apoptosis pathway in patients with early recurrent and non-recurrent breast cancer

Network rewiring analysis is also applicable to mechanistic studies and helps identify underlying key players that cause phenotypic differences. For example, 50% of estrogen receptor-positive breast cancers recur following treatment, but the mechanisms involved in cancer recurrence remain unknown. Understanding of the mechanisms of breast cancer recurrence can provide critical information for early detection and prevention. We used gene expression data from a clinical study [38] to learn differences in the apoptosis pathway in primary tumors between patients with recurrent and non-recurrent disease. We compared the pathway changes in tumors obtained from patients whose breast cancer recurred within 5 years after treatment and from patients who remained recurrence-free for at least 8 years after treatment. There were 47 and 48 tumor samples in the recurring and non-recurring groups, respectively. Gene expression data were generated using Affymetrix U133A arrays. We used the apoptosis pathway from KEGG as prior knowledge.

Following the same presentation as in the yeast study, red edges are connections established in patients with recurrent disease, and green edges are connections unique to patients without recurrent disease. Differences in the signaling among genes in the apoptosis pathway between patients whose cancer recurred or who remained cancer-free are shown in Figure 6.

Figure 6.

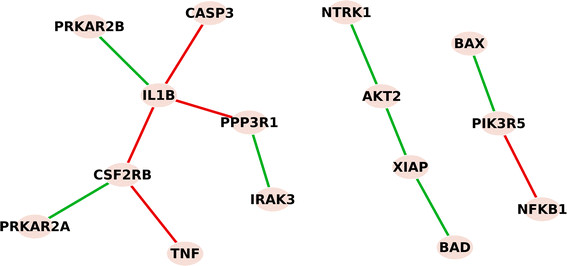
Rewiring of apoptosis pathway in breast cancer patients with and without recurrence. Red edges are unique connections in patients with recurrent breast cancer, where inflammatory/immune response genes IL1B, NFκB and TNFα that are all linked to increased resistance to breast cancer treatment were found. Green edges are unique connections in patients with breast cancer that did not recur, where paths to both anti-apoptotic XIAP/AKT2 and proapoptotic BAX and BAD were formed.

Three inflammatory/immune response genes (IL1B, NFκB and TNFα) that are all linked to increased resistance to breast cancer treatment were identified in the recurrent tumors. These genes formed a path to inhibit proapoptotic CASP3 and PPP3R1[39], and to activate the pro-survival genes PIK3R5 or CSF2RB that maintain cell survival. In contrast, green edges that were present in non-recurrent tumors form paths to both anti-apoptotic XIAP/AKT2 and proapoptotic BAX and BAD gene functions.

When we overlaid the differential network over the KEGG [19] apoptosis pathway we noticed additional differences in the signaling patterns. Using the same color-coded presentation, we show the learned differential network in Figure 7. In the recurrent breast cancers (red edges), the molecular activities mainly affect the initial apoptotic signals outside the cell and within the cell membrane (ligands and their receptors), while inside the cell there is no clear signaling cascade affected to determine cell fate. The only route affected within the cell is IL1B-induced inhibition of proapoptotic CASP3. In non-recurrent breast cancer, the affected network involves both signals received from activation of the membrane receptors and a cascade of signaling pathways inside the cell to promote both apoptosis and survival. Since a balance between apoptosis and survival is necessary for damaged cells to be eliminated and repaired cells to survive [40], it is logical that both pathways would be activated concurrently. Interestingly, the imbalance of apoptotic and survival signals and the inhibition of CASP3 in recurrent cancer both lead to the resistance of cell death, reported as a major hallmark of cancer [41].

Figure 7.

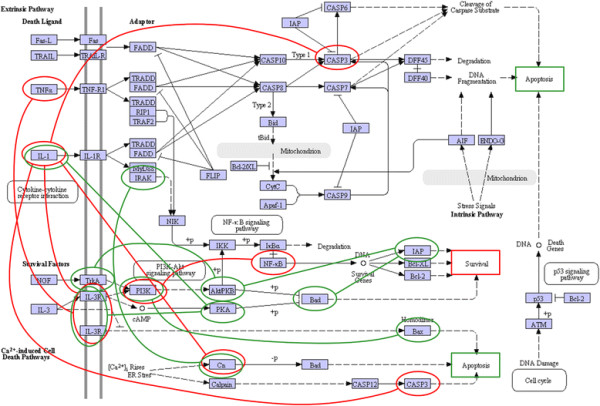
Differential dependency network presented over the KEGG[[19]] apoptosis pathway. Recurrent breast cancers (featured by red edges) showed the imbalance between apoptosis and survival with only one route into the cell through IL1B-induced inhibition of proapoptotic CASP3. Non-recurrent breast cancer had a cascade of signaling pathways inside the cell that provides the balance between apoptosis and survival.

In conclusion, the apoptosis pathway rewiring analysis identified key mechanistic signaling differences in tumors from patients whose breast cancer did or did not recur. These differences provide a promising ground for novel hypotheses to determine factors affecting breast cancer recurrence.

Conclusions

To address the challenges concerning differential network inference using data-knowledge integrated approaches, we formulated the problem of learning the condition‐specific network structure and topological changes as a convex optimization problem. Model regularization and prior knowledge were utilized to navigate through the vast solution space. An efficient algorithm was developed to make the solution scalable by exploring the special structure of the problem. Prior knowledge was carefully and efficiently incorporated in seeking the balance between the prior knowledge support and data-derived evidence. The proposed method can efficiently utilize prior knowledge in the network inference while remaining robust to false positive edges in the knowledge. The statistical significance of rewiring and desired type I error rate were assessed and validated. We evaluated the proposed method using synthetic data sets in various cases to demonstrate the effectiveness of this method in learning both common and differential networks, and the simulation results further corroborated our theoretical analysis. We then applied this approach to yeast oxidative stress data to study the cellular dynamic response to this environmental stress by rewiring network structures. Results were highly consistent with previous findings, providing meaningful biological insights into the problem. Finally, we applied the methods to breast cancer recurrence data and obtained biologically plausible results. In the future, we plan to incorporate more types of biological prior information, e.g., protein‐DNA binding information in ChIP‐chip data and protein‐protein interaction data, to improve the use of condition-specific prior knowledge.

Abbreviations

kDDN: Knowledge-fused differential dependency network

TP: True positives

FP: False positives

kDDN.dt: kDDN with no knowledge

kDDN.tk: kDDN with true knowledge

kDDN.fk: kDDN with random knowledge

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

YT and BZ designed the method and drafted the manuscript along with ZZ and YW. YT and BZ carried out the experimental validation of the methods. EPH, RC, IMS, JX and DMH helped with the methodology development and provided important biological interpretation of the results. RC and DMH helped with the yeast study. RC, ZZ and IMS helped with the breast cancer study. EPH helped with the muscular dystrophy study. All authors read and approved the final manuscript.

Supplementary Material

Additional file 1:

Supplementary methods and experimental results. Details of theoretical proofs and algorithms, more synthetic and real data comparisons, and validations are included in this file.

Acknowledgements

This work is supported in part by the National Institutes of Health under Grants CA160036, CA164384, NS29525, CA149147 and HL111362. This work is also supported in part by grant U24CA160036, from the National Cancer Institute Clinical Proteomic Tumor Analysis Consortium (CPTAC).