Solid-State NMR Structure Determination from Diagonal-Compensated, Sparsely Nonuniform-Sampled 4D Proton–Proton Restraints

Abstract

We report acquisition of diagonal-compensated protein structural restraints from four-dimensional solid-state NMR spectra on extensively deuterated and ¹H back-exchanged proteins. To achieve this, we use homonuclear ¹H–¹H correlations with diagonal suppression and nonuniform sampling (NUS). Suppression of the diagonal allows the accurate identification of cross-peaks which are otherwise obscured by the strong autocorrelation or whose intensity is biased due to partial overlap with the diagonal. The approach results in unambiguous spectral interpretation and relatively few but reliable restraints for structure calculation. In addition, the diagonal suppression produces a spectrum with low dynamic range for which ultrasparse NUS data sets can be readily reconstructed, allowing straightforward application of NUS with only 2% sampling density with the advantage of more heavily sampling time-domain regions of high signal intensity. The method is demonstrated here for two proteins, α-spectrin SH3 microcrystals and hydrophobin functional amyloids. For the case of SH3, suppression of the diagonal results in facilitated identification of unambiguous restraints and improvement of the quality of the calculated structural ensemble compared to nondiagonal-suppressed 4D spectra. For the only partly assigned hydrophobin rodlets, the structure is yet unknown. Applied to this protein of biological significance with large inhomogeneous broadening, the method allows identification of unambiguous crosspeaks that are otherwise obscured by the diagonal.

Introduction

In recent years, solid-state NMR has evolved as a general tool to probe the structure and dynamics of biological macromolecules¹⁻⁵ and a wide range of other materials.⁶⁻¹¹ The technique has found particular applicability in the investigation of solid systems that have a partial intrinsic disorder, such as fibrillar proteins¹²⁻¹⁵ or membrane proteins,^3,16−21 which are embedded in a dynamic environment or display mobility themselves. Structural assessment by NMR is to a great extent based on the availability of individual distances between protein spin pairs. Existing methods have demonstrated highly accurate structures mostly based on a high number of crosspeaks per residue in few spectral dimensions.²²⁻²⁵ The usefulness of spatial correlations, however, depends on reliable assignments and sufficient spectral resolution.

When applied to proteins with many resonances or for samples with structural heterogeneity and/or dynamic behavior, substantial peak overlap is encountered. To reduce the probability of shift degeneracy, recent efforts in solid-state NMR have been directed toward extending the commonly encountered ¹³C and ¹⁵N spectral dimensions to additional nuclei, particularly ¹H. The accessibility of proton chemical shifts by fast magic angle spinning (fast MAS) and tailored deuteration approaches²⁶⁻³⁰ has greatly facilitated powerful ¹H/¹⁵N/¹³C triple-resonance approaches recently.³¹⁻³⁴ Techniques currently developed for spinning frequencies of up to 100 kHz and higher allow narrow proton line widths even in the absence of deuteration.³⁵⁻³⁷ Proton detection has so far been successful in providing improved resolution and reliability in a new generation of solid-state NMR experiments mainly for resonance assignment and characterization of dynamics.

The most important approach for measuring distance restraints and other distance-related information to enable structure calculation relies on magnetization transfers between spins in spatial proximity. Commonly applied methods using fully protonated samples measure ¹³C–¹³C or ¹³C–¹⁵N contacts,³⁸⁻⁴² often enabled by exploitation of the proton-dipolar-coupling network, and yield large quantities of close and predominantly intraresidual contacts.^22,25 Extensive deuteration approaches yield a reduced set of restraints,^43,44 but these exclusively connect amide and/or methyl protons over relatively long distances and with high resolution. Also, they are little affected by spin diffusion and dipolar truncation. Accordingly, these correlations have the potential to provide accurate and nonredundant restraints for unambiguously identifiable pairs of residues.

Recently, excellent methyl–methyl correlations have been recorded with solid-state NMR approaching spectral qualities of solution NMR on samples with stoichiometrically protonated methyl groups (CD₂H).⁴³ This is facilitated by the fast methyl rotations and is achievable even at intermediate MAS frequencies.⁴⁵ For the more comprehensive set of distances between amides, ¹H^N-back-substituted preparations have been used at intermediate MAS frequencies of 10–40 kHz.^31,44,46 A partial back-exchange has the advantage of reducing spin diffusion, indirect transfer processes, and dipolar truncation effects^26,32,46,47 but comes at the price of larger sample volumes required. For very fast MAS above 60 kHz, fully ¹H-back-exchanged proteins and lower sample volumes are used to achieve the highest possible signal-to-noise.^29,34 In both cases, however, single-quantum single-quantum (SQ-SQ) correlations can lead to compromised spectra due to large autocorrelation peaks. The difficulty is analogous to the case encountered in solution-state NOESY data.

Several different approaches have been dedicated to overcome problems associated with an intense diagonal signal.⁴⁸⁻⁵⁵ In solution NMR, interleaved experiments for subtraction^49,50 as well as spin-state-selective variants based on the ST2 polarization-transfer scheme have been used.⁵¹⁻⁵³ Both methods sacrifice on the order of 50% of the sensitivity. Elegant pulse schemes have been developed for solid-state NMR that result in scaling of signal intensity dependent upon the distance from the diagonal.^54,55 In principle, DQ-filtered recoupling, using schemes like DREAM⁴¹ or Post-C7,⁵⁶ can obviate the need for diagonal suppression. (See a review by Demers et al.⁵⁷ for a comparison of different recoupling schemes at fast MAS.)

Diagonal peaks bear little structural information and can potentially be up to orders of magnitude stronger than the correlations of interest. The presence of this intense autocorrelation is currently a significant hindrance to obtaining quality ¹H–¹H structural restraints near the diagonal. An easily implementable cancellation of the diagonal is presented here, which is expected to be especially desirable also for overcoming the following problems: First, particular diagonal-related difficulties are expected for future structure calculation from sparse aliphatic protonation, which now enables straightforward access to full sets of sharp side-chain proton resonances.²⁸ The extensive dilution of the aliphatic protons necessary for this effect will go in hand with extremely large diagonal-to-cross-peak ratios. Second, evolution times in higher dimensional spectra are typically truncated even with nonuniform sampling. This results in severe artifacts from strong peaks, which are also difficult to recognize in higher dimensional space. In contrast to their overall feasibility for spectral resolution, higher dimensional spectra are thus particularly affected by interfering diagonal signals and their artifacts. Third, α-helical proteins and inhomogeneous samples represent additional challenges in the presence of intense diagonal signal due to little spectral amide peak resolution.

A powerful current method for encoding high-quality and large-quantity nonredundant proton–proton contacts in proteins is homonuclear, doubly heteronuclear-edited ¹H–¹H 4D spectra.^53,58,59 Severe signal truncation in the presence of three indirect dimensions can be circumvented by nonuniform sampling (NUS) of only a subset of the indirect points by covering a sufficiently large Nyquist grid, which is needed to obtain narrow line widths.^60,61 Given that in the solid state, spectral acquisition is usually dominated by sensitivity rather than resolution, NUS with high sparsity has rarely been implemented. However, increased sensitivity is obtained through predominant sampling of higher signal-to-noise data found at short indirect evolution times as well.⁶² This is pronounced for 4D approaches, where the enhancement is obtained in three indirect dimensions.⁶¹ Poisson distribution of sampling gaps⁶³ and reconstruction by the iterative soft thresholding (hmsIST) algorithm⁶⁴ turns out to be a powerful means for achieving both improvements in resolution and signal-to-noise in solid-state NMR spectroscopy.

Accurate and unambiguous structural restraints are demonstrated here from 4D NUS spectra with ultrasparse Poisson-gap sampling and diagonal compensation. We show that the near absence of diagonal peaks enables artifact-free spectra despite nonuniform sampling at an ultrasparse sampling rate of as low as 2%. The diagonal is suppressed by subtraction of compensating scans recorded without mixing in only a fraction of the time used for the regular spectrum, resulting in identification of cross-peaks that would otherwise be obscured by the diagonal.

Experimental Section

Sample Preparation

The two proteins used for this study are the SH3 domain of α-spectrin and EAS_Δ15 hydrophobin rodlets. Samples were prepared as described previously using 25% and 100% ¹H back-substitution of amide protons, respectively, in otherwise deuterated, ¹³C and ¹⁵N-labeled protein.^32,65 Hence, methyl groups only bear protons to the extent defined by incompleteness of commercially available deuterated D₂O and glucose (97% ²D) here, corresponding to an abundance of ∼9%. In the case of the SH3 domain, paramagnetic doping was applied as described previously using 100 mM [Cu^II(edta)]^2–.⁶⁶ In the case of the hydrophobin, rodlets were formed in the absence of doping agent and subsequently incubated overnight in a 75 mM [Cu^II(edta)]^2– solution. For the SH3 domain, approximately 3.5 mg was centered in a 2.5 mm rotor using self-made spacers of Teflon tape in the top and bottom of the rotor. For the hydrophobin rodlets, roughly 1 mg protein was spun into a 1.3 mm rotor and sealed with fluorinated rubber plugs to prevent loss of water.

Spectral Acquisition

SH3 spectra were recorded at 700 MHz Larmor frequency using a Bruker Avance narrow-bore spectrometer with a triple-resonance probehead. Magic Angle Spinning was set to 25-kHz rotation at approximately 10 °C. Interscan delays were chosen to be 0.5 s.

Spectral widths in indirect dimensions were set to 12 and 26 ppm for ¹H and ¹⁵N/¹³C with indirect evolution times of 5 ms in each case. Mixing was achieved using 8 ms RFDR⁶⁷ with 180° pulses of 4.7 μs (ν_RF = 106 kHz). In a time-shared⁶⁸ 4D experiment, methyl resonances in indirect heteronuclear dimensions can be separated from the amide signals by their corresponding proton chemical shift if the indirect ¹H spectral width is large enough to avoid folding (here 12 ppm). Hydrophobin spectra were recorded as nontime-shared versions in a 1.3 mm rotor at 1 GHz Larmor frequency and 60 kHz MAS at approximately 20 °C. Indirect spectral widths were set to 4.6 and 28.6 ppm for ¹H and ¹⁵N, respectively. Carriers were set to the center of the amide bulk in both cases. Mixing was achieved using 6.7 ms RFDR with 180° pulses of 2.5 μs (ν_RF = 200 kHz). Four identical data sets with RFDR mixing were recorded, and one data set was recorded in the absence of mixing. Each data set was shifted independently to compensate for drift of the B₀ field before further processing.

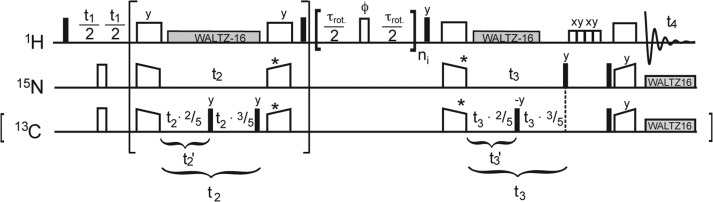
Figure 1 depicts a 4D experimental scheme using dipolar transfers between protons and heteronuclei and time-shared⁶⁸ indirect heteronuclear evolution periods. The pulse program used (for Bruker software) can be found on the Linser group webpage (mpibpc.mpg.de/linser) or can be obtained from the authors. Incrementation of ¹³C is scaled down by a factor of 2.5 by temporary storage of ¹³C magnetization along the axis of B₀ after 40% of the incremented time. This leads to correct scaling (in ppm) when treating the indirect dimensions as ¹⁵N and also serves to keep the evolution time short with respect to evolution of ¹³C–¹³C scalar couplings. Nonuniform sampling for 4D experiments was implemented via a variable counter (vc) list with a predefined 2% schedule. To avoid aliasing artifacts, sampling gaps should be kept small but as random as possible, which is achieved by Poisson distribution centered at zero value.⁶³ We recorded eight successive scans according to States-TPPI phase-sensitive incrementation of the three indirect dimensions for each set of indirect evolution increments.

Figure 1.

Practical implementation of diagonal-free 4D proton–proton correlations. Pulse scheme for NUS time-shared HXXH 4D correlations. Large brackets indicate the HXH pathway extractable for 3D HXH correlations. Mixing via RFDR is elicited by n_i = {t_mix/τ_rot, t_mix/τ_rot, 0} and n_i = {t_mix/τ_rot, t_mix/τ_rot, t_mix/τ_rot, t_mix/τ_rot, 0} for successive scans in the case of 25% and 100% ¹H back-exchange, respectively. Time-shared evolution (by including the small brackets) is provided by simultaneous H/X cross-polarization transfer steps for amides and methyl groups and storage of ¹³C magnetization to achieve scaling of indirect evolution increments.^44,68 Phases of the first proton πι/2 pulse and the CP pulses marked by asterisks were cycled for phase-sensitive incrementation.

The 2D reference spectrum plotted under the 4D planes in Figure 2A,B and Supporting Information, Figures 1 and 6 was recorded using the same (truncated) scheme without F1 incrementation and without mixing.

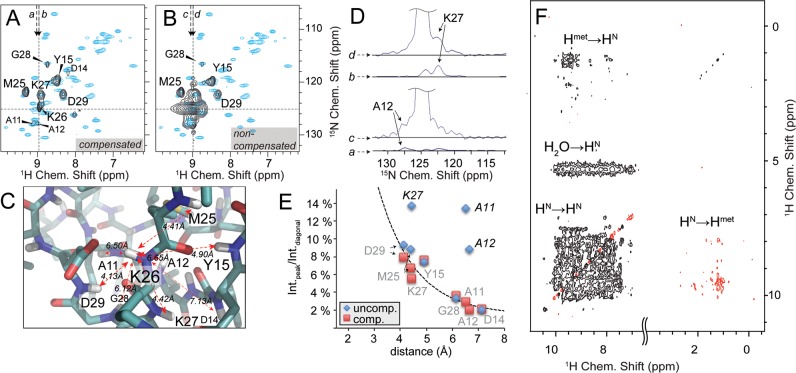
Figure 2.

4D spectroscopy and diagonal compensation. (A) A representative F3(¹⁵N)/F4(¹H) 2D slice as an excerpt of a NUS diagonal-free 4D experiment (black contours), with indirect F1(¹H)/F2(¹⁵N) chemical shifts set as indicated by dashed lines, showing spatial contacts of K26 H^N. *L61 is a bleed-through and has maximum intensity at different F1/F2 shifts. (B) The nondiagonal-free spectrum at identical shifts. In both slices the reference 2D HN correlation (cyan contours) is overlaid for better overview. (C) Neighboring amides of K26 as a representative residue as seen in the crystal structure of the SH3 domain of α-spectrin (PDB: 2NUZ) and their distances to K26 H^N. D) Traces along F3 through K26/K27 and K26/A12 cross peaks (as shown by arrows in A and B), which are in relative proximity to the diagonal. Whereas K27 peak intensity (traces b vs d) is doubled in comparison to its expected value, intensities of distant A12 (traces c vs a) are fully dominated by the diagonal. The same is true also for A11 (as can be seen in E). (E) 4D peak volumes extracted from the respective 2D slice and plotted over their corresponding internuclear distances (extracted from X-ray structure 2NUZ). Peaks significantly deviating from a consistent distance/intensity relation (delineated by the dashed line) incur erroneous distance restraints. The error introduced by noise is on the order of the symbol sizes used. (F) The set of resonances recorded in regular homonuclear correlation experiments consist of amide/amide cross peaks, whereas only one peak per amino acid pair is observed. Thus, every cross peak contains useful and nonredundant information. For time-shared versions and adequate protein labeling, additional correlations are recorded involving methyls. This 2D plane was recorded using the shortened version of the pulse scheme shown in Figure 1. Negative contours are shown in red. See Supporting Information, Figure 2 for the same spectrum without diagonal compensation.

2D spectra were processed using Topspin, and 4D data was processed using NMRpipe.⁶⁹ For the 4D spectra, Fourier transformation of the direct dimension was followed by the hmsIST routine⁶⁴ with 200 iterations and subsequent reshuffling of transients for phase-sensitive recording and time increments in order to allow for standard FFT of the indirect dimensions. Apodization was performed using a sine bell shifted by π/2 for all dimensions and 2048 × 64 × 64 × 64 points for the direct and indirect ones. The nmrPipe processing scripts are provided on the Linser group webpage. The hmsIST routine⁶⁴ as well as a sampling schedule generator can be obtained on the Wagner lab webpage (gwagner.med.harvard.edu/intranet/hmsIST/).

Spectra were converted to ucsf format with the routine included in the Sparky program⁷⁰ and used for analysis in CcpNmr.⁷¹

Assigned 4D HN-HN cross-peaks were converted into distance restraints with a uniform calibration procedure to convert peak intensity into distance. Structure ensembles were calculated with a simulated annealing procedure implemented in ARIA⁷²/CNS⁷³. Backbone dihedral angle restraints were predicted from chemical shifts⁷⁴ and used in addition of the HN-HN distance restraints. Structure calculations and distances calibration are presented in detail in the Supporting Information.

Results

In contrast to solution NMR approaches,⁴⁹⁻⁵³ we find that diagonal compensation in the solid state can be achieved with little sensitivity loss compared with the noncompensated spectrum. For SH3 and hydrophobin, only ∼27% and ∼13% of the sensitivity needs to be sacrificed for diagonal compensation. The reason is that in the absence of dipolar mixing (i.e., in scans that can be subtracted for elimination of the diagonal), signal intensity is significantly higher (see below) relative to the regular scans that include the desired information (regular scans refer to scans carrying both diagonal and cross peaks). This effect is due to pulse imperfections, relaxation, and rf-inhomogeneity during the dipolar mixing sequence in the latter. In addition, the diagonal signals become significantly dispersed into cross-peak signals in the course of magnetization transfer to nearby nuclei. Accordingly, highest sensitivity is obtained by recording and subtracting single diagonal-only compensating scans from the sum of multiple regular transients. For the SH3 domain with 25% proton back-exchange, diagonal signal in compensation scans is approximately three times more intense than in the regular scans on average. This allows experiments of highest signal-to-noise with an accordingly low number of interleaved compensation transients. When optimized, 27% of the sensitivity is sacrificed (see Supporting Information for more details). Hydrophobin spectra were recorded with a 100% proton back-protonation at 60 kHz MAS using a 1 GHz spectrometer. For this labeling scheme, diagonal-signal intensity is expectedly lower than obtained with stochastic partial protonation. Hardly any price has to be paid here in terms of additional measurement time since a very low number of compensation scans is necessary to eliminate the smaller diagonal in this case. Diagonal signal in compensation scans is here more than six times more intense than in the regular scans on average. One scan without mixing was recorded here for every 4 regular scans with recoupling and required further downscaling to 0.6 upon processing. This is commensurate with an additional time requirement of 14% for diagonal compensation. Due to site-specific differences in protein mobility and the density of the proton dipolar-coupling network, small residual diagonal peaks are observed for a subset of the protein residues after compensation with intensities on the order of weak cross peaks as expected.

Given the much smaller sensitivity loss for tailored compensation approaches in the solid state compared to solution NMR, zero-quantum (ZQ) recoupling techniques can be implemented without diagonal-related problems at low cost. ZQ recoupling sequences like RFDR⁶⁷ have been used much for proton–proton recoupling in deuterated solids.^31,34,44,75 This common use for informative distance restraints in structure calculations is further facilitated when diagonal signal is suppressed.

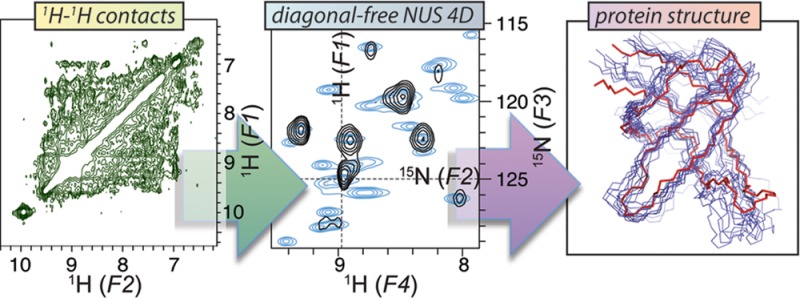
We generated diagonal-compensated NUS HXXH 4D experiments according to the scheme in Figure 1. Both the moiety from which magnetization is transferred and the moiety where it can be detected after mixing are encoded using a proton and a heteronuclear chemical shift evolution. For a structure of the well-characterized SH3 domain of α-spectrin based on sparse amide restraints, we employed ultrasparse (2%) Poisson-gap sampling, diagonal compensation (one out of three transients), and two heteronuclear time-shared dimensions. In this way spectra with excellent resolution were obtained within 4 days of total measurement time. Ultrasparse sampling allows flexible choices for numbers of regular and compensation scans even in the 4D. The spectra obtained (Figure 2A,F), provide high resolution as well as signal-to-noise ratios without potential artifacts. Also, due to the absence of diagonal signals and the performance of the hmsIST reconstruction, there is no detectable t₁ noise. Figure 4B–D classify the kind of restraints obtained. A structure calculation on the basis of these restraints is described below.

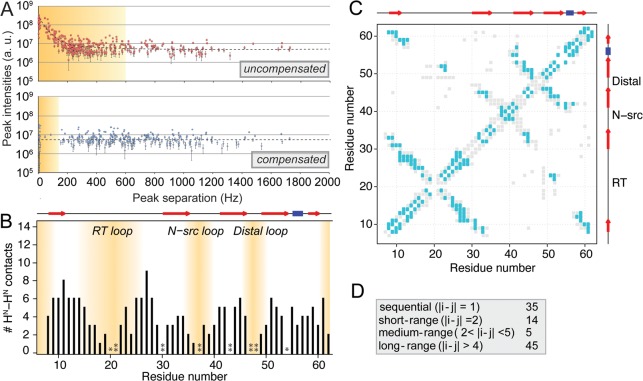
Figure 4.

Correlations obtained in homonuclear ¹H–¹H experiments on perdeuterated SH3. (A) All peak-like intensity above the noise level, picked at root resonance combinations (H/N HSQC shift pairs) only and representing potential (but not necessarily real) cross peaks. Orange shading represents the minimum space affected by diagonal signal, within which a great part of all peak-like intensity actually represents artifact peaks. Note the logarithmic scale of the Y-axis. Error bars refer to the noise level in the spectrum. Peak intensities were normalized using the F52/K26 cross peak as a representative peak, well separated from the diagonal. (B) Numbers of amide–amide contacts observed for a 4D version recorded on the SH3 domain of α-spectrin (black bars). Less peak intensity and fewer contacts are seen in the flexible loop regions (orange shades). Most contacts are long-range contacts and thus of high benefit for structure calculation. One asterisk indicates Pro residues, two asterisks denote those residues which are exchange-broadened in HN correlations and/or have not be assigned unambiguously. (C) Contact map of all visible correlations (cyan rectangles) overlaid on all residue pairs within 7.5 Å (gray rectangles). (D) Classification of the extracted (nonredundant) distance restraints.

In the absence of diagonal compensation, a large region of each 2D slice (on the order of 1.5 and 10 ppm wide for ¹H and ¹⁵N, respectively) would be affected by the presence of the diagonal in a four-dimensional (4D) experiment. The improvement with diagonal suppression is shown in Figure 2 for SH3, by comparing the compensated spectrum (Figure 2A) with the regular 4D (Figure 2B). Without compensation, significant errors in intensity are introduced for those peaks that are close to the diagonal (Figure 2D). With diagonal compensation, on the other hand, peak intensities within the set of restraints obtained for a specific residue follow a consistent trend dependent on the internuclear distance in the majority of cases (see Figure 2E).

A benefit of diagonal-compensated HXXH spectroscopy is obtained for proteins with heterogeneously or homogeneously broadened resonances, which are particularly affected by diagonal obstructions covering large parts of the spectral space. ¹H/¹H proximities can be derived from application of diagonal-compensated NUS-4D ¹H/¹H correlations for structural assessment of hydrophobin rodlets (shown in Figure 3). These rodlets are partially disordered functional amyloids from fungal spores.^77,78 Even though EM pictures (see the negative-stain representation in Figure 3A) of rodlets formed from the amphipathic monomer (Figure 3B) are macroscopically well ordered, the atomic order seems to be limited to a relatively small portion (<50%) of the protein sequence with a β-sheet character.^65,76 (See Figure 3D for a comparison of the ¹H^N bulk resolution with the microcrystalline SH3 domain.) ¹³C resonances from only ∼20 residues in the well-structured region of the sample could be identified and assigned to amino acid types using ¹³C–¹³C homonuclear correlation spectroscopy (DARR⁴⁰ mixing) and a 3D NCACX spectrum initially.⁶⁵ Here, the initial noncompensated 4D and 3D ¹H–¹H spectra were almost entirely noninterpretable, forming the motivation to seek for general high-signal-to-noise diagonal-free strategies. Figure 3E,F shows a comparison between standard and diagonal-free homonuclear correlations in the case of 4D HNNH correlations. Backbone assignments and structure calculation for this protein are in progress.

Figure 3.

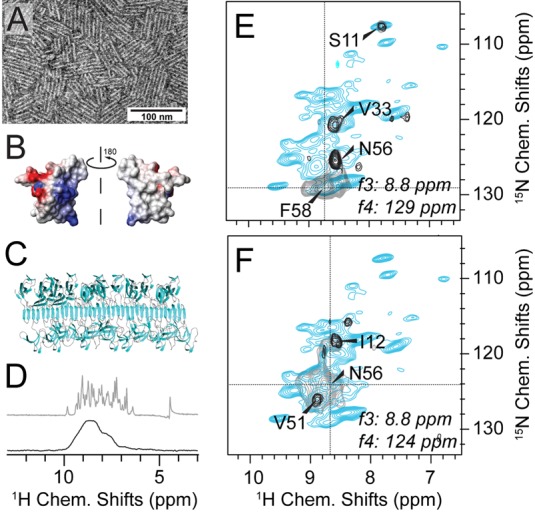
Diagonal-compensated 4D ¹H/¹H correlations in spectra of hydrophobin rodlets lacking crystalline order. (A) Negative-stain EM image of EAS_Δ15 hydrophobin rodlets. (B) Surface charge representation of the amphipathic hydrophobin monomer (PDB 2K6A). (C) Hypothetical model of the rodlet structure as a functional fungal amyloid obtained using molecular docking with the solution structure of monomeric EAS_Δ15 and mutagenesis and other biophysical data.⁷⁶ (D) ¹H amide resolution of the rodlets (black, bottom) compared to the microcrystalline SH3 domain (gray, top). Both spectra are shown without apodization or truncation of the FID. (E and F) Representative 2D slices from an HNNH 4D experiment. Diagonal compensation was achieved (black contours) applying 1 out of 5 scans without dipolar recoupling. (Gray contours display noncompensated scans only, blue contours represent an overlaid reference HN correlation.) Proximities seen in (E) are expected on the basis of the monomer structure.⁷⁷ The peaks labeled in (F) cannot be explained by the monomer fold and hint to major structural rearrangements upon rodlet assembly. Hydrophobin spectra were recorded on deuterated hydrophobin EAS_Δ15 rodlets, 100% ¹H back-exchanged at labile sites in a 1.3 mm rotor at 1 GHz ¹H Larmor frequency and 60 kHz MAS. Proton-detected experiments used for obtaining backbone assignments are described in the Supplement.

For the SH3 domain, we generated and analyzed structures calculated from sparse 4D restraints (see the Supporting Information for a detailed description). The calculation focuses on the set of peaks representing correctly assigned amide-to-amide distances only. (Methyl-amide contacts obtained with this labeling scheme are much sparser, they are not affected by diagonal signal, and it has been shown previously that methyl–amide restraints improve structural quality, see details in the Supporting Information. For assignment fidelity effects, see below.) Here from 161 resolved 4D amide–amide peaks, 99 unique ¹H^N–¹H^N distance restraints could be extracted (see Figure 4B,C). The final set of nonredundant restraints consists of 35 sequential (|i – j| = 1), 14 short-range (|i – j| = 2), 5 medium-range (2 < |i – j| <5), and 45 long-range (|i – j| > 4) restraints. Similar to methyl NOEs in structure calculation of large proteins in solution, amide–amide distances as shown here thus represent structural restraints of particular, nontrivial character, especially of value for defining β-sheet and α-helical secondary structures, but also for the overall protein fold. Figure 5A shows a backbone representation of the 10 lowest-energy structures based on restraints only from confirmed, correct amide–amide cross peaks as seen in the diagonal-free spectrum.

Figure 5.

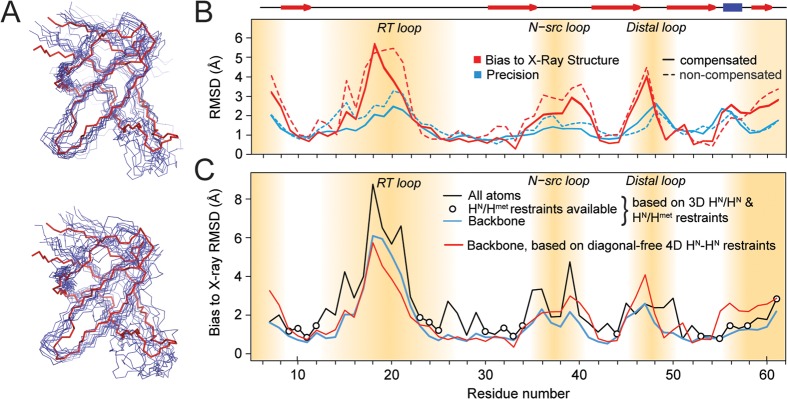
Structure calculation from ¹H–¹H restraints. (A) Backbone representation of the structural ensembles obtained from diagonal-free 4D correlations superimposed on the reference X-ray structure (PDB: 2NUZ, shown in red). Top: Calculation using peak integrals from diagonal-compensated spectra; bottom: using integrals of the same peaks without compensation. (B) Representation of backbone structure accuracy (bias to the X-ray structure 2NUZ, red) and precision (blue, RMSD to mean) based on high-quality diagonal-free 4D restraints (solid lines). Dashed lines correspond to structures from noncompensated restraints. Secondary structure elements are shown on top with red arrows (strands) and a blue bar (helix). The flexible termini and loop regions are indicated by brown shades, where few contacts are available. All other regions are not far from 1 Å resolution. (C) Comparison of backbone structure accuracy (bias to the X-ray structure 2NUZ) using additional methyl restraints (blue) and using amide–amide contacts only (red). All-atom RMSDs (black) are similar to backbone RMSDs in the presence of amide–methyl restraints (bullets), demonstrating the general potential of methyl-based restraints to further improve accuracy. Methyl data shown here for comparison were acquired using the time-shared experiment in its (truncated) 3D version. See the Supporting Information for details on methyl data.

At the level of data quality obtained, the structural quality (with a backbone precision of 1.28 ± 0.21 Å) is very close to the potential optimum expected for the kind and number of restraints used: Using the same set of amide–amide restraints, but with “true” crystal-structure distances, a backbone precision of 1.15 ± 0.22 Å would be obtained.

The improvement in the backbone fold accuracy (from 2.05 to 1.69 Å) upon structure calculation with diagonal compensation in comparison to a calculation without compensation seems modest (RMSDs with respect to the crystal-structure, see also Supporting Information, Figure 10). The structural restraints that this comparison is based on, however, differ here only due to improved integration of cross-peaks, whereas the kinds of restraints taken into account are identical and only from correctly assigned peaks in both calculations. The quality of de novo structures obtained from noncompensated spectra only, on the other hand, would be dominated by the lower reliability of identification and assignment of cross peaks. The probability for correct peak selection is difficult to quantify. Nevertheless, significant qualitative differences in spectral interpretability are evident from the relative space covered by diagonal signal.

In addition, Figure 4A shows peak-like intensity in a 4D experiment plotted over the distance of each of those signals to the diagonal. Peak intensity is taken to be the intensity above the noise level at all H/N/N/H combinations at which cross peaks could potentially be located on the basis of HSQC root resonances. Sufficiently distant from the diagonal, these data purely represent real cross peaks of structural relevance. With less separation of cross-peaks from the diagonal, however, unreal “peaks” show up that would not be expected on the basis of atomic distances. These false peaks are inadvertently introduced into structure calculations for proteins of unknown structure (particularly for automated peak picking) unless large areas around the diagonal are avoided for peak picking or circumvented by diagonal compensation.

Discussion

Distances based on unambiguous amide–amide spectra are valuable for identification of a backbone fold and can be supplemented by methyl–methyl⁴³ and methyl–amide⁴⁴ restraints to provide high-resolution structures if these are suitably labeled. A more comprehensive set of distances may be obtained by incorporation of other side chain protons in partially or fully side chain-protonated samples,^28,30,36,79 however, increasing numbers of peaks will always also lead to increasing ambiguity in assignment and structural data. Different kinds of structural data obtained with different approaches are usually not mutually exclusive and can be combined with each other.^{23,24,31,80,81} If resolved ¹³C-edited distance restraints from protonated samples are available, which is less likely for increasing molecular weight, these can always be integrated into the structure calculation as unambiguous or ambiguous²⁵ restraints. Where better suited, paramagnetic restraints⁸² and surface contacts⁸³ can be easily combined with proton-detected methods.³⁴

Ultrasparse NUS 4D HXXH spectra turn out to be highly reliable in terms of unambiguous peak identification and assignment and provide sparse and nonredundant long-range distance restraints. This makes them a well suited basis for proton-distance-based structure assessment of proteins. In contrast to solution NMR, even though generally much sharper peaks are obtained and significant sacrifice of sensitivity results from both subtraction of transients⁴⁹ as well as from elimination of coherences,⁵³ diagonal-compensated 4D spectroscopy in the solid state has not been used so far for structure elucidation. Providing a valuable tool with respect to the increasing use of proton spins in the solid state, this or modified approaches have the potential to facilitate acquisition of structure-relevant data on deuterated samples with different degrees of protons selectively introduced at various protein sites.

Whereas amide and methyl restraints are able to mostly deliver a reliable protein fold, dilute side-chain protonation in terms of random adjoining protonation (RAP labeling)²⁸ is expected to be of major advantage for correct side chain orientation and packing in future studies. For this and stochastic labeling generally (implying a reduced labeling percent causing larger diagonal to cross-peak ratios), diagonal compensation will be very well suited. Also for heterogeneous preparations, as shown for (but not limited to) hydrophobins with a 100% back-protonation at 60 kHz MAS and 1 GHz Larmor frequency, significant benefits of diagonal compensation become obvious from the average ¹H line width of ca. 0.25 ppm (250 Hz), which translates into short indirect acquisition times and a significant portion of the total spectral space to practically be covered by diagonal signal. Thus, spectral interpretability as well as distance-restraint data quality is significantly increased upon diagonal compensation.

In agreement to previous studies,^31,34 the efficiency of RFDR recoupling was not seen to be compromised by fast spinning and accordingly short pulse widths (2.5 μs 180°-pulse length at a rotor period of 16.7 μs). We used RFDR as a robust and easy-to-implement scheme with a high relative signal-to-noise even after diagonal suppression. It is also compatible with the large ¹H bandwidths required for time-shared (amide–methyl) spectra. In principle, however, RFDR could be replaced by other robust and well-working zero- or double-quantum recoupling schemes when requirements for ¹H rf power and bandwidths are met. For spectra with small diagonal-to-cross peak intensity ratios, negligible costs of measurement time apply for acquisition of compensation scans, so acquisition of compensation scans can always be easily implemented. Better data quality and interpretability with compensation can then save a multitude of the additional measurement time at the analysis and calculation state.

Spin-diffusion processes and dipolar truncation effects are expected to be more significant for increasing back-substitution levels at amide sites.^57,84 These issues lead, respectively, to less reliable and fewer long-range restraints for fully back-exchanged or stoichiometrically methyl-labeled samples. On the other hand, nanomolar sample amounts of stoichiometrically amide-protonated proteins can be employed here due to greater overall sensitivity when 1.3 mm rotors and 100% proton back-substitution at 60 kHz are used. This has advantages when samples are particularly difficult to make or costly (like for CHD₂-methyl labeling).

Both for 25% ¹H back-exchange and intermediate MAS as well as 100% back-exchange and ultrafast spinning, correlations of the kind shown are straightforward and will be useful in future studies. This is true even despite the lower number of expected contacts for 100% back-exchange at 60 kHz.

Conclusions

We have shown that the approach presented here yields proton–proton distance restraints for partially deuterated proteins and represents a reduced set of structural data that are sparse in quantity but highly nonredundant and accurate. Importantly, structural restraints can be correctly identified and evaluated. We obtain highly resolved correlations in conjunction with very good sensitivity from diagonal-compensated, ¹H, ¹⁵N/¹³C, ¹⁵N/¹³C, ¹H-edited 4D experiments with ultrasparse Poisson-gap sampling. Fully demonstrated here using the small protein SH3 and a relatively well-dispersed spectrum, it also becomes evident that the reduction in signal overlap is a critical advancement in facilitating the characterization of challenging targets like the more heterogeneous hydrophobin rodlets. An SH3 structure based on restraints obtained using this approach is characterized by a relatively high accuracy with respect to the minimal set of unambiguous structural restraints with mainly long-range character. This opens the door for successful structure assessment of large or poorly ordered proteins.

We believe that the quality of data obtainable, in combination with the simplicity and efficacy of the concept, will lead to proton-based structure elucidation as a major anchor point in the evolving field of fast-MAS solid-state NMR. This applies in particular to the steadily increasing MAS frequencies under which detection of side chain protons can be resolved without extensive deuteration. The methodologies are expected to be useful for improved structural characterization of membrane proteins and fibrillar or prion proteins.

Supporting Information Available

Time-shared spectral data, effects of diagonal compensation for spinning side bands, sensitivity considerations, bidirectionality in 4D spectra, structure calculation, and distance-integral correlations. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^# Technische Universität München, Germany, 85748 München, Germany.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States