Integrating Social Contact and Environmental Data in Evaluating Tuberculosis Transmission in a South African Township

Abstract

Background. Population models of tuberculosis transmission have not accounted for social contact structure and the role of the environment in which tuberculosis is transmitted.

Methods. We utilized extensions to the Wells–Riley model of tuberculosis transmission, using exhaled carbon dioxide as a tracer gas, to describe transmission patterns in an endemic community. Drawing upon social interaction data and carbon dioxide measurements from a South African township, we created an age-structured model of tuberculosis transmission in households, public transit, schools, and workplaces. We fit the model to local data on latent tuberculosis prevalence by age.

Results. Most tuberculosis infections (84%) were estimated to occur outside of one's own household. Fifty percent of infections among young adults (ages 15–19) occurred in schools, due to high contact rates and poor ventilation. Despite lower numbers of contacts in workplaces, assortative mixing among adults with high rates of smear-positive tuberculosis contributed to transmission in this environment. Households and public transit were important sites of transmission between age groups.

Conclusions. Consistent with molecular epidemiologic estimates, a minority of tuberculosis transmission was estimated to occur within households, which may limit the impact of contact investigations. Further work is needed to investigate the role of schools in tuberculosis transmission.

Tuberculosis transmission has been classically modeled as a mass-action process in a homogenous population, wherein individuals randomly contact one another and in which types and duration of contacts are not considered [1–3]. There is substantial evidence to suggest that the duration and environment in which contacts occur are key determinants of the risk of tuberculosis transmission [4]. Additionally, as with many other diseases, age-specific mixing patterns likely play an important role in tuberculosis transmission dynamics.

Tuberculosis is spread by droplet nuclei, which may remain suspended in the air for 30 minutes in the absence of air exchange. The impact of the indoor environment in tuberculosis transmission was first rigorously studied in the late 1950s by Wells and Riley, who exposed guinea pigs to air from a tuberculosis ward and measured infection rates under controlled conditions [5, 6]. Models derived from the Wells–Riley findings have focused on single environments to characterize point-source outbreaks or nosocomial transmission [7, 8]. Environmental settings have not been factored into broader models evaluating endemic transmission. This may be in part due to logistical difficulties in measuring ventilation, as well as characterizing contact patterns in various environments. The former obstacle has been surmounted in part due to the use of exhaled carbon dioxide as a natural tracer gas to evaluate air exchange [9], which can be done with increasingly low-cost and portable devices. Additionally, recent efforts to quantify social contact patterns have yielded rich data on age-assortativeness and variability of contacts between settings [10–12].

By integrating data on social interactions and environmental context, we developed a new approach to project the impact of age-specific contact patterns and estimate where tuberculosis transmission occurs. We utilized local data from a study of social interactions together with measurements of carbon dioxide in common indoor environments, to model tuberculosis transmission in a South African township.

METHODS

Wells and Riley derived an equation describing the risk of tuberculosis infection (P) in an indoor environment as a function of the number of infectious individuals in a space (I), the breathing rate (p), the rate of generating infectious quanta (q; quanta/hour), the duration of exposure (t), and the room ventilation rate (Q) [6]:

$$P=1-\exp \left(-\frac{Ipqt}{Q}\right).$$

Rudnick and Milton extended this work to non-steady-state situations and described the use of carbon dioxide as a natural tracer gas to overcome the need for resource-intensive measurements of conventional room ventilation analysis [13]. This approach involves estimating the proportion of air in a room that was expired by its occupants (the “rebreathed fraction,” f) by evaluating the excess carbon dioxide (CO₂) in the room over outdoor air CO₂. Using this rebreathed fraction, the probability of infection, as a function of time and number of infectious individuals (I) among all individuals (n) in a room, can be estimated through the following relationship (see Supplementary Data):

$$P=1-\exp \left(-\frac{\overline{f}Iqt}{n}\right).$$

We extended this work to describe endemic tuberculosis transmission in an age-structured model with multiple transmission environments.

We drew on data from 571 residents in a Cape Town township that contained information on the number of indoor contacts and time spent in various locations, stratified by 10 age groups (0–4, 5–9, 10–14, 15–19, 20–24, 25–29, 30–34, 35–39, 40–44, and ≥45 years) [14]. More than 97% of indoor contact-time occurred in 5 locations: own households, other households, schools, workplaces, and public transit [14]. Although the majority of time spent indoors was spent in households (Supplementary Figure 1), most daily contacts occurred outside the home, with school accounting for the largest number of contacts among children and transit and workplaces serving as the environment for most contacts among adults (Supplementary Figure 2). Compared with other settings, the number of contacts observed in public transit were highly dispersed with a long right tail; a number of individuals reported a very high contact number (>50) (Supplementary Figure 1).

Additionally, using portable CO₂ detection devices (EasyView 80 CO₂ analyzer, Extech Instruments, and custom-developed monitors using COZIR Ambient sensors, Gas Sensing Solutions Ltd), ambient air in 4 environments—public transit vehicles, schools/crèches, workplaces, and households—was sampled by 9 volunteers to assess mean and ranges for CO₂ concentration (Table 1). Volunteers collected 17 124 observations of CO₂ concentration in various locations throughout day and night. We used the mean and standard error of sets of concentration observations for each setting. We utilized tuberculosis notification data (29 478 cases reported in 2009) and estimated age-stratified incidence rates of smear-positive and smear-negative tuberculosis.

Table 1.

Model Parameters and Data Sources

Parameter	Symbol	Value	Range	Reference
Relative infectiousness, smear-negative tuberculosis	NA	0.2	…	[15–17]
Duration of infectiousness	NA	12 mo	4–18	[18, 19]
Excess CO2 concentrationa, household	[CO2]h-[CO2]o	635 ppm	453–817	Observed
Excess CO2 concentration, public transit	[CO2]p-[CO2]o	1464 ppm	397–2531	Observed
Excess CO2 concentration, school/crèche	[CO2]s-[CO2]o	1404 ppm	1227–1581	Observed
Excess CO2 concentration, workplace	[CO2]w-[CO2]o	538	359–717	Observed
Contacts per day in each location	Ck	Variable by age	Variable by age	[14]
Hours spent in each location	Tk	Variable by age	Variable by age	[14]
Infectious quanta production	q	Fit	Fit	…

Abbreviations: CO₂, carbon dioxide; NA, not applicable; ppm, parts per million.

^a Excess CO₂ concentration refers to the difference between the indoor CO₂ and the outdoor CO₂, which varied by location and time of day. Range of values reflects 95% confidence intervals.

We assessed the risk of transmission in each environment as a function of the number of individuals in the environment, the amount of time spent in the environment, the rebreathed fraction calculated from the CO₂ concentration, and the probability that there was an infectious individual present in the environment given age-specific tuberculosis prevalence, estimated from age-stratified notification data (Supplementary Figure 3) and adjusted for population age structure estimated by census data (Supplementary Figure 4). A contact matrix reflecting the age assortativeness of mixing was estimated by weighting reported number of contacts for each age group by the proportion of contact-time reported for each age group in each environment; in other words, the probability of a person with age i contacting a person with age j in environment k is proportionate to the fraction of total contact time in environment k that was reported by individuals of age j (see Supplementary Data). Therefore, exposure to other individuals was proportionate to the amount of time spent in each environment; the exception was interactions in schools, which were modeled such that all contact time among children was within their own 5-year age strata. This was done because mixing between age groups in schools was thought to be limited, as children spend most of their time in classrooms with other children of the same age. We weighted the infectiousness of smear-negative tuberculosis by 0.2, consistent with estimates from several contact investigation studies [15–17].

Using the risk derived from the modified Wells–Riley equation, we projected the annual risk of tuberculosis infection (ARI), by age, from the daily risk of infection in each environment. We then used these age-structured estimates for ARI to project the latent tuberculosis prevalence by age, according to the following equation [20]:

$$\text{Latent}\text{tuberculosis}\text{prevalence}\text{at}\text{age}a=1-\prod _{i=1}^a(1-\text{ARI}(i)).$$

We fit our model to age-structured data on latent tuberculosis prevalence from the same study community as the survey [21] by varying the quantum production rate and using a simplex descent algorithm to minimize the least-squares residuals between modeled and observed data.

To evaluate uncertainty in our projections resulting from our data, we used Latin hypercube sampling to draw from distributions of contacts and time spent in each environment for each age group and CO₂ measurements for each environment [22]. We drew from 1000 sets of parameters to generate median and 95% credible intervals. We used broad 1-way sensitivity analysis to evaluate 2 key parameters for which there is great uncertainty: the duration of tuberculosis prior to diagnosis and the proportion of contacts in each setting that are recurring. We generated estimates of the quantum production rate and the proportion of tuberculosis transmitted in each setting.

This model drew upon data that were collected as part of a study that was approved by the Human Research Ethics Committee of the University of Cape Town. Written informed consent was obtained from all participants. Parental/guardian consent was obtained for participants under 18 years of age, and signed assent forms were obtained from adolescents aged 12–17 years.

RESULTS

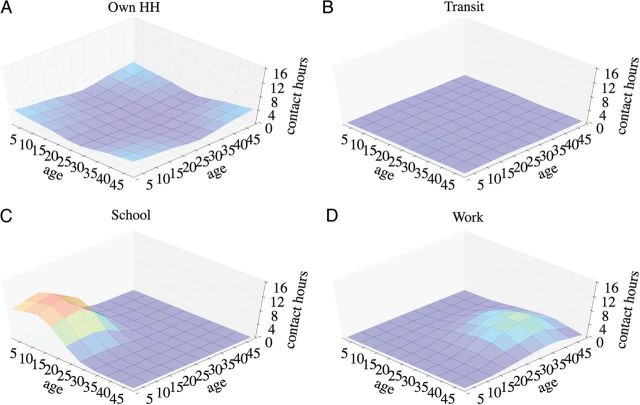
We found significant assortativeness of contact-time among children in schools and among adults in workplaces, in contrast to general mixing between children and adults that occurred in households and in public transit (Figure 1). Carbon dioxide levels were highest in schools and public transit, followed by homes and workplaces (Table 1). There were higher levels of variation in CO₂ estimates from public transit compared with other environments.

Figure 1.

Estimated contact-hours between individuals of various age groups in 4 locations (A, own household; B, public transit; C, schools; D, workplaces), with Gaussian smoothing applied to the contour. Abbreviation: HH, household.

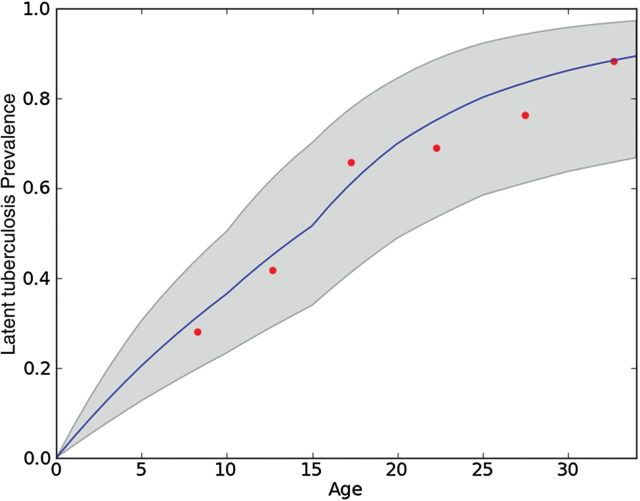
We fit the modeled latent tuberculosis prevalence to empiric measurements from a recent community survey [21] (Figure 2). The projected age-weighted mean annual risk of tuberculosis infection overall was 6.6% (95% credible interval, 3.1%–10.6%); the risk varied from 4.4% among children aged 5–9 to 9.1% among young adults aged 15–19 (Supplementary Figure 5). The majority of tuberculosis transmission was estimated to occur outside of one's own household, for all age groups (weighted mean percentage transmission within own household, 15.6%; Figure 3). Schools/crèches accounted for about a quarter of infections among children aged 0–14 years; however, up to half of tuberculosis transmission in young adults age 15–19 was estimated to occur in schools. A substantial proportion of tuberculosis transmission among adults was estimated to take place in workplaces (weighted mean, 41.4%), where there was high-level mixing among age groups with the highest prevalence of smear-positive tuberculosis (Supplementary Figure 3). Owing to migration in recent years, working-aged adults represent the largest population in this community, which strongly influenced the weighted mean for transmission in workplaces. Public transit was estimated to account for 7.9%–34.8% of transmission in all age groups (weighted mean, 21.9%).

Figure 2.

Modeled (blue line) and observed (red points) latent tuberculosis prevalence by age group, where duration of infectiousness is 12 months and all contacts were recurrent except those in public transit. The gray shaded area reflects 95% credible intervals for model estimates.

Figure 3.

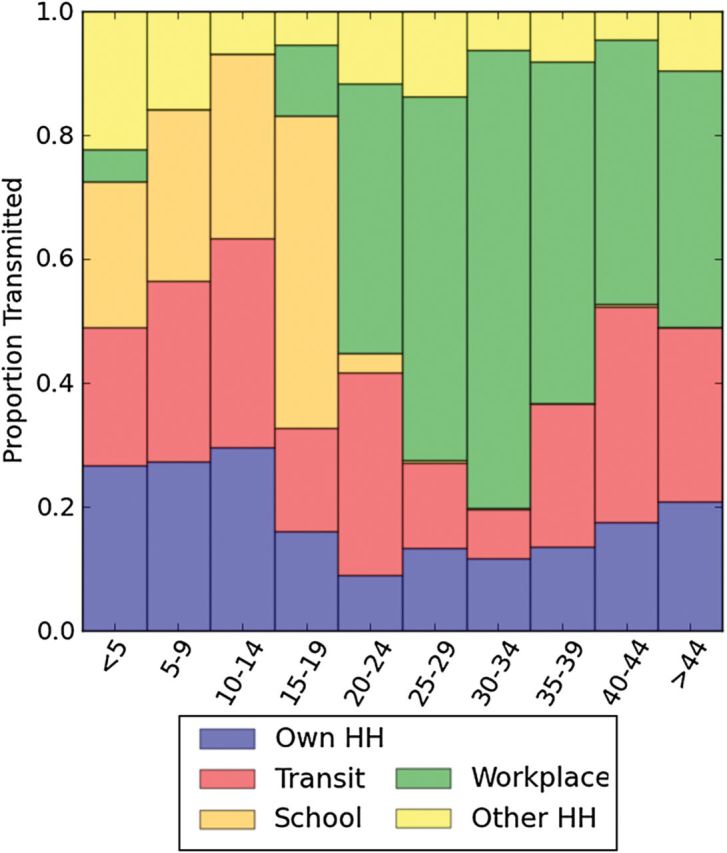
Estimated proportion of tuberculosis infections acquired in each setting, according to age group. Abbreviation: HH, household.

Among the most uncertain parameters in modeling transmission of tuberculosis through Wells–Riley approaches is the rate of infectious quanta production, q. We found that two factors, both of which are not well known, substantially impact the estimate of q. The first is the duration of infectiousness of undiagnosed tuberculosis, which has been variably estimated as being from 4 months to over 18 months [18, 19]. With shorter duration of infectiousness, a higher quantum production rate is required to achieve the same force of infection. We used a base case of 12 months as this reflected local data from this community [18]. Our estimate of q with this duration of infectiousness was 0.89 quanta/hour (Supplementary Table 1), but varied from 5.69 quanta/hour to 0.44 quanta/hour with duration of 4–18 months.

The second most influential factor in the estimate of q was the proportion of contacts that were recurrent. We evaluated 3 scenarios: (1) all contacts in all settings were recurrent; (2) no contacts were recurrent; (3) all contacts were recurrent in households, schools, and workplaces, but not in public transit. Recurrent contacts implied that the same individuals were contacted each day; for example, if a person contacted 3 individuals per day in the household, it was the same 3 individuals every day (eg, family members). We assumed the third scenario for our base case. Our estimate of q varied from 0.27 quanta/hour in scenario 2 (none recurrent) to 0.94 quanta/hour in scenario 1 (all recurrent). The scenario of no recurrent contacts had poor model fit compared with scenarios 1 and 3.

Despite the uncertainty wrought by these parameters, the main results in terms of where tuberculosis is transmitted were robust to reasonable uncertainty ( Supplementary Table 1). The percentage of tuberculosis cases transmitted in the household varied from 5.4% to 24.2% when varying duration of infectiousness from 4 to 18 months, respectively, and from 59.5% to 15.5% when varying proportion of recurrent contacts from 0% to 100%.

DISCUSSION

Mathematical models of tuberculosis transmission have relied upon abstract effective contact rates that do not account for the environment of contacts or the mixing patterns that characterize social interactions [1–3]. We have demonstrated how measurements of carbon dioxide in indoor environments can be combined with social mixing data to describe tuberculosis transmission in an endemic community. Although this approach is subject to limitations in terms of data on transmission risks and simplifying assumptions concerning social interactions, it nevertheless offers a straightforward approach to understanding the importance of various environments and contact patterns in driving tuberculosis transmission. Moreover, this approach can be done using easily obtainable data and simple deterministic models, in contrast to detailed social network enumeration approaches [23, 24], and could be applied to other infectious diseases spread by droplet nuclei, such as measles and varicella.

Epidemiologists have long cited crowding and population density in urban environments as key factors contributing to the spread of tuberculosis [25, 26]; however, a detailed understanding of how these factors influence tuberculosis transmission has been lacking. Data used for this model, for example, demonstrate that close indoor contact rates in South African townships are substantially higher than in Europe and rural Vietnam [10, 11]. By integrating this data with duration of exposure and the ventilation characteristics of the environment, we estimate that a substantial proportion of tuberculosis transmission occurs outside of households. Indeed, molecular epidemiologic studies have suggested that only 19% of tuberculosis cases in South African townships arise from transmission within one's own household [27], whereas our model similarly estimated that 16% of tuberculosis transmission occurs in this setting. Age-stratified molecular epidemiologic data on household transmission are not currently available, but as these data emerge in the future, they could be used to further validate models of this nature. However, because of delay between infection and onset disease in tuberculosis, it is difficult to use molecular epidemiologic approaches to evaluate the location of transmission, particularly between casual or nonrecurring contacts. Our approach enables the prediction of where tuberculosis is transmitted, as well as which age groups are driving transmission. The use of detailed social network studies combined with recent advantages in whole-genome sequencing of Mycobacterium tuberculosis may be useful in validating predictions from this approach [23, 24, 28, 29].

By understanding where tuberculosis transmission occurs, we may be able to better project the impact of control interventions. For example, contact investigations targeting household members may fail to identify the majority of tuberculosis cases in this setting. In other settings, household contacts may account for a larger proportion of tuberculosis transmission, and simple data can provide insights to inform this. Schools are characterized by high social contact rates and high proportions of rebreathed air; we projected that this was a particularly high-risk environment for transmission among young adults aged 15–19. Among younger children, who have a lower prevalence of smear-positive tuberculosis, infection risk in schools was estimated to be more limited. In contrast to schools, households and public transit are important areas for general mixing between age groups and likely drive transmission from adults to children. This modeling approach could be used to evaluate thresholds for CO₂ levels in congregate settings, such as schools, public transit, and workplaces and to project the impact of environmental interventions, such as ventilation systems (mechanical or natural) or the use of upper-room ultraviolet germicidal irradiation.

Among the most important and uncertain parameters in understanding the transmission of tuberculosis is the infectious quanta production rate. Wells and Riley estimated this in their original experiments to be 1.25 quanta/hour, derived from hospitalized patients at the beginning of their tuberculosis treatment [6]. Escombe and colleagues repeated these studies in a tuberculosis ward in Peru and reported considerable variability, from 0 quant/hour to over 200 quanta/hour [30]. Their mean estimate was 8.2 quanta/hour, which was affected by a few outliers. However, both sets of estimates were made by studying the infections induced among guinea pigs by hospitalized patients with a confirmed diagnosis of tuberculosis. The extent to which this can be generalized to individuals in a community setting with undiagnosed disease, many of whom may have few to no symptoms, is unclear. We estimated this rate by fitting our model to data on latent infections. Our estimates were heavily dependent upon assumptions about the recurrence of contacts and the duration of infectiousness, and ranged from 0.27 quanta/hour to 5.69 quanta/hour, with a base case estimate of 0.89 quanta/hour. Recurrence of contacts leads to local saturation of infections (by depletion of susceptible contacts of an infectious person) and requires a higher quantum generation rate to achieve a comparable population level of transmission. In general, however, these estimates were lower than those of Wells–Riley and Escombe et al, which may indicate that individuals are less infectious earlier in their course of illness. More detailed enumeration of social contact patterns, including frequency of recurrent contacts, may lead to improved estimates of infectiousness.

Our approach and results are subject to limitations of our assumptions and available data. We fit our model to age-structured data on latent tuberculosis prevalence, which does not account for cohort effects of differences in tuberculosis transmission rates over time. Estimates of the annual risk of infection have remained fairly stable for at least 15 years in this area [31], although earlier differences in the annual risk of infection, if present, would lead to errors in estimating the annual risk of infection, particularly in older adults. We projected latent tuberculosis prevalence by age according to annual risk of infection, as commonly done in tuberculosis epidemiology [20]; however, this does not account for mortality due to tuberculosis, which has a small impact on latent tuberculosis prevalence estimates. We did not consider “self-quarantine” in this model, wherein individuals who feel ill due to undiagnosed disease stay at home, reducing their contact with others [32]. Given the disparity in duration of reported symptoms prior to tuberculosis diagnosis (around 4 weeks in most studies) and estimates of the duration of infectiousness (12 months), it is likely that self-quarantine does not account for a significant reduction in mixing. We did not have empirical data on age-assortativeness of contacts; therefore, we estimated age-assortativeness based on age-specific time reported in each setting. Additionally, there are currently no available data on the proportion of contacts that are recurring, or the frequency of recurrences; such data could be obtained through self-report or novel approaches to defining social networks that involve radiofrequency identification tags [33]. Nevertheless, our results remained fairly robust to reasonable assumptions concerning these uncertain parameters. Children are likely much less infectious than adults with tuberculosis; in the absence of better data, we assumed that differences in infectiousness were explained by smear status. This led to almost negligible transmission from the youngest children in this model. We did not incorporate heterogeneity in infectiousness, although multiple experimental data suggest tremendous interindividual variability in infectiousness [6, 30, 34]. Furthermore, there is likely intraindividual variability in infectiousness over time, as individuals develop higher burdens of disease. Combined with skewed distributions of contact rates and contact time, these factors may help explain the observed phenomena of superspreading [35]. As better data on variability in infectiousness become available, future work with agent-based models may build on this approach to yield more nuanced insights into transmission patterns. We did not attempt to adjust notification data, which was stratified by smear status, for dynamic changes in smear status that likely occur over time. There are conflicting data on the smear-adjusted relative infectiousness of individuals with human immunodeficiency virus (HIV) infection [36, 37] and the relative duration of active tuberculosis [18, 19]; we used data from a large survey done in this community that found the duration of undiagnosed tuberculosis to be equal among HIV-infected and -uninfected individuals. Our results demonstrate that the duration of infectiousness is a key influential parameter in understanding the social and environmental contributions to tuberculosis transmission; further epidemiological studies are greatly needed to provide additional estimates of this parameter in other settings and to elucidate the interindividual variability in duration of infectiousness. We did not explicitly model dynamics of progression from tuberculosis infection to disease, but rather focused on modeling location and age structure of transmission assuming a stable epidemic. This approach could easily be extended to dynamic models. As with “mass action” models of infectious disease transmission, this model does not account for clustering of tuberculosis within local social networks over time, which could further drive heterogeneity of tuberculosis risk.

There have been a number of studies in recent years characterizing social contact patterns in various settings [10–12]. We have demonstrated how such information can be combined with simple, easily obtainable environmental data to describe tuberculosis transmission patterns and estimate where transmission is taking place. This approach may enable us to better understand the impact of crowding and population density in sustaining tuberculosis endemicity, as well as to target interventions to improve control of tuberculosis.

Supplementary Data

Supplementary materials are available at The Journal of Infectious Diseases online (http://jid.oxfordjournals.org/). Supplementary materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supplementary data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.